Калькулятор натуральных дробей: Онлайн сервис для вычислений обыкновенной и десятичной дробями, сложение, вычитание, умножение и деление десятичной и обыкновенной дробей.

Содержание

Как переводить дробные числа в десятичные. Калькулятор онлайн.Перевод десятичной дроби в обыкновенную

Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления. В таких случаях говорят, что выполнено деление с остатком , и решение записывают в таком виде:
497: 4 = 124 (1 остаток).

Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое , 4 — делитель . Результат деления при делении с остатком называют неполным частным . В нашем случае это число 124. И, наконец, последний компонент, которого нет в обычном делении, — остаток . В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело . Считают, что при таком делении остаток равен нулю. В нашем случае остаток равен 1.

Остаток всегда меньше делителя.

Проверку при делении можно сделать умножением. Если, например, имеется равенство 64: 32 = 2, то проверку можно сделать так: 64 = 32 * 2.

Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.

Частное от деления натуральных чисел можно записать в виде дроби.

Числитель дроби — это делимое, а знаменатель — делитель.

Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление . Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».

Частное от деления натуральных чисел m и n можно записать в виде дроби $\frac{m}{n} $, где числитель m — делимое, а знаменатель п — делитель:
$m:n = \frac{m}{n} $

Верны следующие правила:

Чтобы получить дробь $\frac{m}{n} $, надо единицу разделить на n равных частей (долей) и взять m таких частей.

Чтобы получить дробь $\frac{m}{n} $, надо число m разделить на число n.

Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть.

Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.

Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
$\large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} $

Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
$\large \frac{a}{b} = \frac{a: m}{b: m} $
Это свойство называют основным свойством дроби .

Два последних преобразования называют сокращением дроби .

Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют

приведением дробей к общему знаменателю .

Правильные и неправильные дроби. Смешанные числа

Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например, дробь $\frac{3}{4} $ означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими дробями, как, например, $\frac{5}{5} $ или $\frac{8}{5} $? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби, у которых числитель больше знаменателя или равен ему, называют неправильными дробями . Остальные дроби, т. е. дроби, у которых числитель меньше знаменателя, называют правильными дробями .

Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.

Если число состоит из целой части и дроби, то такие дроби называются смешанными .

Например:
$5:3 = 1\frac{2}{3} $ : 1 — целая часть, а $\frac{2}{3} $ — дробная часть.

Если числитель дроби $\frac{a}{b} $ делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель разделить на это число:
$\large \frac{a}{b} : n = \frac{a:n}{b} $

Если числитель дроби $\frac{a}{b} $ не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её знаменатель умножить на это число:
$\large \frac{a}{b} : n = \frac{a}{bn} $

Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда, когда трудно с первого взгляда определить, делится числитель дроби на n или нет.

Действия с дробями. Сложение дробей.

С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей. Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму $\frac{2}{7} $ и $\frac{3}{7} $. Легко понять, что $\frac{2}{7} + \frac{2}{7} = \frac{5}{7} $

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.

Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
$\large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} $

Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
$\large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} $

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.

Сложение смешанных дробей

Такие записи, как $2\frac{2}{3} $, называют смешанными дробями . При этом число 2 называют целой частью смешанной дроби, а число $\frac{2}{3} $ — ее дробной частью . Запись $2\frac{2}{3} $ читают так: «две и две трети».

При делении числа 8 на число 3 можно получить два ответа: $\frac{8}{3} $ и $2\frac{2}{3} $. Они выражают одно и то же дробное число, т.е $\frac{8}{3} = 2 \frac{2}{3} $

Таким образом, неправильная дробь $\frac{8}{3} $ представлена в виде смешанной дроби $2\frac{2}{3} $. В таких случаях говорят, что из неправильной дроби выделили целую часть .

Вычитание дробей (дробных чисел)

Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит найти такое число, которое при сложении со вторым дает первое. Например:
$\frac{8}{9}-\frac{1}{9} = \frac{7}{9} $ так как $\frac{7}{9}+\frac{1}{9} = \frac{8}{9} $

Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель оставить прежним.

С помощью букв это правило записывается так:
$\large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} $

Умножение дробей

Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе — знаменателем.

С помощью букв правило умножения дробей можно записать так:
$\large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} $

Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать смешанные дроби.

Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.

Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное свойство умножения относительно сложения.

Деление дробей

Возьмем дробь $\frac{2}{3} $ и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь $\frac{3}{2} $. Эту дробь называют обратной дроби $\frac{2}{3} $.

Если мы теперь «перевернем» дробь $\frac{3}{2} $, то получим исходную дробь $\frac{2}{3} $. Поэтому такие дроби, как $\frac{2}{3} $ и $\frac{3}{2} $ называют

взаимно обратными .

Взаимно обратными являются, например, дроби $\frac{6}{5} $ и $\frac{5}{6} $, $\frac{7}{18} $ и $\frac{18}{7} $.

С помощью букв взаимно обратные дроби можно записать так: $\frac{a}{b} $ и $\frac{b}{a} $

Понятно, что произведение взаимно обратных дробей равно 1 . Например: $\frac{2}{3} \cdot \frac{3}{2} =1 $

Используя взаимно обратные дроби, можно деление дробей свести к умножению.

Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.

Используя буквы, правило деления дробей можно записать так:
$\large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} $

Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления дробей, его надо предварительно представить в виде неправильной дроби.

Большое количество учащихся, и не только, задаются вопросом, как перевести дробь в число. Чтобы это сделать, имеется несколько достаточно простых и понятных способов. Выбор конкретного способа зависит от предпочтений решающего.

В первую очередь нужно знать, как дроби записываются. А записываются они следующим образом:

Обыкновенная. Пишется с числителем и знаменателем через наклонную или столбиком (1/2).
Десятичная. Пишется через запятую (1,0, 2,5 и так далее).

Перед тем как приступить к решению, нужно знать, что такое неправильная дробь, ведь она встречается достаточно часто. Она имеет числитель больше знаменателя, например, 15/6. Неправильную дробь также можно решать такими способами, без каких-либо усилий и затрат времени.

Смешанное число — это когда в результате выходит целое число и дробная часть, к примеру 52/3.

Любое натуральное число можно записать дробью с совершенно разными натуральными знаменателями, например:1= 2/2=3/3 = и т.д.

Перевести можно еще и с помощью калькулятора, но не все они имеют такую функцию. Существует специальный инженерный калькулятор, где есть такая функция, но не всегда есть возможность его использовать, особенно в школе. Поэтому лучше разобраться в данной теме.

Первым делом стоит обратить внимание на то, какая дробь. Если ее можно с легкостью множить до 10 на одинаковые с числителем значения, то можно воспользоваться первым способом. Например: обыкновенная ½ умножаете в числителе и знаменателе на 5 и получаете 5/10, которое можно записать как 0,5.

Данное правило основано на том, что десятичная всегда имеет в знаменателе круглое значение, такое как 10,100,1000 и так далее.

Из этого выходит, что если множить числитель и знаменатель, то нужно добиваться получения в знаменателе именно такого значения в результате умножения, независимо от того, что выходит в числителе.

Стоит помнить, что некоторые дроби нельзя перевести, для этого необходимо перед началом решения проверить ее.

Например: 1,3333, где цифра 3 повторяется до бесконечности, причем калькулятор тоже не избавит от нее. Решением такой проблемы может быть только округление таким образом, чтобы получилось целое число, если это возможно. Если такой возможности не имеется, то следует вернуться в начало примера и проверить правильность решения задачи, возможно, была допущена ошибка.

Рисунок 1-3. Перевод дробей путем умножения.

Рассмотрим для закрепления описанной информации следующий пример перевода:

Например, необходимо перевести 6/20 в десятичную. Первым делом ее следует проверить, как показано на рисунке 1.
Только после того как убедились, что можно разложить, как в данном случае на 2 и 5, нужно приступать к самому переводу.
Наиболее простым вариантом будет умножить знаменатель, получив результат 100, является 5, так как 20х5=100.
Следуя примеру на рисунке 2, в итоге получится 0,3.

Можно закрепить результат и еще раз все просмотреть по рисунку 3. Для того чтобы полностью разобраться в теме и больше не прибегать к изучению этого материала. Эти знания помогут не только ребенку, но и взрослому человеку.

Перевод путем деления

Второй вариант перевода дробей является немного сложней, но более популярным. Таким методом в основном пользуются в школах учителя для объяснения. В целом, он намного проще объясняется и быстрее понимается.

Стоит помнить, что для правильного преобразования простой дроби необходимо ее числитель поделить на знаменатель. Ведь если задуматься, то решение это и есть процесс деления.

Для того чтобы понять это простое правило, нужно рассмотреть следующий пример решения:

Возьмем 78/200, которую нужно перевести в десятичную. Для этого следует 78 разделить на 200, то есть числитель на знаменатель.
Но перед тем как начать, стоит провести проверку, как показано на рисунке 4.
После того как убедились, что ее можно решить, следует приступать к процессу. Для этого стоит разделить числитель на знаменатель в столбик или уголком, как показано на рисунке 5. В начальных классах школ учат такому делению, и трудностей с этим не должно возникнуть.

На рисунке 6 показаны примеры наиболее распространенных примеров, их просто можно запомнить, чтобы при необходимости не тратить время для решения. Ведь в школе на каждую контрольную или самостоятельную работы дается мало времени для решения, поэтому не стоит тратить его на то, что можно выучить и просто помнить.

Перевод процентов

Переводить проценты в десятичное число тоже достаточно легко. Этому начинают учить в 5 классе, а в некоторых школах еще раньше. Но если ваш ребенок на уроке математики не понял эту тему, можно наглядно ему еще раз объяснить. Для начала следует выучить определения понятия, что такое процент.

Процент — это одна сотая часть от какого-либо числа, другими словами, абсолютная произвольная. Например, от 100 это будет 1 и так далее.

На рисунке 7 показан наглядный пример перевода процентов.

Чтобы перевести процент, надо всего лишь убрать значок %, а затем разделить его на 100.

Еще 1 пример показан на рисунке 8.

Если надо провести обратную «конвертацию», необходимо все сделать с точностью до наоборот. Другими словами, число необходимо умножить на сто и после приписать значок процентов.

А для того чтобы обычную перевести в проценты, также можно использовать этот пример. Только изначально следует перевести дробь в число и только потом в проценты.

Исходя из описанного выше, можно легко понять принцип перевода. С помощью этих способов можно ребенку объяснять тему, если он ее не понял или не присутствовал на уроке в момент ее прохождения.

И никогда не будет необходимости нанимать репетитора, чтобы он объяснил ребенку, как перевести дробь в число или процент.

То нажмите на кнопки, и задача выполнена. В результате у вас получится либо целое число, либо десятичная дробь. Десятичная дробь может получится с длинным остатком после . В этом случае дробь нужно округлить до определенного, нужного вам разряда, используя округления (цифры до 5 округляются в меньшую сторону, от 5 включительно и более — в большую сторону).

Если калькулятора под рукой не , но придется . Напишите числитель дроби со знаменателем, между ними уголочек, означающий . К примеру, переведите в число дробь 10/6. Для начала 10 разделите на 6. Получится 1. Запишите результат по уголком. Перемножьте 1 на 6, получится 6. Вычтите 6 из 10. Получится остаток 4. Остаток нужно снова разделить на 6. Допишите к 4 цифру 0, и разделите 40 на 6. Получится 6. Запишите 6 в результат, после запятой. Перемножьте 6 на 6. Получится 36. Вычтите 36 из 40. Получится вновь остаток 4. Далее можно не продолжать, поскольку становится очевидным, что результатом будет число 1,66(6). Округлите данную дробь до того разряда, который вам необходим. Например, 1,67. Это и есть окончательный результат.

Связанная статья

Источники:

перевод дробей с целым числом

Дроби нужны для обозначения чисел, которые состоят из одной или нескольких частей единицы. Термин «дробь» произошел от латинского fractura, которое имеет значение «дробить, ломать». Различаются обыкновенные и десятичные дроби. При этом в обыкновенных дробях единицу можно разделить на любое количество частей, а в десятичной — это количество должно быть кратно 10. Любая дробь может иметь быть как обычной, так и десятичной.

Вам понадобится

Для подсчета результата вам понадобится калькулятор или листок и ручка.

Инструкция

Итак, для начала возьмите обыкновенную дробь и разделите ее на части. Например, 2 1\8, в которой 2 — это целая часть, а 1\8 дробь. Из нее можно увидеть, что число разделили на 8 , но взяли лишь одну. Часть, которую взяли, числитель, а количество частей, на которое делят, — знаменатель.

Обратите внимание

Зачастую встречаются дроби, которые нельзя полностью перевести в десятичные. В этом случае на помощь приходит округление. Если вы хотите округлить до тысячных, то посмотрите на четвертое число после запятой. Если оно меньше 5, то запишите в ответ, первые три цифры после запятой без изменения, в противном случае к последней цифре из трех необходимо прибавить единицу. Например, 0, 89643123 можно записать как 0,896, а вот 0, 89663123 — 0,897.

Полезный совет

Если вы подсчитываете результат вручную, то перед делением дробь лучше максимально сократить, а также выделить из нее целые части.

Источники:

как перевести дроби

Дробь является одним из элементов формул, для ввода которых в текстовом процессоре Word существует инструмент Microsoft Equation. С помощью него можно вводить любые сложные математические или физические формулы, уравнения и другие элементы, включающие в себя специальные символы.

Инструкция

Чтобы запустить инструмент Microsoft Equation необходимо пройти по адресу: «Вставка» -> «Объект», в открывшемся диалоговом окне, на первой вкладке из списка нужно выбрать Microsoft Equation и нажать «Ок» или два раза кликнуть на выбранном пункте. После запуска редактора , перед вами откроется панель инструментов и в отобразится поле для ввода : прямоугольник в пунктирной . Панель инструментов разделена на секции, в каждой из них находится набор знаков действий или выражений. При нажатии на одну из секций, развернется список находящихся в ней инструментов. Из открывшегося списка необходимо выбрать нужный символ и кликнуть на нем. После выбора, указанный символ появится в выделенном прямоугольнике в документе.

Секция, в которой располагаются элементы для написания дробей, находится во второй строке панели инструментов. При наведении на нее курсора мыши, вы увидите подсказку «Шаблоны дробей и радикалов». Кликните секцию один раз и разверните список. В выпавшем меню есть шаблоны для дробей с горизонтальной и косой . Среди появившихся вариантов вы можете выбрать тот, который подходит для вашей задачи. Кликните на нужном варианте. После нажатия, в поле для ввода, которое открылось в документе, появится символ дроби и места для ввода числителя и знаменателя, обрамленные пунктирной линией. Курсор по умолчанию автоматически устанавливается в поле для ввода числителя. Введите числитель. Помимо цифр можно так же вводить символы, буквы или знаки действий. Их можно вводить как с клавиатуры, так и из соответствующих секций панели инструментов Microsoft Equation. После вода числителя, нажатием клавиши TAB, перейдите к знаменателю. Перейти можно и кликнув мышью в поле для ввода знаменателя. Как только написана, кликните указателем мыши в любом месте документа, панель инструментов закроется, ввод дроби будет завершен. Чтобы отредактировать , дважды нажмите на ней левой кнопкой мыши.

Если при открытии меню «Вставка» -> «Объект», в списке вы не обнаружили инструмента Microsoft Equation, его необходимо установить. Запустите установочный диск, образ диска или файл дистрибутива Word. В появившемся окне инсталлятора выберите «Добавить или удалить компоненты. Добавление или удаление отдельных компонентов» и нажмите «Далее». В следующем окне отметьте пункт «Расширенная настройка приложений». Нажмите «Далее». В следующем окне найдите пункт списка «Средства Office» и нажмите на плюсик слева. В развернувшемся списке, нас интересует пункт «Редактор формул». Кликните на значок рядом с надписью «Редактор формул» и, в открывшемся меню, нажмите «Запускать с компьютера». После этого нажмите «Обновить» и дождитесь пока пройдет установка необходимого компонента.

Материалов по дробям и изучать последовательно. Ниже для вас подробная информация с примерами и пояснениями.

1. Смешанное число в обыкновенную дробь. Запишем в общем виде число:

Запоминаем простое правило – целую часть умножаем на знаменатель и прибавляем числитель, то есть:

Примеры:

2. Наоборот, обыкновенную дробь в смешанное число. *Конечно, это возможно сделать только с неправильной дробью (когда числитель больше знаменателя).

При «небольших» числах никаких действий, в общем, и не нужно делать, результат «видно» сразу, например, дроби:

*Подробнее:

15:13 = 1 остаток 2

4:3 = 1 остаток 1

9:5 = 1 остаток 4

А вот если числа будут более, то без вычислений не обойтись. Здесь всё просто – делим уголком числитель на знаменатель до тех пор пока остаток не получится менее делителя. Схема деления:

Например:

*Числитель у нас – это делимое, знаменатель – это делитель.

Получаем целую часть (неполное частное) и остаток. Записываем – целое, затем дробь (в числителе остаток, а знаменатель оставляем тот же):

3. Десятичную переводим в обыкновенную.

Частично в первом пункте, где рассказывали про десятичные дроби мы уже коснулись этого. Как слышим так и записываем. Например — 0,3; 0,45; 0,008; 4,38; 10,00015

Первые три дроби у нас без целой части. А четвёртая и пятая её имеют, переведём их в обыкновенные, это делать уже умеем:

*Мы видим, что дроби можно ещё и сократить, например 45/100 =9/20, 38/100=19/50 и другие, но мы здесь делать этого не будем. По сокращению вас ожидает отдельный пункт ниже, где подробно всё разберём.

4. Обыкновенную переводим в десятичную.

Тут не всё так просто. По каким-то дробям сразу видно и ясно, что с ней сделать, чтобы она стала десятичной, например:

Используем наше замечательное основное свойство дроби – умножаем числитель и знаменатель соответственно на 5, 25, 2, 5, 4, 2, получим:

Если имеется целая часть, то тоже ничего сложного:

Умножаем дробную часть соответственно на 2, 25, 2 и 5, получим:

А есть такие, по которым без опыта и не определить, что их можно перевести в десятичные, например:

На какие числа умножать числитель и знаменатель?

Тут опять на помощь приходит проверенный способ – деление уголком, способ универсальный, им для перевода обыкновенной дроби в десятичную можно пользоваться всегда:

Так вы сможете всегда определить переводится ли дробь в десятичную. Дело в том, что не каждую обыкновенную дробь можно перевести в десятичную, например такие как 1/9, 3/7, 7/26 не переводятся. А что же тогда получается за дробь при делении 1 на 9, 3 на 7, 5 на 11? Отвечаю – бесконечная десятичная (говорили о них в пункте 1). Разделим:

На этом всё! Успеха вам!

С уважением, Александр Крутицких.

Дробь может быть преобразована в целое число либо в десятичную дробь. Неправильная дробь, числитель которой больше знаменателя и делится на него без остатка, переводится в целое число, например: 20/5. Делим 20 на 5 и получаем число 4. Если дробь правильная, то есть числитель меньше знаменателя, то тогда преобразовать ее в число (десятичную дробь). Больше информации о дробях вы сможете почерпнуть из нашего раздела — .

Способы преобразования дроби в число

Первый способ, как перевести дробь в число годится для дроби, которую можно преобразовать в число, являющееся десятичной дробью. Сначала выясним, можно ли перевести заданную дробь в дробь десятичную. Для этого обратим внимание на знаменатель (цифра, которая под чертой или справа от наклонной). Если знаменатель можно разложить на множители (в нашем примере — 2 и 5), которые могут повторяться, то данную дробь реально преобразовать в конечную десятичную дробь. Например: 11/40 =11/(2∙2∙2∙5). Данная обыкновенная дробь переведется в число (десятичную дробь) с конечным количеством знаков после запятой. А вот дробь 17/60 =17/(5∙2∙2∙3) переведется в число с бесконечным количеством знаков после запятой. То есть при точном вычислении числового значения довольно трудно определить конечный знак после запятой, поскольку таких знаков бесконечное множество. Поэтому для решения задач обычно требуется округлить значение до сотых или тысячных. Дальше — необходимо умножить и числитель, и знаменатель на такое число, чтобы в знаменателе получились цифры 10, 100, 1000 и т. д. Например: 11/40 =(11∙25)/(40∙25) =275/1000 =0,275
Второй способ, как перевести дробь в число — более простой: необходимо числитель поделить на знаменатель. Для применения этого способа просто произведем деление, а полученное число и будет той искомой десятичной дробью. Например, надо перевести дробь 2/15 в число. Делим 2 на 15. Получаем 0, 1333… — бесконечная дробь. Записываем так: 0,13(3). Если дробь неправильная, то есть числитель больше знаменателя (например, 345/100), то в результате преобразования ее в число получится целое числовое значение или десятичная дробь с целой дробной частью. В нашем примере это будет 3,45. Чтобы преобразовать смешанную дробь такого вида, как 3 2 / 7 , в число, то нужно сначала превратить ее в неправильную дробь: (3∙7+2)/7 =23/7. Далее делим 23 на 7 и получаем число 3,2857143, которое сокращаем до 3,29.

Самый простой способ по переводу дроби в число — это использование калькулятора или иного вычислительного прибора. Укажем сначала числитель дроби, потом нажмем кнопку со значком «разделить» и набираем знаменатель. После нажатия клавиши «=» мы получаем искомое число.

Сокращение дробей с корнями онлайн калькулятор.

Умножение, деление и сокращение алгебраических дробей

Дети в школе учат правила сокращения дробей в 6 классе. В этой статье мы сначала расскажем вам о том, что же означает это действие, затем разъясним, как сократимую дробь перевести в несократимую. Следующим пунктом будут правила сокращения дробей, а затем уже постепенно подберемся к примерам.

Что значит «сократить дробь «?

Итак, все мы знаем, что обычные дроби делятся на две группы: сократимые и несократимые. Уже по названиям можно понять, что те, что сократимые — сокращаются, а те, которые несократимые — не сокращаются.

Сократить дробь — это значит разделить ее знаменатель и числитель на их (отличный от единицы) положительный делитель. В результате, конечно, выходит новая дробь с меньшим знаменателем и числителем. Полученная дробь будет равна исходной дроби.

Стоит отметить, что в книгах по математике с заданием «сократите дробь » это значит, что нужно исходную дробь привести именно к этому несократимому виду. Если говорить простыми словами, то деление знаменателя и числителя на их наибольший общий делитель и есть сокращение.

Как сократить дробь. Правила сокращения дробей (6 класс)

Итак, здесь всего два правила.

Первое правило сокращения дробей: сначала нужно будет найти наибольший общий делитель знаменателя и числителя вашей дроби.
Второе правило: делить знаменатель и числитель на наибольший общий делитель, в конечном итоге получить несократимую дробь.

Как сократить неправильную дробь?

Правила сокращения дробей идентичны правилам сокращения неправильных дробей.

Для того чтобы сократить неправильную дробь, для начала нужно будет расписать на простые множители знаменатель и числитель, а уже потом общие множители сокращать.

Сокращение смешанных дробей

Правила сокращения дробей также распространяется на сокращение смешанных дробей. Есть лишь небольшая разница: целую часть мы можем не трогать, а дробную сократить или смешанную дробь перевести в неправильную, затем сократить и опять перевести в правильную дробь.

Сократить смешанные дроби можно двумя способами.

Первый: расписать дробную часть на простые множители и целую часть тогда не трогать.

Второй способ: перевести сначала в неправильную дробь, расписать на обычные множители, потом сократить дробь. Уже полученную неправильную дробь перевести в правильную.

Примеры можно увидеть на фото выше.

Мы очень надеемся, что смогли помочь вам и вашим детям. Ведь на уроках они очень часто бывают невнимательными, поэтому приходится заниматься интенсивнее на дому самостоятельно.

Сокращение дробей нужно для того, чтобы привести дробь к более простому виду, например, в ответе полученном в результате решения выражения.

Сокращение дробей, определение и формула.

Что такое сокращение дробей? Что значит сократить дробь?

Определение:
Сокращение дробей – это разделение у дроби числитель и знаменатель на одно и то же положительное число не равное нулю и единице. В итоге сокращения получается дробь с меньшим числителем и знаменателем, равная предыдущей дроби согласно .

Формула сокращения дробей основного свойства рациональных чисел.

$\frac{p \times n}{q \times n}=\frac{p}{q}$

Рассмотрим пример:
Сократите дробь $\frac{9}{15}$

Решение:
Мы можем разложить дробь на простые множители и сократить общие множители.

$\frac{9}{15}=\frac{3 \times 3}{5 \times 3}=\frac{3}{5} \times \color{red} {\frac{3}{3}}=\frac{3}{5} \times 1=\frac{3}{5}$

Ответ: после сокращения получили дробь $\frac{3}{5}$. По основному свойству рациональных чисел первоначальная и получившееся дробь равны.

$\frac{9}{15}=\frac{3}{5}$

Как сокращать дроби? Сокращение дроби до несократимого вида.

Чтобы нам получить в результате несократимую дробь, нужно найти наибольший общий делитель (НОД) для числителя и знаменателя дроби.

Есть несколько способов найти НОД мы воспользуемся в примере разложением чисел на простые множители.

Получите несократимую дробь $\frac{48}{136}$.

Решение:
Найдем НОД(48, 136). Распишем числа 48 и 136 на простые множители.
48=2⋅2⋅2⋅2⋅3
136=2⋅2⋅2⋅17
НОД(48, 136)= 2⋅2⋅2=6

$\frac{48}{136}=\frac{\color{red} {2 \times 2 \times 2} \times 2 \times 3}{\color{red} {2 \times 2 \times 2} \times 17}=\frac{\color{red} {6} \times 2 \times 3}{\color{red} {6} \times 17}=\frac{2 \times 3}{17}=\frac{6}{17}$

Правило сокращения дроби до несократимого вида.

Нужно найти наибольший общий делитель для числители и знаменателя.
Нужно поделить числитель и знаменатель на наибольший общий делитель в результате деления получить несократимую дробь.

Пример:
Сократите дробь $\frac{152}{168}$.

Решение:
Найдем НОД(152, 168). Распишем числа 152 и 168 на простые множители.
152=2⋅2⋅2⋅19
168=2⋅2⋅2⋅3⋅7
НОД(152, 168)= 2⋅2⋅2=6

$\frac{152}{168}=\frac{\color{red} {6} \times 19}{\color{red} {6} \times 21}=\frac{19}{21}$

Ответ: $\frac{19}{21}$ несократимая дробь.

Сокращение неправильной дроби.

Как сократить неправильную дробь?
Правила сокращения дробей для правильных и неправильных дробей одинаковы.

Рассмотрим пример:
Сократите неправильную дробь $\frac{44}{32}$.

Решение:
Распишем на простые множители числитель и знаменатель. А потом общие множители сократим.

$\frac{44}{32}=\frac{\color{red} {2 \times 2 } \times 11}{\color{red} {2 \times 2 } \times 2 \times 2 \times 2}=\frac{11}{2 \times 2 \times 2}=\frac{11}{8}$

Сокращение смешанных дробей.

Смешанные дроби по тем же правилам что и обыкновенные дроби. Разница лишь в том, что мы можем целую часть не трогать, а дробную часть сократить или смешанную дробь перевести в неправильную дробь, сократить и перевести обратно в правильную дробь.

Рассмотрим пример:
Сократите смешанную дробь $2\frac{30}{45}$.

Решение:
Решим двумя способами:
Первый способ:
Распишем дробную часть на простые множители, а целую часть не будем трогать.

$2\frac{30}{45}=2\frac{2 \times \color{red} {5 \times 3}}{3 \times \color{red} {5 \times 3}}=2\frac{2}{3}$

Второй способ:
Переведем сначала в неправильную дробь, а потом распишем на простые множители и сократим. Полученную неправильную дробь переведем в правильную.

$2\frac{30}{45}=\frac{45 \times 2 + 30}{45}=\frac{120}{45}=\frac{2 \times \color{red} {5 \times 3} \times 2 \times 2}{3 \times \color{red} {3 \times 5}}=\frac{2 \times 2 \times 2}{3}=\frac{8}{3}=2\frac{2}{3}$

Вопросы по теме:
Можно ли сокращать дроби при сложении или вычитании?
Ответ: нет, нужно сначала сложить или вычесть дроби по правилам, а только потом сокращать. Рассмотрим пример:

Вычислите выражение $\frac{50+20-10}{20}$ .

Решение:
Часто допускают ошибку сокращая одинаковые числа в числителе и знаменателе в нашем случаем число 20, но их сокращать нельзя пока не выполните сложение и вычитание.

$\frac{50+\color{red} {20}-10}{\color{red} {20}}=\frac{60}{20}=\frac{3 \times 20}{20}=\frac{3}{1}=3$

На какие числа можно сокращать дробь?
Ответ: можно сокращать дробь на наибольший общий делитель или обычный делитель числителя и знаменателя.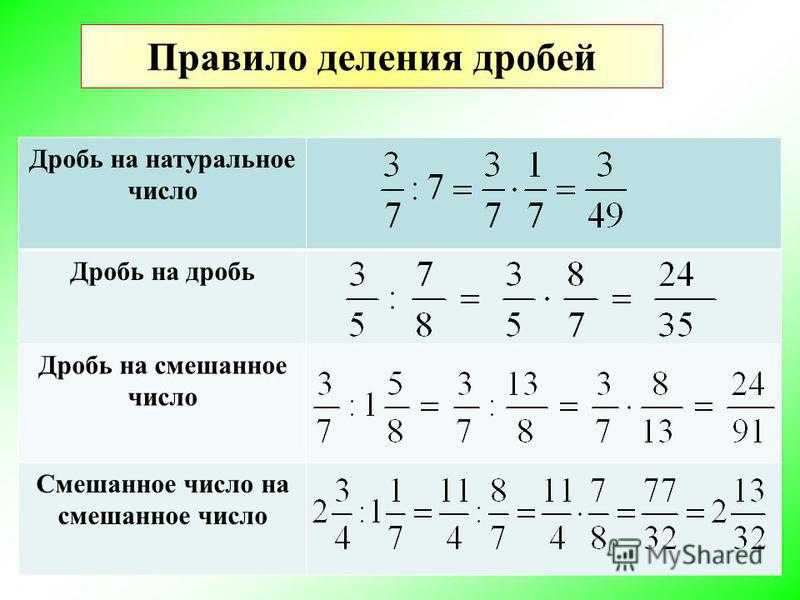 Например, дробь $\frac{100}{150}$.

Распишем на простые множители числа 100 и 150.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
Наибольшим общим делителем будет число НОД(100, 150)= 2⋅5⋅5=50

$\frac{100}{150}=\frac{2 \times 50}{3 \times 50}=\frac{2}{3}$

Получили несократимую дробь $\frac{2}{3}$.

Но необязательно всегда делить на НОД не всегда нужна несократимая дробь, можно сократить дробь на простой делитель числителя и знаменателя. Например, у числа 100 и 150 общий делитель 2. Сократим дробь $\frac{100}{150}$ на 2.

$\frac{100}{150}=\frac{2 \times 50}{2 \times 75}=\frac{50}{75}$

Получили сократимую дробь $\frac{50}{75}$.

Какие дроби можно сокращать?
Ответ: сокращать можно дроби у которых числитель и знаменатель имеют общий делитель. Например, дробь $\frac{4}{8}$. У числа 4 и 8 есть число, на которое они оба делятся это число 2. Поэтому такую дробь можно сократить на число 2.

Пример:
Сравните две дроби $\frac{2}{3}$ и $\frac{8}{12}$.

Эти две дроби равны. Рассмотрим подробно дробь $\frac{8}{12}$:

$\frac{8}{12}=\frac{2 \times 4}{3 \times 4}=\frac{2}{3} \times \frac{4}{4}=\frac{2}{3} \times 1=\frac{2}{3}$

Отсюда получаем, $\frac{8}{12}=\frac{2}{3}$

Две дроби равны тогда и только тогда, когда одна из них получена путем сокращения другой дроби на общий множитель числителя и знаменателя.

Пример:
Сократите если возможно следующие дроби: а) $\frac{90}{65}$ б) $\frac{27}{63}$ в) $\frac{17}{100}$ г) $\frac{100}{250}$

Решение:
а) $\frac{90}{65}=\frac{2 \times \color{red} {5} \times 3 \times 3}{\color{red} {5} \times 13}=\frac{2 \times 3 \times 3}{13}=\frac{18}{13}$
б) $\frac{27}{63}=\frac{\color{red} {3 \times 3} \times 3}{\color{red} {3 \times 3} \times 7}=\frac{3}{7}$
в) $\frac{17}{100}$ несократимая дробь
г) $\frac{100}{250}=\frac{\color{red} {2 \times 5 \times 5} \times 2}{\color{red} {2 \times 5 \times 5} \times 5}=\frac{2}{5}$

Чтобы понять, как сокращать дроби, сначала рассмотрим один пример.

Сократить дробь — значит, разделить числитель и знаменатель на одно и то же . И 360, и 420 оканчиваются на цифру, поэтому можем сократить эту дробь на 2. В новой дроби и 180, и 210 тоже делятся на 2, сокращаем и эту дробь на 2. В числах 90 и 105 сумма цифр делится на 3, поэтому оба эти числа делятся на 3, сокращаем дробь на 3. В новой дроби 30 и 35 оканчиваются на 0 и 5, значит, оба числа делятся на 5, поэтому сокращаем дробь на 5. Получившаяся дробь шесть седьмых — несократимая. Это — окончательный ответ.

К этому же ответу можем прийти другим путем.

И 360, и 420 оканчиваются нулем, значит, они делятся на 10. Сокращаем дробь на 10. В новой дроби и числитель 36, и знаменатель 42 делятся на 2. Сокращаем дробь на 2. В следующей дроби и числитель 18, и знаменатель 21 делятся на 3, значит, сокращаем дробь на 3. Пришли к результату — шесть седьмых.

И еще один вариант решения.

В следующий раз рассмотрим примеры сокращения дробей.

Вот и добрались до сокращения. Применяется здесь основное свойство дроби. НО! Не всё так просто. Со многими дробями (в том числе из школьного курса) вполне можно им обойтись. А если взять дроби «покруче»? Разберём подробнее! Рекомендую посмотреть материалов с дробями.

Итак, мы уже знаем, что числитель и знаменатель дроби можно умножать и делить на одно и тоже число, дробь от этого не изменится. Рассмотрим три подхода:

Подход первый.

Для сокращения делят числитель и знаменатель на общий делитель. Рассмотрим примеры:

Сократим:

В приведенных примерах мы сразу видим какие взять делители для сокращения. Процесс несложен – мы перебираем 2,3.4,5 и так далее. В большинстве примеров школьного курса этого вполне достаточно. А вот если будет дробь:

Тут процесс с подбором делителей может затянуться надолго;). Конечно, такие примеры лежат вне школьного курса, но справляться с ними нужно уметь. Чуть ниже рассмотрим как это делается. А пока вернёмся к процессу сокращения.

Как рассмотрено выше, для того чтобы сократить дробь, мы осуществляли деление на определённый нами общий делитель(ли). Всё правильно! Стоит лишь добавить признаки делимости чисел:

— если число чётное то оно делится на 2.

— если число из последних двух цифр делится на 4, то и само число делится на 4.

— если сумма цифр из которых состоит число делится на 3, то и само число делится на 3. Например 125031, 1+2+5+0+3+1=12. Двенадцать делится на 3, значит и 123031 делится на 3.

— если в конце числа стоит 5 или 0, то число делится на 5.

— если сумма цифр из которых состоит число делится на 9, то и само число делится на 9. Например 625032 =.> 6+2+5+0+3+2=18. Восемнадцать делится на 9, значит и 623032 делится на 9.

Второй подход.

Если кратко суть, то на самом деле всё действо сводится к разложению числителя и знаменателя на множители и далее к сокращению равных множителей в числителе и знаменателе (данный подход – это следствие из первого подхода):

Визуально, чтобы не запутаться и не ошибиться равные множители просто перечёркивают. Вопрос – а как разложить число на множители? Нужно определить перебором все делители. Это тема отдельная, она несложная, посмотрите информацию в учебнике или интернете. Никаких великих проблем с разложением на множители чисел, которые присутствуют в дробях школьного курса, вы не встретите.

Формально принцип сокращения можно записать так:

Подход третий.

Тут самое интересное для продвинутых и тех, кто хочет им стать. Сократим дробь 143/273. Попробуйте сами! Ну и как, быстро получилось? А теперь смотрите!

Переворачиваем её (числитель и знаменатель меняем местами). Делим уголком полученную дробь переводим в смешанное число, то есть выделяем целую часть:

Уже проще. Мы видим, что числитель и знаменатель можно сократить на 13:

А теперь не забываем снова перевернуть дробь обратно, давайте запишем всю цепочку:

Проверено – времени уходит меньше, чем на перебор и проверку делителей. Вернёмся к нашим двум примерам:

Первый. Делим уголком (не на калькуляторе), получим:

Эта дробь попроще конечно, но с сокращением опять проблема. Теперь отдельно разбираем дробь 1273/1463, переворачиваем её:

Тут уже проще. Можем рассмотреть такой делитель как 19. Остальные не подходят, это видно: 190:19= 10, 1273:19 = 67. Ура! Запишем:

Следующий пример. Сократим 88179/2717.

Делим, получим:

Отдельно разбираем дробь 1235/2717, переворачиваем её:

Можем рассмотреть такой делитель как 13 (до 13 не подходят):

Числитель 247:13=19 Знаменатель 1235:13=95

*В процессе увидели ещё один делитель равный 19. Получается, что:

Теперь записываем исходное число:

И не важно, что будет больше в дроби – числитель или знаменатель, если знаменатель, то переворачиваем и действуем как описано. Таким образом мы можем сократить любую дробь, третий подход можно назвать универсальным.

Конечно, два примера рассмотренные выше это непростые примеры. Давайте попробуем эту технологию на уже рассмотренных нами «несложных» дробях:

Две четвёртых.

Семьдесят две шестидесятых. Числитель больше знаменателя, переворачивать не нужно:

Разумеется, третий подход применили к таким простым примерам просто как альтернативу. Способ, как уже сказано, универсальный, но не для всех дробей удобный и корректный, особенно это относится к простым.

Многообразие дробей велико. Важно, чтобы вы усвоили именно принципы. Строгого правила по работе с дробями просто нет. Посмотрели, прикинули каким образом удобнее действовать и вперёд. С практикой придёт навык и будете щёлкать их как семечки.

Вывод:

Если видите общий(ие) делитель(и) для числителя и знаменателя, то используйте их для сокращения.

Если умеете быстро раскладывать на множители число, то разложите числитель и знаменатель, далее сокращайте.

Если никак не можете определить общий делитель, то воспользуйтесь третьим подходом.

*Для сокращения дробей важно усвоить принципы сокращения, понимать основное свойство дроби, знать подходы к решению, быть крайне внимательным при вычислениях.

И запомните! Дробь принято сокращать до упора, то есть сокращать её пока есть общий делитель.

C уважением, Александр Крутицких.

Остаток всегда меньше делителя.

Частное от деления натуральных чисел можно записать в виде дроби.

Числитель дроби — это делимое, а знаменатель — делитель.

Верны следующие правила:

Чтобы получить дробь $\frac{m}{n} $, надо единицу разделить на n равных частей (долей) и взять m таких частей.

Чтобы получить дробь $\frac{m}{n} $, надо число m разделить на число n.

Два последних преобразования называют сокращением дроби .

Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к общему знаменателю .

Правильные и неправильные дроби.

Смешанные числа

Если число состоит из целой части и дроби, то такие дроби называются смешанными .

Например:
$5:3 = 1\frac{2}{3} $ : 1 — целая часть, а $\frac{2}{3} $ — дробная часть.

Действия с дробями. Сложение дробей.

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.

Сложение смешанных дробей

Вычитание дробей (дробных чисел)

С помощью букв это правило записывается так:
$\large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} $

Умножение дробей

С помощью букв правило умножения дробей можно записать так:
$\large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} $

Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.

Деление дробей

Если мы теперь «перевернем» дробь $\frac{3}{2} $, то получим исходную дробь $\frac{2}{3} $. Поэтому такие дроби, как $\frac{2}{3} $ и $\frac{3}{2} $ называют взаимно обратными .

Взаимно обратными являются, например, дроби $\frac{6}{5} $ и $\frac{5}{6} $, $\frac{7}{18} $ и $\frac{18}{7} $.

С помощью букв взаимно обратные дроби можно записать так: $\frac{a}{b} $ и $\frac{b}{a} $

Понятно, что произведение взаимно обратных дробей равно 1 . Например: $\frac{2}{3} \cdot \frac{3}{2} =1 $

Используя взаимно обратные дроби, можно деление дробей свести к умножению.

Используя буквы, правило деления дробей можно записать так:
$\large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} $

Таблица квадратов натуральных чисел | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Квадратом называется вторая степень любого действительного или комплексного числа. Например, 3² можно назвать «три во второй степени», «три в квадрате» или «квадрат числа три». Происхождение этого названия берет свое начало из геометрии Пифагора, где для нахождения площади квадрата необходимо умножить его сторону саму на себя, таким образом, возведя ее во вторую степень. Со временем эти два понятия стали взаимозаменяемы, и сейчас вторая степень называется квадратом. Чтобы найти квадрат любого двузначного числа, используя таблицу, необходимо найти строку с цифрой десятков и столбец с цифрой единиц, на их пересечении будет находиться число-квадрат. Выделенные строка и столбец подсвечиваются цветом. Ниже таблицы приведены примеры для нахождения квадрата числа, разделенные на столбцы по десяткам.

единицы десятки	0	1	2	3	4	5	6	7	8	9
0	0	1	4	9	16	25	36	49	64	81
1	100	121	144	169	196	225	256	289	324	361
2	400	441	484	529	576	625	676	729	784	841
3	900	961	1024	1089	1156	1225	1296	1369	1444	1521
4	1600	1681	1764	1849	1936	2025	2116	2209	2304	2401
5	2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
6	3600	3721	3844	3969	4096	4225	4356	4489	4624	4761
7	4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
8	6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
9	8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

Таблица квадратов до 10 1² = 1 2² = 4 3² = 9 4² = 16 5² = 25 6² = 36 7² = 49 8² = 64 9² = 81 10² = 100	Таблица квадратов до 20 11² = 121 12² = 144 13² = 169 14² = 196 15² = 225 16² = 256 17² = 289 18² = 324 19² = 361 20² = 400	Таблица квадратов до 30 21² = 441 22² = 484 23² = 529 24² = 576 25² = 625 26² = 676 27² = 729 28² = 784 29² = 841 30² = 900	Таблица квадратов до 40 31² = 961 32² = 1024 33² = 1089 34² = 1156 35² = 1225 36² = 1296 37² = 1369 38² = 1444 39² = 1521 40² = 1600	Таблица квадратов до 50 41² = 1681 42² = 1764 43² = 1849 44² = 1936 45² = 2025 46² = 2116 47² = 2209 48² = 2304 49² = 2401 50² = 2500

Таблица квадратов до 60 51² = 2601 52² = 2704 53² = 2809 54² = 2916 55² = 3025 56² = 3136 57² = 3249 58² = 3364 59² = 3481 60² = 3600	Таблица квадратов до 70 61² = 3721 62² = 3844 63² = 3969 64² = 4096 65² = 4225 66² = 4356 67² = 4489 68² = 4624 69² = 4761 70² = 4900	Таблица квадратов до 80 71² = 5041 72² = 5184 73² = 5329 74² = 5476 75² = 5625 76² = 5776 77² = 5929 78² = 6084 79² = 6241 80² = 6400	Таблица квадратов до 90 81² = 6561 82² = 6724 83² = 6889 84² = 7056 85² = 7225 86² = 7396 87² = 7569 88² = 7744 89² = 7921 90² = 8100	Таблица квадратов до 100 91² = 8281 92² = 8464 93² = 8649 94² = 8836 95² = 9025 96² = 9216 97² = 9409 98² = 9604 99² = 9801 100² = 10000

Калькулятор

фракций | Justfreetools

Введите дроби, выберите операцию и нажмите кнопку «Рассчитать».

Результат

Расчет

Калькулятор упрощения дробей »

Пример сложения дробей

1/2 + 1/3 = (1×3+1×2) / (2×3) = 5/6

Пример вычитания дробей

1/2 — 1/3 = (1×3 — 1×2) / (2×3) = 1/6

Пример умножения дробей

1/2 × 1/3 = (1×1) / ( 2×3) = 1/6

Пример деления дробей

1/2 ÷ 1/3 = 1/2 × 3/1 = (1×3) / (2×1) = 3 / 2 = 1 1/ 2

В настоящее время у нас есть около 5611 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и программных функций для студентов, преподавателей и учителей, дизайнеров и просто для всех.

Вы можете найти на этой странице финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы автокредита и калькуляторы лизинга, калькуляторы процентов, калькуляторы выплат, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, калькуляторы финансов, калькуляторы подоходного налога , калькуляторы сложных процентов, калькулятор зарплаты, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор ИМТ, калькуляторы калорий, калькулятор жировых отложений, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, калькулятор процентов, генератор случайных чисел, калькулятор треугольника, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор среднего балла, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, генератор паролей калькулятор преобразования tor и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebook (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook). Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других сайтов социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все видео, которые вы загружаете, загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, ALT-кодах для Mac, Windows и Linux и других полезных советах и инструментах (как написать смайлики онлайн и т. д.)

Есть много очень полезных бесплатных онлайн-инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или пришлете нам какие-либо предложения по другим инструментам, которые придут вам на ум. Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или нуждается в лучшем переводе, сообщите нам об этом. Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее.

Ниже перечислены наиболее часто используемые многими пользователями по всему миру.

Бесплатные онлайн-калькуляторы и инструменты
Калькуляторы часовых поясов/часов/дат
Бесплатные онлайн-калькуляторы перевода единиц
Бесплатные онлайн-инструменты для веб-дизайна
Бесплатные онлайн-инструменты для электричества и электроники
Математика
Инструменты PDF
Код
Экология
Прочее
Бесплатные онлайн-загрузчики для социальных сетей
Бесплатные онлайн-калькуляторы и инструменты для электротехники
Бесплатные онлайн финансовые калькуляторы и инструменты
Бесплатные онлайн калькуляторы оценок и инструменты
Бесплатные онлайн калькуляторы освещения и инструменты
Бесплатные онлайн математические калькуляторы и инструменты
Бесплатные онлайн калькуляторы проводов и инструменты
Бесплатные онлайн детские калькуляторы и инструменты
Бесплатные онлайн-калькуляторы тела и инструменты
Калькулятор преобразования переменного тока в постоянный
Сложение дробей бесплатный онлайн-калькулятор
Сложение бесплатный онлайн-калькулятор
Antilog бесплатный онлайн-калькулятор
Arccos бесплатный онлайн-калькулятор
Arcsin бесплатный онлайн-калькулятор
Arctan бесплатный онлайн-калькулятор
Average бесплатный онлайн-калькулятор
Base бесплатный онлайн-калькулятор
Binary бесплатный онлайн-калькулятор 6 37 09 09 бесплатно 90 90 Косинус калькулятор онлайн бесплатно
Деление дробей онлайн калькулятор бесплатно
Деление бесплатно онлайн калькулятор
Формула экспоненциального роста/убывания онлайн калькулятор бесплатно
Экспоненты онлайн калькулятор
Факториал бесплатный онлайн калькулятор
Дроби бесплатный онлайн калькулятор
Наибольший общий множитель бесплатный онлайн калькулятор
Наименьшее общее кратное бесплатный онлайн калькулятор
Логарифм бесплатный онлайн калькулятор
Умножение дробей бесплатный онлайн калькулятор
Натуральный логарифм бесплатный онлайн калькулятор
Процентный безошибочный онлайн-калькулятор
Процентное изменение бесплатный онлайн-калькулятор
Процентный бесплатный онлайн-калькулятор
Процентное увеличение/уменьшение бесплатный онлайн-калькулятор
Теорема Пифагора бесплатный онлайн-калькулятор
Квадратное уравнение Радикальное уравнение и корни онлайн
бесплатно 900 s калькулятор
Бесплатный онлайн генератор случайных чисел
Генератор случайных чисел 0-1
Генератор случайных чисел 0-10
Генератор случайных чисел 0-100
Генератор случайных чисел 0-9
Генератор случайных чисел 0-99
Генератор случайных чисел 1-10
Генератор случайных чисел 1-100
3-2 Генератор случайных чисел Генератор случайных чисел 1-20
Генератор случайных чисел 1-3
Генератор случайных чисел 1-4
Генератор случайных чисел 1-5
Генератор случайных чисел 1-6
Калькулятор коэффициентов
Функционал онлайн калькулятор
Упрощение дробей онлайн калькулятор
Синус онлайн калькулятор
Корень квадратный онлайн калькулятор
Стандартное отклонение онлайн калькулятор
Вычитание дробей онлайн калькулятор
Тангенс калькулятор онлайн
7 90 бесплатно онлайн-калькулятор
Тригонометрия бесплатный онлайн-калькулятор
Дисперсия бесплатный онлайн-калькулятор
Средневзвешенный бесплатный онлайн-калькулятор

И мы все еще разрабатываем больше. Наша цель — стать универсальным сайтом для людей, которым нужно быстро рассчитать или найти быстрый ответ для основных конверсий.

Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Поэтому все наши инструменты и сервисы абсолютно бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый из них строгому всестороннему тестированию. Однако, пожалуйста, сообщите нам, если вы заметите малейшую ошибку — ваш вклад чрезвычайно ценен для нас. Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран.

Мы получили ваше сообщение, мы свяжемся с вами в ближайшее время.

Ой! Что-то пошло не так, обновите страницу и повторите попытку.

10 Лучший калькулятор дробей | Обзоры и рейтинги 2022

Разнообразие доступных продуктов и услуг легко ошеломить. Вы можете запутаться во всех вариантах и не знать, чего хотите. Вот почему очень важно перед покупкой задать себе следующие вопросы:

Есть ли гарантия на товар?
Какова политика возврата этого продукта?
Доступна ли служба поддержки клиентов для этого продукта?
Где купить товар?
Сколько это стоит?

Если вы ответили утвердительно на все вопросы, то поздравляем! Вы нашли дробный калькулятор для вас! Но если нет, продолжайте читать, потому что мы предоставим больше полезной информации.

Цена

Часто люди покупают калькулятор дробей дешевле, чем следовало бы, потому что он продается со скидкой. Обычно это импульсивная покупка, и покупатель может не понимать всех последствий этого конкретного решения. Одна проблема заключается в том, что продукты, купленные дешево, обычно уступают более дорогим. Когда вы покупаете что-то дешевое, невозможно узнать, во что вы ввязываетесь, не потратив некоторое время на то, чтобы сначала изучить это!

Другая проблема с более доступными продуктами заключается в том, что они выходят из строя быстрее, чем качественные. В долгосрочной перспективе ремонт или замена этих элементов может стоить в два раза больше денег из-за их некачественного мастерства и недостатков дизайна. Чем дороже аутентичный продукт, тем он будет лучше. Это приводит к тому, что некоторые люди покупают продукты, которые они не могут себе позволить только из-за их цены, а другие решают ничего не покупать.

Компании, продающие отличные товары, должны сообщать, насколько более дешевая каждая покупка приведет к нематериальным выгодам и ощутимой экономии с течением времени. Следовательно, клиенты знают, во что они ввязываются, прежде чем принять окончательное решение о том, хотят ли они получить ваш товар по более высокой цене.

Качество

Качество продукта можно определить по способу его изготовления, материалам, используемым в производстве, и используемому процессу. Качественные продукты имеют более высокие стандарты, чем вредные продукты, а это означает, что они служат дольше и не так легко ломаются. Чтобы узнать, качественный ли продукт, следует посмотреть, из каких материалов он был изготовлен, как он был собран или изготовлен, а также есть ли отзывы других покупателей, которые его приобрели.

Если компания существует уже давно, она знает, что ее продукция должна быть высокого качества, иначе она не выживет. Иногда может быть трудно отличить калькулятор дробей от того, который стоит купить. Было бы полезно, если бы вы обращали внимание на многие вещи при покупке товара, но гарантия качества тоже имеет значение.

Гарантия качества означает, что продукты соответствуют определенным производственным стандартам, чтобы соответствовать ожиданиям клиентов в отношении конечного продукта. Просматривая товары на Amazon или в других интернет-магазинах, ознакомьтесь с их отзывами, прежде чем принимать решение о покупке. Если кто-то, купивший такую же вещь, как и вы, пожаловался на ее низкое качество, то, возможно, сначала подумайте о покупке в другом месте!

Отзывы покупателей

Не всегда легко понять, какой продукт подойдет именно вам. Есть так много вариантов, и может быть трудно сказать, какие из них стоят вашего времени. Я обнаружил, что лучший способ определить, хороший продукт или плохой, — это прочитать отзывы клиентов на таких сайтах, как Amazon, Facebook и Google. Эти страницы позволяют клиентам, которые использовали продукты раньше, высказать честное мнение о них другим потребителям, рассматривающим их варианты. Вам не нужно пробовать что-то лично — просто прочитайте, что говорят другие!

Гарантийная политика

Всегда лучше покупать товары стоимостью менее 500, 400, 200, 100 или 50 долларов с гарантией, потому что это дает вам душевное спокойствие. Вы всегда можете вернуть товар, если он не оправдает ваших ожиданий, и вам вернут ваши деньги, но только в том случае, если он находится в пределах гарантийного срока. Важно знать, как долго длится этот срок, прежде чем покупать продукт. Например, некоторые гарантии действуют в течение одного года, а другие — до трех и более лет, в зависимости от вашей услуги или покупки.

Если вы ищете отличное качество, не беспокоясь о таких вещах, убедитесь, что при покупке любого продукта стоимостью более 2000 долларов США доступна расширенная гарантия. Калькулятор дробей — это тот, который имеет хорошую гарантийную политику, чтобы убедиться, что вы защищены в случае, если что-то пойдет не так.

Оптимальный срок действия гарантии составляет в среднем около двух лет. Если он продлится дольше этого срока, вероятно, имеется проблема с качеством. Один из способов определить, какие продукты имеют лучшие гарантии и политики, — это просмотреть отзывы клиентов в Интернете.

Вы можете узнать, что люди говорят о своем опыте и чем они отличаются от других компаний. Чтение обзоров также поможет вам узнать, чего ожидать от вашего опыта, поэтому стоит потратить некоторое время, прежде чем совершать покупку!

Служба поддержки клиентов

Правильная политика обслуживания клиентов важна как никогда. Клиенты ищут отзывы о вашей компании и принимают решение о покупке, основываясь на том, что они думают о ваших продуктах и услугах, а также на том, что вы делаете, чтобы помочь им, если они недовольны своей покупкой.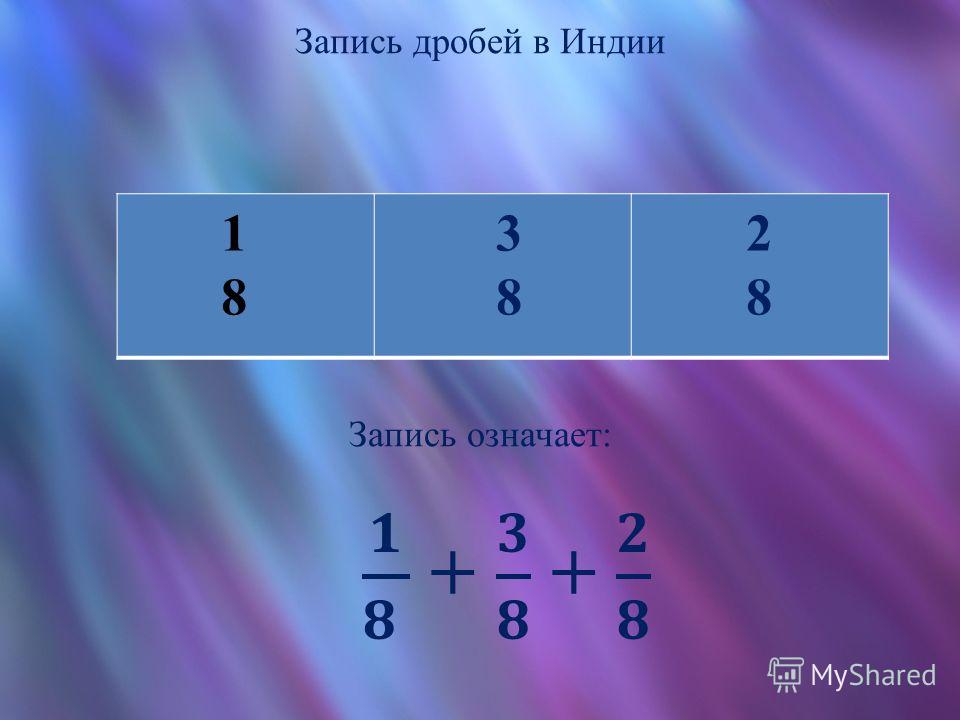 Если вы хотите, чтобы клиенты были довольны, пришло время позаботиться о них, внедрив некоторые или все эти пять лучших практик в свою стратегию обслуживания клиентов.

Общеизвестно, что качественная продукция требует отличного обслуживания клиентов. Однако стоит отметить, что это относится не только к самому продукту. Компания также должна быть отзывчивой и готова ответить на любые вопросы или опасения по поводу своего продукта с непредубежденностью и доброжелательным отношением. Чтобы представители службы поддержки клиентов могли эффективно выполнять свою работу, им нужны соответствующие инструменты для эффективной обработки ваших запросов.

Они могут варьироваться от телефонных звонков для заказов, размещенных по телефону, электронных писем для получения информации о том, когда ваша посылка будет доставлена или какой размер вы заказали, если она не подходит правильно, и т. д., до каналов социальных сетей, таких как Facebook или Twitter, где потенциальные клиенты могут связаться, прежде чем совершить покупку.

Правила возврата

Важно знать правила возврата перед покупкой продукта. Если товар неисправен или не работает, вы хотите вернуть свои деньги и купить что-то другое. Также полезно знать, понравится ли вам предмет или нет, поскольку все мы зря тратим деньги на вещи, которые нам в конечном итоге не понравились.

Существует несколько важных правил возврата, поэтому стоит ознакомиться с ними и прочитать обзоры продуктов, прежде чем покупать их. Лучшие компании всегда заботятся о своих клиентах, и они часто делают все возможное со своими гарантиями и гарантиями, делая возврат намного менее стрессовым, чем мог бы быть.

Узнать качество.

Желаете приобрести калькулятор дробей по минимально возможной цене? Поскольку доступно так много различных продуктов, определить, какой из них подойдет именно вам, непросто. На калькулятор фракций могут влиять несколько факторов, таких как ингредиенты, отзывы, корпоративная история, обслуживание клиентов и цена.

Чтобы товары с отличными оценками в каждой категории, попадающие в диапазон вашего бюджета, отображались при рассмотрении всех этих факторов, вы также должны учитывать свой бюджет. Самый важный аспект любой покупки — знать заранее, что вы покупаете, чтобы гарантировать высокое качество.

Проведение домашней работы перед покупкой — лучший способ сэкономить на продукте, который вам не подойдет. Убедитесь, что вы получаете качественный калькулятор дробей, который будет работать на вас, а не тот, который был признан «средним», прочитав обзоры или проведя обширное исследование. Пожалуйста, сделайте свое исследование, прежде чем покупать что-либо, чтобы не получить средний продукт!

Внимательно читайте обзоры

Количество вариантов, доступных людям, которые ищут калькулятор дробей до 1000, 500, 200, 100 или 50 долларов на Facebook или Reddit, может быть ошеломляющим. Отзывы помогают определить, подходит ли вам этот калькулятор дробей. Благодаря отзывам вам будет легче принять решение, если вы знаете, что об этом думают другие.

Покупая что-то новое, люди часто колеблются, потому что не уверены, как это повлияет на них, или потому что им нужны дополнительные предметы, чтобы эффективно использовать свою покупку. В этой ситуации могут быть полезны отзывы. Прежде чем совершить покупку, они могут дать представление о том, будет ли товар соответствовать вашим потребностям и ожиданиям, предотвращая угрызения совести покупателя в будущем.

Обзоры — это отличный способ узнать, как другие люди используют и думают о калькуляторе дробей. Вы должны прочитать каждый и рассмотреть, какие из них взяты из надежных источников. Если товар получил достаточно благоприятных отзывов, покупка его по сравнению с другим с сопоставимыми характеристиками или более высокими оценками может быть предпочтительнее.

Проверить рейтинг клиентов

Как говорится, «вы получаете то, за что платите». Может быть сложно решить, в какой из множества доступных продуктов стоит инвестировать наши деньги. Однако, если вы проведете некоторое исследование и получите доступ к некоторым отзывам клиентов, вы сможете решить, подходит ли вам продукт или нет.

Мы проведем вас через процесс поиска отзывов клиентов о любом продукте в Интернете, выполнив 3 простых шага, чтобы помочь вам.

Для начала введите название элемента в поле поиска Google. В большинстве случаев список лучших результатов от известных продавцов, таких как Amazon, Walmart или Target, должен отображаться как потенциальные совпадения.
Когда дело доходит до выбора калькулятора дробей до 1000 долларов, у вас есть много вариантов. Совершение покупки на основе отзывов клиентов является одним из наиболее важных решений.
Возможно, стоит подумать о покупке такого калькулятора для себя, если, например, кто-то говорит, что его калькулятор дробей имеет все нужные ему функции и дешевле, чем другие лучшие продукты в этой категории.

Изучите продукт перед его покупкой

Гарантия — это сервисное соглашение, которое защищает покупателя от дефектов продукта. Депозит либо включен в первоначальную покупку продукта, либо может быть получен при покупке расширенной гарантии.

Если компания, у которой вы покупаете, не предоставляет гарантии, возможно, стоит обратиться к другому поставщику, прежде чем совершать покупку.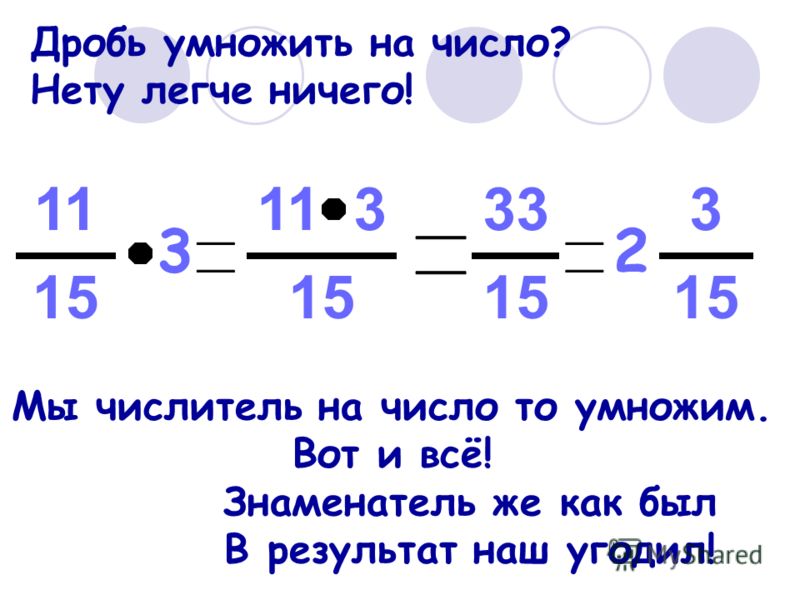 Прежде чем совершить онлайн-покупку, вы можете проверить веб-сайт компании, чтобы узнать больше о ее гарантиях.

Это позволит вам выяснить, предлагают ли они различные варианты или только один вариант для своих товаров и существуют ли какие-либо ограничения в отношении того, кто имеет право на этот контракт на обслуживание. Перед совершением важно знать об этих вещах.

Гарантия имеет решающее значение для многих людей, приобретающих калькулятор дробей. Годовой ограниченной гарантии производителя может быть достаточно, если вы хотите вернуть или заменить дефектный товар. Если ни один из этих вариантов вам не нужен, может быть достаточно более короткой и простой политики.

При проверке в Интернете в магазине, где вы планируете совершить покупку, внимательно прочитайте информацию о гарантии, чтобы узнать, какое покрытие будет предлагаться на вашу покупку, прежде чем она попадет к вам на порог.

Калькулятор дробей

Для правильного использования этого сайта вам необходимо включить javascript в вашем браузере!

Вы используете устаревший браузер . Пожалуйста обновите свой браузер, чтобы улучшить свой опыт.

Если ваша профессия требует выполнения множества операций с дробями, то эти приложения — то, что вам нужно для эффективной и быстрой работы. Какими бы ни были ваши потребности в расчете фракций, мы обеспечим вас.

Лучшие приложения

Приложения с наивысшим рейтингом в категории

Калькулятор фракций Plus

DigitAlchemy LLC

Калькулятор дробей Plus — лучшее и простое решение для дробей в повседневной жизни

Калькулятор дробей Plus — лучшее и простое решение для дробей в повседневной жизни. Вычислять дроби: складывать, вычитать, делить и умножать. Легко конвертируйте дроби в десятичные.

— Хотите проверить математические упражнения ваших детей? Теперь это больше не проблема, потому что вы можете просматривать дроби за считанные секунды.
— Вам нужно скорректировать количество рецептов для более длительного гостя…

Калькулятор фракций Plus #1

DigitAlchemy LLC

Калькулятор дробей Plus — лучшее и простое решение для дробей в повседневной жизни

Калькулятор дробей и прогресс

Chien Ming Chen

Простой в использовании калькулятор дробей

Простой в использовании калькулятор дробей. С процессом расчета

Калькулятор дробей можно использовать для проверки домашнего задания учащегося.
Формула только для справки, так как в разных регионах действуют разные алгоритмы.
Совершенно бесплатно.

Тоже хорошо

Приложения со средним баллом

Construction Master Pro Calc

Calculated Industries

БЕСПЛАТНАЯ пробная версия перед покупкой. Apple не взимает плату с вашей учетной записи Apple во время бесплатной пробной версии.

Сэкономьте время и уменьшите количество дорогостоящих ошибок во всех ваших работах с помощью отмеченного наградами и ведущего в отрасли калькулятора строителя Construction Master® Pro с дробью на футы и дюймы!

Уже более 30 лет портативный калькулятор Calculated Industries Construction Master…

БЕСПЛАТНО Подробнее

Мастер по строительству 5

Расчетные отрасли

Вот уже более 30 лет портативный калькулятор Calculated Industries Construction Master является надежным помощником лучших плотников и строителей по всей Северной Америке и за ее пределами.

Как…

БЕСПЛАТНО Подробнее

Мастер измерения Pro

Расчетные отрасли

Калькулятор преобразования фут-дюйм-дробей и метрических единиц от Calculated Industries®

Приложение Measure Master Pro от Calculated Industries дает вам возможность выполнять преобразование американских и метрических единиц на вашем iPhone или iPad.

Всегда получайте профессиональные результаты с помощью этого удобного и простого в использовании инструмента для проектов, связанных с измерениями.

Идеально подходит для дизайнеров, продавцов, столяров…

БЕСПЛАТНО Подробнее

jCalc – Калькулятор

Джон Эриксен

Простой. Мощный. Легко использовать. jCalc — это научный калькулятор, который имеет смысл.

Характеристики

Ввод дробей и десятичных знаков:
• [1] [.] [2] = 1,2
• [1] [н/д] [2] = 1/2
• [1] [н/д] [2] [Nn/d] [3] = 1_2/3

Формат ответа:
• 1–16 знаков после запятой
• Иррациональные, рациональные, десятичные и научные результаты
• Тригонометрические функции в радианах, градусах и градианах

Конвертировать …

БЕСПЛАТНО Подробнее

Научный калькулятор Elite

Cyberprodigy LLC

Scientific Calculator Elite™ — один из самых полных научных калькуляторов, доступных для iOS. Этот полнофункциональный научный калькулятор выглядит и работает как настоящий.

Ищете дроби? Преобразование единиц измерения и расчеты с размерными единицами? Без рекламы? Все это и многое другое можно найти с помощью Scientific Calculator Elite™.

Научный расчет…

$4,99 Подробнее

Калькулятор дробей Pro Plus

Елена Полянская

Лучший и самый простой способ решения повседневных проблем с дробями. Калькулятор дробей поможет вам проверить домашнее задание, поработать над проектом, скорректировать количество рецепта. Привлекательный и эффектный.

ОСОБЕННОСТИ:
— Проверка математических дробей занимает всего несколько секунд!
— Складывать, вычитать, умножать, делить дроби быстро и четко.
— Дисплей с тройной клавиатурой позволяет…

$0,99 Подробнее

Калькулятор футов и дюймов

Megabyte Software Inc.

• Преобразование измерений в дюймы, футы, ярды, метры, мили, километры, акры, квадратные футы, гектары, кубические футы, досковые футы и т.д.
• Ввод и вычисление футов, дюймов и дюймов в виде дробей
• Возможность округления дюймов до ближайших 1/32, 1/16, 1/8 и т. д.
• Сложение и вычитание измерений в различных единицах
• Полный калькулятор дробей: добавить,…

БЕСПЛАТНО Подробнее

Калькулятор дробей Pro

lindahl studios LLC

Fraction Calculator Pro – лучшее приложение в App Store для расчетов на основе дробей. Складывать, вычитать, умножать и делить, у нас есть все. В зависимости от результата приложение отображает ответ в виде неправильной и правильной дроби, а также десятичной дроби. Однако мы не загромождаем экран…

2,99 $ Подробнее

Калькулятор дробей + десятичные дроби

Visual Math Interactive Sdn. д.

Представляем первый в мире калькулятор дробей с дополнительными функциями, такими как сокращение или упрощение дробей, преобразование дробей в десятичные и калькулятор десятичных дробей в дроби. Все это в одном изящном приложении. Откройте для себя простой способ решения повседневных задач на дроби. Складывайте, вычитайте, умножайте, делите и даже преобразовывайте дроби быстро и четко. Калькулятор дробей Visual Math Interactive…

БЕСПЛАТНО Подробнее

Расчет дробей от PalaSoftware

PalaSoftware Inc.

Калькулятор дробей ведет себя точно так же, как калькулятор, за одним исключением: вы работаете с дробями. Так что теперь, когда домашняя работа (конечно, проверка) требует дробей, или ваш столярный проект требует, чтобы вы прибавляли восьмые и шестнадцатые десятки раз, или, может быть, вы просто хотите иметь возможность…

0,99 $ Подробнее

дюймCALC+

River Studio

ПРОФЕССИОНАЛЬНЫЙ УРОВЕНЬ [ФУТ • ДЮЙМ • ДОЛЯ] КАЛЬКУЛЯТОР

MACWORLD **** «Простота использования inchCALC+ в сочетании с его расширенными функциями делает его необычайно хорошим дополнением к переполненному жанру». 3/9/09

inchCALC+ — современный строительный калькулятор / конвертер для людей, которые работают с размерами в ФУТАХ• ДЮЙМАХ• Дробях, используемых на…

4,99 $ Подробнее

ArchiCalc

Томас Боеман

ArchiCalc — калькулятор размеров для архитекторов и строителей. Он разработан, чтобы сделать работу с британскими и метрическими размерами плавной и легкой. Разработанный архитектором для архитекторов, ArchiCalc работает естественным интуитивно понятным способом с числами, длинами, площадями и объемами. Метрические и имперские единицы можно складывать вместе…

$3,99 Подробнее

ConcreteCalc Pro

Расчетные отрасли

Advanced Concrete Construction-Math Calculator от Calculated Industries

Официальный ConcreteCalc Pro от Calculated Industries теперь доступен для пользователей iPhone и iPad. И хотя это, возможно, очевидно, если вы перейдете с устройства iOS на устройство, отличное от iOS, вам НУЖНО будет купить новую лицензию, поскольку они несовместимы.

Помогает бетону,…

39,99 $ Подробнее

Справка по дробям

Дэвид Кэдди

Облегчает решение и изучение дробей!

Справка по дробям — это калькулятор дробей и образовательный инструмент, который позволяет быстро решать задачи с дробями.

Особенности:

— Точное решение уравнений дробей (сложение, вычитание, умножение и деление)
— Просмотр подробной работы, чтобы узнать, как был определен окончательный ответ*
— Работа со смешанными/частичными…

БЕСПЛАТНО Подробнее

Калькулятор дробей 4 в 1

Intemodino Group s.r.o.

Все, что вам нужно для преобразования, расчета, упрощения и сравнения дробей в одном приложении!

Конвертер дробей и калькулятор идеально подходит для инженеров, плотников, строителей, студентов и всех, кому нужно комплексное приложение для дробей.

► ПРЕОБРАЗОВАТЕЛЬ Дробей
— Преобразует дроби в десятичные и наоборот.
— Поддерживает правильные и неправильные дроби, смешанные числа, завершающие и повторяющиеся…

$3,99 Подробнее

Калькулятор дробей

xNeat.com

Отмеченный наградами калькулятор дробей футов и дюймов и конвертер метрических единиц для iPhone и iPad. Разработан с учетом простоты, удобства и красоты!

ХАРАКТЕРИСТИКИ:

— Элегантный и интуитивно понятный интерфейс
— Преобразователь десятичной дроби в дробную
— Преобразование дробной части в десятичную
— Одновременное отображение уравнения и результата
— Расширенное редактирование с помощью простого возврата. ..

БЕСПЛАТНО Подробнее

Калькулятор фракций

Essence Computing

Вам трудно вычислять дроби? Вам нужна помощь в понимании того, как складывать, вычитать, делить и умножать дроби? Ну, если вы это сделаете, то это приложение для вас. Он не только вычисляет для вас ответы, но и всесторонне объясняет, как был получен ответ….

0,99 $ Подробнее

FraCa (калькулятор дробей)

Thomas Burow

FraCa — калькулятор дробей.

FraCa обеспечивает вычисления с использованием сложения, вычитания, умножения и деления. Кроме того, возможно сокращение фракций. Можно использовать обыкновенные дроби и смешанные числа.

Кроме того, FraCa обеспечивает расчет со скобками и простую функцию памяти.

БЕСПЛАТНО Подробнее

HeavyCalc Pro

Расчетные отрасли

Ярд, фут-дюйм-дробь, метрическая математика для тяжелого строительства от Calculated Industries®

Официальный Heavy Calc Pro от Calculated Industries теперь доступен для пользователей iPhone и iPad.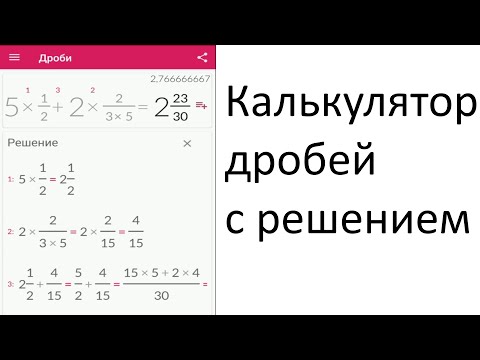 И хотя это, возможно, очевидно, если вы перейдете с устройства iOS на устройство без iOS, вам НУЖНО будет купить новую лицензию, поскольку они…

$39,99 Подробнее

Fractions Pro

Intemodino Group s.r.o.

Получите универсальный многофункциональный калькулятор с дробями, предназначенный для выполнения математических, инженерных, научных и технических расчетов любой сложности. Мощный, простой в использовании и хорошо продуманный усовершенствованный калькулятор дробей позволяет выполнять вычисления с правильными и неправильными дробями, смешанными числами, десятичными и целыми числами. Благодаря новой улучшенной конструкции, добавлены…

$4,99 Подробнее

Калькулятор дробей с шагами

Intemodino Group s.r.o.

Калькулятор дробей с шагами поможет вам быстро решить домашние задачи или проверить свои результаты.

Калькулятор дробей выполняет основные операции с дробями, смешанными числами и целыми числами.

Особенности:
• Калькулятор дробей для двух и трех дробей.
• Основные вычисления: сложение, вычитание, умножение и деление.
• Поддерживает дроби, смешанные числа и целые числа.
•…

1,99 $ Подробнее

Калькулятор дробей Lite

Corporate Smalltalk Consulting Ltd

5 3/16 + (12,11 — 1/8)*2,0 = 11663/400

Чтобы получить ответ, который вы можете представить как 29 63/400 или 29,1575

Калькулятор дробей — это калькулятор дробей, который выполняет смешанные или целые дроби и десятичная арифметика с поддержкой скобок «(«. Это покрывает большую часть работы, которую вам нужно сделать…

БЕСПЛАТНО Подробнее

Другие приложения

Может подойти для особых случаев

Строительный калькулятор

xNeat.com

Удостоенный наград строительный калькулятор для iPhone и iPad. Разработан с учетом простоты, удобства и красоты!

ХАРАКТЕРИСТИКИ:

Идеально подходит для тех, кто работает в строительстве, деревообработке и для студентов, чтобы проверить свою домашнюю работу!

Если вам нужны более продвинутые функции, вы можете перейти на одну или несколько из следующих:

— Расчет лестниц
— Расчет стропил
— Работа и преобразование между всеми размерными форматами здания: футы-дюймы-доли, дюймы-доли , ярды, десятичные футы (10-е, 100-е), десятичные дюймы и метрические единицы (км, м, см, мм)
— Несколько тем на выбор

Наслаждайтесь БЕСПЛАТНЫМ калькулятором дробей без рекламы и подсказок. Если вам это нравится, поддержите нас, обновив приложение или оставив положительный отзыв.

Спасибо 🙂

Калькулятор дробей XL

Intemodino Group s.r.o.

Лучшее приложение для понимания, изучения, преподавания и вычисления дробей!

Калькулятор дробей XL — это простой в использовании калькулятор дробей с пошаговыми инструкциями, которые позволяют быстро решать задачи с дробями и значительно облегчают изучение дробей.
Калькулятор дробей XL поможет вам быстро решить домашние задания или проверить свои результаты.

Калькулятор дробей с шагами выполняет основные операции с дробями, смешанными числами и целыми числами.

Особенности:

• Калькулятор дробей для арифметических операций с двумя, тремя, четырьмя, пятью и шестью дробями.

• Показывает подробности расчета.

• Основные расчеты: сложение, вычитание, умножение и деление.

• Поддерживает дроби, смешанные числа и целые числа.

• Поддерживает отрицательные значения.

• Лента истории для просмотра последних вычислений.

• Кнопки «Назад» и «Вперед» для проверки или вызова последних расчетов.

• Отправляет результаты и историю по электронной почте.

• «Отменить» для команды «Очистить».

Дробь — калькулятор дробей

Клинт Ньюсом

Калькулятор, который вам всегда был нужен, но никогда не был у вас. Калькулятор дробей складывает, вычитает, умножает и делит дроби, так что вам не нужно конвертировать, но если вам нужно преобразовать в десятичные дроби или просто нужен обычный калькулятор, дробь тоже это сделает! Переключайте режимы для преобразования футов и дюймов в футы или дюймы и даже метры или миллиметры. С дробью вы можете переключаться между четырьмя различными калькуляторами. Первая страница приложения представляет собой калькулятор дробей. Вторая страница представляет собой стандартный калькулятор. Третья страница, перевернутая в альбомную ориентацию, представляет собой калькулятор целых чисел и дробей, поэтому вы можете рассчитать все свои измерения и дробные потребности. Четвертая страница напоминает рулетку (не в масштабе) с прокруткой измерений до одного дюйма, так что вы можете считать, как если бы вы это делали с рулеткой. Все страницы функционируют как преобразование единиц измерения с возможностью преобразования дробей в десятичные, футы и дюймы, только футы, только дюймы, метры и миллиметры. Каждая страница также предназначена для удобного и эргономичного использования с учетом ваших потребностей.

Калькулятор простых дробей

Intemodino Group s.r.o.

Удобный калькулятор, который поможет вам сократить дроби и смешанные числа.

Особенности:
Сокращает дроби до наименьших значений.
Поддерживает правильные и неправильные дроби и смешанные числа.
Подробные результаты.
Находит наибольший общий делитель (НОД) числителя и знаменателя.
Разложение числителя и знаменателя на простые множители.
Сохраняет список истории.
Отправляет результаты и историю по электронной почте.

Решатель систем уравнений

Intemodino Group s. r.o.

Калькулятор решает системы линейных уравнений с двумя и тремя переменными.

• Системный решатель 2×2
Решает системы двух линейных уравнений с двумя переменными путем подстановки или с использованием правила Крамера.

• Системный решатель 3×3
Решает системы из трех линейных уравнений с тремя переменными с использованием правила Крамера.
Для решения систем уравнений 3×3 необходимо выбрать альбомную ориентацию.

Особенности:
Показывает пошаговое решение.
Поддерживает целые, дробные и десятичные коэффициенты.
Показывает результаты в виде десятичных и дробных чисел.
Сохраняет историю с возможностью вызова предыдущих уравнений.
Отправляет результаты и историю по электронной почте.
Поддерживает книжную и альбомную ориентацию.

Калькулятор дробей — удобный математический помощник

ROMAN GAL

Хотите улучшить свои школьные оценки? Используйте его сейчас, потому что это абсолютно бесплатно! Мы представляем вам отличную функциональность с отличным дизайном, потому что нам нравится разрабатывать простые и мощные приложения.

Не стесняйтесь писать отзыв, нам нужно ваше мнение.

Калькулятор дробей

Студия серых карт

Калькулятор дробей вычисляет простые и сложные задачи с дробями.
Вы можете комбинировать правильные и неправильные дроби, смешанные числа и десятичные дроби в одной операции.
Вы можете ввести до десяти членов (дробных, целых или десятичных дробей) в свой расчет, каждый из которых может содержать до 3 цифр.
В случае ошибки можно удалить любую цифру в целом числе, числителе или знаменателе и ввести правильную.
Калькулятор сначала выполняет умножение и деление, а затем сложение и вычитание. Это гарантирует, что проблемы с большим количеством членов будут правильно рассчитаны.
Результаты больше 1 отображаются в виде смешанного числа, неправильной дроби и десятичного числа. Результаты меньше 1 отображаются в виде правильной дроби и десятичного числа.
Вводить дроби легко: у вас есть специальная клавиатура для целых чисел, числителя и знаменателя!
Это приложение оптимизировано для iPhone 5, iPhone 6 и iPhone 6 Plus.

Как переводить дробные числа в десятичные. Калькулятор онлайн.Перевод десятичной дроби в обыкновенную

Правильные и неправильные дроби. Смешанные числа

Действия с дробями. Сложение дробей.

Сложение смешанных дробей

Вычитание дробей (дробных чисел)

Умножение дробей

Деление дробей

Перевод путем деления

Перевод процентов

Способы преобразования дроби в число

Сокращение дробей с корнями онлайн калькулятор.

Что значит «сократить дробь «?

Как сократить дробь. Правила сокращения дробей (6 класс)

Как сократить неправильную дробь?

Сокращение смешанных дробей

Сокращение дробей, определение и формула.

Как сокращать дроби? Сокращение дроби до несократимого вида.

Правило сокращения дроби до несократимого вида.

Сокращение неправильной дроби.

Сокращение смешанных дробей.

Правильные и неправильные дроби.

Действия с дробями. Сложение дробей.

Сложение смешанных дробей

Вычитание дробей (дробных чисел)

Умножение дробей

Деление дробей

Таблица квадратов натуральных чисел | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

фракций | Justfreetools

Пример сложения дробей

Пример вычитания дробей

Пример умножения дробей

Пример деления дробей

10 Лучший калькулятор дробей | Обзоры и рейтинги 2022

Цена

Качество

Отзывы покупателей

Гарантийная политика

Служба поддержки клиентов

Правила возврата

Узнать качество.

Внимательно читайте обзоры

Проверить рейтинг клиентов

Изучите продукт перед его покупкой

Калькулятор дробей

Лучшие приложения

Калькулятор фракций Plus

Калькулятор фракций Plus #1

Калькулятор дробей и прогресс

Тоже хорошо

Construction Master Pro Calc

Мастер по строительству 5

Мастер измерения Pro

jCalc – Калькулятор

Научный калькулятор Elite

Калькулятор дробей Pro Plus

Калькулятор футов и дюймов

Калькулятор дробей Pro

Калькулятор дробей + десятичные дроби

Расчет дробей от PalaSoftware

дюймCALC+

ArchiCalc

ConcreteCalc Pro

Справка по дробям

Калькулятор дробей 4 в 1

Калькулятор дробей

Калькулятор фракций

FraCa (калькулятор дробей)

HeavyCalc Pro

Fractions Pro

Калькулятор дробей с шагами

Калькулятор дробей Lite

Другие приложения

Строительный калькулятор

Калькулятор дробей XL

Дробь — калькулятор дробей

Калькулятор простых дробей

Решатель систем уравнений

Калькулятор дробей — удобный математический помощник

Калькулятор дробей

Добавить комментарий Отменить ответ