Калькулятор онлайн градиент функции: Градиент функции онлайн

Содержание

Калькулятор Градиента — Mathcracker.Com

Инструкции: Используйте этот калькулятор градиента, чтобы вычислить вектор частных производных для многомерной функции, которую вы предоставляете, показывая все шаги. Пожалуйста, введите многопараметрическую функцию в форму ниже.

Калькулятор градиента

Этот калькулятор градиента с шагами поможет вам найти вектор градиента данной многомерной функции, которую вы предоставляете. Эта функция должна быть допустимой, дифференцируемой функцией с 2 или более переменными.

Предоставляемая вами функция должна сопровождаться полным определением имени переменной и функции, например f(x, y) = x^2 + y^2 или f(x,y,z) = xy+z*sin. (ху) и т. д.

Как только действительная функция с несколькими переменными предоставлена, все, что осталось сделать, это нажать кнопку «Рассчитать», чтобы получить все показанные шаги.

Градиенты представляют собой естественное расширение производных для ситуации с несколькими переменными, в которой скорость изменения лучше определяется вектором, чем числом.

Что такое градиент

Проще говоря, градиент — это вектор, содержащий все частные производные первого порядка функции многих переменных \(f\). Тогда для функции двух переменных \(f(x, y)\) ее градиент будет двумерным вектором \(\nabla f(x, y) = \displaystyle \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right)\).

Точно так же для функции трех переменных \(f(x, y, z\) ее градиентом будет трехмерный вектор \(\nabla f(x, y, z) = \displaystyle \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\right)\) и так далее.

Шаги для вычисления градиента

Шаг 1: Определите функцию f, с которой вы хотите работать, и укажите количество задействованных переменных.

Шаг 2: Найдите первый заказ Частичная производная по каждой из переменных
Шаг 3: Создайте градиент как вектор, который содержит все частные производные первого порядка, найденные на шаге 2.

При желании вы можете упростить, если это возможно, после завершения шага 3. Затем с помощью градиента у вас есть версия того, что является производной для одномерной функции, в данном случае для многомерной функции.

Применение градиента

Так же, как и в случае одномерных функций при поиске критических точек нам нужно найти точки, в которых производная равна нулю, для многомерных функций нам нужно искать точки, в которых градиент равен нулю, чтобы найти критические точки.

Кроме того, эквивалент тестов второй производной представлен в виде правила Гессе для многомерных функций.

Советы и рекомендации

Помните, что Градиент определяется для многомерных функций с двумя или более переменными. 2 \) равен:

\[ \nabla f = \left(2x,2y,2z\right)\]

Пример расчета градиента

Для следующей функции: \(f(x, y) = xy\) найдите ее градиент.

Отвечать: Для этого примера у нас есть функция двух переменных x и y: \(\displaystyle f(x,y)=xy\).

Во-первых, дифференцируя по x

\( \displaystyle \frac{\partial }{\partial x}\left(xy\right)\)

Поскольку это постоянное время \(x\), мы сразу получаем: \(\frac{\partial }{\partial x}\left( xy \right) = y\)

\( \displaystyle = \,\,\)

\(\displaystyle y\)

Теперь продифференцируем по y

\( \displaystyle \frac{\partial }{\partial y}\left(xy\right)\)

Поскольку это постоянное время \(y\), мы сразу получаем: \(\frac{\partial }{\partial y}\left( xy \right) = x\)

\( \displaystyle = \,\,\)

\(\displaystyle x\)

Заключение: Непосредственно получаем, что градиент функции \(\displaystyle f(x,y)=xy \) равен:

\[ \nabla f = \left(y, x\right)\]

Еще примеры градиентов

Вычислите соответствующий градиент \( f(x, y) = x^2 — y^2 — xy \). 2-xy \) равен:

\[ \nabla f = \left(2x-y,-x-2y\right)\]

Другие производные калькуляторы

Используя производный калькулятор определенно может облегчить вашу жизнь, поскольку позволит вам отслеживать все Правила производных .

Большинство из правила дифференциации используемые для одномерных функций, имеют эквивалент для многомерных функций. Таким образом, Правило цепи , Правило Продукта а также правило квоты также будет работать для многомерной функции, учитывая правильные размеры.

Калькуляторы

Общие калькуляторы

Расчет содержания вещества в растворе (пересчет процентов в граммы)

Расчет количества дней между двумя датами

Расчет эквивалентных доз глюкокортикостероидов

Калькулятор расчета дефицита калия и объема растворов для его возмещения

Расчет скорости инфузии препарата через линеомат (скорость титрования)

Тест Фагерстрема — оценка степени никотиновой зависимости

Профессиональный калькулятор расчета времени выведения алкоголя

Калькулятор расчета индекса курения

Калькулятор расчета дефицита натрия и объема растворов для его возмещения

Калькулятор расчета площади поверхности тела

Калькулятор расчета скорости внутривенного капельного введения препарата

Калькулятор расчета времени выведения алкоголя и концентрации в крови

Акушерство

Шкала оценки состояния новорожденного

Определение степени зрелости шейки матки

Определение предполагаемой даты родов

Биофизический профиль плода

Оценка наличия и тяжести гипоксии плода в антенатальный период

Догоспитальная оценка степени тяжести гестоза

Оценка наличия и тяжести гипоксии плода в антенатальный период

Оценка степени тяжести нефропатии при гестозах

Анестезиология и реаниматология

Интерпретация кислотно-щелочного состояния крови

Шкала для оценки пробуждения пациента после анестезиологического пособия

Расчет альвеолярно-артериального градиента

Измерение степени тяжести пациентов в ОРИТ

Расчет объема инфузионной терапии при ожогах

Шкала Кормака–Лехана — классификация структур гортани

Шкала клинической оценки инфекций легких

Система оценки риска трудной интубации

Градация глубины комы у интубированных больных

Шкала оценки глубины коматозных состояний

Расчет риска кардиальных осложнений в некардиальной хирургии

Соотношение введенной и выделенной организмом жидкости

Калькулятор расчета дефицита калия и объема растворов для его возмещения

Оценка риска развития дессиминированного внутрисосудистого свертывания

Оценка степени нарушения сознания и комы

Оценка выраженности повреждений легких

Оценка трудности интубации трахеи по анатомическим ориентирам

Шкала вероятного анестезиологического риска перед оперативным лечением

Шкала оценки полиорганной дисфункции Маршалла

Оценка тяжести состояния пациентов с COVID-19

Динамическая оценка послеоперационной боли у детей от 8 мес до 13 лет

Оценка функции обмена кислорода в легких

Расчет объема инфузионной терапии при ожогах по Паркланду

Оценка состояния после пробуждения от наркоза

Шкала возбуждения-седации Ричмонда

Шкала оценки риска интраоперационных сердечно-сосудистых осложнений

Калькулятор расчета дефицита натрия и объема растворов для его возмещения

Оценка органной недостаточности, риска смертности и сепсиса в ОРИТ

Гастроэнтерология

Шкала бальной оценки (диагностические критерии) аутоиммунного гепатита

Индекс активности болезни Крона (Crohn’s Disease Activity Index, CDAI, индекс Беста)

Объективизация клинической оценки степени дегидратации при ОКИ

Оценка тяжести цирроза печени и выживаемости пациента

Шкала для оценки тяжести течения заболевания у детей с гастроэнтеритом

Оценка терминальных стадий заболеваний печени и прогноза жизни

Педиатрический индекс активности болезни Крона (Pediatric Crohn’s Disease Activity Index, PCDAI)

Шкала для оценки тяжести течения острого гастроэнтерита

Гериатрия

Шкала оценки уровня повседневной активности и нуждаемости в уходе

Шкала для диагностики сосудистой деменции

Шкала оценки психоэмоционального состояния пожилого человека

Методика оценки индивидуальной потребности в социальных услугах

Шкала оценки возможности выполнения сложных действий

Шкала оценки вероятности риска падения

Шкала оценки риска развития пролежней у пациента

Кардиология

Оценка риска раннего развития инсульта после перенесенной ТИА

Расчет корригированного интервала QT

Расчет риска инсульта при фибрилляции и трепетании предсердий

Расчет риска кровотечения у пациентов с ОКС без подъема ST

Оценка риска антитромбоцитарной терапии после стентирования

Оценка десятилетнего риска инсульта при сердечно сосудистых заболеваниях

Риск летальности и развития инфаркта миокарда на госпитальном этапе

Оценка риска большого кровотечения при мерцательной аритмии

Оценка шести недельного риска серьезного кардиального события

Оценка риска большого кровотечения при фибрилляции предсердий

Оценка фатального риска при сердечно-сосудистых заболеваниях

Расчет среднего артериального давления

Расчет массы миокарда левого желудочка по данным эхокардиографии

Оценка риска антитромбоцитарной терапии во время коронарного стентирования

Оценка риска большого кровотечения у стабильных пациентов с атеросклерозом

Оценка возможности достижения антикоагуляции при применении варфарина

Оценка фатального риска при сердечно-сосудистых заболеваниях

Дифференциальная диагностика патологической элевации сегмента ST

Оценка риска инфаркта и смерти при ОКС без подъема сегмента ST

Неврология

Оценка риска раннего развития инсульта после перенесенной ТИА

Шкала оценки риска развития пролежней у пациента

Расчет риска инсульта при фибрилляции и трепетании предсердий

Опросник для определения нарушений сна: бессоницы, апноэ, нарколепсии

Оценка десятилетнего риска инсульта при сердечно сосудистых заболеваниях

Шкала для диагностики сосудистой деменции

Оценка локомоторной функции пациента

Оценка риска хирургической летальности при нетравматическом САК

Шкала самооценки бытовых возможностей повседневной жизни

Шкала оценки риска развития пролежней у пациента

Шкала для оценки состояния больного рассеянным склерозом

Оценка инвалидности и исходов реабилитации после инсульта

Шкала для планирования тромболитической терапии при ишемическом инсульте

Нефрология

Оценка риска развития контраст-индуцированной нефропатии

Расчет фракционной экскреции натрия и оценка типа олигоурии

Калькулятор расчета адекватности проведенного гемодиализа

Расчет скорости клубочковой фильтрации у взрослых

Расчет скорости клубочковой фильтрации у детей

Оценка степени тяжести нефропатии при гестозах

Онкология

Шкала оценки общего состояния онкологического больного

Шкала оценки общего статуса онкологического больного

Стратификация риска ВТЭО у онкологических пациентов

Оценка риска кровотечения

Расчет риска кровотечения у пациентов с ОКС без подъема ST

Оценка риска большого кровотечения при мерцательной аритмии

Оценка риска большого кровотечения при фибрилляции предсердий

Оценка риска развития кровотечения согласно рекомендациям ISTH

Оценка риска развития дессиминированного внутрисосудистого свертывания

Оценка риска большого кровотечения у стабильных пациентов с атеросклерозом

Определение риска при кровотечениях из верхних отделов ЖКТ

Оценка вероятности ТЭЛА

Оценка риска развития ВТЭО у пациентов хирургического профиля

Индекс Geneva — оценка вероятности развития ТЭЛА

Оценки риска тромбоэмболии глубоких вен и ТЭЛА у нехирургических больных

Прогноз риска венозной тромбоэмболии при госпитализации

Стратификация риска ВТЭО у онкологических пациентов

Выявление риска ТГВ и ТЭЛА в стационаре у нехирургических больных

Оценка риска 30-ти дневной летальности у пациентов с ТЭЛА

Wells Criteria — оценка вероятности развития ТЭЛА

Педиатрия

Расчет площади ожоговой поверхности у детей по таблице Лунда и Браудера

Рейтинговая шкала аутизма у детей для первичного скрининга

Объективизация клинической оценки степени дегидратации при ОКИ

Шкала для оценки тяжести течения заболевания у детей с гастроэнтеритом

Шкала для определения выраженности боли у новорожденных

Шкала для оценки острой и хронической боли у новорожденных по внешним признакам

Шкала для оценки тяжести респираторных нарушений у новорожденных

Поведенческая шкала оценки боли у младенцев и детей до 7 лет

Динамическая оценка послеоперационной боли у детей от 8 мес до 13 лет

Педиатрический индекс активности болезни Крона (Pediatric Crohn’s Disease Activity Index, PCDAI)

Шкала для оценки тяжести респираторных нарушений у недоношенных

Расчет скорости клубочковой фильтрации у детей

Шкала для оценки тяжести течения острого гастроэнтерита

Психиатрия

Скрининговая шкала оценки наличия и уровня депрессии

Рейтинговая шкала аутизма у детей для первичного скрининга

Шкала оценки тяжести алкогольного абстинентного синдрома

Предварительная оценка тревожных расстройств

Скрининг тревоги и депрессии у пациентов стационара

Шкала количественной оценки динамики депрессивных проявлений

Шкала оценки психоэмоционального состояния пожилого человека

Проведение диагностики наличия и тяжести депрессии

Шкала оценки уровня реактивной и личностной тревожности Спилберга-Ханина

Определение выраженности маниакальных симптомов

Реабилитология

Шкала оценки уровня повседневной активности и нуждаемости в уходе

Оценка уровня боли у неконтактного пациента

Шкала оценки риска развития пролежней у пациента

Оценка локомоторной функции пациента

Методика оценки индивидуальной потребности в социальных услугах

Шкала оценки возможности выполнения сложных действий

Шкала самооценки бытовых возможностей повседневной жизни

Шкала оценки вероятности риска падения

Шкала оценки риска развития пролежней у пациента

Оценка инвалидности и исходов реабилитации после инсульта

Индекс мобильности — клиническая оценкя мобильности пациента

Шкала оценки риска развития пролежней у пациента

Рентгенология

Расчет индекса вымывания контраста из надпочечников при КТ исследовании

Расчет эффективной эквивалентной дозы облучения при КТ исследовании

Спорт

Калькулятор полного максимума — макс. вес штанги в одном повторении

Количество повторений с определённым весом при известном полном максимуме

Расчет веса при заданном количестве повторений

Расчет значения, для сравнения поднятых весов спортсменов с разным весом

Терапия

Индекс активности болезни Крона (Crohn’s Disease Activity Index, CDAI, индекс Беста)

Шкала клинической оценки инфекций легких

Оценка степени тяжести внебольничной пневмонии

Оценки риска тромбоэмболии глубоких вен и ТЭЛА у нехирургических больных

Прогноз риска венозной тромбоэмболии при госпитализации

Альгофункциональный индекс Лекена — оценка степени тяжести остеоартозов

Оценка выраженности повреждений легких

Оценка тяжести состояния пациентов с COVID-19

Выявление риска ТГВ и ТЭЛА в стационаре у нехирургических больных

Шкала определения тяжести внегоспитальной пневмонии

Выявление пациентов с тяжелой внебольничной пневмонией

Физиология

Расчет базового обмена веществ — количества сжигаемых калорий

Расчет идеального веса по формуле Брока

Расчет количества калорий расходуемых при ходьбе

Калькулятор расчета индексов центрального ожирения

Расчет идеального веса по формуле Devine

Расчет идеального веса по таблице Егорова Левитского

Соотношение введенной и выделенной организмом жидкости

Онлайн калькуляторы для расчета идеального веса

Расчет индекса массы тела

Калькулятор расчета индекса Кетле

Расчет идеального веса по формуле Лоренца

Калькулятор расчета процента жира в организме

Хирургия

Расчет площади ожоговой поверхности у детей по таблице Лунда и Браудера

Расчет объема инфузионной терапии при ожогах

Оценка риска развития ВТЭО у пациентов хирургического профиля

Расчет объема инфузионной терапии при ожогах по Паркланду

Шкала оценки тяжести состояния больных с острым панкреатитом

Определение риска при кровотечениях из верхних отделов ЖКТ

Калькулятор градиента — MathCracker.

2 или f(x,y,z) = xy+z*sin(xy) и т. д.

После того, как действительная функция с несколькими переменными предоставлена, все, что осталось сделать, это нажать кнопку «Рассчитать», чтобы получить все показанные шаги.

Что такое градиент

Проще говоря, градиент — это вектор, содержащий все частные производные первого порядка функции многих переменных \(f\). Итак, для функции две переменные \(f(x, y)\), его градиент будет двумерным вектором \(\nabla f(x, y) = \displaystyle \left(\frac{\partial f}{\partial x} , \frac{\partial f}{\partial y}\right)\).

Аналогично, для функции трех переменных \(f(x, y, z\), его градиент будет трехмерным вектором \(\nabla f(x, y, z) = \displaystyle \left(\frac{\partial f}{\ частичный х}, \ гидроразрыв {\ парциальное е} {\ парциальное у}, \frac{\partial f}{\partial z}\right)\) и так далее.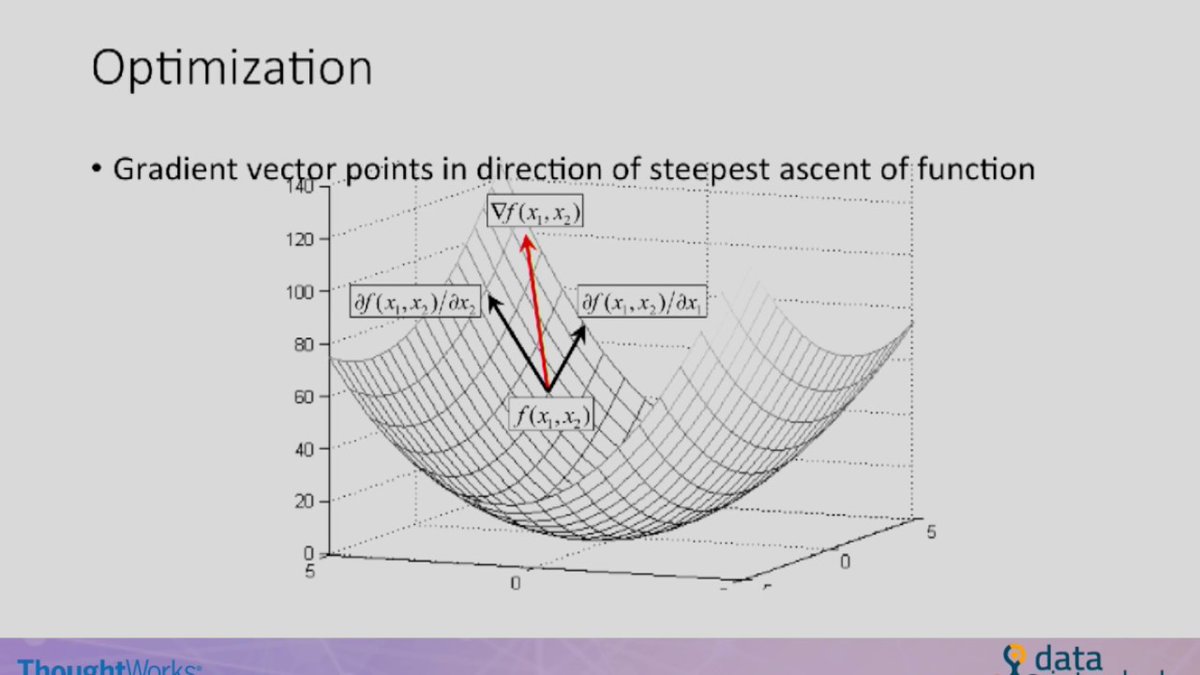

Шаги для вычисления градиента

Шаг 1: Определите функцию f, с которой вы хотите работать, и укажите количество задействованных переменных
Шаг 2: Найти частную производную первого порядка по каждой из переменных
Шаг 3: Построить градиент как вектор, содержащий все частные производные первого порядка, найденные на шаге 2

При желании вы можете упростить, если это возможно, после выполнения шага 3. Затем с градиентом у вас есть версия того, что является производной для одномерной функции, в данном случае для многомерной функции.

Применение градиента

То же, что и в случае одномерных функций, при поиске критических точек нужно найти точки, в которых производная равна нулю, для многомерных функций нам нужно искать точки, в которых градиент равен нулю, чтобы найти критические точки.

Кроме того, эквивалент тестов второй производной представлен в форме правила Гессе для многомерных функций.

Советы и рекомендации

Помните, что градиент определяется для многомерных функций с двумя или более переменными. Кроме того, имейте в виду, что градиент является вектором, где каждый из компонентов является функцией. Точнее, каждая его компонента является частной производной первого порядка. 92\) равно:

\[ \nabla f = \left(2x,2y,2z\right)\]

Пример вычисления градиента

Для следующей функции: \(f(x, y) = xy\) найдите ее градиент.

Решение: В этом примере у нас есть функция двух переменных x и y: \(\displaystyle f(x,y)=xy\).

Сначала дифференцируем по x

\( \displaystyle \frac{\partial }{\partial x}\left(xy\right)\)

Так как это постоянное время \(x\) , мы сразу получаем: \(\frac{\partial }{\partial x}\left( xy \right) = y\)

\( \displaystyle = \,\,\)

\(\displaystyle y\)

Теперь выполним дифференцирование по y

\( \displaystyle \frac{\partial }{\partial y} \left(xy\right)\)

Поскольку это константа, умноженная на \(y\), мы напрямую получаем: \(\frac{\partial }{\partial y}\left( xy \right) = x\ )

\( \displaystyle = \,\,\)

\(\displaystyle x\)

Вывод: Непосредственно получаем, что градиент функции \(\displaystyle f(x,y)=xy \) равно: 92-ху \) равно:

\[ \nabla f = \left(2x-y,-x-2y\right)\]

Другие калькуляторы производных

Использование калькулятора производных определенно может облегчить вашу жизнь, так как позволит отслеживать всех производных правил.

Большинство правил дифференцирования, используемых для одномерных функций, имеют эквиваленты для многомерных функций. Сюда, цепное правило, правило произведения и правило частного также будут работать для многовариантная функция с учетом правильных размеров.

Нахождение градиента векторной функции | by Chi-Feng Wang

Часть 3 книги «Шаг за шагом: математика за нейронными сетями»

Заглавное изображение: Источник

В части 1 нам дали задачу: вычислить градиент этой функции потерь:

Изображение 1 : Функция потерь

Чтобы найти градиент, мы должны найти производную функции. Во второй части мы научились вычислять частную производную функции по каждой переменной. Однако большинство переменных в этой функции потерь являются векторами. Возможность найти частную производную векторных переменных особенно важна, поскольку нейронная сеть имеет дело с большими объемами данных. Векторные и матричные операции — это простой способ представления операций с таким большим количеством данных. Как именно можно найти градиент векторной функции?

Градиент скалярной функции

Допустим, у нас есть функция, f(x,y) = 3x²y . Наши частные производные:

Изображение 2: Частные производные

Если мы организуем эти частные производные в горизонтальный вектор, мы получим градиент из f(x,y) или ∇ f(x,y) :

Изображение 3: Градиент f(x,y)

6yx — это изменение f(x,y) по отношению к изменению x , а 3x² — это изменение f(x,y) относительно изменения y .

Что происходит, когда у нас есть две функции? Давайте добавим еще одну функцию, g(x,y) = 2x+y⁸ . Частные производные:

Изображение 4: Частичные для g(x,y)

Таким образом, градиент g(x,y):

Изображение 5: Градиент g(x,y)

Представление функций

Когда мы имеем несколько функций с несколькими параметрами, часто бывает полезно представить их в более простом виде. Мы можем объединить несколько параметров функций в один векторный аргумент, x , это выглядит следующим образом:

Изображение 6: Вектор x

Таким образом, f(x,y,z) станет f(x₁,x₂,x₃) , которое станет f( x ).

Мы также можем объединить несколько функций в вектор, например: x ), f₂( x ), f₃( x )…fn( x )]

Для нашего предыдущего примера с двумя функциями, f(x,y) ⇒ f( x ) и g(x,y) ⇒ g( x ). Здесь вектор x = [x₁, x₂], где x₁=x и x₂=y . Чтобы упростить его еще больше, мы можем объединить наши функции: [f ( x ), g ( x )] = [f₁ ( x ), f₂ ( x )] = f (x) = у.

Изображение 8: Уравнения внутри векторной функции y

Часто количество функций и количество переменных совпадают, поэтому для каждой переменной существует решение.

Градиент векторной функции

Теперь, когда у нас есть две функции, как нам найти градиент обеих функций? Если мы организуем оба их градиента в одну матрицу, мы перейдем от векторного исчисления к матричному исчислению. Эта матрица и организация градиентов нескольких функций с несколькими переменными известны как матрица Якоби .

Изображение 9: Якобиан

Существует несколько способов представления якобиана. Этот макет, в котором мы накладываем градиенты по вертикали, известен как 9.0267 схема числителя , но в других статьях будет использоваться схема знаменателя , которая просто переворачивает его по диагонали: x) = x , где fi( x ) = xi , и найдите его градиент:

Изображение 11: Функция тождества

Так же, как мы создали наш предыдущий якобиан, мы можем найти градиенты каждой скалярной функции и сложите их вертикально, чтобы создать якобиан функции тождества:

Изображение 12: Якобиан функции тождества

Поскольку это функция тождества, f₁( x ) = x₁, f₂( x ) = x₂ и так далее. Следовательно,

Изображение 13: Якобиан функции тождества

Частная производная функции по переменной, не входящей в функцию, равна нулю. Например, частная производная 2x² относительно y равна 0. Другими словами,

Изображение 14: Частная производная функции относительно переменной, которая не входит в функцию, равна нулю

Следовательно, все, что не находится на диагонали якобиана, становится равным нулю. Между тем, частная производная любой переменной по отношению к самой себе равна 1. Например, частная производная x по отношению к x равна 1. Таким образом, якобиан принимает вид:

Изображение 15: Якобиан тождественной функции

Градиент поэлементных комбинаций векторных функций

Поэлементные бинарные операторы являются операциями (такими как сложение w + x или w > x , который возвращает вектор единиц и нулей), который последовательно применяет оператор, начиная с первого элемента обоих векторов, чтобы получить первый элемент вывода, затем второй элемент обоих векторов, чтобы получить второй элемент продукции… и так далее.

В этой статье представлены поэлементные бинарные операции с такими обозначениями:

Изображение 16: Поэлементная бинарная операция с f(x) и g(x)

Здесь ◯ означает любой поэлементный оператор (например, +), а не композиция функций.

Так как же найти градиент поэлементной операции двух векторов?

Так как у нас есть два набора функций, нам нужны два якобиана, один представляющий градиент относительно x и один относительно w :

Изображение 17: Якобиан относительно w и x

Большинство арифметических операций, которые нам понадобятся, являются простыми, поэтому f(w) часто представляет собой просто вектор w . Другими словами, fi(wi) = wi . Например, операция w+x соответствует этой категории, так как ее можно представить как f(w)+g(x) , где fi(wi) + gi(xi) = wi +xi.

При этом условии каждый элемент в двух якобианах упрощается до:

Изображение 18: Элементы в якобиане

На диагонали i=j, поэтому существует значение частной производной. Однако вне диагонали i≠j, так что частные производные становятся равными нулю:

Изображение 19: Диагональный якобиан

Мы можем представить это более кратко как:

Изображение 20: Якобиан относительно w и x

Попробуем найти градиент функции w+x . Мы знаем, что все, что находится за пределами диагонали, равно 0. Значения частичных чисел по диагонали относительно w и x равны:

диагональ равна 1. Это выглядит знакомо… это единичная матрица!

Попробуем с умножением: ш*х . Значения парциалов по диагонали относительно w 90 268 и 90 267 x 90 268: x равен диаг.( x ) , а градиент относительно x w*x равен диаг.( w ).

Применяя те же шаги для вычитания и деления, мы можем суммировать все это:

Изображение 23: Градиенты обычных поэлементных бинарных операций

Градиент векторных сумм

Одной из наиболее распространенных операций глубокого обучения является операция суммирования.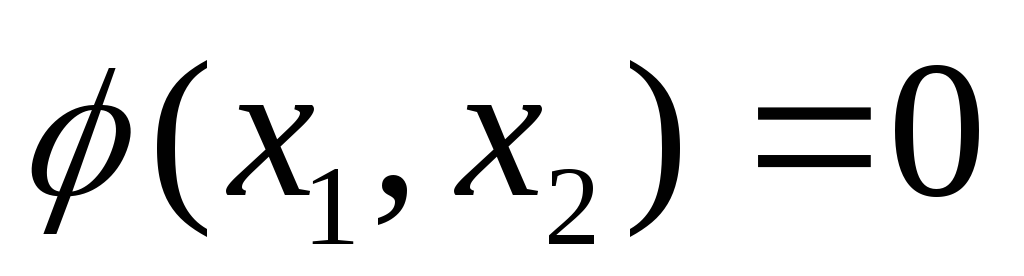 Как мы можем найти градиент функции y=sum( x ) ?

y=сумма( x ) также может быть представлена как: сумма( x )

А поскольку частная производная функции по переменной, не входящей в функцию, равна нулю, ее можно упростить следующим образом: результатом является горизонтальный вектор.

Как насчет градиента y=sum( x z) ? Единственное отличие состоит в том, что мы умножаем каждое частичное число на константу z:

. Изображение 27: Градиент y=sum( x z) относительно x

Хотя это производная относительно x , производная относительно скаляра z просто число:

Изображение 28: Градиент y=sum( x z) относительно z

Градиент комбинаций векторных функций цепных правил

В части 2 мы узнали о цепных правилах с несколькими переменными. Однако это работает только для скаляров. Давайте посмотрим, как мы можем интегрировать это в векторные вычисления!

Возьмем векторную функцию, y = f (x) и найдите его градиент. Давайте определим функцию как:

Изображение 29: y = f (x)

Оба f₁(x) и f₂(x) являются составными функциями. Введем промежуточные переменные для f₁(x) и f₂(x) и перепишем нашу функцию: наше цепное правило с несколькими переменными для вычисления производной вектора и . Просто вычислите производную от f₁(x) и f₂(x) и поместите их друг над другом:

Изображение 31: Градиент y = f ( g (x))

Вуаля! У нас есть градиент. Однако мы пришли к нашему решению со скалярными правилами, просто сгруппировав числа вместе в вектор. Есть ли способ представить правило цепочки с несколькими переменными для векторов?

Прямо сейчас наш градиент вычисляется с помощью:

Изображение 32: Градиент y = f ( g (x))

Обратите внимание, что первый член градиентов как f₁(x) , так и f₂(x) включает часть g₁ x , а второй член градиентов как f₁(x) , так и f₂(x) включает частичное значение g₂ на x .

Калькулятор Градиента — Mathcracker.Com

Калькулятор градиента

Что такое градиент

Шаги для вычисления градиента

Применение градиента

Советы и рекомендации

Пример расчета градиента

Еще примеры градиентов

Другие производные калькуляторы

Калькуляторы

Общие калькуляторы

Акушерство

Анестезиология и реаниматология

Гастроэнтерология

Гериатрия

Кардиология

Неврология

Нефрология

Онкология

Оценка риска кровотечения

Оценка вероятности ТЭЛА

Педиатрия

Психиатрия

Реабилитология

Рентгенология

Спорт

Терапия

Физиология

Хирургия

Калькулятор градиента — MathCracker.

Что такое градиент

Шаги для вычисления градиента

Применение градиента

Советы и рекомендации

Пример вычисления градиента

Другие калькуляторы производных

Нахождение градиента векторной функции | by Chi-Feng Wang

Часть 3 книги «Шаг за шагом: математика за нейронными сетями»

Градиент скалярной функции

Представление функций

Градиент векторной функции

Градиент поэлементных комбинаций векторных функций

Градиент векторных сумм

Градиент комбинаций векторных функций цепных правил

Добавить комментарий Отменить ответ