Точки разрыва функции
Перейдем к изучению так называемых «точек разрыва» функции. Вспомним, что по определению точка (в окрестности которой задана функция ), называется точкой непрерывности данной функции, если выполнено: или (что то же самое, но теперь более удобное для нас) . Естественно принять следующее определение. Точка называется точкой разрыва функции , если она не является точкой непрерывности этой функции, т.е. в этой точке нарушается хотя бы одно из следующих условий (которые в совокупности и составляли условие непрерывности функции):
1. Существуют оба односторонних предела и , причем , . 2. 3.
В зависимости от того, какое из перечисленных выше условий непрерывности функции нарушается, точки разрыва классифицируются различным образом.
1 .
Пусть нарушено только третье условие непрерывности. Это значит, что
существуют оба односторонних предела
и
,
,
но .
Пример 1.
Исследовать на непрерывность функцию . Решение. Функция определена на всей
числовой прямой и задана двумя формулами,
а потому на подозрении в отсутствии
непрерывности может быть только точка
стыка различных формул .
Исследуем функцию на непрерывность в
этой точке. Посчитаем односторонние
пределы
и
при
.
Вспоминая первый замечательный предел,
получаем, что и .
Таким образом, оба односторонних предела
совпадают: ,
но .
В этом случае точка
по
приведенной выше классификации является
точкой устранимого разрыва. Таким
образом, заданная функция непрерывна
на всей числовой прямой, за исключением
точки
,
которая является точкой устранимого
разрыва.
2 . Пусть первое условие непрерывности не нарушено (т.е. существуют оба односторонних предела и , причем , ), но нарушено второе (а потому, автоматически, и третье) условие, т.е. . В этом случае точка х0называется точкой разрыва первого рода (или скачком ), а число называют величиной скачка. Типичная картина скачка (в точке ) показана на рисунке.
Пример 2: Исследовать на непрерывность функцию:
.
Решение. Найдем
область определения этой функции. При
всех функция определяется верхней формулой.
Для всех таких чисел выражение под
знаком логарифма положительно, а потому
все они входят в область определения
функции. Для всех вычисление функции по нижней формуле
тоже не вызывает никаких трудностей.
{поскольку при вычислении левого предела мы приближаемся числами к 2 слева (т.е. со стороны чисел, которые меньше 2), то под знаком предела в качестве должна фигурировать верхняя формула, задающая для } = = = , то есть . Далее, , то есть . Поскольку , то точка разрыва первого рода ( скачок ). Величина скачка .
3.
Если нарушено первое условие
непрерывности, т.е. хотя бы один из
односторонних пределов не существует
или равен ∞ (т.е. А = ± ∞ или В = ± ∞ ), то точка
называется точкой
разрыва второго рода (или бесконечный
скачок ).
Пример 3: Исследуем на непрерывность функцию . Ее график (гипербола) изображен на рисунке. Поскольку функция задана одной формулой, то она непрерывна во всех точках, кроме, быть может, , которая не принадлежит ее области определения. Исследуем точку . Вычисляем левый и правый пределы (такие односторонние пределы выше уже вычислялись): , т.е. . Далее, , т.е. . Поэтому − точка разрыва второго рода ( бесконечный скачок ). Соответствующее поведение графика этой функции вблизи точки разрыва изображено на рисунке.
Рассмотрим примеры на тему непрерывности функции.
Пример 4. Исследовать на непрерывность функцию .
Решение. Функция
определена при всех (при
знаменатель обращается в 0).
Поскольку она задана одной формулой,
то (по Правилу 1 в параграфе «Свойства
функций, непрерывных в точке» ) она
непрерывна на всей числовой прямой, за
исключением, быть может, точки 1.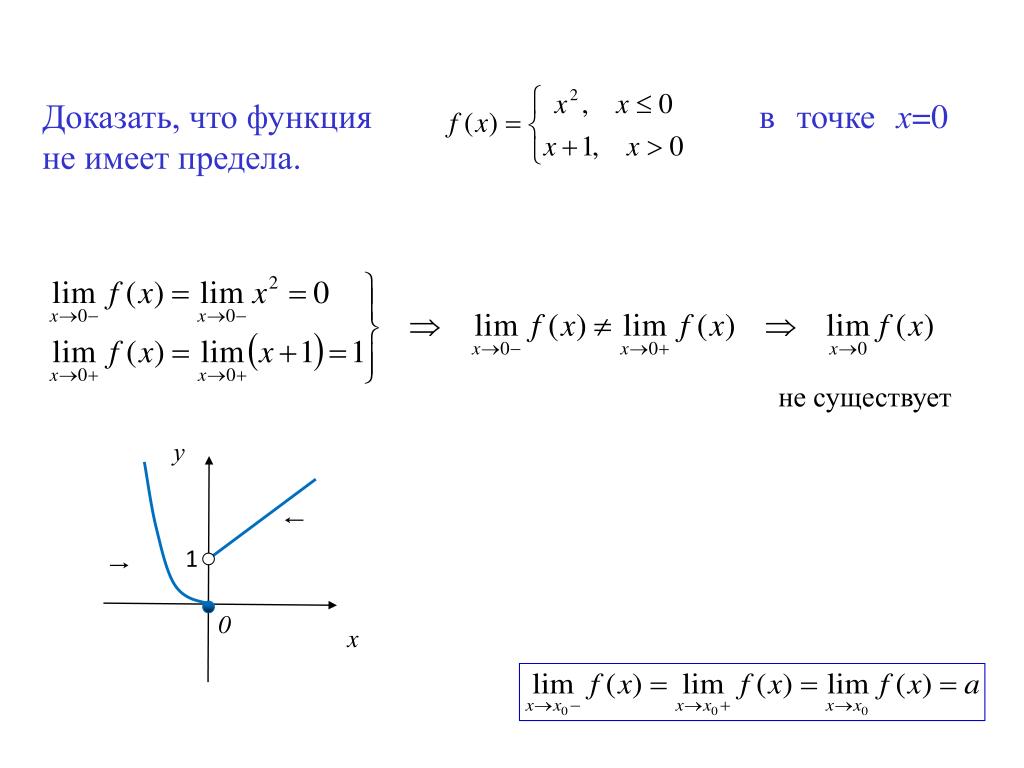
Исследуем отдельно на непрерывность-разрывность
точку .
Вычисляем односторонние пределы:
. Если помните, когда при вычислении предела после подстановки вместо его предельного значения получается , то это было названо псевдонеопределенностью и давало бесконечность. Знак этой бесконечности определяется знаком функции . При приближении к 1 числитель этой дроби становится положительным, так как приближается к положительному числу 1. Поскольку приближается к 1 слева (т.е. со стороны чисел, которые меньше 1), то и знаменатель этой дроби тоже становится положительным. Таким образом, дробь приближается к бесконечности, оставаясь положительной. Поэтому . Аналогично, легко получить, что правый предел (при приближении к 1 справа знаменатель становится отрицательным). По приведенной выше классификации есть точка разрыва 2 рода.
Пример 5. Исследовать на непрерывность функцию .
Решение.
Область
определения: .
Так как функция задана одной формулой,
то она непрерывна на всей числовой
прямой, за исключением, быть может, числа 0.
Исследуем отдельно точку
.
Для начала вспомним, как определяется
модуль числа: .
Теперь вычислим односторонние пределы: {
приближается к
Пример 6. Исследовать на непрерывность функцию .
Решение. Область
определения
.
Так как функция задана одной формулой,
то она непрерывна на всей числовой
прямой, за исключением, быть может, числа 0.
Исследуем отдельно точку
.
Для этого вспомним не раз уже вычисленные
выше следующие односторонние пределы: , .
Тогда , . Таким образом, один (правый) из
односторонних пределов оказался
бесконечным.
Этого уже достаточно, чтобы
по принятой выше классификации объявить
точку
точкой разрыва 2-го рода.
Пример 7. Исследовать на непрерывность функцию .
Решение. Начало решения точно такое же. Область определения . Так как функция задана одной формулой, то она непрерывна на всей числовой прямой, за исключением, быть может, числа 0. Исследуем отдельно точку . Теперь воспользуемся вычисленными в предыдущем примере пределами: и . Тогда предел слева . Запишем предел справа: ={для избавления от неопределенности разделим числитель и знаменатель на }= . Итак, односторонние пределы , а . По классификации точек разрыва есть точка разрыва 1-го рода (скачок). Величина скачка .
Пример 8. При каком значении параметра функция непрерывна на всей числовой прямой.
Решение. При
любом значении
параметра
функция определена на всей числовой
прямой и задается двумя формулами на
разных интервалах по
: и .
Для непрерывности в данной точке должны выполняться условия: , то есть . Очевидно, что это выполнено только при . Итак, только при заданная функция непрерывна на всей числовой прямой.
Предметы |
||||
| Математика История Экономическая теория | ||||
Математика |
||||
Теория Задания С2 Задания С3 Задания С4 Задания С5 Задания С6 |
|
|||
История |
||||
Первобытные люди
|
||||
Экономическая теория |
||||
Предмет экономическая теория
|
||||
| При создании сайта была использована литература. | ||||
|
• 10-11 Алгебра и начала математического анализа. А.Н.Колмогоров. |
||||
Возникновение религии.
Уильям Стаффорд. Томас Ман
Деньги как средство платежа. Мировые деньги.
А.Г.Мордкович.
т. I Карл Маркс.MDMath
MDMath Echo CalculatorsНормальные диапазоны количественной оценки камеры и значения раздела
| Левый желудочек | Правый желудочек |
| Индекс корня аорты AVA (уравнение непрерывности VMax) AVA (уравнение непрерывности VTI) Коэффициент скорости аортального клапана dP/dt (сократимость ЛЖ) dP/dt (сократимость ПЖ) Давление в левом предсердии (MR) Объем ЛП (метод биплана) ФВ ЛЖ (метод Дюмениля) ФВ ЛЖ (модифицированное уравнение хинонов) ФВ ЛЖ (упрощенное уравнение хинонов) | Фракционное укорочение ЛЖ Масса ЛЖ и индекс массы ЛЖ Диастолическая функция ЛЖ Диаг.  (нормальный LVEF) LV Давление наполнения Расчетное. (Сниженная ФВ ЛЖ или N ФВ ЛЖ с диастолической дисф.) Модифицированное уравнение Бернулли Индекс работоспособности миокарда (ЛЖ) Индекс работоспособности миокарда (RV) Площадь митрального клапана (PHT) Оценка митральной вальвулопластики (MGH) Протез а/в (DVI) | Протез AV (EOA) PCWP по E/e’ (формула Nagueh) PISA (митральная регургитация) PISA (митральный стеноз) Протез MV (DVI) Протез MV (EOA) Qp/Qs RVSP (TR) Ударный объем, сердечный выброс Размеры синуса Вальсальвы |
| Макс. Прогнозируемая частота сердечных сокращений достигнута Максимальная прогнозируемая частота сердечных сокращений к возрасту | Mets & VO2 (беговая дорожка) Изделие с нормальным давлением |
| Индекс массы тела (ИМТ) | Площадь поверхности тела (BSA) |
Автор: Chi-Ming Chow MD MSc FRCPC
Разработчик: Эдвард Бравер BSc (с отличием)
Иллюстратор: Эллен Хо BFA
Отказ от ответственности: Предоставленные калькуляторы не предназначены для замены профессиональной консультации и не должны использоваться для медицинской диагностики.
Все расчеты должны быть подтверждены квалифицированными медицинскими работниками перед клиническим использованием или в диагностических целях. Авторы не претендуют на точность информации, содержащейся здесь. Авторы не делают никаких заявлений, выраженных или подразумеваемых, относительно подлинности, точности, надежности, полноты или своевременности предоставленных материалов, программного обеспечения, текста, графики и ссылок. Ни при каких обстоятельствах авторы, их поставщики, аффилированные лица или любые третьи стороны не несут никакой ответственности за любой ущерб, возникший в результате использования любой предоставленной информации.
Информация: Этот набор эхокардиографических калькуляторов (ранее известный как CardioMath) уже более десяти лет используется тысячами клиницистов практически из всех стран мира. Канадское общество эхокардиографии является их домом в Интернете с 2005 года.
Уравнение непрерывности (принцип непрерывности) – ЭКГ и ЭХО
Уравнение непрерывности: то, что входит, должно выйти
Как обсуждалось ранее, ударный объем обычно рассчитывается путем измерения площади и VTI (интеграл скорость-время) в LVOT (выносящий тракт левого желудочка).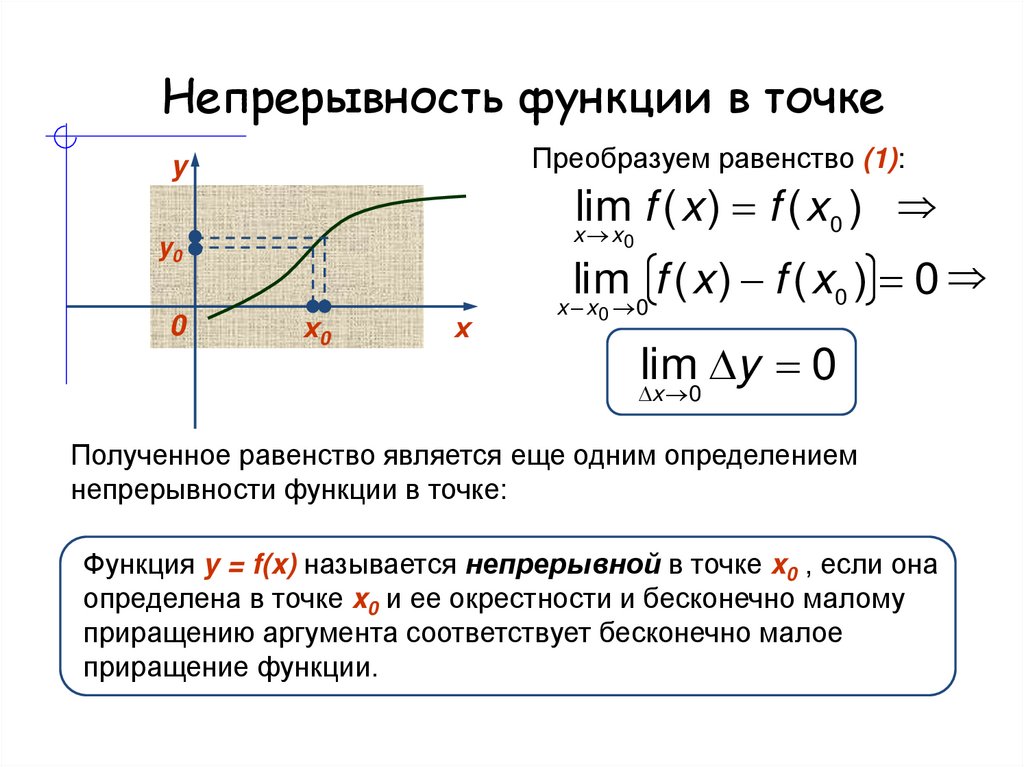
Однако ударный объем также можно рассчитать путем количественного определения объема крови, протекающей через митральный или трехстворчатый клапан. Это объясняется принципом непрерывности (уравнением непрерывности) , который гласит, что объем крови, поступающей в камеру, должен быть равен объему, вытекающему из той же камеры (рис. 1). Таким образом, объем крови, протекающей через митральный клапан в диастолу, равен объему, протекающему через аортальный клапан в систолу (рис. 2). Уравнение неразрывности объясняется тем, что скорость крови обратно пропорциональна площади отверстия; скорость увеличивается с уменьшением площади отверстия, и наоборот .
Ударный объем, количество крови, выбрасываемой в аорту, рассчитывается путем измерения площади и VTI в LVOT:
SV = площадь LVOT • VTI LVOT
SV = ударный объем; LVOT = выходной тракт левого желудочка; VTI = интеграл скорости от времени.
Согласно формуле, ударный объем является произведением площади и VTI в LVOT. Однако уравнение непрерывности утверждает, что ударный объем можно рассчитать путем количественной оценки объема, протекающего через митральный клапан, трехстворчатый клапан или клапан легочной артерии. Эти объемы можно рассчитать по тому же принципу, что и для аорты (, т.е. произведение площади и VTI). Хотя уравнение непрерывности верно, в подавляющем большинстве случаев ударный объем измеряется в ВОЛЖ, что объясняется следующим:
- Аортальный клапан легко визуализировать, а качество изображения обычно высокое в нескольких проекциях.
- Диаметр аортального клапана относительно постоянен во время систолы; это важно, потому что репрезентативный диаметр имеет решающее значение для расчета площади.
- Обычно регургитации в аортальном клапане нет или она незначительна. Распространенность недостаточности трехстворчатого клапана и недостаточности клапана легочной артерии относительно высока.
Для расчета потока (объема) через митральный клапан измеряют максимальный диаметр клапана в диастолу в апикальной четырехкамерной проекции. VTI получают в той же проекции с объемом образца, помещенным в центр митрального кольца.
SV митральный = площадь митральный • VTI митральный
Для расчета потока через трехстворчатый клапан диаметр и VTI измеряются в RVOT (выносящий тракт правого желудочка). Измерения производятся в плоскости аортального клапана в парастернальной проекции по короткой оси.
SV трикуспидальный = площадь RVOT • VTI RVOT
Уравнение непрерывности и клапанная регургитация крови, оттекающей из левого желудочка (через аортальный клапан). Другими словами, ударный объем через аортальный клапан эквивалентен ударному объему через митральный клапан. Этот принцип можно использовать для количественной оценки регургитации и стеноза. Например, при митральной регургитации объем регургитации можно количественно определить, рассчитав разницу в ударном объеме через аортальный и митральный клапаны по формуле:
RV митральный = SV митральный – SV аорта
RV = объем регургитации; митральный = митральный клапан.