Компьютерра: Секреты калькулятора Windows
АрхивУтилиты
автор : Петр Каньковски 07.09.2004
Как извлечь кубический корень, подсчитать среднеквадратичное отклонение, перевести число из одной системы в другую — обо всем этом вы узнаете в сегодняшнем выпуске рубрики RTFM.
Как извлечь кубический корень, подсчитать среднеквадратичное отклонение, перевести число из одной системы в другую — обо всем этом вы узнаете в сегодняшнем выпуске рубрики RTFM.
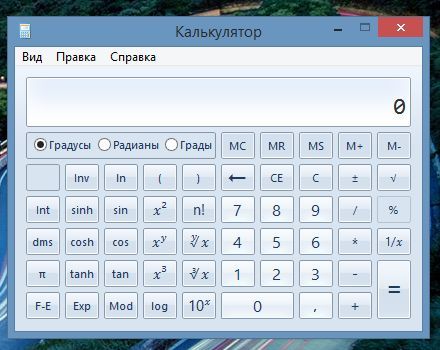
Начнем с того, что простой калькулятор («Пуск > Программы > Стандартные > Калькулятор») можно переключить в режим инженерных вычислений («Вид > Инженерный»).
Чтобы узнать о назначении каждой кнопки, щелкните по ней правой кнопкой мыши и выберите пункт «Что это такое?». Будут показаны краткое описание, пример и «горячая» клавиша. Нажимать кнопки калькулятора мышью довольно неудобно, поэтому часто используемые клавиши стоит запомнить.
Подсказка к кнопке калькулятора
Системы счисления (двоичная, десятичная, восьмеричная, шестнадцатеричная) переключаются клавишами F5-F8, а градусы-радианы-грады — F2, F3, F4. На большинстве клавиатур F5-F8 отделены от F1-F4, поэтому запомнить их довольно легко. Нетрудно также запомнить по первым буквам S — синус, T — тангенс, P — число «пи». Чтобы возвести число в квадрат, нужно нажать Shift+2, а в третью степень — Shift+3.
В калькуляторе Windows XP появилась удобная возможность разделять группы из трех разрядов пробелами (например, 1 048 576 вместо 1048576). Выберите «Вид > Количество цифр в группе», чтобы переключиться в этот режим.
Обратите внимание на галочки Inv и Hyp (клавиши I и H). Если установлена Inv, то функция меняется на обратную, например, синус на арксинус, логарифм — на показательную функцию. Если вам нужно извлечь кубический корень из числа, нажмите I, затем Shift+F3. Галочка Hyp предназначена для вычисления гиперболических функций.
Для большинства пользователей назначение кнопок Sta, Ave, Dat остается тайной за семью печатями. Для вычисления простых статистических функций они используют Excel и пребывают в растерянности, если не находят его на чужом компьютере. Между тем, калькулятор Windows тоже может считать среднее арифметическое, среднеквадратичное отклонение (с параметрами n и n — 1) и сумму квадратов. Это может пригодиться в экстренных случаях (когда под рукой нет Excel или какой-нибудь математической программы).
Статистические вычисления
Нажмите кнопку Sta или Ctrl+S, затем вернитесь в окно калькулятора и вводите данные выборки, нажимая после каждого из них Ins. Можно сначала выполнить необходимые расчеты, а затем занести их в окно «Статистика». Кнопки Ave, Sum, s предназначены для вычисления статистических функций (чтобы прочитать описание, щелкните одну из них правой кнопкой мыши и выберите «Что это такое?»). Обратите внимание, что каждую из этих кнопок можно использовать с флажком Inv.
Корень из 3 онлайн калькулятор. Простые и не очень способы того, как вычислить кубический корень
Размещенный на нашем сайте. Извлечение корня из числа часто используется в различных расчетах, а наш калькулятор — это отличный инструмент для подобных математических вычислений.
Онлайн калькулятор с корнями позволит быстро и просто сделать любые расчеты, содержащие извлечение корня. Корень третьей степени посчитает также легко, как и квадратный корень из числа, корень из отрицательного числа, корень из комплексного числа, корень из числа пи и т.д.
Вычисление корня из числа возможно вручную. Если есть возможность вычислить целый корень числа, то просто находим значение подкоренного выражения по таблице корней. В остальных случаях приближенное вычисление корней сводится к разложению подкоренного выражения на произведение более простых множителей, которые являются степенями и их можно убрать за знак корня, максимально упрощая выражение под корнем.
Но не стоит использовать такое решение корня. И вот, почему. Во-первых, придется потратить массу времени на подобные расчеты. Числа в корне, а точнее сказать, выражения могут быть достаточно сложными, а степень не обязательно квадратичной или кубической. Во-вторых, не всегда устраивает точность таких вычислений. И, в-третьих, есть онлайн калькулятор корней, который сделает за вас любое извлечение корня в считанные секунды.
И вот, почему. Во-первых, придется потратить массу времени на подобные расчеты. Числа в корне, а точнее сказать, выражения могут быть достаточно сложными, а степень не обязательно квадратичной или кубической. Во-вторых, не всегда устраивает точность таких вычислений. И, в-третьих, есть онлайн калькулятор корней, который сделает за вас любое извлечение корня в считанные секунды.
Извлечь корень из числа — значит найти такое число, которое при его возведении в степень n будет равно значению подкоренного выражения, где n — это степень корня, а само число — основание корня. Корень 2 степени называют простым либо квадратным, а корень третьей степени — кубическим, опуская в обоих случаях указание степени.
Решение корней в онлайн калькуляторе сводится лишь к написанию математического выражения в строке ввода. Извлечение из корня в калькуляторе обозначается как sqrt и выполняется с помощью трех клавиш — извлечение квадратного корня sqrt(x), извлечение корня кубического sqrt3(x) и извлечение корня n степени sqrt(x,y). Более детальная информация о панели управления представлена на странице .
Более детальная информация о панели управления представлена на странице .
Извлечение квадратного корня
Нажатие этой кнопки вставит в строке ввода запись извлечения из квадратного корня: sqrt(x), вам нужно только внести подкоренное выражение и закрыть скобку.
Пример решения квадратных корней в калькуляторе:
Если под корнем отрицательное число, а степень корня четная, то ответ будет представлен в виде комплексного числа с мнимой единицей i.
Квадратный корень из отрицательного числа:
Корень третьей степени
Используйте эту клавишу, когда нужно извлечь кубический корень. Она вставляет в строке ввода запись sqrt3(x).
Корень 3 степени:
Корень степени n
Естественно, онлайн калькулятор корней позволяет извлекать не только квадратный и кубический корень из числа, но также корень степени n. Нажатие этой кнопки выведет запись вида sqrt(x x,y).
Корень 4 степени:
Точный корень n степени из числа можно извлечь только, если само число является точным значением степени n. В противном же случае расчет получится приблизительным, хотя и очень близким к идеалу, так как точность вычислений онлайн калькулятора достигает 14 знаков после запятой.
В противном же случае расчет получится приблизительным, хотя и очень близким к идеалу, так как точность вычислений онлайн калькулятора достигает 14 знаков после запятой.
Корень 5 степени с приблизительным результатом:
Корень из дроби
Вычислить корень калькулятор может из различных чисел и выражений. Нахождение корня дроби сводится к отдельному извлечению корня из числителя и знаменателя.
Квадратный корень из дроби:
Корень из корня
В случаях когда корень выражения находится под корнем, по свойству корней их можно заменить одним корнем, степень которого будет равняться произведению степеней обоих. Проще говоря, чтобы извлечь корень из корня, достаточно перемножить показатели корней. В приведенном на рисунке примере выражение корень третьей степени корня второй степени можно заменить одним корнем 6-ой степени. Указывайте выражение так, как вам удобно. Калькулятор в любом случае все рассчитает верно.
Пример, как извлечь корень из корня:
Степень в корне
Корень степени калькулятор позволяет рассчитать в одно действие, без предварительного сокращения показателей корня и степени.
y».
Корень третьей степени можно вычислить и в программе MS Excel. Для этого введите в любую клетку «=» и выберите значок «вставка » (fx). Выберите в появившемся окошке функцию «СТЕПЕНЬ» и нажмите кнопку «Ок». В появившемся окошке введите значение числа, для которого необходимо вычислить корень третьей степени. В «Степень» введите число «1/3». Число 1/3 набирайте именно в таком виде – как обыкновенную . После этого нажмите кнопку «Ок». В той клетке таблицы, где создавалась , появится кубический корень из заданного числа.
Если корень третьей степени приходится вычислять постоянно, то немного усовершенствуйте описанный выше метод. В качестве числа, из которого требуется извлечь корень, укажите не само число, а клетку таблицы. После этого, просто каждый раз вводите в эту клетку исходное число – в клетке с формулой будет появляться его кубический корень.
Видео по теме
Обратите внимание
Заключение. В данной работе были рассмотрены различные методы вычисления значений кубического корня.
Выяснилось, что значения кубического корня можно находить с помощью метода итераций, также можно аппроксимировать кубический корень, возводить число в степень 1/3, искать значения корня третьей степени с помощью Microsoft Office Ecxel, задавая формулы в ячейках.
Полезный совет
Корни второй и третьей степени употребляются особенно часто и поэтому имеют специальные названия. Квадратный корень: В этом случае показатель степени обычно опускается, а термин «корень» без указания степени чаще всего подразумевает квадратный корень. Практическое вычисление корней Алгоритм нахождения корня n-ной степени. Квадратные и кубические корни обычно предусмотрены во всех калькуляторах.
Источники:
- корень третий степени
- Как извлечь квадратный корень в N степени в Excel
Операцию нахождения корня третьей степени обычно называют извлечением «кубического» корня, а заключается она в нахождении такого вещественного числа, возведение которого в куб даст значение равное подкоренному числу.
Операция извлечения арифметического корня любой степени n эквивалентна операции возведения в степень 1/n. Для практического вычисления кубического корня можно использовать несколько способов. Из большого числа без калькулятора мы уже разобрали. В этой статье рассмотрим как извлечь кубический корень (корень третьей степени). Оговорюсь, что речь идёт о натуральных числах. Как вы думаете, сколько времени нужно, чтобы устно вычислить такие корни как:
Совсем немного, а если потренируетесь два-три раза минут по 20, то любой такой корень вы сможете извлечь за 5 секунд устно.
*Нужно отметить, что речь идёт о таких числах стоящих под корнем, которые являются результатом возведения в куб натуральных чисел от 0 до 100.
Мы знаем, что:
Так вот, число а, которое мы будем находить – это натуральное число от 0 до 100. Посмотрите на таблицу кубов этих чисел (результаты возведения в третью степень):
Вы без труда сможете извлечь кубический корень из любого числа в этой таблице.
Что нужно знать?1. Это кубы чисел кратных десяти:
Я бы даже сказал, что это «красивые» числа, запоминаются они легко. Выучить несложно.
2. Это свойство чисел при произведении.
Его суть заключается в том, что при возведении в третью степень какого-либо определённого числа, результат будет иметь особенность. Какую?
Например, возведём в куб 1, 11, 21, 31, 41 и т.д. Можно посмотреть по таблице.
1 3 = 1, 11 3 = 1331, 21 3 = 9261, 31 3 = 26791, 41 3 = 68921 …
То есть, при возведении в куб числа с единицей на конце в результате у нас всегда получится число с единицей в конце.
При возведении в куб числа с двойкой на конце в результате всегда получится число с восьмёркой в конце.
Покажем соответствие в табличке для всех чисел:
Знания представленных двух моментов вполне достаточно.
Рассмотрим примеры:
Извлечь кубический корень из 21952.
Данное число находится в пределах от 8000 до 27000. Это означает, что результат корня лежит в пределах от 20 до 30.
Число 29952 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 28.
Извлечь кубический корень из 54852.
Данное число находится в пределах от 27000 до 64000. Это значит, что результат корня лежит в пределах от 30 до 40. Число 54852 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 38.
Извлечь кубический корень из 571787.
Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 571787 заканчивается на 7. Такой вариант возможен только тогда, когда в куб возводится число с тройкой в конце. Таким образом, результат корня равен 83.
Извлечь кубический корень из 614125.
Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 614125 заканчивается на 5.
Такой вариант возможен только тогда, когда в куб возводится число с пятёркой в конце. Таким образом, результат корня равен 85.
Думаю, что вы теперь без труда сможете извлечь кубический корень из числа 681472.
Конечно, чтобы извлекать такие корни устно, нужна небольшая практика. Но восстановив две указанные таблички на бумаге, вы без труда в течение минуты, в любом случае, такой корень извлечь сможете.
После того, как нашли результат обязательно сделайте проверку (возведите его с третью степень). *Умножение столбиком никто не отменял 😉
На самом ЕГЭ задач с такими «страшненькими» корнями нет. Например, в требуется извлечь кубический корень из 1728. Думаю, что это теперь для вас не проблема.
Если вы знаете какие-то интересные приёмы вычислений без калькулятора, присылайте, со временем опубликую. На этом всё. Успеха Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Если под рукой есть калькулятор, извлечь кубический корень из любого числа не составит никаких проблем.
Но если калькулятора нет или вы просто хотите произвести впечатление на окружающих, извлеките кубический корень вручную. Большинству людей описываемый здесь процесс покажется довольно сложным, но с практикой извлекать кубические корни станет намного легче. Перед тем как приступить к чтению данной статьи, вспомните основные математические операции и вычисления с числами в кубе.
Шаги
Часть 1
Извлечение кубического корня на простом примере
Запишите задачу. Извлечение кубического корня вручную похоже на деление в столбик, но с некоторыми нюансами. Сначала запишите задачу в определенной форме.
- Запишите число, из которого нужно извлечь кубический корень. Число разбейте на группы по три цифры, причем отсчет начните с десятичной запятой. Например, нужно извлечь кубический корень из 10. Напишите это число так: 10, 000 000. Дополнительные нули призваны повысить точность результата.
- Возле и над числом нарисуйте знак корня.
2 = 1. Таким образом, первый множитель равен сумме следующих чисел: 1200 + 60 + 1 = 1261. Запишите это число слева от вертикальной черты.
Умножьте и вычтите. Умножьте последнюю цифру ответа (в нашем примере это 1) на найденный множитель (1261): 1*1261 = 1261. Запишите это число под 2000 и вычтите его из 2000. Вы получите 739 (это второй остаток).
Подумайте, является ли полученный ответ достаточно точным. Делайте это каждый раз, после того как завершите очередное вычитание. После первого вычитания ответ был равен 2, что не является точным результатом. После второго вычитания ответ равен 2,1.
- Чтобы проверить точность ответа, возведите его в куб: 2,1*2,1*2,1 = 9,261.
- Если вы считаете, что ответ достаточно точный, вычисления можно не продолжать; в противном случае проделайте еще одно вычитание.
Найдите второй множитель. Чтобы попрактиковаться в вычислениях и получить более точный результат, повторите действия, которые описаны выше.
{3}=729} , то значение кубического корня из 600 лежит между 8 и 9. Поэтому используйте числа 512 и 729 в качестве верхнего и нижнего пределов ответа.
Оцените второе число. Первое число вы нашли благодаря знанию кубов целых чисел. Теперь целое число превратите в десятичную дробь, приписав к нему (после десятичной запятой) некоторую цифру от 0 до 9. Необходимо найти десятичную дробь, куб которой будет близок, но меньше исходного числа.
- В нашем примере число 600 находится между числами 512 и 729. Например, к первому найденному числу (8) припишите цифру 5. Получится число 8,5.
- В нашем примере: 8 , 5 ∗ 8 , 5 ∗ 8 , 5 = 614 , 1. {\displaystyle 8,5*8,5*8,5=614,1.}
Сравните куб полученного числа с исходным числом. Если куб полученного числа больше исходного числа, попробуйте оценить меньшее число. Если же куб полученного числа намного меньше исходного числа, оценивайте большие числа до тех пор, пока куб одного из них не превысит исходное число.
{3}=614,1} . Исходное число 600 ближе к 592, чем к 614. Поэтому к последнему числу, которое вы оценили, припишите цифру, которая ближе к 0, чем к 9. Например, таким числом является 4. Поэтому возведите в куб число 8,44.
Если нужно, оцените другое число. Сравните куб полученного числа с исходным числом. Если куб полученного числа больше исходного числа, попробуйте оценить меньшее число. Короче говоря, нужно найти такие два числа, кубы которых чуть больше и чуть меньше исходного числа.
- В нашем примере 8 , 44 ∗ 8 , 44 ∗ 8 , 44 = 601 , 2 {\displaystyle 8,44*8,44*8,44=601,2} . Это чуть больше исходного числа, поэтому оцените другое (меньшее) число, например, 8,43: 8 , 43 ∗ 8 , 43 ∗ 8 , 43 = 599 , 07 {\displaystyle 8,43*8,43*8,43=599,07} . Таким образом, значение кубического корня из 600 лежит между 8,43 и 8,44.
Выполняйте описанный процесс до тех пор, пока не получите ответ, точность которого вас устроит. Оцените следующее число, сравните его с исходным, затем, если нужно, оцените другое число и так далее.
{3}=599,93} , то есть результат меньше исходного числа менее чем на 0,1.
Сколько гневных слов произнесено в его адрес? Порой кажется, что кубический корень невероятно сильно отличается от квадратного. На самом деле разница не настолько велика. Особенно, если понять, что они только частные случаи общего корня n-ой степени.
Зато с его извлечением могут возникнуть проблемы. Но чаще всего они связаны с громоздкостью вычислений.
Что нужно знать о корне произвольной степени?
Во-первых, определение этого понятия. Корнем n-ой степени из некоторого «а» называется такое число, которое при возведении в степень n дает исходное «а».
Причем бывают четные и нечетные степени у корней. Если n — четное, то подкоренное выражение может быть только нулем или положительным числом. В противном случае вещественного ответа не будет.
Когда же степень нечетная, то существует решение при любом значении «а». Оно вполне может быть и отрицательным.
Во-вторых, функцию корня всегда можно записать, как степень, показателем которой является дробь.
Иногда это бывает очень удобным.
Например, «а» в степени 1/n как раз и будет корнем n-ой степени из «а». В этом случае основание степени всегда больше нуля.
Аналогично «а» в степени n/m будет представлено, как корень m-ой степени из «а n ».
В-третьих, для них справедливы все действия со степенями.
- Их можно перемножать. Тогда показатели степеней складываются.
- Корни можно разделить. Степени нужно будет вычесть.
- И возвести в степень. Тогда их следует перемножить. То есть ту степень, которая была, на ту, в которую возводят.
В чем сходства и различия квадратного и кубического корней?
Они похожи, как родные братья, только степень у них разная. И принцип их вычисления одинаков, различие только в том, сколько раз должно число на себя умножиться, чтобы получить подкоренное выражение.
А о существенном отличии было сказано чуть выше. Но повториться не будет лишним. Квадратный извлекается только из неотрицательного числа.
В то время, как вычислить кубический корень из отрицательной величины не составит труда.
Извлечение кубического корня на калькуляторе
Каждый человек хоть раз делал это для квадратного корня. А как быть если степень «3»?
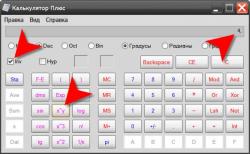
На обычном калькуляторе имеется только кнопочка для квадратного, а кубического — нет. Здесь поможет простой перебор чисел, которые трижды умножаются на себя. Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.
А что в инженерном виде калькулятора в компьютере? Ура, здесь есть кубический корень. Эту кнопочку можно просто нажать, и программа выдаст ответ. Но это не все. Здесь можно вычислить корень не только 2 и 3 степени, но и любой произвольной. Потому что есть кнопка у которой в степени корня стоит «у». То есть после нажатия этой клавиши потребуется ввести еще одно число, которое будет равно степени корня, а уже потом «=».
Извлечение кубического корня вручную
Этот способ потребуется, когда калькулятора под рукой нет или воспользоваться им нельзя.
Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.
Сначала посмотреть, а не получается ли полный куб от какого-нибудь целого значения. Может быть под корнем стоит 2, 3, 5 или 10 в третьей степени?
- Мысленно разделить подкоренное выражение на группы по три цифры от десятичной запятой. Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
- Определить число, куб которого меньше целой части подкоренного выражения. Его записать в промежуточный ответ над знаком корня. А под этой группой расположить его куб.
- Выполнить вычитание.
- К остатку приписать первую группу цифр после запятой.
- В черновике записать выражение: а 2 * 300 * х + а * 30 * х 2 + х 3 . Здесь «а» — это промежуточный ответ, «х» является числом, которое меньше получившегося остатка с приписанными к нему числами.
- Число «х» нужно записать после запятой промежуточного ответа. А значение всего этого выражения записать под сравниваемым остатком.
- Если точности достаточно, то расчеты прекратить. В противном случае нужно возвращаться к пункту под номером 3.
Наглядный пример вычисления кубического корня
Он нужен потому, что описание может показаться сложным. На рисунке ниже показано, как извлечь кубический корень из 15 с точностью до сотых.
Единственной сложностью, которую имеет этот метод, заключается в том, что с каждым шагом числа увеличиваются многократно и считать в столбик становится все сложнее.
- 15> 2 3 , значит под целой частью записана 8, а над корнем 2.
- После вычитания из 15 восьми получается остаток 7. К нему нужно приписать три нуля.
- а = 2. Поэтому: 2 2 * 300 * х +2 * 30 * х 2 + х 3
- Методом подбора получается, что х = 4. 1200 * 4 + 60 * 16 + 64 = 5824.
- Вычитание дает 1176, а над корнем появилось число 4.
- Приписать к остатку три нуля.
- а = 24. Тогда 172800 х + 720 х 2 + х 3
- х = 6. Вычисление выражения дает результат 1062936.
Остаток: 113064, над корнем 6.
- Снова приписать нули.
- а = 246. Неравенство получается таким: 18154800х + 7380х 2 + х 3
- х = 6. Расчеты дают число: 109194696, Остаток: 3869304. Над корнем 6.
Ответом получается число: 2, 466. Поскольку ответ должен быть дан до сотых, то его нужно округлить: 2,47.
Необычный способ извлечения кубического корня
Его можно использовать тогда, когда ответом является целое число. Тогда кубический корень извлекается разложением подкоренного выражения на нечетные слагаемые. Причем таких слагаемых должно быть минимально возможное число.
К примеру, 8 представляется суммой 3 и 5. А 64 = 13 + 15 + 17 + 19.
Ответом будет число, которое равно количеству слагаемых. Так корень кубический из 8 будет равен двум, а из 64 — четырем.
Если под корнем стоит 1000, то его разложением на слагаемые будет 91 + 109 + 93 + 107 + 95 + 105 + 97 + 103 + 99 + 101. Всего 10 слагаемых. Это и есть ответ.
Калькулятор кубического корня — Мастер математики
В математике «кубический корень» означает «число, которое нужно умножить три раза, чтобы получить исходное число».
Онлайн-калькулятор кубического корня показывает кубический корень указанного значения. Кубический корень отображается за считанные секунды благодаря онлайн-калькулятору кубического корня The Mathematics Master, который выполняет вычисления быстрее. Символ ‘∛’ обозначает кубический корень.
Значение Х:
Содержание
Кубический корень Определение
Реальный куб и корни дерева могут быть первыми образами, которые приходят на ум, когда мы слышим термины «куб» и «корень». Это не? Ну концепция та же. Корень относится к первоисточнику или отправной точке. Следовательно, мы должны рассмотреть, куб какого числа мы должны взять, чтобы получить данное число.
Формула кубического корня
Кубический корень из целого числа можно вычислить по следующей формуле:
Кубический корень из \(x = \sqrt[3]{x} = \sqrt[3]{(y × y × y)} = y\),
Здесь y — кубический корень из x.
Кроме того, если y имеет целочисленное значение, число x будет идеальным кубом.
Применение формулы кубического корня
Основные области применения формулы кубического корня перечислены ниже.
- Для решения кубических уравнений
- Для определения размерности куба, если известен объем
- Для указания точных размеров квартиры и т. д.
Как пользоваться калькулятором кубического корня?
Если вы не знаете, как вычислить кубический корень на калькуляторе, выполните следующие действия:
- Заполните поле ввода значением подкоренной черты внутри кубического корня.
- Чтобы получить значение кубического корня, нажмите кнопку «Решить».
- В поле вывода будет отображаться кубический корень указанного числа на последнем шаге.
Как найти кубический корень на калькуляторе?
Сначала необходимо ввести числовое значение, для которого необходимо вычислить кубический корень.
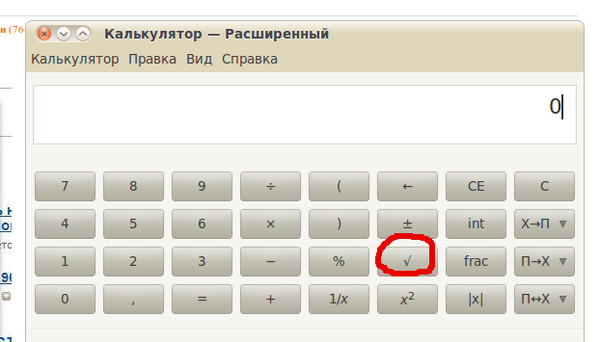
- Дважды нажмите корневую клавишу √
- Нажмите x (несколько знаков)
- Введите √ (основной ключ) четыре раза
- Нажмите x (несколько знаков)
- Нажмите √ (корень) восемь раз
- Нажмите x (несколько знаков)
- Нажмите клавишу √ (корень) дважды в последний раз
- Теперь нажмите = (знак равенства)! Вот ваш окончательный результат
Часто задаваемые вопросы
Что такое кубический корень числа?
Число, полученное при возведении числа в куб кубического корня исходного числа.
Так, например, мы знаем, что \( 2 × 2 × 2 = 8\), а кубический корень из 8 равен 2.
Как быстрее всего определить кубический корень числа?
Метод простой факторизации используется для быстрого получения кубического корня из идеальных кубов.
Не можете найти свой запрос?
Заполните форму ниже с вашим запросом, и мы свяжемся с вами в течение 24 часов.
САМЫЕ ПОПУЛЯРНЫЕ
Наиболее часто используемые бесплатные онлайн-калькуляторы
Алгебра
Квадратичный калькулятор
Квадратичный калькулятор используется для нахождения…
Подробнее
Арифметика
SIG Figulator
. Онлайн -калькулятор рис. Может преобразовать …
Читать больше
Алгебра
Дискриминационный калькулятор
Дискриминант Каллера может использоваться для … 9003 9009 2 ч. Подробнее
Координатная геометрия
Калькулятор скалярного произведения
Калькулятор скалярного произведения.
..
Подробнее
Проценты
Калькулятор среднего процента
Несмотря на то, что выяснение среднего Percen …
Читать Подробнее
Алгебра
Завершение квадратного калькулятора
Завершение квадратного калькулятора — FR …
Читать больше
Арифметика
квадратный корень
Арифметика
квадратного корня. Вы должны быть знакомы с квадратными…
Подробнее
Алгебра
Калькулятор теоремы Пифагора
Используя теорему Пифагора, вычисление Пифагора…
Подробнее
Учебный центр
Самые популярные блоги среди людей
Декартова система координат – размеры, формула…
Декартовы координаты, иногда называемые прямоугольными координатами, т… эти советы и рекомендации.
..
Математические вопросы могут пугать многих учащихся. Это особенно т…
Подробнее
Как построить график параболы – формула, свойства,…
Когда вы выпускаете стрелу или бросаете камень, он летит дугой в воздух и…
Подробнее
Посетить все блоги
квадратный корень из 12 — Google Поиск
AlleBilderShoppingVideosMapsNewsBücher
suchoptionen
квадратный корень(12) =
3,46410162
Что такое упрощенный квадратный корень 2 из 13 900?
Откуда 12 квадратный корень?
Почему квадратный корень из 12 рациональный?
Как найти квадратный корень из 12? — Cuemath
www.cuemath.com › алгебра › квадратный корень из 12
Квадратный корень из 12 выражается как √12 в радикальной форме и как (12)½ или (12)0,5 в экспоненте форма. Квадратный корень из 12, округленный до 5 десятичных .
..
Является ли квадратный корень из 12 рациональным… · Как найти квадратный корень из 12…
Квадратный корень из 12 — YouTube
www.youtube. com › смотреть
26.07.2021 · В этом видео я показываю как упростить квадратный корень из 12,оценку и квадратный корень до 5 знаков.
Dauer: 1:54
Прислан: 26.07.2021квадратный корень из 12 — YouTube
www.youtube.com › смотреть
29.01.2019 · Колледж Алгебра. квадратный корень из 12. 32K просмотров 3 года назад. Математик Зеро. Математик Зеро. 6 …
Dauer: 1:18
Прислан: 29.01.2019Квадратный корень из 12 в радикальной форме — Byjus
byjus.com › Математика › Квадратные корни
Квадратный корень из 12 представлен в радикальная форма как √12, что равно 2√3. Так как 2√3 не может быть дополнительно упрощено, следовательно, такие корни равны …
Простые числа от 1 до 50: делимые числа
Латинские буквы от 1 до 100: длина окружности
Рациональные числа: угол отражения
График обратных тригонометрических функций: тождества по математике для 9 классаwww.
playosmo.com › … › Квадратный корень
Квадратный корень из 12 математически представляется как √12. Число 12 — четное число, а 1, 2, 3, 4, 6 и 12 — делители 12.
Квадратный корень из 12 — значение, метод расчета, примеры решений )½ или (12)0,5 · Квадратный корень из 12 в подкоренной форме: √12 или 2 √3 …
Упрощение квадратного корня из 12 — Mathway
www.mathway.com › Popular-задачи › Algebra
Бесплатное средство решения математических задач отвечает на ваши домашние вопросы по алгебре, геометрии, тригонометрии, исчислению и статистике с пошаговыми объяснениями, …
Чему равен квадратный корень из 12? — Quora
www.quora.com › Что такое квадратный корень из 12
Квадратный корень из 12 равен 3,6.
Чему равен квадратный корень из 12 в подкоренной форме? — Quora
www.quora.com › Что такое квадратный корень из 12 в радикальной форме
Итак, 12 = 4*3, √12 = √4 * √3.

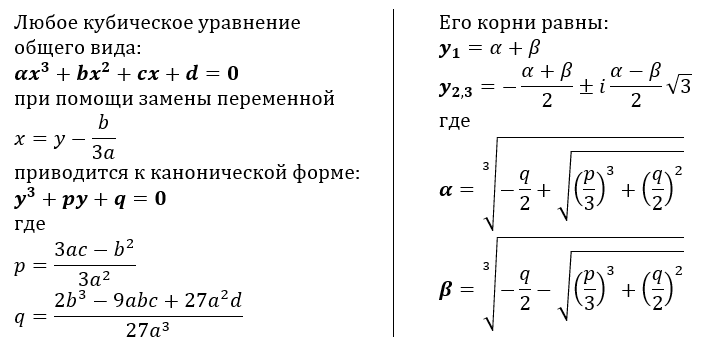 y».
y». Выяснилось, что значения кубического корня можно находить с помощью метода итераций, также можно аппроксимировать кубический корень, возводить число в степень 1/3, искать значения корня третьей степени с помощью Microsoft Office Ecxel, задавая формулы в ячейках.
Выяснилось, что значения кубического корня можно находить с помощью метода итераций, также можно аппроксимировать кубический корень, возводить число в степень 1/3, искать значения корня третьей степени с помощью Microsoft Office Ecxel, задавая формулы в ячейках.

 Число 29952 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 28.
Число 29952 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 28. Такой вариант возможен только тогда, когда в куб возводится число с пятёркой в конце. Таким образом, результат корня равен 85.
Такой вариант возможен только тогда, когда в куб возводится число с пятёркой в конце. Таким образом, результат корня равен 85. Но если калькулятора нет или вы просто хотите произвести впечатление на окружающих, извлеките кубический корень вручную. Большинству людей описываемый здесь процесс покажется довольно сложным, но с практикой извлекать кубические корни станет намного легче. Перед тем как приступить к чтению данной статьи, вспомните основные математические операции и вычисления с числами в кубе.
Но если калькулятора нет или вы просто хотите произвести впечатление на окружающих, извлеките кубический корень вручную. Большинству людей описываемый здесь процесс покажется довольно сложным, но с практикой извлекать кубические корни станет намного легче. Перед тем как приступить к чтению данной статьи, вспомните основные математические операции и вычисления с числами в кубе. 2 = 1. Таким образом, первый множитель равен сумме следующих чисел: 1200 + 60 + 1 = 1261. Запишите это число слева от вертикальной черты.
2 = 1. Таким образом, первый множитель равен сумме следующих чисел: 1200 + 60 + 1 = 1261. Запишите это число слева от вертикальной черты. {3}=729}
, то значение кубического корня из 600 лежит между 8 и 9. Поэтому используйте числа 512 и 729 в качестве верхнего и нижнего пределов ответа.
{3}=729}
, то значение кубического корня из 600 лежит между 8 и 9. Поэтому используйте числа 512 и 729 в качестве верхнего и нижнего пределов ответа. {3}=614,1}
. Исходное число 600 ближе к 592, чем к 614. Поэтому к последнему числу, которое вы оценили, припишите цифру, которая ближе к 0, чем к 9. Например, таким числом является 4. Поэтому возведите в куб число 8,44.
{3}=614,1}
. Исходное число 600 ближе к 592, чем к 614. Поэтому к последнему числу, которое вы оценили, припишите цифру, которая ближе к 0, чем к 9. Например, таким числом является 4. Поэтому возведите в куб число 8,44. {3}=599,93}
, то есть результат меньше исходного числа менее чем на 0,1.
{3}=599,93}
, то есть результат меньше исходного числа менее чем на 0,1. Иногда это бывает очень удобным.
Иногда это бывает очень удобным. В то время, как вычислить кубический корень из отрицательной величины не составит труда.
В то время, как вычислить кубический корень из отрицательной величины не составит труда. Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.
Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.
 Остаток: 113064, над корнем 6.
Остаток: 113064, над корнем 6. Онлайн-калькулятор кубического корня показывает кубический корень указанного значения. Кубический корень отображается за считанные секунды благодаря онлайн-калькулятору кубического корня The Mathematics Master, который выполняет вычисления быстрее. Символ ‘∛’ обозначает кубический корень.
Онлайн-калькулятор кубического корня показывает кубический корень указанного значения. Кубический корень отображается за считанные секунды благодаря онлайн-калькулятору кубического корня The Mathematics Master, который выполняет вычисления быстрее. Символ ‘∛’ обозначает кубический корень. Кроме того, если y имеет целочисленное значение, число x будет идеальным кубом.
Кроме того, если y имеет целочисленное значение, число x будет идеальным кубом.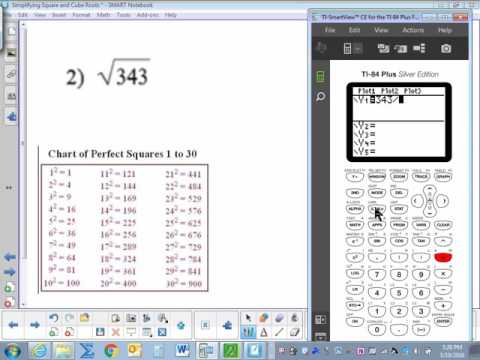 Так, например, мы знаем, что \( 2 × 2 × 2 = 8\), а кубический корень из 8 равен 2.
Так, например, мы знаем, что \( 2 × 2 × 2 = 8\), а кубический корень из 8 равен 2. ..
.. ..
.. ..
.. playosmo.com › … › Квадратный корень
playosmo.com › … › Квадратный корень