Калькулятор онлайн угол между прямыми: Онлайн калькулятор. Угол между прямыми

Содержание

Угол между прямой и плоскостью.

Навигация по странице:

Определение угла между прямой и плоскостью
Формула для вычисления угла между прямой и плоскостью
Вывод формулы вычисления угла между прямой и плоскостью
Примеры задач на вычисление угла между прямой и плоскостью

Онлайн калькулятор. Угол между прямой и плоскостью.

Определение.

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.

Формула вычисления угла между прямой и плоскостью

Если в пространстве заданы направляющий вектор прямой L

s = {l; m; n}

и уравнение плоскости

Ax + By + Cz + D = 0,

то угол между этой прямой и плоскостью можно найти используя формулу

sin φ =	\| A · l + B · m + C · n \|
	√A² + B² + C² · √l² + m² + n²

Вывод формулы для вычисления угла между прямой и плоскостью

Из уравнения прямой можно найти направляющий вектор прямой

s = {l; m; n}

Из уравнения плоскости вектор нормали плоскости имеет вид

q = {A; B; C}

Из формул скалярного произведения векторов найдем косинус угла между нормалью к плоскости и направляющим вектором прямой

cos ψ =	\| q · s \|
	\| s \| · \|q \|

Так как φ = 90° — ψ, то синус угла между прямой и плоскостью sin φ = cos ψ.

Расписав скалярное произведение векторов и модуль векторов через их координаты, получим формулу для вычисления угла между прямой и плоскостью.

Пример вычисления угла между прямой и плоскостью

Пример 1.

Найти угол между прямой

x — 4	=	y + 2	= —	z — 6
2	=	6	= —	3

и плоскостью x — 2y + 3z + 4 = 0.

Решение.

Из уравнения прямой найдем направляющий вектор прямой

s = {2; 6; -3}

Из уравнения плоскости найдем вектор нормали плоскости

q = {1; -2; 3}

Воспользовавшись формулой, найдем угол между прямой и плоскостью

sin φ =	\| 2 · 1 + 6 · (-2) + (-3) · 3 \|	=
	√2² + 6² + (-3)² · √1² + (-2)² + 3²

sin φ =	\| 2 — 12 — 9 \|	=	19	=	19
	√4 + 36 + 9 · √1 + 4 + 9		√49 · √14		7√14

Ответ:

sin φ =	19
	7√14

Аналитическая геометрия: Вступление и оглавлениеРасстояние между двумя точками. Середина отрезка. Координаты середины отрезка.Уравнение прямой.Уравнение плоскости.Расстояние от точки до плоскости.Расстояние между плоскостями.Расстояние от точки до прямой на плоскости.Расстояние от точки до прямой в пространстве.Угол между плоскостями.Угол между прямой и плоскостью.

Онлайн калькуляторы. Аналитическая геометрия. Декартовые координаты.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Найти угол между прямой и плоскостью в пространстве — онлайн калькулятор

Справочник
Онлайн-калькуляторы
Тесты с ответами

Углом между прямой и плоскостью в пространстве называется угол между прямой и ее проекцией на эту плоскость.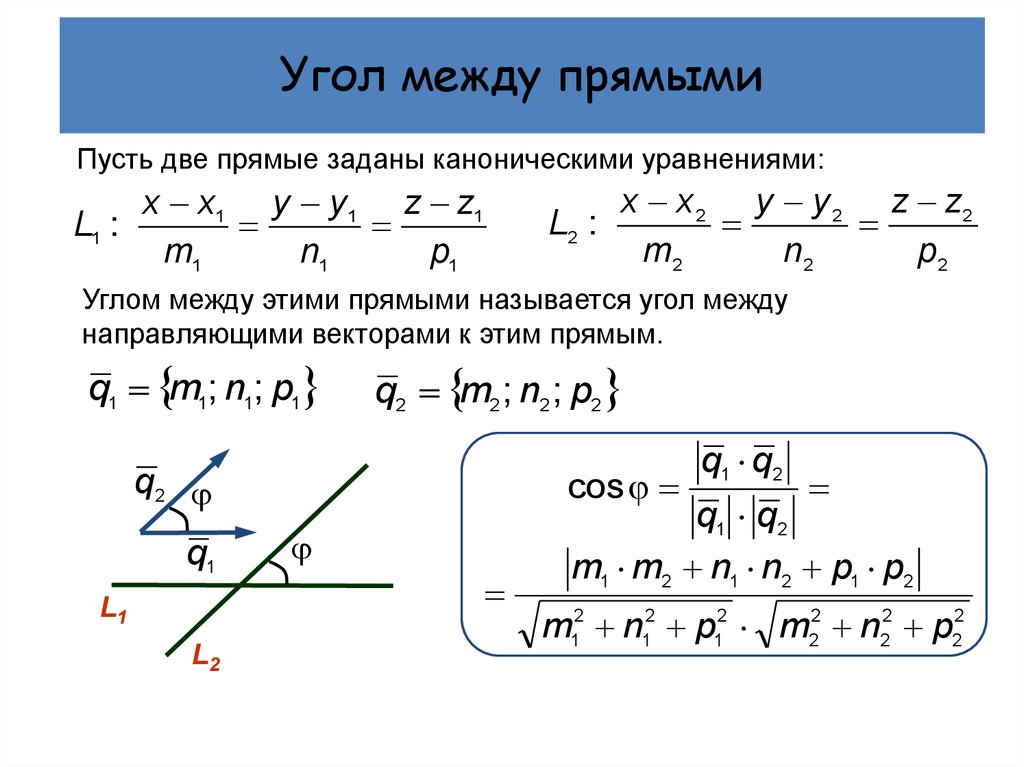 Чтобы наглядно представить задание и получить подробные вычисления, воспользуйтесь нашим сервисом.

На сайте собраны программы, которые позволяют ввести данные из условия задачи и сразу увидеть решение и ответ. Сервис помогает облегчить учебный процесс школьникам, студентам, автоматизировать работу учителям.

1. Выберите, в какой форме представлено уравнение прямой.

Вариант 1

2. Введите данные из условия задачи.

Вариант 1

3. Отправьте задание на вычисление кнопкой «Рассчитать» и получите подробное решение и ответ.

Вариант 2

2. Введите данные из условия задачи.

Вариант 2

3. Отправьте задание на вычисление кнопкой «Рассчитать» и получите подробное решение и ответ.

Ответ:

Решение

Ответ:

list» :key=»`error-${eIdx}`» v-html=»e»/>

Похожие калькуляторы:

Длина отрезка. Расстояние между точками
Середина отрезка
Каноническое уравнение прямой проходящей через две точки
Параметрическое Уравнение прямой проходящей через две точки

Расстояние от точки до прямой на плоскости
Уравнение плоскости (координаты трех точек)
Уравнение плоскости (координаты вектора нормали и точки)
Точка пересечения прямых (с угловыми коэффициентами)

Расстояние от точки до прямой в пространстве
Расстояние от точки до плоскости
Расстояние между плоскостями
Угол между плоскостями

Нахождение угла между прямой и плоскостью.

Онлайн-калькулятор

Определение угла между прямой и плоскостью происходит по формуле:

если направляющий вектор прямой L ,

а уравнение плоскости

Калькулятор получает входные данные, на их основе производит пошаговый расчет. От вас не требуется производить никаких действий вручную. Сразу после ввода условия вы получаете вычисления и ответ.

Почему сервис часто используют:

Бесплатные расчеты. Программа заменяет школьнику репетитора. Теперь можно самостоятельно разбираться в непонятной теме с помощью готового чертежа, формулы, последовательных вычислений.
Экономия времени. Отсутствие регистрации позволяет получить подсказку на зачете. Проверка выполненных заданий теперь сводится только к вводу данных, сверке с готовым решением и результатом.

Нет ограничений по количеству запросов на расчет. Тренироваться в вычислениях можно столько, сколько необходимо для освоения материала в удобное для вас время.

На сайте круглосуточно доступен консультант. Свяжитесь с ним, если у вас все равно остались трудности в понимании темы. В нашем штате достаточно опытных преподавателей, которые смогут объяснить материал, решить задачи или оказать дистанционную помощь по невысокой цене.

Понравился калькулятор? Поделись с друзьями!

Разделы калькуляторов

Процент
Решение матриц
Точка, прямая, плоскость
Конвертеры
Объем фигур
Калькуляторы площади фигур
Решение уравнений
Операции над векторами
Периметр фигур

Поможем с любой работой

Дипломные работы
Курсовые работы
Рефераты
Контрольные работы
Решение задач
Отчеты по практике

Все наши услуги

Узнай бесплатно стоимость работы

Не получается написать работу самому?

Доверь это кандидату наук!

Формула для нахождения пеленга или курсового угла между двумя точками: Широта и долгота —

Формула для нахождения пеленга или курсового угла между двумя точками. Азимут или угол курса используется для определения навигации , как правило, в области авиационной или морской навигации или навигации транспортных средств или при работе по наземной съемке. Так какой курс или пеленг? Как мы можем найти азимут между двумя точками на земле с помощью формулы? Или Как мы можем найти другую точку, когда дана одна точка, фактическое пройденное расстояние и азимут? Давайте обсудим все эти моменты, а затем на примере и поэкспериментируем с инструментом для расчета пеленга, представленным в посте.

Инструмент ГИС для расчета пеленга
IGISMap Bearing Angle Tool

Формула для определения азимута или угла направления между двумя точками: Широта Долгота линия, соединяющая цель и опорную точку. В то время как Направление – это угол или направление, в котором вы сейчас движетесь. Это означает, что для достижения определенного пункта назначения вам необходимо скорректировать направление курса с помощью азимута.

Вообще «компас» — это инструмент, который дает вам информацию о направлении для навигации. Вы должны обратиться к формуле расстояния Haversine , прежде чем читать этот пост.

Расчет азимута или угла направления между двумя точками:

Итак, если вы из поля ГИС или имеете дело с приложением ГИС , вы должны знать азимут и как рассчитать азимут по формуле. Посмотрим на формулу и инструмент для подшипника:

Пусть ‘ R’ – радиус Земли,
‘ L’ – долгота,
‘θ’ – широта,
‘ β ‘ азимут.

Обозначьте точки A и B как две разные точки , где ‘ La’ – долгота точки A, а ‘θa’ – широта точки A. Аналогичным образом предположим, что для точки B. Азимут будет измеряться с северного направления, т.е. Азимут 0° означает север, азимут 90° — восток, азимут 180° — юг, а 270° — запад.

Примечание: Если азимут обозначен +ve или -ve инициалами, значения которых находятся в диапазоне от 0° до 180°, то -ve обозначается для южной и западной сторон.

Формула для определения азимута, когда заданы широта и долгота двух разных точек:

Азимут от точки А до точки В можно рассчитать как

β = atan2(X,Y),

где, X и Y являются двумя величинами и могут быть рассчитаны как:

X = cos θb * sin ∆L

Y = cos θa * sin θb – sin θa * cos θb * cos ∆L

Возьмем пример для расчета пеленга между двумя разными точками по формуле:

9 90 Kanas City:

St Louis: 38,627089, -90,200203

SO X и Y можно рассчитать,

x = Cos (38,627089) * SIN (4,38101)

x = COS (38,627089) * SIN (4,38101)

9000 2

9967

676 9000 2

Y = cos(39.099912) * sin(38.627089) – sin(39.099912) * cos(38.627089) * cos(4.38101)

Y = 0.77604737571 * 0.62424

8 – 0.6306746155 * 0.78122541965 * 0.99707812506

Y = -0.00681261948

***Convert θ into radians***

So as, β = atan2(X,Y) = atan2(0.05967668696, -0.00681261948) = 1.684463062558 radians

convert it into degree

β = 96.51 °

Это означает, что из Канзас-Сити, если мы переедем 96.51 ° азимут, мы достигнем Сент-Луиса.

Вы также можете посмотреть видео объяснение угла азимута.

Проверьте следующие инструменты Igismap для работы с углом подшипника

Инструмент угла подшипника Igismap
Угол подшипника

Igismap Угловой Угол Угол

4004 40019

IGISMAP Угловой для подшипника

4004 4004

IGISMAP Углов. платформа, предоставляющая несколько ГИС-приложений, наиболее важных в области геопространственной аналитики. Особенностью IGISMAP в индустрии ГИС является его пользовательский интерфейс/UX, который помогает пользователю легко выполнять геопространственные операции.
Угол азимута Инструмент IGISMap можно использовать для создания геопространственного пути на основе угла азимута, расстояния и местоположения. Путь представляет собой одну или несколько прямых линий, соединенных между точками, нанесенными по порядку. Пользователь может нанести необходимые местоположения, просто нажав на карту или введя адрес или координаты. Путь, созданный в Угол азимута , будет доступен как слой ГИС в IGISMap. Этот слой ГИС можно загрузить как данные ГИС в любом формате, таком как Shapefile, GeoJSON, CSV или KML.
Проверьте https://map.igismap.com/bearing-angle, чтобы открыть Угол азимута
Формула для нахождения точки широты и долготы, когда заданы пеленг, расстояние и другая широта
Предположим условие, где вы хотите узнать где приземлится самолет , если у вас есть следующие данные об этом самолете, то есть фактическое расстояние он пролетит, азимут и начальная точка (широта, долгота) ?
Пусть первая точка широта будет LA1,
Долгота AS LO1,
D — расстояние,
R как радиус Земли,
AD — угловая дистанция, то есть D/R и
.
θ быть азимутом,
**Вот формула для нахождения второй точки, когда известны первая точка, азимут и расстояние: Ad + cos la1 * sin Ad * cos θ),** и

долгота второй точки = lo2 = lo1 + atan2(sin θ * sin Ad * cos la1 , cos Ad – sin la1 * sin la2)

Вы можете найти оба инструмента на отдельной странице, с картой Google, работающей над ним: (обновление будет через 2 дня, пожалуйста, посетите нас снова)

Инструмент для определения азимута, когда даны две точки
Инструмент для поиска другой точки, когда азимут, расстояние и одна из дается точка.

Надеюсь, эта статья обязательно поможет вам найти подшипник или товарная позиция . Вы можете поделиться дополнительными данными, связанными с азимутом или любой вещью, которую вы используете для расчета азимута и того, как вы используете навигацию с азимутом.

Если вам трудно понять расчет пеленга, вы можете прокомментировать ниже, так что мы обсудим далее нахождение пеленга или угла курса .

Зарегистрируйтесь и войдите в IGISMap Tool, чтобы проверить другие инструменты ГИС.

Теперь мы есть и на Youtube. Пожалуйста, поставьте лайк, поделитесь и подпишитесь на наш канал Карта IGIS

Калькулятор рабочего угла трансмиссии | Запчасти Спайсер

Литература

Используйте Калькулятор рабочего угла трансмиссии, чтобы найти рабочий угол каждого карданного шарнира в вашей трансмиссии.

Измерьте углы каждого компонента трансмиссии — ведущего элемента, приводного вала (валов), ведомого элемента — чтобы определить рабочие углы карданного шарнира.

Подробнее…

Измерьте углы каждого компонента трансмиссии — ведущего элемента, приводного вала (валов), ведомого элемента — чтобы найти рабочие углы карданного шарнира.

Рабочий угол универсального шарнира — это угол, который возникает между ведущим элементом и приводным валом, а также между ведомым элементом и приводным валом, когда они не выровнены по вертикали.

ПРИМЕЧАНИЕ. Этот калькулятор не учитывает составные углы привода (горизонтальные смещения).

Вам понадобится спиртовой уровень или цифровой транспортир с точностью до ¼ градуса. Вы будете измерять углы в разных точках:

От коробки передач
Вдоль трансмиссии
Задняя часть заднего моста

Введите угол с точностью до ¼ градуса вместе с наклоном (вверх или вниз):

Вверх: поднимается от передней части к задней части автомобиля
Вниз: Опускается спереди назад

Три способа измерения:

Используйте адаптер для цифрового транспортира, который позволяет измерять уклоны непосредственно на крышках подшипников в легких условиях или в устройствах с быстроразъемными соединениями
Снимите крышку подшипника и снимите мерки непосредственно с вилки
Снимите стопорное кольцо и снимите мерки с крышки подшипника с помощью адаптера

Советы по измерению:

Измерение вдоль фактической осевой линии выходного вала
Измерить на плоской поверхности под углом 90 градусов или параллельно выходному валу коробки передач
Измерение истинной осевой линии

Основные правила:

Рабочие углы универсального шарнира на каждом конце карданного вала всегда должны быть не менее половины градуса
Рабочие углы универсального шарнира на каждом конце карданного вала всегда должны быть равны в пределах одного градуса друг от друга (половина градуса для домов на колесах и валов перед раздаточной коробкой или вспомогательными устройствами)
Для работы без вибраций рабочий угол универсального шарнира не должен превышать трех градусов. Если они есть, убедитесь, что они не превышают максимальные рекомендуемые углы.

Приводной вал об/мин	Макс. Рабочий угол	Межосевой
Приводной вал об/мин	Макс. Рабочий угол	Параллельный	Пересечение
5000	3,2°	—	—
4500	3,7°	—	—
4000	4,2°	—	—
3500	5,0°	—	—
3000	5,8°	—	—
2500	7,0°	—	—
2000	8,7°	—	—
1500	11,5°	—	—

Следует помнить:

Углы, показанные на приведенной выше диаграмме, являются максимальными рабочими углами карданного шарнира, рекомендованными инженерами Spicer, и напрямую связаны со скоростью карданного вала.
No related posts.