Калькулятор дробей онлайн (с подробным решением)
Если вам необходимо произвести математические операции с дробями воспользуйтесь нашим онлайн калькулятором:
+−×÷
=
Просто заполните необходимые поля и получите ответ и подробное решение.
Данный калькулятор может работать как с положительными, так и с отрицательными дробями.
При этом нужно помнить, что:
− ac = a− c = − ac
Всегда нужно использовать только последний вариант.
Сложение дробей
С одинаковыми знаменателями
При сложении дробей с одинаковыми знаменателями складываются только числители, а знаменатель остаётся прежним.
Формула
ac + bc = a + bc
Пример
Для примера сложим следующие дроби с равными знаменателями:
27 + 47 = 2 + 47 = 67
С разными знаменателями
При сложении дробей с разными знаменателями для начала необходимо привести дроби к общему знаменателю.
А затем сложить числители.
Формула (универсальная)
ac + bd = a⋅d + b⋅cc⋅d
Пример №1
Для примера сложим следующие дроби с разными знаменателями:
12+13=1⋅32⋅3+1⋅23⋅2=36+26=3+26=56
Пример №2
Существуют также частные случаи, когда знаменатель одной дроби можно привести к знаменателю второй. Например:
12+14=1⋅22⋅2+14=24+14=2+14=34
Этот же пример можно решить и применяя вышеуказанную универсальную формулу:
12+14=1⋅42⋅4+1⋅24⋅2=48+28=4+28=68=34
Обратите внимание, что мы сократили дробь:
68=3 ⋅ 24 ⋅ 2=34
Сложение смешанных чисел
Смешанные числа — это такие числа, у которых есть как дробная часть, так и целая.
Преобразуя в неправильную дробь
Для начала смешанное число (дробь) нужно преобразовать в неправильную дробь, а потом можно складывать как в предыдущих примерах.
Формула
a bc + d ef = b + a ⋅ cc + e + d ⋅ ff
Пример
Для примера сложим два смешанных числа:
312+123=1+3⋅22+2+1⋅33=72+53=7⋅32⋅3+5⋅23⋅2=216+106=21+106=316=5⋅6+16=5⋅
+ 16=516
Обратите внимание, что из полученной неправильной дроби мы выделили целую часть:
316=5⋅6+16=5⋅66 + 16=516
Складывая целую и дробную части отдельно
Целую и дробную части смешанных чисел можно складывать по отдельности.
Формула
a bc + d ef = (a + d) + (bc + ef)
Пример
Решим предыдущий пример этим способом:
3 12 + 1 23 = (3+1)+(12+23) = 4+1⋅32⋅3+2⋅23⋅2=4+36+46=4+3+46=4+76=4+116 = 516
Вычитание дробей
Вычитание дробей происходит по тем же принципам, что и сложение.
С одинаковыми знаменателями
Формула
ac − bc = a − bc
Пример
Для примера вычтем одну дробь из другой с равными знаменателями:
35−25=3−25=15
С разными знаменателями
Тут также, как и при сложении, дроби нужно подвести под общий знаменатель, а затем вычитать.
Формула
ac − bd = a⋅d − b⋅cc⋅d
Пример
Для примера вычтем одну дробь из другой, с разными знаменателями:
34−13=3⋅34⋅3−1⋅43⋅4=912−412=9−412=512
Вычитание смешанных чисел
Для начала смешанные числа преобразуем в неправильные дроби, потом приводим полученные дроби к общему знаменателю, а затем вычтем одну из другой. Далее выделяем целую часть если она есть.
Формула
a bc − d ef = b + a ⋅ cc − e + d ⋅ ff
Пример
312−123=1+3⋅22−2+1⋅33=72−53=7⋅32⋅3−5⋅23⋅2=216−106=21−106=116=1⋅6+56=1⋅+ 56=156
Умножение дробей
При умножении дробей неважно одинаковые или разные у них знаменатели. Числитель одной дроби умножается на числитель другой, а знаменатели тоже перемножаются между собой.
Формула
ac ⋅ be = a ⋅ bc ⋅ e
Давайте рассмотрим несколько примеров:
Пример №1
Умножим дроби с одинаковыми знаменателями:
13⋅23=1⋅23⋅3=29
Пример №2
Умножим дроби с разными знаменателями:
13⋅24=1⋅23⋅4=212=1⋅
6⋅
=16
Пример №3
Умножим смешанные числа:
112⋅223=1+1⋅22⋅2+2⋅33=32⋅83=3⋅82⋅3=246=4
Деление дробей
При делении одной дроби на другую также неважно одинаковые или разные у них знаменатели.
Чтобы разделить одну дробь на другую нужно перемножить числитель первой дроби и знаменатель второй, а знаменатель первой умножить на числитель второй.
Формула
ac : be = a ⋅ ec ⋅ b
Давайте рассмотрим несколько примеров:
Пример №1
Разделим одну дробь на другую с таким же знаменателем:
23:13=23⋅31=2⋅33⋅1=63=2
Пример №2
Делим дроби с разными знаменателями:
Пример №3
Деление смешанных чисел:
412:223=1+4⋅22:2+2⋅33=92:83=92⋅38=9⋅32⋅8=2716=1⋅16+1116=1⋅
+ 1116=11116
См. также
Привести дробь к новому знаменателю. Онлайн калькулятор.
Для приведения обыкновенной дроби вида a/b к новому знаменателю, необходимо числитель и знаменатель дроби домножить на дополнительный множитель.
Разберём пример.
Приведём дробь 3/4 к знаменателю 12. Найдём дополнительный множитель — для этого разделим 12 на 4 получится 12 / 4 = 3. Домножим числитель и знаменатель дроби на 3 получится дробь 9/12
=
3 × 3
3 × 4
=
Перед преобразованием дроби к новому знаменателю дробь необходимо сократить.
Разберём пример. Приведём дробь 6/8 к знаменателю 12. Знаменатель 8 не делит нацело новый знаменатель, из этого можно предположить что дробь 6/8 невозможно привести к знаменателю 12. Но если мы сократим дробь 6/8 = 3/4 то дробь без проблем можно привести к знаменателю 12. Домножив числитель и знаменатель на 3 3/4 = 9/12.
=
2 × 3
2 × 4
=
=
3 × 3
3 × 4
=
Как привести смешанное число к новому знаменателю
Для приведения смешанного числа к новому знаменателю, необходимо смешанное число преобразовать в неправильную дробь. Затем числитель и знаменатель дроби домножить на дополнительный множитель.
Разберём пример. Приведём дробь 5 целых 3/4 к знаменателю 12.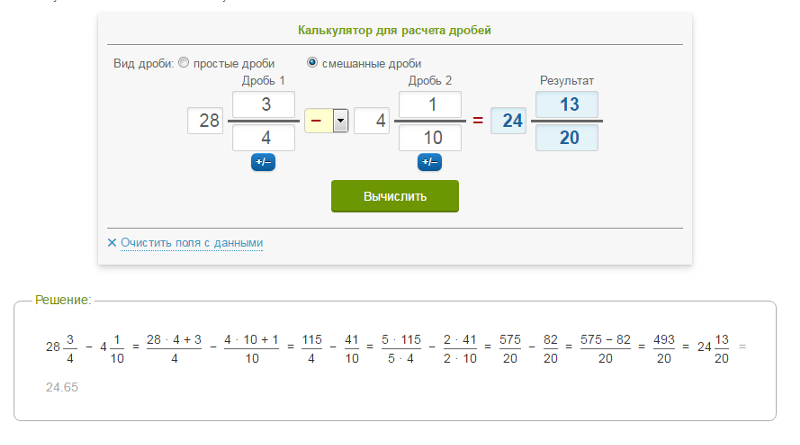
Преобразуем смешанное число в неправильную дробь. 5 целых 3/4 = 23/4 Найдём дополнительный множитель — для этого разделим 12 на 4 получится 12 / 4 = 3. Домножим числитель и знаменатель дроби на 3 получится дробь 69/12
=
5 × 4 + 3
4
=
=
3 × 23
3 × 4
=
Как привести десятичную дробь к новому знаменателю
Для приведения десятичной дроби к новому знаменателю, необходимо десятичную дробь преобразовать в обыкновенную дробь. Затем числитель и знаменатель дроби домножить на дополнительный множитель.
Разберём пример. Приведём десятичную дробь 2.5 к знаменателю 4.Преобразуем десятичную дробь в обыкновенную дробь. 2.5 =5/2 Найдём дополнительный множитель — для этого разделим 4 на 2 получится 4 / 2 = 2. Домножим числитель и знаменатель дроби на 2 получится дробь 10/4
=
2.5 × 10
1 × 10
=
=
5 × 5
2 × 5
=
=
5 × 2
2 × 2
=
Как привести обыкновенную дробь к новому знаменателю
Для приведения обыкновенной дроби к новому знаменателю, необходимо числитель и знаменатель дроби домножить на дополнительный множитель.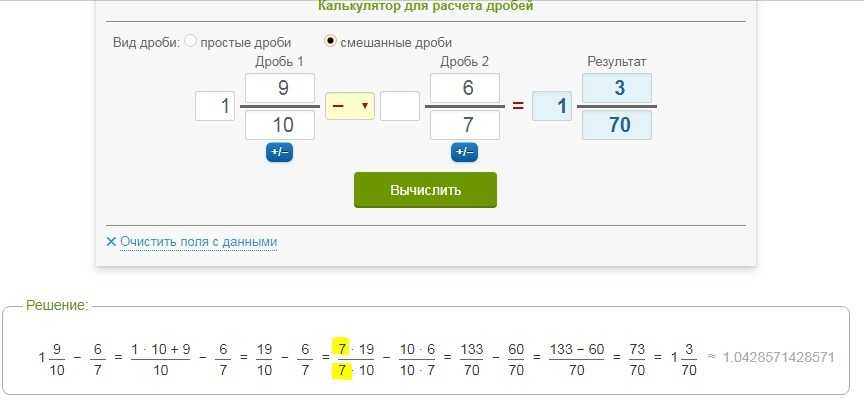
Разберём пример. Приведём обыкновенную дробь 2/7 к знаменателю 14. Найдём дополнительный множитель — для этого разделим 14 на 7 получится 14 / 7 = 2. Домножим числитель и знаменатель дроби на 2 получится дробь 4/14
=
2 × 2
2 × 7
=
Привести дробь 8/21 к знаменателю 22
Привести дробь 10/17 к знаменателю 10
Привести дробь 11/20 к знаменателю 12
Привести дробь 20/9 к знаменателю 25
Привести дробь 11/20 к знаменателю 19
Привести дробь 4/15 к знаменателю 16
Похожие калькуляторы
Перевести бесконечную периодическую дробь в обыкновенную дробь
Перевести десятичную дробь в обыкновенную
Деление дробей
Умножение дробей
Преобразовать смешанную дробь в неправильную дробь
Преобразовать неправильная дробь в смешанную дробь
Сравнение дробей
Сложение дробей
Вычитание дробей
Приведение дробей к наименьшему общему знаменателю
Сократить дробь
Калькулятор дробей — примеры, онлайн-калькулятор дробей
Калькулятор дробей выполняет сложение, вычитание, умножение и деление двух заданных дробей.
Дроби — это числовые значения, представляющие часть целого. Простая дробь задается обозначением — числитель/знаменатель.
Что такое калькулятор дробей?
Калькулятор дробей — это онлайн-инструмент, который можно использовать для сложения, вычитания, умножения и деления дробей с одинаковыми или разными знаменателями. Это обеспечивает быстрый и простой способ решения сложных проблем, а также подсчет результатов в течение нескольких секунд. Чтобы использовать Калькулятор дробей , введите значения в поля ввода, указанные ниже.
Калькулятор дробей
ПРИМЕЧАНИЕ. Вводите значения не более 4 цифр.
Как пользоваться калькулятором дробей?
Выполните следующие простые действия, чтобы сложить, умножить, вычесть или разделить любые две дроби с помощью онлайн-калькулятора дробей:
- Шаг 1: Перейдите к онлайн-калькулятору дробей Cuemath.
- Шаг 2: Введите значения в поля ввода калькулятора дробей и выберите операцию, которую хотите выполнить.
- Шаг 3: Нажмите кнопку «Рассчитать», чтобы сложить, вычесть, умножить и разделить две дроби.
- Шаг 4: Нажмите кнопку «Сброс», чтобы очистить поля и ввести новые значения.
Как работает калькулятор дробей?
Числитель дроби используется для описания количества равных частей целого, а знаменатель показывает полную часть или целое. Следует отметить, что для существования дроби знаменатель должен быть ненулевым.
- Сложение : Чтобы сложить дроби, первый шаг — иметь одинаковые знаменатели. Для определения общего знаменателя возьмите их НОК. Затем умножьте знаменатель на число, которое дает то же значение, что и НОК. На это число также будет умножаться числитель. Как только обе дроби будут иметь одинаковые знаменатели, сложите числители.
- Вычитание : Вычитание двух дробей можно выполнять только в том случае, если обе дроби имеют общие знаменатели. Используя метод НОК, дроби можно преобразовать так, чтобы они имели одинаковые знаменатели, а затем вычесть числители.
- Умножение : Умножение дробей намного проще, чем сложение или вычитание. Сначала умножьте числители, затем умножьте знаменатели. После этого сократите дробь до наименьшего значения, чтобы получить окончательный ответ.
- Деление : Деление дробей аналогично умножению. Здесь мы умножаем первую дробь на обратную (обратную) второй и упрощаем ее до наименьшей формы.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Запишитесь на бесплатный пробный урок
Решенные примеры на калькуляторе дробей
Пример 1:
Добавьте (2/3) + (5/6) и проверьте это с помощью калькулятора дробей.
Решение:
Поскольку знаменатели не совпадают, находим НОК.
НОК (3, 6) = 6
(2/3) + (5/6) = [(2 × 2)/(3 × 2)] + (5/6)
= 4/6 + 5/6
= (4 + 5)/6 = 9/6 = 3/2
Пример 2:
Вычтите (7/8) — (1/4) и проверьте это с помощью калькулятора дробей.
Решение:
НОК (8, 4) = 8
(7/8) — (1/4) = (7/8) — [(1 × 2)/(2 × 4)]
= 7/8 — 2/8
= (7 — 2)/8 = 5/8
Пример 3:
Умножить (4/15) × (9/16) и проверьте его с помощью калькулятора дробей. Пример 4:
Разделите (2/3) ÷ (4/5) и проверьте это с помощью калькулятора дробей.
Решение:
Обратное число 4/5 равно 5/4.
(2/3) ÷ (4/5) = (2/3) × (5/4)
= 10/12
= 5/6
Точно так же вы можете попробовать калькулятор дробей для выполнения сложения , вычитание, умножение и деление двух дробей для следующего:
- (5/11) + (4/7)
- (14.11) — (2/3)
- (2/9) × (3/8)
- Дроби
- Смешанные фракции
Калькулятор дробей — MathCracker.com
Инструкции: Используйте этот калькулятор дробей, чтобы вычислить любую предоставленную вами операцию дроби или вычисление, показывая все шаги.
Пожалуйста, введите в
расчет дроби, который вы хотите выполнить в поле формы ниже.
Подробнее об этом калькуляторе дробей
Этот калькулятор позволит вам складывать дроби , умножать дроби , делить дроби и т. д., а также любые допустимые операция дроби, показывающая все шаги. Вам нужно предоставить допустимое выражение, включающее дроби. Это может быть что-то простое, например, «1/2 + 1/3» или что-то в этом роде. более сложные, такие как «(1/3+1/4)(1/5+1/6)».
Как только вы введете правильное выражение, включающее дробь, все, что вам нужно сделать, это нажать кнопку «Рассчитать», и вам будут предоставлены все шаги расчеты.
Алгебра дробей включает преобразование дробей, например, использование общего знаменателя и использование основных арифметических правил.
В целом, процесс расчета может
быть трудоемким, хотя это можно делать систематически, без особых проблем.
Как складывать дроби?
Сложение дробей — один из самых важных и базовых навыков, которые вы будете использовать при вычислении операций с дробями. Обычно нужно начинать с поиска общего знаменателя, но часто вы будете использовать следующую формулу для сложения дроби:
\[\displaystyle \frac{a}{b} + \frac{c}{d} = \displaystyle \frac{ad + cb}{bd} \]
Как складывать дроби?
- Шаг 1: Определите числитель и знаменатель первой и второй дроби
- Шаг 2: Предположим, что a и b — числитель и знаменатель первой дроби, а c и d — числитель и знаменатель второй дроби
- Шаг 3: Используйте формулу сложения: в полученной дроби в числителе ad + cb, а в знаменателе bd
Вычитание дробей просто получается из суммы дробей: Чтобы вычесть две дроби, вы просто умножаете вторую на -1 и прибавляете к первой .
Как умножать дроби?
Вторым краеугольным камнем для проведения общих расчетов дробей является умножение дробей. В этом случае нет необходимости находить общий знаменатель, вы просто умножьте числители и знаменатели вместе:
\[\displaystyle \frac{a}{b} \times \frac{c}{d} = \displaystyle \frac{ac}{bd} \]
Каковы шаги для умножения дробей?
- Шаг 1: Определите числитель и знаменатель первой и второй дроби
- Шаг 2: Предположим, что a и b — числитель и знаменатель первой дроби, а c и d — числитель и знаменатель второй дроби
- Шаг 3: Используйте формулу сложения: в полученной дроби в числителе ad + cb, а в знаменателе bd
Подобно тому, что произошло со сложением и вычитанием, деление дробей просто происходит от умножения дробей: Чтобы разделить две дроби, вы просто умножаете
первый к обратная дробь второй (обратная дробь получается заменой числителя на знаменатель в дроби).
Зачем заботиться о вычислении дробей?
Дроби являются одним из краеугольных камней алгебры и любого общего алгебраического выражения для вычисления. Фракции простые операнды, но которые могут быть составлены в более сложные термины с помощью таких операций, как сумма, умножение и т. д., а затем с помощью функций мы можем создавать еще больше продвинутые выражения.
Центр всех алгебраических калькуляторов начинается со степени основных чисел дробей.
Пример: вычисление суммы дробей
Вычислить следующее: \(\frac{1}{3} + \frac{5}{4} — \frac{5}{6}\)
Решение :
Нам нужно вычислить и упростить следующее выражение: \(\displaystyle \frac{1}{3}+\frac{5}{4}-\frac{5}{6}\).
Получается следующий расчет:
\( \displaystyle \frac{1}{3}+\frac{5}{4}-\frac{5}{6}\)
Усиление для получения общего знаменателя 12
«=»
\(\displaystyle \frac{1}{3}\cdot\frac{4}{4}+\frac{5}{4}\cdot\frac{3}{3}-\frac{5}{6} \cdot\frac{2}{2}\)
Нахождение общего знаменателя: 12
«=»
\(\displaystyle \frac{1\cdot 4+5\cdot 3-5\cdot 2}{12}\)
Расширение каждого члена: \(4+5 \умножить на 3-5 \умножить на 2 = 4+15-10\)
«=»
\(\displaystyle \frac{4+15-10}{12}\)
Добавление каждого термина
«=»
\(\displaystyle \frac{9}{12}\)
Мы можем вынести 3 как из числителя, так и из знаменателя.
«=»
\(\displaystyle \frac{3\cdot 3}{3\cdot 4}\)
Теперь мы сокращаем 3 из числителя и знаменателя.
«=»
\(\displaystyle \frac{3}{4}\)
, который завершает расчет.
Пример: вычисление другой дроби
Вычислить \( \left(\frac{2}{3} \times \frac{6}{5} \right)+ \frac{2}{5} \).
Решение:
Нам нужно вычислить и упростить следующее выражение: \(\displaystyle \left(\frac{2}{3}\cdot\frac{6}{5}\right)+\frac{2} {5}\).
Получается следующий расчет:
\( \displaystyle \left(\frac{2}{3} \times \frac{6}{5} \right)+ \frac{2}{5} \)
Мы можем умножить члены сверху и снизу, как в \(\displaystyle\frac{ 2}{ 3} \times \frac{ 6}{ 5}= \frac{ 2 \times 6}{ 3 \times 5} \ )
«=»
\(\displaystyle \frac{2\cdot 6}{3\cdot 5}+\frac{2}{5}\)
Мы можем вынести член \(\displaystyle 3\) в числителе и знаменатель в \(\displaystyle \frac{ 2 \times 6}{ 3 \times 5}\)
«=»
\(\displaystyle \frac{2\cdot 2}{5}+\frac{2}{5}\)
После исключения общих факторов
«=»
\(\displaystyle \frac{4}{5}+\frac{2}{5}\)
Используем общий знаменатель: 5
«=»
\(\displaystyle \frac{4+2}{5}\)
Добавление каждого термина
«=»
\(\displaystyle \frac{6}{5}\)
, что завершает расчет.