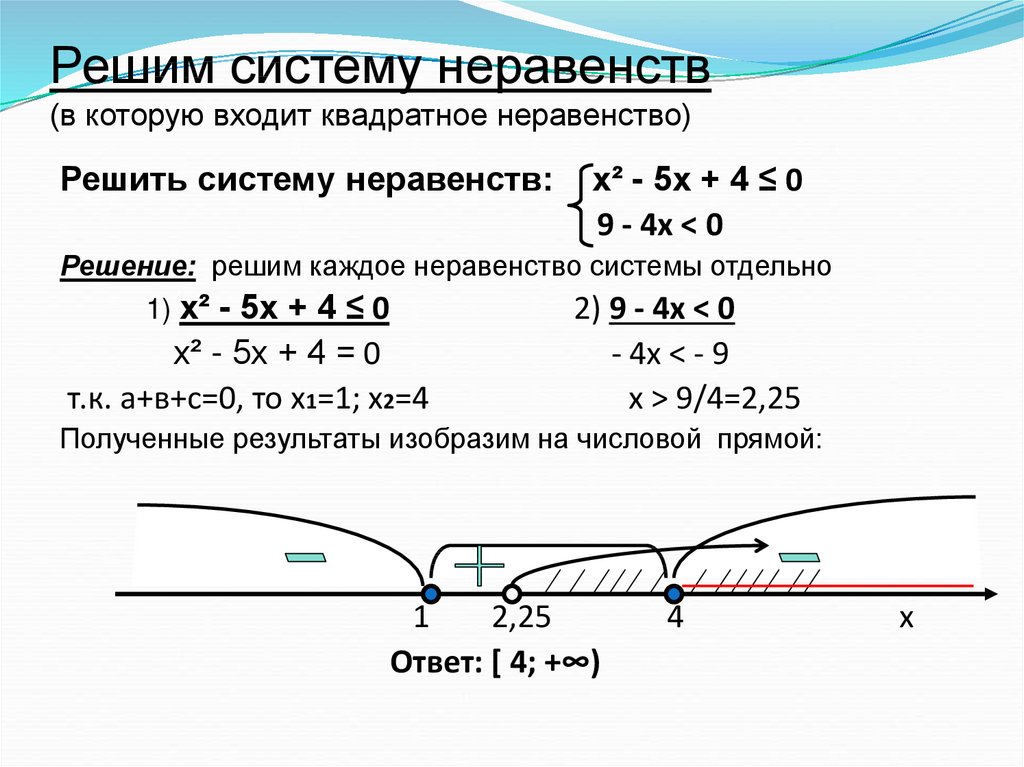
Калькулятор систем линейных неравенств: Калькулятор систем неравенств

Указанные выше примеры содержат также:

модуль или абсолютное значение: absolute(x) или |x|
квадратные корни sqrt(x),
кубические корни cbrt(x)
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
показательные функции и экспоненты exp(x)
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс acot(x)
натуральные логарифмы ln(x),
десятичные логарифмы log(x)
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x), гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x)
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x), арккосеканс acsc(x), гиперболический секанс sech(x), гиперболический косеканс csch(x), гиперболический арксеканс asech(x), гиперболический арккосеканс acsch(x)
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x)
знак числа:
sign(x)
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности), функция Лапласа laplace(x)
Факториал от x:
x! или factorial(x)
Гамма-функция gamma(x)
Функция Ламберта LambertW(x)
Тригонометрические интегралы: Si(x), Ci(x), Shi(x), Chi(x)

Содержание

Правила ввода

Можно делать следующие операции

2*x: — умножение
3/x: — деление
x^2: — возведение в квадрат
x^3: — возведение в куб
x^5: — возведение в степень
x + 7: — сложение
x — 6: — вычитание
Действительные числа: вводить в виде 7. 5, не 7,5

Постоянные

pi: — число Пи
e: — основание натурального логарифма
i: — комплексное число
oo: — символ бесконечности

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:

«Решение систем линейных неравенств» | Методическая разработка по алгебре (9 класс):

Опубликовано 13.02.2021 — 1:57 — Перцева Елена Валентиновна

подготовка к контрольной работе(для дистанционного обучения)

Скачать:

Предварительный просмотр:

Тема урока: «Решение систем линейных неравенств»

Назовите и запишите промежутки, изображённые на рисунке

Самостоятельная работа

Заполнить таблицу:

1	2	3	4	5	6	7	8

Тест

На каком рисунке изображено множество решений системы

А.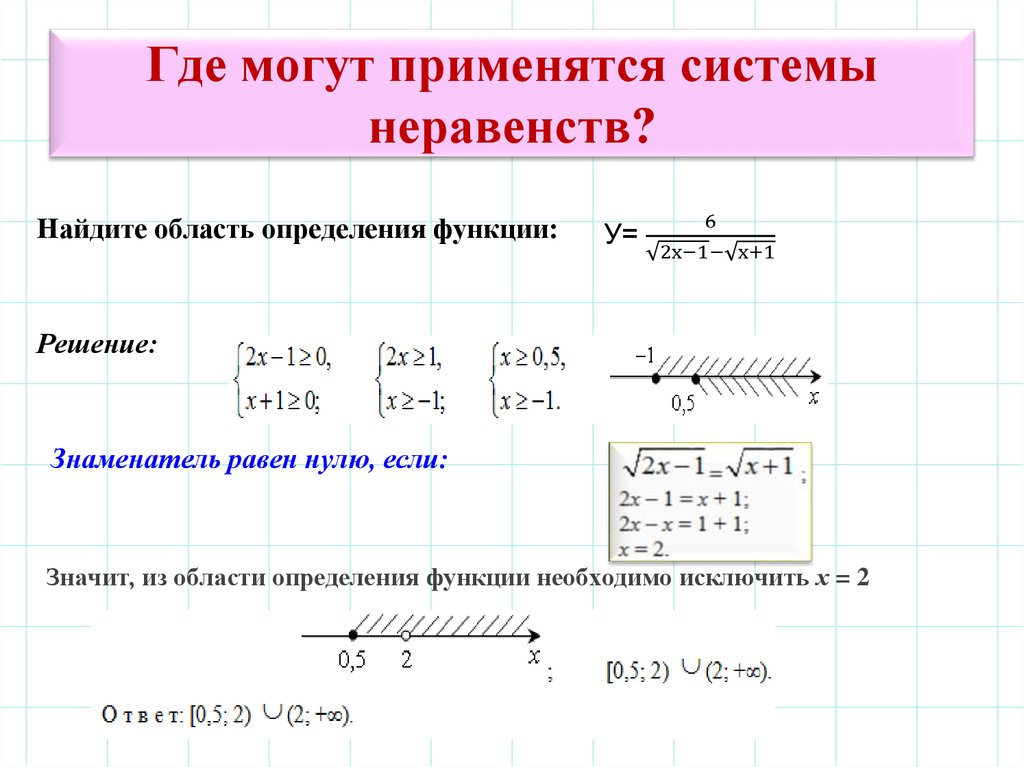 Б. В.

2 — 3 — 3 2 — 3 2

Запишите обозначение промежутка :

— 10 5

А. (-10; — 5) Б. В.

Решите неравенство 2 – 5х

А. (0,4; + ∞) Б. [0,4; + ∞) В. (- ∞; 0,4)

При каких значениях параметра а двучлен 12 – а принимает положительные значения?

А. а > 12 Б. а > — 12 В. а

При каких значениях у дробь меньше дроби ?

А. (- ∞; 4,4) Б. (- ∞; — 4,4) В.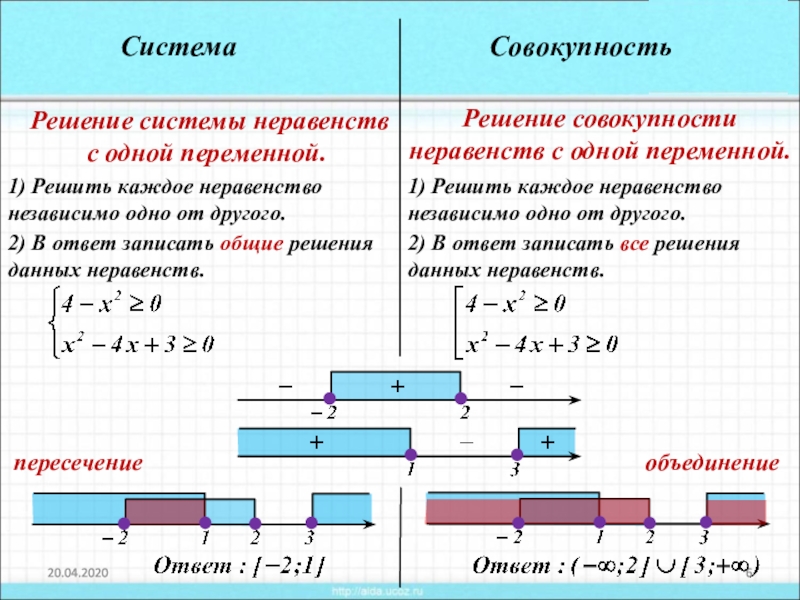 (4,4; + ∞)

Найдите наибольшее целое решение неравенства

А. – 2 Б. 0 В. – 1

Промежутку [- 2,5; 2,4] принадлежит число …

А. – 2,6 Б. 0 В. 3

Для любых значений х верно неравенство:

А. (х – 2)2 0

В. (х + 3)2 > 0 Г. х2 – 10х + 25 ≥ 0

Ответы

1	2	3	4	5	6	7	8

Используя числовую ось, найдите пересечение промежутков:

А. Б. В.

Изучение новых знаний

При решении систем неравенств мы будем использовать следующий алгоритм:

Решить каждое из неравенств системы;
Изобразить множество решений каждого неравенства на числовой оси;
Найти на числовой оси пересечение промежутков (если оно есть) и записать его с помощью неравенства или обозначения промежутка (или сделать вывод об отсутствии решения системы).

1.Решите систему неравенств:

А.

Б.

В.

2.Найти наименьшее целое решение системы неравенств:

1. 2. 3.

3.Найти наибольшее целое решение системы неравенств:

1. 2. 3.

По теме: методические разработки, презентации и конспекты

«Решение систем линейных уравнений» Урок обобщающего повторения

Урок разноуровневого обощающего повторения. ..

Методическая разработка урока алгебры в 7 классе «Различные способы решения систем линейных уравнений» способы решения систем уравнений

Урок алгебры в 7 классе направлен на обобщение и систематизацию различных способов решения систем уравнений: метода сравнения, сложения, подстановки, графического метода, метода Крамера, выбора рацион…

«Решение систем линейных неравенств»

урок изучения и первичного закрепления знаний.Цель урока: повторить решение линейных неравенств; ознакомить с алгоритмом решения систем линейных неравенств; сформировать умение решать системы линейных…

Конспект урока алгебры 8 класс по теме «Решение систем линейных неравенств»

Конспект урока алгебры 8 класс по теме «Решение систем линейных неравенств» с приложением презентации в программе SmartNotebook….

Урок по теме : «Решение систем линейных неравенств»

Повторить решение линейных неравенств; ознакомить с алгоритмом решения систем линейных неравенств; сформировать умение решать системы линейных неравенств любой сложности. …

Решение систем линейных неравенств. 7 класс

Решение систем линейных неравенств…

Конспект урока » Решение систем линейных неравенств» 7 класс

Решение систем линейных неравенств…

Калькулятор и решение неравенств

— SnapXam

Получите подробные решения ваших математических задач с помощью нашего пошагового калькулятора неравенств

. Практикуйте свои математические навыки и учитесь шаг за шагом с помощью нашего математического решателя. Проверьте все наши онлайн-калькуляторы здесь!

(◻)

—

◻/◻

◻ ²

◻ ^◻

√◻

√

^◻ √ ◻

^◻ √

∞

бревно

бревно _◻

LIM

D/DX

D ^□ _x

∫

∫ ^◻

| ◻ |

sin

cos

tan

cot

sec

csc

asin

acos

atan

acot

asec

acsc

sinh

cosh

TANH

COTH

SECH

CSCH

ASINH

ACOSH

ATANH

ACOTH

ASECH

ACSCH

Пример

Решенные проблемы

Сложные задачи

Пример решения неравенств

$4\left(x+2\right)-3\left(x-5\right)<-x+13$

Умножить один член $4$ на каждый член многочлена $\left(x+2\right)$

$4x+2\cdot 4-3\left(x-5\right)<-x+13 $

Умножить $2$ на $4$

$4x+8-3\влево(x-5\вправо)<-x+13$

Умножить один член $-3$ на каждый член полинома $\left(x-5\right)$

$4x+8-3x-5\cdot -3<-x+13$

Умножить $-5$ на $-3$

$4x+8-3x+15<-x+13$

Добавьте значения $8$ и $15$

$23+4x-3x<-x+13$

Объединение одинаковых выражений $4x$ и $-3x$

$23+x<-x+13$

Условия группировки

$23+x+x<13$

Объединение одинаковых терминов $x$ и $x$

$23+2x<13$

Перенос члена $23$ в другую часть неравенства с обратным знаком

$2x<-10$

Разделить обе части неравенства на $2$

$x<-5$

Окончательный ответ

$x<-5$

Проблемы с математикой?

Доступ к подробным пошаговым решениям тысяч проблем, число которых растет с каждым днем!

Калькулятор неравенства с шагами | Решатель неравенства

Калькулятор неравенства

Введите математическое выражение. ..

РАДДЕГ

Триггерные функции

Решить для:xyztabcdfghjklmnopqrsuvw

Решить для: xyztabcdfghjklmnopqrsuvw

Добро пожаловать в наш Калькулятор неравенства ! Этот мощный инструмент позволяет легко решить любое неравенство всего за несколько простых шагов. Просто введите неравенство в предоставленное поле ввода и нажмите кнопку «Рассчитать». Калькулятор неравенства предоставит вам пошаговое решение.

Независимо от того, являетесь ли вы студентом, пытающимся сдать экзамены по математике, или профессионалом, который ищет быстрый и точный способ решения неравенств, наш Калькулятор неравенства станет для вас идеальным инструментом. Попробуйте прямо сейчас и убедитесь, насколько это может быть полезно!

Допустимые функции и символы	Описание
квт()	Квадратный корень
лн()	Натуральный логарифм
лог() 9	Экспоненты
абс()	Абсолютное значение
sin(), cos(), tan(), csc(), sec(), кроватка()	Основные тригонометрические функции
asin(), acos(), atan(), acsc(), asec(), acot()	Обратные тригонометрические функции
sinh(), cosh(), tanh(), csch(), sech(), coth()	Гиперболические функции
asinh(), acosh(), atanh(), acsch(), asech(), acoth()	Обратные гиперболические функции
число пи	PI-номер (π = 3,14159. ..)
е	Число Непера (e= 2,71828…)
я	Для обозначения мнимой составляющей комплексного числа.

Таблица 1: Допустимые функции и символы

Содержание

1 Калькулятор неравенства
2 Определение неравенства | Что такое неравенство в математике?
3 Виды неравенств
4 Как решать неравенства
- 4. 1 Решение линейных неравенств
- 4.2 Решение квадратных неравенств
- 4.3 Как решать абсолютные неравенства

Определение неравенства | Что такое неравенство в математике?

Неравенство в математике — это утверждение, в котором значение одного выражения сравнивается со значением другого с использованием одного из следующих символов неравенства :

Меньше: <
Меньше или равно: ≤
Больше чем: >
Больше или равно: ≥

Неравенства используются для описания ситуаций, когда одно значение не равно другому значению. Они часто используются в алгебре для описания условий, которые должны быть соблюдены, чтобы решение было действительным.

Например:

x + 3 < 5 — это неравенство, говорящее, что «x + 3 меньше 5»
y ≥ 10 — это неравенство, которое говорит, что «y больше или равно 10»

Решением неравенства является набор значений, которые делают неравенство верным. Например, решением неравенства x + 3 < 5 является множество всех значений x, меньших 2 (поскольку 5 – 3 = 2). Решением неравенства y ≥ 10 является множество всех значений y, которые больше или равны 10.

Типы неравенств

Существует несколько типов неравенств:

Линейные неравенства: Это неравенства, которые включают только одну переменную и могут быть представлены в виде «ax + b < c» или «ax + b > c», где a, b и c — константы, а x — переменная. Пример линейного неравенства: «2x + 3 < 7».
Квадратные неравенства: Это неравенства, которые включают переменную, возведенную во вторую степень, например «x
2 + 2x + 1 < 0″. Квадратные неравенства можно решить, найдя значения x, которые делают неравенство верным, а затем проверив эти значения, чтобы определить, какие из них являются допустимыми решениями.
Неравенства абсолютного значения: это неравенства, которые включают абсолютное значение переменной, например «|x – 3| < 4”. Неравенства абсолютного значения можно решить, разбив их на два отдельных неравенства и решив каждое отдельно.
Рациональные неравенства: Это неравенства, включающие рациональные выражения, такие как «1/x < 2». Рациональные неравенства можно решить, найдя значения x, которые делают неравенство верным, а затем проверив эти значения, чтобы определить, какие из них являются допустимыми решениями.

Это лишь несколько примеров существующих видов неравенства. Есть много других типов неравенств, которые можно использовать в различных математических контекстах и при решении задач.

Как решать неравенства

Решение линейных неравенств

Большинство методов решения линейных уравнений применимы к вычислению линейных неравенств. Поэтому, чтобы найти решение действительного неравенства, вы можете прибавить или вычесть любое действительное число к обеим частям неравенства, а также вы можете умножить или разделить обе части на любое положительное действительное число, чтобы получить эквивалентные неравенства.

Чтобы проиллюстрировать вышеизложенное ниже, я представляю, как мы можем решить следующее линейное неравенство:

5x+3x−8>3

Шаг 1: Упростите обе части неравенства.

8x−8>3

Шаг 2: Добавьте 8 к обеим сторонам.

8x -8+8> 3+8

8x> 11

Шаг 3: Разделите обе стороны на 8.

‌‌> ‌‌

x> ‌‌

Решение: