Калькулятор сложения матриц онлайн: Онлайн калькулятор. Сложение и вычитание матриц

Как вычесть матрицу из матрицы. Действия с матрицами

Следует заметить, что данной операции поддаются только матрицы одинакового размера. При сложении двух матриц попарно суммируются все их элементы, а при вычитании мы, соответственно, имеем дело с их попарной разностью. Получив детальное и пошаговое решение, вы сможете лучше разобраться с процессом нахождения суммы и разности матриц.

Итак, перед вами две матрицы, и вам необходимо узнать их сумму, либо же разность. И то, и другое вы сможете легко и оперативно сделать, если воспользуетесь нашим онлайн калькулятором. Он будет очень вам полезен, если вы желаете разобраться в алгоритме данных операций. Теория не всегда способна дать чёткий ответ на все вопросы, куда лучше с этой задачей справляются практические расчёты. Используя онлайн калькулятор, вы получите подробную схему, по которой происходит вычитание или сложение матриц. К тому же, вы можете сначала попробовать просчитать всё самостоятельно, а затем перепроверить себя здесь.

Данный онлайн калькулятор имеет предельно простую инструкцию. Указать размеры каждой из матриц вы сможете, нажимая на иконки «+» или «-» слева от матриц и под ними. Далее вам потребуется ввести все элементы. И затем, нажав кнопку «Вычислить», вы сможете быстро получить искомое значение вместе с развёрнутым алгоритмом вычислений.

Данное методическое пособие поможет Вам научиться выполнять действия с матрицами : сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы. Весь материал изложен в простой и доступной форме, приведены соответствующие примеры, таким образом, даже неподготовленный человек сможет научиться выполнять действия с матрицами. Для самоконтроля и самопроверки Вы можете бесплатно скачать матричный калькулятор >>> .

Я буду стараться минимизировать теоретические выкладки, кое-где возможны объяснения «на пальцах» и использование ненаучных терминов. Любители основательной теории, пожалуйста, не занимайтесь критикой, наша задача –

научиться выполнять действия с матрицами .

Для СВЕРХБЫСТРОЙ подготовки по теме (у кого «горит») есть интенсивный pdf-курс Матрица, определитель и зачёт!

Матрица – это прямоугольная таблица каких-либо элементов . В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.

Обозначение: матрицы обычно обозначают прописными латинскими буквами

Пример: рассмотрим матрицу «два на три»:

Данная матрица состоит из шести элементов :

Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет:

Это просто таблица (набор) чисел!

Также договоримся

не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!

Рассматриваемая матрица имеет две строки:

и три столбца:

СТАНДАРТ : когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».

Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной , например: – матрица «три на три».

Если в матрице один столбец или одна строка , то такие матрицы также называют векторами .

На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: . По существу, координаты точки записаны в матрицу «один на два». Кстати, вот Вам и пример, почему порядок чисел имеет значение: и – это две совершенно разные точки плоскости.

Теперь переходим непосредственно к изучению действий с матрицами :

1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу) .

Вернемся к нашей матрице . Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.

Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак :

У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.

Обратный пример: . Выглядит безобразно.

Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак :

Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому что есть такая математическая народная примета:

чем больше минусов – тем больше путаницы и ошибок .

2) Действие второе. Умножение матрицы на число .

Пример:

Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.

Еще один полезный пример:

– умножение матрицы на дробь

Сначала рассмотрим то, чего делать НЕ НАДО :

Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если – окончательный ответ задания).

И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:

Из статьи

Математика для чайников или с чего начать , мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.

Единственное, что желательно сделать в этом примере – это внести минус в матрицу:

А вот если бы ВСЕ элементы матрицы делились на 7 без остатка , то тогда можно (и нужно!) было бы поделить.

Пример:

В этом случае можно и НУЖНО умножить все элементы матрицы на , так как все числа матрицы делятся на 2 без остатка .

Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.

3) Действие третье. Транспонирование матрицы .

Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.

Пример:

Транспонировать матрицу

Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:

– транспонированная матрица.

Транспонированная матрица обычно обозначается надстрочным индексом или штрихом справа вверху.

Пошаговый пример:

Транспонировать матрицу

Сначала переписываем первую строку в первый столбец:

Потом переписываем вторую строку во второй столбец:

И, наконец, переписываем третью строку в третий столбец:

Готово. Грубо говоря, транспонировать – это значит повернуть матрицу набок.

4) Действие четвертое. Сумма (разность) матриц .

Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.

Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!

Пример:

Сложить матрицы и

Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы :

Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов .

Пример:

Найти разность матриц ,

А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу :

Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.

5) Действие пятое. Умножение матриц .

Какие матрицы можно умножать?

Чтобы матрицу можно было умножить на матрицу нужно,

чтобы число столбцов матрицы равнялось числу строк матрицы .

Пример:
Можно ли умножить матрицу на матрицу ?

Значит, умножать данные матрицы можно.

А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!

Следовательно, выполнить умножение невозможно:

Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.

Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
Например, для матриц, и возможно как умножение , так и умножение

Сложение матриц $ A $ и $ B $ это арифметическая операция, в результате которой, должна получаться матрица $ C $, каждый элемент которой равен сумме соответствующих элементов складываемых матриц:

$$ c_{ij} = a_{ij} + b_{ij} $$

Более подробно формула сложения двух матриц выглядит так:

$$ A + B = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} + \begin{pmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{pmatrix} = $$

$$ = \begin{pmatrix} a_{11} + b_{11} & a_{12}+b_{12} & a_{13}+b_{13} \\ a_{21}+b_{21} & a_{22}+b_{22} & a_{23}+b_{23} \\ a_{31}+b_{31} & a_{32}+b_{32} & a_{33}+b_{33} \end{pmatrix} = C $$

Обратите внимание, что складывать и вычитать матрицы можно только одинаковой размерности. При сумме или разности будет получаться матрица $ C $ такой же размерности как и слагаемые (вычитаемые) матрицы $ A $ и $ B $. Если матрицы $ A $ и $ B $ отличаются друг от друга размерами, то сложение (вычитание) таких матриц будет ошибкой!

В формуле складываются матрицы 3 на 3, значит и получиться должна матрица 3 на 3.

Вычитание матриц полностью аналогично по алгоритму сложения, только знак минус. Каждый элемент искомой матрицы $ C $ получается благодаря вычитанию соответствующих элементов матриц $ A $ и $ B $:

$$ c_{ij} = a_{ij} — b_{ij} $$

Запишем подробную формулу вычитания двух матриц:

$$ A — B = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} — \begin{pmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{pmatrix} = $$

$$ = \begin{pmatrix} a_{11} — b_{11} & a_{12}-b_{12} & a_{13}-b_{13} \\ a_{21}-b_{21} & a_{22}-b_{22} & a_{23}-b_{23} \\ a_{31}-b_{31} & a_{32}-b_{32} & a_{33}-b_{33} \end{pmatrix} = C $$

Стоит так же заметить, что нельзя складывать и вычитать матрицы с обычными числами, а так же с другими какими-то элементами

Будет полезно знать для дальнейших решений задач с матрицами знать свойства сложения (вычитания).

Свойства

1. Если матрицы $ A,B,C $ одинаковые по размеру, тогда для них действует свойство ассоциативности: $$ A + (B + C) = (A + B) + C $$
2. Для каждой матрицы существует нулевая матрица, обозначаемая $ O $, при сложении (вычитании) с которой исходная матрица не изменяется: $$ A \pm O = A $$
3. Для каждой ненулевой матрицы $ A $ есть противоположная матрица $ (-A) $ сумма с которой обращается в нуль: $$ A + (-A) = 0 $$
4. При сложении (вычитании) матриц допустимо свойство коммутативности, то есть матрицы $ A $ и $ B $ можно менять местами: $$ A + B = B + A $$ $$ A — B = B — A $$

Примеры решений

Пример 1

Даны матрицы $ A = \begin{pmatrix} 2&3 \\ -1& 4 \end{pmatrix} $ и $ B = \begin{pmatrix} 1&-3 \\ 2&5 \end{pmatrix} $. Выполнить сложение матриц, а затем вычитание.

Решение

Первым делом проверяем матрицы на размерность. У матрицы $ A $ размерность $ 2 \times 2 $, у второй матрицы $ B $ размерность тоже $ 2 \times 2 $. Это значит, что с данными матрицами можно провести совместную операцию по сложению и вычитанию. Напомним, что для суммы нужно выполнить попарное сложение соответствующих элементов матриц $ A \text{ и } B $. $$ A + B = \begin{pmatrix} 2&3 \\ -1& 4 \end{pmatrix} + \begin{pmatrix} 1&-3 \\ 2&5 \end{pmatrix} = $$ $$ = \begin{pmatrix} 2 + 1 & 3 + (-3) \\ -1 + 2 & 4 + 5 \end{pmatrix} = \begin{pmatrix} 3 & 0 \\ 1 & 9 \end{pmatrix} $$ Аналогично сумме находим разность матриц с помощью замены знака «плюс» на «минус»: $$ A — B = \begin{pmatrix} 2&3 \\ -1& 4 \end{pmatrix} + \begin{pmatrix} 1&-3 \\ 2&5 \end{pmatrix} = $$ $$ = \begin{pmatrix} 2 — 1 & 3 — (-3) \\ -1 — 2 & 4 — 5 \end{pmatrix} = \begin{pmatrix} 1 & 6 \\ -3 & -1 \end{pmatrix} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ A + B = \begin{pmatrix} 3 & 0 \\ 1 & 9 \end{pmatrix}; A — B = \begin{pmatrix} 1 & 6 \\ -3 & -1 \end{pmatrix} $$

В статье: «Сложение и вычитание матриц» были даны определения, правила, замечания, свойства операций и практические примеры решения.

Сложение матриц:

Вычитание и сложение матриц сводится к соответствующим операциям над их элементами. Операция сложения матриц вводится только для матриц одинакового размера, т. е. для матриц , у которых число строк и столбцов соответственно равно. Суммой матриц А и В, называется матрица С, элементы которой равны сумме соответствующих элементов. С = А + В c ij = a ij + b ij Аналогично определяется разность матриц .

Умножение матрицы на число:

Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число. Произведением матрицы А на число k называется матрица В, такая что

b ij = k × a ij . В = k × A b ij = k × a ij . Матрица — А = (-1) × А называется противоположной матрице А.

Свойства сложения матриц и умножения матрицы на число:

Операции сложения матриц и умножения матрицы на число обладают следующими свойствами: 1. А + В = В + А; 2. А + (В + С) = (А + В) + С; 3. А + 0 = А; 4. А — А = 0; 5. 1 × А = А; 6. α × (А + В) = αА + αВ; 7. (α + β) × А = αА + βА; 8. α × (βА) = (αβ) × А; , где А, В и С — матрицы, α и β — числа.

Умножение матриц (Произведение матриц):

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы . Произведением матрицы А m×n на матрицу В n×p , называется матрица С m×p такая, что с ik = a i1 × b 1k + a i2 × b 2k + … + a in × b nk , т. е. находиться сумма произведений элементов i — ой строки матрицы А на соответствующие элементы j — ого столбца матрицы В. Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А × Е = Е × А = А, где А квадратная матрица , Е — единичная матрица того же размера.

Свойства умножения матриц:

Умножение матриц не коммутативно, т.е. АВ ≠ ВА даже если определены оба произведения. Однако, если для каких — либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными. Самым характерным примером может служить единичная матрица , которая является перестановочной с любой другой матрицей того же размера. Перестановочными могут быть только квадратные матрицы одного и того же порядка. А × Е = Е × А = А

Умножение матриц обладает следующими свойствами: 1. А × (В × С) = (А × В) × С; 2. А × (В + С) = АВ + АС; 3. (А + В) × С = АС + ВС; 4. α × (АВ) = (αА) × В; 5. А × 0 = 0; 0 × А = 0; 6. (АВ) Т = В Т А Т; 7. (АВС) Т = С Т В Т А Т; 8. (А + В) Т = А Т + В Т;

2. Определители 2-го и 3-го порядков. Свойства определителей.

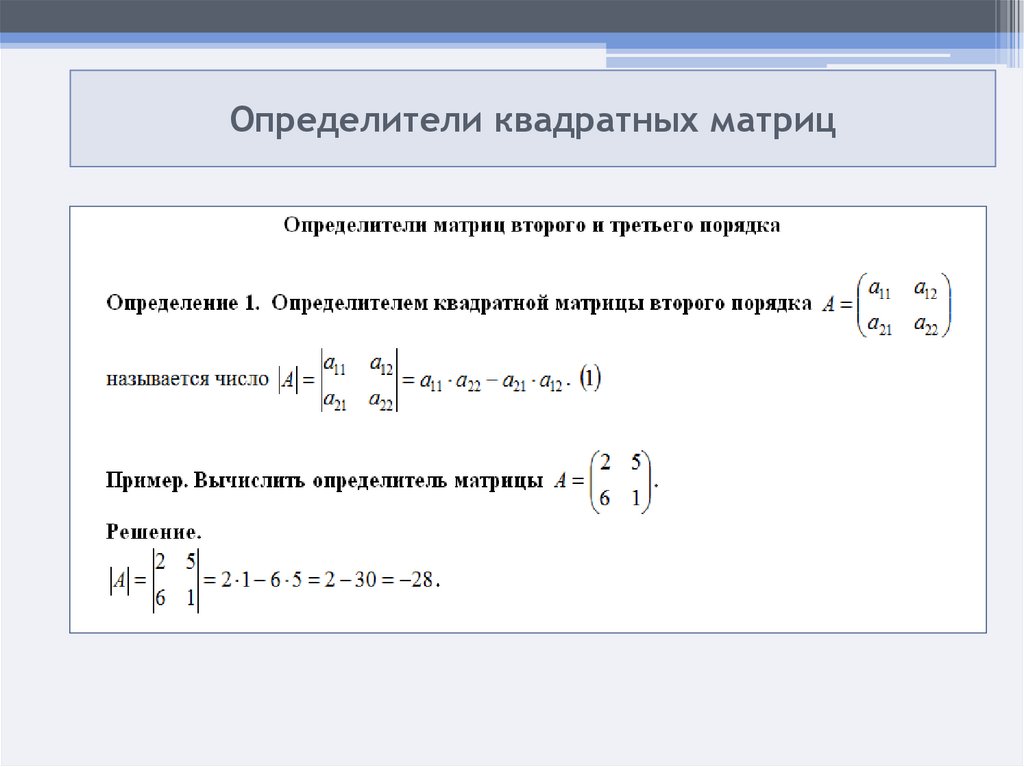
Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:

Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:

Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы . Каждое слагаемое состоит из произведения трех сомножителей.

Знаки, с которыми члены определителя матрицы входят в формулу нахождения определителя матрицы третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса.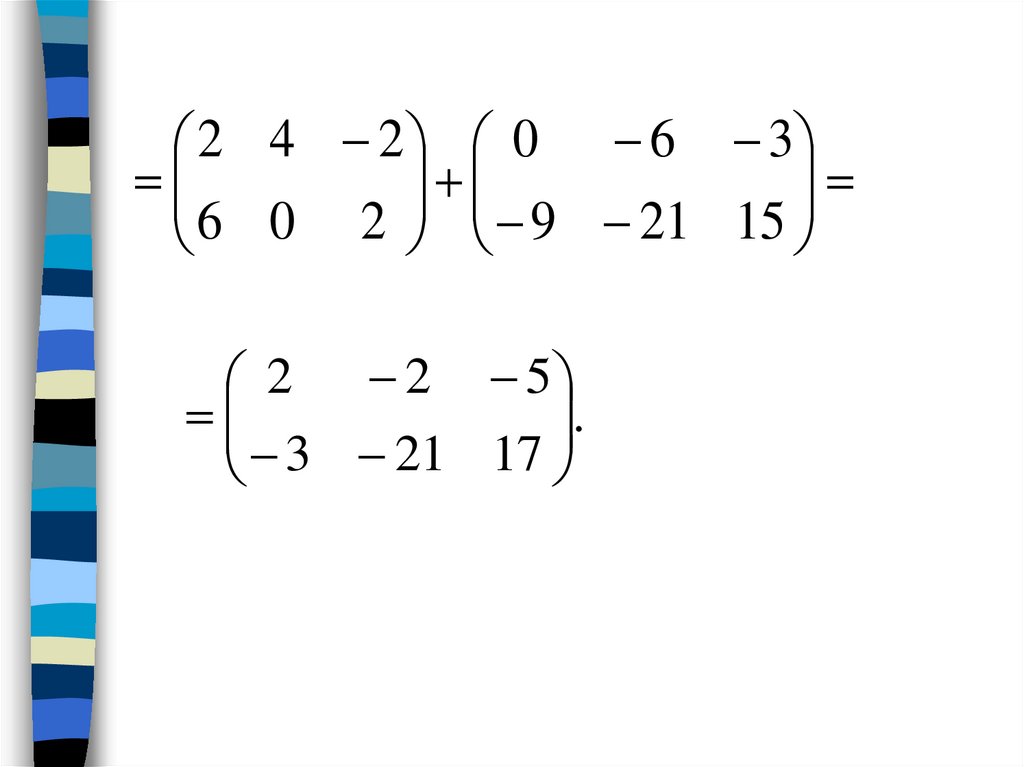 Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.

Определить количество слагаемых, для нахождения определителя матрицы , в алгебраической сумме, можно вычислив факториал: 2! = 1 × 2 = 2 3! = 1 × 2 × 3 = 6

Свойства определителей матриц

Свойства определителей матриц:

Свойство № 1:

Определитель матрицы не изменится, если его строки заменить столбцами, причем каждую строку столбцом с тем же номером, и наоборот (Транспонирование). |А| = |А| Т

Следствие:

Столбцы и строки определителя матрицы равноправны, следовательно, свойства присущие строкам выполняются и для столбцов.

Свойство № 2:

При перестановке 2-х строк или столбцов определитель матрицы изменит знак на противоположный, сохраняя абсолютную величину, т.е.:

Свойство № 3:

Определитель матрицы , имеющий два одинаковых ряда, равен нулю.

Свойство № 4:

Общий множитель элементов какого-либо ряда определителя матрицы можно вынести за знак определителя .

Следствия из свойств № 3 и № 4:

Если все элементы некоторого ряда (строки или столбца) пропорциональны соответствующим элементам параллельного ряда, то такой определитель матрицы равен нулю.

Свойство № 5:

определителя матрицы равны нулю, то сам определитель матрицы равен нулю.

Свойство № 6:

Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель матрицы можно представить в виде суммы 2-х определителей по формуле:

Свойство № 7:

Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель матрицы не изменит своей величины.

Пример применения свойств для вычисления определителя матрицы :

Калькулятор матриц



Калькулятор матриц

Калькулятор матриц с подробным решением поможет вычислить матрицу онлайн — бесплатно!

Введите матрицу, нажав на кнопку «матрица». Появится матрица 2 на 2. Каждая ячейка матрицы должна быть в фигурных скобках {}.

Введите данные в ячейку, кликнув мышью внутри фигурных скобок либо перейдите туда, используя кнопки влево и вправо. Чтобы добавить ячейку, установите курсор вне фигурных скобок с помощью мыши либо кнопок влево, вправо и нажмите кнопку добавления элемента. Появятся фигурные скобки, введите туда значение элемента. Для добавления строки нажмите кнопку добавления строки.

Наш искусственный интеллект решает сложные математические задания за секунды

Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!

Пример:

Пример:

Пример:

Переменные: Параметры:

Матрицы применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. При этом количество строк матрицы соответствует числу уравнений, а количество столбцов – количеству неизвестных. Как результат – решение систем линейных уравнений сводится к операциям над матрицами.

Матрица записывается в виде прямоугольной таблицы элементов кольца или поля (к примеру, целых, комплексных или действительных чисел). Является совокупностью строк и столбцов, на пересечении которых находятся ее элементы. Размер матрицы задается количеством строк и столбцов.

При решении матриц имеются определённые правила. Например, можно сложить или отнять любую строку матрицу с другой любой строкой матрицы. При этом решения системы уравнений данных матриц не поменяются. Таким образом, если мы решаем уравнения, представленные матрицей вручную, то подобными манипуляциями мы должны привести матрицу к определённому виду, например обнулить по диагонали все значения матрицы, получив искомые корни.

Если Вам решать матрицы не хочется вручную, то можете воспользоваться онлайн калькулятором решения матриц, который выдаст Вам решение любой матрицы автоматически.

Так же читайте нашу статью «Решить систему уравнений методом сложения онлайн решателем»

Воспользоваться инженерным калькулятором, решить квадратное уравнение или решить систему уравнений вы сможете на сайте pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей группе Вконтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Калькулятор сложения матриц с шагами и решением

Введение в калькулятор сложения матриц

Калькулятор суммы матриц с шагами — это онлайн-инструмент, который вычисляет сложение двух матриц. Он использует простую формулу сложения матриц, добавляя соответствующие записи в калькулятор в дополнение к двум матрицам. Он применяет формулу сложения в том же порядке для обеих двух матриц.

В матричной алгебре мы обычно применяем разные операции над матрицами одного порядка. Операции с матрицей меньшего порядка, то есть 2 на 2, проще, чем решение матриц 4 на 4 из-за длительных вычислений. Вот почему мы представляем онлайн-инструмент, который может вычислять сложение матриц до порядка 4 на 4.

Формула, используемая Matrix Add Calculator

Матрица представляет собой прямоугольный массив чисел, расположенных в строках и столбцах. Матрица, содержащая m строк и n столбцов, показанная ниже,

$$ \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix} $$ Где m= количество строк n= количество столбцов К матрицам можно применять сложение и вычитание, как в обычная алгебра. Таким образом, сложение двух матриц A и B порядка m×n можно определить как: $$ A+B \;=\; \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33 } \end{bmatrix} \;+\; \begin{bmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33 } \end{bmatrix} $$

Калькулятор сложения матриц использует приведенную выше формулу для вычисления сложения двух матриц. Отсюда также следует условие сложения матриц, согласно которому порядок обеих матриц должен быть одинаковым для выполнения сложения.

Как пользоваться Калькулятором суммы матриц?

Есть несколько простых шагов, чтобы использовать этот инструмент и решить вопрос: как сложить две матрицы? Вот эти шаги:

1. На первом шаге вы должны ввести количество строк и столбцов для матрицы A.
2. Теперь введите значения всех элементов матрицы A.
3. Снова введите количество строк и столбцов матрицы B, а затем введите значения всех элементов матрицы B.
4. Нажмите кнопку расчета.

Вы получите сложение матриц после нажатия на кнопку расчета.

Зачем использовать калькулятор сложения для матрицы?

В матричной алгебре существует несколько операций умножения матриц. Но также существуют различные условия, связанные с каждой операцией. Точно так же существует условие для добавления двух матриц, что порядок обеих матриц должен быть одинаковым.

Когда вы вычисляете сложение двух матриц вручную, есть много шансов, что вы можете забыть добавить какую-либо запись в матрицу. Или, иногда, вы можете не следовать дополнительному условию матрицы. Вот почему вам нужно использовать этот инструмент.

Преимущества использования Калькулятора формул сложения матриц

Матрица широко применяется в математике, поскольку она помогает решать линейные уравнения. Он имеет множество применений в научных областях. Этот калькулятор можно использовать для расчета сложения матриц. Потому что решатель сложения матриц имеет много полезных применений в дополнение к двум матрицам. Эти преимущества:

1. Калькулятор суммы матриц может сэкономить ваше время на вычислении долгосрочного сложения матриц и предоставить вам подробное решение о том, как сложить две матрицы.
2. Калькулятор сложения матриц поможет вам не пропустить ни одной записи.
3. Это может помочь вам решить многие задачи, связанные с наукой и линейными уравнениями.
4. Калькулятор добавления матриц — это бесплатный онлайн-инструмент, поэтому вам не нужно платить комиссию.
Калькулятор суммы матриц
5. предоставляет пошаговую процедуру для понимания каждого шага, выполняемого этим инструментом.

Как найти калькулятор сложения матриц?

Вы можете найти этот инструмент, выполнив поиск на сайте www.calculatores.com. На этом сайте будет список математических инструментов. Вы можете выбрать инструмент добавления матрицы из этого списка.

Хамза Харун

Последнее обновление 05 апреля 2022 г.

Я автор контента и создатель контента. Мне нравится писать контент на разные темы. Помимо писательства, я SEO-ASO-SMM специалист и любитель футбола.

Калькулятор матриц онлайн — расчет суммы двух матриц

Сумма матриц, расчет онлайн

Сводка :

Калькулятор матриц позволяет онлайн вычислить сумму двух матриц с шагом вычисления.

matrix_sum онлайн

---

Описание :

Калькулятор может рассчитать онлайн сумму двух матриц . Калькулятор матриц может вычислять сумму матриц , коэффициенты которых имеют буквы или цифры, это формальный калькулятор вычисления матрицы.

Вычисление суммы матриц

Калькулятор может вычислить сумму двух матриц с результатами в точной форме: для вычисления суммы матриц `((3,3,4),(1,2,0),(-5,1,1))+((3,3,4),(1,4,0) ,(2,1,1))`, введите matrix_sum(`[[3;1;-5];[3;2;1];[4;0;1]];[[3;1;2];[3;4;1];[4; 0;1]]`), после расчета возвращается результат.

Калькулятор допускает символьные вычисления, можно использовать и буквы, чтобы вычислить сумму двух матриц следующим образом: `((а,3),(а/2,4))+((а,1),(а/2,2))`, введите matrix_sum(`[[а;а/2];[3;4]];[[а;а/2];[1;2]]`), после расчета возвращается результат.

Синтаксис:

matrix_sum(матрица;матрица)

---

Примеры:

matrix_sum(`[[3;1;-5];[3;2;1];[4;0;1]];[ [3;1;2];[3;4;1];[4;0;1]]`) возвращает `[[6;2;-3];[6;6;2];[8;0;2]]`

Расчет онлайн с помощью matrix_sum (калькулятор суммы матриц)

См. также

Список связанных калькуляторов:

• Матричный калькулятор : matrix_calculator. Калькулятор матриц позволяет производить расчеты с матрицами онлайн.
• Калькулятор определителя: определитель. Функция определителя вычисляет онлайн определитель векторов или определитель матрицы.
• Разница между двумя матрицами: matrix_difference. Калькулятор матриц позволяет вычислить в режиме онлайн разницу между двумя матрицами с пошаговым расчетом.
• Калькулятор обратной матрицы: inverse_matrix. Функция inverse_matrix позволяет вычислить в режиме онлайн обратную матрицу.
• Калькулятор матрицы продуктов: matrix_product. Калькулятор матриц позволяет в режиме онлайн рассчитать произведение двух матриц с шагом вычисления.
• Решение системы линейных уравнений :solve_equations. Решатель систем линейных уравнений позволяет решать уравнения с несколькими неизвестными: система уравнений с 2 ​​неизвестными, система уравнений с 3 неизвестными, система с n неизвестными.
• Калькулятор матрицы суммы: matrix_sum. Калькулятор матриц позволяет вычислить онлайн сумму двух матриц с шагом расчета.

  No related posts.