Предел функции, правило Лопиталя
Применение правила Лопиталя необходимо для вычисления пределов при получении неопределенностей вида 00 и ∞∞.
Имеются неопределенности вида 0·∞ и ∞-∞.
Самой важной частью правила Лопиталя является дифференцирование функции и нахождение ее производной.
Определение 1Когда limx→x0f(x)g(x)=00 или ∞∞ и функции f(x), g(x) являются дифференцируемыми в пределах точки х0, тогда limx→x0f(x)g(x)=limx→x0f'(x)g'(x).
Если неопределенность нерешаема после применения правила Лопиталя, тогда необходимо снова его применить. Для полного понятия рассмотрим несколько примеров.
Пример 1Произвести вычисления, применив правило Лопиталя limx→0sin2(3x)x·cos(x).
Решение
Для решения по правилу Лопиталя для начала необходимо произвести подстановку. Получаем, что limx→0sin2(3x)x·cos(x)=sin2(3·0)0·cos(0)=00.
Теперь можно переходить к вычислению пределов, используя правило. Получаем, что
limx→0sin2(3x)x·cos(x)=00=limx→0sin2(3x)’x·cos(x)’=limx→02sin(3x)(sin(3x))’x’·cos(x)+x·(cos(x))’==limx→06 sin(3x)cos(3x)cos(x)-x·sin(x)=6sin(3·0)cos(3·0)cos(0)-0·sin(0)=01=0
Ответ: limx→0sin2(3x)x·cos(x)=0.
Вычислить предел заданной функции limx→∞ln(x)x.
Решение
Производим постановку бесконечностью. Получаем, что
limx→∞ln(x)x=ln(∞)∞=∞∞
Полученная неопределенность указывает на то, что необходимо применить правило Лопиталя. Имеем, что
limx→∞ln(x)x=∞∞=limx→∞ln(x)’x’=limx→∞1×1=1∞=0
Ответ: limx→∞ln(x)x=0
Пример 3Вычислить предел заданной функции limx→0+0(x4ln(x))
Решение
Производим подстановку значения x. получаем, что
limx→0+0(x4ln(x))=(0+0)4·ln(0+0)=0·(-∞)
Решение привело к неопределенности вида ноль умноженный на отрицательную бесконечность. Это указывает на то, что необходимо обратиться к таблице неопределенностей и принять решения для выбора метода нахождения этого предела. После преобразования применяем правило Лопиталя. Получаем, что
limx→0+0(x4ln(x))=0·(-∞)=limx→0+0ln(x)x-4=ln(0+0)(0+0)-4=-∞+∞
Приход к неопределенности говорит о том, что необходимо повторное применение этого правила.
Имеем, что
limx→0+0(x4ln(x))=0·(-∞)=limx→0+0ln(x)x-4=-∞+∞==limx→0+0(ln(x))'(x-4)’=limx→0+01x-4-5=-14limx→0+01x-4=-14·1(0+0)-4==-14·(0+0)4=0
Ответ: limx→0+0(x4ln(x))=0
Пример 4Выполнить вычисление предела функции limx→0ctg2(x)-1×2.
Решение
После подстановки получаем
limx→0ctg2(x)-1×2=∞-∞
Наличие неопределенности указывает на то, что следует использовать правило Лопиталя. Получаем, что
limx→0ctg2(x)-1×2=∞-∞=limx→0cos2(x)sin2(x)-1×2==limx→0x2cos2(x)-sin2(x)x2sin2(x)=limx→0x cos x-sin xx cos x+sin xx2sin2(x)==limx→0x cos x-sin xx sin2(x)x cos x+sin xx=limx→0xcos x-sinxxsin2(x)cos x+sin xx==limx→0cos x+sin xxlimx→0xcos x-sin xxsin2(x)=2limx→0x cosx-sin xx sin2 (x)==20·cos(0)-sin(0)0·sin2(0)=00
Для последнего перехода использовался первый замечательный предел. После чего приходим к решению по Лопиталю. Получим, что
2limx→0x cosx-sin xx sin2 (x)=00=2limx→0(x cosx -sin x)'(x sin2(x))’==2limx→0cos x-x sin x-cos xsin2(x)+2x sin x cos x=2limx→0-xsin(x)+2x cos x=00
Так как неопределенность не ушла, необходимо еще одно применение правила Лопиталя.
Получаем предел вида
2limx→0-xsin(x)+2x cos x=00=2limx→0-x’sin(x)+2x cos x’==2limx→01cos x+2cos x-2xsin x=-2·13·cos(0)-2·0·sin(0)=-23
Ответ: limx→0ctg2(x)-1×2=-23
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
замечательный предел
This site uses cookies. Some of these cookies are essential to the operation of the site, while others help to improve your experience by providing insights into how the site is being used. For more information, please see the ProZ.com privacy policy.
Cookie settings
- KudoZ™ Top
русский => немецкий
Математика и статистика
немецкий translation: der wichtige Grenzwert oder der wichtige Limes
| 14:45 Jan 11, 2006 |
| Перевод в паре русский => немецкий [PRO] Science — Математика и статистика | |||
|---|---|---|---|
| |||
| Выбранный ответ от: Jarema Украина Local time: 06:31 | ||
Grading comment
| |||
Der Grenzwert einer Funktion ist derjenige Wert, den die Funktion haben müsste, um an der jeweiligen Stelle stetig zu sein.| Все предложенные варианты перевода | ||||
|---|---|---|---|---|
| 4 | der wichtige Grenzwert oder der wichtige Limes |
| ||
| 3 | massgebend |
|
29 мин степень уверенности:
| замечательный п& der wichtige Grenzwert oder der wichtige Limes Пояснение: In der Mathematik bezeichnet der Limes oder Grenzwert einer Folge denjenigen Wert, den man sich als das Folgenglied mit Index „unendlich“ vorstellen kann. http://de.wikipedia.org/wiki/Limes_(Mathematik)#Wichtige_Gre… ————————————————— Çíàþ òî÷íî, ïåðåâîäèë ìàòåìàòè÷åñêèå òåêñòû è êîíñóëüòèðîâàëñÿ. Äà è ñàì âûñøóþ ìàòåìàòèêó èçó÷àë. |
| |
Grading comment
| ||
| Login to enter a peer comment (or grade) | ||
Der Grenzwert einer Funktion ist derjenige Wert, den die Funktion haben müsste, um an der jeweiligen Stelle stetig zu sein.1 час степень уверенности:
| çàìå÷àòåëüíûé ïðåäåë massgebend Пояснение: |
| |
| Login to enter a peer comment (or grade) | ||
Login or register (free and only takes a few minutes) to participate in this question.
You will also have access to many other tools and opportunities designed for those who have language-related jobs (or are passionate about them). Participation is free and the site has a strict confidentiality policy.
Return to KudoZ list
KudoZ™ translation help
Сеть KudoZ — система, позволяющая переводчикам и другим участникам сайта оказывать друг другу помощь в переводе и интерпретации отдельных терминов, словосочетаний и коротких фраз.
- Overview
- Latest translation questions
- Ask a translation question
See also:
ProZ.com term search
Search millions of term translations
Стандартное отклонение и стандартная ошибка в Excel: функции и примеры формул
В учебнике объясняется сущность стандартного отклонения и стандартной ошибки среднего, а также какая формула лучше всего используется для расчета стандартного отклонения в Excel.
В описательной статистике среднее арифметическое (также называемое средним) и стандартное отклонение являются двумя тесно связанными понятиями.
Но если первое понятно большинству, то второе понимают немногие. Цель этого руководства — пролить свет на то, что на самом деле представляет собой стандартное отклонение и как его рассчитать в Excel.
Что такое стандартное отклонение?
Стандартное отклонение — это мера, показывающая, насколько значения набора данных отклоняются (разбросаны) от среднего значения. Другими словами, стандартное отклонение показывает, близки ли ваши данные к среднему значению или сильно колеблются.
Стандартное отклонение предназначено для того, чтобы помочь вам понять, действительно ли среднее значение возвращает «типичные» данные. Чем ближе стандартное отклонение к нулю, тем ниже изменчивость данных и тем надежнее среднее значение. Стандартное отклонение, равное 0, указывает на то, что каждое значение в наборе данных точно равно среднему значению. Чем выше стандартное отклонение, тем больше вариаций в данных и тем менее точным является среднее значение.
Чтобы лучше понять, как это работает, взгляните на следующие данные:
Для биологии стандартное отклонение равно 5 (округлено до целого числа), что говорит нам о том, что большинство результатов не отличаются от среднего значения более чем на 5 баллов.
Это хорошо? Что ж, да, это указывает на то, что оценки студентов по биологии довольно постоянны.
Для математики стандартное отклонение равно 23. Это показывает, что существует огромная дисперсия (разброс) в баллах, а это означает, что некоторые учащиеся справились намного лучше, а некоторые намного хуже, чем в среднем.
На практике стандартное отклонение часто используется бизнес-аналитиками в качестве меры инвестиционного риска: чем выше стандартное отклонение, тем выше волатильность доходности.
Стандартное отклонение выборки в сравнении со стандартным отклонением генеральной совокупности
В отношении стандартного отклонения вы можете часто слышать термины «выборка» и «совокупность», которые относятся к полноте данных, с которыми вы работаете. Основное отличие заключается в следующем:
- Население включает в себя все элементы из набора данных.
- Выборка — это подмножество данных, которое включает один или несколько элементов генеральной совокупности.
Исследователи и аналитики оперируют стандартным отклонением выборки и генеральной совокупности в различных ситуациях. Например, при подведении итогов экзаменов класса учащихся учитель будет использовать стандартное отклонение совокупности. Статистики, рассчитывающие средний балл SAT по стране, будут использовать стандартное отклонение выборки, потому что им представлены данные только выборки, а не всего населения.
Понимание формулы стандартного отклонения
Причина, по которой характер данных имеет значение, заключается в том, что стандартное отклонение генеральной совокупности и стандартное отклонение выборки рассчитываются по немного отличающимся формулам:
Стандартное отклонение выборки | Стандартное отклонение населения |
Где:
- x i являются отдельными значениями в наборе данных
- x — среднее значение всех x значений
- n — общее количество x значений в наборе данных
Возникли трудности с пониманием формул? Разбивка их на простые шаги может помочь.
Но сначала давайте поработаем над некоторыми примерами данных:
1. Рассчитать среднее значение
Сначала вы находите среднее значение всех значений в наборе данных ( x в формулах выше). При расчете вручную вы складываете числа, а затем делите сумму на количество этих чисел, например:
.(1+2+4+5+6+8+9)/7=5
Чтобы найти среднее значение в Excel, используйте функцию СРЗНАЧ, например. =СРЗНАЧ(A2:G2)
2. Для каждого числа вычтите среднее значение и возведите результат в квадрат
Это часть формулы стандартного отклонения, которая гласит: ( x i — x) 2
Чтобы представить себе, что происходит на самом деле, взгляните на следующие изображения.
В этом примере среднее значение равно 5, поэтому мы вычисляем разницу между каждой точкой данных и 5.
Затем вы возводите в квадрат разности, превращая их все в положительные числа:
3. Сложите квадраты разностей
Чтобы сказать «суммировать» в математике, вы используете сигма Σ.
Итак, теперь мы складываем квадраты разностей, чтобы завершить эту часть формулы: Σ( x i — x) 2
16 + 9 + 1 + 1 + 9+ 16 = 52
4. Разделить общую сумму квадратов разностей на количество значений
До сих пор формулы стандартного отклонения выборки и стандартного отклонения совокупности были идентичными. На данный момент они разные.
Для стандартного отклонения выборки вы получаете дисперсию выборки путем деления общих квадратов разностей на размер выборки минус 1:
52 / (7-1) = 8,67
Для стандартного отклонения совокупности , вы найдете среднее квадратов разностей путем деления суммы квадратов разностей на их количество:
52/7 = 7,43
Почему такая разница в формулах? Потому что в формуле выборочного стандартного отклонения вам нужно скорректировать смещение в оценке среднего значения выборки вместо истинного среднего значения генеральной совокупности.
И вы делаете это, используя n — 1 вместо n , что называется поправкой Бесселя.
5. Извлеките квадратный корень
Наконец, извлеките квадратный корень из приведенных выше чисел, и вы получите стандартное отклонение (в приведенных ниже уравнениях, округленное до 2 знаков после запятой):
| Стандартное отклонение выборки | Стандартное отклонение населения |
| √8,67 = 2,94 | √7,43 = 2,73 |
В Microsoft Excel стандартное отклонение вычисляется таким же образом, но все вышеуказанные вычисления выполняются скрыто. Ключевым моментом для вас является выбор правильной функции стандартного отклонения, о чем следующий раздел даст вам некоторые подсказки.
Как рассчитать стандартное отклонение в Excel
Всего существует шесть различных функций для определения стандартного отклонения в Excel. Какой из них использовать, зависит в первую очередь от характера данных, с которыми вы работаете — будь то вся совокупность или выборка.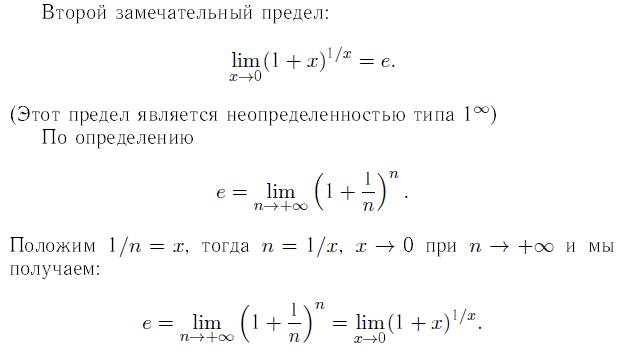
Функции для расчета стандартного отклонения выборки в Excel
Для расчета стандартного отклонения на основе выборки используйте одну из следующих формул (все они основаны на методе «n-1», описанном выше).
Функция Excel СТАНДОТКЛОН
СТАНДОТКЛОН(число1,[число2],…) — самая старая функция Excel для оценки стандартного отклонения на основе выборки, доступная во всех версиях Excel с 2003 по 2019.
В Excel 2007 и более поздних версиях STDEV может принимать до 255 аргументов, которые могут быть представлены числами, массивами, именованными диапазонами или ссылками на ячейки, содержащие числа. В Excel 2003 функция может принимать не более 30 аргументов.
Учитываются логические значения и текстовые представления чисел, указанные непосредственно в списке аргументов. В массивах и ссылках учитываются только числа; пустые ячейки, логические значения ИСТИНА и ЛОЖЬ, текстовые и ошибочные значения игнорируются.
Примечание.
СТАНДОТКЛОН Excel — это устаревшая функция, которая сохраняется в более новых версиях Excel только для обратной совместимости. Однако Microsoft не дает никаких обещаний относительно будущих версий. Поэтому в Excel 2010 и более поздних версиях рекомендуется использовать СТАНДОТКЛОН.С вместо СТАНДОТКЛОН.
Функция Excel СТАНДОТКЛ.С
СТАНДОТКЛОН.С(число1,[число2],…) — это улучшенная версия СТАНДОТКЛОН, представленная в Excel 2010.
Как и СТАНДОТКЛОН, функция СТАНДОТКЛОН.С вычисляет выборочное стандартное отклонение набора значений на основе классической формулы выборочного стандартного отклонения, рассмотренной в предыдущем разделе.
Функция Excel STDEVA
СТАНДОТКЛОН(значение1, [значение2], …) — еще одна функция для расчета стандартного отклонения выборки в Excel. Он отличается от двух предыдущих только способом обработки логических и текстовых значений:
- Подсчитываются все логических значений , независимо от того, содержатся ли они в массивах или ссылках или введены непосредственно в список аргументов (ИСТИНА оценивается как 1, ЛОЖЬ оценивается как 0).
- Текстовые значения в массивах или ссылочных аргументах считаются равными 0, включая пустые строки («»), текстовые представления чисел и любой другой текст. Текстовые представления чисел, указанные непосредственно в списке аргументов, учитываются как числа, которые они представляют (вот пример формулы).
- Пустые ячейки игнорируются.
Примечание. Чтобы образец формулы стандартного отклонения работал правильно, предоставленные аргументы должны содержать не менее двух числовых значений, в противном случае #DIV/0! возвращается ошибка.
Функции для расчета стандартного отклонения генеральной совокупности в Excel
Если вы имеете дело со всей совокупностью, используйте одну из следующих функций для расчета стандартного отклонения в Excel. Эти функции основаны на методе «n».
Функция Excel СТАНДОТКЛОН
СТАНДОТКЛОН(число1,[число2],…) — это старая функция Excel для нахождения стандартного отклонения совокупности.
В новых версиях Excel 2010, 2013, 2016 и 2019 она заменена улучшенной функцией СТАНДОТКЛОН.П, но по-прежнему сохранена для обратной совместимости.
Функция Excel STDEV.P
СТАНДОТКЛОН.П(число1,[число2],…) — это современная версия функции СТАНДОТКЛОН, обеспечивающая повышенную точность. Он доступен в Excel 2010 и более поздних версиях.
Как и их аналогичные образцы стандартного отклонения, в массивах или ссылочных аргументах функции СТАНДОТКЛОН и СТАНДОТКЛОН.П считают только числа. В списке аргументов также учитываются логические значения и текстовые представления чисел.
Функция Excel СТАНДОТКЛОНПА
СТАНДОТКЛОНПА(значение1, [значение2], …) вычисляет стандартное отклонение совокупности, включая текстовые и логические значения. Что касается нечисловых значений, СТАНДОТКЛОНПА работает точно так же, как функция СТАНДОТКЛОН.
Примечание. Какую бы формулу стандартного отклонения Excel вы ни использовали, она вернет ошибку, если один или несколько аргументов содержат значение ошибки, возвращаемое другой функцией или текстом, который нельзя интерпретировать как число.
Какую функцию стандартного отклонения Excel использовать?
Различные функции стандартного отклонения в Excel определенно могут вызвать путаницу, особенно у неопытных пользователей. Чтобы выбрать правильную формулу стандартного отклонения для конкретной задачи, просто ответьте на следующие 3 вопроса:
- Вы рассчитываете стандартное отклонение выборки или генеральной совокупности?
- Какую версию Excel вы используете?
- Включает ли ваш набор данных только числа или логические значения и текст?
Для расчета стандартного отклонения на основе числовой выборки используйте функцию СТАНДОТКЛОН.С в Excel 2010 и более поздних версиях; СТАНДОТКЛОН в Excel 2007 и более ранних версиях.
Чтобы найти стандартное отклонение совокупности , используйте функцию СТАНДОТКЛОН.П в Excel 2010 и более поздних версиях; STDEVP в Excel 2007 и более ранних версиях.
Если вы хотите включить в расчет логических или текстовых значений, используйте либо СТАНДОТКЛОН (выборочное стандартное отклонение), либо СТАНДОТКЛОНПА (стандартное отклонение генеральной совокупности).
Хотя я не могу придумать ни одного сценария, в котором любая функция может быть полезна сама по себе, они могут пригодиться в более крупных формулах, где один или несколько аргументов возвращаются другими функциями в виде логических значений или текстовых представлений чисел.
Чтобы помочь вам решить, какая из функций стандартного отклонения Excel лучше всего подходит для ваших нужд, просмотрите следующую таблицу, в которой обобщается уже изученная вами информация.
| СТАНДОТКЛОН | СТАНДОТКЛОН.S | СТДЕВП | СТАНДОТКЛОН.P | СТДЕВА | СТДЕВПА | |
| Версия Excel | 2003 — 2019 | 2010 — 2019 | 2003 — 2019 | 2010 — 2019 | 2003 — 2019 | 2003 — 2019 |
| Образец | ✓ | ✓ | ✓ | |||
| Население | ✓ | ✓ | ✓ | |||
| Логические значения в массивах или ссылках | Игнорируется | Оценено (ИСТИНА=1, ЛОЖЬ=0) | ||||
| Текст в массивах или ссылках | Игнорируется | Оценивается как ноль | ||||
| Логические значения и «текстовые числа» в списке аргументов | Оценено (ИСТИНА=1, ЛОЖЬ=0) | |||||
| Пустые ячейки | Игнорируется | |||||
Примеры формулы стандартного отклонения Excel
После того, как вы выбрали функцию, соответствующую вашему типу данных, не должно возникнуть сложностей с написанием формулы — синтаксис настолько прост и прозрачен, что не оставляет места для ошибок 🙂 Следующие примеры демонстрируют пару стандартных отклонений Excel формулы в действии.
Расчет стандартного отклонения выборки и генеральной совокупности
В зависимости от характера ваших данных используйте одну из следующих формул:
- Чтобы рассчитать стандартное отклонение на основе всей совокупности , т. е. полного списка значений (в данном примере B2:B50), используйте функцию СТАНДОТКЛОН.П:
=СТАНДОТКЛОН.П(B2:B50) - Чтобы найти стандартное отклонение на основе выборки , которая составляет часть или подмножество генеральной совокупности (В2:В10 в этом примере), используйте функцию СТАНДОТКЛОН.С:
=СТАНДОТКЛОН.С(B2:B10)
Как видно на скриншоте ниже, формулы возвращают несколько разные числа (чем меньше выборка, тем больше разница):
В Excel 2007 и более ранних версиях вместо этого следует использовать функции СТАНДОТКЛОН и СТАНДОТКЛОН:
- Чтобы получить стандартное отклонение совокупности:
=СТАНДОТКЛОН(B2:B50) - Для расчета стандартного отклонения выборки:
=СТАНДОТКЛОН(B2:B10)
Расчет стандартного отклонения для текстовых представлений чисел
При обсуждении различных функций для расчета стандартного отклонения в Excel мы иногда упоминали «текстовое представление чисел», и вам может быть интересно узнать, что это на самом деле означает.
В этом контексте «текстовые представления чисел» — это просто числа, отформатированные как текст. Как такие числа могут появиться в ваших рабочих листах? Чаще всего они экспортируются из внешних источников. Или, возвращаемые так называемыми текстовыми функциями, предназначенными для манипулирования текстовыми строками, например. TEXT, MID, RIGHT, LEFT и т. д. Некоторые из этих функций могут работать и с числами, но их вывод всегда является текстом, даже если он очень похож на число.
Чтобы лучше проиллюстрировать это, рассмотрим следующий пример. Предположим, у вас есть столбец кодов товаров, например «Джинсы-105», где цифры после дефиса обозначают количество. Ваша цель — извлечь количество каждого элемента, а затем найти стандартное отклонение извлеченных чисел.
Перетащить количество в другой столбец не проблема:
=ВПРАВО(A2,LEN(A2)-ПОИСК("-",A2,1))
Проблема заключается в том, что использование формулы стандартного отклонения Excel для извлеченных чисел возвращает #DIV/0! или 0, как показано на скриншоте ниже:
Почему такие странные результаты? Как упоминалось выше, выходом функции ПРАВИЛЬНО всегда является текстовая строка.
Но ни STDEV.S, ни STDEVA не могут обрабатывать числа, отформатированные как текст в ссылках (первый просто игнорирует их, а второй считает нулями). Чтобы получить стандартное отклонение таких «текстовых чисел», вам нужно указать их непосредственно в списке аргументов, что можно сделать, внедрив все ПРАВИЛЬНЫЕ функции в вашу формулу СТАНДОТКЛОН.С или СТАНДОТКЛОН:
=СТАНДОТКЛОН.S(ПРАВО(A2,ДЛСТР(A2)-ПОИСК("-",A2,1)), ПРАВО(A3,ДЛСТР(A3)-ПОИСК("-",A3,1)), ПРАВО (A4,ДЛСТР(A4)-ПОИСК("-",A4,1)), ВПРАВО(A5,ДЛСТР(A5)-ПОИСК("-",A5,1)))
=СТАНДОТКЛОН(ПРАВО(A2,ДЛСТР(A2)-ПОИСК("-",A2,1)), ПРАВО(A3,ДЛСТР(A3)-ПОИСК("-",A3,1)), ПРАВО(A4 ,ДЛСТР(A4)-ПОИСК("-",A4,1)), ВПРАВО(A5,ДЛСТР(A5)-ПОИСК("-",A5,1)))
Формулы немного громоздки, но это может быть рабочим решением для небольшой выборки. Для большего, не говоря уже о всем населении, это точно не вариант. В этом случае более элегантным решением было бы использование функции VALUE для преобразования «текстовых чисел» в числа, которые может понять любая формула стандартного отклонения (обратите внимание на числа, выровненные по правому краю на снимке экрана ниже, в отличие от текстовых строк, выровненных по левому краю).
на скриншоте выше):
Как рассчитать стандартную ошибку среднего в Excel
В статистике есть еще одна мера для оценки изменчивости данных — стандартная ошибка среднего , которую иногда сокращают (хотя и некорректно) до просто «стандартная ошибка». Стандартное отклонение и стандартная ошибка среднего — это два тесно связанных понятия, но не одно и то же.
В то время как стандартное отклонение измеряет изменчивость набора данных от среднего значения, стандартная ошибка среднего (SEM) оценивает, насколько вероятно, что среднее значение выборки будет отличаться от истинного среднего значения генеральной совокупности. Другими словами, если вы взяли несколько выборок из одной и той же совокупности, стандартная ошибка среднего показала бы дисперсию между этими средними выборками. Поскольку обычно мы вычисляем только одно среднее для набора данных, а не несколько средних, стандартная ошибка среднего оценивается, а не измеряется.
В математике стандартная ошибка среднего рассчитывается по следующей формуле:
Где SD — стандартное отклонение, а n — размер выборки (количество значений в выборке).
На листах Excel вы можете использовать функцию СЧЕТ, чтобы получить количество значений в выборке, КОРЕНЬ, чтобы извлечь квадратный корень из этого числа, и СТАНДОТКЛОН.С, чтобы вычислить стандартное отклонение выборки.
Сложив все это вместе, вы получите стандартную ошибку формулы среднего в Excel:
СТАНДОТКЛОН.С( диапазон )/КОРЕНЬ(СЧЁТ( диапазон ))
Если исходные данные представлены в формате B2:B10, наша формула SEM будет выглядеть следующим образом:
=СТАНДОТКЛОН.С(B2:B10)/КОРЕНЬ(СЧЁТ(B2:B10))
Результат может быть примерно таким:
Как добавить столбцы стандартного отклонения в Excel
Чтобы визуально отобразить границу стандартного отклонения, вы можете добавить полосы стандартного отклонения на диаграмму Excel. Вот как:
- Создайте график обычным способом (вкладка Вставка > группа Графики ).
- Щелкните в любом месте графика, чтобы выбрать его, затем нажмите кнопку Chart Elements .
- Щелкните стрелку рядом с Столбики ошибок и выберите Стандартное отклонение . Чтобы отобразить стандартную ошибку среднего, выберите Standard Error .
При этом будут вставлены одни и те же планки погрешностей для всех точек данных.
Дополнительные сведения см. в разделе Как добавить планки погрешностей в диаграммы Excel.
Вот как сделать стандартное отклонение в Excel. Я надеюсь, что вы найдете эту информацию полезной. В любом случае, я благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе.
Вас также может заинтересовать
Основные части речи — Грамматика
Существительное
Название чего-либо, например человека, животного, места, предмета или понятия. Существительные обычно используются как подлежащие, дополнения, объекты предлогов и модификаторы других существительных.
- Я закончил исследование.
- I = субъект
- Мэгги написала диссертацию .
- диссертация = объект
- Автор представил результаты в главе 4 .
- в главе 4 = объект предлога
- Его исследования выводы могут способствовать социальным изменениям.
- исследование = модификатор
Глагол
Выражает действия человека, животного, места, предмета или понятия. В английском языке глаголы следуют за существительным.
- нужно приложить немало усилий, чтобы получить докторскую степень.
- Она усердно изучала для теста.
- Написать диссертацию сложно. (Глагол «быть» также иногда называют связкой или глаголом-связкой. Он связывает подлежащее, в данном случае «написание диссертации», с дополнением или сказуемым предложения, в данном случае «трудно». «)
«)Прилагательное
Описывает существительное или местоимение. Прилагательные обычно стоят перед существительным или после глагола состояния, например, глагол «быть».
- прилежный 9Студентка 0555 досрочно выполнила задание.
- Прилежный описывает студента и стоит перед существительным студент .
- трудно совмещать время на учебу и рабочие обязанности.
- Трудный ставится после глагола to be и описывает, что значит балансировать время.
Помните, что прилагательные в английском языке не имеют формы множественного числа. Одна и та же форма прилагательного используется как для единственного, так и для множественного числа существительных.
- А разные идея
- Некоторые разные идеи
- НЕПРАВИЛЬНО: несколько
отличийидей
Наречие
Это дает больше информации о глаголе и о том, как было выполнено действие.
Наречия сообщают, как, где, когда, почему и т. д. В зависимости от контекста наречие может стоять до или после глагола, в начале или в конце предложения.
- Прошел курс с энтузиазмом .
- С энтузиазмом описывает, как он прошел курс, и отвечает на вопрос как .
- Стивен недавно записался на программу Graduate Certificate in Communication в Walden.
- Недавно изменяет глагол enroll и отвечает на вопрос when .
- Затем, Я убедился, что большинство моих источников прошли экспертную оценку.
- Затем описывает и изменяет все предложение. См. эту ссылку на переходы для получения дополнительных примеров конъюнктивных наречий (наречия, которые соединяют одну идею с другой, чтобы улучшить связность письма).
Местоимение
Это слово заменяет существительное или именную группу (например, оно, она, он, они, тот, те,…).
- Смит (2014) провел собеседование с заявителями, когда они прибыли.
- они = заявители
- Он интересовался идеями которые ранее никогда не записывались, а не теми которые уже были опубликованы.
- He = Смит; что = идеи; те = эти идеи
Определитель
Это слово делает ссылку существительного более конкретной (например, его, ее, мой, их, тот, а, этот, эти, … ).
- Джонс опубликовала свою книгу в 2015 году.
- Книга была очень популярна.
Предлог
Этот предлог стоит перед существительным или именным словосочетанием и связывает его с другими частями предложения. Обычно это отдельные слова (например, on, at, by ,… ), но может содержать до четырех слов (например, насколько, в дополнение к, в результате, …).
- Я решил взять интервью у учителей в ближайшем ко мне районе .
- Диктофон был помещен рядом с интервьюируемым.
- Я остановил запись в середине интервью из-за низкого заряда батареи.
Союз
Слово, соединяющее два предложения. Это может быть координация (простой способ запомнить это — запомнить ФАНБОЙЦЫ = для, и, ни, но, или, тем не менее, так) или подчиненный (например, потому что, хотя, когда, …).
- Результаты были незначительными, поэтому была принята альтернативная гипотеза.
- Хотя результаты кажутся многообещающими, в этой области необходимо провести дополнительные исследования.
Вспомогательные глаголы
Вспомогательные глаголы. Они используются для образования полных глаголов.
- Первичные вспомогательные глаголы (be, have, do) показывают прогрессивное, пассивное, совершенное и отрицательное время глаголов.
