Классификация треугольников по сторонам по углам: Виды треугольников по углам и сторонам

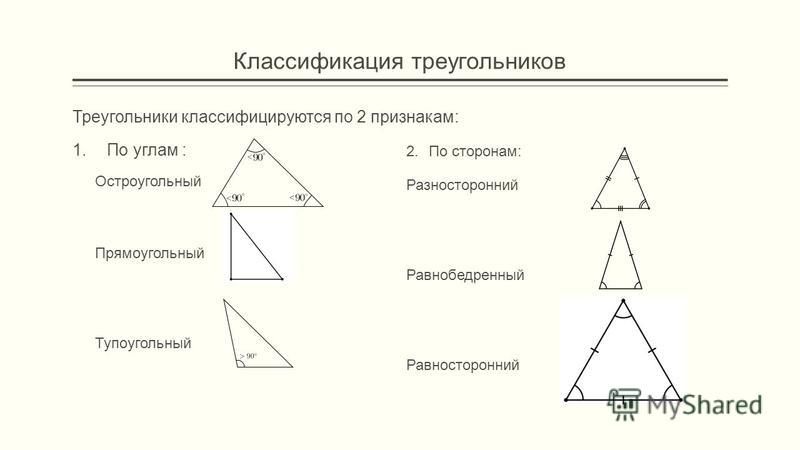
4 класс. Математика. Виды треугольников. — Виды треугольников по названию углов.

Комментарии преподавателя

На этом уроке мы рассмотрим виды треугольников и научимся строить прямоугольный треугольник на нелинованной бумаге. Вначале вспомним определение треугольника и его элементы, какие существуют виды углов, узнаем, как на нелинованной бумаге построить прямой угол. Далее узнаем, как делятся треугольники на виды в зависимости от типа углов в них. Рассмотрим несколько задач на нахождение вида треугольников и на построение 

 Треугольник и его элементы

Тре­уголь­ник – это гео­мет­ри­че­ская фи­гу­ра, со­сто­я­щая из трех точек, не ле­жа­щих на одной пря­мой и трех со­еди­ня­ю­щих их от­рез­ков. В любом тре­уголь­ни­ке раз­ли­ча­ют сле­ду­ю­щие эле­мен­ты:

Вер­ши­ны (рис. 1). Это точки.

Рис. 1. Эле­мен­ты тре­уголь­ни­ка: вер­ши­ны

Сто­ро­ны (Рис. 2). Это от­рез­ки.

Рис. 2. Эле­мен­ты тре­уголь­ни­ка: сто­ро­ны

Углы (Рис. 3)

Рис. 3. Эле­мен­ты тре­уголь­ни­ка: углы

 Виды углов

Раз­вер­ну­тый угол. (Рис. 4)

Угол на­зы­ва­ет­ся раз­вер­ну­тым, если его сто­ро­ны лежат на одной пря­мой.

Рис. 4. Виды углов: раз­вер­ну­тый

Пря­мой угол (Рис. 5)

Пря­мой угол со­став­ля­ет по­ло­ви­ну раз­вер­ну­то­го.

Рис. 5. Виды углов: пря­мой угол

Пря­мой угол можно по­лу­чить путем скла­ды­ва­ния бу­ма­ги. Сло­жив лист два­жды, мы по­лу­чим мо­дель пря­мо­го угла, его со­став­ля­ют линии сгиба.

При­ло­жим мо­дель угла к углу на чер­те­же (Рис. 5) таким об­ра­зом, чтобы углы и сто­ро­ны сов­па­ли (Рис. 6).

Рис. 5. Мо­дель угла и угол на чер­те­же

Рис. 6. Мо­дель угла, при­ло­жен­ная к углу на чер­те­же

Мы убе­ди­лись, что на чер­те­же дей­стви­тель­но изоб­ра­жен пря­мой угол.

Для удоб­ства опре­де­ле­ния, пря­мой угол или нет, ис­поль­зу­ют осо­бый ин­стру­мент – пря­мо­уголь­ный тре­уголь­ник (Рис. 7).

Рис. 7. Пря­мо­уголь­ный тре­уголь­ник

Непря­мые углы де­лят­ся на ост­рые (Рис. 8) и тупые (Рис. 11).

Рис. 8. Виды углов: ост­рый угол Ост­рый угол мень­ше пря­мо­го (Рис. 10). Рис. 10. Срав­не­ние остро­го и пря­мо­го угла

Рис. 11. Виды углов: тупой угол Тупой угол боль­ше пря­мо­го (Рис. 12). Рис. 12. Срав­не­ние ту­по­го и пря­мо­го угла

 Виды треугольников

Пря­мо­уголь­ный тре­уголь­ник (Рис. 13). Угол  – пря­мой.

Рис. 13. Виды тре­уголь­ни­ков: пря­мо­уголь­ный тре­уголь­ник

Ост­ро­уголь­ный тре­уголь­ник (Рис. 14). Все углы  дан­но­го тре­уголь­ни­ка ост­рые.

Рис. 14. Виды тре­уголь­ни­ков: ост­ро­уголь­ный тре­уголь­ник

Ту­по­уголь­ный тре­уголь­ник (Рис. 15). Угол  – тупой.

Рис. 15. Виды тре­уголь­ни­ков: ту­по­уголь­ный тре­уголь­ник 

 Задание 1 (определение вида треугольников)

На­зо­ви­те но­ме­ра ту­по­уголь­ных, ост­ро­уголь­ных и пря­мо­уголь­ных тре­уголь­ни­ков на ри­сун­ке 16.

Рис. 16. Ил­лю­стра­ция к за­да­нию 1

Тре­уголь­ник номер 1 – ост­ро­уголь­ный, у него все углы ост­рые. Тре­уголь­ни­ки номер 3 и 4 – ту­по­уголь­ные, каж­дый из них имеет один тупой угол. Фи­гу­ра номер 2 – пря­мо­уголь­ный тре­уголь­ник. Про­ве­рим, дей­стви­тель­но ли эта фи­гу­ра имеет пря­мой угол, с по­мо­щью пря­мо­уголь­но­го тре­уголь­ни­ка (Рис. 17).

Рис. 17. Про­вер­ка тре­уголь­ни­ка номер 2

Мы видим, что вер­ши­ны и сто­ро­ны пря­мо­го угла сов­па­ли, зна­чит, угол пря­мой, а тре­уголь­ник пря­мо­уголь­ный.

 Задание 2 (построение прямоугольного треугольника)

По­строй­те на нели­но­ван­ной бу­ма­ге тре­уголь­ник , чтобы угол  был пря­мым, длина сто­ро­ны  рав­ня­лась 15 см, а длина сто­ро­гы  – 20 см.

По­стро­им точку  (Рис. 18).

Рис. 18. Точка 

Про­ве­дем через точку  пря­мую (Рис. 19).

Рис. 19. Пря­мая, про­ве­ден­ная через точку 

Для по­стро­е­ния пря­мо­го угла вос­поль­зу­ем­ся пря­мо­уголь­ным тре­уголь­ни­ком. При­ло­жим тре­уголь­ник так, чтобы вер­ши­на пря­мо­го угла сов­па­ла с точ­кой , а одна из сто­рон сов­па­ла с лучом, как по­ка­за­но на рис. 20.

Рис. 20. По­стро­е­ние пря­мо­го угла

Про­ве­дем по вто­рой сто­роне пря­мо­го угла тре­уголь­ни­ка луч из точки  и по­лу­чим пря­мой угол (Рис. 21).

Рис. 21. По­лу­чен­ный пря­мой угол

Вы­пол­ним по­стро­е­ние сто­рон тре­уголь­ни­ка. По­стро­им от­ре­зок , ко­то­рый равен 15 см (Рис. 22).

Рис. 22. От­ре­зок 

По­стро­им от­ре­зок , ко­то­рый равен 20 см (Рис. 23).

Рис. 23. От­ре­зок 

Со­еди­ним по­лу­чен­ные точки от­рез­ком . Мы по­лу­чи­ли пря­мо­уголь­ный тре­уголь­ник  (Рис. 24) с пря­мым углом  и сто­ро­на­ми  см и  см.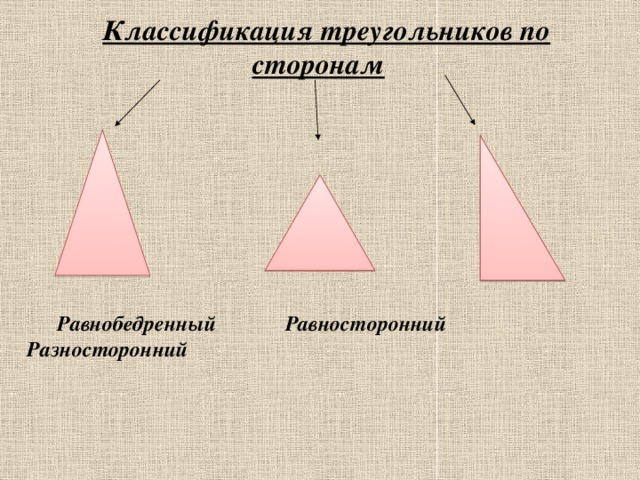

Рис. 24. Тре­уголь­ник 

 Виды треугольников в зависимости от длины сторон

В за­ви­си­мо­сти от длины сто­рон можно вы­де­лить раз­но­сто­рон­ние и рав­но­бед­рен­ные тре­уголь­ни­ки. Вспом­ним, если у тре­уголь­ни­ка длины всех сто­рон раз­лич­ные, то такой тре­уголь­ник на­зы­ва­ет­ся раз­но­сто­рон­ним. Если в тре­уголь­ни­ке две сто­ро­ны по длине равны, то такой тре­уголь­ник на­зы­ва­ет­ся рав­но­бед­рен­ным, а рав­ные по длине сто­ро­ны на­зы­ва­ют бо­ко­вы­ми сто­ро­на­ми тре­уголь­ни­ка, а тре­тья сто­ро­на на­зы­ва­ет­ся ос­но­ва­ни­ем тре­уголь­ни­ка.

 Задание 3 (построение прямоугольного равнобедренного треугольника и прямоугольника)

По­строй­те рав­но­бед­рен­ный тре­уголь­ник  с пря­мым углом  и сто­ро­на­ми  и  по 20 см. До­пол­ни­те этот тре­уголь­ник до пря­мо­уголь­ни­ка.

По­стро­им точку  (Рис. 25).

Рис. 25. Точка 

Про­ве­дем через точку  пря­мую (Рис. 26).

Рис. 26. Пря­мая, про­ве­ден­ная через точку 

Для по­стро­е­ния пря­мо­го угла вос­поль­зу­ем­ся пря­мо­уголь­ным тре­уголь­ни­ком. При­ло­жим пря­мо­уголь­ный тре­уголь­ник так, чтобы вер­ши­на пря­мо­го угла сов­па­ла с точ­кой , а одна из сто­рон тре­уголь­ни­ка – с лучом (Рис. 27).

Рис. 27. По­стро­е­ние пря­мо­го угла

По­стро­им по вто­рой сто­роне пря­мо­го угла луч из точки . По­лу­чим пря­мой угол (Рис. 28).

Рис. 28. Пря­мой угол

Вы­пол­ним по­стро­е­ние сто­рон тре­уголь­ни­ка. От­ло­жим на каж­дом луче от­ре­зок, рав­ный 20 см, и обо­зна­чим точки бук­ва­ми  и  (Рис. 29).

Рис. 29. Сто­ро­ны бу­ду­ще­го тре­уголь­ни­ка

Со­еди­ним по­лу­чен­ные точки от­рез­ком (Рис. 29). Мы по­лу­чи­ли пря­мо­уголь­ный тре­уголь­ник  с пря­мым углом  и сто­ро­на­ми  и  по 20 см.

Рис. 29. Тре­уголь­ник 

Вы­пол­ним вто­рую часть за­да­ния: до­стро­им этот тре­уголь­ник до пря­мо­уголь­ни­ка. В пря­мо­уголь­ни­ке все углы пря­мые. По­стро­им пря­мой угол с вер­ши­ной . Для этого при­ло­жим пря­мо­уголь­ный тре­уголь­ник таким об­ра­зом, чтобы его вер­ши­на сов­па­ла с точ­кой , а одна из сто­рон сов­па­ла со сто­ро­ной  (Рис. 30).

Рис. 30. По­стро­е­ние пря­мо­го угла с вер­ши­ной 

Про­ве­дем луч из точки  по вто­рой сто­роне тре­уголь­ни­ка (Рис. 31).

Рис. 31. Луч из точки 

У пря­мо­уголь­ни­ка про­ти­во­по­лож­ные сто­ро­ны равны. От­ло­жим от­ре­зок на новом луче, ко­то­рый равен по длине от­рез­ку , то есть 20 см и обо­зна­чим эту сто­ро­ну  (Рис. 32).

Рис. 32. По­стро­е­ние сто­ро­ны 

Со­еди­ним точки  и  от­рез­ком. Мы по­лу­чи­ли пря­мо­уголь­ник  (Рис. 33).

Рис. 33. Пря­мо­уголь­ник 

Об­ра­ти­те вни­ма­ние, в пря­мо­уголь­ни­ке  все сто­ро­ны равны, зна­чит, по­лу­чил­ся квад­рат (Рис. 34).

Рис. 34. По­лу­чен­ный квад­рат

 Заключение

Мы се­год­ня по­зна­ко­ми­лись с ви­да­ми тре­уголь­ни­ков: ост­ро­уголь­ным, ту­по­уголь­ным и пря­мо­уголь­ным, и учи­лись стро­ить пря­мо­уголь­ный тре­уголь­ник на нели­но­ван­ной бу­ма­ге с по­мо­щью ин­стру­мен­та «пря­мо­уголь­ный тре­уголь­ник».

 Источник конспекта: http://interneturok.ru/ru/school/matematika/4-klass/tema-3/vidy-treugolnikov-postroenie-pryamougolnogo-treugolnika-na-nelinovannoy-bumage?konspekt

Источник видео: http://www.youtube.com/watch?v=xQQgjf2Wla4

Виды треугольников по величине углов

Урок 49. Математика 3 класс ФГОС

Матюша вновь рассказывает о трёх разных видах треугольников. На этот раз они различаются по величине углов. И конечно, для закрепления проводится работа по распознаванию различных видов треугольников.

Конспект урока «Виды треугольников по величине углов»

Здравствуйте, ребята.

Сегодня я хочу начать нашу встречу с загадки.

Он и острый, да не нос,

И прямой, да не вопрос,
И тупой он, да не ножик, —
Что ещё таким быть может?

Догадались? Это угол. Помните, какими бывают углы? Мы с вами говорили о трёх видах углов. Есть углы прямые, которые можно увидеть на линейке-угольнике. Есть острые углы – они раскрыты меньше прямого угла. И есть тупые углы, которые раскрыты больше прямого угла. А сегодня мы с вами поговорим о том, что, оказывается, в зависимости от величины углов, треугольники тоже делятся на три вида.

Вот посмотрите на эти треугольники.

Видите, какие они разные? Они отличаются друг от друга по размеру и форме. Но сейчас мы возьмём треугольники под номерами два, пять и шесть и проверим в каждом из них при помощи линейки-угольника один наиболее широко раскрытый, то есть самый большой угол. Вы видите, что углы, которые мы проверили, больше, чем прямой угол, то есть они

тупые.

А теперь давайте посмотрим треугольники под номерами один, три, семь. Опять проверяем самые большие углы в каждом из них.

А вот в них углы совпадают с прямым углом линейки-угольника. Значит, эти углы тоже прямые.

Проверяем оставшиеся треугольники. У этих треугольников нет прямых и тупых углов, то есть все углы – острые.

Вот у нас появилось три группы треугольников. В первой группе в каждом треугольнике есть один тупой угол. И, несмотря на то, что остальные два угла острые, такие треугольники называются тупоугольными.

Во второй группе в каждом из треугольников один из углов – прямой. И, несмотря на то, что остальные два угла острые, такие треугольники называются прямоугольными.

В третьей группе – треугольники, в которых все углы острые. Такие треугольники называются остроугольными.

Если мы вспомним виды треугольников по их сторонам, то можно сказать, что тупоугольные треугольники могут быть разносторонними и равнобедренными.

То же можно сказать и о прямоугольных треугольниках. И они бывают разносторонними и равнобедренными.

А вот остроугольные треугольники могут быть не только разносторонними и равнобедренными, но и равносторонними.

Но при этом равносторонние треугольники могут быть только остроугольными.

А теперь я предлагаю вам посмотреть вот на эти треугольники, и на глаз, без измерений, определить вид этих треугольников в зависимости от их углов.

Определите сначала номера прямоугольных треугольников, затем – тупоугольных, и – остроугольных.

Ну а теперь давайте проверим, справились ли вы с заданием.

Про третью группу треугольников мы говорим, что у них острые углы. А про тех ребят, которые справились с заданием, можно сказать, что у них острый глаз.

А сейчас, ребята давайте повторим то, что вы сегодня от меня услышали.

Если в треугольнике есть тупой угол, такой треугольник называют тупоугольным.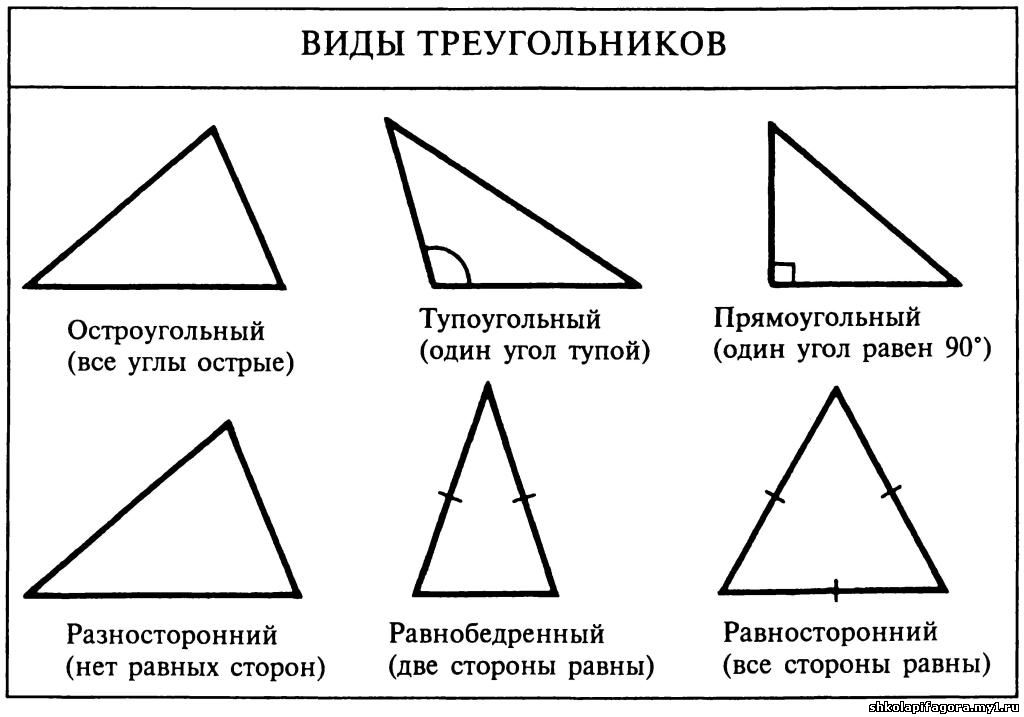

Если в треугольнике есть прямой угол, такой треугольник называют прямоугольным.

Если в треугольнике все углы острые, такой треугольник называют остроугольным.

Я надеюсь, вы не забыли, что в тупоугольном треугольнике только один угол может быть тупым, а два остальных обязательно будут острыми. Точно так же и в прямоугольном – один прямой и два острых.

Ну вот теперь можно и попрощаться с вами, ребята. До следующей встречи, мои друзья.

Предыдущий урок 48 Умножение и деление. Приёмы устных вычислений

Следующий урок 50 Приём письменного умножения на однозначное число

Получите полный комплект видеоуроков, тестов и презентаций Математика 3 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Классификация треугольников.

Определение, типы, примеры

Классификация треугольников производится по длине их сторон и величине углов. Треугольник — это простой многоугольник с 3 сторонами, 3 внутренними углами и 3 вершинами, которые соединены друг с другом и обозначаются символом △. Это наиболее распространенная форма, встречающаяся в математике и природе, и бывает разных типов. В этой статье подробно рассматривается классификация треугольников вместе с несколькими решенными примерами, чтобы лучше понять концепцию.

1.	Классификация треугольников
2.	Классификация треугольников по сторонам
3.	Классификация треугольников на основе углов
4.	Классификация треугольников на основе углов и сторон
5.	Часто задаваемые вопросы о классификации треугольников

Классификация треугольников

Классификация треугольников производится на основе их сторон и углов.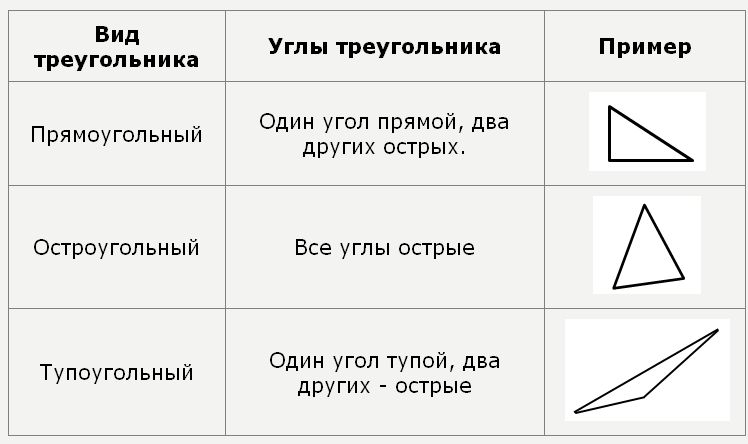 Другими словами, характеристики размера и формы треугольника помогают отличить тип треугольника. В таблице ниже показаны различные типы треугольников в зависимости от их углов и сторон.

На основе сторон	На основе углов	На основе сторон и углов
Равносторонний треугольник	Острый угол	Равноугольный треугольник
Равнобедренный треугольник	Тупой угол	Прямоугольный равнобедренный треугольник
Разносторонний треугольник	Прямой угол	Тупоугольный равнобедренный треугольник
		Острый равнобедренный треугольник
		Правосторонний треугольник
		Тупоугольный разносторонний треугольник
		Острый лестничный треугольник

Рассмотрим каждый тип подробно.

Классификация треугольников по сторонам

Треугольник состоит из трех сторон, но фактором для их классификации является длина сторон. Он конкретно основан на соотношении длин сторон друг к другу, а не на единице измерения. Следовательно, треугольники классифицируются по количеству сторон с одинаковой длиной, равных друг другу или не равных вовсе. Треугольники бывают трех типов: равносторонний треугольник, разносторонний треугольник и равнобедренный треугольник.

Равносторонний треугольник

Равносторонний треугольник является наиболее распространенным типом, используемым при изучении основ формы. Здесь три стороны равны друг другу вместе с тремя углами, равными 60°. Равносторонний треугольник считается правильным многоугольником с равными углами и сторонами.

Равнобедренный треугольник

Слово «равнобедренный» происходит от греческого слова «изо», что означает «такой же», и «скелос», что означает «нога». У этого типа треугольника две стороны одинаковой длины.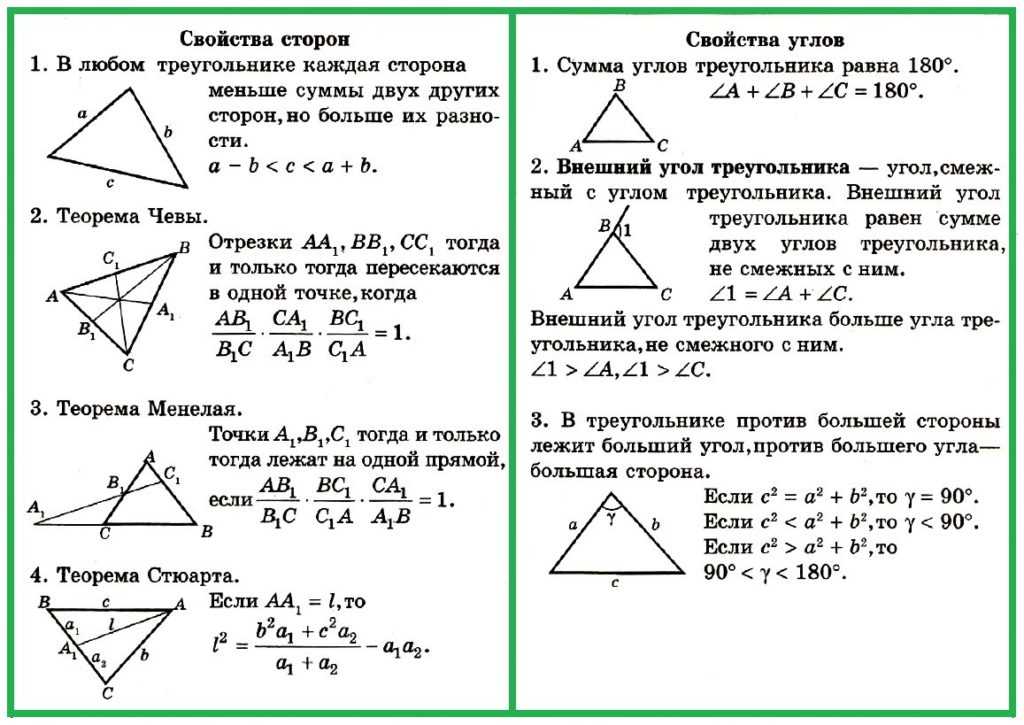 Две равные стороны равнобедренного треугольника называются катетами 9.0129 , а угол между ними называется углом при вершине или углом при вершине.

Разносторонний треугольник

Разносторонний треугольник — это треугольник, все три стороны которого имеют разную длину, а также три угла разной величины. Эта фигура не имеет линии симметрии, т. е. где бы ни проводилась линия через разносторонний треугольник, левая и правая стороны линии никогда не будут равны друг другу.

Классификация треугольников на основе углов

Треугольники также можно классифицировать на основе углов. Все треугольники имеют три внутренних угла, сумма угловых измерений которых составляет 180 ° с различными комбинациями углов в зависимости от типа треугольника. Три различных типа: остроугольный треугольник, тупоугольный треугольник и прямоугольный треугольник.

Остроугольный треугольник

Остроугольный треугольник — это тип треугольника, в котором все три внутренних угла являются острыми или меньше 90°.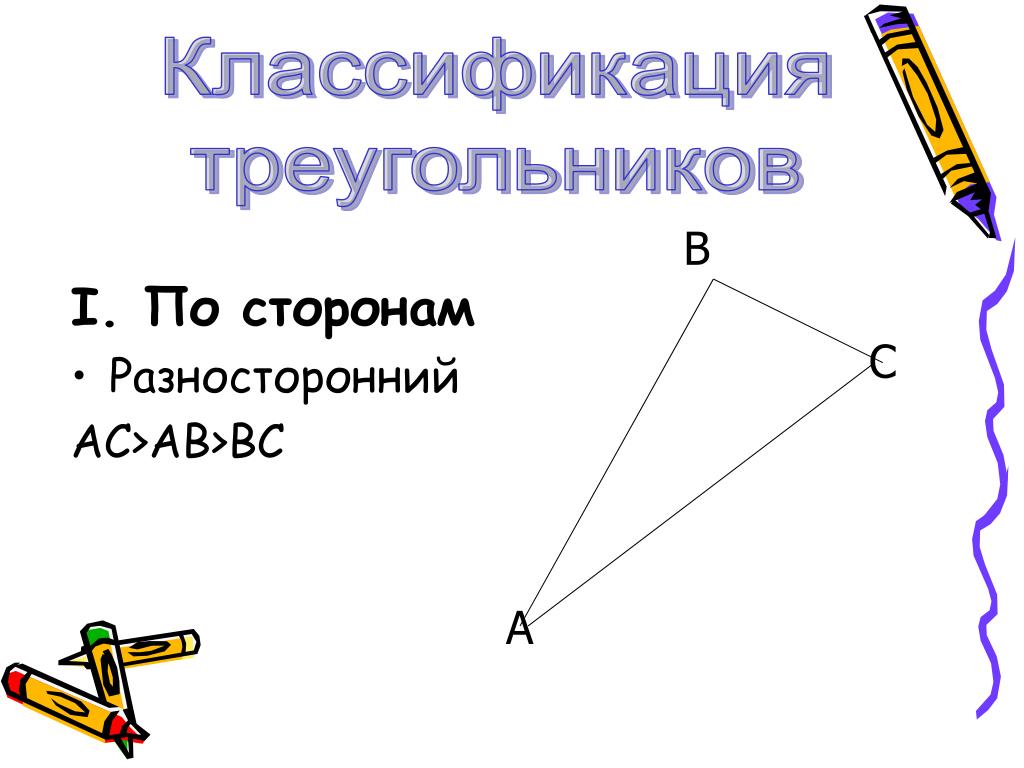 Стороны остроугольного треугольника могут быть равными или неравными в зависимости от того, является ли треугольник равносторонним, равнобедренным или разносторонним.

Прямоугольный треугольник

Прямоугольный треугольник — это треугольник, один из углов которого равен 90 градусов. Угол в 90 градусов называется прямым углом, поэтому треугольник с прямым углом называется прямоугольным. Здесь связь между сторонами понимается с помощью правила Пифагора. Сторона, противоположная прямому углу, является наибольшей стороной и называется гипотенузой.

Тупоугольный треугольник

Тупоугольный треугольник или тупоугольный треугольник — это тип треугольника, у которого один из углов при вершине больше 90°, а сумма двух других углов меньше 90°. Сторона, противоположная тупому углу, считается самой длинной.

Классификация треугольников по углам и сторонам

Различные типы треугольников также классифицируются в соответствии с их сторонами и углами следующим образом:

• Равносторонний или равносторонний треугольник: Когда все стороны и углы треугольника равны, он называется равносторонним или равноугольным треугольником.
• Равнобедренный прямоугольный треугольник : Треугольник, в котором две стороны равны и один угол равен 90°, называется равнобедренным прямоугольным треугольником. Итак, в равнобедренном прямоугольном треугольнике две стороны и два острых угла равны.
• Тупоугольный равнобедренный треугольник : Треугольник, в котором 2 стороны равны и один угол тупой, называется тупоугольным равнобедренным треугольником.
• Остроугольный равнобедренный треугольник : Треугольник, в котором все 3 угла острые, а 2 стороны имеют одинаковую меру, называется остроугольным равнобедренным треугольником.
• Прямоугольный разносторонний треугольник : Треугольник, в котором любой из углов является прямым, а все три стороны неравны, называется прямоугольным разносторонним треугольником.
• Тупоугольный треугольник : Треугольник с тупым углом и сторонами разной меры называется тупоугольным треугольником.
• Остроугольный треугольник : Треугольник, у которого 3 неравные стороны и 3 острых угла, называется остроугольным треугольником.

☛ Связанные темы

Ниже перечислены несколько тем, связанных с классификацией треугольников, взгляните!

• Построение треугольников
• Подобные треугольники
• Свойства треугольника
• Периметр треугольника
• Конгруэнтность треугольников

Часто задаваемые вопросы о классификации треугольников

Что такое классификация треугольников в геометрии?

Треугольники классифицируются по 2 группам, т. е. по сторонам и углам, и всего шести типов. В зависимости от сторон треугольники делятся на равносторонние, равнобедренные и разносторонние. Основываясь на их углах, 3 типа треугольников перечислены как остроугольный треугольник, тупоугольный треугольник и прямоугольный треугольник.

Какие 3 треугольника классифицируются на основе их углов?

В зависимости от углов треугольники делятся на остроугольные, прямоугольные и тупоугольные.

• Остроугольный треугольник: В остроугольном треугольнике все углы меньше 90°.
• Прямоугольный треугольник: Когда один угол треугольника равен 90°, такой треугольник называется прямоугольным.
• Тупоугольный треугольник: Когда один из углов треугольника тупой, такой треугольник называется тупоугольным.

Какие треугольники классифицируют по сторонам?

В зависимости от сторон треугольники делятся на 3 типа.

• Равносторонний треугольник: Когда все три стороны имеют одинаковую длину, треугольник считается равносторонним.
• Равнобедренный треугольник: Если две стороны треугольника равны, такой треугольник называется равнобедренным.
• Разносторонний треугольник: Если все стороны треугольника имеют разную длину, такой треугольник называется разносторонним.

Какие треугольники имеют 3 линии симметрии?

Все равносторонние треугольники имеют 3 оси симметрии, так как три оси симметрии могут проходить через вершину этого треугольника.

Какие треугольники имеют симметрию отражения?

Все равносторонние и равнобедренные треугольники обладают симметрией отражения.

Какие существуют 6 типов треугольников?

Можно перечислить 6 типов треугольников: остроугольный треугольник, тупоугольный треугольник, прямоугольный треугольник, равносторонний треугольник, равнобедренный треугольник и разносторонний треугольник.

В чем разница между равносторонним и равносторонним треугольником?

Оба треугольника считаются правильными многоугольниками. Основное различие между этими двумя треугольниками заключается в том, что равносторонний треугольник или многоугольник имеет конгруэнтные стороны, как ромб, тогда как равноугольный треугольник или многоугольник имеет конгруэнтные внутренние углы, как прямоугольник. Если многоугольник одновременно равносторонний и равноугольный, он считается правильным многоугольником.

Какие бывают треугольники? Определение, примеры, факты

Что такое треугольник?

Треугольник — это многоугольник, состоящий из трех сторон. Точка, в которой встречаются две стороны треугольника, называется вершиной и образует внутренний угол. Все треугольники имеют три стороны, три вершины и три внутренних угла.

Рассмотрим треугольник с тремя вершинами, поскольку A, B и C обозначены как △ABC, как показано ниже.

Рекомендуемые рабочие листы:

Основные свойства треугольников

• Треугольник имеет три внутренних угла, а сумма всех внутренних углов треугольника равна 180°. Это известно как свойство суммы углов треугольника.

• Треугольник имеет три стороны. Суммарная длина любых двух сторон треугольника больше, чем мера третьей стороны. Это также известно как свойство неравенства треугольника.

• Самая длинная сторона треугольника находится напротив его наибольшего угла, а сторона, противоположная наименьшему углу, является самой короткой стороной треугольника.

Рекомендуемые игры:

Какие существуют типы треугольников?

Треугольник — это замкнутая двумерная фигура с тремя сторонами. Существуют разные названия типов треугольников. По длине сторон различают три типа треугольников: разносторонние, равнобедренные и равнобедренные. Название треугольника также зависит от величины его внутреннего угла: острый (если все углы меньше 90°), прямой (если один угол равен 90°) и тупой (если один угол больше 90°).0°)

На приведенном ниже рисунке показаны различные типы треугольников и их свойства.

Классификация треугольников по длинам сторон

Существует три типа треугольников, основанных на величине их сторон.

Разносторонние треугольники

Все стороны разностороннего треугольника имеют разную длину. Следовательно, три внутренних угла отличны друг от друга.

Равнобедренные треугольники

У равнобедренного треугольника две стороны одинаковой длины. Углы, противолежащие этим равным сторонам, равны.

Равносторонний треугольник

Три стороны равностороннего треугольника имеют одинаковую длину. Следовательно, каждый внутренний угол равностороннего треугольника равен 60°.

Классификация треугольников на основе внутренних углов

В геометрии существуют различные типы углов, основанные на измерении. Внутренние углы треугольника могут быть трех видов: острые, прямые и тупые углы, как показано ниже.

Существует три типа треугольников, основанных на величине внутренних углов.

Остроугольные треугольники

Все внутренние углы остроугольного треугольника являются острыми, т. е. их мера меньше 90°.

Прямоугольные треугольники

Прямоугольным треугольником называется треугольник, у которого один внутренний угол равен 90° или прямой угол. Гипотенуза, сторона, противоположная прямому углу, является самой длинной стороной в прямоугольном треугольнике.

Тупоугольные треугольники

Треугольник с одним внутренним углом больше 90° или тупым углом называется тупоугольным треугольником.

Решенные примеры

Пример 1. Классифицируйте треугольник как равносторонний, равнобедренный или разносторонний.

Решение:

Изучите длины сторон, чтобы убедиться, что они равны. Все стороны треугольника отличны друг от друга.

Следовательно, треугольник разносторонний.

Пример 2. Классифицируйте треугольник как остроугольный, прямоугольный и тупоугольный.

Решение:

Изучите величину каждого внутреннего угла данного треугольника и сравните ее с 90°. Все углы треугольника меньше 90°.

Следовательно, треугольник остроугольный.

3. В равнобедренном треугольнике ABC ∠A = 100° и ∠B  = ∠C. Найдите меру ∠C.

Решение:

Следуя свойству суммы углов треугольника, получаем °

 Поскольку ∠B  = ∠C, мера ∠C = 80° ÷ 2 = 40°

Практические задачи

1

Какой тип треугольника изображен на изображении ниже?

Прямоугольный треугольник

Тупоугольный треугольник

Равносторонний треугольник

Равнобедренный треугольник

Правильный ответ: Равнобедренный треугольник
Две стороны треугольника равны. Следовательно, это равнобедренный треугольник.

2

Если два угла треугольника равны 45° и 60°, чему равен третий угол? Классифицировать треугольник.

105°; тупой

57°; разносторонний

75°; острый

75°; тупой

Правильный ответ: 75°; острый
В соответствии со свойством суммы углов третий угол должен быть 180° — 45° — 60° или 75°. Все
внутренних углов меньше 90°. Следовательно, треугольник остроугольный.

3

Что из перечисленного не может быть сторонами разностороннего треугольника?

7 футов, 13 футов, 14 футов

6 см, 8 см, 10 см

24 м, 10 м, 26 м

15 см, 15 см, 15√2 см

Правильный ответ: 15 см , 15 см, 15√2 см
Все стороны разностороннего треугольника должны иметь разную длину.

4

В прямоугольном треугольнике, если угол A равен 30°, найдите B.

30

60°

90°

150°

В соответствии со свойством сумма углов 90 909° , ∠B = 180° -∠C -∠A = 180° — 90° — 30° = 60°

Вывод

В этой статье мы узнали о типах треугольников. Их можно классифицировать по сторонам и углам. Чтобы узнать больше математических тем в увлекательной и интерактивной форме, посетите SplashLearn, игровую обучающую платформу.

Часто задаваемые вопросы

Что такое треугольник?

Треугольник — это замкнутая двумерная фигура с тремя сторонами, тремя углами и тремя вершинами. Треугольник также является многоугольником.

Всегда ли внутренние углы равностороннего треугольника равны 60°?

Да. У равностороннего треугольника три равные стороны, и все три внутренних угла равны. Применяя свойство суммы углов, мы можем сказать, что каждый угол равностороннего треугольника должен быть равен 180°÷3 или 60°9.0003

Может ли равнобедренный треугольник быть тупым?

У равнобедренного треугольника две стороны равны, а углы, лежащие при этих сторонах, равны. В равнобедренном треугольнике равные углы острые. Третий угол может быть острым, тупым или прямым.