Код шеннона фано онлайн калькулятор: Онлайн калькулятор: Кодирование Шеннона — Фано

Онлайн калькулятор: Кодирование Шеннона — Фано

Кодирование Шеннона — Фано

Этот калькулятор по таблице вероятностей символов выдает коды Шеннона — Фано

Немного теории по кодированию Шеннона — Фано можно найти сразу под калькулятором.

Кодирование Шеннона — Фано

Таблица вероятности символов

	Имя	Значение

Записей:

51020501001000

Таблица вероятности символов

Значение

Импортировать данныеОшибка импорта

Данные

Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: Lorem ipsum;50.5

Загрузить данные из csv файла

Точность вычисления

Знаков после запятой: 2

Средняя длина символа

 

Энтропия

 

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Кодирование Шеннона — Фано

Кодирование Шеннона — Фано получило свое наименование в области сжатия данных благодаря авторам Клоду Шеннону и Роберту Фано. Данный способ кодирования информации представляет собой технику создания префиксного кода, основанного на наборе символов и их вероятностей (оценочных или измеренных). Этот код не вполне оптимален, в том смысле, что он не дает минимально возможной длинны кода, как, например Код Хаффмана.

При кодировании методом Шеннона — Фано, символы распределяются в порядке от наиболее вероятных к наименее вероятным и затем разделяются на два набора, чьи суммарные вероятности максимально приближены друг к другу. Далее формируется первый разряд кода всех символов: символы из первого набора получают двоичный «0», символы из второго — «1». Процесс деления на две части и получения следующих разрядов повторяется для полученных наборов аналогичным образом, до тех пор, пока в полученном наборе не остается по одному символу. Когда набор уменьшается до одного символа — код символа полностью сформирован.

Этот алгоритм производит довольно эффективный код переменной длины, когда наборы имеют одинаковую суммарную вероятность. Единственный бит, отличающий их друг от друга используется с максимальной эффективностью.
Однако, метод Шеннона — Фано не всегда дает оптимального префиксного кода; набор вероятностей {0.35, 0.17, 0.17, 0.16, 0.15} — один из примеров, по которому будет сформирован неоптимальный код этим способом.

По этой причине, код Шеннона — Фано почти никогда не используется. Код Хаффмана — почти такой же простой с точки зрения вычислительной сложности, но он производит наиболее короткий по длине код.¹

---

1. Алгоритм Шеннона — Фано ↩

Ссылка скопирована в буфер обмена

Похожие калькуляторы

• • Код Хаффмана для последовательности символов
• • Код Хаффмана
• • Построение таблицы частот
• • Формула Шеннона
• • Частная условная энтропия

 алгоритм код кодирование Компьютеры теория информации Шеннон — Фано энтропия

 PLANETCALC, Кодирование Шеннона — Фано

Timur2022-05-30 09:55:26

Код Шеннона-Фано

Код Шеннона-Фано

Пример 2. Закодируем буквы алфавита из примера 1 в коде Шеннона-Фано.

Все буквы записываются в порядке убывания их вероятностей, затем делятся на равновероятные группы, которые обозначаются 0 и 1, затем вновь делятся на равновероятные группы и т.д. (см.табл.4.1)

Таблица 4.1.

X	P					Коды
x1	1/4	0	0	——-	——-	00
x2	1/4		1	——-	——-	01
x3,	1/8	1	0	0	——-	100
x4	1/8			1	——-	101
x5	1/16		1	0	0	1100
x6	1/16				1	1101
x7	1/16			1	0	1110
x8	1/16				1	1111

Средняя длина полученного кода будет равна

Итак, мы получили оптимальный код. Длина этого кода совпала с энтропией. Данный код оказался удачным, так как величины вероятностей точно делились на равновероятные группы. 

Пример 3.

Возьмем 32 две буквы русского алфавита. Частоты этих букв известны. В алфавит включен и пробел, частота которого составляет 0,145. Метод кодирования представлен в таблице 4.2.

Таблица 4.2.

Буква	Рi	1	2	3	4	Код
ب	0. 145	0	0	0	—	000
о	0. 095			1	—	001
е	0.074		1	0	0	0100
а	0. 064				1	0101
и	0.064			1	0	0110
н	0. 056				1	0111
т	0.056	1 …	0  …	0	—
с	0. 047			1 …	0 … 1
…	…
ф	0. 03

Средняя длина данного кода будет равна,  бит/букву;

Энтропия  H=4.42 бит/буква.  Эффективность полученного кода можно определить как отношение энтропии к средней длине кода. Она равна 0,994. При значении равном единице код является оптимальным. Если бы мы кодировали кодом равномерной длины , то эффективность была бы значительно ниже.

Онлайн-калькулятор: Калькулятор кодировки Шеннона-Фано

  Professional  Компьютеры

Этот онлайн-калькулятор генерирует кодировку Шеннона-Фано на основе набора символов и их вероятностей

Этот онлайн-калькулятор производит кодировку Шеннона-Фано набор символов с учетом их вероятностей. Немного теории можно найти под калькулятором.

Кодирование Шеннона–Фано

Таблица вероятностей символов

	  Name	  Value

Items per page:

51020501001000

Symbols probability table

Ошибка импорта данныхИмпорт

«Для разделения полей данных используется один из следующих символов: табуляция, точка с запятой (;) или запятая (,)» Пример: Lorem ipsum;50. 5

Загрузить данные из файла .csv.

• Перетащите файлы сюда

Точность вычислений

Знаки после запятой: 2

Взвешенная длина пути

 

Энтропия Шеннона

 

Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.

Кодирование Шеннона-Фано

В области сжатия данных кодирование Шеннона-Фано, названное в честь Клода Шеннона и Роберта Фано, представляет собой метод построения префиксного кода на основе набора символов и их вероятностей (оцененных или измеренных) . Он неоптимален в том смысле, что он не обеспечивает наименьшую возможную ожидаемую длину кодового слова, как при кодировании Хаффмана.

При кодировании Шеннона–Фано символы располагаются в порядке от наиболее вероятного к наименее вероятному, а затем делятся на два набора, суммарные вероятности которых максимально близки к равным. Затем всем символам назначаются первые цифры их кодов; символы в первом наборе получают «0», а символы во втором наборе получают «1». Пока остаются какие-либо наборы с более чем одним элементом, тот же процесс повторяется для этих наборов, чтобы определить последовательные цифры их кодов. Когда набор был сокращен до одного символа, это означает, что код символа завершен и не будет формировать префикс кода любого другого символа.

Алгоритм производит довольно эффективное кодирование переменной длины; когда два меньших набора, полученных в результате разбиения, на самом деле имеют равную вероятность, один бит информации, используемый для их различения, используется наиболее эффективно. К сожалению, Шеннон-Фано не всегда дает оптимальные префиксные коды; набор вероятностей {0,35, 0,17, 0,17, 0,16, 0,15} является примером вероятности, которой будут присвоены неоптимальные коды кодированием Шеннона – Фано.

По этой причине Шеннон-Фано почти не используется; Кодирование Хаффмана почти так же просто в вычислительном отношении и создает префиксные коды, которые всегда достигают наименьшей ожидаемой длины кодового слова при ограничениях, что каждый символ представлен кодом, состоящим из целого числа битов. ¹

---

1. Википедия: кодирование Шеннона-Фано ↩

URL скопирован в буфер обмена

Аналогичные калькуляторы

• • Кодировка Шеннона
• • Кодировка Хаффмана
• • Преобразователи кодов Грея
• • Азбука Морзе. Мутатор
• • Азбука Морзе
• • Раздел Компьютеры ( 65 калькуляторов )

  #coding #алгоритм Шеннона-Фано код кодирование Компьютеры кодирование энтропия теория информации Шеннон-Фано

  PlanetCalc, калькулятор кодирования Shannon-Fano

 Timur  2020-12-03 12:02:34

Shannon FANO ELIAS ELIAS ELIAS ALGODING ALGORITMENTISMENT ALGORITMENTISMEMEMNT

.

Алгоритм кодирования Shannon Fano Elias является предшественником арифметического кодирования, в котором вероятности используются для определения кодовых слов. Это схема кодирования без потерь, используемая в цифровой связи. Теория вероятностей сыграла важную роль в электронных системах связи. Это связано с тем, что информация в сигнале обычно сопровождается шумом. На стороне получателя, когда мы говорим о восстановлении сигнала сообщения, мы в основном говорим об оценке исходного сигнала из принятого сигнала, сопровождаемого шумом. В цифровой связи мы говорим о декодировании принимаемых битов сообщения с некоторой вероятностью ошибок.

В этой статье описывается простая процедура построения, использующая кумулятивную функцию распределения (CDF) для генерации кодовых слов с помощью LabVIEW. Длина кодового слова кодирования Шеннона Фано Элиаса удовлетворяет неравенству Крафта. Поэтому он используется для создания декодируемого кода для источника информации.

Процедура кода Шеннона Фано Элиаса может быть применена к последовательности случайных величин. Вероятность и CDF можно вычислять последовательно с символами в блоке или группе данных, гарантируя линейный рост вычислений с длиной блока.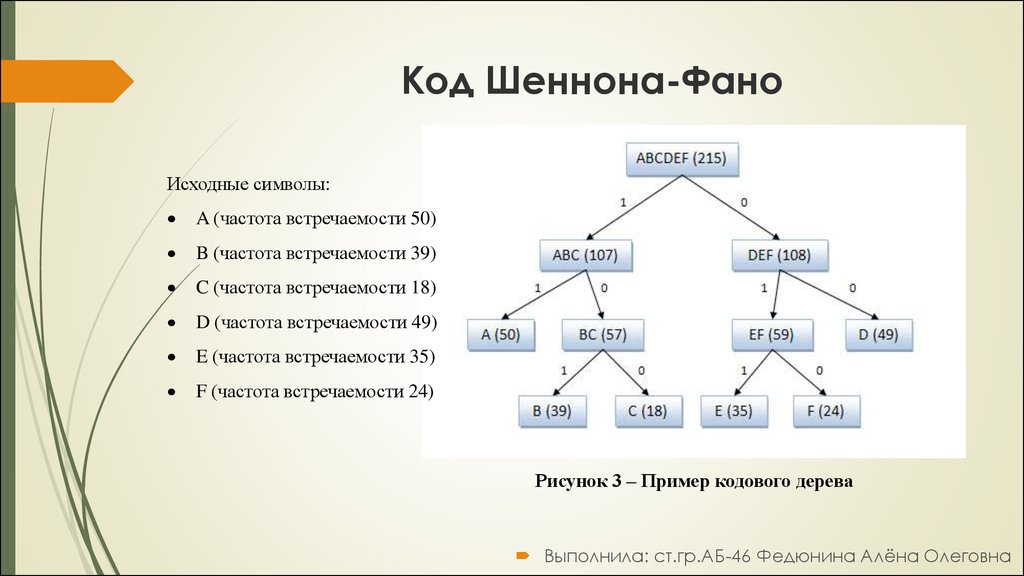 Непосредственное применение кода Шеннона Фано Элиаса также требует арифметики, точность которой растет с увеличением размера блока.

Shannon Fano Elias Алгоритм кодирования

— Реклама —

В цифровой связи исходный кодер преобразует ввод, то есть последовательность символов, в двоичную последовательность нулей и единиц. Каждый исходный символ представлен некоторой последовательностью закодированных символов, называемых кодовыми словами.

Процедура алгоритма кодирования Шеннона Фано Элиаса выглядит следующим образом:

Шаг 1

Расположите символы в порядке убывания вероятности.

Этап 2

Рассчитать кумулятивную вероятность.

σ1=0; σ2=p1+σ1; σ3=p2+σ2; и т.д…

Шаг 3

Рассчитать модифицированную кумулятивную функцию распределения.

Fbar(x)=σi+p(xi)/2

Шаг 4

Найдите длину кодового слова.

l(x)=[log1/p(x)]+1

Шаг 5

Сгенерируйте кодовое слово, найдя двоичное значение Fbar(x) относительно длины l(x).

Пример

Рассмотрим источник с пятью символами с вероятностями 0,3, 0,25, 0,2, 0,15 и 0,1 (см. таблицу).

Реализация алгоритма Шеннона Фано Элиаса в LabVIEW

Программы LabVIEW или виртуальные инструменты (VI) имеют лицевые панели и блок-схемы.

Передняя панель (рис. 1) — пользовательский интерфейс. Блок-схема (рис. 2) представляет собой программирование пользовательского интерфейса. После построения лицевой панели на блок-диаграмму добавляется код, использующий графическое представление функций для управления объектами лицевой панели. Код на блок-диаграмме представляет собой графический код, также известный как G-код или код блок-схемы.

Рис. 1: Передняя панель кодирования Шеннона Фано ЭлиасаРис. 2: Блок-схема кодирования Шеннона Фано Элиаса

Для реализации алгоритма Шеннона Фано Элиаса в LabVIEW требуются следующие компоненты:

Сортировка одномерного массива

Эта функция возвращает отсортированную версию массива с элементами, расположенными в порядке возрастания.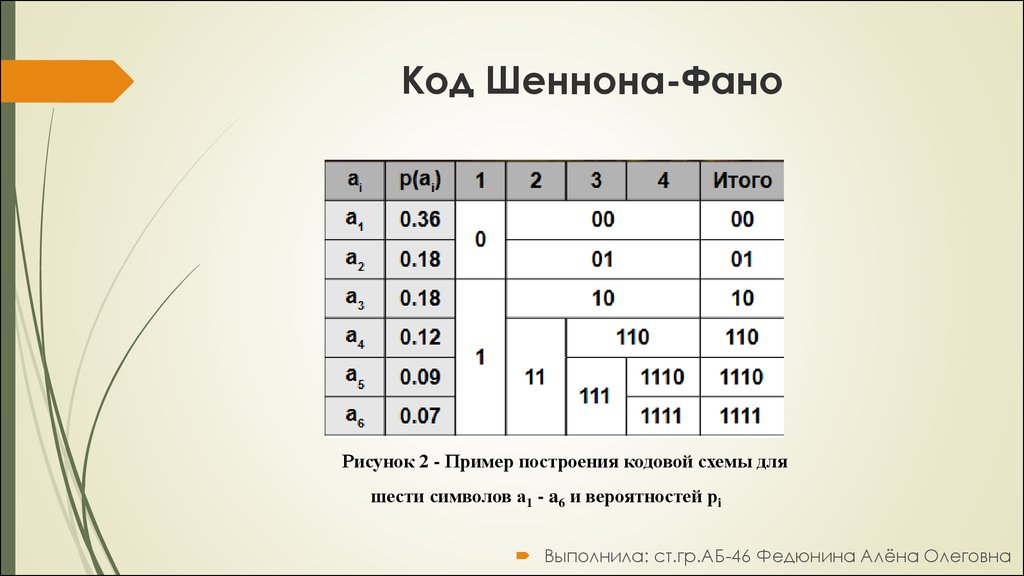 Если массив представляет собой массив кластеров, функция сортирует элементы, сравнивая первые элементы. Если первые элементы совпадают, функция сравнивает второй и последующие элементы. Панель соединителя отображает типы данных по умолчанию для этой полиморфной функции.

Обратный одномерный массив

Эта функция меняет порядок элементов в массиве на обратный, причем массив может быть любого типа. Панель соединителя отображает типы данных по умолчанию для этой полиморфной функции.

Индексный массив

Эта функция возвращает элемент или подмассив n-мерного массива по индексу. Когда вы подключаете массив к этой функции, функция автоматически изменяет размер, чтобы отображать входные индексы для каждого измерения в массиве, который вы подключаете к n-мерному массиву.

Вы также можете добавить дополнительные элементы или терминалы подмассива, изменив размер функции. Панель соединителя отображает типы данных по умолчанию для этой полиморфной функции.

Разделить

Если вы подключаете к этой функции два значения осциллограммы или два значения типа динамических данных, на функции появляются клеммы ввода и вывода ошибок. Панель соединителя отображает типы данных по умолчанию для этой полиморфной функции.

Добавить

Если вы подключаете к этой функции два значения осциллограммы или два значения типа динамических данных, на функции появляются входные и выходные терминалы ошибки. Вы не можете добавить два значения метки времени вместе. Размеры двух матриц, которые вы хотите добавить, должны быть одинаковыми.

В противном случае эта функция возвращает пустую матрицу. Панель соединителя отображает типы данных по умолчанию для этой полиморфной функции.

Основание логарифма 2

Если x равно 0, log2(x) равно отрицательной бесконечности. Если x не является комплексным и меньше 0, log2(x) равно NaN. Панель соединителя отображает типы данных по умолчанию для этой полиморфной функции.

Округление до +бесконечности

Например, если введено значение 3,1, результат равен 4. Если введено значение -3,1, результат равен -3. Панель соединителя отображает типы данных по умолчанию для этой полиморфной функции.

Построить массив кластеров

Эта функция объединяет каждый входной элемент в кластер и собирает все кластеры элементов в массив кластеров. Панель соединителя отображает типы данных по умолчанию для этой полиморфной функции.

Описание блок-схемы

Рис. 3: Преобразование десятичной дроби в двоичную

Шаг 1

Начните с десятичной дроби и умножьте на 2. Целая числовая часть результата представляет собой первую двоичную цифру справа от точка.

Шаг 2

Отбросить целую числовую часть предыдущего результата и снова умножить остаток. Целая числовая часть этого нового результата — это вторая двоичная цифра справа от точки.

Продолжайте процесс, пока не получите 0 в качестве десятичной части или пока не распознаете бесконечно повторяющийся шаблон.

Шаг 3

Не учитывать целую числовую часть предыдущего результата и еще раз умножить на 2. Целая числовая часть результата теперь является следующей двоичной цифрой справа от точки. Продолжайте процесс в зависимости от длины.

Процедура тестирования

1. Загрузите и установите LabVIEW.
2. Нажмите LabVIEW на рабочем столе.
3. Открытый Shannonfanoeliasfinal.vi
4. Укажите исходные символы для x1, x2 и т. д., вероятности P1, P2 и т. д. При применении входного значения вероятности сумма будет равна 1, так как общая вероятность символа должна быть равна 1.
5. Нажмите «Выполнить». Сгенерированный код должен удовлетворять префиксным и мгновенным свойствам.

Примечание. Shannonfanoelias.vi — главный ВП. У нас есть двоичный convert.vi вместе с этим основным VI. Если при открытии основного ВП вы сталкиваетесь с какой-либо ошибкой или вопросительным знаком, дважды щелкните этот вопросительный знак.