Коэффициент корреляции рангов спирмена: Методы статистики

Методы статистики

Коэффициент ранговой корреляции Спирмена – это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.

Чарльз Эдвард Спирмен

1. История разработки коэффициента ранговой корреляции

Данный критерий был разработан и предложен для проведения корреляционного анализа в 1904 году Чарльзом Эдвардом Спирменом, английским психологом, профессором Лондонского и Честерфилдского университетов.

2. Для чего используется коэффициент Спирмена?

Коэффициент ранговой корреляции Спирмена используется для выявления и оценки тесноты связи между двумя рядами сопоставляемых количественных показателей. В том случае, если ранги показателей, упорядоченных по степени возрастания или убывания, в большинстве случаев совпадают (большему значению одного показателя соответствует большее значение другого показателя — например, при сопоставлении роста пациента и его массы тела), делается вывод о наличии прямой корреляционной связи. Если ранги показателей имеют противоположную направленность (большему значению одного показателя соответствует меньшее значение другого — например, при сопоставлении возраста и частоты сердечных сокращений), то говорят об обратной связи между показателями.

Коэффициент корреляции Спирмена обладает следующими свойствами:
1. Коэффициент корреляции может принимать значения от минус единицы до единицы, причем при rs=1 имеет место строго прямая связь, а при rs= -1 – строго обратная связь.
2. Если коэффициент корреляции отрицательный, то имеет место обратная связь, если положительный, то – прямая связь.
3. Если коэффициент корреляции равен нулю, то связь между величинами практически отсутствует.
4. Чем ближе модуль коэффициента корреляции к единице, тем более сильной является связь между измеряемыми величинами.

3. В каких случаях можно использовать коэффициент Спирмена?

В связи с тем, что коэффициент является методом непараметрического анализа, проверка на нормальность распределения не требуется.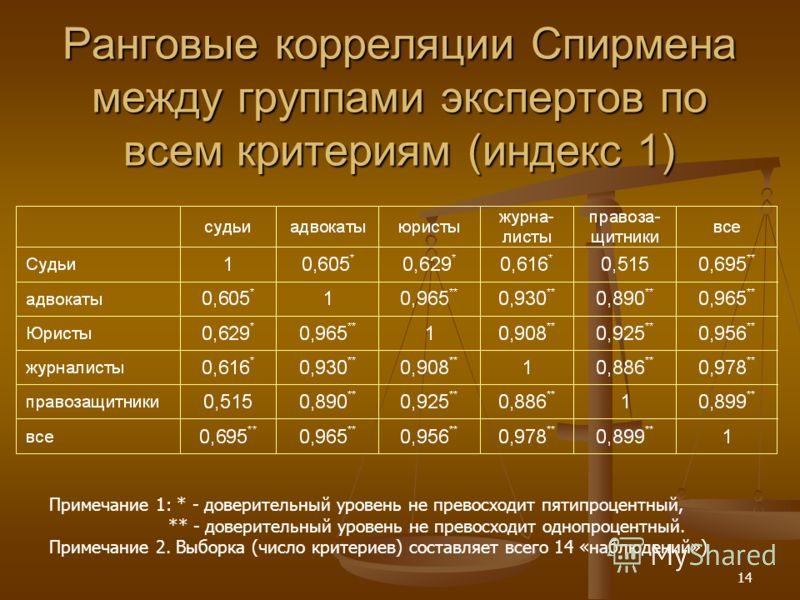

Сопоставляемые показатели могут быть измерены как в непрерывной шкале (например, число эритроцитов в 1 мкл крови), так и в порядковой (например, баллы экспертной оценки от 1 до 5).

Эффективность и качество оценки методом Спирмена снижается, если разница между различными значениями какой-либо из измеряемых величин достаточно велика. Не рекомендуется использовать коэффициент Спирмена, если имеет место неравномерное распределение значений измеряемой величины.

4. Как рассчитать коэффициент Спирмена?

Расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:

1. Сопоставить каждому из признаков их порядковый номер (ранг) по возрастанию или убыванию.
2. Определить разности рангов каждой пары сопоставляемых значений (d).
3. Возвести в квадрат каждую разность и суммировать полученные результаты.
4. Вычислить коэффициент корреляции рангов по формуле:
5. Определить статистическую значимость коэффициента при помощи
   t-критерия, рассчитанного по следующей формуле:

5.

Как интерпретировать значение коэффициента Спирмена?

При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента меньше 0,3 — признаком слабой тесноты связи; значения более 0,3, но менее 0,7 — признаком умеренной тесноты связи, а значения 0,7 и более — признаком высокой тесноты связи.

Также для оценки тесноты связи может использоваться шкала Чеддока:

Абсолютное значение rxy	Теснота (сила) корреляционной связи
менее 0.3	слабая
от 0.3 до 0.5	умеренная
от 0.5 до 0.7	заметная
от 0.7 до 0.9	высокая
более 0.9	весьма высокая

Статистическая значимость полученного коэффициента оценивается при помощи t-критерия Стьюдента. Если расчитанное значение t-критерия меньше табличного при заданном числе степеней свободы, статистическая значимость наблюдаемой взаимосвязи — отсутствует. Если больше, то корреляционная связь считается статистически значимой.

Расчет коэффициента ранговой корреляции Спирмена

«-//W3C//DTD HTML 3.2 Final//RU\»>

Расчет коэффициента ранговой корреляции Спирмена

---

1. Определить, какие два признака или две иерархии признаков будут участвовать в сопоставлении как переменные A и B.

2. Проранжировать значения переменной A, начисляя ранг 1 наименьшему значению, в соответствии с правилами ранжирования. Занести ранги в первый столбец таблицы по порядку номеров испытуемых или признаков.

3. Проранжировать значения переменной B, в соответствии с теми же правилами. Занести ранги во второй столбец таблицы по порядку номеров испытуемых или признаков.

4. Подсчитать разности d между рангами A и B по каждой строке таблицы и занести в третий столбец таблицы.

5. Занести каждую разность в квадрат: d

   2. Эти значения занести в четвертый столбец таблицы.

6. Подсчитать сумму d².

7. При наличии одинаковых рангов расчитать поправки:

   
   
   где a — объем каждой группы одинаковых рангов в ранговом ряду A;
   b — объем каждой группы одинаковых рангов в ранговом ряду B.

8. Расчитать коэффициент ранговой корреляции r_s по формуле:

   1. при отсутствии одинаковых рангов

      
      
      

   2. при наличии одинаковых рангов

      
      
      

      где sum(d²) — сумма квадратов разностей между рангами;
      T_a и T_b — поправки на одинаковые ранги;
      N — количество испытуемых или признаков, участвовавших в ранжировании.

9. Определить по таблице критические значения r

   s для данного N. Если r_s превышает критическое значение или по крайней мере равен ему, корреляция достоверно отличается от 0.

Источник: Сидоренко Е. В. Методы математической обработки в психологии — CПб.: ООО &quotРечь&quot, 2001, с.223.

---

© Куксов А. Ю., 2005

Ранговая корреляция Спирмена в Excel: формула и график

В учебном пособии простым языком объясняются основы корреляции Спирмена и показано, как рассчитать коэффициент ранговой корреляции Спирмена в Excel.

При выполнении корреляционного анализа в Excel в большинстве случаев вы будете иметь дело с корреляцией Пирсона. Но поскольку коэффициент корреляции Пирсона измеряет только линейную связь между двумя переменными, он не работает для всех типов данных — ваши переменные могут быть сильно связаны нелинейным образом, а коэффициент по-прежнему будет близок к нулю. В таких обстоятельствах вы можете использовать ранговую корреляцию Спирмена вместо Пирсона.

Корреляция Спирмена — основы

Корреляция Спирмена — это непараметрическая версия коэффициента корреляции Пирсона, которая измеряет степень связи между двумя переменными на основе их рангов.

Программа Pearson Product Moment Correlation проверяет линейную связь между двумя непрерывными переменными. Линейная означает зависимость, при которой две переменные изменяются в одном направлении с постоянной скоростью.

Ранговая корреляция Спирмена оценивает монотонную связь между ранжированными значениями. В монотонной зависимости переменные также имеют тенденцию изменяться вместе, но не обязательно с постоянной скоростью.

Когда делать корреляцию Спирмена

Корреляционный анализ Спирмена должен использоваться в любом из следующих обстоятельств, когда основные предположения корреляции Пирсона не выполняются:

1. Если ваши данные демонстрируют нелинейность отношения или нормально не распределены.
2. Если хотя бы одна переменная равна порядковому номеру . Если ваши значения можно расположить в порядке «первый, второй, третий…», вы имеете дело с порядковыми данными.
3. При наличии значительных выбросов . В отличие от корреляции Пирсона, корреляция Спирмена не чувствительна к выбросам, поскольку она выполняет расчеты по рангам, поэтому разница между фактическими значениями не имеет значения.

Например, вы можете использовать корреляцию Спирмена, чтобы найти ответы на следующие вопросы:

• Люди с более высоким уровнем образования больше заботятся об окружающей среде?
• Связано ли количество симптомов у пациента с его готовностью принимать лекарства?

Коэффициент корреляции Спирмена

В статистике коэффициент корреляции Спирмена представлен либо r _s , либо греческой буквой ρ («ро»), поэтому его часто называют ро Спирмена .

Коэффициент ранговой корреляции Спирмена измеряет как силу, так и направление взаимосвязи между рангами данных. Это может быть любое значение от -1 до 1, и чем ближе абсолютное значение коэффициента к 1, тем сильнее связь:

• 1 — полная положительная корреляция
• -1 — идеальная отрицательная корреляция
• 0 нет корреляции

Формула ранговой корреляции Спирмена

В зависимости от наличия или отсутствия связей в ранжировании (один и тот же ранг, присвоенный двум или более наблюдениям), коэффициент корреляции Спирмена можно рассчитать по одной из следующих формул.

Если есть нет равных рангов , подойдет более простая формула:

Где:

• d _i разница между парой рядов
• n количество наблюдений

Чтобы иметь дело с связанными рангами , необходимо использовать полную версию формулы корреляции Спирмена, которая представляет собой слегка модифицированную версию r Пирсона:

Где:

• R(x) и R(y) — ранги x и y переменные
• R(x) и R(y) — средние ранги

Как рассчитать корреляцию Спирмена в Excel с помощью функции КОРРЕЛ

К сожалению, в Excel нет встроенной функции для расчета коэффициента ранговой корреляции Спирмена.

Однако это не означает, что вам придется ломать голову над приведенными выше формулами. Немного поэкспериментировав с Excel, мы можем придумать гораздо более простой способ корреляции Спирмена.

В качестве примера попробуем выяснить, имеет ли какое-либо отношение наша физическая активность к нашему кровяному давлению. В столбце B у нас есть количество минут, которые 10 мужчин того же возраста ежедневно проводят в тренажерном зале, а в столбце C у нас есть их систолическое артериальное давление.

Чтобы найти коэффициент корреляции Спирмена в Excel, выполните следующие действия:

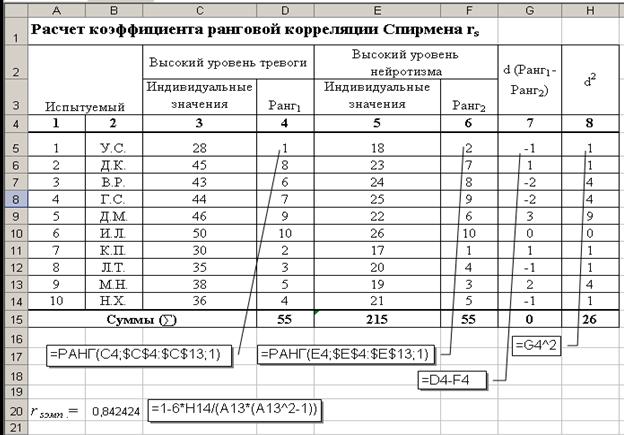
1. Ранжируйте свои данные

   Поскольку корреляция Спирмена оценивает связи между двумя переменными на основе их рангов, вам необходимо ранжировать исходные данные. Это можно быстро сделать с помощью функции Excel RANK.AVG.

   Чтобы ранжировать первую переменную (физическую активность), введите приведенную ниже формулу в D2, а затем перетащите ее вниз в D11:

   =РАНГ. СРЕДНЕЕ(B2,$B$2:$B$11,0)

   Чтобы ранжировать вторую переменную (артериальное давление), поместите следующую формулу в ячейку E2 и скопируйте ее вниз по столбцу:

   =РАНГ.СРЕДНЕЕ(C2,$C$2:$C$11,0)

   Чтобы формулы работали правильно, убедитесь, что диапазоны заблокированы абсолютными ссылками на ячейки.

   На этом этапе ваши исходные данные должны выглядеть примерно так:
   

2. Найти коэффициент корреляции Спирмена
   Теперь, когда ранги установлены, мы можем использовать функцию Excel CORREL для получения ро Спирмена:

   =КОРРЕЛ(D2:D11, E2:E11)

   Формула возвращает коэффициент -0,7576 (округленный до 4 цифр), который показывает достаточно сильную отрицательную корреляцию и позволяет сделать вывод, что чем больше человек тренируется, тем ниже у него артериальное давление.

   Коэффициент корреляции Пирсона для той же выборки (-0,7445) указывает на несколько более слабую корреляцию, но все же статистически значимую:
   

Прелесть этого метода в том, что он быстрый, простой и работает независимо от того, есть ничья в рейтинге или нет.

Рассчитать коэффициент корреляции Спирмена в Excel по традиционной формуле

Если вы не совсем уверены, что функция КОРРЕЛ вычислила право Спирмена, вы можете проверить результат с помощью традиционной формулы, используемой в статистике. Вот как:

1. Найдите разницу между каждой парой рангов ( d ), вычитая один ранг из другого:

   =D2-E2

   Эта формула помещается в F2, а затем копируется вниз по столбцу. 92

   Эта формула относится к столбцу G.

2. Сложите квадраты разностей:

   =СУММ(G2:G11)

   Эта формула может быть адресована любой пустой ячейке, в нашем случае G12.

   Из следующего снимка экрана вы, вероятно, лучше поймете расположение данных:
   

3. В зависимости от того, имеет ли ваш набор данных какие-либо связанные ранги или нет, используйте одну из этих формул для расчета коэффициента корреляции Спирмена.

В нашем примере ничьих нет, поэтому можно использовать более простую формулу:

.

При d ² равном 290 и n (число наблюдений) равном 10 формула претерпевает следующие преобразования:

В результате получается -0,757575758, что полностью согласуется с коэффициентом корреляции Спирмена, рассчитанным в предыдущем примере.

В Microsoft Excel вышеуказанные расчеты можно выполнить с помощью следующего уравнения: 92-1)))

Где G12 — сумма квадратов разностей рангов (d ² ).

Как сделать корреляцию Спирмена в Excel с помощью графика

Коэффициенты корреляции в Excel измеряют только линейные (Пирсон) или монотонные (Спирмен) отношения. Однако возможны и другие ассоциации. Таким образом, независимо от того, какую корреляцию вы делаете, всегда полезно представить взаимосвязь между переменными на графике.

Чтобы построить график корреляции ранжированных данных, вам нужно сделать следующее:

1. Вычислите ранги с помощью функции RANK.AVG, как описано в этом примере.
2. Выберите два столбца с рангами.
3. Вставьте точечную диаграмму XY. Для этого нажмите на иконку Scatter chart на вкладке Inset , в группе Chats .
4. Добавьте на график линию тренда. Самый быстрый способ — нажать кнопку Элементы диаграммы > Добавить линию тренда… .
5. Отображение значения R-квадрата на графике. Дважды щелкните линию тренда, чтобы открыть ее панель, переключитесь на Параметры линии тренда и выберите поле Показать значение R-квадрата на графике .
6. Показать больше цифр в значении R ² для большей точности.

В результате вы получите наглядное представление о соотношении рангов. Дополнительно вы получите Коэффициент детерминации (R ² ), квадратный корень из которого представляет собой коэффициент корреляции Пирсона (r). Но поскольку вы построили ранжированные данные, это r Пирсона есть не что иное, как rho Спирмена.

Примечание. R-квадрат всегда является положительным числом, поэтому выведенный коэффициент ранговой корреляции Спирмена также всегда будет положительным. Чтобы добавить соответствующий знак, просто посмотрите на линию на графике корреляции: наклон вверх указывает на положительную корреляцию (знак плюс), а наклон вниз указывает на отрицательную корреляцию (знак минус).

В нашем случае R ² равно 0,5739210285. Используйте функцию SQRT, чтобы найти квадратный корень:

=КОРЕНЬ(0,5739210285)

… и вы получите уже знакомый коэффициент 0,757575758.

Нисходящий наклон на графике демонстрирует отрицательную корреляцию, поэтому мы добавляем знак минус и получаем правильный коэффициент корреляции Спирмена, равный -0,757575758.

Вот как можно рассчитать ранговый коэффициент корреляции Спирмена в Excel. Чтобы поближе ознакомиться с примерами, обсуждаемыми в этом руководстве, вы можете загрузить наш образец книги ниже.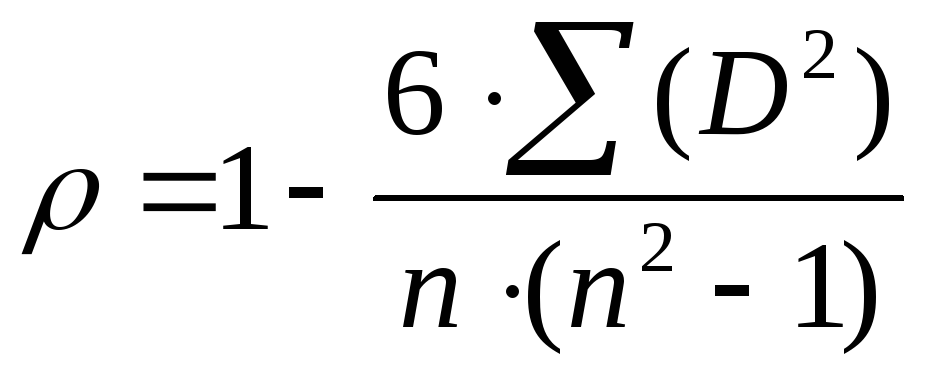 Я благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!

Рабочая тетрадь

Корреляция рангов Спирмена в Excel (файл .xlsx)

Вас также может заинтересовать

Как выполнить ранговый корреляционный тест Спирмена в Excel

В этом руководстве я покажу вам, как выполнить ранговый корреляционный тест Спирмена в Microsoft Excel. Сюда входит определение коэффициента корреляции Спирмена, а также значения p для статистического теста.

Что такое тест корреляции Спирмена?

Критерий ранговой корреляции Спирмена — это непараметрическая мера ранговой корреляции. Это статистический тест, используемый для определения силы и направления связи между двумя ранжированными переменными.

Ранее я обсуждал, как выполнить тест корреляции Пирсона в Excel.

Выходные данные представлены в виде коэффициента корреляции Спирмена (r _s ), который представляет собой значение в диапазоне от -1 до 1, указывающее силу связи.

Следующие значения r _s указывают направление и силу ассоциации.

• r _s = -1 : Совершенно отрицательная ассоциация
• R _S = 0 : NO Association
• R _S = +1 : A Perfect Poploick Association Associal Associal Aslieval

. В Excel нет функции для расчета коэффициента корреляции Спирмена. Во-первых, нам нужно ранжировать две переменные, чтобы иметь возможность рассчитать коэффициент корреляции по рангам.

Затем этот коэффициент корреляции можно использовать для создания статистики t, которая затем может использоваться для определения значения p.

1. Вычислить ранги переменных

Первым шагом является создание двух новых переменных, которые будут рангами. Здесь я скажу Excel ранжировать данные в порядке возрастания. Это присвоит ранг 1 наименьшему значению и так далее и тому подобное.

Для этого воспользуемся формулой RANK.AVG. Эта формула ранжирует значения в порядке возрастания. Обратите внимание, что если есть два одинаковых значения, их ранг будет усреднен.

В пустом столбце щелкните первую ячейку и добавьте следующую формулу.

 =RANK.AVG(число, ссылка, [порядок]) 

Замените входные требования на…

• число: Ячейка, содержащая первое значение данных, которое вы хотите ранжировать
• ссылка: Выбрать все данных – это требуется в качестве ссылки
• [порядок]: Введите значение 1, чтобы ранжировать значение в порядке возрастания

Теперь повторите этот процесс для остальных точек данных.

Простой способ сделать это — заблокировать ввод ссылки (диапазон ячеек, содержащий все данные) и перетащить формулу вниз.

Чтобы заблокировать ячейки, добавьте символ $ перед буквами столбцов и номерами строк.

Теперь вы можете безопасно щелкнуть и перетащить формулу вниз, чтобы заполнить остальные разряды. Поскольку ячейки ссылок заблокированы, они останутся прежними.

Сделав это, перейдите к следующей переменной и повторите процесс. Вы должны получить две новые переменные, содержащие значения ранжирования для исходных переменных.

2. Рассчитать коэффициент корреляции Спирмена в Excel

Для расчета коэффициента корреляции Спирмена мы можем использовать формулу КОРРЕЛ с вновь созданными ранговыми переменными в качестве входных данных.

В новую ячейку введите следующую формулу.

 =CORREL(массив1, массив2) 

Замените входные требования на…

• массив1: Диапазон ячеек для переменной первого ранга
• массив2: Диапазон ячеек для переменной второго ранга41 5

  В приведенном выше примере коэффициент корреляции Спирмена (r _с ) равно 0,63.

  3. Подсчитайте количество пар

  Следующим шагом является определение количества пар (n). Вы можете просто подсчитать их вручную, если ваши данные малы. Для больших наборов данных используйте формулу COUNT.

  Обратите внимание, данные должны быть парными. Если в одной из пар отсутствуют значения, необходимо удалить эту пару из анализа.

  4. Рассчитать t-статистику

  Далее нам нужно рассчитать t-статистику, чтобы иметь возможность определить значение p. 92))

  Замените требования к вводу на…

  • R _S : . Клетка, содержащая коэффициент корреляции
  • N:
    . Содержание. для преобразования значения коэффициента в абсолютное значение (положительное число). Это работает, когда у вас есть отрицательное значение коэффициента. В противном случае без формулы ABS будет ошибка.

    4. Расчет степеней свободы

    Далее нам нужно рассчитать количество степеней свободы (DF).

    DF можно найти, вычитая 2 из n.

    Итак, в новую ячейку введите следующую формулу.

    No related posts.