Коэффициент Стьюдента в зависимости от количества наблюдений n и от значения доверительной вероятности
n-1 | 0,95 | 0,99 |
3 4 5 6 7 8 9 10 12 14 16 18 20 22 24 26 28 30 | 3,182 2,776 2,571 2,447 2,306 2,262 2,228 2,179 2,145 2,120 2,101 2,086 2,074 2,064 2,056 2,048 2,043 1,960 | 5,841 4,604 4,032 3,707 2,998 3,355 3,250 3,169 3,055 2,977 2,921 2,878 2,845 2,819 2,797 2,779 2,763 2,750 2,576 |
4. 3.
Если класс точности прибора указан
двумя цифрами в виде дроби к/н,
то:
3.
Если класс точности прибора указан
двумя цифрами в виде дроби к/н,
то:
. (7)
В последних двух случаях в качестве значения х принимают среднее (наиболее вероятное) значение измеряемой величины.
Если класс точности прибора не указан, то в качестве значения приборной погрешности принимают половину цены наименьшего деления шкалы (для секундомера — цену одного деления шкалы).
5. Рассчитывают доверительную границу приборной погрешности.
При доверительной вероятности = 0,95 значение приборной погрешности определяется соотношением:
х
6.
Согласно [1] приборная погрешность –
это одна из составляющих систематической
погрешности. Результирующее значение
систематической погрешности следует
рассчитывать по формуле:
Результирующее значение
систематической погрешности следует
рассчитывать по формуле:
Δсист = k (Δ12+ Δ22+ Δi2 + … + Δm2)1/2,
где Δi– составляющая погрешности;
k – коэффициент, определяемый доверительной вероятностью. При = 0,95 этот коэффициент равен 1,1.
При доверительной вероятности = 0,99 значение коэффициента k определяется в соответствии с таблицей 1 – в зависимости от количества суммируемых составляющих погрешности m и от соотношения главных (по значению) составляющих этой погрешности: l = Δ1 / Δ2; (Δ1 > Δ2).
Таблица 2
m | l | |||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
2 | 1,22 | 1,17 | 1,12 | 1,09 | 1,07 | 1,06 | 1,05 | |
3 | 1,38 | 1,31 | 1,24 | 1,18 | 1,14 | 1,11 | 1,09 | 1,05 |
4 | 1,41 | 1,36 | 1,29 | 1,22 | 1,17 | 1,14 | 1,12 | 1,10 |
> 4 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 |
7. Вычисляют результирующую
доверительную погрешность прямого
измерения х.
Значение этой величины определяют две
составляющие: случайная погрешность
хсл , и систематическая погрешность хсист,
включающая приборную погрешность
Вычисляют результирующую
доверительную погрешность прямого
измерения х.
Значение этой величины определяют две
составляющие: случайная погрешность
хсл , и систематическая погрешность хсист,
включающая приборную погрешность
(1). Если выполняется неравенство:
2хсист хсл,
то систематической погрешностью по сравнению со случайной пренебрегают.
(2). Если
Если
хсист 5хсл,
то случайной погрешностью по сравнению с систематической пренебрегают.В общем случае границу абсолютной погрешности результата измерений вычисляют по формуле:
х= (хсл 2 + хсист2)1/2 . (8)
7. Окончательный результат записывают в виде:
. (9)
Запись в виде (9) означает, что с вероятностью 0,95 истинное значение измеряемой величины х0 заключено в интервале от ( ) до ( ) и с вероятностью 0,05 – находится вне его. При этом доверительный интервал равен .
Относительная погрешность результата серии наблюдений равна:
%.
Помогите решить / разобраться (Ф)
| Tatyana_math |
| ||
22/05/12 |
| ||
| |||
| Ms-dos4 |
| |||
25/02/08 |
| |||
| ||||
| Tatyana_math |
| ||
22/05/12 |
| ||
| |||
| Ms-dos4 |
| |||
25/02/08 |
| |||
| ||||
| nestoronij |
| ||
09/02/12 |
| ||
| |||
| Tatyana_math |
| ||
22/05/12 |
| ||
| |||
| Ms-dos4 |
| |||
25/02/08 |
| |||
| ||||
| Tatyana_math |
| ||
22/05/12 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 8 ] |
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Понимание анализа предметов | Office of Educational Assessment
Анализ заданий — это процесс, в ходе которого учащиеся изучают ответы на отдельные задания теста (вопросы) с целью оценки качества этих заданий и теста в целом. Анализ элементов особенно ценен для улучшения элементов, которые будут снова использоваться в последующих тестах, но его также можно использовать для устранения двусмысленных или вводящих в заблуждение элементов в рамках одного тестирования. Кроме того, анализ заданий полезен для повышения навыков инструкторов в построении тестов и выявления конкретных областей содержания курса, которые требуют большего внимания или ясности. Отдельные анализы предметов могут быть запрошены для каждой необработанной оценки 1 создано во время данного запуска ScorePak®.
Анализ элементов особенно ценен для улучшения элементов, которые будут снова использоваться в последующих тестах, но его также можно использовать для устранения двусмысленных или вводящих в заблуждение элементов в рамках одного тестирования. Кроме того, анализ заданий полезен для повышения навыков инструкторов в построении тестов и выявления конкретных областей содержания курса, которые требуют большего внимания или ясности. Отдельные анализы предметов могут быть запрошены для каждой необработанной оценки 1 создано во время данного запуска ScorePak®.
Анализ элемента образца (30 K PDF)
Основное предположение ScorePak® состоит в том, что анализируемый тест состоит из элементов, измеряющих одну предметную область или базовую способность. Качество теста в целом оценивается путем оценки его «внутренней состоятельности». Качество отдельных заданий оценивается путем сравнения ответов учащихся по заданиям с их общими результатами теста.
Ниже приводится описание различных статистических данных, представленных в отчете об анализе элементов ScorePak®. Этот отчет состоит из двух частей. В первой части оцениваются предметы, из которых состоял экзамен. Вторая часть показывает статистику, обобщающую производительность теста в целом.
Этот отчет состоит из двух частей. В первой части оцениваются предметы, из которых состоял экзамен. Вторая часть показывает статистику, обобщающую производительность теста в целом.
Статистика элементов
Статистика элементов используется для оценки производительности отдельных элементов теста при допущении, что общее качество теста зависит от качества его элементов. Отчет об анализе элемента ScorePak® содержит следующую информацию об элементе:
Номер элемента
Это номер вопроса, взятый из листа ответов учащегося и ключевого листа ScorePak®. В стандартном листе ответов можно набрать до 150 пунктов.
Среднее и стандартное отклонение
Среднее значение — это «средний» ответ учащегося на задание. Он рассчитывается путем сложения количества баллов, набранных всеми учащимися по предмету, и деления этой суммы на количество учащихся.
Стандартное отклонение, или S.D., является мерой разброса баллов учащихся по этому пункту. То есть это указывает на то, насколько «размазанными» были ответы. Стандартное отклонение элемента является наиболее значимым при сравнении элементов, которые имеют более одной правильной альтернативы, и когда используется оценка по шкале. По этой причине он обычно не используется для оценки тестов в классе.
Стандартное отклонение элемента является наиболее значимым при сравнении элементов, которые имеют более одной правильной альтернативы, и когда используется оценка по шкале. По этой причине он обычно не используется для оценки тестов в классе.
Сложность задания
Для заданий с одним правильным вариантом, оцениваемым в один балл, сложность задания представляет собой просто процент учащихся, ответивших на задание правильно. В этом случае он также равен среднему значению элемента. Индекс сложности предмета варьируется от 0 до 100; чем выше значение, тем проще вопрос. Когда альтернатива оценивается не в один балл, или когда на вопрос имеется более одной правильной альтернативы, сложность задания определяется как средний балл по этому вопросу, деленный на наибольшее количество баллов за любой вариант. Сложность задания важна для определения того, усвоили ли учащиеся тестируемую концепцию. Он также играет важную роль в способности элемента различать учащихся, которые знают тестируемый материал, и тех, кто не знает. У задания будет низкая дискриминация, если оно настолько сложное, что почти все ошибаются или угадывают его, или настолько простое, что почти все понимают его правильно.
У задания будет низкая дискриминация, если оно настолько сложное, что почти все ошибаются или угадывают его, или настолько простое, что почти все понимают его правильно.
Чтобы максимизировать различение предметов, желательные уровни сложности должны быть немного выше среднего между шансом и идеальными оценками для предмета. (Например, вероятность ответа на вопросы с пятью вариантами равна 20, поскольку можно ожидать, что пятая часть учащихся, отвечающих на вопрос, выберет правильный вариант путем угадывания.) Идеальные уровни сложности для заданий с множественным выбором с точки зрения различения потенциальные:
| Формат | Идеальная сложность | |
|---|---|---|
| Множественный выбор из пяти ответов | 70 | |
| Четыре ответа с множественным выбором | 74 | |
| Три ответа с множественным выбором | 77 | |
| Верно-ложно (два ответа с множественным выбором) | 85 |
(От Лорда Ф. М. «Связь надежности теста с множественным выбором с распределением трудностей с заданиями», Психометрика, 1952, 18, 181-194.)
М. «Связь надежности теста с множественным выбором с распределением трудностей с заданиями», Психометрика, 1952, 18, 181-194.)
ScorePak® произвольно классифицирует сложность задания как «легкую», если индекс составляет 85% или выше; «умеренный», если он составляет от 51 до 84%; и «жесткий», если он составляет 50% или ниже.
Различение заданий
Различение заданий относится к способности задания различать учащихся на основе того, насколько хорошо они знают тестируемый материал. Различные процедуры ручного подсчета традиционно использовались для сравнения ответов на задания с общими результатами теста с использованием групп учащихся с высокими и низкими баллами. Компьютеризированный анализ обеспечивает более точную оценку способности различения элементов, поскольку он учитывает ответы всех учащихся, а не только групп с высокими и низкими баллами.
Индекс различения элементов, предоставляемый ScorePak®, представляет собой корреляцию Pearson Product Moment 2 между ответами учащихся на определенный элемент и общими баллами по всем другим элементам теста. Этот индекс является эквивалентом точечно-двусерийного коэффициента в этом приложении. Он обеспечивает оценку степени, в которой отдельный элемент измеряет то же самое, что и остальные элементы.
Этот индекс является эквивалентом точечно-двусерийного коэффициента в этом приложении. Он обеспечивает оценку степени, в которой отдельный элемент измеряет то же самое, что и остальные элементы.
Поскольку индекс различения отражает степень, в которой элемент и тест в целом измеряют единую способность или атрибут, значения коэффициента будут иметь тенденцию быть ниже для тестов, измеряющих широкий диапазон областей содержания, чем для более однородных тестов. . Индексы различения предметов всегда должны интерпретироваться в контексте типа анализируемого теста. Элементы с низкими индексами дискриминации часто сформулированы неоднозначно и должны быть проверены. Элементы с отрицательными индексами следует изучить, чтобы определить, почему было получено отрицательное значение. Например, отрицательное значение может указывать на то, что элемент был неправильно введен, так что учащиеся, которые знали материал, как правило, выбирали неключевой, но правильный вариант ответа.
Тесты с высокой внутренней непротиворечивостью состоят из заданий, в основном имеющих положительную связь с общим результатом теста.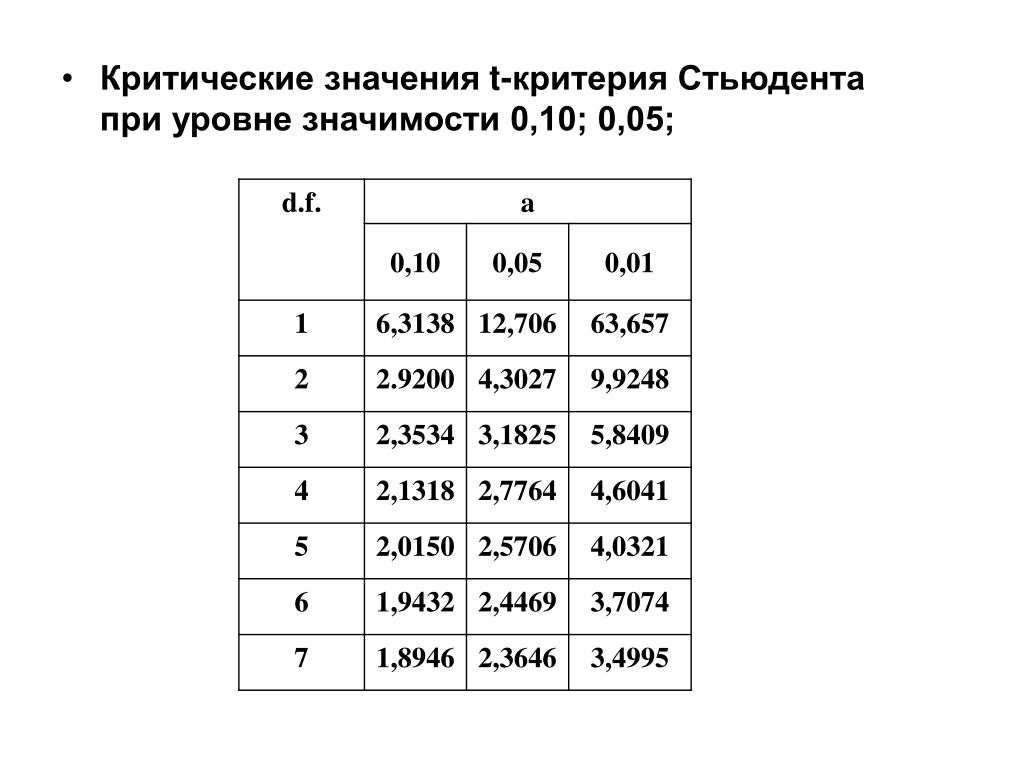 На практике значения индекса различения редко превышают 0,50 из-за различной формы распределений пунктов и общих баллов. ScorePak® классифицирует различение предметов как «хорошее», если индекс выше 0,30; «удовлетворительно», если он находится между 0,10 и 0,30; и «плохо», если он ниже 0,10.
На практике значения индекса различения редко превышают 0,50 из-за различной формы распределений пунктов и общих баллов. ScorePak® классифицирует различение предметов как «хорошее», если индекс выше 0,30; «удовлетворительно», если он находится между 0,10 и 0,30; и «плохо», если он ниже 0,10.
Альтернативный вес
В этой колонке показано количество баллов, присуждаемых за каждый вариант ответа. Для большинства тестов будет один правильный ответ, которому будет присвоен один балл, но ScorePak® допускает несколько правильных вариантов, каждому из которых может быть присвоен разный вес.
Среднее значение
Средний общий балл за тест (за вычетом этого пункта) показан для учащихся, выбравших каждый из возможных вариантов ответа. Эту информацию следует рассматривать вместе с индексом дискриминации; более высокие общие результаты тестов должны быть получены учащимися, выбравшими правильную или наиболее взвешенную альтернативу. Следует изучить неправильные альтернативы с относительно высокими средними значениями, чтобы определить, почему «лучшие» учащиеся выбрали именно эту альтернативу.
Частоты и распространение
Сообщается количество и процент учащихся, выбравших каждый вариант. На гистограмме справа показан процент выбора каждого ответа; каждый «#» представляет приблизительно 2,5%. Часто выбранные неправильные альтернативы могут указывать на распространенные среди учащихся заблуждения.
Распределение сложности и дискриминации
В конце отчета об анализе заданий тестовые задания перечислены в соответствии с их степенями сложности (легкий, средний, сложный) и дискриминацией (хорошо, удовлетворительно, плохо). Эти распределения обеспечивают краткий обзор теста и могут использоваться для выявления элементов, которые не работают должным образом и которые, возможно, можно улучшить или отбросить.
Статистика теста
Для оценки производительности теста в целом предоставляются две статистики.
Коэффициент надежности
Надежность теста относится к степени, в которой тест может дать согласованные результаты. Конкретный коэффициент надежности, рассчитанный ScorePak®, отражает три характеристики теста:
Конкретный коэффициент надежности, рассчитанный ScorePak®, отражает три характеристики теста:
- Взаимокорреляции между элементами — чем больше относительное количество положительных взаимосвязей и чем сильнее эти взаимосвязи, тем выше надежность. Индексы различения элементов и коэффициент надежности теста связаны в этом отношении.
- Длина теста — тест с большим количеством элементов будет иметь более высокую надежность при прочих равных условиях.
- Содержание теста — как правило, чем разнообразнее тестируемый предмет и используемые методы тестирования, тем ниже надежность.
Коэффициенты надежности теоретически находятся в диапазоне значений от нуля (нет надежности) до 1,00 (полная надежность). На практике их приблизительный диапазон составляет от 0,50 до 0,90 примерно для 95% тестов в классе, оцениваемых ScorePak®. Высокая надежность означает, что вопросы теста, как правило, «стягиваются». Студенты, которые правильно ответили на данный вопрос, с большей вероятностью правильно ответили на другие вопросы. Если бы параллельный тест был разработан с использованием аналогичных элементов, относительные баллы учащихся изменились бы незначительно. Низкая надежность означает, что вопросы, как правило, не связаны друг с другом с точки зрения того, кто на них ответил правильно. Полученные результаты тестов отражают особенности заданий или ситуации тестирования в большей степени, чем знания учащихся по предмету.
Если бы параллельный тест был разработан с использованием аналогичных элементов, относительные баллы учащихся изменились бы незначительно. Низкая надежность означает, что вопросы, как правило, не связаны друг с другом с точки зрения того, кто на них ответил правильно. Полученные результаты тестов отражают особенности заданий или ситуации тестирования в большей степени, чем знания учащихся по предмету.
Как и в случае со многими статистическими данными, интерпретировать значение коэффициента надежности вне контекста опасно. Высокая надежность должна требоваться в ситуациях, когда для принятия важных решений используется один результат теста, например, экзамены на получение профессиональной лицензии. Поскольку классные экзамены обычно объединяются с другими баллами для определения оценок, стандарты для одного теста не должны быть такими строгими. Следующие общие рекомендации можно использовать для интерпретации коэффициентов надежности для аудиторных экзаменов:
| Надежность | Интерпретация |
|---|---|
. 90 и выше 90 и выше | Превосходная надежность; на уровне лучших стандартизированных тестов |
| .80 – .90 | Очень хорошо для классного теста |
| .70 – .80 | Подходит для классного теста; в диапазоне большинства. Вероятно, есть несколько элементов, которые можно было бы улучшить. |
| .60 – .70 | Несколько низкий. Этот тест необходимо дополнить другими мерами (например, большим количеством тестов) для определения оценок. Есть, вероятно, некоторые элементы, которые можно было бы улучшить. |
| .50 – .60 | Предлагает пересмотреть тест, если только он не слишком короткий (десять или меньше пунктов). Тест определенно должен быть дополнен другими мерами (например, большим количеством тестов) для оценки. |
| .50 или ниже | Сомнительная надежность. Этот тест не должен сильно влиять на оценку курса, и его необходимо пересмотреть. |
Мерой надежности, используемой ScorePak®, является Альфа Кронбаха.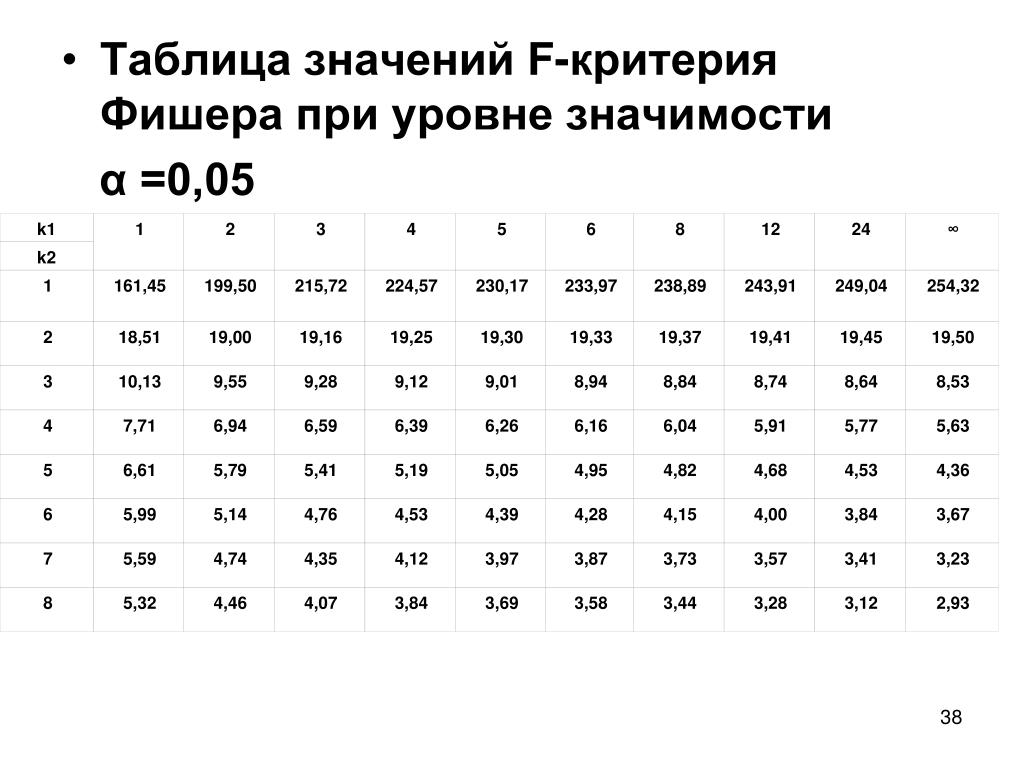 Это общая форма более часто встречающегося KR-20, и ее можно применять к тестам, состоящим из заданий с разным количеством баллов, присваиваемых за разные варианты ответов. Когда коэффициент альфа применяется к тестам, в которых каждый пункт имеет только один правильный ответ и все правильные ответы оцениваются в одинаковое количество баллов, результирующий коэффициент идентичен КР-20.
Это общая форма более часто встречающегося KR-20, и ее можно применять к тестам, состоящим из заданий с разным количеством баллов, присваиваемых за разные варианты ответов. Когда коэффициент альфа применяется к тестам, в которых каждый пункт имеет только один правильный ответ и все правильные ответы оцениваются в одинаковое количество баллов, результирующий коэффициент идентичен КР-20.
(Дальнейшее обсуждение надежности теста можно найти в J. C. Nunnally, Psychometric Theory. New York: McGraw-Hill, 1967, стр. 172-235, особенно см. формулы 6-26, стр. 196.)
Стандарт Ошибка измерения
Стандартная ошибка измерения напрямую связана с надежностью теста. Это показатель степени изменчивости в успеваемости отдельного учащегося из-за случайной ошибки измерения. Если бы можно было проводить бесконечное количество параллельных тестов, можно было бы ожидать, что оценка учащегося будет меняться от одного теста к другому из-за ряда факторов. Для каждого учащегося баллы образуют «нормальное» (колоколообразное) распределение. Предполагается, что среднее значение распределения является «истинной оценкой» учащегося и отражает то, что он или она «действительно» знает о предмете. Стандартное отклонение распределения называется стандартной ошибкой измерения и отражает величину изменения в баллах учащегося, которое можно было бы ожидать от одного тестирования к другому.
Предполагается, что среднее значение распределения является «истинной оценкой» учащегося и отражает то, что он или она «действительно» знает о предмете. Стандартное отклонение распределения называется стандартной ошибкой измерения и отражает величину изменения в баллах учащегося, которое можно было бы ожидать от одного тестирования к другому.
В то время как надежность теста всегда варьируется от 0,00 до 1,00, стандартная ошибка измерения выражается по той же шкале, что и результаты теста. Например, умножение всех результатов теста на константу приведет к умножению стандартной ошибки измерения на ту же константу, но оставит неизменным коэффициент надежности.
Общее эмпирическое правило для прогнозирования количества изменений, которое можно ожидать в результатах отдельных тестов, заключается в умножении стандартной ошибки измерения на 1,5. Лишь в редких случаях можно ожидать, что оценка учащегося увеличится или уменьшится более чем на эту сумму между двумя подобными тестами. Чем меньше стандартная ошибка измерения, тем точнее измерение, обеспечиваемое тестом.
Чем меньше стандартная ошибка измерения, тем точнее измерение, обеспечиваемое тестом.
(Дальнейшее обсуждение стандартной ошибки измерения можно найти в J. C. Nunnally, Psychometric Theory. New York: McGraw-Hill, 1967, стр. 172-235, см. особенно формулы 6-34, стр. 201.)
Предостережение при интерпретации результатов анализа элементов
Каждый из различных статистических показателей элементов, предоставляемых ScorePak®, предоставляет информацию, которую можно использовать для улучшения отдельных элементов теста и повышения качества теста в целом. Такие статистические данные всегда должны интерпретироваться в контексте типа проводимого теста и тестируемых лиц. В. А. Меренс и И. Дж. Леманн приводят следующие предостережения при использовании результатов анализа заданий (Измерение и оценка в образовании и психологии. Нью-Йорк: Холт, Райнхарт и Уинстон, 19).73, 333-334):
- Данные анализа элемента не являются синонимами достоверности элемента.
 Внешний критерий необходим для точного суждения о достоверности тестовых заданий. Используя внутренний критерий общей оценки теста, анализ элементов отражает внутреннюю согласованность элементов, а не достоверность.
Внешний критерий необходим для точного суждения о достоверности тестовых заданий. Используя внутренний критерий общей оценки теста, анализ элементов отражает внутреннюю согласованность элементов, а не достоверность. - Индекс дискриминации не всегда является мерой качества товара. Существует множество причин, по которым элемент может иметь низкую различительную способность: (а) чрезвычайно сложные или простые задания будут иметь низкую способность различения, но такие задания часто необходимы для адекватной выборки содержания и целей курса; (б) элемент может показывать низкую способность различения. дискриминация, если тест измеряет множество различных областей содержания и когнитивных навыков. Например, если в большинстве тестов измеряется «знание фактов», то элемент, оценивающий «способность применять принципы», может иметь низкую корреляцию с общим баллом теста, однако оба типа заданий необходимы для измерения достижения целей курса.
- Данные анализа предмета являются предварительными.
 На такие данные влияют тип и количество тестируемых учащихся, применяемые учебные процедуры и случайные ошибки. Если возможно повторное использование предметов, следует регистрировать статистику для каждого введения каждого предмета.
На такие данные влияют тип и количество тестируемых учащихся, применяемые учебные процедуры и случайные ошибки. Если возможно повторное использование предметов, следует регистрировать статистику для каждого введения каждого предмета.
1 Необработанные баллы — это баллы, которые рассчитываются путем подсчета листов ответов по ключевому листу ScorePak®. Названия необработанных оценок: от EXAM1 до EXAM9, от QUIZ1 до QUIZ9, от MIDTRM1 до MIDTRM3 и FINAL. ScorePak® не может анализировать баллы, взятые из бонусного раздела бланков ответов учащихся или рассчитанные на основе других баллов, поскольку такие баллы не выводятся из отдельных элементов, к которым может получить доступ ScorePak®. Кроме того, для разных версий одного и того же экзамена необходимо запрашивать отдельные анализы. Вернитесь к тексту. (якорь рядом с примечанием 1 в тексте)
2 Корреляция — это статистика, которая показывает степень линейной зависимости между двумя переменными. Если значение одной переменной связано со значением другой, говорят, что они «коррелированы». В позитивных отношениях значение одной переменной имеет тенденцию быть высоким, когда значение другого высокое, и низким, когда другое низкое. В отрицательных отношениях значение одной переменной имеет тенденцию быть высоким, когда другое низким, и наоборот. Возможные значения коэффициентов корреляции находятся в диапазоне от -1,00 до 1,00. Сила связи показана абсолютным значением коэффициента (то есть, насколько велико число, положительное оно или отрицательное). Знак указывает направление связи (будь то положительное или отрицательное). Вернитесь к тексту.
Если значение одной переменной связано со значением другой, говорят, что они «коррелированы». В позитивных отношениях значение одной переменной имеет тенденцию быть высоким, когда значение другого высокое, и низким, когда другое низкое. В отрицательных отношениях значение одной переменной имеет тенденцию быть высоким, когда другое низким, и наоборот. Возможные значения коэффициентов корреляции находятся в диапазоне от -1,00 до 1,00. Сила связи показана абсолютным значением коэффициента (то есть, насколько велико число, положительное оно или отрицательное). Знак указывает направление связи (будь то положительное или отрицательное). Вернитесь к тексту.
Т-распределение Стьюдента
Определение :
При взятии некоторых образцов из нормальной совокупности, дисперсия которой известна, распределение выборки значит нормально. Однако, когда дисперсия населения неизвестна, распределение не нормальное, а студенческое-т, у которого хвост длиннее.
Это означает тот факт, что выборочное среднее с неизвестной дисперсией генеральной совокупности склонно экстремальное значение. Если вместо этого вы используете нормальное распределение для проверки гипотез распределения t вероятность ошибки становится больше.
Формула :
Предположим, у нас есть простой случайная выборка размера n, взятая из нормальной популяции со средним и стандартное отклонение . Позволять обозначают выборочное среднее и s, стандартное отклонение выборки. Тогда количество
имеет распределение с n-1 степеней свободы.
Обратите внимание, что различное распределение t для каждого размера выборки, другими словами, это класс дистрибутивов. Когда мы говорим о конкретном распределении t, мы должны укажите степени свободы. Степени свободы для этой t-статистики получается из выборочного стандартного отклонения s в знаменателе уравнения 1.

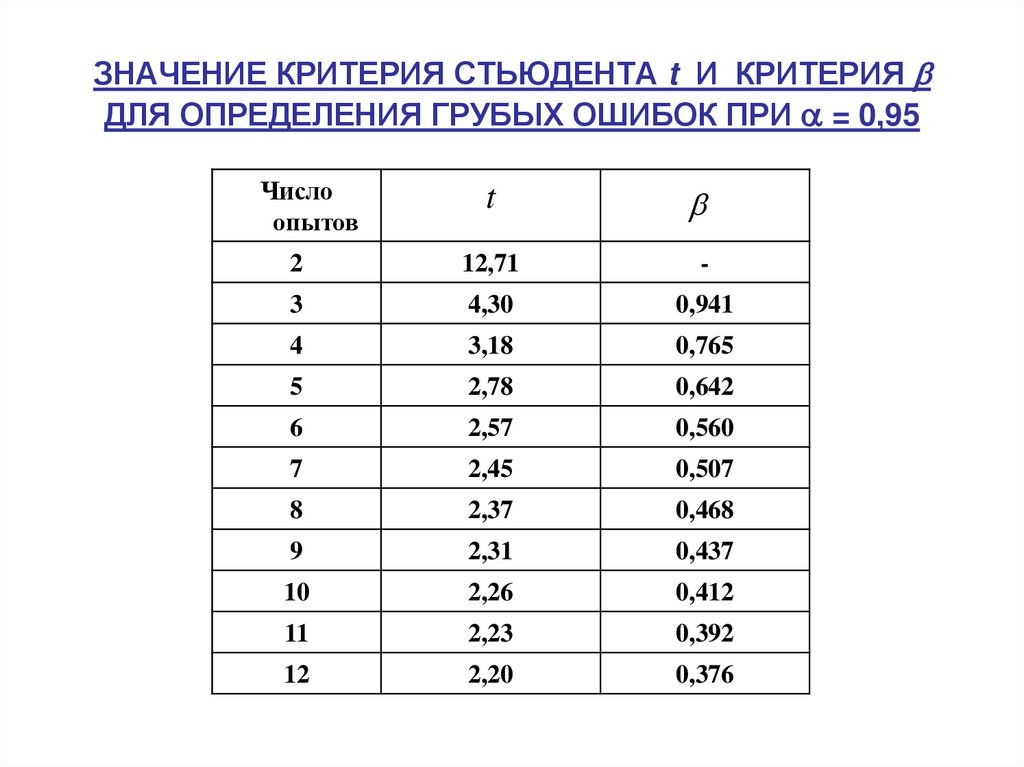
Кривые t-плотности симметричны и имеют форму колокола, как нормальное распределение, и имеют пик в 0. Однако разброс больше, чем у стандартного нормального распределения. Это связано с тем, что в формуле (1) знаменатель равен s, а не σ. Поскольку s — случайная величина, меняющаяся в зависимости от выборки, изменчивость t больше, что приводит к большему разбросу.
Чем выше степень свободы, тем ближе t-плотность к нормальной плотности. Это отражает тот факт, что стандартное отклонение s приближается для большого размера выборки n. Вы можете визуализируйте это в апплете ниже, перемещая ползунки.
Недвижимость :
Распределение Стьюдента t отличается для разных объемов выборки.Распределение Стьюдента t обычно имеет форму колокола, но при меньших размерах выборки увеличивается изменчивость (плоская). Другими словами, распределение менее остроконечное, чем нормальное распределение и с более толстыми хвостами.
Среднее равно нулю (как стандартное нормальное распределение).По мере увеличения размера выборки, распределение приближается к нормальному распределению. При n > 30 различия составляют незначительный.
Распределение симметричен относительно среднего.
Дисперсия больше больше единицы, но приближается к единице сверху по мере увеличения размера выборки (=1 для стандартного нормального распределения).Стандарт населения отклонение неизвестно.
Население составляет в основном нормальный (унимодальный и в основном симметричный)
Метод:
Т распределительный стол
Иллюстрации :
Текущая ставка на производство 5 предохранители в компании Neary Electric Co. стоят 250 ампер в час. Новая машина была закуплены и установлены, что, по словам поставщика, увеличит дебит.
Выборка из 10 случайно выбранных часов за последний месяц показало, что среднечасовая производительность новой машины составляла 256 штук, а выборка стандартное отклонение 6 в час. На уровне значимости 0,05 Нири может сделать вывод, что новая машина быстрее?
Шаг 1: H0: M <= 250 h2: M>250
Шаг 2: H0 отклоняется, если t>1,833, df = 9
Шаг 3: t = [256 — 250]/[6/кв.кв.(10] = 3,16
Шаг 4: H0 отклонен. Новый машина быстрее.
Заявки:
Часто бывает так, что один хочет рассчитать размер выборки, необходимый для получения определенного уровня уверенность в результатах опроса. К сожалению, этот расчет требует предварительного знание стандартного отклонения населения (). Реально, неизвестно. Часто будет проведена предварительная выборка, чтобы разумная оценка этого можно определить критический параметр популяции.

 com/TR/Share_G/grafik.jpg
com/TR/Share_G/grafik.jpg 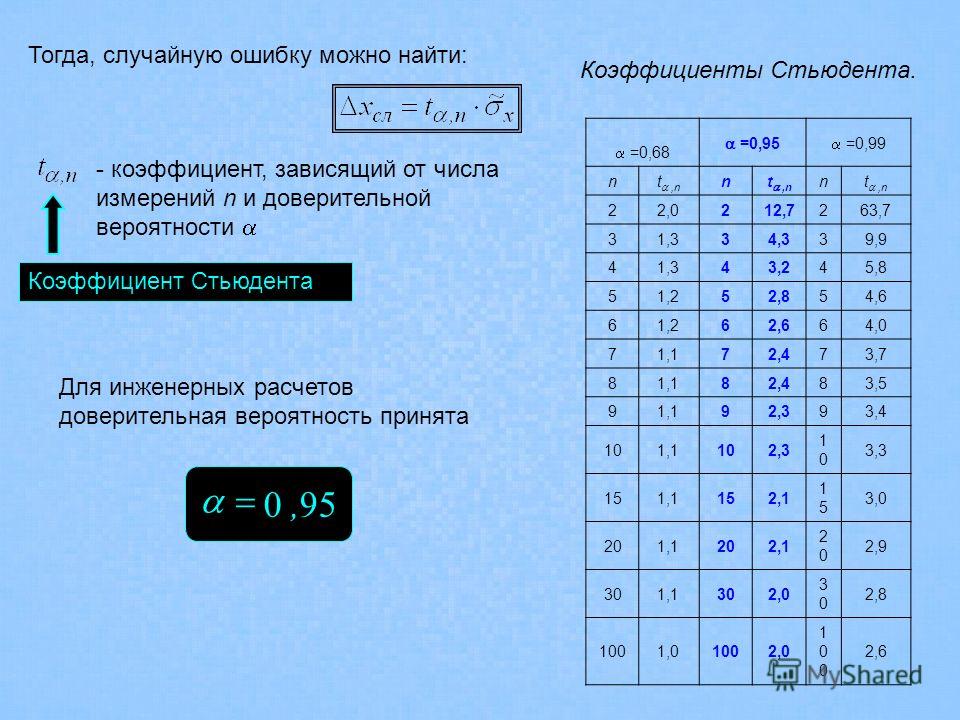 12.2013, 20:24
12.2013, 20:24  12.2013, 20:26
12.2013, 20:26  12.2013, 22:36
12.2013, 22:36  12.2013, 19:33
12.2013, 19:33  12.2013, 20:23
12.2013, 20:23  12.2013, 19:05
12.2013, 19:05  Внешний критерий необходим для точного суждения о достоверности тестовых заданий. Используя внутренний критерий общей оценки теста, анализ элементов отражает внутреннюю согласованность элементов, а не достоверность.
Внешний критерий необходим для точного суждения о достоверности тестовых заданий. Используя внутренний критерий общей оценки теста, анализ элементов отражает внутреннюю согласованность элементов, а не достоверность. На такие данные влияют тип и количество тестируемых учащихся, применяемые учебные процедуры и случайные ошибки. Если возможно повторное использование предметов, следует регистрировать статистику для каждого введения каждого предмета.
На такие данные влияют тип и количество тестируемых учащихся, применяемые учебные процедуры и случайные ошибки. Если возможно повторное использование предметов, следует регистрировать статистику для каждого введения каждого предмета. Это означает
тот факт, что выборочное среднее с неизвестной дисперсией генеральной совокупности склонно
экстремальное значение. Если вместо этого вы используете нормальное распределение для проверки гипотез
распределения t вероятность ошибки становится больше.
Это означает
тот факт, что выборочное среднее с неизвестной дисперсией генеральной совокупности склонно
экстремальное значение. Если вместо этого вы используете нормальное распределение для проверки гипотез
распределения t вероятность ошибки становится больше. 
 По мере увеличения размера выборки,
распределение приближается к нормальному распределению. При n > 30 различия составляют
незначительный.
По мере увеличения размера выборки,
распределение приближается к нормальному распределению. При n > 30 различия составляют
незначительный.  Выборка из 10 случайно выбранных часов за последний месяц
показало, что среднечасовая производительность новой машины составляла 256 штук, а выборка
стандартное отклонение 6 в час. На уровне значимости 0,05 Нири может
сделать вывод, что новая машина быстрее?
Выборка из 10 случайно выбранных часов за последний месяц
показало, что среднечасовая производительность новой машины составляла 256 штук, а выборка
стандартное отклонение 6 в час. На уровне значимости 0,05 Нири может
сделать вывод, что новая машина быстрее? 