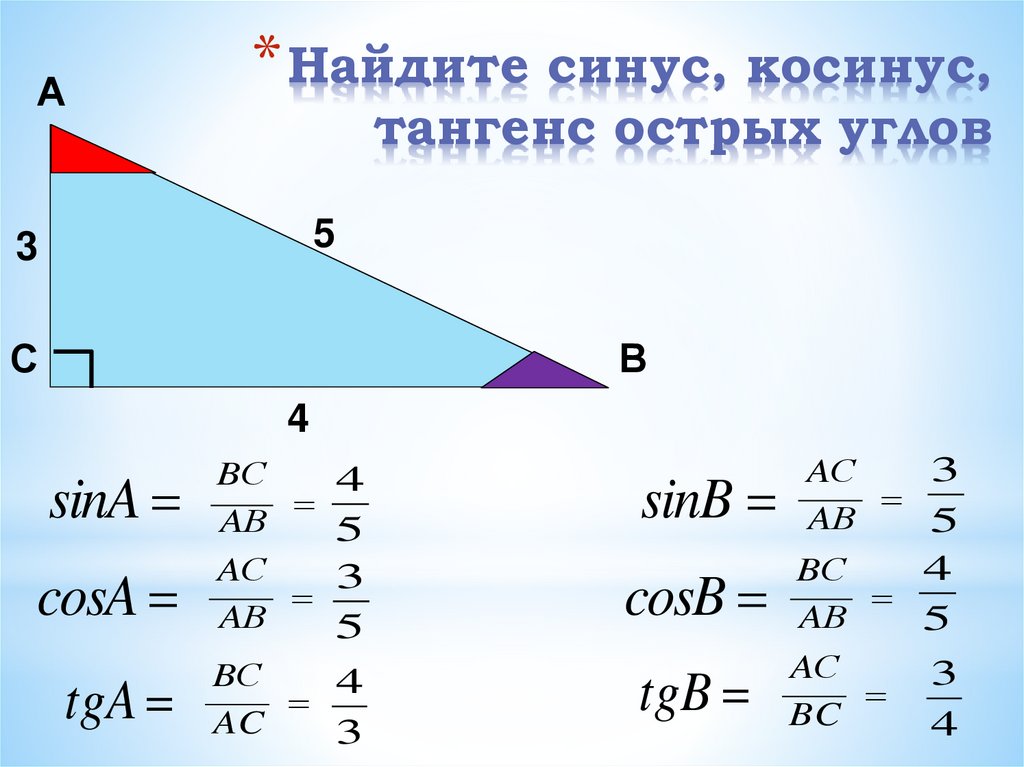
Как пользоваться формулами приведения. Изменение синуса, косинуса и тангенса при возрастании угла
Здоровье детей
Тригонометрия.Формулы приведения.
Формулы приведения не нужно учить их нужно понять. Понять алгоритм их вывода. Это очень легко!
Возьмем единичную окружность и расставим все градусные меры (0°; 90°; 180°; 270°; 360°) на ней.
Разберем в каждой четверти функции sin(a) и cos(a).
Запомним, что функцию sin(a) смотрим по оси Y, а функцию cos(a) по оси X.
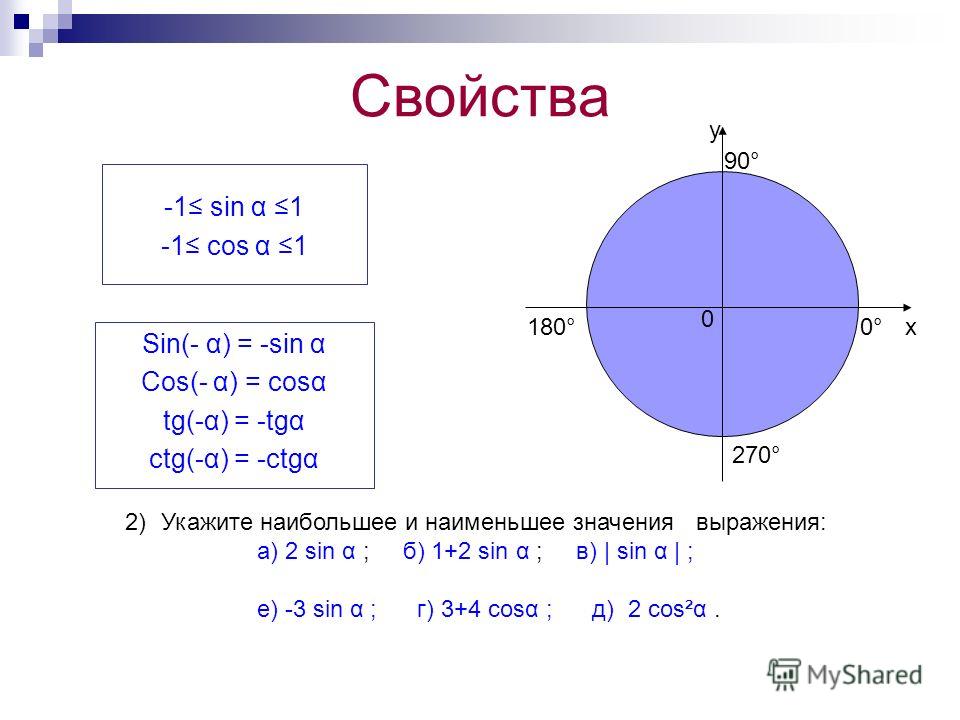
В первой четверти видно, что функция sin(a)>0
И функция cos(a)>0
Первую четверть можно описать через градусную меру, как (90-α) или (360+α).
Во второй четверти видно, что функция sin(a)>0 , потому что ось Y положительна в этой четверти.
А функция cos(a) , потому что ось X отрицательна в этой четверти.
Вторую четверть можно описать через градусную меру, как (90+α) или (180-α).
В третьей четверти видно, что функции sin(a) Третья четверть можно описать через градусную меру, как (180+α) или (270-α).
В четвертой четверти видно, что функция sin(a) , потому что ось Y отрицательна в этой четверти.
А функция cos(a)>0 , потому что ось X положительна в этой четверти.
Четвертую четверть можно описать через градусную меру, как (270+α) или (360-α).
Теперь рассмотрим сами формулы приведения.
Запомним простой алгоритм :
1. Четверть. (Всегда смотрите в какой вы четверти находитесь).
2. Знак. (Относительно четверти смотрите положительны или отрицательный функции косинуса или синуса).
3. Если у вас есть в скобочках (90° или π/2) и (270° или 3π/2), то функция меняется .
И так начнем разбирать по четвертям данный алгоритм.
Выясни чему будет равно выражение cos(90-α)
Рассуждаем по алгоритму:
1. Четверть первая.
Будет cos(90-α) = sin(α)
Выясни чему будет равно выражение sin(90-α)
1. Четверть первая.
Будет sin(90-α) = cos(α)
Выясни чему будет равно выражение cos(360+α)
Рассуждаем по алгоритму:
1. Четверть первая.
Четверть первая.
2. В первой четверти знак у функции косинуса положительный.
Будет cos(360+α) = cos(α)
Выясни чему будет равно выражение sin(360+α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(360+α) = sin(α)
Выясни чему будет равно выражение cos(90+α)
Рассуждаем по алгоритму:
1. Четверть вторая.
3. В скобочках есть (90° или π/2), то функция меняется с косинуса на синус.
Будет cos(90+α) = -sin(α)
Выясни чему будет равно выражение sin(90+α)
1. Четверть вторая.
3. В скобочках есть (90° или π/2), то функция меняется с синуса на косинус.
Будет sin(90+α) = cos(α)
Выясни чему будет равно выражение cos(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции косинуса отрицательный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет cos(180-α) = cos(α)
Выясни чему будет равно выражение sin(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(180-α) = sin(α)
Рассуждаю про третью и четвертую четверть подобным образом составим таблицу:
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Урок и презентация на тему: «Применение формул приведения при решении задач»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
1С: Школа. Интерактивные задания на построение для 7-10 классов
1С: Школа. Решаем задачи по геометрии. Интерактивные задания на построение в пространстве для 10–11 классов
Решаем задачи по геометрии. Интерактивные задания на построение в пространстве для 10–11 классов
Что будем изучать:
1. Немного повторим.
2. Правила для формул приведения.
3. Таблица преобразований для формул приведения.
4. Примеры.
Повторение тригонометрических функций
Ребята, с формулами привидения вы уже сталкивались, но так их еще не называли. Как думаете: где?
Посмотрите на наши рисунки. Правильно, когда вводили определения тригонометрических функций.
Правило для формул приведения
Давайте введем основное правило: Если под знаком тригонометрической функции содержится число вида π×n/2 + t, где n – любое целое число, то нашу тригонометрическую функцию можно привести к более простому виду, которая будет содержать только аргумент t. Такие формулы и называют формулами привидения.
Вспомним некоторые формулы:
- sin(t + 2π*k) = sin(t)
- cos(t + 2π*k) = cos(t)
- sin(t + π) = -sin(t)
- cos(t + π) = -cos(t)
- sin(t + π/2) = cos(t)
- cos(t + π/2) = -sin(t)
- tg(t + π*k) = tg(x)
- ctg(t + π*k) = ctg(x)
формул привидения очень много, давайте составим правило по которому будем определять наши тригонометрические функции при использовании формул привидения :
- Если под знаком тригонометрической функции содержатся числа вида: π + t, π — t, 2π + t и 2π — t, то функция не изменится, то есть, например, синус останется синусом, котангенс останется котангенсом.

- Если под знаком тригонометрической функции содержатся числа вида: π/2 + t, π/2 — t,
3π/2 + t и 3π/2 — t, то функция изменится на родственную, т. е. синус станет косинусом, котангенс станет тангенсом. - Перед получившийся функцией, надо поставить тот знак, который имела бы преобразуемая функция при условии 0
Эти правила применимы и когда аргумент функции задан в градусах!
Так же мы можем составить таблицу преобразований тригонометрических функций:
Примеры применения формул приведения
1.Преобразуем cos(π + t). Наименование функции остается, т.е. получим cos(t). Далее предположим, что π/2
2. Преобразуем sin(π/2 + t). Наименование функции изменяется, т.е. получим cos(t). Далее предположим что 0 sin(t + π/2) = cos(t)
4. Преобразуем ctg(270 0 + t). Наименование функции изменяется, то есть получим tg(t). Далее предположим что 0
Далее предположим что 0
Задачи с формулами приведения для самостоятельного решения
Ребята, преобразуйте самостоятельно, используя наши правила:
1) tg(π + t),
2) tg(2π — t),
3) ctg(π — t),
4) tg(π/2 — t),
5) ctg(3π + t),
6) sin(2π + t),
7) sin(π/2 + 5t),
8) sin(π/2 — t),
9) sin(2π — t),
10) cos(2π — t),
11) cos(3π/2 + 8t),
12) cos(3π/2 — t),
13) cos(π — t).
Они относятся к разделу «тригонометрия» в математике. Суть их заключается в приведении тригонометрических функций углов к более «простому» виду. О важности их знания написать можно много. Этих формул аж 32 штуки!
Не пугайтесь, учить их не надо, как и многие другие формулы в курсе математики. Лишней информацией голову забивать не нужно, необходимо запоминать «ключики» или законы, и вспомнить или вывести нужную формулу проблемой не будет. Кстати, когда я пишу в статьях «… нужно выучить!!!» – это значит, что действительно, это необходимо именно выучить.
Если вы с формулами приведения не знакомы, то простота их вывода вас приятно удивит – есть «закон», при помощи которого это легко сделать. И любую из 32 формул вы напишите за 5 секунд.
Перечислю лишь некоторые задачи, которые будут на ЕГЭ по математике, где без знания этих формул есть большая вероятность потерпеть фиаско в решении. Например:
– задачи на решение прямоугольного треугольника, где речь идёт о внешнем угле, да и задачах на внутренние углы некоторые из этих формул тоже необходимы.
– задачи на вычисление значений тригонометрических выражений; преобразования числовых тригонометрических выражений; преобразования буквенных тригонометрических выражений.
– задачи на касательную и геометрический смысл касательной, требуется формула приведения для тангенса, а также другие задачи.
– стереометрические задачи, по ходу решения не редко требуется определить синус или косинус угла, который лежит в пределах от 90 до 180 градусов.
И это лишь те моменты, которые касаются ЕГЭ. А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.
А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.
Так что же к чему приводится и как оговоренные формулы упрощают для нас решение задач?
Например, вам нужно определить синус, косинус, тангенс или котангенс любого угла от 0 до 450 градусов:
угол альфа лежит пределах от 0 до 90 градусов
* * *Итак, необходимо уяснить «закон», который здесь работает:
1. Определите знак функции в соответствующей четверти.
Напомню их:
2. Запомните следующее:
функция изменяется на кофункцию
функция на кофункцию не изменяется
Что означает понятие — функция изменяется на кофункцию?
Ответ: синус меняется на косинус или наоборот, тангенс на котангенс или наоборот.
Вот и всё!
Теперь по представленному закону запишем несколько формул приведения самостоятельно:
Данный угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:
Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:
Угол лежит в первой четверти, синус в первой четверти положителен. Не меняем функцию на кофункцию, так как у нас 360 градусов, значит:
Вот вам ещё дополнительное подтверждение того, что синусы смежных углов равны:
Угол лежит во второй четверти, синус во второй четверти положителен. Не меняем функцию на кофункцию, так как у нас 180 градусов, значит:
Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.
***
В статье на решение был отмечен такой факт – синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём.
И еще одна задача B11 на ту же тему — из реального ЕГЭ по математике.
Задача. Найдите значение выражения:
В этом коротком видеоуроке мы узнаем, как применять формулы приведения для решения реальных задач B11 из ЕГЭ по математике. Как вы видите, перед нами — два тригонометрических выражения, каждое из которых содержит синусы и косинусы, а также довольно зверские числовые аргументы.
Прежде чем решать эти задачи, давайте вспомним, что такое формулы приведения. Итак, если у нас есть выражения вида:
То мы можем избавиться от первого слагаемого (вида k · π/2) по специальным правилам. Начертим тригонометрическую окружность, отметим на ней основные точки: 0, π/2; π; 3π/2 и 2π. Затем смотрим на первое слагаемое под знаком тригонометрической функции. Имеем:
- Если интересующее нас слагаемое лежит на вертикальной оси тригонометрического круга (например: 3π/2; π/2 и т.д.), то исходная функция заменяется на ко-функцию: синус заменяется косинусом, а косинус — наоборот, синусом.
- Если же наше слагаемое лежит на горизонтальной оси, то исходная функция не меняется. Просто убираем первое слагаемое в выражении — и все.
Таким образом, мы получим тригонометрическую функцию, не содержащую слагаемых вида k
· π/2. Однако на этом работа с формулами приведения не заканчивается. Дело в том, что перед нашей новой функцией, полученной после «отбрасывания» первого слагаемого, может стоять знак плюс или минус. Как определить этот знак? Вот сейчас и узнаем.
Как определить этот знак? Вот сейчас и узнаем.
Представим, что угол α, оставшийся внутри тригонометрической функции после преобразований, имеет очень малую градусную меру. Но что значит «малая мера»? Допустим, α ∈ (0; 30°) — этого вполне достаточно. Рассмотрим для примера функцию:
Тогда, следуя нашим предположениям, что α ∈ (0; 30°), заключаем, что угол 3π/2 − α лежит в третьей координатной четверти, т.е. 3π/2 − α ∈ (π; 3π/2). Вспоминаем знак исходной функции, т.е. y = sin x на этом интервале. Очевидно, что синус в третьей координатной четверти отрицателен, поскольку по определению синус — это ордината конца подвижного радиуса (короче синус — это координата y ). Ну, а координата y в нижней полуплоскости всегда принимает отрицательные значения. Значит, и в третьей четверти y тоже отрицателен.
На основании этих размышлений мы можем записать окончательное выражение:
Задача B11 — 1 вариант
Вот эти же самые приемы вполне подходят для решения задачи B11 из ЕГЭ по математике. Разница лишь в том, что во многих реальных задачах B11 вместо радианной меры (т.е. чисел π, π/2, 2π и т.д.) используется градусная мера (т.е. 90°, 180°, 270° и т.д.). Давайте посмотрим на первую задачу:
Разница лишь в том, что во многих реальных задачах B11 вместо радианной меры (т.е. чисел π, π/2, 2π и т.д.) используется градусная мера (т.е. 90°, 180°, 270° и т.д.). Давайте посмотрим на первую задачу:
Сначала разберемся с числителем. cos 41° — это нетабличное значение, поэтому мы ничего не можем сделать с ним. Пока так и оставим.
Теперь смотрим на знаменатель:
sin 131° = sin (90° + 41°) = cos 41°
Очевидно, что перед нами формула приведения, поэтому синус заменился на косинус. Кроме того, угол 41° лежит на отрезке (0°; 90°), т.е. в первой координатной четверти — именно так, как требуется для применения формул приведения. Но тогда 90° + 41° — это вторая координатная четверть. Исходная функция y = sin x там положительна, поэтому мы и поставили перед косинусом на последнем шаге знак «плюс» (другими словами не поставили ничего).
Осталось разобраться с последним элементом:
cos 240° = cos (180° + 60°) = −cos 60° = −0,5
Здесь мы видим, что 180° — это горизонтальная ось. Следовательно, сама функция не поменяется: был косинус — и останется тоже косинус. Но вновь возникает вопрос: плюс или минус будет стоять перед полученным выражением cos 60°? Заметим, что 180° — это третья координатная четверть. Косинус там отрицательный, следовательно, перед косинусом в итоге будет стоять знак «минус». Итого, получаем конструкцию −cos 60° = −0,5 — это табличное значение, поэтому все легко считается.
Следовательно, сама функция не поменяется: был косинус — и останется тоже косинус. Но вновь возникает вопрос: плюс или минус будет стоять перед полученным выражением cos 60°? Заметим, что 180° — это третья координатная четверть. Косинус там отрицательный, следовательно, перед косинусом в итоге будет стоять знак «минус». Итого, получаем конструкцию −cos 60° = −0,5 — это табличное значение, поэтому все легко считается.
Теперь подставляем полученные числа в исходную формулу и получаем:
Как видим, число cos 41° в числителе и знаменателе дроби легко сокращается, и остается обычное выражение, которое равно −10. При этом минус можно либо вынести и поставить перед знаком дроби, либо «держать» рядом со вторым множителем до самого последнего шага вычислений. Ответ в любом случае получится −10. Все, задача B11 решена!
Задача B14 — 2 вариант
Переходим ко второй задаче. Перед нами снова дробь:
Ну, 27° у нас лежит в первой координатной четверти, поэтому здесь ничего менять не будем. А вот sin 117° надо расписать (пока без всякого квадрата):
А вот sin 117° надо расписать (пока без всякого квадрата):
sin 117° = sin (90° + 27°) = cos 27°
Очевидно, перед нами снова формула приведения : 90° — это вертикальная ось, следовательно, синус поменяется на косинус. Кроме того, угол α = 117° = 90° + 27° лежит во второй координатной четверти. Исходная функция y = sin x там положительна, следовательно, перед косинусом после всех преобразований все равно остается знак «плюс». Другими словами, там ничего не добавляется — так и оставляем: cos 27°.
Возвращаемся к исходному выражению, которое требуется вычислить:
Как видим, в знаменателе после преобразований возникло основное тригонометрическое тождество: sin 2 27° + cos 2 27° = 1. Итого −4: 1 = −4 — вот мы и нашли ответ ко второй задаче B11.
Как видите, с помощью формул приведения такие задачи из ЕГЭ по математике решаются буквально в пару строчек. Никаких синусов суммы и косинусов разности. Все, что нам нужно помнить — это только тригонометрический круг.
Для использования формул приведения существует два правила.
1. Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg. Если же угол можно представить в виде (π ±a) или (2*π ±a), то название функции остается без изменений.
Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет.
2. Правило «каким ты был, таким ты и остался».
Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс». Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».
На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.
Вычислить Sin(150˚)
Воспользуемся формулами приведения:
Sin(150˚) находится во второй четверти, по рисунку видим что знак sin в этой четверти равен +. Значит у приведенной функции тоже будет знак «плюс». Это мы применили второе правило.
Это мы применили второе правило.
Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.
При желании все формулы приведения можно свести в одну таблицу. Но все же легче запомнить эти два правила и пользоваться ими.
Нужна помощь в учебе?
Предыдущая тема:
Как использовать формулы приведения в тригонометрии. Изменение синуса, косинуса и тангенса при возрастании угла
Тема урока
- Изменение синуса, косинуса и тангенса при возрастании угла.
Цели урока
- Познакомиться с новыми определениями и вспомнить некоторые уже изученные.
- Познакомится с закономерностью изменений значений синуса косинуса и тангенса при возрастании угла.
- Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.

- Воспитательные — посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.
Задачи урока
- Проверить знания учащихся.
План урока
- Повторение ранее изученного материала.
- Задачи на повторение.
- Изменение синуса, косинуса и тангенса при возрастании угла.
- Практическое применение.
Повторение ранее изученного материала
Начнем с самого начала и вспомним то что будет полезно освежить в памяти. Что же такое синус, косинус и тангенс и к какому разделу геометрии относятся эти понятия.
Тригонометрия — это такое сложное греческое слово: тригонон — треугольник, метро — мерять. Стало быть по-гречески это означает: мерятся треугольниками.
Предмети > Математика > Математика 8 классДанная статья посвящена подробному изучению тригонометрических формул приведения. Дан полный список формул приведения, показаны примеры их использования, приведено доказательство верности формул.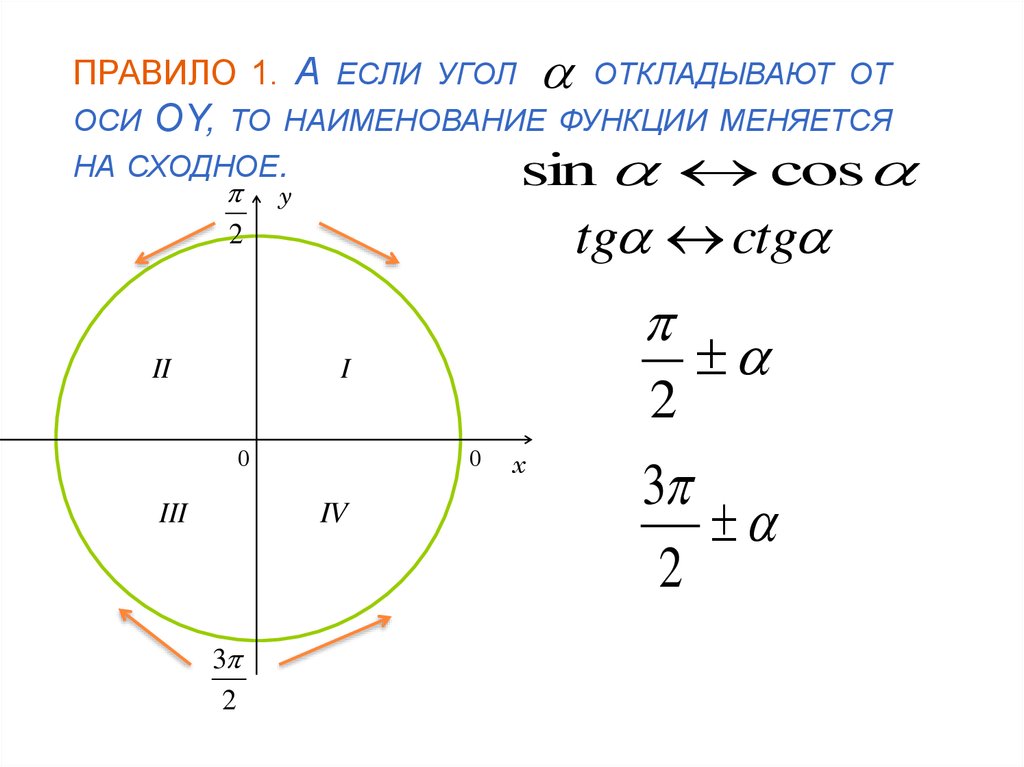 Также в статье дано мнемоническое правило, которое позволяет выводить формулы приведения, не запоминая каждую формулу.
Также в статье дано мнемоническое правило, которое позволяет выводить формулы приведения, не запоминая каждую формулу.
Yandex.RTB R-A-339285-1
Формулы приведения. Список
Фомулы приведения позволяют приводить основные тригонометрические функции углов произвольной величины к функциям углов, лежащих в интервале от 0 до 90 градусов (от 0 до π 2 радиан). Оперировать углами от 0 до 90 градусов гораздо удобнее, чем работать со сколь угодно большими значениями, поэтому формулы приведения широко применяются при решении задач тригонометрии.
Прежде, чем мы запишем сами формулы, уточним несколько важных для понимания моментов.
- Аргументами тригонометрических функций в формулах приведения являются угды вида ± α + 2 π · z , π 2 ± α + 2 π · z , 3 π 2 ± α + 2 π · z . Здесь z — любое целое число, а α — произвольный угол поворота.
- Не обязательно учить все формулы приведения, количество которых довольно внушительно. Существует мнемоническое правило, которо позволяет легко вывести нужную формулу.
 Речь о мнемоническом правиле пойдет позже.
Речь о мнемоническом правиле пойдет позже.
Теперь перейдем непосредственно к формулам приведения.
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов. запишем все формулы в виде таблицы.
Формулы приведения
sin α + 2 π z = sin α , cos α + 2 π z = cos α t g α + 2 π z = t g α , c t g α + 2 π z = c t g α sin — α + 2 π z = — sin α , cos — α + 2 π z = cos α t g — α + 2 π z = — t g α , c t g — α + 2 π z = — c t g α sin π 2 + α + 2 π z = cos α , cos π 2 + α + 2 π z = — sin α t g π 2 + α + 2 π z = — c t g α , c t g π 2 + α + 2 π z = — t g α sin π 2 — α + 2 π z = cos α , cos π 2 — α + 2 π z = sin α t g π 2 — α + 2 π z = c t g α , c t g π 2 — α + 2 π z = t g α sin π + α + 2 π z = — sin α , cos π + α + 2 π z = — cos α t g π + α + 2 π z = t g α , c t g π + α + 2 π z = c t g α sin π — α + 2 π z = sin α , cos π — α + 2 π z = — cos α t g π — α + 2 π z = — t g α , c t g π — α + 2 π z = — c t g α sin 3 π 2 + α + 2 π z = — cos α , cos 3 π 2 + α + 2 π z = sin α t g 3 π 2 + α + 2 π z = — c t g α , c t g 3 π 2 + α + 2 π z = — t g α sin 3 π 2 — α + 2 π z = — cos α , cos 3 π 2 — α + 2 π z = — sin α t g 3 π 2 — α + 2 π z = c t g α , c t g 3 π 2 — α + 2 π z = t g α
В данном случае формулы записаны с радианами. Однако можно записать их и с использованием градусов. Достаточно только перевести радианы в градусы, заменив π на 180 градусов.
Однако можно записать их и с использованием градусов. Достаточно только перевести радианы в градусы, заменив π на 180 градусов.
Примеры использования формул приведения
Покажем, как пользоваться формулами приведения и как указанные формулы применяются при решении практических примеров.
Угол под знаком тригонометрической функции можно представить не одним, а множеством способов. Например, аргумент тригонометрической функции может быть представлен в видах ± α + 2 π z , π 2 ± α + 2 π z , π ± α + 2 π z , 3 π 2 ± α + 2 π z . Продемонстрируем это.
Возьмем угол α = 16 π 3 . Это угол можно записать так:
α = 16 π 3 = π + π 3 + 2 π · 2 α = 16 π 3 = — 2 π 3 + 2 π · 3 α = 16 π 3 = 3 π 2 — π 6 + 2 π
В зависимости от представления угла используется соответствующая формула приведения.
Возьмем тот же угол α = 16 π 3 и вычислим его тангенс
Пример 1. Использование формул приведения
α = 16 π 3 , t g α = ?
Представим угол α = 16 π 3 в виде α = π + π 3 + 2 π · 2
Этому представлению угла будет соответствовать формула приведения
t g (π + α + 2 π z) = t g α
t g 16 π 3 = t g π + π 3 + 2 π · 2 = t g π 3
Воспользовавшись таблицей, укажем значение тангенса
Теперь используем другое представление угла α = 16 π 3 .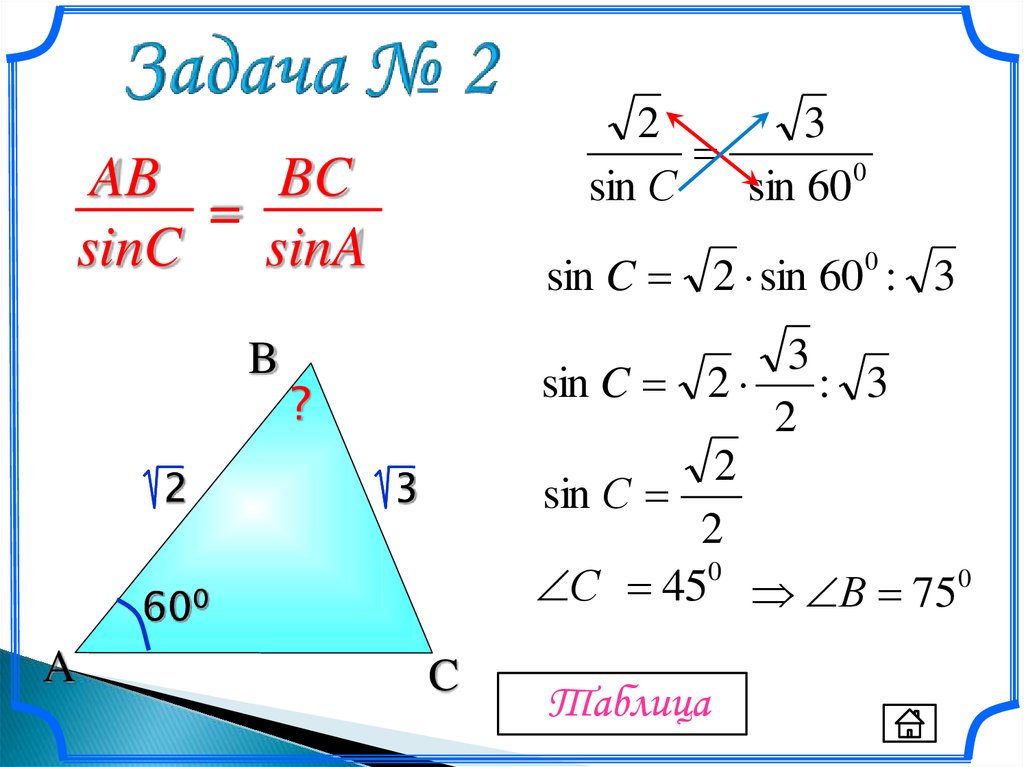
Пример 2. Использование формул приведения
α = 16 π 3 , t g α = ? α = — 2 π 3 + 2 π · 3 t g 16 π 3 = t g — 2 π 3 + 2 π · 3 = — t g 2 π 3 = — (- 3) = 3
Наконец, для третьего представления угла запишем
Пример 3. Использование формул приведения
α = 16 π 3 = 3 π 2 — π 6 + 2 π t g 3 π 2 — α + 2 π z = c t g α t g α = t g (3 π 2 — π 6 + 2 π) = c t g π 6 = 3
Теперь приведем пример на использование формул приведения посложнее
Пример 4. Использование формул приведения
Представим sin 197 ° через синус и косинус острого угла.
Для того, чтобы можно было применять формулы приведения, нужно представить угол α = 197 ° в одном из видов
± α + 360 ° · z , 90 ° ± α + 360 ° · z , 180 ° ± α + 360 ° · z , 270 ° ± α + 360 ° · z . Согласно условию задачи, угол должен быть острым. Соответственно, у нас есть два способа для его представления:
197 ° = 180 ° + 17 ° 197 ° = 270 ° — 73 °
Получаем
sin 197 ° = sin (180 ° + 17 °) sin 197 ° = sin (270 ° — 73 °)
Теперь посмотрим на формулы приведения для синусов и выберем соответствующие
sin (π + α + 2 πz) = — sinα sin (3 π 2 — α + 2 πz) = — cosα sin 197 ° = sin (180 ° + 17 ° + 360 ° · z) = — sin 17 ° sin 197 ° = sin (270 ° — 73 ° + 360 ° · z) = — cos 73 °
Мнемоническое правило
Формул приведения много, и, к счастью, нет необходимости заучивать их наизусть.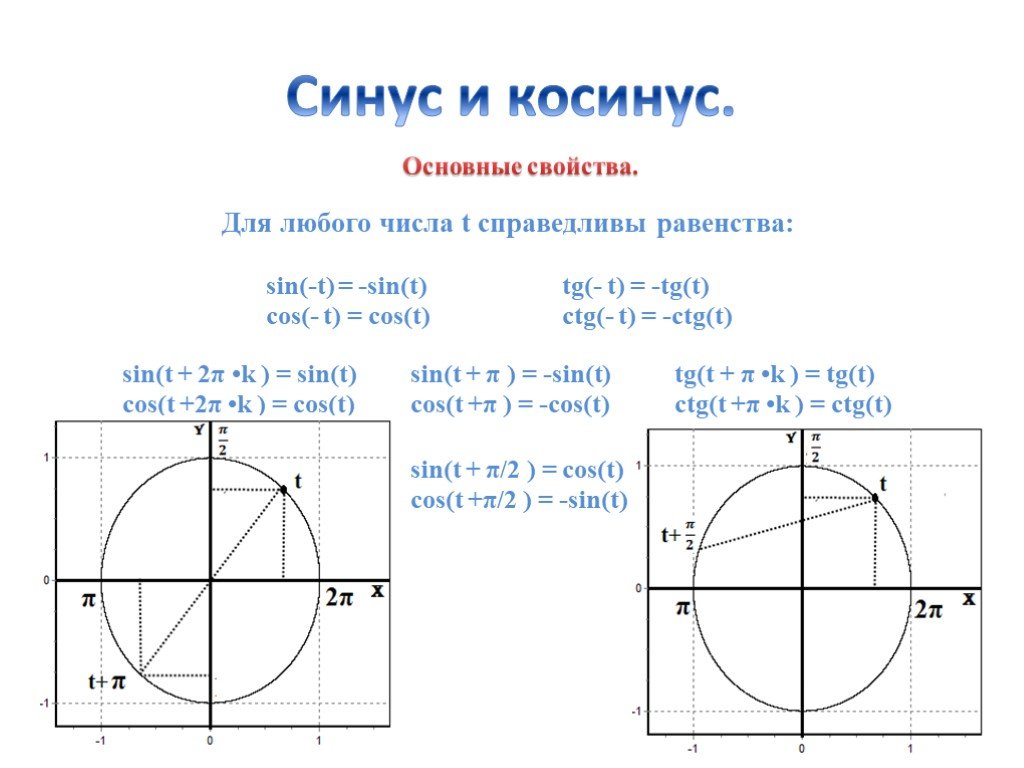 Существуют закономерности, по которым можно выводить формулы приведения для разных углов и тригонометрических функций. Эти закономерности называются мнемоническим правилом. Мнемоника — искусство запоминания. Мнемоническое правило состоит из трех частей, или содержит три этапа.
Существуют закономерности, по которым можно выводить формулы приведения для разных углов и тригонометрических функций. Эти закономерности называются мнемоническим правилом. Мнемоника — искусство запоминания. Мнемоническое правило состоит из трех частей, или содержит три этапа.
Мнемоническое правило
1. Аргумент исходной функции представляется в одном из видов
± α + 2 πz π 2 ± α + 2 πz π ± α + 2 πz 3 π 2 ± α + 2 πz
Угол α должен лежать в пределах от 0 до 90 градусов.
2. Определяется знак исходной тригонометрической функции. Такой же знак будет иметь функция, записываемая в правой части формулы.
3. Для углов ± α + 2 πz и π ± α + 2 πz название исходной функции остается неизменным, а для углов π 2 ± α + 2 πz и 3 π 2 ± α + 2 πz соответственно меняется на «кофункцию». Синус — на косинус. Тангенс — на котангенс.
Чтобы пользоваться мнемоническим праилом для формул приведения нужно уметь определять знаки тригонометрических функций по четвертям единичной окружности. Разберем примеры применения мнемонического правила.
Разберем примеры применения мнемонического правила.
Пример 1. Использование мнемонического правила
Запишем формулы приведения для cos π 2 — α + 2 πz и t g π — α + 2 πz . α — улог первой четверти.
1. Так как по условию α — улог первой четверти, мы пропускаем первый пункт правила.
2. Определим знаки функций cos π 2 — α + 2 πz и t g π — α + 2 πz . Угол π 2 — α + 2 πz также является углом первой четверти, а угол π — α + 2 πz находится во второй четверти. В первой четверти функция косинуса положительна, а тангенс во второй четверти имеет знак минус. Запишем, как будут выглядеть искомые формулы на этом этапе.
cos π 2 — α + 2 πz = + t g π — α + 2 πz = —
3. Согласно третьему пункту для угла π 2 — α + 2 π название функции изменяется на конфуцию, а для угла π — α + 2 πz остается прежним. Запишем:
cos π 2 — α + 2 πz = + sin α t g π — α + 2 πz = — t g α
А теперь заглянем в формулы, приведенные выше, и убедимся в том, что мнемоническое правило работает.
Рассмотрим пример с конкретным углом α = 777 ° . Приведем синус альфа к тригонометрической функции острого угла.
Пример 2. Использование мнемонического правила
1. Представим углол α = 777 ° в необходимом виде
777 ° = 57 ° + 360 ° · 2 777 ° = 90 ° — 33 ° + 360 ° · 2
2. Исходный угол — угол первой четверти. Значит, синус угла имеет положительный знак. В итоге имеем:
3. sin 777 ° = sin (57 ° + 360 ° · 2) = sin 57 ° sin 777 ° = sin (90 ° — 33 ° + 360 ° · 2) = cos 33 °
Теперь рассмотрим пример, который показывает, как важно правильно определить знак тригонометрической функции и правильно представить угол при использовании мнемонического правила. Повторим еще раз.
Важно!
Угол α должен быть острым!
Вычислим тангенс угла 5 π 3 . Из таблицы значений основных тригонометрических функций можно сразу взять значение t g 5 π 3 = — 3 , но мы применим мнемоническое правило.
Пример 3. Использование мнемонического правила
Представим угол α = 5 π 3 в необходимом виде и воспользуемся правилом
t g 5 π 3 = t g 3 π 2 + π 6 = — c t g π 6 = — 3 t g 5 π 3 = t g 2 π — π 3 = — t g π 3 = — 3
Если же представить угол альфа в виде 5 π 3 = π + 2 π 3 , то результат применениея мнемонического правила будет неверным.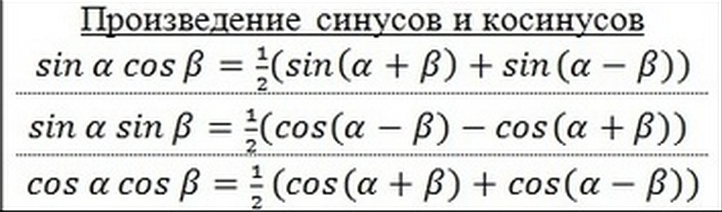
t g 5 π 3 = t g π + 2 π 3 = — t g 2 π 3 = — (- 3) = 3
Неверный результат обусловлен тем, что угол 2 π 3 не явдяется острым.
Доказательство формул приведения основывается на свойствах периодичности и симметричности тригонометрических функций, а также на свойстве сдвига на углы π 2 и 3 π 2 . Доказательство справедливости всех формул приведения иожно проводить без учета слагаемого 2 πz , так как оно обозначает изменение угла на целое число полных оборотов и как раз отражает свойство периодичности.
Первые 16 формул следуют напрямую из свойств основных тригонометрических функций: синуса, косинуса, тангенса и котанганса.
Приведем доказательство формул приведения для синусов и косинусов
sin π 2 + α = cos α и cos π 2 + α = — sin α
Посмотрим на единичную окружность, начальная точка которой после повоторота на угол α перешла в точку A 1 x , y , а после поворота на угол π 2 + α — в точку A 2 . Из обеих точек проведем перпендикуляры к оси абсцисс.
Два прямоугольных треугольника O A 1 H 1 и O A 2 H 2 равны по гипотенузе и прилежащим к ней углам. Из расположения точек на окружности и равенства треугольников можно сделать вывод о том, что точка A 2 имеет координаты A 2 — y , x . Используя определения синуса и косинуса, запишем:
Из расположения точек на окружности и равенства треугольников можно сделать вывод о том, что точка A 2 имеет координаты A 2 — y , x . Используя определения синуса и косинуса, запишем:
sin α = y , cos α = x , sin π 2 + α = x , cos π 2 + α = y
sin π 2 + α = cos α , cos π 2 + α = — sin α
С учетом основных тождеств тригонометрии и только что доказанного, можно записать
t g π 2 + α = sin π 2 + α cos π 2 + α = cos α — sin α = — c t g α c t g π 2 + α = cos π 2 + α sin π 2 + α = — sin α cos α = — t g α
Для доказательства формул приведения с аргументом π 2 — α его необходимо представить в виде π 2 + (- α) . Например:
cos π 2 — α = cos π 2 + (- α) = — sin (- α) = sin α
В доказательстве используются свойства тригонометрических функций с аргументами, противоположными по знаку.
Все остальные формулы приведения можно доказать на базе записанных выше.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Для использования формул приведения существует два правила.
1. Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg. Если же угол можно представить в виде (π ±a) или (2*π ±a), то название функции остается без изменений.
Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет.
2. Правило «каким ты был, таким ты и остался».
Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс». Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».
На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.
Вычислить Sin(150˚)
Воспользуемся формулами приведения:
Sin(150˚) находится во второй четверти, по рисунку видим что знак sin в этой четверти равен +. Значит у приведенной функции тоже будет знак «плюс». Это мы применили второе правило.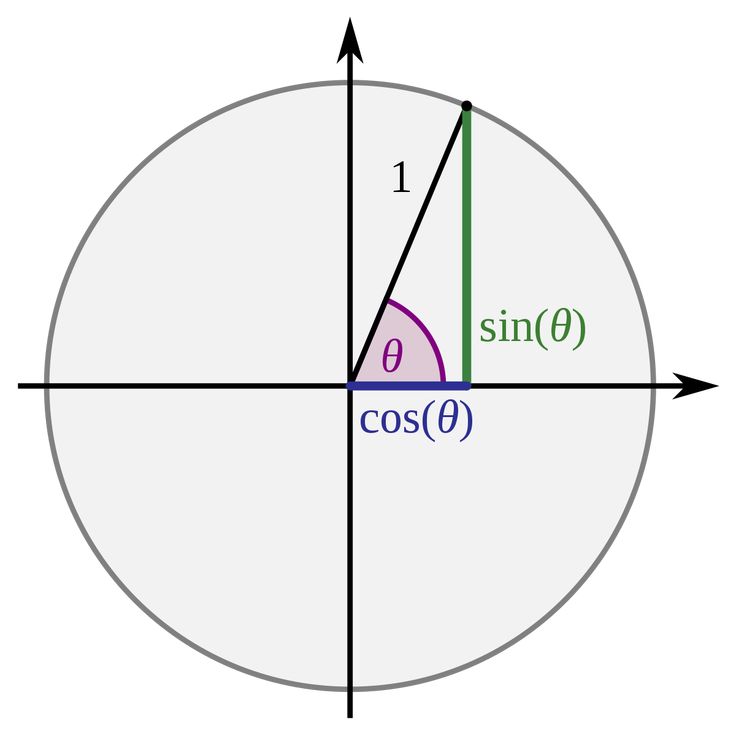
Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.
При желании все формулы приведения можно свести в одну таблицу. Но все же легче запомнить эти два правила и пользоваться ими.
Как запомнить формулы приведения тригонометрических функций? Это легко, если использовать ассоциацию.Данная ассоциация придумана не мной. Как уже говорилось, хорошая ассоциация должна «цеплять», то есть вызывать яркие эмоции. Не могу назвать эмоции, вызываемые этой ассоциацией, позитивными. Но она дает результат — позволяет запоминать формулы приведения, а значит, имеет право на существование. В конце концов, если она вам не понравится, вы же ее можете не использовать, правильно?
Формулы приведения имеют вид: sin(πn/2±α), cos(πn/2±α), tg(πn/2±α), ctg(πn/2±α). Запоминаем, что +α дает движение против часовой стрелки, — α — движение по часовой стрелке.
Для работы с формулами приведения нужны два пункта:
1) ставим знак, который имеет начальная функция (в учебниках пишут: приводимая. Но, чтобы не запутаться, лучше назвать ее начальной), если считать α углом I четверти, то есть маленьким.
Но, чтобы не запутаться, лучше назвать ее начальной), если считать α углом I четверти, то есть маленьким.
2) Горизонтальный диаметр — π±α, 2π±α, 3π±α… — в общем, когда нет дроби — название функции не меняет. Вертикальный π/2±α, 3π/2±α, 5π/2±α…- когда дробь есть — название функции меняет: синус — на косинус, косинус — на синус, тангенс — на котангенс и котангенс — на тангенс.
Теперь, собственно, ассоциация:
вертикальный диаметр (есть дробь) —
пьяный стоит. Что с ним случится рано
или поздно? Правильно, упадет.
Название функции изменится.
Если же диаметр горизонтальный — пьяный уже лежит. Спит, наверное. С ним уже ничего не случится, он уже принял горизонтальное положение. Соответственно, название функции не меняется.
То есть sin(π/2±α), sin(3π/2±α), sin(5π/2±α) и т.д. дают ±cosα,
а sin(π±α), sin(2π±α), sin(3π±α), … — ±sinα.
Как , уже знаем.
Как это работает? Смотрим на примерах.
1) cos(π/2+α)=?
Становимся на π/2.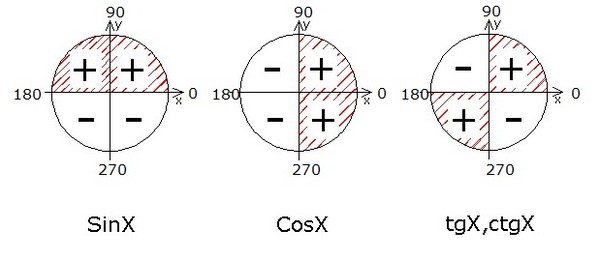 Поскольку +α — значит, идем вперед, против часовой стрелки. Попадаем во II четверть, где косинус имеет знак «-«. Название функции меняется («пьяный стоит», значит — упадет). Итак,
Поскольку +α — значит, идем вперед, против часовой стрелки. Попадаем во II четверть, где косинус имеет знак «-«. Название функции меняется («пьяный стоит», значит — упадет). Итак,
cos(π/2+α)=-sin α.
Становимся на 2π. Так как -α — идем назад, то есть по часовой стрелке. Попадаем в IV четверть, где тангенс имеет знак «-«. Название функции не меняется (диаметр горизонтальный, «пьяный уже лежит»). Таким образом, tg(2π-α)=- tgα.
3) ctg²(3π/2-α)=?
Примеры, в которых функция возводится в четную степень, решаются еще проще. Четная степень «-» убирает, то есть надо только выяснить, меняется название функции или остается. Диаметр вертикальный (есть дробь, «пьяный стоит», упадет), название функции меняется. Получаем: ctg²(3π/2-α)= tg²α.
С центром в точке A .
α — угол, выраженный в радианах.
Определение
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2 π .
Четность
Функция синус — нечетная. Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
рабочих листов | TPT
by
My Teaching Pal
12,50 $
8,00 $
Bundle
Предложите своим ученикам практиковать все, что связано с алфавитом, с помощью этого ОГРОМНОГО комплекта рабочих листов по алфавиту. Студенты будут работать над идентификацией букв, начальными звуками, формированием букв, различением строчных и прописных букв и многим другим. В этот пакет включены 4 различных типа рабочих листов, которые охватывают каждую букву алфавита. Всего включено 104 рабочих листа. Что включено: ♥ Рабочие листы по алфавиту — Работа с буквами ♥ Рабочие листы для начальных звуков — цвет по моему звуку ♥ Алфавит M
Студенты будут работать над идентификацией букв, начальными звуками, формированием букв, различением строчных и прописных букв и многим другим. В этот пакет включены 4 различных типа рабочих листов, которые охватывают каждую букву алфавита. Всего включено 104 рабочих листа. Что включено: ♥ Рабочие листы по алфавиту — Работа с буквами ♥ Рабочие листы для начальных звуков — цвет по моему звуку ♥ Алфавит M
Предметы:
Английский язык искусства, Фоника, написание
Оценки:
Prek — K
Типы:
, печатные изготовления, рабочие листы
My Nerdy Учитель от Alina V
$ 100.00.00
$ 19.004 1
$ 19.004 1
$ 19.004 1
$ 19.004 70004 70004 $ 19.004 70004 $ 19.004 1
$ 19.004
$ 19.004
$ 19.004
$ 19.004
$ 19.004
$ 19.004
$
$ nerdy.
⭐⭐⭐ СРОЧНАЯ РАСПРОДАЖА ⭐⭐⭐Получите меганабор The Ultimate Reading Intervention ВСЕГО за 19 долларов! (СТОИМОСТЬ 100 долл. США) Вы ищете веселые и увлекательные занятия по интервенции при чтении, связанные с наукой о чтении? Получите МЕГА-НАБОР Ultimate Phonics Reading Intervention всего за 19 долларов США.! Спешите, время истекает! Ваши студенты станут бегло читать, используя эти забавные действия. Требуется низкая подготовка. Просто распечатайте и приступайте к работе. Эти занятия помогут вашим ученикам практиковать фонетические модели, которые вы преподаете.
США) Вы ищете веселые и увлекательные занятия по интервенции при чтении, связанные с наукой о чтении? Получите МЕГА-НАБОР Ultimate Phonics Reading Intervention всего за 19 долларов США.! Спешите, время истекает! Ваши студенты станут бегло читать, используя эти забавные действия. Требуется низкая подготовка. Просто распечатайте и приступайте к работе. Эти занятия помогут вашим ученикам практиковать фонетические модели, которые вы преподаете.
CCSS:
RF.K.1, RF.K.1a, RF.K.1b, RF.K.1c, RF.K.1d…
по
My Nerdy Teacher by Alina V
100,00 $
19,00 $
⭐⭐⭐ FLASH SAFE ⭐⭐⭐Получите Мега-пакет Decodable Readers Passages всего за 19 долларов! Спешите, время истекает! Ваши ученики могут практиковаться в чтении весело и увлекательно, используя эти декодируемые тексты. Наука чтения AlignedLow Требуется подготовка. Просто распечатайте и идите. Эти декодируемые отрывки помогут вашим ученикам практиковать фонетические модели, которым вы их учите. Идеально подходит для центров, домашних заданий, утренней работы и многого другого. Печатные и цифровые (Google Slides™) Идеально подходит для дошкольного детского сада, 1-й класс
Идеально подходит для центров, домашних заданий, утренней работы и многого другого. Печатные и цифровые (Google Slides™) Идеально подходит для дошкольного детского сада, 1-й класс
Предметы:
Акустика, Чтение, Письмо
Классы:
К — 2-й
Виды:
Занятия, Центры, Печатные формы
CCSS, RF.K.3.K. .K.3c, RF.1.2c, RF.1.2d…
by
Aimee’s Edventures LLC
$10,75
$5,50
У меня разрывалось сердце, когда я смотрел, как мои ученики бродят по комнате, пытаясь не заплакать, когда я сказал: «Пожалуйста, найдите партнера». Вот я и создал эти открытки! Теперь их любят тысячи учителей, которые преследуют одну и ту же цель: включить всех учащихся в свой класс. Эти партнерские карточки позволяют быстро и легко настроить дифференцированную работу в малых группах и идеально подходят для детей с любым уровнем способностей. Самое приятное то, что им не нужно угадывать, кто их партнер, это прямо на карте (whi
Объекты:
Вернуться в школу, сообщество классных комнат, управление классной комнатой
Оценки:
Не Оценка. Little Learners
Little Learners
128,00 $
34,99 $
Это годичный набор из 576 дифференцированных отрывков и вопросов для понимания прочитанного во 2-м классе на трех разных уровнях. Эти отрывки для беглого чтения меняют правила игры! Цифровые отрывки и вопросы для понимания прочитанного во 2-м классе также включены! ⭐️Загрузите файл предварительного просмотра, чтобы увидеть каждый заголовок! ⭐️Хотите улучшить беглость чтения? Каждый отрывок для понимания прочитанного во 2-м классе включает подсчет слов и трекер беглости. Идеально подходит для повторного чтения и практики беглости чтения.
Предметы:
Английский язык, чтение, стратегии чтения
Классы:
Типы:
Оценка, распечатки
CCSS:
, RL.2.1, RL.2.2 .2.5…
по
My Teaching Pal
Этот пакет заполнен рабочими листами, чтобы помочь вашим ученикам практиковать диграфы. Он включает рабочие листы для орграфов ch, sh, th, ph и wh. Бонусное включение диграфов ph и wh идеально подходит для того, чтобы бросить вызов вашим ученикам с более высокими способностями. Пакет включает в себя 42 увлекательных рабочих листа, которые позволяют учащимся практиковаться в написании диграфов, чтении диграфов, определении звуков диграфов и многому другому! Он идеально подходит для общеклассных занятий, математических станций, быстрых финишеров, домашних заданий и
Бонусное включение диграфов ph и wh идеально подходит для того, чтобы бросить вызов вашим ученикам с более высокими способностями. Пакет включает в себя 42 увлекательных рабочих листа, которые позволяют учащимся практиковаться в написании диграфов, чтении диграфов, определении звуков диграфов и многому другому! Он идеально подходит для общеклассных занятий, математических станций, быстрых финишеров, домашних заданий и
Субъекты:
АНГЛИЙСКИЙ ЯЗЫКИ, Фоника, чтение
Оценки:
K — 2 -е место
Типы:
Центры, печатные изготовления, листы
с горой.
Bundle
Этот НАБОР из трех ресурсов со скидкой включает 90 печатных (и ЦИФРОВЫХ!) страниц для обучения, повторения и применения навыков чтения и письма! В комплект включены следующие ресурсы: Использование иллюстраций для обучения навыкам чтения 40 страниц, обучающих 8 основным навыкам чтения. Каждому навыку чтения посвящено пять страниц! Использование иллюстраций для обзора смешанных навыков чтения20 страниц, посвященных основным навыкам чтения. На каждой странице рассматриваются различные навыки чтения. Использование иллюстраций для обучения изобразительному языку15, стр.
На каждой странице рассматриваются различные навыки чтения. Использование иллюстраций для обучения изобразительному языку15, стр.
Subjects:
English Language Arts, Reading, Reading Strategies
Grades:
3rd — 5th
Types:
Centers, Printables
by
My Teaching Pal
$22.00
$15.00
Bundle
В этом наборе 263 ОГРОМНЫХ математических листа для первого класса! Рабочие листы охватывают сложение и вычитание, числа и разрядность, 2D и 3D фигуры, данные и графики, дроби и разбиение на части и время. Эти веселые рабочие листы отлично подходят для использования в течение всего года, они идеально подходят для общеклассных занятий, математических станций, быстрых финишеров, домашних заданий и повторения. Этот комплект состоит из следующих пакетов: Рабочие листы для сложения и вычитания для первого классаРабочие листы для первого класса 2D и 3D
Субъекты:
Основные операции, математика, номера
Оценки:
Типы:
печатные изделия, рабочие книги, рабочие листы
на
Melissa Mazur
$ 15. 00
00
$ 12.00 9000 3
. содержат 30 готовых к печати отрывков (15 художественных и 15 научно-популярных). Каждый уровневый отрывок находится в диапазоне 520L и 830L и содержит от 196 до 222 слов. Используйте вопросы на понимание, чтобы оценить понимание после того, как учащиеся прочитают текст! *ОБНОВЛЕНИЕ* Теперь вы можете поделиться этим со своими учениками в цифровом виде! Этот ресурс был создан с помощью Google Forms. Для использования у вас должна быть электронная почта Google. Каждому проходу можно присвоить в Google Classr
Предметы:
Чтение
Классы:
Типы:
Деятельность, Оценка
CCSS:
RF.3.4, RF.3.4a, RF.004b, RF.004c Также включены 9 в: RF.004c 9 in:9004c НАБОР отрывков для понимания прочитанного и беглого чтения — скидка 30%
by
My Nerdy Teacher by Alina V
Вы ищете веселые и увлекательные рабочие листы по алфавиту от А до Я для своих учеников? Этот пакет идеально подходит для тех, кто рано заканчивает работу, утренней работы, выполнения домашних заданий и многого другого. Каждый рабочий лист включает 5 различных заданий, которые ваши ученики могут использовать, чтобы узнать все о прописных и строчных буквах. — — — — — — — — — > Проверьте наш БЕСКОНЕЧНЫЙ НАБОР АЛФАВИТА и получите этот ресурс с огромной скидкой!! <- - - - - - - - -ВКЛЮЧЕННЫЕ МЕРОПРИЯТИЯ: • Произнеси по буквам! Напишите буквы в коробках • Раскрасьте! Цвет
Каждый рабочий лист включает 5 различных заданий, которые ваши ученики могут использовать, чтобы узнать все о прописных и строчных буквах. — — — — — — — — — > Проверьте наш БЕСКОНЕЧНЫЙ НАБОР АЛФАВИТА и получите этот ресурс с огромной скидкой!! <- - - - - - - - -ВКЛЮЧЕННЫЕ МЕРОПРИЯТИЯ: • Произнеси по буквам! Напишите буквы в коробках • Раскрасьте! Цвет
Предметы:
Акустика, Изобразительное искусство
Классы:
PreK — K
Виды:
Задания, Печатные формы, Рабочие листы
CCSS,
.К.К.а, РФ. K.1b, RF.K.1c, RF.K.1d… Также включено в: Рабочий лист «Начало звуков». 123 центра обучения грамоте для первоклассников и второклассников обеспечивают идеальный способ обеспечить увлекательную, дифференцированную практику ELA в течение всего года. Все центры имеют аналогичный формат, что делает их идеальными для самостоятельной практики, оставляя вам больше времени для обучения с меньшим количеством перерывов! Отлично подходит для центров или быстро заканчивающих, с этим пакетом вы сможете легко дифференцировать потребности всех ваших учеников с огромным выбором игр на выбор. Каждое общее ядро соответствует
Каждое общее ядро соответствует
Предметы:
Английский язык, акустика, правописание
Классы:
1-2
CCSS:
RF.1.1a, RF.1.2, RF.1.2a, RF.1.2b, RF.1.2b, RF.1.2b, RF.1.2b, RF.1.2b, RF.1.2b c…
by
Кейтлин Олбани
Внутри вы найдете 60 отрывков для понимания детского сада! Эти отрывки отлично подходят для детей младшего возраста, а также подойдут для первоклассников или первоклассников, в зависимости от того, как вы их используете. В комплекте много разнообразия. Пожалуйста, проверьте изображения и предварительный просмотр, чтобы увидеть, подойдут ли эти отрывки для ваших учеников. Отрывки разбиты на три категории… Первые 20 отрывков: Основная история с 3 вопросами. Студентам дается два ответа на выбор на каждый вопрос. Вторые 20 отрывков: Базовый
Subjects:
English Language Arts, Reading, Reading Strategies
Grades:
K — 1st
Types:
Centers, Printables, Worksheets
by
My Teaching Pal
$13. 75
75
$10.00
Bundle
В этот комплект входит множество занимательных математических заданий для учащихся детского сада. Он идеально подходит для общеклассных занятий, математических станций, быстрых финишеров, домашних заданий и повторения. Рабочие листы охватывают сложение и вычитание до 10, разрядное значение, 2D и 3D-фигуры и числа до 20. Включено в общей сложности 126 рабочих листов, которые отлично подходят для использования круглый год. Этот комплект состоит из следующих пакетов: Рабочие листы для детского сада на сложение и вычитание. Детский сад Числа до 20. Работа 9.0003
Субъекты:
Основные операции, математика, номера
Оценки:
Prek — 1st
Типы:
Центры, печатные изделия, рабочие листы
с горой. Bundle
Читайте и понимайте художественную литературу и информационные тексты с помощью идеального комплекта для чтения и повторения. Это лучший набор для проверки навыков чтения на ВЕСЬ ГОД. «Быстрое чтение и повторение» — идеальный способ вовлечь учащихся в актуальную и тщательную проверку навыков чтения! Этот набор обзоров — идеальный способ поддерживать навыки чтения у ваших учеников ИЛИ помочь вам обучить их навыкам. Его можно использовать в центрах, небольших группах, всем классом или в качестве домашнего задания для повторения основного информационного текста com
«Быстрое чтение и повторение» — идеальный способ вовлечь учащихся в актуальную и тщательную проверку навыков чтения! Этот набор обзоров — идеальный способ поддерживать навыки чтения у ваших учеников ИЛИ помочь вам обучить их навыкам. Его можно использовать в центрах, небольших группах, всем классом или в качестве домашнего задания для повторения основного информационного текста com
Субъекты:
Краткое чтение, Английское языковое искусство, стратегии чтения
Оценки:
4 -й — 5th
Типы:
Действия, Центры
CCS:
RL.4.1, RL.4.2, RL.4.3 , RL.4.4, RL.4.5…
by
Kaitlynn Albani
Внутри вы найдете 6 забавных и уникальных шрифтов в ZIP-файле! Большинство символов ударения включено во все шрифты. Пожалуйста, проверьте предварительный просмотр, чтобы увидеть все шрифты, включенные в этот набор! Примечания. Включено 5 шрифтов + 1 шрифт для каракулей. Все шрифты с заглавными буквами Elementary. Проверьте предварительный просмотр, чтобы увидеть все шрифты в действии! $ СЭКОНОМЬТЕ ДЕНЬГИ $ БОЛЕЕ 400 ШРИФТОВ + КАЖДЫЙ НОВЫЙ ШРИФТ БЕСПЛАТНО! ПРОВЕРЬТЕ РАСТУЩИЙ НАБОР ШРИФТОВ ЗДЕСЬУсловия использования * Шрифты
Проверьте предварительный просмотр, чтобы увидеть все шрифты в действии! $ СЭКОНОМЬТЕ ДЕНЬГИ $ БОЛЕЕ 400 ШРИФТОВ + КАЖДЫЙ НОВЫЙ ШРИФТ БЕСПЛАТНО! ПРОВЕРЬТЕ РАСТУЩИЙ НАБОР ШРИФТОВ ЗДЕСЬУсловия использования * Шрифты
Предметы:
Для всех предметов, Товары для продавцов ТРТ, Специальность
Классы:
PreK — 12th, Высшее образование, Обучение взрослых, Персонал by
Polka Dots Please
14,00 $
10,00 $
Bundle
Вы понимаете важность практики словесного зрения! Эти карточки со словами для зрения помогают детям читать часто встречающиеся слова по отдельности и в расшифровываемых предложениях! Каждая карточка помогает читателям улучшить свои навыки распознавания слов, беглости и декодирования! Они идеально подходят для чтения с гидом, уроков чтения и выполнения домашних заданий. Нажмите на предварительный просмотр, чтобы увидеть, что делает эти карточки такими особенными! Исследование чтения поддерживает изучение новых слов в предложении. Что включено? 400 карточек со словами с расшифровкой
Что включено? 400 карточек со словами с расшифровкой
Subjects:
Phonics, Reading, Reading Strategies
Grades:
PreK — 3rd
Types:
Flash Cards, Printables, Word Walls
by
The Little Ladybug Shop
$10.95
$6.95
Развивайте своих читателей с помощью этого замечательного пакета отрывков и вопросов для понимания прочитанного для 3–5 классов (теперь доступны цифровые варианты)! Пакет «Отрывки для чтения» включает в себя 20 недель еженедельной практики, идеально подходящей для: разминки, работы с колокольчиками, домашних заданий или быстрой оценки. Учащиеся могут использовать эти наборы самостоятельно, в группах по обучению грамоте, в группах по чтению с гидом для выполнения домашних заданий или в качестве замены. Эти занятия проверяют навыки учащихся без утомительной болтовни, а также позволяют научить их
Субъекты:
Закрытие чтения, ELA Test Prep, Стратегии чтения
Оценки:
3 -е — 5 -е
Типы:
Действия, печатные изготовления
CCS:
RL. 3.1, RL.3.2, RL.3.444. , RL.4.1, RL.4.2…
3.1, RL.3.2, RL.3.444. , RL.4.1, RL.4.2…
Также включено в: Документальная поэзия Отрывки и вопросы для понимания прочитанного 3-й 4-й класс
by
ThatKinderMama
10,00 $
Это четырехнедельный блок иллюстраций в помощь писателям детского сада/первого класса. стать уверенными в своих навыках рисования и раскрашивания. Учащиеся начальных классов научатся рисовать фигуры и людей с разными выражениями лица, прическами и оттенками кожи. Это иллюстративное исследование настраивает учащихся детского сада на успех до конца года во время писательского семинара. Учащиеся могут обращаться к своей тетради для направленного рисования в течение года, если они забывают, как рисовать объект, который они уже выучили
Предметы:
Искусство и музыка, Снова в школу, Письмо
Классы:
PreK — 1st
Типы:
Уроки, Печатные формы
Также включены в: LEGROWND Writing Units | Мастерская писателей
by
Учительница с обсыпанным верхом
$18. 00
00
Писать от руки должно быть весело и для старших школьников! Это набор ежедневных листов для практики почерка, которые ученики действительно будут просить! Этот набор для рукописного ввода отлично подходит для учащихся, которые уже знают, как составлять буквы, но просто не могут замедлить темп и писать аккуратно! Практика письма для всех возрастов! ВКЛЮЧЕННЫЕ ЗАНЯТИЯ: 26 страниц глупых предложений с алфавитом, 20 страниц положительных утверждений, 20 страниц потрясающих фактов о животных, 20 страниц общих фактов, 20 страниц удивительных математических фактов, 20 страниц Space 9.0003
Предметы:
Английский язык, правописание, письмо
Классы:
1–6
Типы:
Упражнения, оценка
Также включено в: Рабочие листы для рукописного ввода | CURSIVE PRINT D’NEALIAN BUNDLE для старших школьников
by
Kim Miller
Эти ПРОСТЫЕ без суеты редактируемые шаблоны информационных бюллетеней в классе идеально подходят для использования в течение всего года и облегчают общение с родителями! Держите родителей в курсе того, что происходит в вашем классе в течение года. Независимо от того, отправляете ли вы информационный бюллетень домой еженедельно или ежемесячно, эти шаблоны облегчат вам задачу, а редактировать их очень просто! В эту загрузку включены: 24 различных ЦВЕТНЫХ шаблона информационного бюллетеня (цветной и черно-белый) 24 различных ЧЕРНО-БЕЛЫХ шаблона информационного бюллетеня шаблоны информационных бюллетеней
Независимо от того, отправляете ли вы информационный бюллетень домой еженедельно или ежемесячно, эти шаблоны облегчат вам задачу, а редактировать их очень просто! В эту загрузку включены: 24 различных ЦВЕТНЫХ шаблона информационного бюллетеня (цветной и черно-белый) 24 различных ЧЕРНО-БЕЛЫХ шаблона информационного бюллетеня шаблоны информационных бюллетеней
Объекты:
Вернуться в школу, для всех предметных областей, для всех предметов
Оценки:
Prek — 5th
Типы:
Формы классных комнат, для родителей
на
Pocket of Presedhool
Community Helpers. Центры математики и грамотности заполнены веселыми практическими занятиями на школьную тематику, которые помогут вашим ученикам построить математические концепции и грамотность! Теперь включает в себя два занятия по мелкой моторике, один центр письма, шесть заданий по обучению грамоте и восемь заданий по математике. Охватываемые навыки грамотности включают определение букв, начальные звуки, почерк, написание дружеских писем, группы рифм/слов, слоги, построение словарного запаса слов, слов, виденных, и письмо / ведение журнала. Охватываемые математические навыки от одного до
Охватываемые математические навыки от одного до
Предметы:
Английский язык, математика
Классы:
PreK — K
Типы:
Мероприятия, центры
& Детский сад
by
Тара Уэст
$14.00
FirstieMath® Intervention: 30-недельный комплексный и систематический учебный курс по математике. Что такое вмешательство FirstieMath™? FirstieMath® Intervention — это очень универсальная учебная программа по математике, созданная учителем для учителей! Программа универсальна для реализации и разного уровня учащихся. Вы можете успешно использовать эту программу в своих интервенционных группах, группах RTI, математических группах с гидом, общегрупповой математике или в качестве ресурса для несертифицированных сотрудников, помогающих в 9.0003
Субъекты:
Математика, ментальная математика, номера
Оценки:
K — 1 -е
Типы:
Урок, печатные изготовления
на
ЧТО Я УЧИТ
. Ваши студенты ищут немного O ‘ удача ирландцев в этот День Святого Патрика? Подарите им свой собственный четырехлистный клевер, полный волшебства и очарования, с этим веселым мастерством ко Дню Святого Патрика! С помощью этого клевера учащиеся будут размышлять о том, как им «везет» в жизни. Это также отлично подходит для SEL или социально-эмоционального обучения! Проведите мозговой штурм со своими учениками, составьте список «счастливых» вещей до занятия и позвольте им выбрать четыре, которые наполнят их жизнь волшебством. Это мастерство ко Дню Святого Патрика в
Ваши студенты ищут немного O ‘ удача ирландцев в этот День Святого Патрика? Подарите им свой собственный четырехлистный клевер, полный волшебства и очарования, с этим веселым мастерством ко Дню Святого Патрика! С помощью этого клевера учащиеся будут размышлять о том, как им «везет» в жизни. Это также отлично подходит для SEL или социально-эмоционального обучения! Проведите мозговой штурм со своими учениками, составьте список «счастливых» вещей до занятия и позвольте им выбрать четыре, которые наполнят их жизнь волшебством. Это мастерство ко Дню Святого Патрика в
Предметы:
Для всех предметных областей, День Святого Патрика
Классы:
1–4
Типы:
Мероприятия, Идеи для доски объявлений
Тематическая доска объявлений
на
Чем занять детей
37,00 $
11,00 $
В этом полном наборе с алфавитом есть все, что нужно для обучения учащихся названиям букв, звукам букв, мелкой моторике, почерку и многому другому! Этот пакет предназначен для дошкольников, pre-k, переходного детского сада и учащихся детского сада. Дети любят делать поделки с алфавитом, якорные диаграммы, лабиринты, мазки, рисование алфавита, вырезание и вставку, рабочие листы и игры. получается
Дети любят делать поделки с алфавитом, якорные диаграммы, лабиринты, мазки, рисование алфавита, вырезание и вставку, рабочие листы и игры. получается
Предметы:
Снова в школу, Акустика, Чтение
Классы:
PreK — 1st
Типы:
Занятия, плакаты, рабочие листы
CCSS:
43 9.Ka, RF.Ka, RF.Ka, RF.Ka, RF.Ka, RF.Ka, 9.0043 9.0004 , RF.K.1b, RF.K.1c, RF.K.1d…
Также включено в: Полная учебная программа для детского сада – Математические разделы – Чтение – Акустика – Письмо
Амплитуда, период и фазовый сдвиг
Вы должны знать, что
три слагаемых: амплитуда, период и
среднее значение фазового сдвига,
в контексте разговора об обобщенных синусоидальных и косинусоидальных кривых, показанных ниже:
Как обсуждается ниже,
учитывая любую обобщенную кривую синуса или косинуса,
вы должны быть в состоянии
определить его амплитуду, период и фазовый сдвиг.
Пример вопроса:
Укажите амплитуду, период и фазовый сдвиг $\,y = 5\sin(3x-1)\,.$
В следующем разделе вы напишете
уравнение кривой с заданными амплитудой, периодом и фазовым сдвигом.
Пример вопроса:
Напишите уравнение синусоиды с амплитудой $\,5\,$, периодом $\,3\,$ и фазовым сдвигом $\,2\,.$
Краткое изложение основных понятий
АМПЛИТУД:
| |
ПЕРИОД:
| |
ФАЗОВЫЙ СДВИГ:
|
Учитывая обобщенную синусоидальную/косинусную кривую: 90 555 Найдите амплитуду, период и фазовый сдвиг
ПРИМЕР:
Укажите амплитуду, период и фазовый сдвиг $\,y = 5\sin(3x-1)\,.$
РЕШЕНИЕ:
| Аргумент имеет вид $\,kx + B\,.$ Выражение имеет вид $\,a\sin(kx+B)\,.$ Здесь $\,a = 5\,$ $\,k = 3\,$ и $\,B = -1\,.$ Амплитуда $\,|a| = |5| = 5\,.$ Период равен $\,\displaystyle\frac{2\pi}{|k|} = \frac{2\pi}{3}\,. Установка $\,3x-1 = 0\,$ дает $\,\displaystyle x = \frac{1}{3}\,$; фазовый сдвиг равен $\,\displaystyle\frac{1}{3}\,.$ Альтернативный фазовый сдвиг: $\,\displaystyle\frac{-B}{k} = \frac{-(-1)}3 = \frac{1}{3}\,$ |
ПРИМЕР:
Укажите амплитуду, период и фазовый сдвиг $\displaystyle\,y = -3\cos 2(x+\frac{\pi}{5})\,.$
РЕШЕНИЕ:
| Аргумент имеет вид $\,k(x + b)\,.$ Выражение имеет вид $\,a\cos k(x + b)\,.$ Здесь $\,a = -3\,$ $\,k = 2\,$ и $\displaystyle\,b = \frac{\pi}{5}\,.$ Амплитуда $\,|a| = |-3| = 3\,. |



 Речь о мнемоническом правиле пойдет позже.
Речь о мнемоническом правиле пойдет позже. )
)  $
Если $\,а
$
Если $\,а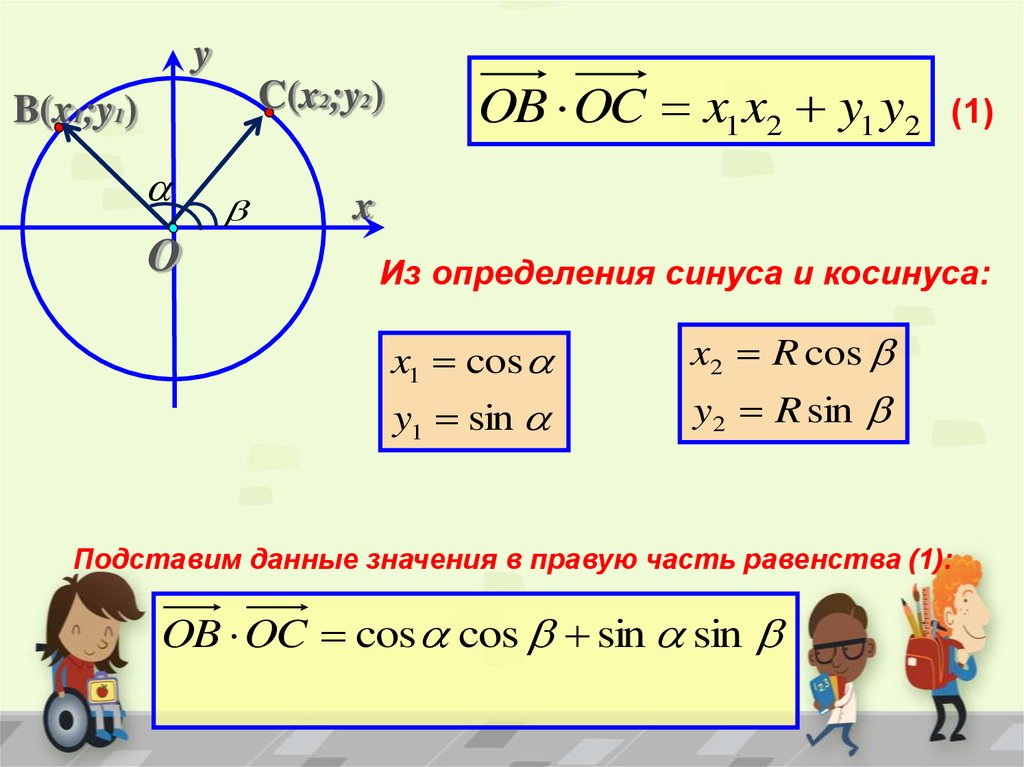 Периодические функции и
Период периодической функции.
Периодические функции и
Период периодической функции. $
$


 Затем применяется горизонтальное растяжение/сжатие, которое снова перемещает точку.
В этом случае в формулу фазового сдвига входят как $\,B\,$, так и $\,k\,.$
Затем применяется горизонтальное растяжение/сжатие, которое снова перемещает точку.
В этом случае в формулу фазового сдвига входят как $\,B\,$, так и $\,k\,.$ $
$
 $
$