Решение комбинаторных задач. 5-й класс
Тип урока: формирование и совершенствование умений и навыков.
Цели урока:
- Образовательные: закрепить умение решения комбинаторных задач на примере составления многозначных чисел из предложенных цифр с помощью перечисления комбинаций (дерева возможных вариантов), подсчет общего числа комбинаций по правилу умножения.
- Развивающие: развитие математического мышления; развитие познавательного интереса учащихся; развитие умения самостоятельно выбирать способ решения и умения обосновать выбор;
- Воспитательные: формирование навыков самоконтроля, воспитание самостоятельности и настойчивости в достижении цели.
Оборудование: карточки с заданиями
для индивидуальной работы, карточки с решением
задач для самопроверки, карточки-«подсказки» для
решения задач.
Структура урока:
- Организационный момент
- Актуализация опорных знаний и умений учащихся (устный опрос)
- Формирование и закрепление знаний и умений:
- Коллективная работа над задачами
- Индивидуальная работа над задачами
- Подведение итогов урока
- Домашнее задание
Показатель реального результата достижения цели урока: самостоятельное выполнение заданий на составление многозначных чисел с применением дерева возможных вариантов и подсчет общего числа комбинаций по правилу умножения в знакомой и измененной ситуациях.
ХОД УРОКА
1. Устный опрос
2. Натуральные числа
– Какие числа называются
натуральными? (Числа, используемые при счете
предметов)
– С помощью каких «знаков» можно
написать любое натуральное число? (С помощью
цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
– Как называется группа из трех цифр в
записи числа, считая справа налево? (Класс)
– Как называется место, занимаемое
цифрой в записи числа? (Разряд)
– Сколько разрядов в каждом классе? (Три)
– Что обозначает цифра 0 в десятичной
записи числа? (Отсутствие единиц данного
разряда)
– Какая цифра не может стоять в старшем
разряде числа? (0)
3.
Комбинаторные задачи
– Какие задачи называются
комбинаторными? (Задачи, в которых идет речь о
тех или иных комбинациях объектов)
– Какими способами мы умеем решать
комбинаторные задачи? (С помощью правила
умножения и с помощью дерева возможных
вариантов)
– В чем заключается правило
умножения? (Если первый элемент в
комбинации можно выбрать а способами,
после чего второй элемент b способами, то общее
число комбинаций из двух элементов будет a .
b).
– В чем заключается правило решения
задач с помощью дерева вариантов?
4. Работа по теме урока:
1 этап.
Коллективная работа над задачами
№ 1
Запишите все трехзначные числа, для записи которых употребляются только цифры 1 и 2.
– Какая цифра может стоять в разряде
сотен? (1 или 2)
– Какая цифра может стоять в разряде
десятков в каждом из полученных двух случаев? (1
или 2)
– Какая цифра может стоять в разряде
единиц в каждом из полученных четырех случаев? (1
или 2)
По ходу рассуждений выполняется схема на доске
Получили 8 чисел: 111, 112, 121, 122, 211, 212, 221, 222
№ 2
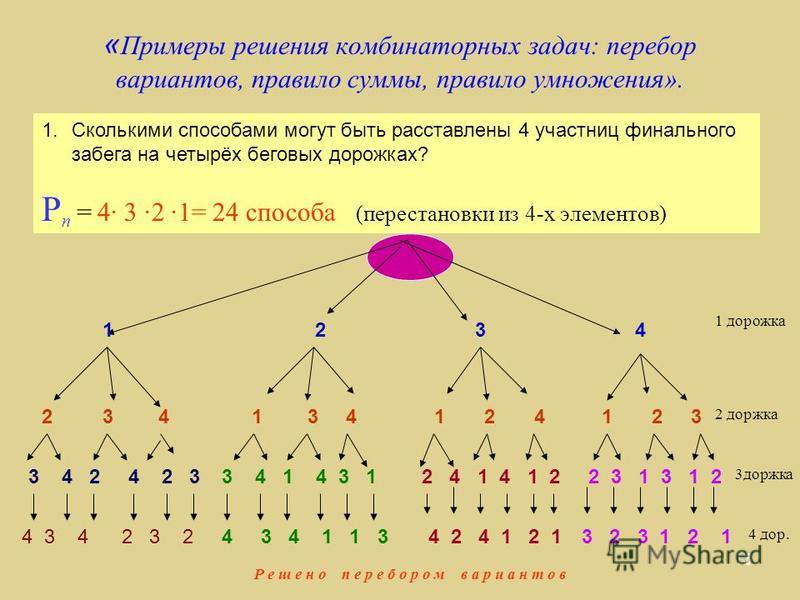
Сколько трехзначных чисел можно составить из цифр 2, 4, 6, 8, если цифры в записи числа не повторяются?
– Сколько цифр дано? (Четыре)
– Какое условие поставлено? (Цифры не
должны повторяться)
– Какая цифра может стоять на первом
месте?
– Если цифру поставили на первое место,
может она занимать второе, третье место? (Нет)
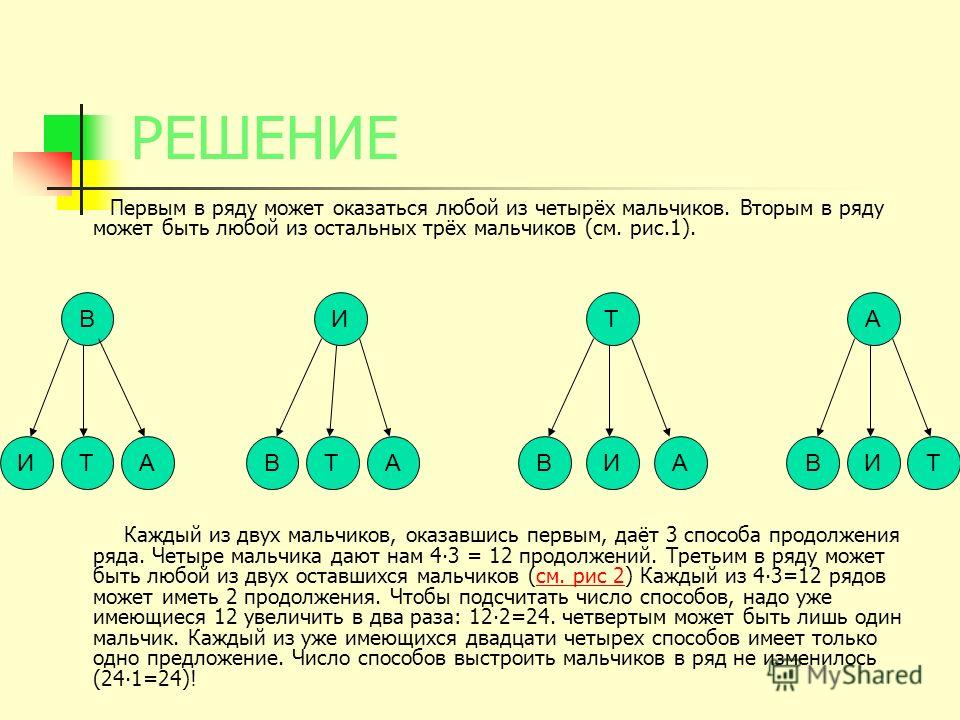
Первой цифрой числа может быть любая из четырех
данных цифр, второй – любая из трех других.
А
третьей – любая из двух оставшихся. Всего из
данных цифр можно составить
4 . 3 . 2 = 24
трехзначных числа.
Ответ: 24 числа.
Вывод: для удобства перечисления всех возможных вариантов мы пользовались деревом вариантов. При большом количестве комбинаций дерево быстро ветвится и становится необозримым. Поэтому для подсчета количества комбинаций, если не требуется перечислить все комбинации, лучше пользоваться правилом умножения.
2 этап. Индивидуальная работа над задачами
Индивидуальная работа над задачами состоит из двух шагов:
Шаг 1 задачи № 3 и № 4. Задачи решаются
самостоятельно с последующей самопроверкой по
карточке с решением, выданным учителем. (Приложение 1)
Если учащиеся справились с решением задач № 3 и №
4, то им предлагаются задачи № 5, № 6, № 7
Если учащийся не справился с задачами № 3 и № 4,
ему предлагаются аналогичные задачи № 3.
1 и №
4.1. Если учащийся справляется с задачами № 3.1 и
№ 4.1, он решет № 5, № 6, № 7.
В случае, если учащиеся затрудняются в решении
задач № 3.1, № 4.1, № 5, № 6, № 7 им выдаются
карточки-«подсказки». (Приложение
2)
№ 3
Запишите все трехзначные числа, для записи которых используются цифры 5 и 7.
№ 4
Запишите все трехзначные числа, для записи которых используются цифры 0, 2, 5, если цифры в записи не повторяются.
№ 3.1
Запишите все трехзначные числа, для записи которых используются цифры 2 и 9
№ 4.1
Запишите все трехзначные числа, в записи которых используются цифры 0, 3, 7. Если цифры в записи не повторяются.
№ 5
Сколько двухзначных чисел можно составить из цифр 0, 2, 4, 6, если цифры в записи числа не повторяются? Запишите все эти числа.
№ 6
Сколько трехзначных чисел можно составить из
нечетных цифр, если цифры в записи числа не
повторяются? Запишите первые 12 чисел, если
составленные числа расположены в порядке
возрастания.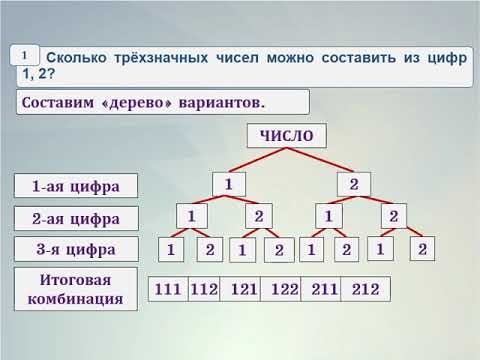
№ 7
Сколько существует трехзначных чисел, в записи которых нет цифры 3?
Ответы:
№ 3.1 222, 229, 292, 299,
922, 929, 992, 999
№ 4.1 307, 370, 703, 730
№ 5 3 .
3 = 9 чисел 20, 24, 26, 40, 42, 46, 60, 62, 64
№ 6 5 .
4 . 3 = 60 чисел 135, 137, 139, 153, 157, 159, 173, 175,
179, 193, 195, 197
№ 7 8 .
9 . 9 = 648 чисел
5. Итог урока
– Чем удобно пользоваться при
перечислении всех возможных комбинаций?
– Почему при большом количестве
комбинаций неудобно пользоваться деревом
вариантов?
– Какое правило вы знаете для подсчета
количества комбинаций? Сформулируйте его.
6.
7. Оценивание работы на уроке каждого учащегося в соответствии с количеством и номерами решенных задач и взятых подсказок.
8. Задание на дом
– Составить и решить две комбинаторных задачи на составление многозначных чисел из предложенных цифр.
Презентация к уроку математики 5 класс «Комбинаторные задачи»
Комбинаторные задачи
УМК: А.Г. Мерзляк и др.
5 класс
Разработано учителем математики МБОУ — Полужская ООШ им.Ф.Е.Стрельца.
Басовой Е.В.
2020 г.
Прозвенел уже звонок,
Встали тихо, замолчали,
Всё, что нужно, вы достали.
Приготовились к уроку,
В нём иначе нету проку.
Здравствуйте, садитесь,
Больше не вертитесь.
Мы урок начнем сейчас,
Интересен он для вас.
Слушай всё внимательно,
Поймешь всё обязательно.
Математика уступает свои крепости лишь сильным и смелым.
(А.П. Конфорович)
Какой рисунок солнышка соответствует твоему настроению на начало урока
3
1
2
Повторение
1. Чему равен объём куба, ребро которого равно 8 дм?
2. Чему равен объём прямоугольного параллелепипеда с с измерениями и 2см, 6 см и 10 см?
3.Вычислите сумму
27 + 16 + 33 + 24.
4. Из цифр 7, 4, 5 составили трёхзначные числа. Сколько чисел получится и какие это числа, если цифры не повторяются?
Задача
Решение
М
Д
Б
Д
Б
М
Б
М
Д
М
Д
М
Б
Б
Д
БДМ БМД ДБМ ДМБ МБД МДБ
Нередко в повседневной жизни мы встречаемся с задачами, решение которых требует рассмотрения всех возможных случаев, или, как ещё принято говорить, всех возможных комбинаций .
Поэтому такие задачи называют комбинаторными
Комбинаторные
задачи
Слово «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять».
Термин «комбинаторика» был введён знаменитым Готфридом Вильгельмом Лейбницем, — всемирно известным немецким учёным.
Занимался идеями комбинаторного искусства.
Комбинаторика — раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить.
Методы решения комбинаторных задач
— Метод перебора вариантов:
если нужных комбинаций не слишком много, то все их можно просто
Перечислить, или, как говорят перебрать все возможности.
-Изображение дерева возможных вариантов: позволяет наглядно представить
все варианты.
- Правило умножения:
- Применяется, когда количество возможных вариантов достаточно велико.
Задача № 1
В 5 классе в пятницу 3 урока: математика, литература, родной язык. Сколько вариантов расписания можно составить?
Задача №2
У Арсения есть три книги: красная, зелёная и фиолетовая. Сколько существует способов расставить эти книги на полку?
Задача № 3
Сколько различных трёхзначных чисел можно составить из цифр 1, 3, 5? (Цифры НЕ могут повторяться!)
Задача № 4
Сколько различных трёхзначных чисел можно составить из цифр 2, 4, 6? (Цифры НЕ могут повторяться!)
Решение задачи № 3
Цифры
5
3
1
3
5
1
1
5
3
1
5
1
3
5
3
Ответ: 6 чисел (135, 153, 315, 351, 513, 531)
Физкультминутка
- Потрудились – отдохнем.
- Встанем, глубоко вздохнем.
- Руки в стороны, вперед,
- Влево, вправо поворот.
- Три наклона, прямо встать,
- Руки вниз и вверх поднять.
- Руки плавно опустили,
- Всем улыбки подарили .
Задача № 5
Сколько различных завтраков, состоящих из 1 напитка и 1 вида выпечки, можно составить из чая, кофе, бутерброда, печенья и вафель?
Решение задачи № 5
Завтрак
Ответ: 6 завтраков.
Задача № 6
У ослика Иа-Иа есть три надувных шарика: красный, зелёный и жёлтый. Он хочет подарить их Винни-Пуху, Пятачку и Кролику. Сколько у ослика есть вариантов сделать подарки своим друзьям?
Решение задачи № 6
Ответ: 6 вариантов.
Проблемный вопрос:
Может ли нам комбинаторика помочь в реальной жизни?
Области
применения
комбинаторики:
ГИА
Домашнее задание
Прочитать параграф 24(стр.
160-163)
№ 646, 648,652, 662, 4(стр163)
Рефлексия
Мне было интересно. Я доволен своей работой на уроке
На уроке я работал неплохо, но не всё было понятно
На уроке мне было трудно
Искусство решения проблем
В комбинаторике рассмотрение дела — это метод подсчета, который включает в себя разделение задачи на несколько частей, подсчет этих частей по отдельности, а затем суммирование итогов каждой части. Кейсворк — это очень общий подход к решению проблем, и поэтому он имеет широкое применение.
Содержимое
- 1 Примеры
- 1.1 Пример 1
- 1.2 Пример 2
- 1.3 Пример 3
- 1.4 Другие примеры
- 2 Ресурсы
- 3 См. также
Примеры
Вот несколько примеров, демонстрирующих делопроизводство в действии. В отличие от вариантов, приведенных в этой статье, большинство проблем не могут быть полностью решены с помощью работы с кейсами.
Тем не менее, это важно как промежуточный шаг во всей математике, а не только в соревнованиях.
В то время как есть проблемы, где рассмотрение дела дает наиболее элегантное решение, в тех случаях, когда существует более короткий ответ, рассмотрение дела может рассматриваться как грубая сила. Это особенно верно, если в этом альтернативном решении используется дополнительный подсчет.
Пример 1
Сколько слов имеют длину менее четырех букв и содержат только буквы A, B, C, D и E? Здесь «слово» относится к любой последовательности букв.
Решение : Мы делим задачу на случаи в зависимости от длины слова.
Случай 1 : Слово состоит из одной буквы. Ясно, что есть такие слова.
Случай 2 : Слово состоит из двух букв. При построении множества этих слов есть варианты на первую букву и варианты на вторую букву, значит есть из этих слов.
Случай 3 : Слово состоит из трех букв. По той же логике, что и выше, у нас есть варианты для первой буквы, варианты для второго и варианты для третьего.
Тогда есть из этих писем.
Суммируя все наши случаи, есть слова, которые состоят менее чем из четырех букв и содержат только буквы A, B, C, D и E.
Пример 2
Сколько положительных целых чисел удовлетворяют уравнению ?
Решение : Мы используем делопроизводство на основе значения x.
Случай 1 : . Тогда эта проблема становится , так что есть возможные значения для и, следовательно, решения, когда это одно.
Случай 2 : . Тогда эта проблема становится , так что возможны значения для , и, следовательно, решения, когда равно два.
Если , проблема становится . Но вопрос требует положительного ответа, поэтому решений нет, когда . Таким образом, существуют положительные целые решения уравнения.
Пример 3
2004 AIME II Задача 4. Сколько положительных целых чисел, меньших 10 000, имеют не более двух разных цифр?
Решение : Позвольте и быть двумя цифрами числа.
Используйте разбор дела в зависимости от того, сколько цифр в номере.
Вариант 1 : Одноразрядный номер. Все числа в этой категории удовлетворяют заданному условию, значит, есть такие.
Случай 2 : Номер двузначный. Опять же, все числа в этой категории имеют две разные цифры, поэтому есть и такие.
Случай 3 : Номер трехзначный. Возможные случаи в этой категории: и Используя конструктивный подход, есть цифры для того, что может быть первым числом, нуль исключен, чтобы сохранить число трехзначным. Вторая цифра может быть цифрой, включая ноль и удаляя номер первой цифры. Тогда есть из этих чисел.
Случай 4 : Четырехзначный номер. Возможные случаи в этой категории: и Используя ту же логику, что и раньше, первая цифра имеет варианты, как и вторая. Тогда есть из этих чисел.
Таким образом, существуют целые числа, меньшие которых имеют не более двух различных цифр.
Другие примеры
- 2000 AIME 1 Задача 5
Ресурсы
- AoPS Casework Counting Part 1
- Подсчет дел AoPS, часть 2
См.
также- Дополнительный счет
- Конструктивный счет
- Пересчет
Глава 2 Раздел 2 (стр. 26-27)
Глава 2 Раздел 3 (стр. 32-33)
Обзор главы 2 (стр. 33-36)
Глава 3 Раздел 1 (стр. 42-47)
| ||||
