Квадратный корень из комплексного числа » Аналитическая геометрия f(x)dx.Ru
п.6. Извлечение квадратного корня из комплексного числа. Формула квадратных корней из комплексного числа.
В дальнейшем нам понадобится одна числовая функция:
обозначим .
Эту функцию называют знаком числа х и читается она так: «сигнум икс».
Теорема. Пусть . Тогда
(7) , где квадратные корни в скобках являются арифметическими квадратными корнями из положительных чисел.
Доказательство. Как мы уже выяснили существует ровно два квадратных корня из комплексного числа, причем они являются противоположными числами. Пусть , где . Тогда или . Возведем в квадрат левую часть этого равенства и воспользуемся условиями равенства двух комплексных чисел. Получаем:
(8) .
Возведем в квадрат каждое уравнение этой системы: . Прибавим второе уравнение к первому:
.
Здесь – обычный арифметический квадратный корень из положительного действительного числа. Далее, если полученная система имеет решение, то по обратной теореме Виета и являются корнями квадратного уравнения . Находим дискриминант . Отсюда . Оба корня квадратного уравнения оказываются положительными, т.к., очевидно, . При выборе корней учитываем равенства (8), а именно . Отсюда следует, что и
Далее, если полученная система имеет решение, то по обратной теореме Виета и являются корнями квадратного уравнения . Находим дискриминант . Отсюда . Оба корня квадратного уравнения оказываются положительными, т.к., очевидно, . При выборе корней учитываем равенства (8), а именно . Отсюда следует, что и
. Осталось правильно выбрать знаки перед знаками радикалов. Из равенств (8) следует, что . Положим , тогда , откуда и следует доказываемая формула. Теорема доказана.
Пример. Вычислить .
Решение. Используем только что доказанную формулу корней. Здесь . Подставляем в формулу и получаем:
.
Ответ: .
Замечание. Можно не запоминать формулу (7) ввиду ее громоздкости, а при решении использовать алгоритм доказательства теоремы. Решим таком образом предыдущий пример.
Пусть . Тогда . Это возможно лишь тогда равны вещественные и мнимые части обоих комплексных чисел: . Возводим оба уравнения системы в квадрат: . Прибавляем второе уравнение к первому: . Применяем обратную теорему Виета:
Применяем обратную теорему Виета:
. Решаем квадратное уравнение: . Так как , то . Принимаем . Так как , то . Получили один из двух корней: . Второй корень противоположен первому.
Ответ: .
Конечно, этот способ, в отличие от первого, занимает у нас некоторое время, но зато алгоритмы запоминаются лучше, нежели формулы.
Нам будет интересен частный случай формулы (7), когда мнимая часть числа z равна нулю.
Следствие. Пусть – произвольное действительное число. Тогда имеет место следующая формула:
(9) .
Доказательство очевидно, достаточно подставить в формулу (7) и вспомнить, что арифметический квадратный корень из квадрата действительного числа равен его модулю: .
Теперь, если , то формула (9) дает оба корня из положительного действительного числа а: .
Не будем забывать, что квадратный корень в левой части формулы (9) обозначает все множество корней из комплексного числа , а квадратные корни в правой части формулы (9) обозначают арифметические квадратные корни из неотрицательных действительных чисел. Обозначение одно и то же, с помощью знака радикала, а смысл различный.
Обозначение одно и то же, с помощью знака радикала, а смысл различный.
Пусть теперь . Тогда и формула (9) дает равенство: . Здесь – арифметический квадратный корень из положительного числа .
Случай очевиден: .
Интерес представляет случай корня квадратного из отрицательного числа. Сформулируем этот случай отдельно в виде следствия.
Следствие. Пусть и . Тогда оба квадратных корня из числа z могут быть найдены по формуле:
(10) .
Примеры: , , .
Замечание. Обратите внимание на последнее равенство:
.
Это верное равенство, т.е. по определению есть множество всех корней из числа –1, в то время как равенство неверное, с этой точки зрения! Именно поэтому нельзя переносить свойства корней из действительных чисел на корни из комплексных чисел, как показывает следующий простой пример.
Пример. Найдите ошибку в следующих преобразованиях:
.
С другой стороны, легко доказать следующую теорему.
Теорема. (О вынесении действительного множителя из под знака корня.) Пусть, n – произвольное натуральное число. Тогда
(11) ,
где есть обычный арифметический корень из положительного числа.
Доказательство. Равенство (11) здесь нужно понимать как равенство двух множеств: – множество всех корней n-й степени из комплексного числа , – множество всех корней n-й степени из комплексного числа z,
.
Отсюда вытекает и способ доказательства. Мы докажем, что оба множества состоят из одних и тех же элементов.
Пусть . Тогда . Отсюда следует, что . Обратно, Пусть . Тогда . Следовательно, , ч.т.д. Теорема доказана.
Замечание. Предыдущее следствие можно вывести и из только что доказанной теоремы.
Следствие. Пусть и Тогда .
Доказательство. Рассматриваем отрицательное число а как комплексное число . Тогда доказываемое равенство сразу же следует из только что доказанной теоремы: .
Пример. Вычислить .
Решение. Применим только что доказанную теорему: .
Применим только что доказанную теорему: .
Ответ: .
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 2 из 6Следующая ⇒ Пусть комплексное число записано в тригонометрической форме . Запишем его корень также в тригонометрической форме записи По определению корня имеем . Возводя в степень по формуле Муавра, получаем . Отсюда находим модуль корня и аргумент ; . Итак, корень степени n из комплексного числа извлекается по формуле
где
Для любого комплексного числа различных корней степени n ровно n штук. Все они расположены на окружности с центром в начале координат с радиусом и делят эту окружность на n равных частей. Пример 2.Вычислить . Запишем число i в тригонометрической форме . Применим формулу извлечения корня из комплексного числа при . Подставляя получаем различные значения корня
Извлечение корня квадратного из комплексного числа в алгебраической форме записи.
Запишем квадратный корень из числа в алгебраической форме . Возведем это равенство в квадрат: Приравнивая действительные и мнимые части, а также, учитывая, что модуль числа равен квадрату модуля его корня, получаем систему Решая эту систему, находим , откуда .
Пример 3.Вычислить . Действительная и комплексная части равны a=3 и b=4. Вычислим по найденной формуле действительную и комплексную части его корня Итак, .
Многочлены. Разложение на множители.
Рассмотрим многочлен степени n с комплексными коэффициентами от комплексной переменной , где комплексная переменная; комплексные числа. Любой многочлен можно поделить на многочлен с остатком, то есть представить в виде где – делитель, – остаток, – частное.
Определение.Число z0называется корнем многочлена , если =0.
Теорема Безу.Число является корнем многочлена тогда и только тогда, если делится нацело на .
Доказательство. Необходимость. Пусть – корень многочлена . Поделим на многочлен с остатком: , где R – число. Положим в этом равенстве . Так как – корень, то , следовательно и делится нацело на . Достаточность. Пусть делится на без остатка, тогда . Подставляя в это равенство , получаем , следовательно, по определению, является корнем многочлена .
Определение.Число – корень многочлена кратности k , если многочлен можно представить в виде , где не является корнем многочлена , то есть .
Утверждение.Число является корнем кратности k многочлена тогда и только тогда, если является корнем этого многочлена и всех его производных до порядка включительно, то есть а .
Доказательство. Необходимость. Пусть известно, что , где . Очевидно, что , то есть является корнем многочлена. Покажем, что является корнем производных многочлена до порядка включительно. Вычислим производную порядка по формуле Ньютона-Лейбница При все слагаемые в правой части в точке будут равны нулю, и тогда . Если же , то в точке все слагаемые, кроме последнего, равны нулю. Последнее же слагаемое отлично от нуля в силу условия . Отсюда Достаточность. Разложим многочлен в точке по формуле Тейлора Так как первые k слагаемых в правой части обращаются в ноль, то многочлен можно представить в виде . При этом многочлен в точке в ноль не обращается, так как по условию. Тогда будет корнем кратности k по определению.
Основная теорема алгебры (без доказательства). Пусть многочлен от комплексной переменной степени n, с комплексными коэффициентами. , где – корень кратности
Лемма 1.Если z0 – корень кратности k многочлена , то сопряжённое число является корнем кратности k для сопряженного многочлена .
Доказательство. Если z0– корень кратности k многочлена , то многочлен можно представить в виде , где . Возьмём сопряжённое к левой и правой частям последнего равенства . По свойствам сопряжённых чисел имеем . В левой части этого равенства стоит значение сопряженного многочлена в точке и оно представимо в виде где Положив в этой формуле , получим . Обозначим , тогда , где Это и означает, что – корень кратности k многочлена .
Лемма 2. Пусть – многочлен с действительными коэффициентами, но от комплексной переменной. Если корень кратности k многочлена , то также является корнем кратности k многочлена .
Доказательство. По лемме 1 число является корнем кратности k сопряженного многочлена . Поскольку коэффициентымногочлена действительны, то сопряженный многочлен совпадает с самим многочленом и число является корнем кратности k многочлена . Теорема.Многочлен от действительной переменной с действительными коэффициентами представляется в виде произведения линейных множителей и квадратных с отрицательным дискриминантом: , где – действительный корень кратности ; ; .
Доказательство. Рассмотрим многочлен как многочлен от комплексной переменной . Тогда, по основной теореме алгебры, его можно представить в виде , где – корень кратности . Если — действительное число, то скобку не преобразовываем. Если то , где . По лемме 2, если – корень кратности для , то также корень кратности для . Сопряженное число запишется как , тогда произведение можно представить в виде степени, в основании которой лежит квадратный трехчлен с отрицательным дискриминантом так как . Таким образом, разложили многочлен в произведение линейных множителей и квадратных с отрицательным дискриминантом. Положив , получим искомое разложение для .
⇐ Предыдущая123456Следующая ⇒ Читайте также: Психологические особенности спортивного соревнования Приготовление дезинфицирующих растворов различной концентрации Занятость населения и рынок труда Социальный статус семьи и её типология |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 546; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. 3 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | Risolvere per ? | cos(x)=1/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | Risolvere per x | sin(x)=-1/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | Преобразовать из градусов в радианы | 225 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Risolvere per ? | cos(x)=( квадратный корень из 2)/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Risolvere per x | cos(x)=( квадратный корень из 3)/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | Risolvere per x | sin(x)=( квадратный корень из 3)/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | График | g(x)=3/4* корень пятой степени из x | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | Найти центр и радиус | x^2+y^2=9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | Преобразовать из градусов в радианы | 120 град. {n}$ равен одному из значений аргумента числа $z$. Из этого равенства находим {n}$ равен одному из значений аргумента числа $z$. Из этого равенства находим
$\omega \frac{ \phi_{0} + 2k \pi}{n}$. (5) и оказывается, что при разных значениях $k$ получаются, вообще говоря, разные значения корня $w$. Обозначим значение $\omega$, соответствующее каждому выбору числа $k$, через $\omega_{k}$:
$w_{k} = \sqrt[n]{r} \left ( \cos \frac{\phi_{0} + 2k \pi}{n} + i \sin \frac{\phi_{0} + 2k \pi}{n} \right )$. (6) Покажем, что все эти значения различны, а при остальных возможных значениях $k$ новых значений корня $w$ уже не получится. Для этого заметим, что разность аргументов $\omega_{k}$ и $\omega_{l}$ будет равна $\omega_{k} — \omega_{l} = \frac{ \phi_{0} + 2k \pi}{n} — \frac{\phi_{0} + 2l \pi}{n} = 2 \pi \cdot \frac{k-l}{n}$ Числа $w_{k}$ и $w_{l}$ совпадут в том и только в том случае, если $k – l$ делится на $n$ нацело. В случае $z = 0$ единственное значение $\sqrt[n]{0}$ также равно нулю; для достижения общности формулировки можно говорить, что корень степени $n$ из нуля также имеет $n$ значений, которые все совпадают между собой (и равны нулю). Пример 1. Найти все значения корней: а) $\sqrt[4]{-16}$; б) $\sqrt[3]{27}$.
Пример 2. Вычислить: a) $\sqrt[4]{-8-8\sqrt{3i}}$; б) $\sqrt[3]{27i}$.
Учебные материалы по математике | Корень n – ой степени из комплексного числаРассмотрим два комплексных числа с1 и с2, с2 ≠ 0. . По определению частного с1 = с·с2 = ·с2. Arg c1 = Arg + Arg c2 Arg = Arg c1 — Arg c2 Итак, с = = [cos(Arg c1 — Arg c2)+i·sin(Arg c1 — Arg c2)] Комплексное число с = изображается вектором, который получается из вектора с1 путем его сжатия в раз, затем поворотом полученного вектора на угол (-Arg c2) 6. Корень n – ой степени из комплексного числаВозьмем произвольное комплексное число с и натуральное число n 2. Комплексное число Z называется корнем n–ой степени из комплексного числа c, если Zn = c. Найдем все значения корня n–ой степени из комплексного числа с. Пусть c=|c|·(cos Arg c+i·sin Arg с), а Z = |Z|·(сos Arg Z + i·sin Arg Z), где Z корень n—ой степени из комплексного числа с. Тогда должно быть = c = |c|·(cos Arg c+i·sin Arg с). Отсюда следует, что и n·Arg Z = Arg с Arg Z = (k=0,1,…). Следовательно, Z = (cos + i·sin ), (k=0,1,…). Легко увидеть, что любое из значений , (k=0,1,…) отличается от одного из соответствующих значений ,(k = 0,1,…,n-1) на кратное 2π. , (k = 0,1,…,n-1). 7. Предел последовательности комплексных чиселКомплексно-значная функция натурального аргумента называются последовательностью комплексных чисел и обозначается (сn) или с1, с2, …, сn. сn = аn+bn·i (n = 1,2, …) комплексные числа. с1, с2, … — члены последовательности; сn – общий член Комплексное число с = a+b·i называется пределом последовательности комплексных чисел (cn), где сn = аn+bn·i (n = 1, 2, …), где для любого , что при всех n > N выполняется неравенство . Последовательность, имеющая конечный предел называется сходящейся последовательностью. Теорема. Для того, чтобы последовательность комплексных чисел (сn) (сn = аn+bn·i) сходилась к числу с = a+b·i, необходимо и достаточно, чтобы выполнялось равенство lim an = a, lim bn = b. Теорема. Пусть последовательность комплексных чисел (сn) и (zn) сходятся соответственно к с и z, тогда справедливо равенства lim(сn zn) = c z, lim(сn·zn) = c·z. Если доподлинно известно, что z не равно 0, то справедливо равенство . 8. Понятие функции комплексного переменного.Рассмотрим в комплексной плоскости (Z) два множества E и D (не пустые). Отображение множества на множество называется функцией комплексного переменного (D может принадлежать другой плоскости (W)). Любому Z0, принадлежащему E, указан каким-то способом одним элемент из D). Пусть Z = x+i·y, W = u+i·v. Функция u(x,y) называется вещественной частью функции f(Z), а v(x,y) мнимой частью f(Z). Таким образом, Ref(Z) = u(x,y) , Imf(Z) = v(x,y). Например, для функции W = Z2 = (x +i·y)2 = x2 – y2 + 2·i·x·y вещественная часть ReZ2 = x2 – y2, ImZ2 = 2·x·y. Геометрически, как отображение множества на множество . Корень из комплексного числа в алгебраической форме. Комплексные числа и алгебраические действия над нимиРассмотрим квадратное уравнение . Определим его корни . Не существует действительного
числа, квадрат которого равен -1. Но если формулой определить
оператор i как мнимую единицу, то решение этого уравнения можно записать
в виде . При этом и
— комплексные числа, в которых -1
это действительная часть, 2 или во втором случае -2 – мнимая часть. Мнимая
часть – это также действительное (вещественное) число. Мнимая часть,
умноженная на мнимую единицу, означает уже мнимое число . В общем виде комплексное число имеет вид z = x + iy , где x, y – вещественные числа, – мнимая единица. В ряде прикладных наук, например, в электротехнике, электронике, теории сигналов мнимая единица обозначается через j . Вещественные числа x = Re{z} и y = Im{ z} называются вещественной и мнимой частями числа z. Выражение называется алгебраической формой записи комплексного числа. Любое действительное число есть частный случай комплексного числа в виде . Мнимое число тоже частный случай комплексного числа . Определение множества комплексных чисел С Это выражение читается следующим образом: множество С , состоящее из элементов , таких что x и y принадлежат множеству действительных чисел R и — это мнимая единица. Отметим, что и т.д. Два комплексных числа и равны, если и только если равны их
действительные и мнимые части, т. Комплексные числа и функции широко используются в науке и технике, в частности, в механике, анализе и расчете цепей переменного тока, аналоговой электронике, в теории и обработке сигналов, в теории автоматического управления и др. прикладных науках.
Сложение двух комплексных чисел состоит в сложении их действительных и мнимых частей, т.е. Соответственно разность двух комплексных чисел Комплексное число называется комплексно сопряженным числу z = x + iy. Комплексно сопряженные числа z и z * отличаются знаками мнимой части. Очевидно, что . Любое равенство между комплексными выражениями остается справедливым, если в этом равенстве всюду i заменить на — i , т.е. перейти к равенству сопряженных чисел. Числа i и – i алгебраически неразличимы, поскольку . Произведение (умножение) двух комплексных чисел может быть вычислено следующим образом: Деление двух комплексных чисел: Пример :
Комплексное
число графически можно представить в прямоугольной системе координат. На оси Ox будем располагать действительные части x , она называется действительной (вещественной) осью , на оси Oy –мнимые части y комплексных чисел. Она носит название мнимой оси . При этом каждому комплексному числу соответствует определенная точка плоскости, и такая плоскость называется комплексной плоскостью . Точке А комплексной плоскости будет соответствовать вектор ОА . Число x называется абсциссой комплексного числа , число y – ординатой . Пара комплексно сопряженных чисел отображается точками, расположенными симметрично относительно действительной оси. Если на плоскости задать полярную
систему координат , то каждое комплексное число z определяется полярными координатами . Модуль комплексного числа всегда неотрицательный. Аргумент комплексного числа не определяется однозначно. Главное значение аргумента должно удовлетворять условию . Каждой точке комплексной плоскости соответствует также общее значение аргумента . Аргументы, отличающиеся значением, кратным 2π, считаются равными. Аргумент числа нуль не определен. Главное значение аргумента определяют по выражениям: Очевидно, что При этом Представление комплексного числа z в виде называется тригонометрической формой комплексного числа. Пример .
Разложение в ряд Маклорена для функций действительного аргумента имеет вид: Для экспоненциальной функции комплексного аргумента z разложение имеет аналогичный характер . Разложение в ряд Маклорена для экспоненциальной функции мнимого аргумента можно представить как Получившееся тождество называется формулой Эйлера . Для отрицательного аргумента оно имеет вид Комбинируя эти выражения, можно определить следующие выражения для синуса и косинуса . Пользуясь формулой Эйлера, из тригонометрической формы представления комплексных чисел можно получить показательную (экспоненциальную, полярную) форму комплексного числа, т.е. его представление в виде , где — полярные координаты точки с прямоугольными координатами (x, y ). Число, сопряженное комплексному числу , в показательной форме записывается следующим образом . Для показательной формы легко определить следующие формулы умножения и деления комплексных чисел Т.е., в показательной форме
произведение и деление комплексных чисел выполняется проще, чем в
алгебраической форме. При умножении модули сомножителей перемножаются, а
аргументы складываются. При делении модуль числителя делится на модуль знаменателя, и из аргумента числителя вычитается аргумент знаменателя. Используя показательную форму комплексных чисел, можно получить выражения для известных тригонометрических тождеств. Например, из тождества с помощью формулы Эйлера можно записать Приравнивая действительную и мнимую части в данном выражении, получаем выражения для косинуса и синуса суммы углов
Возведение комплексного числа в натуральную степень n производится по формуле Пример . Вычислим . Представим число в тригонометрической форме ’ Применяя формулу возведения в степень, получим Положив в выражении значение r = 1, получим так называемую формулу Муавра , при помощи которой можно
определять выражения синусов и косинусов кратных углов. Корень n –й степени из комплексного числа z имеет n различных значений, определяемых по выражению Пример . Найдем . Для этого выразим комплексное число () к тригонометрической форме . По формуле вычисления корня из комплексного числа, получаем Логарифм комплексного числа z – это число w , для которого . Натуральный логарифм комплексного числа имеет бесконечное множество значений и вычисляется по формуле Состоит из действительной (косинусоидальной) и мнимой (синусоидальной) части. Такое напряжение можно представлять как вектор длиной U m , начальной фазой (углом) , вращающийся с угловой скоростью ω . При этом если комплексные функции
складываются, то складываются их вещественные и мнимые части. Если комплексная
функция умножается на константу или вещественную функцию, то её вещественная и
мнимая части умножаются на тот же множитель. Дифференцирование / интегрирование
такой комплексной функции сводится к дифференцированию / интегрированию вещественной
и мнимой части. Например, дифференцирование выражения комплексного напряжения заключается в умножении его на iω — вещественная часть функции f(z), а – мнимая часть функции. Примеры: . Значение z изображается точкой в комплексной плоскости z, а соответствующее значение w — точкой в комплексной плоскости w . При отображении w = f(z) линии плоскости z переходят в линии плоскости w , фигуры одной плоскости в фигуры другой, но формы линий или фигур могут существенно измениться. 2 + 25 = 0$, и я нашел четыре ответа: $z = \pm\sqrt{3 \pm 4i}$.Однако кто-то в комментарии сказал, что ответ будет $2+i$, $2-i$, $-2+i$, $-2-i$. Я не могу понять, как мы можем найти эти корни из ответа, который я нашел. Как мы должны вычислить квадратный корень из комплексного числа?
$\endgroup$ 3 $\begingroup$ Подсказка: 92$, так что $x = \pm \sqrt {\frac{5+3}2} = \pm 2$ и $y = \frac 4 {2x} = \pm 1$ (с тем же знаком, что и $x $). $\endgroup$ 1 $\begingroup$
Если $z$ неположительное действительное число, квадратные корни равны $\pm\sqrt{-z}\cdot\mathrm i$. В противном случае квадратные корни $z$ равны 92$, следовательно, $r=5$, $z+r=8+4\mathrm i$, то есть $z+r=4(2+\mathrm i)$, $|z+r|=4|2 +\mathrm i|=4\sqrt5$ и квадратные корни $$ \pm\sqrt5\cdot\frac{4(2+\mathrm i)}{4\sqrt5}=\pm(2+\mathrm i). $$ Для несколько меньшего примера , составленного из , рассмотрим $z=3+2\mathrm i$, тогда тождество выше показывает, что квадратные корни $z$ равны $$ \pm\frac{3+\sqrt{13}+2\mathrm i}{\sqrt2\cdot\sqrt{3+\sqrt{13}}}. $$ $\endgroup$ 4 Твой ответЗарегистрируйтесь или войдите в системуЗарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и пароль Опубликовать как гостьЭлектронная почта Требуется, но никогда не отображается Опубликовать как гостьЭлектронная почта Требуется, но не отображается Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie . определение — Чему равен квадратный корень из комплексного числа i?
В этом корень проблемы: людей учат, что $i$ «определяется как» нечто, а не то, что оно происходит естественным образом из геометрии и арифметики проблемы. Потому что, если что-то «определяется как» то и это, оно автоматически становится бесспорным и необъяснимым. Если бы числа были обнаружены в правильном порядке и в правильном порядке , то вы бы поняли, почему $i$ является тем, чем оно является, потому что оно естественным образом вытекает из арифметики. Вот как вы можете самостоятельно открыть $i$, уже имея его правильную геометрическую интерпретацию:
Теперь у нас есть все необходимое, чтобы открыть $i$ (и $-1$ по пути тоже!): Каков ответ на следующую геометрическую прогрессию?: $$1:x = x:1 $$ Или словами: Вы делаете что-то со своей единицей ($1$), чтобы получить $x$. Очевидный ответ: просто ничего не делать. Пусть $x = 1$ (число $1$ — это число, которое не меняет никакого другого числа при умножении на него; это число 9).0027 мультипликативная идентичность ). Давайте проверим: подставьте $1$ вместо $x$, и вы получите: $$1:(1) = (1):1$$ Но есть еще один ответ на эту загадку: вы можете повернуть свой блок на $180°$ , заставляя его работать в направлении , противоположном . То есть другой ответ: $x = -1$, что противоположно $1$. Давайте проверим: $$1:(-1) = (-1):1$$ Приведенная выше пропорция говорит, что все, что вы делаете со своей единицей ($1$), чтобы получить $-1$ (что превращает ее в $180°$), вы делаете то же самое с полученным таким образом $-1$ (то есть также поворачиваете его на $180°$), чтобы вернуть свою стандартную единицу $1$. И это правда: Поверните свой блок 92 = 1$. Тогда и $1$, и $-1$ являются квадратными корнями из единицы. Таким же образом вы можете обнаружить $i$, воображаемую единицу . Просто задайте себе следующий вопрос: каково среднее геометрическое между $1$ (ваша стандартная единица измерения) и недавно обнаруженным $-1$? Или в символах: $$1 : x = x : -1$$ Чтобы превратить $1$ в $-1$, вам нужно буквально повернуть его на $180°$. Но тут нужно как-то сделать половину того хода, дважды. И что такое пол-оборота $180°$? Конечно, это $90°$! 🙂 Таким образом, ваш $x$, представляющий собой квадратный корень из $-1$ (то есть операцию, которую вам нужно дважды применить к вашей единице, чтобы превратить ее в $-1$), оказывается (ха :P) равным быть на уровне $90°$ по отношению к вашей стандартной единице. $$1 : \sqrt{-1} = \sqrt{-1} : 1$$, или в современных обозначениях: $$1 : i = i : -1$$ Но помните, что всегда есть два ответа на такие геометрические прогрессии. Другой в данном случае противоположен $i$, то есть $-1$. Давайте проверим: $$1 : -\sqrt{-1} = -\sqrt{-1} : 1$$, или в современных обозначениях: $$1 : -i = -i : -1$$ что тоже верно, и вы также можете проверить это геометрически: умножение на $-i$ поворачивает на $270°$ (или, как я предпочитаю это видеть: на $-9{\ frac {1} {2}} = \ sqrt {-1} \ lor — \ sqrt {- 1} = i \ lor -i $ $ Теперь к вашему первоначальному вопросу:
Чтобы узнать, каковы квадратные корни из $i$, вам нужно сделать то же самое, что вы делали до этого момента: вам нужно найти среднее геометрическое между $1$ и $i$. $$1 : x = x : i$$ То есть вам нужно что-то сделать с вашей единицей, чтобы получить это число, а затем сделать то же самое снова с этим числом, чтобы получить $i$. Какая операция, примененная дважды, поворачивается на 9 долларов?0°$? Самый очевидный ответ: просто поверните на половину от этого угла, что составляет $45°$, или $\frac{\pi}{4}$. Вы не меняете длину своей единицы ($i$ также является единицей длины), а только ее направление. Таким образом, ответом является число, которое представляет собой вашу единицу измерения, повернутую на $45°$ и остающуюся длиной в единицу. Если бы вы получили его сложением, вам пришлось бы переместить $\frac{1}{\sqrt{2}}$ в направлении вашего юнита, а затем еще $\frac{1}{\sqrt{2 }}$ в направлении, перпендикулярном ему (то есть в направлении вашей воображаемой единицы $i$). Таким образом, ответ в прямоугольной/аддитивной форме: $\frac{1}{\sqrt{2}} + \frac{i}{\sqrt{2}}$. Или в геометрии: 92 = -1$.
Выпалить какие угодно определения всегда легко. Сложный квадратный корень | плюс.maths.orgЭта статья о комплексных числах немного продвинута. См. здесь базовое введение в комплексные числа. Каждое положительное действительное число имеет два квадратных корня, один из которых является отрицательным из другого. Их легко отличить, указав, смотрите ли вы на положительный или отрицательный квадратный корень. Это означает, что вы можете однозначно определить функцию квадратного корня по всем неотрицательным действительным числам (положительные действительные числа и 0). График положительной функции квадратного корня, заданной для неотрицательных действительных чисел. Когда дело доходит до квадратного корня из комплексных чисел, все немного сложнее. Формула ЭйлераВо-первых, вспомните, что комплексное число может быть записано как где и и — действительные числа. Вы можете связать комплексное число с точкой на плоскости, которая имеет декартовы координаты. Комплексное число, представленное точкой на плоскости в декартовых координатах. Формула Эйлера говорит нам, что ее также можно записать как где полярные координаты точки на плоскости, связанной с . Вот расстояние от этой точки до точки и угол, образованный линией, соединяющей точку с положительной осью (измеряется против часовой стрелки). Комплексное число, представленное точкой на плоскости в полярных координатах. См. эту статью, чтобы узнать, почему это так. Это представление комплексных чисел мы будем использовать в этой статье. Причина в том, что извлечение квадратного корня из числа требует возведения этого числа в степень. Использование экспоненциального представления комплексных чисел упрощает эту задачу. Прежде чем продолжить, отметим две вещи. Во-первых, для любого положительного действительного числа и угла мы имеем Вы можете убедиться в том, что это так, заметив, что точка с полярными координатами совпадает с точкой с полярными координатами. Это потому, что угол соответствует полному обороту окружности, поэтому добавление полярного угла возвращает вас к тому, с чего вы начали. Второе, что следует отметить, это то, что мы также можем сказать, что мы подразумеваем под где положительный. мы можем думать о комплексном числе как представленном точкой на расстоянии от , с углом, измеренным по часовой стрелке, а не против часовой стрелки, в направлении от положительной -оси. Отрицательный угол можно интерпретировать как угол, измеренный по часовой стрелке от положительной оси x . Извлечение квадратного корняКогда дело доходит до квадратного корня из комплексного числа, у нас снова есть два варианта, как и для квадратных корней из действительных чисел. Первый Давайте просто проверим, работает ли это: по мере необходимости. Второй вариант: Еще раз проверим: по мере необходимости. Два квадратных корня (показаны красным) для z (показаны синим). Наши два выражения, называются двумя ветвями квадратного корня. Определение функцииНачнем с определения нашей функции извлечения квадратного корня из неотрицательной вещественной прямой. Мы определим функцию так, чтобы для действительного числа в этой неотрицательной действительной строке функция соответствовала положительному квадратному корню. Это означает, что нам нужно выбрать первую из двух ветвей выше, поэтому Давайте посмотрим, что произойдет, если мы распространим это определение на небольшой сектор комплексной плоскости, содержащий неотрицательную вещественную прямую. Приведенный ниже апплет Geogebra показывает, что с этим определением проблем нет. Это недвусмысленно, а также дает нам непрерывную функцию: когда вы используете ползунки для изменения и , вы видите, что (показано красным) постоянно изменяется по мере изменения (показано синим). Почему мы не можем одинаково определить нашу функцию на всем плане? Рассмотрим, что происходит, когда вы приближаетесь к точке отрицательной реальной линии сверху и снизу. Мы можем подойти к точке сверху, рассматривая точки с возрастанием от до . Так как наша функция стоимость приближается Чтобы подойти к нашей точке снизу, мы можем смотреть на точки с уменьшением от до . значение сейчас приближается к Следовательно, если мы определили нашу функцию как на всей комплексной плоскости, она не будет непрерывной на отрицательной действительной прямой. Когда мы приближаемся к точке на отрицательной действительной линии сверху, функция приближается к , но когда мы приближаемся снизу, функция приближается к . Вы можете увидеть это в апплете Geogebra ниже. Используйте ползунок для перемещения его в направлении (вправо) и в направлении (влево). Проблема разрыва возникает не только потому, что мы выбрали «неправильную» ветвь для определения нашей функции. аналогичным образом, он также был бы прерывистым на отрицательной действительной прямой. Таким образом, комплексный квадратный корень — это многозначная функция, которую нельзя однозначно определить на всей комплексной плоскости таким образом, чтобы сделать ее непрерывной. Новая поверхностьОднако есть хитрый трюк, который поможет нам обойти эту проблему. Идея состоит в том, чтобы создать новую поверхность, на которой можно непрерывно определить функцию для комплексного квадратного корня. Начнем с того, что возьмем две копии комплексной плоскости и разрезаем каждую вдоль отрицательной вещественной оси (такой разрез называется 9-кратным разрезом).0027 ветка срезана ). На одной копии этой разрезанной комплексной плоскости мы определяем , а с другой определяем Теперь приклеиваем верхний край среза первой копии к нижнему краю среза второй копии, и наоборот (это сложно представить, но держитесь). Чтобы проиллюстрировать это, посмотрите на точки на первой копии с . По мере приближения к верхнему краю выреза в первой копии плоскости функция приближается к Теперь посмотрите на точки на второй копии с помощью , и уменьшите по направлению к Это означает, что вы приближаетесь к нижнему краю разреза на второй копии плоскости. Поскольку на этой второй копии функция определяется как стоимость приближается по мере приближения. А поскольку верхняя кромка разреза в первой копии плоскости была приклеена к нижнему краю разреза во второй копии плоскости, функция теперь непрерывна на линии, полученной от склеивания двух края. Это иллюстрация римановой поверхности, полученной в результате разрезания и склеивания: Риманова поверхность, связанная с комплексным квадратным корнем, представленная в трех измерениях. Петля вокруг точки 0 на этой поверхности (которая находится прямо в центре) проведет вас один раз вокруг верхнего листа и один раз вокруг нижнего листа. Рисунок: Ян Хоманн. Когда вы пытаетесь создать эту поверхность в трех измерениях, вы сталкиваетесь с проблемами: как только вы приклеите верхний край среза одной копии плоскости к нижнему краю среза другой копии плоскости, два оставшихся свободных края разреза оказываются на разных сторонах поверхности, которую вы уже создали. Таким образом, единственный способ склеить эти свободные края вместе — позволить поверхности пройти сквозь себя. Комплексный квадратный корень — не единственная многозначная функция. Другой пример — комплексный логарифм, который на самом деле имеет бесконечно много значений. В этом случае ассоциированная риманова поверхность представляет собой красивую бесконечную лестницу (конечное сечение которой показано ниже). Риманова поверхность, ассоциированная с комплексным логарифмом. Рисунок: Леонид 2, CC BY-SA 3.0. Об этой статьеМарианна Фрейбергер является редактором Plus . Эта статья является частью нашего сотрудничества с Институтом математических наук имени Исаака Ньютона (INI), международным исследовательским центром и нашим соседом по математическому кампусу Кембриджского университета. INI привлекает ведущих ученых-математиков со всего мира и открыт для всех. Что такое квадратный корень из комплексного числа? (2 метода решения) — JDM EducationalМы знаем, как найти квадратный корень из действительного числа, но как насчет квадратного корня из комплексного или мнимого числа? Как оказалось, мы можем это сделать, но есть еще кое-что. Итак, что такое квадратный корень из комплексного числа? Квадратный корень из комплексного числа Z — это комплексное число S, удовлетворяющее условию Z = S 2 . Обратите внимание, что -S (отрицательное значение S) также является квадратным корнем из Z. Мы можем использовать полярную форму, чтобы найти квадратный корень из комплексного числа. Для мнимого числа bi квадратные корни равны √(b/2) + i√(b/2) и -√(b/2) – i√(b/2). Конечно, мы также можем использовать алгебру, чтобы найти квадратный корень из комплексного числа. Однако формулы могут оказаться немного сложными. В этой статье мы поговорим о том, как найти квадратный корень из комплексного числа и квадратный корень из мнимого числа, используя формулу и полярную форму. Начнем. Что такое квадратный корень из комплексного числа?Квадратный корень из комплексного числа Z — это еще одно комплексное число S, удовлетворяющее уравнению знакомы с квадратными корнями действительных чисел:
Помните, что действительное число — это комплексное число a + bi, где b = 0. есть число a + bi, где b не равно нулю). Комплексное число a + bi имеет действительную часть «a» (отложенную по горизонтальной оси Re) и мнимую часть «bi» (отложенную по вертикальной оси Im).Начнем с того, как найти квадратный корень из i, мнимой единицы. Что такое квадратный корень из i? Квадратный корень из i — это комплексное число √(1/2) + i√(1/2). Существует второй квадратный корень из i, который является отрицательным значением первого корня: -√(1/2) – i√(1/2). Вот один из способов найти квадратный корень из i с помощью алгебры. Квадратный корень из i — комплексное число, поэтому мы назовем его a + bi. По определению квадратного корня:
Теперь мы напишем два уравнения: одно для действительных частей с каждой стороны уравнения, а другое для мнимых частей на каждая часть уравнения:
Первое уравнение (действительные части) имеет разность квадратов в левой части, которая легко размножается:
 Таким образом, либо a = -b, либо a = b. Таким образом, либо a = -b, либо a = b.Мы попробуем оба этих случая во втором уравнении: Случай 1: a = -b Это не работает, так как b должно быть действительным числом. Теперь пробуем второй случай: Случай 2: a = b Поскольку a = b, у нас есть два возможных решения для квадратного корня из i: Итак, воображаемая единица i имеет два различных квадратных корня. Теперь мы можем использовать квадратный корень из i, чтобы найти квадратный корень из любого мнимого числа. Что такое квадратный корень из мнимого числа?Квадратный корень из мнимого числа bi — это комплексное число √(b/2) + i√(b/2). Существует второй квадратный корень из I, который является отрицательным значением этого первого корня: -√(b/2) – i√(b/2). Чтобы убедиться в этом, мы можем просто возвести это комплексное число в квадрат, используя FOIL, комбинируя одинаковые термины и упрощая, используя i 2 = -1: Возведя в квадрат отрицательный корень, -√(b/2) – i√(b/2), мы получим тот же результат, поскольку негативы станут положительными при возведении в квадрат. Итак, два квадратных корня мнимого числа bi равны: Как найти квадратный корень из комплексного числа (2 метода)Что, если у нас есть комплексное число a + bi, где и a, и b не равны нулю? В некоторых случаях нахождение квадратного корня немного сложнее при использовании алгебры — в этом случае нам может понадобиться использовать другой метод. Метод 1: найти квадратный корень из комплексного числа с помощью алгебры (FOIL и решить систему уравнений)Чтобы найти квадратный корень из комплексного числа c + di, мы можем использовать метод, аналогичный тому, который мы использовали раньше, чтобы найти квадратный корень i. Квадратный корень из a + bi — комплексное число, поэтому мы назовем его c + di. По определению квадратного корня: Теперь напишем два уравнения: одно для действительных частей с каждой стороны уравнения, а другое для мнимые части с каждой стороны уравнения: = [C = B/2D] = 4d 2 — D 2 = A Теперь нам нужно решить это квадратное уравнение относительно x с коэффициентами A = 4, B = 4a и C = -b 2 . Используя квадратичную формулу, мы получаем: x = -1/2(a + √(a 2 + b 2 )) и x = -1/2(a — √(a 2 + b 2 )) Поскольку x = d 2 , нам потребуется извлечь квадратный корень из каждого из этих выражений, чтобы найти d. Поскольку d — действительное число, нам нужно извлечь квадратный корень из положительного числа, т.е. x = -1/2(a – √(a 2 + b 2 )). Итак, d = √(-1/2(a – √(a 2 + b 2 )) и d = -√(-1/2(a – √(a 2 + b 2 ))). Мы также можем найти c, используя уравнение c = b/2d. Пример: Найдите квадратный корень из 4 + 3i.В этом случае у нас есть комплексное число 4 + 3i с a = 4 и b = 3. Тогда: Мы также можем найти c = Итак, квадратный корень из 4 + 3i равен c + di = 3/√2 + i√(1/2). Мы можем проверить это, возведя 3/√2 + i√(1/2) в квадрат, чтобы получить 3 + 4i. Отрицательное значение этого комплексного числа, -3/√2 – i√(1/2), также является квадратным корнем из 3 + 4i. Метод 2: нахождение квадратного корня комплексного числа с использованием полярной формы (модуль и аргумент) Чтобы найти квадратный корень из комплексного числа, гораздо проще сначала преобразовать его в полярную форму, а затем извлечь квадратный корень. Чтобы преобразовать комплексное число a + bi в полярную форму, нам нужно вычислить как модуль, так и аргумент. Модуль R (действительное число) определяется уравнением
Аргумент A (угол) определяется уравнением
Полярная форма комплексного числа A + BI составляет
13, где R. MODULULE 928.3.LULULE RA 928. a 2 + b 2 ), а A — аргумент tan -1 (b/a). Другими словами,
Примечание: помните, что a и A не обязательно являются одним и тем же числом! Получив полярную форму, мы можем найти квадратный корень. Таким образом, квадратный корень из a + bi = Re iA равен:
Отрицательное значение этого числа, -(√R)*e iA/2 , также является квадратным корнем из a + bi. Давайте рассмотрим пример того, как это работает. Пример: найти квадратный корень из 4 + 3i с помощью полярной формыДля комплексного числа 4 + 3i мы имеем a = 4 и b = 3. Модуль R равен:
The argument A is:
Тогда полярная форма комплексного числа 4 + 3i:
To take the square root, we take the square root of the modulus and half of the argument to get:
Преобразуя это обратно в комплексное число, мы получаем приблизительно 2,1213 + 0,7071i из нашего решения √(1/2). ЗаключениеТеперь вы знаете, как найти квадратный корень из мнимого числа и квадратный корень из комплексного числа. Вы также знаете, как преобразовать комплексное число в полярную форму. Вы можете узнать больше о квадратных корнях в моей статье здесь. Вы также можете узнать все о том, для чего используются квадратные корни, в моей статье здесь. Вы можете узнать, как извлекать квадратный корень вручную из моей статьи здесь. Надеюсь, эта статья была вам полезна. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию. Не забудьте подписаться на мой канал YouTube и получать обновления о новых математических видео! Подпишитесь на наш канал на YouTube! ~Джонатон Видео с вопросами: Нахождение квадратных корней комплексных чиселСтенограмма видеоОпределите набор решений уравнение 𝑧 в квадрате равно двум плюс два корня три 𝑖 в множестве комплексных числа. Чтобы решить это уравнение для 𝑧,
нам нужно найти квадратный корень из обеих частей. Теперь с правой стороны от нашего
уравнение, мы видим, что у нас есть комплексное число. Он имеет действительную часть двойки и
мнимая часть корня два из трех. Чтобы найти корни комплексных чисел,
мы знаем, что можем использовать теорему де Муавра. Теорема де Муавра для корней
утверждает, что мы можем найти 𝑛-й корень комплексного числа вида 𝑟 cos 𝜃 плюс
𝑖 sin 𝜃 вычислив 𝑟 в степени один на 𝑛 раз потому что 𝜃 плюс два 𝜋
𝑘 над 𝑛 плюс 𝑖 грех 𝜃 плюс два 𝜋𝑘 над 𝑛, где 𝑘 принимает целые значения
от нуля до 𝑛 минус один. Но тут мы замечаем, что комплекс
число в нашем уравнении записывается в прямоугольной форме, а не в полярной форме. И так набросаем комплекс
номер два плюс два корень три 𝑖 на диаграмме Аргана, чтобы помочь нам преобразовать его. Так как комплексное число имеет действительное
часть двойки и мнимую часть двойки корня три, представим ее точкой
чьи декартовы координаты равны двойке, два корня три. Мы знаем, что 𝑟 — это модуль, и
это длина отрезка, соединяющего эту точку с началом координат. Мы можем использовать формулу расстояния, чтобы
найти модуль. То есть находим квадратный корень из
сумма квадратов действительной и мнимой частей. Далее мы хотим найти
аргумент. Теперь мы знаем, что аргумент
угол, который этот отрезок образует с положительной действительной осью, измеренный в
направление против часовой стрелки. Итак, для построения комплексных чисел
в первом квадранте мы можем использовать отношение тангенсов. В данном случае сторона, противоположная
прилежащий угол 𝜃 равен двум корням из трех единиц, а сторона, примыкающая к нему, равна двум
единицы. Делим и числитель, и
знаменатель этой дроби на два. Теперь мы готовы применить De
Теорема Муавра с 𝑛 равна двум. Модуль равен четырем в степени
одна половина. Но, конечно, четыре в степени
половина — это квадратный корень из четырех, так что всего два. Общая форма аргументации
наше решение 𝜋 на три плюс два 𝜋𝑘 больше двух. Чтобы найти точные решения, мы
собираюсь заменить 𝑘 равно нулю, а 𝑘 равно единице в этом выражении. Когда 𝑘 равно нулю, мы получаем
два cos 𝜋 на три плюс ноль больше двух плюс 𝑖 грех 𝜋 на три плюс ноль больше
два. Когда мы это делаем, мы находим первый
решение нашего уравнения должно быть в два раза больше, чем 𝜋 на шесть плюс 𝑖 грех на 𝜋 на
шесть. Но потому что 𝜋 на шесть — это корень три
больше двух, а грех 𝜋 на шесть равен половине, и поэтому мы можем распределить эти
скобки. Дважды квадратный корень из трех
больше двух — это квадратный корень из трех. И два раза пополам 𝑖 просто 𝑖, и так
у нас есть первое решение нашего уравнения. Чтобы найти второй, мы собираемся
подставьте 𝑘 равно единице в общую форму. На этот раз мы получаем аргумент 𝜋
на три плюс два 𝜋 больше двух. 𝜋 на три плюс два 𝜋 становится
семь 𝜋 больше трех. И затем, когда мы разделим это на
два, мы получаем семь 𝜋 на шесть. Мы оцениваем косинус семи 𝜋 на шесть, и мы получаем отрицательный корень три над двумя. Точно так же грех семи 𝜋 на шесть отрицательная половина. Наконец, мы распределяем те скобки, и это дает нам второе решение нашего уравнения как отрицательный корень три минус 𝑖. Итак, мы использовали метод Де Муавра. теорема для решения уравнения. Запишем это в обозначении множества как показано. Итак, мы видим, что набор решений к нашему уравнению в множестве комплексных чисел есть множество, включающее в себя элементы корня три плюс 𝑖 и отрицательный корень три минус 𝑖. Какие, к черту, мнимые числа?ComplexesQuadratic Formula Purplemath До сих пор вам говорили, что вы не можете извлечь квадратный корень из отрицательного числа. Раньше каждое число было положительным после возведения его в квадрат. Таким образом, вы не могли бы извлечь квадратный корень из отрицательного значения и ожидать чего-то разумного. Содержание продолжается ниже MathHelp.comКомплексные числа Теперь, однако, вам говорят, что вы можете извлечь квадратный корень из отрицательного числа, но для этого потребуется использовать новое число. Это новое число было изобретено («обнаружено»?) во времена Реформации. В то время никто не верил, что это новое число найдет какое-либо применение в «реальном мире», кроме упрощения вычислений, связанных с решением определенных уравнений, поэтому новое число рассматривалось как притворное число, придуманное для удобства. Но— Если подумать, разве не являются изобретениями всех чисел ? Числа не растут на деревьях; они живут в наших головах. Вот и изобрели новый. Этот новый номер назывался « i », что означает «воображаемый», потому что «все знали», что i не было «настоящим». (Кстати, именно поэтому раньше нельзя было извлечь квадратный корень из отрицательного числа: можно было работать только с «настоящими» числами, т. е. с числами без «9».0027 i «.) Что такое мнимое число?Мнимое число определяется как: и привносит новую гибкость: теперь мы можем делать то, что раньше не могли, а именно, мы можем извлечь квадратный корень из −1. Но это не имеет смысла в контексте математики, которая у нас уже была — и помните, это новое число полезно только до тех пор, пока оно работает с тем, что у нас уже было.0005 Одна из причин, по которой это не сработает, заключается в том, что у нас уже есть два числа, которые возводятся в квадрат до 1; а именно -1 и +1. Во-вторых, по определению i квадратов с точностью до −1. Таким образом, просто неразумно думать, что i также будут возведены в квадрат +1. Поскольку −1 никогда не может равняться +1, приведенное выше «уравнение» не может быть верным. Но где же ошибка в этом уравнении? Мы уже делали это «переместите власть внутрь радикала», и это было нормально. Где на этот раз математика пошла не так? Произошел сбой в средней строке, где возведение в квадрат было взято из-за пределов квадратного корня внутрь. И это указывает на ограничение, связанное с мнимым числом. Что мы приобретаем/теряем с воображаемым? Имея дело с мнимыми числами, мы что-то приобретаем (способность работать с отрицательными числами внутри квадратных корней), но также и что-то теряем (гибкое и удобное правило, которое мы привыкли использовать при возведении квадратных корней в квадрат). Какой пример упрощения с мнимым числом?
Число внутри квадратного корня отрицательное. Чтобы справиться с этим, мне нужно разделить девятку и «минус», поэтому моим первым шагом в моем упрощении будет факторизация. Затем я могу перевести «минус» в его собственный квадратный корень и упростить, используя воображаемое. Моя работа выглядит так: Рекомендации по обозначениям: при переходе от второй строки к третьей преобразование будет « «, а не «». i — это снаружи, а после — символ квадратного корня; он не прыгает обратно с 9. Не делайте ошибку, закрывая это пространство между двумя квадратными корнями, чтобы воображаемое каким-то образом случайно забралось обратно внутрь квадратного корня. Давайте еще немного упростим.
Я разделю «минус» из 25, разделю один квадратный корень на два, преобразую sqrt[−1], упрощу другой квадратный корень и соберу все вместе в конце для моего ответа.
Этот квадратный корень похож на предыдущий, но есть важное отличие; а именно, 25 = 5 2 в предыдущем упражнении было полным квадратом, а 18 = (3 2 )×(2) — нет. Как с этим бороться? Я сделаю упрощение так же, как всегда делал для 18, и я выделю -1 и разберусь с ним отдельно.
Перед этим квадратным корнем стоит знак «минус». Замечу, что число внутри квадратного корня не является полным квадратом и не содержит его. С 6 упрощать нечего. Но я могу работать с этим «минусом» внутри. Итак, я разделю это на части, чтобы вывести воображаемое за пределы радикала, а ведущий «минус» снаружи будет унесен с собой. Честно говоря, единственное «упрощение» здесь было в преобразовании в воображаемую форму. Как складывать и вычитать си ?В ваших вычислениях сложения и вычитания с мнимыми числами вы будете иметь дело с i точно так же, как с x .
Если бы мне дали 2 x + 3 x , я бы просто добавил 2 и 3 и взял с собой x , чтобы получить ответ 5 x . Вместо этого мне дали выражение на букву и . Я разберусь с этим точно так же. 2 i + 3 i = (2 + 3) i = 5 i
Этот работает так же, как и предыдущий. 16 i − 5 i = (16 − 5) i = 11 i Как умножить на мнимое?Для умножения выражений, содержащих мнимую i , умножьте так же, как и для выражений, содержащих переменную, например x . Единственная разница здесь в том, что x 2 — это всего лишь x 2 , но i 2 равно −1, поэтому можно сделать большее упрощение.
Чтобы сделать это упрощение, я буду перемещать множители так, чтобы числовые части и мнимые части были сгруппированы вместе. (3 I ) (4 I ) = (3 · 4) ( I · I ) = (12) ( I 2 ) = (12) (12) (12) (12) (12) (12) (12) −1) = −12
Это умножение имеет три копии и , но это нормально. Два из них умножатся на −1, а последняя копия и будут унесены. ( I ) (2 I ) ( — 3 I ) = (2 · -3) ( I · I · I ) = (–6) ( I ) = (–6) ( i 2 · I )= ( — 6) ( — 1 · I ) = (-6) ( — I ) = 6 I в Последнем Упражнение выше, у нас было i 3 как часть выражения. В процессе упрощения это i 3 упрощенно как i 3 = − i . i 4 = i 2 · i 2 = (−1)(−1) , мы снова вернулись к 1.Эта комбинация степеней, знаков, единиц и i представляет собой цикл, как вы можете видеть ниже: i 1 = i  4 × i 4 = 1 × 1 = 1 4 × i 4 = 1 × 1 = 1Другими словами, чтобы вычислить любую большую степень i , вы можете преобразовать ее в более низкую степень, взяв ближайшее кратное 4, которое не больше чем экспонента и вычитание этого множителя из экспоненты. Например, распространенный вопрос с подвохом в тестах звучит примерно так: «Упростите i 99 », идея в том, что вы попытаетесь умножить i девяносто девять раз, и у вас не хватит времени, а преподаватели получат хороший смех за ваш счет в учительской. Вот как работает ярлык: I 99 = I 96+3 = I (4 × 24) +3 = I 3 = = I 3 = = I 3 = = I 3 = = I 3 . То есть i 99 = i 3 , потому что вы можете просто отрезать i 96 .
Мощность на единицу больше, чем четыре: 17 = 16 +; 1 = 4 × 4 +; 1. Я буду использовать это, чтобы уменьшить мощность до чего-то более разумного: i 17 = i 16 + 1 = i 4 · 4 + 1 = i 1 = i
Показатель здесь довольно большой, но я сразу вижу, что он кратен четырем: 120 = 4×30. Таким образом, деление мощности на четыре не оставляет остатка; У меня есть тридцать копий I 4 = 1. I 120 = I 4 · 30 = I 4 · 30 + 09074 = I 4 · 30 + 09074 9000 2 I 4. 300714 = I 4. 300714 = I 4. 300714 = I 4. 300714 = I 4 = I 4. 0 = 1 Хорошо; эта сила смешна. Когда я вижу что-то необычное, как это, я думаю о том, какие уловки я мог бы применить, чтобы облегчить себе жизнь. В этом случае трюк с силами приведет меня домой. i 64,002 = i 64,000 + 2 = i 4 · 16,000 + 2 = i 2 = −1 Until now, вы работали с «настоящими» числами. Теперь вы узнали, как работать с мнимыми числами. |

 Все правила по сольфеджио
Все правила по сольфеджио



 Тогда он имеет ровно n корней и его можно представить в виде
Тогда он имеет ровно n корней и его можно представить в виде

 Для $k = 0, 1, 2, \cdots , n-1$ разность любых двух значений на $n$ не разделится. Если же теперь брать $k=n, n+1, \cdots$ или $k = — 1, -2$ то значения корней $w_{k}$ будут повторяться:
Для $k = 0, 1, 2, \cdots , n-1$ разность любых двух значений на $n$ не разделится. Если же теперь брать $k=n, n+1, \cdots$ или $k = — 1, -2$ то значения корней $w_{k}$ будут повторяться:

 {\circ}) = — 3i $.
{\circ}) = — 3i $.
 Поэтому
Поэтому
 Очевидно, что задание функции комплексного переменного эквивалентно следующему: каждой паре (Е здесь принадлежит декартовой плоскости) ставится в соответствие два числа v и u. Следовательно, задание функции комплексного переменного W = f(Z) эквивалентно заданию вещественных функций u = u(x,y), v = v(x,y). При этом мы имеем f(Z) = u(x,y) + i·v(x,y).
Очевидно, что задание функции комплексного переменного эквивалентно следующему: каждой паре (Е здесь принадлежит декартовой плоскости) ставится в соответствие два числа v и u. Следовательно, задание функции комплексного переменного W = f(Z) эквивалентно заданию вещественных функций u = u(x,y), v = v(x,y). При этом мы имеем f(Z) = u(x,y) + i·v(x,y).

 е. и .
е. и . Зададим
в плоскости прямоугольную систему координат (x, y).
Зададим
в плоскости прямоугольную систему координат (x, y).  При этом модуль числа – это полярный радиус точки, а угол
— её полярный угол
или аргумент комплексного числа z .
При этом модуль числа – это полярный радиус точки, а угол
— её полярный угол
или аргумент комплексного числа z .
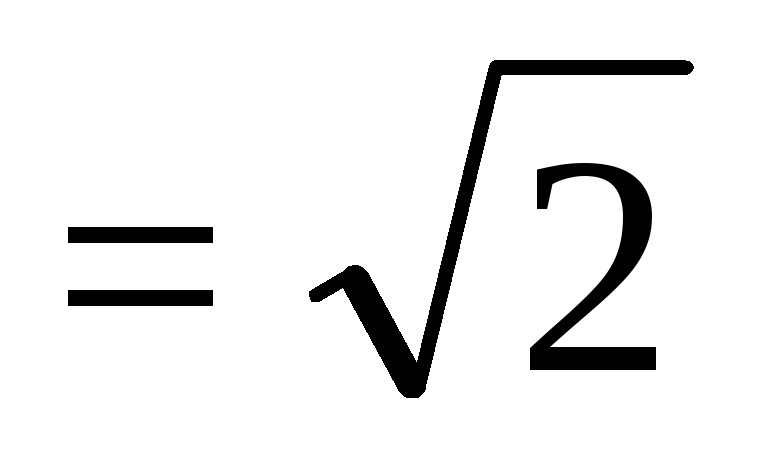 Это правило распространяется на любое число сомножителей.
В частности, при умножении комплексного числа z на i вектор z поворачивается против часовой стрелки на 90
Это правило распространяется на любое число сомножителей.
В частности, при умножении комплексного числа z на i вектор z поворачивается против часовой стрелки на 90

 Это дает два квадратных корня из $3+4i$ .
Это дает два квадратных корня из $3+4i$ . Обозначается как $a:b$.
Обозначается как $a:b$.  Итак, что вам нужно сделать с $1$, чтобы получить $2$? Вам нужно повторить этот шаг устройства дважды. Сделайте то же самое с вашим «большим шагом», $3$: когда вы сделаете два таких шага длиной $3$, вы продвинетесь на стандартные единичные шаги на $6$ дальше. И вот как $2\cdot3=6$. 9{\frac{1}{2}}$ тогда называется средним геометрическим двух крайних значений $a$ и $c$.
Итак, что вам нужно сделать с $1$, чтобы получить $2$? Вам нужно повторить этот шаг устройства дважды. Сделайте то же самое с вашим «большим шагом», $3$: когда вы сделаете два таких шага длиной $3$, вы продвинетесь на стандартные единичные шаги на $6$ дальше. И вот как $2\cdot3=6$. 9{\frac{1}{2}}$ тогда называется средним геометрическим двух крайних значений $a$ и $c$.  Что вам нужно сделать с этим $x$, чтобы вернуть свою единицу ($1$)?
Что вам нужно сделать с этим $x$, чтобы вернуть свою единицу ($1$)? Вы также можете видеть, что если бы вы не знали отрицательных чисел, вы могли бы обнаружить их с помощью геометрической прогрессии: $1$ — это его собственное среднее геометрическое, но также $-1$ — это среднее геометрическое между $1$ и $1$ (или полу- путь между ними при умножении).
Вы также можете видеть, что если бы вы не знали отрицательных чисел, вы могли бы обнаружить их с помощью геометрической прогрессии: $1$ — это его собственное среднее геометрическое, но также $-1$ — это среднее геометрическое между $1$ и $1$ (или полу- путь между ними при умножении). Затем вы можете назвать его воображаемой единицей , как его обычно называют. Проверим:
Затем вы можете назвать его воображаемой единицей , как его обычно называют. Проверим: Или, в символах:
Или, в символах: Но настоящее искусство состоит в том, чтобы давать определения, которые имеют смысл, и понимать, что за ними скрывается , означающее .
Но настоящее искусство состоит в том, чтобы давать определения, которые имеют смысл, и понимать, что за ними скрывается , означающее . Прежде чем мы начнем, давайте быстро взглянем на формулу Эйлера , которая дает нам способ записи комплексных чисел, который удобен, когда дело доходит до извлечения квадратных корней (см. эту статью для более подробной информации о формуле Эйлера).
Прежде чем мы начнем, давайте быстро взглянем на формулу Эйлера , которая дает нам способ записи комплексных чисел, который удобен, когда дело доходит до извлечения квадратных корней (см. эту статью для более подробной информации о формуле Эйлера).
 С
С
 Например, давайте определим
Например, давайте определим Так как наша функция
Так как наша функция Если бы мы решили определить функцию как
Если бы мы решили определить функцию как На полученной поверхности (называемой Риманова поверхность ) функция квадратного корня теперь определяется однозначно и непрерывно.
На полученной поверхности (называемой Риманова поверхность ) функция квадратного корня теперь определяется однозначно и непрерывно.
 Вот почему трехмерное представление этой римановой поверхности, как и приведенное выше, пересекает само себя. Чтобы получить поверхность, которая не пересекается сама с собой, вам нужно перейти в четвертое измерение.
Вот почему трехмерное представление этой римановой поверхности, как и приведенное выше, пересекает само себя. Чтобы получить поверхность, которая не пересекается сама с собой, вам нужно перейти в четвертое измерение. Посетите сайт www.newton.ac.uk, чтобы узнать больше.
Посетите сайт www.newton.ac.uk, чтобы узнать больше. 

 Обратите внимание, что любое комплексное число (кроме нуля) имеет два различных квадратных корня, отрицательных друг для друга.
Обратите внимание, что любое комплексное число (кроме нуля) имеет два различных квадратных корня, отрицательных друг для друга.
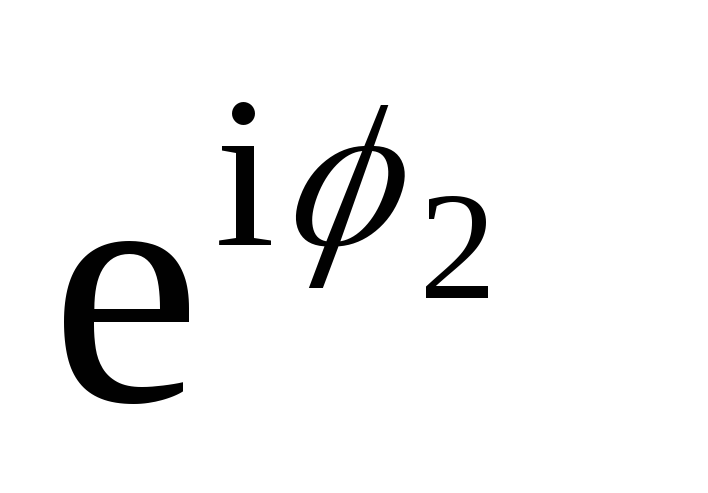 [используется определение i как квадратного корня из -1, или i 2 = -1]
[используется определение i как квадратного корня из -1, или i 2 = -1] 40713 4
40713 4 

 Мы используем половину A в качестве нашего нового угла и берем квадратный корень из модуля R в качестве нашего нового модуля.
Мы используем половину A в качестве нашего нового угла и берем квадратный корень из модуля R в качестве нашего нового модуля. 6435i
6435i 
 Теперь, в случае нашего уравнения,
мы сказали, что собираемся решить, найдя квадратный корень из обеих частей. Итак, мы позволим 𝑛 быть равным
до двух. Это означает, что 𝑘 будет равно
ноль, и он будет равен единице.
Теперь, в случае нашего уравнения,
мы сказали, что собираемся решить, найдя квадратный корень из обеих частей. Итак, мы позволим 𝑛 быть равным
до двух. Это означает, что 𝑘 будет равно
ноль, и он будет равен единице. Так что это квадратный корень из двух
квадрат плюс два корня из трех в квадрате. Два корня из трех в квадрате становятся четырьмя
умножить на три, что равно 12. Таким образом, мы получаем квадратный корень из четырех
плюс 12. Это корень 16, что, конечно,
равно четырем. Длина отрезка равна
четыре единицы, поэтому 𝑟, модуль нашего комплексного числа, равен четырем.
Так что это квадратный корень из двух
квадрат плюс два корня из трех в квадрате. Два корня из трех в квадрате становятся четырьмя
умножить на три, что равно 12. Таким образом, мы получаем квадратный корень из четырех
плюс 12. Это корень 16, что, конечно,
равно четырем. Длина отрезка равна
четыре единицы, поэтому 𝑟, модуль нашего комплексного числа, равен четырем. И мы получаем, что загар 𝜃 равен
квадратный корень из трех. Теперь, на самом деле, мы знаем это
ценность. Мы знаем этот загар 𝜋 на три
радиан равен квадратному корню из трех. Итак, аргумент 𝜃 есть 𝜋 на
три. Итак, у нас есть комплексное число.
написано в полярной форме. Это четыре потому что 𝜋 на три плюс 𝑖
грех 𝜋 на три.
И мы получаем, что загар 𝜃 равен
квадратный корень из трех. Теперь, на самом деле, мы знаем это
ценность. Мы знаем этот загар 𝜋 на три
радиан равен квадратному корню из трех. Итак, аргумент 𝜃 есть 𝜋 на
три. Итак, у нас есть комплексное число.
написано в полярной форме. Это четыре потому что 𝜋 на три плюс 𝑖
грех 𝜋 на три.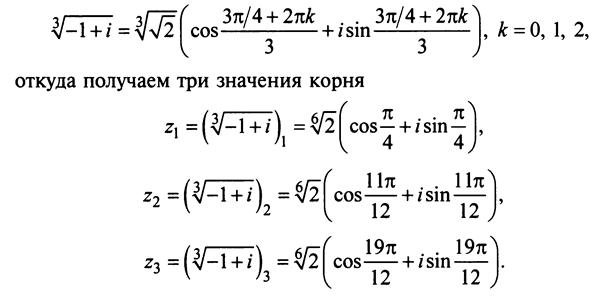 Но конечно 𝜋 на три с плюсом
ноль — это всего лишь 𝜋 на три. Итак, наш числитель равен 𝜋 на три,
и теперь нам нужно разделить это на два.
Но конечно 𝜋 на три с плюсом
ноль — это всего лишь 𝜋 на три. Итак, наш числитель равен 𝜋 на три,
и теперь нам нужно разделить это на два. Итак, у нас есть два раза, потому что
семь 𝜋 на шесть плюс 𝑖 грех семи 𝜋 на шесть.
Итак, у нас есть два раза, потому что
семь 𝜋 на шесть плюс 𝑖 грех семи 𝜋 на шесть. Это потому, что у вас не было чисел, которые были бы отрицательными после того, как вы возвели их в квадрат, поэтому вы не могли «вернуться назад» и вернуться к ним, извлекая квадратный корень.
Это потому, что у вас не было чисел, которые были бы отрицательными после того, как вы возвели их в квадрат, поэтому вы не могли «вернуться назад» и вернуться к ним, извлекая квадратный корень. Мы сделали их все вверх. Так почему же , а не изобретают новый, если он хорошо работает с тем, что у нас уже есть?
Мы сделали их все вверх. Так почему же , а не изобретают новый, если он хорошо работает с тем, что у нас уже есть? В чем смысл i , если он просто дублирует то, что у нас уже есть? Мы хотим, чтобы он делал новых вещей .
В чем смысл i , если он просто дублирует то, что у нас уже есть? Мы хотим, чтобы он делал новых вещей . В частности, при упрощении с помощью мнимого — или, что то же самое, при упрощении с квадратным корнем из −1 — МЫ ВСЕГДА ДОЛЖНЫ ДЕЛАТЬ и -ЧАСТЬ ПЕРВАЯ!
В частности, при упрощении с помощью мнимого — или, что то же самое, при упрощении с квадратным корнем из −1 — МЫ ВСЕГДА ДОЛЖНЫ ДЕЛАТЬ и -ЧАСТЬ ПЕРВАЯ! Воображаемое — это вне этого квадратного корня из девяти, и оно должно оставаться там!
Воображаемое — это вне этого квадратного корня из девяти, и оно должно оставаться там! Но, пока могу взять «минус»; через круглые скобки, я не могу сделать ничего подобного с радикалом. «Минус» снаружи радикала отличается от «минуса» внутри, и я буду иметь дело с ними отдельно.
Но, пока могу взять «минус»; через круглые скобки, я не могу сделать ничего подобного с радикалом. «Минус» снаружи радикала отличается от «минуса» внутри, и я буду иметь дело с ними отдельно.
 Любые квадраты i будут преобразованы в −1, а затем умножены на числовую часть.
Любые квадраты i будут преобразованы в −1, а затем умножены на числовую часть. Это упрощение произошло потому, что i 2 = −1. Мы можем продолжить в больших степенях i :
Это упрощение произошло потому, что i 2 = −1. Мы можем продолжить в больших степенях i : (Девяносто шесть кратно четырем, поэтому i 96 равно 1, что можно игнорировать.) Другими словами, вы можете разделить показатель степени на 4 (используя длинное деление), отбросить ответ и использовать только остаток. Это даст вам часть экспоненты, о которой вы заботитесь. Вот еще несколько примеров:
(Девяносто шесть кратно четырем, поэтому i 96 равно 1, что можно игнорировать.) Другими словами, вы можете разделить показатель степени на 4 (используя длинное деление), отбросить ответ и использовать только остаток. Это даст вам часть экспоненты, о которой вы заботитесь. Вот еще несколько примеров: Упрощение — это Doddle:
Упрощение — это Doddle: