Применение комплексных чисел
Применение комплексных чисел
Общественные науки в целом
Тезисы
Вуз: Независимое исследование (нет вуза)
ID: 5ed3f9ae1db94600015323b5
UUID: ddfe9380-859b-0138-b6a2-0242ac180003
Язык: Русский
Опубликовано: почти 3 года назад
Просмотры: 314
Find:
Highlight allMatch case
Current View
Current View
Automatic ZoomActual SizeFit PageFull Width50%75%100%125%150%200%300%400%
Enter the password to open this PDF file:
File name:
—
—
Title:
—
Author:
—
Subject:
—
Keywords:
—
Creation Date:
—
Modification Date:
—
Creator:
—
PDF Producer:
—
PDF Version:
—
Page Count:
—
Жаркевич И. М. УрГЭУ, Екатеринбург
Применение комплексных чисел.
Выражения вида a + bi, где a и b – любые действительные числа, а i – мнимая
единица, причем i2=-1, называются комплексными числами. Вещественное
число a будем называть вещественной частью комплексного числа a + bi и
обозначать Re (a + bi), а b — его мнимой частью и обозначать
Im(a +
bi). Множество комплексных чисел обозначается С. Множество
действительных чисел R входят в множество С. Понятие комплексного числа
расширяет знание о числовых системах. Комплексное число считается
заданным, если заданы его вещественная и мнимая части, т.е. заданы два
вещественных числа. Поэтому иногда в курсах алгебры комплексные числа
определяют как упорядоченные пары вещественных чисел (a, b).
Комплексные числа и функции от комплексного переменного находят свое
применение в естественных науках и технике. Многие решения
геометрических задач упрощаются, если данные задачи перенести на
комплексную плоскость. Так, многие задачи теории чисел и вещественного
математического анализа удалось решить только с помощью комплексных
чисел.
М. УрГЭУ, Екатеринбург
Применение комплексных чисел.
Выражения вида a + bi, где a и b – любые действительные числа, а i – мнимая
единица, причем i2=-1, называются комплексными числами. Вещественное
число a будем называть вещественной частью комплексного числа a + bi и
обозначать Re (a + bi), а b — его мнимой частью и обозначать
Im(a +
bi). Множество комплексных чисел обозначается С. Множество
действительных чисел R входят в множество С. Понятие комплексного числа
расширяет знание о числовых системах. Комплексное число считается
заданным, если заданы его вещественная и мнимая части, т.е. заданы два
вещественных числа. Поэтому иногда в курсах алгебры комплексные числа
определяют как упорядоченные пары вещественных чисел (a, b).
Комплексные числа и функции от комплексного переменного находят свое
применение в естественных науках и технике. Многие решения
геометрических задач упрощаются, если данные задачи перенести на
комплексную плоскость. Так, многие задачи теории чисел и вещественного
математического анализа удалось решить только с помощью комплексных
чисел.
Рецензии:
Авторизуйтесь, чтобы добавить рецензию
— у работы пока нет рецензий —
Является ли каждое действительное число комплексным числом?
Комплексное число называется суммой действительного числа и мнимого числа. Обычно он обозначается как «z» и записывается в виде a + ib, где a и b — действительные числа, а i = √(-1). Здесь «a» — это действительная часть, которая представлена как Re(z), а «ib» — это мнимая часть, которая представлена как Im(z). Некоторыми примерами комплексных чисел являются 2 + 3i, 5–7i, 3 + i√4 и т. д. Мнимое число обычно выражается либо как «i», либо как «j», значение которого равно √(-1). Следовательно, квадрат мнимого числа дает нам отрицательное значение. Квадратный корень из отрицательных чисел можно вычислить, используя комплексные числа. Некоторые приложения комплексных чисел находятся в обработке сигналов, гидродинамике, квантовой механике, электромагнетизме, анализе вибрации, а также во многих областях научных исследований.
Обычно он обозначается как «z» и записывается в виде a + ib, где a и b — действительные числа, а i = √(-1). Здесь «a» — это действительная часть, которая представлена как Re(z), а «ib» — это мнимая часть, которая представлена как Im(z). Некоторыми примерами комплексных чисел являются 2 + 3i, 5–7i, 3 + i√4 и т. д. Мнимое число обычно выражается либо как «i», либо как «j», значение которого равно √(-1). Следовательно, квадрат мнимого числа дает нам отрицательное значение. Квадратный корень из отрицательных чисел можно вычислить, используя комплексные числа. Некоторые приложения комплексных чисел находятся в обработке сигналов, гидродинамике, квантовой механике, электромагнетизме, анализе вибрации, а также во многих областях научных исследований.
Действительные числа называются объединением множества рациональных чисел и множества иррациональных чисел, т. е. положительные числа, целые числа, целые числа, рациональные числа, иррациональные числа и т. д. являются действительными числами. Некоторые примеры действительных чисел: -4, -7/11, 0, 9, √6, 3,8 и т. д.
д. являются действительными числами. Некоторые примеры действительных чисел: -4, -7/11, 0, 9, √6, 3,8 и т. д.
Число, которое дает отрицательное значение при возведении в квадрат, называется мнимым числом . Это произведение ненулевого действительного числа и мнимой единицы «i», значение которой равно √(-1). Мнимое число также можно определить как квадратный корень из отрицательных чисел. Некоторые примеры мнимых чисел: -2i, √5i, 3i и т. д.
Является ли каждое действительное число комплексным?
Ответ:
Комплексное число обычно состоит из двух частей, т. е. действительной и мнимой частей. Записывается в виде a + ib, где «a» — действительное число, а «ib» — мнимое число. Предположим, что мнимая часть равна 0. Теперь у нас будет только действительная часть числа. Таким образом, каждое действительное число является комплексным числом, если мнимая часть равна нулю. Но помните, что каждое комплексное число не является действительным числом.
Например, мы можем записать 5 как 5+0×(i).
Следовательно, Каждое действительное число является комплексным числом.
Степень i
Буква «i» представляет собой мнимую часть комплексного числа, также известного как «йота». Значение «i» равно √(-1), т. е. i 2 = -1. Йота помогает вычислить квадратный корень из отрицательных чисел. Например, √-9 = √(i 2 × 9) = +3i.
- i = √(-1)
- i 2 = -1
- i 3 = i 2 × i = -i
- i 4 = i 2 × i 2 = (-1) × (-1) = 1
3 i- i 1
- i (4n+1) = i
- i (4n+2) = -1
- i (4n+3) = -i
Графическое представление сложных чисел 7 21 Представление комплексного числа
Комплексное число формы z = a + ib может быть представлено на аргановой плоскости, рассматривая его координаты как (Re(z), Im(z)) = (a, ib). Плоскость Аргана или комплексная плоскость — это евклидова плоскость, относящаяся к комплексным числам, где действительная часть комплексного числа «а» представлена на оси X, а мнимая часть «ib» представлена на оси Y. Модуль комплексного числа (r) — это расстояние комплексного числа, представленного в виде точки на аргановой плоскости (a, ib), т. е. линейное расстояние между началом координат (0, 0) и точкой (a, ib ).
Плоскость Аргана или комплексная плоскость — это евклидова плоскость, относящаяся к комплексным числам, где действительная часть комплексного числа «а» представлена на оси X, а мнимая часть «ib» представлена на оси Y. Модуль комплексного числа (r) — это расстояние комплексного числа, представленного в виде точки на аргановой плоскости (a, ib), т. е. линейное расстояние между началом координат (0, 0) и точкой (a, ib ).
r = √(a 2 + b 2 )
Аргумент комплексного числа представляет собой угол в направлении против часовой стрелки, образованный линией, соединяющей геометрическое представление комплексного числа и начало координат , с положительной осью x.
Argz (θ) = tan −1 (b/a)
Полярная форма комплексного числа
Комплексное число также может быть представлено и идентифицировано на аргановой плоскости с использованием его полярной формы. Чтобы представить комплексное число на плоскости арганда, полярная форма использует модуль и аргумент комплексного числа. Комплексное число z = a + ib выражается как z = r(cosθ + isinθ) в его полярной форме, где r — модуль, а θ — аргумент комплексного числа. Здесь r равно √(a 2 + b 2 ), тогда как θ равно tan -1 (b/a).
Чтобы представить комплексное число на плоскости арганда, полярная форма использует модуль и аргумент комплексного числа. Комплексное число z = a + ib выражается как z = r(cosθ + isinθ) в его полярной форме, где r — модуль, а θ — аргумент комплексного числа. Здесь r равно √(a 2 + b 2 ), тогда как θ равно tan -1 (b/a).
Сопряженное комплексное число
Сопряженное комплексное число — это другое комплексное число, имеющее ту же действительную часть, что и исходное комплексное число, а величина мнимой части такая же, но с обратным знаком. Два комплексных числа называются сопряженными друг другу, если их сумма и произведение являются действительными числами.
- Сопряженным комплексным числом z = a + ib является z̅ = a − ib.
- Сумма комплексного числа и его сопряженного = z + z̅ = (a + ib) + (a − ib) = 2a
- Произведение комплексного числа и его сопряженного = z × z̅ = ( a + ib)×(a − ib)= a 2 +b 2
Обратное значение комплексного числа
При делении двух комплексных чисел используется формула обратного выражения комплексное число. Когда комплексное число делится на другое, результат равен произведению одного комплексного числа на обратную величину другого комплексного числа.
Когда комплексное число делится на другое, результат равен произведению одного комплексного числа на обратную величину другого комплексного числа.
Значение обратной величины комплексного числа z = a + ib равно
z −1 =1/(a + ib) =(a − ib)/(a 2 +b 2 )
Арифметические операции с комплексными числами
Мы можем выполнять различные арифметические операции, такие как сложение, вычитание, умножение и деление, над комплексными числами точно так же, как и над натуральными. Здесь мы должны комбинировать одинаковые члены при выполнении арифметических операций; т. е. мы должны объединить действительное число с действительным числом и мнимое число с мнимым числом.
Сложение комплексных чисел
При сложении двух комплексных чисел действительная часть добавляется к действительной части, а мнимая часть добавляется к мнимой части. Рассмотрим два комплексных числа вида z 1 = a + ib и z 2 = c + id. Теперь
Теперь
z 1 + z 2 = (a + c) + i(b + d).
Вычитание комплексных чисел
Когда комплексное число вычитается из другого, вычитание выполняется отдельно для действительных частей, а затем выполняется для мнимых частей. Рассмотрим два комплексных числа вида z 1 = a + ib и z 2 = c + id. Итак,
z 1 – z 2 = (a-c) +i(b – d)
Умножение комплексных чисел
Процесс умножения двух комплексных чисел аналогичен умножению двух комплексных чисел на два. биномы. Здесь мы используем формулу i 2 = -1. Рассмотрим два комплексных числа вида z 1 = a + ib и z 2 = c + id. Сейчас,
я 1 × z 2 = (a + ib) × (c + id) = (ac – bd) + i(ad + bc)
Деление комплексных чисел
При делении двух комплексных чисел чисел, мы используем формулу обратной комплексного числа. Рассмотрим два комплексных числа вида z 1 = a + ib и z 2 = c + id. Теперь
Рассмотрим два комплексных числа вида z 1 = a + ib и z 2 = c + id. Теперь
z 1 /z 2 = (a + ib) × 1/(c + id) = (a + ib) × (c – id)/(c 2 + d 2 )
Algebraic Identities of Complex Numbers
Following are some algebraic identities of complex numbers:
- (z 1 + z 2 ) 2 = (z 1 ) 2 + 2Z 1 Z 2 + (Z 2 ) 2
- (Z1 — Z2) 2 = (Z 1 ) 2 — 2Z 1 ) 2 — 2Z 1 2 — 2Z 1 ) 2 — 2Z 1 ) 2 — 2Z 1 ) 2 — 2Z 1 ) 2 — 2Z 1 ) 2 — 2Z 1 ) 2 ) 2
- (з 1 ) 2 — (Z 2 ) 2 = (Z 1 + Z 2 ) (Z 1 — Z 2 )
- (Z + + + + ) ) ) ) ) ) ) ) ) ) ) ) ) ) ) ).
3 = (z 1 ) 3 + 3Z 1 Z 2 (Z 1 + Z 2 ) + (Z 2 ) 9035 3 ) + (Z 2 ) 3 4 3 4 3 4 3 4 (z 2 )
3 4) + (Z 2 )
3
6 (Z
2 ). z 2 ) 3 = (z 1 ) 3 – 3z 1 z 2 (z 1 – z 2 0166) — (z 2 ) 3- (z 1 + z 2 + z 3 ) 2 = (Z 1 ) 2 + (Z 1 ) 2 + (Z 1 ) 2 + (Z 1 ) + (Z 1 ) + (Z 1 ) + (Z 1 ) (Z 1 ) (Z 1 ) ( + (z 3 ) 2 + 2z 1 z 2 + 2z 2 z 3 + 2z 3 z 1
Solved Examples on Complex Numbers
Пример 1: Упростить:
а) (3i)(2 + 5i)
б) 8i + 15i – 7i
Решение:
a) (3i) (2 + 5i)
= (3i) (2) + (3i) (5i)
= 6i + 15i 2
мы.
знаем, что i 2 = –1
= 6i + 15(–1)
(3i)(2 + 5i) = 6i – 15
б) 8i + 15i – 7i = 23i – 7i = 16i
Пример 2: Решить: (2+i)/(2-i).
Решение:
Дано: (2+i)/(2-i)
Теперь умножьте числитель и знаменатель на (2+i)
(2+i)/(2-i) × (2+i)/(2+i)
(2+i)(2– i) = (2) 2 – i 2 { Так как i 2 = –1}
= 4 –(–1) = 4+1 = 5
(2+i)/(2-i) × (2+i)/(2+i) = (2+i) 2 /5
= (2 2 + 2×2×i + i 2 )/5
= (4 + 4i –1)/5
= (3 +4i)/5
Следовательно, (2+i)/(2-i) = (3+4i)/5.
Пример 3: Определить сумму и произведение комплексных чисел z 1 = 2 + 3i и z 2 = 1 – i как комплексное число.
Решение:
Дано: z 1 = 2 + 3i
z 2 = 1 — I
Сумма:
Z 1 + Z = Z = Z = Z = Z = Z = Z = Z = Z = Z = Z =
Z 1 + Z .
3i + 1 — I
= (2 + 1) + (3i — I)
z 1 + z 2 = 3 + 2i
Продукт:
z 1 × Z 2 = (2 + 3i) × (1 – i)
= 2(1 – i) + 3i(1 – i)
= 2 – 2i + 3i – 3i 2
= 2 + i – 3(–1) {Так как i 2 = –1}
= 2 + i + 3
6z 9 × z
2 = 5 + i
Пример 4. Определите разность и частное комплексных чисел z 1 = 5 – 4i и z 2 = 3+ i как комплексное число.
Решение:
Дано: z 1 = 5 – 4i
z 2 = 3+ i
Разница:
z 1 – z 2 = 5 – 4i – (3+ i)
= (5 – 3) + (–4i – i)
z 1 2 = 2 – 5i
Деление:
z 1 /z 2 = (5 – 4i)/(3+ i)
= (5 – 4i)/(3+ i) × (3 – i)/(3 – i)
(3 + i)(3 – i) = 3 2 – i 2
= 9 – (–1) = 9 + = 10 {Поскольку, i 2 = –1}
(5 – 4i)/(3+ i) × (3 – i)/(3 – i) = [(5 – 4i)(3 – i)]/10
= (15 – 5i – 12i + 4i 2 )/10
= (15 –17i + 4(–1))/10 {Так как, i 2 = –1}
z 6 1 /z 2 = (11 – 17i)/10
Пример 5.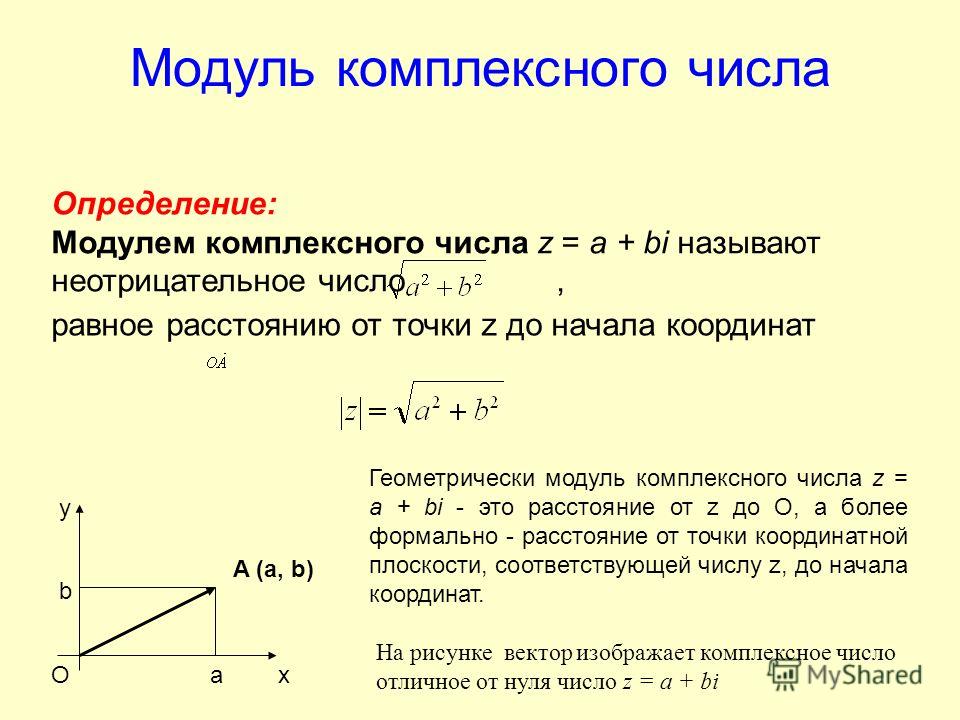 Определите модуль, сопряженное и обратное значение комплексного числа 4 + 3i.
Определите модуль, сопряженное и обратное значение комплексного числа 4 + 3i.
Решение:
Дано: z = 4 + 3i
Модуль = √(42 + 32) = √(16 + 9) = √25 = 5 – 3i
Обратная = 1/(4 + 3i) = (4 – 3i)/(4 2 +3 2 )
=(4 – 3i)/(16 + 9) = (4 – 3i)/25
Обратная величина 4 + 3i = (4 – 3i)/25
Часто задаваемые вопросы по комплексным числам
Вопрос 1: Что такое комплексное число?
Ответ:
Комплексным числом называется сумма действительного числа и мнимого числа. Обычно он обозначается как «z» и записывается в виде a + ib, где a и b — действительные числа, а i = √(-1). Здесь «a» — это действительная часть, которая представлена как Re(z), а «ib» — это мнимая часть, которая представлена как Im(z). Некоторые примеры комплексных чисел: 2 + 3i, 5–7i, 3 + i√4 и т. д.
Вопрос 2: Какова стандартная форма комплексного числа?
Ответ:
Комплексное число обычно выражается как «z» и записывается в его стандартной форме как z = a + ib.
Комплексное число в его стандартной форме состоит из двух частей: действительной части и мнимой части. Здесь «a» — это действительная часть, которая представлена как Re(z), а «ib» — это мнимая часть, которая представлена как Im(z).
Вопрос 3: Как представить комплексное число на графике?
Ответ:
Комплексное число формы z = a + ib может быть представлено на аргановой плоскости, рассматривая его координаты как (Re(z), Im(z)) = (a, ib) . Плоскость Аргана или комплексная плоскость — это евклидова плоскость, относящаяся к комплексным числам, где действительная часть комплексного числа «а» представлена на оси X, а мнимая часть «ib» представлена на оси Y.
Вопрос 4: Что понимают под модулем и аргументом в комплексных числах?
Ответ:
Модуль комплексного числа (r) — это расстояние комплексного числа, представленного в виде точки на плоскости аргана (a, ib), т.
е. линейное расстояние между началом координат (0 , 0) и точку (a, ib).
r = √(a 2 + b 2 )
Аргументом комплексного числа является угол в направлении против часовой стрелки, образованный линией, соединяющей геометрическое представление комплексного числа и начало координат, с положительная ось x.
Argz (θ) = tan −1 (b/a)
Вопрос 5. Какова полярная форма комплексного числа?
Ответ:
Комплексное число также может быть представлено и идентифицировано на аргановой плоскости с помощью его полярной формы. Чтобы представить комплексное число на плоскости арганда, полярная форма использует модуль и аргумент комплексного числа. Комплексное число z = a + ib выражается как z = r(cosθ + isinθ) в его полярной форме, где r — модуль, а θ — аргумент комплексного числа. Здесь r равно √(a 2 + b 2 ), тогда как θ равно tan -1 (b/a).
Комплексные числа | Ultimate Electronics Book
Ultimate Electronics: Практические схемы и анализ
≡ Оглавление
«
1.2
Порядки величины, логарифмические шкалы и децибелы»
1,4
Линейная и нелинейнаяМнимые и комплексные числа и их связь с кругами, синусоидами и обработкой сигналов. 14 минут чтения
В пространстве действительных чисел отрицательные числа не имеют определенного квадратного корня, потому что любое действительное число (положительное или отрицательное), умноженное само на себя, будет иметь положительное произведение.
Однако мы можем произвольно определить значение j
для представления квадратного корня из -1. Обратите внимание, что в электротехнике мы используем j
чтобы не конфликтовать с использованием буквы i
для текущего, и потому что это более отчетливо при записи.
j2=j⋅j=−1j=√−1
Теперь это «мнимое» число.
Эти мнимые числа сами по себе не имеют физического смысла: я могу съесть 3 куска пиццы, но не могу съесть 3j кусочки пиццы. Однако мы покажем, что комплексные числа образуют непротиворечивую область математики и что их тесная связь с окружностями, тригонометрией (синусами и косинусами) и синусоидами делает их мощным и удобным инструментом для отслеживания как величины, так и фазы. синусоидальной волны, когда она распространяется через любую систему.
Складывая действительные и мнимые числа, мы можем получить комплексные числа. Вместо того, чтобы изображать числовую прямую как одну линию от −∞ до +∞ , мы можем представить пространство комплексных чисел как двумерную плоскость: по оси абсцисс — действительные числа, а по оси у — мнимые. Любая точка на двумерной плоскости теперь представляет собой комплексное число: 9.1 вообще, но мы можем представить, что он там.
Мы можем определить основные операции над комплексными числами z=a+bj представляя их как двумерные векторы:
Re(z)=R(z)=R(a+bj)=aIm(z)=I(z)=I(a+bj)=bz1+z2= (a+bj)+(c+dj)=(a+c)+(b+d)jz1−z2=(a+bj)−(c+dj)=(a−c)+(b−d) j
Умножение — более сложный случай, но мы можем расширить произведение и работать почленно, чтобы получить правильный результат:
z1z2=(a+bj)(c+dj)z1z2=ac+adj+bcj+ bdj2z1z2=ac+adj+bcj+bd(−1)z1z2=(ac−bd)+(ad+bc)j
Если мы рассмотрим частный случай умножения на j :
z1j=(a+bj)jz1j=aj+bj2z1j=aj+b(−1)z1j=(−b)+aj
Интересно, что при умножении на j находим
, действительная и мнимая части z1
поменялись местами, и действительная часть тоже получает отрицательный знак.
Геометрически это соответствует повороту на 90 градусов против часовой стрелки вокруг начала координат, при условии, что мы нарисовали действительные числа по оси x и мнимые числа по оси y. Если это неясно, нарисуйте двумерную плоскость с любой точкой (a,b) помечен. Затем нанесите точку (−b,a) .
Умножение на j второй раз (т.е. умножая z1 по Дж дважды) геометрически отображает два поворота на 90 градусов, что в сумме дает поворот на 180 градусов вокруг начала координат: на −j соответствует повороту на 90 градусов по часовой стрелке. В любом направлении эта серия вращений периодична, потому что j4=(−1)2=1 .
Комплексное сопряжение ¯z комплексного числа z определяется как значение с отрицательной мнимой частью:
z=a+bj¯z=a−bjI(¯z)=−I(z)
Комплексное сопряжение важно, потому что оно умножает исходное комплексное число на чисто действительное число:
z¯z= (a+bj)(a−bj)=a2+abj−abj−b2j2=a2+(abj−abj)−b2(−1)=a2+b2
Используя определения комплексного сопряжения и умножения, мы можем определить деление комплексных чисел:
z1z2=a+bjc+djz1z2=z1z2(¯z2¯z2)z1z2=(a+bj)(c−dj)(c+dj)(c−dj)z1z2=(a +bj)(c−dj)c2+d2z1z2=(ac+bd)+(bc−ad)jc2+d2z1z2=(ac+bdc2+d2)+(bc−adc2+d2)j
Обратите внимание, что для двух чисто действительных чисел (т. е. b=0 и d=0
), это упрощается до обычного деления: z1z2=ac
. Действительные числа являются подмножеством комплексных чисел.
е. b=0 и d=0
), это упрощается до обычного деления: z1z2=ac
. Действительные числа являются подмножеством комплексных чисел.
Как упоминалось ранее, комплексные числа можно представить как часть двумерного векторного пространства или представить визуально на плоскости x-y (Re-Im). Эти графические интерпретации порождают два других геометрических свойства комплексного числа: модуль и фазовый угол.
Величина комплексного числа определяется так же, как и в трехмерных векторных пространствах, как общая длина вектора от начала координат:
|z|=√z¯z=√a2+b2
Фазовый угол определяется графически из интерпретации плоскости x-y: это угол против часовой стрелки от положительной оси x к вектору, представленному комплексным числом. Фаза положительного действительного числа равна 0 градусов, а фаза отрицательного действительного числа составляет 180 градусов или π радианы. В общем случае фаза определяется как:
ϕ(z)=tan−1Im(z)Re(z)
определение скрывает тот факт, что комплексное число с отрицательной действительной частью и отрицательной мнимой частью находится в 3-м квадранте: диапазон tan−1
есть [−π2,+π2]
это всего лишь π
радианы или 180 градусов в ширину — он покрывает только половину фазового пространства. (В компьютерном программировании функция «atan2» учитывает эти многоквадрантные проблемы и дает полный 2π
диапазон выходных данных, проверяя знак числителя и знаменателя перед продолжением. Вы должны делать то же самое при работе вручную.)
(В компьютерном программировании функция «atan2» учитывает эти многоквадрантные проблемы и дает полный 2π
диапазон выходных данных, проверяя знак числителя и знаменателя перед продолжением. Вы должны делать то же самое при работе вручную.)
Хотя ранее мы определили комплексное число в терминах декартовой двумерной плоскости с ортогональными действительными и мнимыми частями, альтернативная полярная интерпретация проста, полезна и предлагается по фазе и величине. Пока мы тщательно задаем фазовый угол с полным 2π диапазон, мы можем напрямую сопоставить любое комплексное число с декартовым представлением z=(a,b) к полярному представлению (r, θ) , где г=|z| и θ=ϕ(z) . Чтобы сопоставить между двумя представлениями взад и вперед, обратите внимание, что:
z=a+bj=(r,θ)a=rcosθb=rsinθ
Хотя некоторые операции, такие как сложение и вычитание, проще всего выполнять в декартовом представлении a+bj
, другие операции на самом деле проще в полярном представлении (r, θ)
. В частности, умножение и деление становятся довольно простыми:
В частности, умножение и деление становятся довольно простыми:
При умножении два значения радиуса (или величины) перемножаются, и два фазовых угла складываются. (В качестве упражнения вы можете доказать это себе на бумаге.)
Это полезно, потому что многие электронные системы, такие как усилители и фильтры, могут работать мультипликативно: фильтр может уменьшить входную амплитуду в 110 раз. и применить фазовую задержку -90 градусов. Отслеживая как амплитуду, так и фазу, мы можем рассматривать этот фильтр как аналог умножения входного сигнала на комплексное число zfilter=(r=110,θ=-π2)=-110j . Для краткого намека на то, что будет дальше, вот простой RC-фильтр нижних частот, который ведет себя как это комплексное число (по крайней мере, на определенной частоте, которую мы указали):
RC-фильтр нижних частот как умножение комплексных чисел
Circuitlab. y
то векторное уравнение 9y
y
то векторное уравнение 9y
описывает единичный круг на плоскости x-y.
Оказывается, существует более компактное представление комплексной плоской единичной окружности, и это невероятная часть математики, называемая формулой Эйлера:
ejθ=cosθ+jsinθ
кажутся загадочными, но они невероятно мощные. Естественная базовая константа e возведение в любое мнимое число дает комплексное число с единичной величиной и углом, изменяющимся в зависимости от параметра.
Принимая это как данность на данный момент, это позволяет нам записать комплексное число z очень просто:
z=rejθ
Любое комплексное число можно записать в такой форме, где r и θ — действительные числа, определяющие величину и фазу комплексного числа.
Важно отметить, что из этого определения очень легко работать с правилами умножения и деления комплексных чисел. Поскольку для любых показателей eAeB=e(A+B) и eAeB=e(A−B) :
z1z2=(r1ejθ1)(r2ejθ2)=(r1r2)ej(θ1+θ2)z1z2=r1ejθ1r2ejθ2=r1r2ej(θ1−θ2)
Разумно спросить, что вообще означает возведение числа в мнимое число. Возведение в степень любого основания bn
достаточно ясно, когда n
является положительным целым числом: умножение b
сам по себе н
раз. Когда н
не целое число, это странно: n=12
подразумевает, например, квадратный корень. Но любое возведение в степень можно преобразовать в единицу по основанию e.
, основание натурального логарифма:
Возведение в степень любого основания bn
достаточно ясно, когда n
является положительным целым числом: умножение b
сам по себе н
раз. Когда н
не целое число, это странно: n=12
подразумевает, например, квадратный корень. Но любое возведение в степень можно преобразовать в единицу по основанию e.
, основание натурального логарифма:
ey=bnln(ey)=ln(bn)y=nlnbe(nlnb)=bn
натуральный логарифм. Но чтобы компьютер вычислил любую (нецелую) экспоненту или любой натуральный логарифм, нам нужно найти способ выразить эти операции в терминах базовой арифметики: сложения, умножения, деления и т. д. К счастью, у нас есть то, что называется операцией Тейлора. расширение серии бывших :
ex=1+x+x22!+x33!+x44!+x55!+x66!+x77!+⋯=∞∑n=0xnn!
Это бесконечно длинный ряд, но каждый член представляет собой просто полиномиальный член от x
: достаточно легко вычислить, умножив x
сам по себе целое число раз напрямую. Члены в конечном итоге становятся все меньше и меньше по направлению к 0, потому что факториальная функция в знаменателе растет быстрее, чем полином в числителе, поэтому бесконечный ряд сходится к конечному значению для всех входных данных.
Другие функции, такие как sin(x) и кос(х) также имеют разложения в ряд Тейлора в виде полиномов:
cos(x)=1−x22!+x44!−x66!+…=∞∑n=0,2,4,6,8,… (только четное n)(−1)n2xnn!sin(x) =x−x33!+x55!−x77!+…=∞∑n=1,3,5,7,9,… (только нечетное n)(−1)(n−1)2xnn!
При сравнении ряда Тейлора для cos(x) и грех (х) с этим для бывшего выше вы можете видеть, что происходит кое-что интересное: все бывшие члены с четными степенями xn (в т.ч. n=0 ) содержатся в ряду для cos(x) , и все члены нечетной степени содержатся в ряду для sin(x) – за исключением схемы чередующихся знаков минус!
Теперь давайте посмотрим на единичное мнимое число j=√−1 и посмотрим, что произойдет, если его возвести в n-ю степень:
1=j0=j4=j8=j12=…√−1=j1=j5=j9=j13=…−1=j2=j6=j10=j14 =…−√−1=j3=j7=j11=j15=…
Идея о том, что умножение на j это как поворот на 90 градусов против часовой стрелки в реально-воображаемой плоскости. После четырех оборотов мы вернулись к тому, с чего начали.
Теперь посмотрите только на первую и третью строки, перечисленные здесь:
jn=+1для n=0,4,8,12,… jn=−1для n=2,6,10,14,…
Если вы посмотрите на разложение в ряд Тейлора для cos(x)
, оно имеет (−1)n2
в каждом члене, который точно отображается в эту последовательность для всех четных значений n
. Просто сравнивая значения для четных значений n
, мы можем написать:
Просто сравнивая значения для четных значений n
, мы можем написать:
(−1)n2=jnдля n=0,2,4,6,8,…
Конечно, мы могли бы также заметить, что
(−1)n2=((−1) 12)n=(√−1)n=jn
напрямую, но более конкретно видеть соответствие значений внутри каждого термина.
Для нечетных членов мы находим что-то подобное:
jn=+jдля n=1,5,9,13,…jn=−jдля n=3,7,11,15,…
Если вы посмотрите на разложение в ряд Тейлора для sin(x) , оно имеет (−1)(n−1)2 в каждом сроке. Это дает нам правильную последовательность положительных и отрицательных инверсий, но пропускает j . (Этот недостающий множитель j все в порядке — мы просто умножим на j
(−1)(n−1)2=j(n−1)for n=1,3,5,7,9,…
Итак, наконец, давайте соберем все заново. Вот ряд для cos(θ) :
cos(θ)=∞∑n=0,2,4,6,8,… (только четное n)(−1)n2θnn!cos(θ)=∞∑n=0,2,4,6 ,8,… (только четное n)jnθnn!cos(θ)=∞∑n=0,2,4,6,8,… (только четное n)(jθ)nn!cos(θ)=1−θ22! +θ44!−θ66!+…
А вот ряд для jsin(θ) (мы просто умножили каждый член на j чтобы исправить «недостающее» мнимое значение из приведенной выше последовательности):
jsin(θ)=∞∑n=1,3,5,7,9,… (только нечетное n)j(−1)(n−1 )2θnn!jsin(θ)=∞∑n=1,3,5,7,9,… (только нечетные n)j⋅jn−1θnn!jsin(θ)=∞∑n=1,3,5,7 ,9,… (только нечетные n)jnθnn!jsin(θ)=∞∑n=1,3,5,7,9,… (только нечетные n)(jθ)nn!jsin(θ)=jθ−jθ33! +jθ55!−jθ77!+…
И ряд для ejθ будет действовать аналогично:
ejθ=∞∑n=0(jθ)nn!ejθ=1+jθ+(jθ)22!+(jθ)33!+(jθ)44!+(jθ)55!+(jθ )66!+(jθ)77!+…ejθ=1+jθ−θ22!−jθ33!+θ44!+jθ55!−θ66!−jθ77!+…
Итак, когда мы объединяем cos(θ) (при четных условиях) и jsin(θ) (учитывая нечетные члены), мы точно находим:
ejθ=cos(θ)+jsin(θ)
Это известно как формула Эйлера.
Иногда это оценивается в одной точке θ=π и записывается как:
ejπ+1=0
Это известно как тождество Эйлера, и теперь, надеюсь, вы понимаете, откуда оно взялось: это всего лишь частный случай формулы Эйлера.
Как упоминалось ранее, комплексные числа могут использоваться для представления величины и фазы синусоиды. Эти два значения — амплитуда и фаза — все, что нужно для определения любой синусоиды.
Вспоминая наш предыдущий пример:
RC-фильтр нижних частот как умножение комплексных чисел
Circuitlab.com/c2hz4cg6g2e62
Править — Имитация
На определенной частоте в этом примере фильтр может представлять собой (приблизительно) умножение величины входной синусоидальной волны на 0,1 и (приблизительно) изменение фазы на -90 градусов. (Мы говорим «приблизительно», потому что округлили до хороших значений. Мы обсудим, как анализировать и спроектировать такие фильтры, в следующих главах, но сейчас просто примите как данность, что эта конструкция делает примерно то же самое. .)
.)
Если мы посмотрим на это чисто во временной области, для нашей единственной частоты f=1000Hz , мы могли бы рассмотреть наш ввод x(t) и выход y(t) :
x(t)=sin(2π⋅1000t)y(t)≈110sin(2π⋅1000t−π2)
Это простой линейный фильтр: если мы удвоим величину x(t) , величина y(t) также удваивается. Если мы изменим фазу входа на 20 градусов, мы также изменим фазу выхода на 20 градусов. Тем не менее, как это ни удивительно, было бы очень сложно написать одну общую алгебраическую формулу, описывающую передаточную функцию фильтра y(t)x(t) . Амплитудную часть можно легко вынести за скобки, но фазовая часть заключена в некоторых синусоидальных выражениях.
Вместо этого мы можем думать о наших входных и выходных сигналах как о векторах. Это означает, что вместо обработки x(t)
как функцию времени, мы просто рассматриваем его как одно комплексное число X
который представляет собой синусоиду на нашей конкретной частоте. Величина и фаза X
представляют синусоиду. Точно так же наш вывод — это просто одно комплексное число Y
. Преимущество этого в том, что теперь мы можем очень компактно представить весь наш фильтр (на этой частоте):
Преимущество этого в том, что теперь мы можем очень компактно представить весь наш фильтр (на этой частоте):
Y=(110e−jπ2)⋅X
Здесь мы делаем два больших предположения, чтобы работать с этими комплексными числами, называемыми векторами:
Во-первых, мы предполагаем, что ввод синусоидальной волны означает, что мы получим что-то похожее на синусоидальную волну. (Позже мы покажем, что это всегда верно для линейных систем, не зависящих от времени (LTI), но предположим, что это верно на данный момент.)
Во-вторых, мы предполагаем, что работаем только на одной конкретной частоте (для сейчас) – или, что то же самое, мы предполагаем, что если мы подадим только синусоидальный сигнал на частоте f , мы получим синусоидальный сигнал только при f вне. (Опять же, мы покажем, что это верно для систем LTI. Кроме того, в будущем мы рассмотрим, как комбинировать разные синусоиды на разных частотах — ключевое понимание преобразований Лапласа и Фурье и частотной области.)
Пока нас устраивают эти предположения, теперь мы можем перемещаться между двумя нашими представлениями.
Предположим, что наш входной сигнал равен x(t)=5cos(2π⋅1000t) : мы можем представить это вектором величины 5 и фазы 0, или
X=5ej0=5
Мы можем применить наш фильтр (110e−jπ2) чтобы найти вектор для нашего выхода:
Y=(110e−jπ2)⋅X=(110e−jπ2)⋅(5ej0)=0,5ej(−π2+0)=0,5e−jπ2
Как вернуться назад и далее от векторного представления к представлению во временной области?
Во-первых, обратите внимание, что мы можем записать частоту f = 1000 Гц. как угловая частота, часто обозначаемая греческим символом ω=2πf , поэтому для этого примера ω=2π⋅1000 . Мы делаем это только потому, что писать 2πf становится утомительно. повсюду!
Теперь, чтобы перейти от вектора X=5ej0 к функции x(t) , мы просто умножаем X от ejωt а затем взять действительную часть результата:
ejθ=cos(θ)+jsin(θ)ejωt=cos(ωt)+jsin(ωt)
Это комплексное значение ejωt
наша базовая комплексная синусоида. Обратите внимание, что он отслеживает как косинус, так и синус одной и той же частоты в его действительной и мнимой частях соответственно. Когда мы берем действительную часть R(5ej0ejωt)
находим:
Когда мы берем действительную часть R(5ej0ejωt)
находим:
x(t)=R(X⋅ejωt)=R(5(cos(ωt)+jsin(ωt)))=R(5cos(ωt)+j5sin(ωt))=5cos(ωt)
Это был особенно простым примером, потому что X был чисто реальным. А теперь найдем y(t) из нашего комплексного вектора Y:
y(t)=R(Y⋅ejωt)=R(0,5e−jπ2(cos(ωt)+jsin(ωt))=R(0,5(−j)(cos(ωt )+jsin(ωt)))=R(0,5(−j)cos(ωt)+j0,5(−j)sin(ωt))=R(−j0,5cos(ωt)+0,5sin(ωt)) =0,5sin(ωt)
В этом случае Y было чисто мнимым, и мы находим, что y(t) чисто имеет sin(ωt) срок. Однако в общем случае, если Y имеет ненулевые вещественные и мнимые части, то временная область y(t)=R(Y⋅ejωt) будет иметь как косинус, так и синус.
Обратите внимание, что всегда можно написать линейную комбинацию cos(x) и грех (х) как только cos(x+θ) для некоторого фазового угла θ . В простых 90-градусных случаях у нас может быть простое выражение, такое как:
sin(x)=cos(x−π2)cos(x)=sin(x+π2)
В более сложных случаях для промежуточных значений помните, что:
f(t)=R(ejθejωt)=R(ejθ+jωt)=R(ej(θ+ωt))=R(cos(θ+ωt)+jsin(θ+ωt))=cos (θ+ωt)
Таким образом, для нашего примера выше мы могли бы написать:
y(t)=0,5cos(ωt−π2)
Здесь мы показали, что, хотя очень сложно написать общую алгебраическую функцию для этого простого фильтра, который преобразует нашу входную синусоиду x(t)
непосредственно в выходную синусоиду y(t)
, это на самом деле довольно просто, если мы думаем о входе и выходе как о векторах с комплексными значениями, представляющих величину и фазу соответствующей синусоиды. Затем применение фильтра превращается в простое умножение на комплексное число, что очень просто. И мы можем вернуться от нашего сложного фазора Y
к нашему сигналу во временной области y(t)
путем умножения на нашу комплексную синусоиду ejωt
а затем, наконец, принимая настоящую роль.
Затем применение фильтра превращается в простое умножение на комплексное число, что очень просто. И мы можем вернуться от нашего сложного фазора Y
к нашему сигналу во временной области y(t)
путем умножения на нашу комплексную синусоиду ejωt
а затем, наконец, принимая настоящую роль.
- Запись входной синусоиды x(t) как комплексное число X с амплитудой и фазой, соответствующими входной синусоиде.
- Умножить Х комплексным числом, представляющим эффект фильтра на этой конкретной частоте. Величины будут умножаться, а фазы добавляться, чтобы получить новое комплексное число Y. .
- Преобразование комплексного вектора Y обратно в сигнал временной области y(t) путем умножения Y⋅ejωt а затем взять реальную часть:
y(t)=R(Yejωt)
В следующем разделе, «Линейное и нелинейное», мы переключим передачу и поговорим о линейности и о том, почему она так полезна для понимания и проектирования систем всех видов.
≡ Оглавление
«
1.


 3 = (z 1 ) 3 + 3Z 1 Z 2 (Z 1 + Z 2 ) + (Z 2 ) 9035 3 ) + (Z 2 ) 3 4 3 4 3 4 3 4 (z 2 )
3 = (z 1 ) 3 + 3Z 1 Z 2 (Z 1 + Z 2 ) + (Z 2 ) 9035 3 ) + (Z 2 ) 3 4 3 4 3 4 3 4 (z 2 )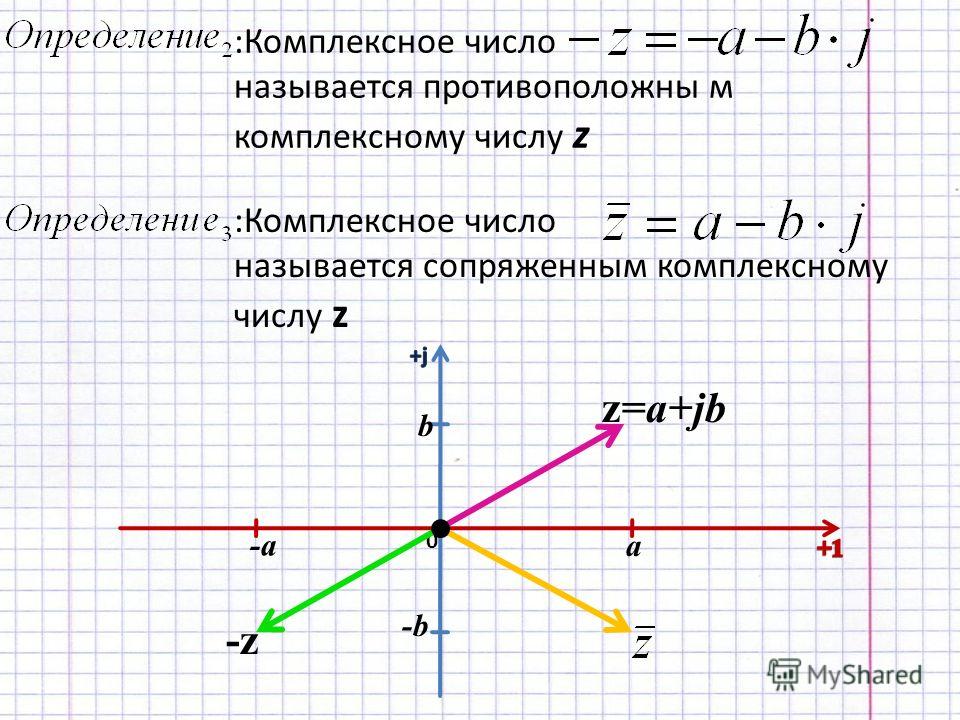 знаем, что i 2 = –1
знаем, что i 2 = –1 3i + 1 — I
3i + 1 — I Комплексное число в его стандартной форме состоит из двух частей: действительной части и мнимой части. Здесь «a» — это действительная часть, которая представлена как Re(z), а «ib» — это мнимая часть, которая представлена как Im(z).
Комплексное число в его стандартной форме состоит из двух частей: действительной части и мнимой части. Здесь «a» — это действительная часть, которая представлена как Re(z), а «ib» — это мнимая часть, которая представлена как Im(z). е. линейное расстояние между началом координат (0 , 0) и точку (a, ib).
е. линейное расстояние между началом координат (0 , 0) и точку (a, ib).