Координатные плоскости: Точки на координатной плоскости | PHP: Абстракция с помощью данных

Координатная плоскость

В повседневной жизни вы могли слышать такую фразу: «Оставьте мне ваши координаты!».

Как вы понимаете эту фразу?

Это выражение означает, что собеседник должен оставить свой адрес или номер телефона, т.е. данные, по которым его можно найти.

Определение

Числа, с помощью которых указывают, где находится некоторый объект, называют его координатами.

С координатами вы уже не раз встречались и в математике. Вы умеете выполнять две операции: отмечать на координатной прямой точку с заданной координатой и, наоборот, определять координату заданной точки. Для этого на прямой выбирают начало отсчёта, положительное направление и единичный отрезок. После этого любая точка прямой получает свою собственную координату. 

Координата точки указывает, таким образом, её место на координатной прямой.

Возникает вопрос: а можно ли определить местоположение точки на плоскости

?

Наверняка, хоть раз в жизни вы играли в такую игру как «Морской бой».

Поле этой игры состоит из квадрата размерами 10 на 10 клеточек. В этом поле изображаются корабли: 1 четырёхклеточный, 2 трёхклеточных, 3 двухклеточных и 4 одноклеточных. При этом между любыми двумя соседними кораблями должен оставаться промежуток не меньше одной клетки.

На экране изображён один из вариантов расположения кораблей. Каждая клеточка квадрата обозначается парой: (буква –число), указанных вдоль нижней и левой сторон квадрата. Например, корабль расположен в клетке (Ж; 4). Суть этой игры найти все корабли соперника первым. При обозначении положения клетки первой указывают её горизонтальную координату, а второй – вертикальную.

Именно в этом и состоит суть координат или, как обычно говорят, системы координат: это правило, по которому определяется положение того или иного объекта.

Системы координат встречаются в нашей жизни постоянно.

Вы знакомы с системой координат в зрительном зале кинотеатра (номер ряда и номер места), в поезде (номер вагона и номер места), с системой географических координат (долгота и широта).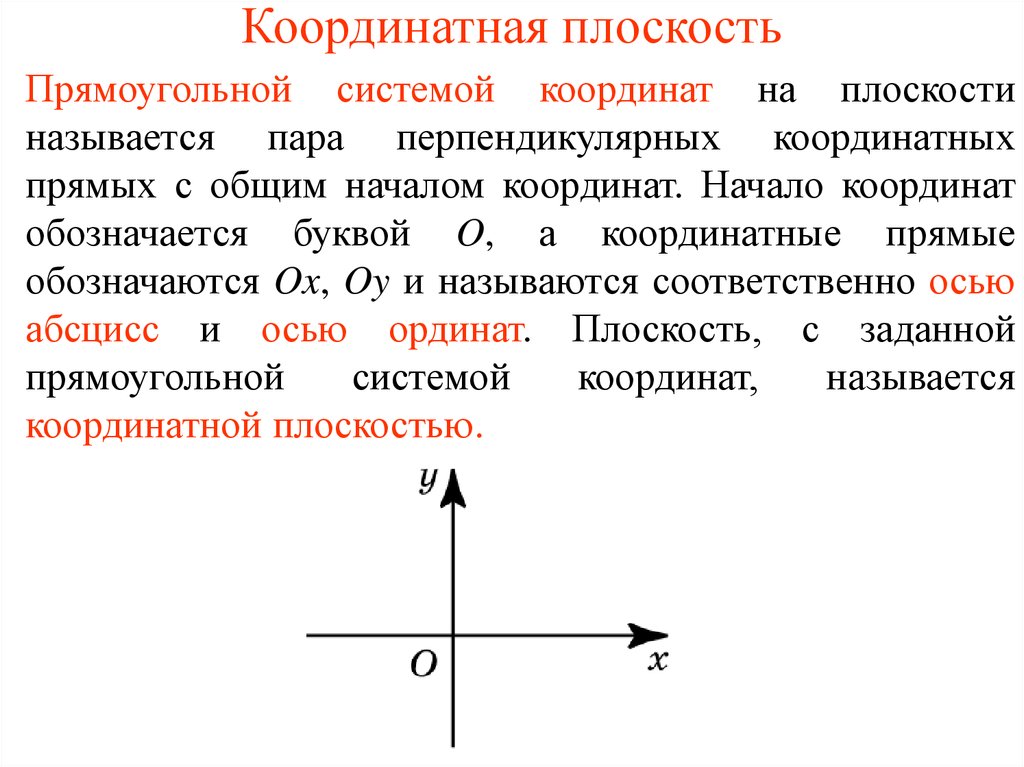

Что нужно знать для того, чтобы найти своё место в кинотеатре? Места в зрительном зале кинотеатра задают двумя числами: первым числом обозначают номер ряда, а вторым – номер кресла в этом ряду. Значит, чтобы правильно занять своё место в зрительном зале необходимо знать две координаты: ряд и место.

Например, в билете указаны: 3 ряд 2 место. Посмотрите где это место расположено.

Обратите внимание, что при определении местоположения нам необходимо знать

две характеристики или два значения.

Подобным образом можно обозначить и положение точки на плоскости.

Рене Декарт –  французский математик ввёл в 1637 году систему координат, которая используется во всем мире и известна каждому школьнику. Её называют также «Декартова система координат».

Чтобы задать декартову прямоугольную систему координат на плоскости проводят две взаимно перпендикулярные координатные прямые х и у, называемые координатными осями.

Точка пересечения осей – «O» называется началом координат.

На каждой оси ОX и ОY задаётся положительное направление и выбирается единичный отрезок.

Каждая из координатных осей имеет своё название: горизонтальную ось называют

осью абсцисс (или осью х), вертикальную ось называют осью ординат (или осью у). Эти прямые составляют систему координат на плоскости.

Определение

Плоскость, на которой задана система координат, называется координатной плоскостью.

Оси разбивают координатную плоскость на четыре части, которые называют координатными четвертями. Их нумеруют римскими цифрами и против часовой стрелки.

Говорят: первая четверть, вторая четверть, третья четверть и четвертая четверть.

Каждая точка такой плоскости имеет две координаты.

Рассмотрим, как определяется положение точки на координатной плоскости.

Например, у нас есть точка М. И нужно определить её координаты. Для этого проведём перпендикуляр из этой точки на горизонтальную ось или ось абсцисс.

Точка пересечения с осью х называется абсциссой точки М.

В нашем случае, абсцисса точки М 3.

Далее, из этой же точки проведём перпендикуляр до пересечения с вертикальной осью, или осью ординат.

Точка пересечения с осью у называется ординатой точки М.

В нашем случае, ордината точки М 5.

Абсцисса и ордината точки М называются координатами этой точки. Их принято записывать рядом с буквой, обозначающей точку, в круглых скобках. Причем, на первом месте всегда пишется абсцисса, а на втором – ордината.

Читают эту запись так: «точка М с абсциссой 3 и ординатой 5», или «точка М с координатами 3 и 5».

Обратите внимание, если переставить координаты местами, то получится совсем другая точка. Например, точка N (5; 3).

Определение

Координаты точки (х;у) на плоскости – это пара чисел, в которой на первом месте стоит абсцисса (х), а на втором – ордината (у) этой точки.

Сделаем вывод: координаты можно указать для любой точки координатной плоскости: для этого надо из точки провести перпендикуляры на координатные оси и определить, какому числу координатной оси  соответствует основание перпендикуляра.

Точки любой прямой, перпендикулярной оси абсцисс, имеют одну и ту же абсциссу.

Например, все точки прямой а имеют абсциссу 4. Все точки оси ординат имеют абсциссу 0, т.е. координаты любой точки оси ординат имеют вид (0; у).

Точки любой прямой, перпендикулярной оси ординат, имеют одну и ту же ординату

.

Например, все точки прямой b имеют ординату -3. Все точки оси абсцисс имеют ординату 0, т.е. координаты любой точки оси абсцисс имеют вид (х; 0).

Начало координат – точка О – лежит и на оси абсцисс, и на оси ординат. Значит, её координаты (0; 0).

Построить точку по её координатам можно несколькими способами.

Например, построим точку А (-5; 7).

Первый способ: на оси х находим  абсциссу точки А. Она у нас равна -5. Проводим перпендикуляр из этой точки относительно оси ОХ. Далее, на оси у, найдём ординату точки. Она равна 7. Проводим перпендикуляр из этой точки относительно оси ОУ. Точка, где пересеклись оба перпендикуляра, и есть искомая точка А.

Второй способ построения точки по заданным координатам. Можно сместиться по оси

ОХ влево на 5 единиц, т.к. абсцисса точки – отрицательное число. А затем, параллельно оси ОX  вверх на 7 единиц, т.к. ордината точки положительное число.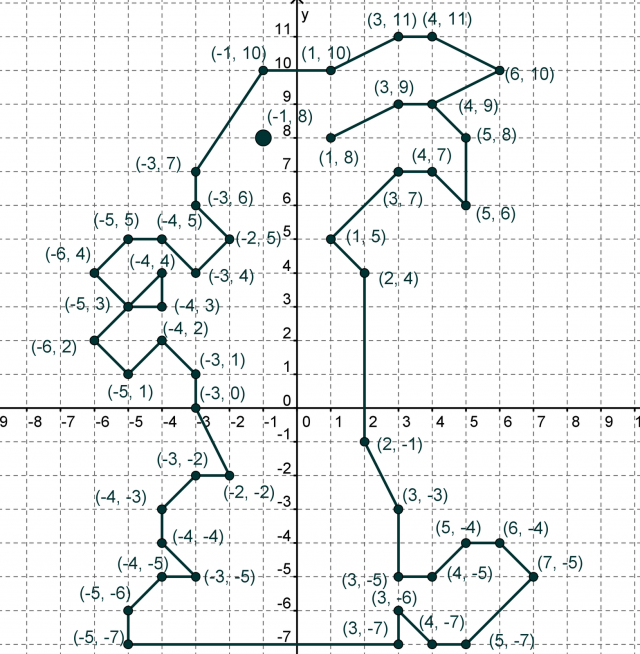 Точка, где пересеклись оба перпендикуляра, и есть искомая точка А.

Сделаем ещё один очень важный вывод:

Каждой точке на координатной плоскости соответствует пара чисел: её абсцисса и ордината. Наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.

Задание

Построите на координатной плоскости точки, а затем последовательно соедините их отрезками.

Какая фигура у нас получилась в итоге? Правильно! Это котик!!!

Координатная плоскость с координатами (6 класс, математика)

4.4

Средняя оценка: 4.4

Всего получено оценок: 186.

4.4

Средняя оценка: 4.4

Всего получено оценок: 186.

Координатная плоскость – это основа многих достижений человечества. Системы навигации, оптические прицелы, радиолокаторы: все это основано на плоских системах координат. Поговорим подробнее о данной теме в рамках курса математики за 6 класс.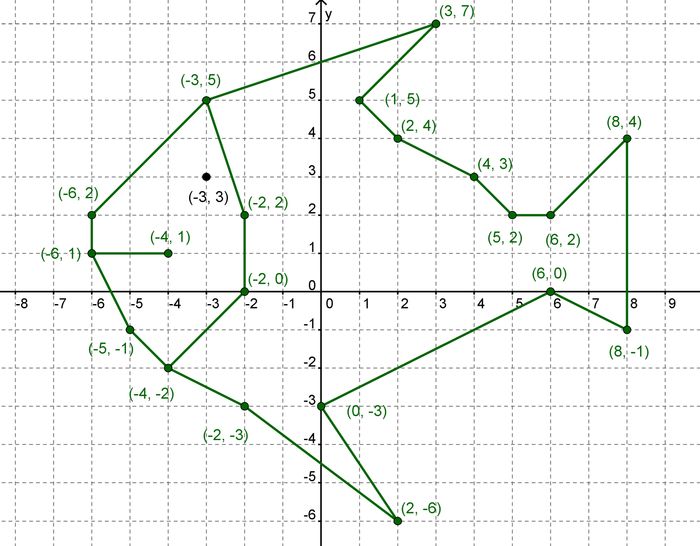

Виды координатных плоскостей.

Многие не знают, что существует два вида координатных плоскостей. Это декартова система координат и полярная система координат.

Первая это всем привычная координатная сетка с двумя координатными осями. Именно такие сетки наносят на оптические прицелы. В этой системе положение точки на плоскости определяется двумя значениями координат.

Рис. 1. Декартова система координат.

Существует и альтернатива: полярная система координат. В этой системе положение точки определяется значением координатной прямой и высотой подъема точки над этой прямой, которая задается углом.

Рис. 2. Полярная система координат.

Этой системой пользовались древние мореплаватели задолго до изобретения более удобной декартовой системы. Но до сих пор полярная система координат имеет свои области применения.

Оси координатной плоскости

Осями координатной плоскости называют две перпендикулярные прямые, на которых отмечаются единичные отрезки начало координат.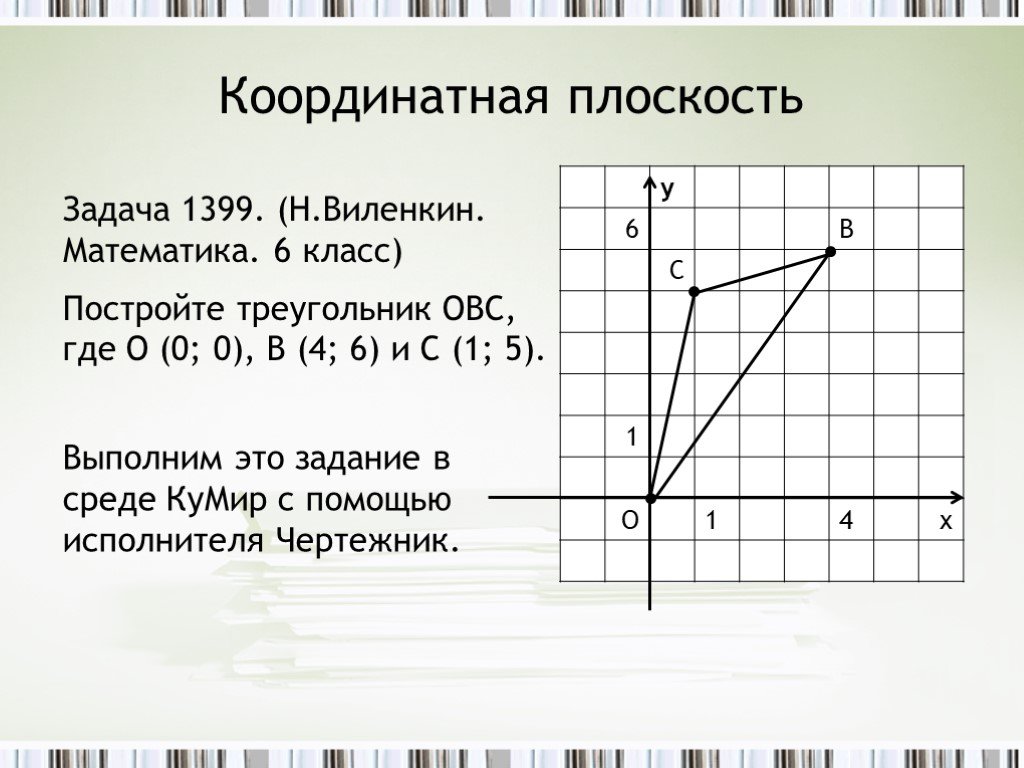 Началом координат и центром системы служит точка пересечения двух прямых.

Единичные отрезки осей могут не совпадать. Так за 1 по оси х может быть принять 1 см, а по оси у 10. Это вполне распространенная практика, которая применяется для более наглядного изображения рисунков, чертежей и графиков в координатной плоскости.

Оси координат традиционно обозначают х и у и называют соответственно осями абсцисс и ординат.

Рис. 3. Декартова система координат в пространстве.

В пространстве используется схожая система координат, только добавляется еще одна координатная ось z.

Определение координат

Для того чтобы определить координаты точки, опускают перпендикуляр на каждую из осей. Получаются два отрезка. Значение длин этих отрезков в заданных единицах длины и будет соответствовать координатам точки.

Соответственно, чтобы по координатам построить точку, нужно провести перпендикуляр из заданных точек на осях. В точке пересечения этих перпендикуляров и будет находиться искомая точка.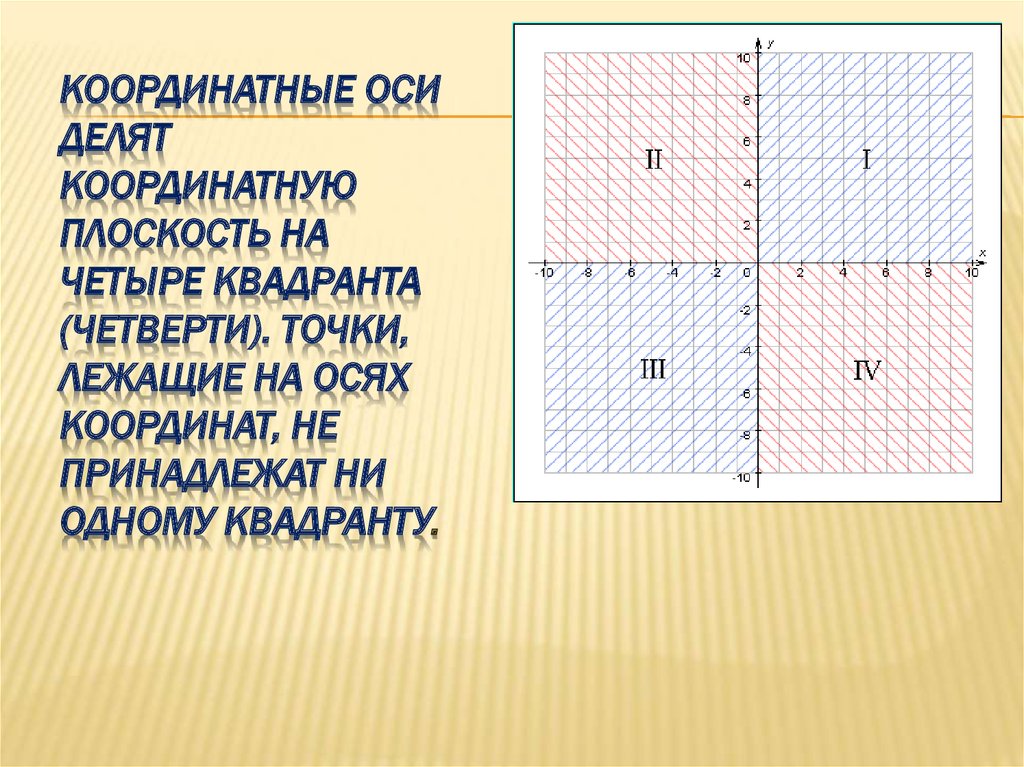

У координатной плоскости есть 4 четверти, в каждой из которых свои границы х и у. Будьте внимательны, координаты вполне могут быть отрицательными. Это всего лишь позволяет определить четверть координатной плоскости.

Что мы узнали?

Мы узнали, что такое координатная плоскость с координатами. Выделили элементы и квадраты координатной плоскости и поговорили о том, какие системы координат существуют. Рассказали о способе определения координат и построения точки по координатам. Выделили несколько нюансов построения координатной плоскости.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Вова Коваленко

  5/5

• Иван Костиков

  4/5

Оценка статьи

4.4

Средняя оценка: 4.4

Всего получено оценок: 186.

---

А какая ваша оценка?

Объяснение урока: Координатные плоскости | Nagwa

В этом объяснителе мы узнаем, как определять различные типы координатных плоскостей и координаты точки и места. точки на плоскости.

Координатные плоскости особенно полезны для определения местоположения объектов по их координатам. На Земле мы обычно используем географические система координат (GCS) на основе широты и долготы. В геометрии мы обычно используем координатную плоскость, где оси перпендикулярны, а расстояния равны. В этом объяснении мы подробнее рассмотрим эту знакомую координатную плоскость, а также несколько альтернативных координатных плоскостей.

Сначала определим координатную плоскость в общих чертах.

Определение: Координатная плоскость

Координатная плоскость образована любыми тремя неколлинеарными точками (𝑂;𝐼,𝐽), где 𝑂 начало координат, линия ⃖⃗𝑂𝐼 является осью 𝑥 с положительным направление в направлении 𝑂𝐼, и линия ⃖⃗𝑂𝐽 это 𝑦-ось с положительным направлением в сторону 𝑂𝐽. Длина отрезка 𝑂𝐼 — это единица длины 𝑥-ось, а 𝑂𝐽 — единичная длина 𝑦-оси.

Из этого определения мы видим, что ортонормированная координатная плоскость является специальной координатной плоскостью, поскольку мы имеем ⃖⃗𝑂𝐼⟂⃖⃗𝑂𝐽 и 𝑂𝐼=𝑂𝐽.

Возьмем три случайные неколлинеарные точки 𝑂, 𝐼 и 𝐽, расположенные в космосе, как показано.

Если мы хотим использовать их для формирования координатной плоскости (𝑂;𝐼,𝐽), нам нужно нарисовать линии ⃖⃗𝑂𝐼 и ⃖⃗𝑂𝐽 для формирования 𝑥- и 𝑦-осей и создайте сетку с линиями, параллельными обеим осям и разнесенными на единичные длины, определенные 𝑂𝐼 и 𝑂𝐽.

Мы можем заметить, что эта координатная плоскость не является ортонормированной, поскольку ⃖⃗𝑂𝐼 и ⃖⃗𝑂𝐽 не перпендикулярны. Мы называем этот тип координатной плоскости наклонной координатной плоскостью .

Ортогональная координатная плоскость – это координатная плоскость, в которой ⃖⃗𝑂𝐼 и ⃖⃗𝑂𝐽 перпендикулярны.

Таким образом, у нас есть три разных типа координатных плоскостей, которые мы сейчас обрисуем.

Определение: типы координатных плоскостей (𝑂; 𝐼, 𝐽)

В косой координатной плоскости , ⃖⃗𝑂𝐼 и ⃖⃗𝑂𝐽 перпендикулярны , а не .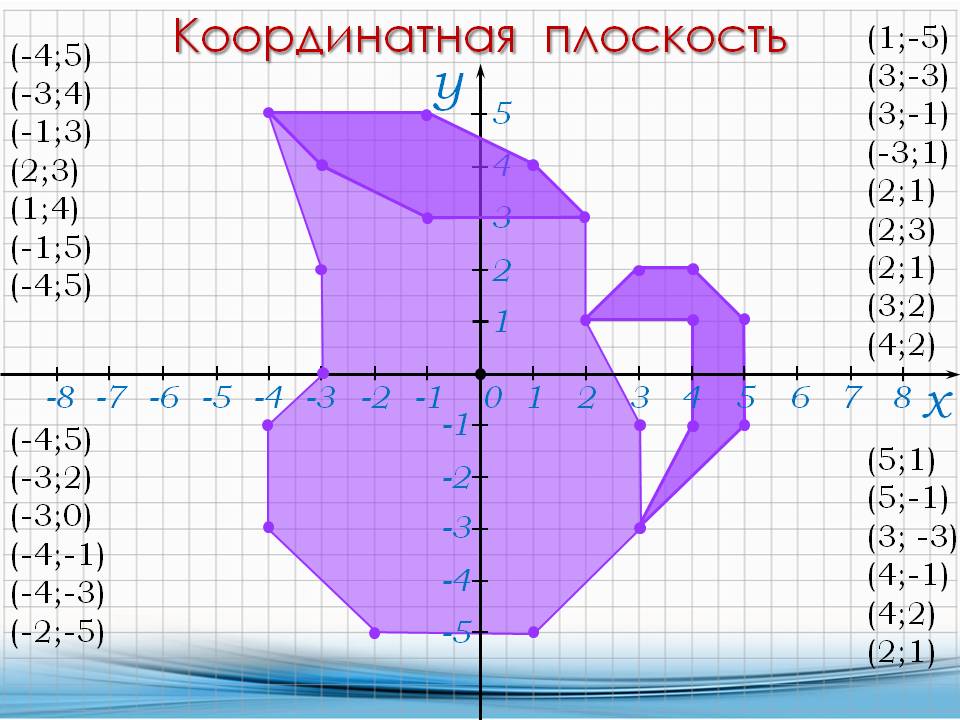

В ортогональной координатной плоскости , ⃖⃗𝑂𝐼⟂⃖⃗𝑂𝐽.

В ортонормированной координатной плоскости , ⃖⃗𝑂𝐼⟂⃖⃗𝑂𝐽 и 𝑂𝐼=𝑂𝐽.

Стоит отметить, что для удобства мы обычно изображаем координатные плоскости с горизонтальной 𝑥-осью всякий раз, когда это возможно, так как это облегчает визуальную интерпретацию.

В нашем первом примере мы собираемся использовать эти определения для определения различных типов координатных плоскостей.

Пример 1. Определение ортонормированных, ортогональных и наклонных координатных плоскостей

𝐴𝐵𝐶 — равнобедренный треугольник с прямым углом 𝐵. Точки 𝐷, 𝐸 и 𝐹 — середины отрезков 𝐴𝐶, 𝐴𝐵 и 𝐵𝐶 соответственно.

1. Какая из следующих плоскостей является ортонормированной координатной плоскостью?
   1. (𝐴; 𝐸, 𝐷)
   2. (𝐵; 𝐶, 𝐸)
   3. (𝐵; 𝐹, 𝐸)
   4. (𝐴; 𝐵, 𝐶)
   5. (𝐶; 𝐴, 𝐵)
2. (𝐶; из следующих плоскостей является ортогональной, но не ортонормированной координатной плоскостью?
   1. (𝐵; 𝐹, 𝐸)
   2. (𝐵; 𝐶, 𝐴)
   3. (𝐷; 𝐵, 𝐶)
   4. (𝐴; 𝐵, 𝐶)
   5. (𝐵; 𝐹, 𝐴)
3. (𝐵; из следующих плоскостей является наклонной координатной плоскостью?
   1. (𝐷;𝐵,𝐶)
   2. (𝐵;𝐶,𝐷)
   3. (𝐵;𝐶,𝐴)
   4. (𝐷;𝐵,𝐴)
   5. (𝐸;𝐵,𝐷)

Ответ

Часть 1

Напомним, что первая точка координатной плоскости является ее началом. Линия от начала до второй точки образует 𝑥-ось, а линия от начала координат до третьей точки образует 𝑦-ось.

В ортонормированной плоскости координат две оси перпендикулярны, а единицы длины, определяемые как расстояния между начало координат и вторая и третья точки соответственно равны.

Пройдемся по всем вариантам и оценим, соблюдается ли первый критерий (оси перпендикулярны).

Вариант А (𝐴;𝐸,𝐷). Треугольник 𝐴𝐵𝐶 находится прямо в 𝐵, что означает что ∠𝐵𝐴𝐶 не является прямым углом. Строки ⃖⃗𝐴𝐸 и ⃖⃗𝐴𝐷 не перпендикулярны.

Вариант B (𝐵;𝐶,𝐸). Поскольку ∠𝐴𝐵𝐶 — прямой угол, линии ⃖⃗𝐵𝐶 и ⃖⃗𝐵𝐸 перпендикулярны.

Вариант C (𝐵;𝐹,𝐸). Поскольку ∠𝐴𝐵𝐶 — прямой угол, линии ⃖⃗𝐵𝐹 и ⃖⃗𝐵𝐸 перпендикулярны.

Вариант D: (𝐴;𝐵,𝐶). Треугольник 𝐴𝐵𝐶 находится прямо в 𝐵, что означает, что ∠𝐵𝐴𝐶 не является прямым углом. Строки ⃖⃗𝐴𝐵 и ⃖⃗𝐴𝐶 не перпендикулярны.

Вариант E (𝐶;𝐴,𝐵). Треугольник 𝐴𝐵𝐶 находится прямо в 𝐵, что означает, что ∠𝐵𝐶𝐴 не является прямым углом. Линии ⃖⃗𝐶𝐵 и ⃖⃗𝐶𝐴 не перпендикулярны.

Итак, только в вариантах B и C оси 𝑥 и 𝑦 перпендикулярны. Теперь нам нужно оценить для каждой из них выполняется ли второй критерий (единичные длины обеих осей равны). Для варианта B это означает, что 𝐵𝐶=𝐵𝐸, а для варианта C означает, что 𝐵𝐹=𝐵𝐸.

Так как треугольник 𝐴𝐵𝐶 равнобедренный и имеет прямой угол при 𝐵, то 𝐵𝐶=𝐵𝐴. Точка 𝐸 — это середина 𝐴𝐵, а 𝐹 — это точка 𝐵𝐶, поэтому 𝐵𝐹=𝐵𝐸. Следовательно, (𝐵;𝐹,𝐸) есть единственная ортонормированная координатная плоскость. Это вариант С.

Часть 2

Напомним, что в ортогональной координатной плоскости две оси перпендикулярны. Нам также сообщили, что координатные плоскости не являются ортонормированными, что означает, что длины между началом координат и второй и третьей точками, соответственно, равны , а не .

Как и в части 1, пройдемся по опциям и сначала исключим координатные плоскости, оси которых не перпендикулярны.

Вариант А (𝐵;𝐹,𝐸). Поскольку ∠𝐴𝐵𝐶 — прямой угол, линии ⃖⃗𝐵𝐹 и ⃖⃗𝐵𝐸 перпендикулярны.

Вариант B (𝐵;𝐶,𝐴). Поскольку ∠𝐴𝐵𝐶 — прямой угол, линии ⃖⃗𝐵𝐶 и ⃖⃗𝐵𝐴 перпендикулярны.

Вариант C (𝐷;𝐵,𝐶). 𝐵𝐷 — это медиана равнобедренный треугольник 𝐴𝐵𝐶 с 𝐵𝐶=𝐵𝐴; следовательно, это также перпендикуляр биссектриса 𝐴𝐶. Следовательно, строки ⃖⃗𝐷𝐵 и ⃖⃗𝐷𝐶 перпендикулярны.

Вариант D: (𝐴;𝐵,𝐶). Треугольник 𝐴𝐵𝐶 находится прямо в 𝐵, что означает, что ∠𝐵𝐴𝐶 не является прямым углом. Линии ⃖⃗𝐴𝐵 и ⃖⃗𝐴𝐶 поэтому не перпендикулярны.

Вариант E (𝐵;𝐹,𝐴). Поскольку ∠𝐴𝐵𝐶 — прямой угол, линии ⃖⃗𝐵𝐶 и ⃖⃗𝐵𝐴 перпендикулярны.

Исключается только вариант D, так как его оси не перпендикулярны, поэтому он не может быть ортогональной системой координат.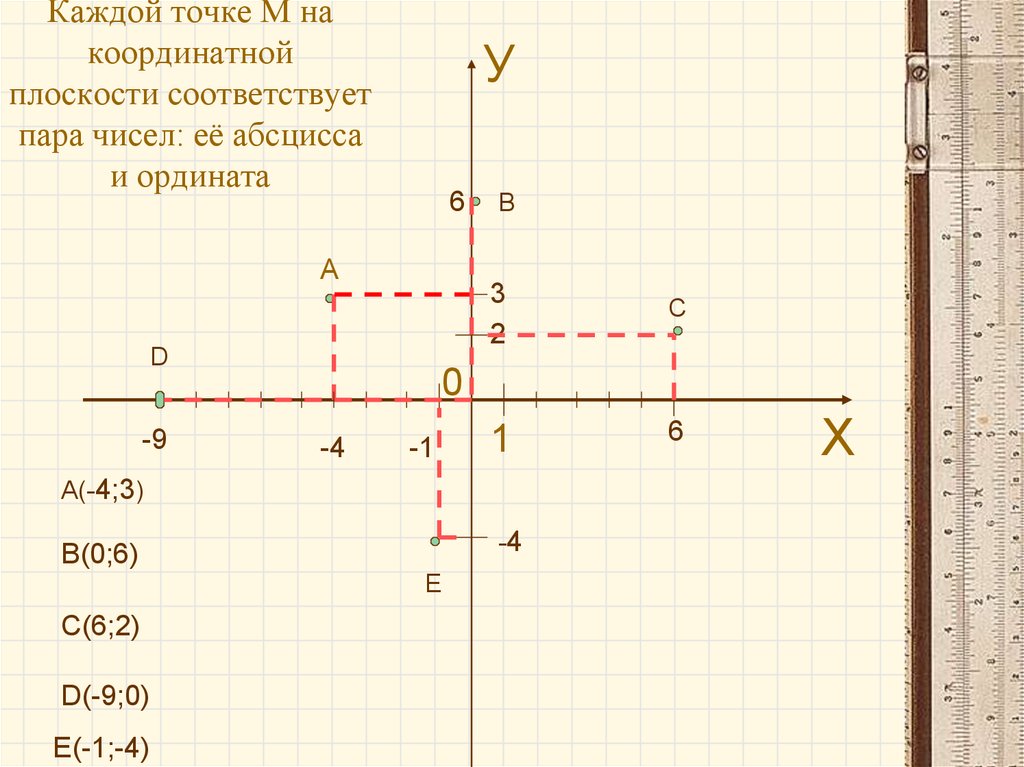

Теперь сравним единичные длины обеих осей.

Вариант А (𝐵;𝐹,𝐸). Как мы показали в части 1, имеем 𝐵𝐹=𝐵𝐸.

Вариант B (𝐵;𝐶,𝐴). Как мы показали в части 1, имеем 𝐵𝐶=𝐵𝐴.

Вариант C (𝐷;𝐵,𝐶). Треугольник 𝐴𝐵𝐶 равнобедренный, значит ∠𝐵𝐴𝐶=∠𝐵𝐶𝐴=45∘. Более того, 𝐵𝐷 также является биссектрисой угла ∠𝐴𝐵𝐶. Следовательно, ∠𝐶𝐵𝐷=902=45∘. Таким образом, треугольник 𝐵𝐶𝐷 равнобедренный и 𝐷𝐵=𝐷𝐶.

Вариант E (𝐵;𝐹,𝐴). У нас есть 𝐵𝐹=12𝐵𝐴 и 𝐵𝐶=𝐵𝐴, так что 𝐵𝐹≠𝐵𝐴. Таким образом,

(𝐵;𝐹,𝐴) является ортогональной координатной плоскостью. Это вариант E.

Часть 3

Нам нужно определить, какая координатная плоскость является наклонной, то есть имеет неперпендикулярные оси.

Проверив все варианты, мы видим, что только (𝐵;𝐶,𝐷) является наклонной координатной плоскостью в виде линий ⃖⃗𝐵𝐶 и ⃖⃗𝐵𝐷 не перпендикулярны. Это вариант Б.

Теперь, когда мы определили эти три разных типа координатных плоскостей, давайте определим координаты на координатной плоскости (𝑂;𝐼,𝐽).

Определение: Координаты

Учитывая координатную плоскость (𝑂;𝐼,𝐽), положение любой точки 𝑀 на плоскости описывается его координатами, отмеченными (𝑥,𝑦).

𝑥 — действительное число на оси 𝑥 точки пересечения параллельной линии к оси 𝑦 и проходящей через 𝑀.

𝑦 — действительное число на оси 𝑦 точки пересечения прямой, параллельной к оси 𝑥 и проходящей через 𝑀.

Используя это определение, мы можем определить координаты (𝑥,𝑦) точки 𝑀 в наклонной плоскости координат, как показано на следующей диаграмме.

Стоит отметить, что по определению координаты 𝐼 в координатной плоскости (𝑂;𝐼,𝐽) равны (1,0), а числа 𝐽 равны (0,1).

В нашем следующем примере мы собираемся использовать наше понимание координат в ортонормированной координатной плоскости.

Пример 2. Определение координат точки по координатам другой точки на координатной плоскости

𝐴 и 𝐵 две точки в ортонормированной координатной плоскости с положительной горизонталью 𝑥-ось направлена ​​вправо, а положительная вертикальная 𝑦-ось направлена ​​вверх. Единица длины осей задаются сеткой. Если координаты 𝐴 равны (1,2), каковы координаты 𝐵?

Ответ

Мы знаем, что точки 𝐴 и 𝐵 лежат в ортонормированной плоскости координат, единицы длины которой даются сеткой. Чтобы найти координаты точки 𝐵, мы сначала определим положение начало координатной плоскости, 𝑂, используя координаты 𝐴, (1,2). Эти координаты означают, что точка 𝐴 расположена на единицу длины справа от начала координат и на 2 единицы длины вверх от начала координат. Другими словами, начало координатной плоскости равно единице. длина слева от 𝐴 и на 2 единицы длины вниз от 𝐴.

Теперь мы можем провести оси координатной плоскости и прочитать координаты точки 𝐵.

Точка 𝐵 находится на расстоянии одной единицы длины от начала координат и находится на оси 𝑥. Следовательно, его координаты (−1,0).

В предыдущем примере мы рассматривали точки в ортонормированной системе координат. В следующем примере мы отразим о различиях между тремя типами координатных плоскостей.

Пример 3. Определение формы четырехугольника в различных типах координатной плоскости

Рассмотрим точки 𝐴(0,0), 𝐵(1,0), 𝐶(1,1) и 𝐷(0,1) в координатной плоскости.

1. Если координатная плоскость является наклонной координатной плоскостью, какой формы четырехугольник 𝐴𝐵𝐶𝐷?
   1. Трапеция
   2. Воздушный змей
   3. Квадрат
   4. Прямоугольник
   5. Параллелограмм
2. Если координатная плоскость является ортогональной координатной плоскостью, то какой формы четырехугольник 𝐶𝐝𝐝𝐝𝐝?
   1. Трапеция
   2. Воздушный змей
   3. Квадрат
   4. Прямоугольник
3. Если координатная плоскость является ортонормированной координатной плоскостью, какой формы четырехугольник 𝐴𝐵𝐶𝐷?
   1. Трапеция
   2. Воздушный змей
   3. Квадрат

Ответ

Часть 1

Нарисуем косую координатную плоскость и расставим точки 𝐶, 𝐶, 𝐶 и 𝐷.

Так как 𝐴 и 𝐷 с одной стороны и 𝐵 и 𝐶 с другой у руки одинаковая 𝑥-координата, у нас есть 𝐴𝐷⫽𝐵𝐶⫽𝑦-ось. Точно так же 𝐴 и 𝐵 с одной стороны а 𝐷 и 𝐶, с другой стороны, имеют одинаковую 𝑦-координату, поэтому 𝐴𝐵⫽𝐷𝐶⫽𝑥-ось. Следовательно, мы можем заключить что 𝐴𝐵𝐶𝐷 — параллелограмм (вариант E).

Часть 2

Поступим, как описано выше, нарисуем ортогональную координатную плоскость и поместим точки 𝐴, 𝐵, 𝐶 и 𝐷.

По тем же причинам, что и в наклонной плоскости координат, 𝐴𝐵𝐶𝐷 является параллелограммом. Однако это особый параллелограмм, так как оси 𝑥 и 𝑦 перпендикулярны. Параллелограмм с прямым углом представляет собой прямоугольник. Следовательно, 𝐴𝐵𝐶𝐷 — прямоугольник (вариант D).

Часть 3

Наконец, для ортонормированной плоскости теперь мы знаем, что 𝐴𝐵=𝐴𝐷. 𝐴𝐵𝐶𝐷 это поэтому особый прямоугольник, где все стороны равны; это квадрат (вариант C).

Давайте потренируемся на следующем примере чтения координат в наклонной координатной плоскости, имея в виду, что сетка в наклонная координатная плоскость образует параллелограммы.

Пример 4. Нахождение координат точки в нескольких конфигурациях для координатной плоскости

𝐴𝐵𝐶𝐷 — параллелограмм, а точки 𝐼, 𝐽, и 𝐿 — середины отрезков 𝐴𝐵, 𝐵𝐶, 𝐶𝐷 и 𝐷𝐴 соответственно.

Найдите координаты точки 𝐶 в каждой из следующих конфигураций координатной плоскости.

1. Координатная плоскость (𝐴;𝐵,𝐷)
2. Координатная плоскость (𝐶;𝐷,𝐵)
3. Координатная плоскость (𝐿;𝐽,𝐷)
4. Координатная плоскость (𝐴;54), 𝐼,𝐼,00051

Ответ

Прежде чем начать, заметим, что поскольку 𝐴𝐵𝐶𝐷 — параллелограмм и точки 𝐼, 𝐽, 𝐾 и 𝐿 — середины отрезков. 𝐴𝐵, 𝐵𝐶, 𝐶𝐷, и 𝐷𝐴, мы имеем ⃖⃗𝐴𝐵⃖⃗𝐴𝐵⃖⃗𝐷𝐶⃖⃗𝐷𝐶 и ⃖⃗𝐴𝐷⃖⃗𝐴𝐷⃖⃗𝐵𝐶⃖⃗𝐵𝐶.

Часть 1

В координатной плоскости (𝐴;𝐵,𝐷) 𝐴 — начало координат, ⃖⃗𝐴𝐵 — ось 𝑥 с единицей длины 𝐴𝐵, а ⃖⃗𝐴𝐷 — 𝑦-ось с 𝐴𝐷 в качестве единицы длины. Следовательно, координаты 𝐵 равны (1,0) и 𝐷 равны (0,1).

Чтобы найти 𝑥-координату точки 𝐶, ищем прямую, параллельную 𝑦-ось (прямая ⃖⃗𝐴𝐷), проходящая через 𝐶; это ⃖⃗𝐵𝐶. Она пересекает ось 𝑥 (прямая ⃖⃗𝐴𝐵) в точке 𝐵, что соответствует 𝑥-координате 1,

Чтобы найти 𝑦-координату точки 𝐶, ищем прямую, параллельную 𝑥-ось (прямая ⃖⃗𝐴𝐵), проходящая через 𝐶; это ⃖⃗𝐷𝐶. Она пересекает ось 𝑦 (прямая ⃖⃗𝐴𝐷) в точке 𝐷, что соответствует 𝑦-координате 1. Координаты 𝐶 в (𝐴;𝐵,𝐷) равны (1,1).

Часть 2

В координатной плоскости (𝐶;𝐷,𝐵) 𝐶 является началом координат. Следовательно, его координаты (0,0).

Часть 3

В координатной плоскости (𝐿;𝐽,𝐷) 𝐿 — начало координат, ⃖⃗𝐿𝐽 — ось 𝑥 с 𝐿𝐽 в качестве ее единичной длины, и ⃖⃗𝐿𝐷 — это ось 𝑦, единицей длины которой является 𝐿𝐷. Следовательно, координаты 𝐽 равны (1,0), а координаты 𝐷 равны (0,1).

Прямая, параллельная оси 𝑦 ⃖⃗𝐿𝐷, проходящая через 𝐶, ⃖⃗𝐽𝐶.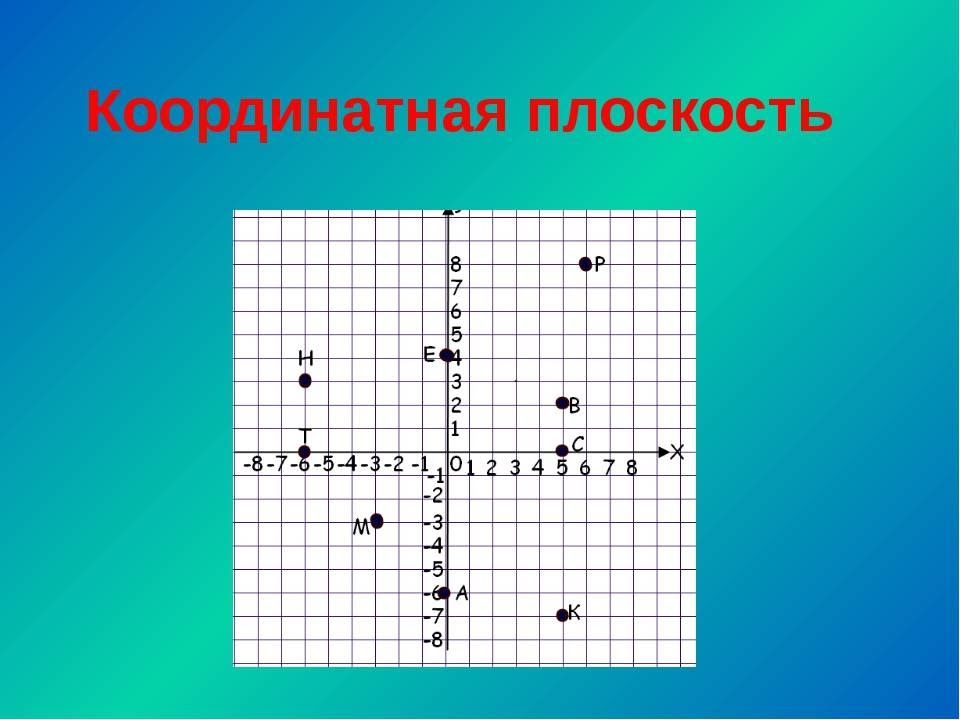 Он пересекает 𝑥-ось ⃖⃗𝐿𝐽 в точке 𝐽, что дает 𝑥-координату 1.

Прямая, параллельная оси 𝑥 ⃖⃗𝐿𝐽, проходящая через 𝐶, ⃖⃗𝐷𝐶. Он пересекает 𝑦-ось ⃖⃗𝐿𝐷 в точке 𝐷, что дает 𝑦-координату 1,

Следовательно, координаты 𝐶 в (𝐿;𝐽,𝐷) равны (1,1).

Часть 4

В координатной плоскости (𝐴;𝐼,𝐿) 𝐴 — начало координат, ⃖⃗𝐴𝐼 — ось 𝑥 с 𝐴𝐼 в качестве единицы длины, а ⃖⃗𝐴𝐿 — это ось 𝑦, единицей длины которой является 𝐴𝐿. Следовательно, координаты 𝐼 равны (1,0), а координаты 𝐿 равны (0,1).

Прямая, параллельная оси 𝑦 ⃖⃗𝐴𝐿, проходящая через 𝐶, ⃖⃗𝐵𝐶. Он пересекает 𝑥-ось ⃖⃗𝐴𝐼 в точке 𝐵. 𝐼 является серединой 𝐴𝐵, мы имеем 𝐴𝐵=2𝐴𝐼, что соответствует 𝑥-координате 2,

Прямая, параллельная оси 𝑥 ⃖⃗𝐴𝐼, проходящая через 𝐶, ⃖⃗𝐷𝐶. Он пересекает 𝑦-ось ⃖⃗𝐴𝐿 в точке 𝐷. Поскольку 𝐿 является серединой 𝐴𝐷, мы имеем 𝐴𝐷=2𝐴𝐿, что соответствует 𝑦-координате 2.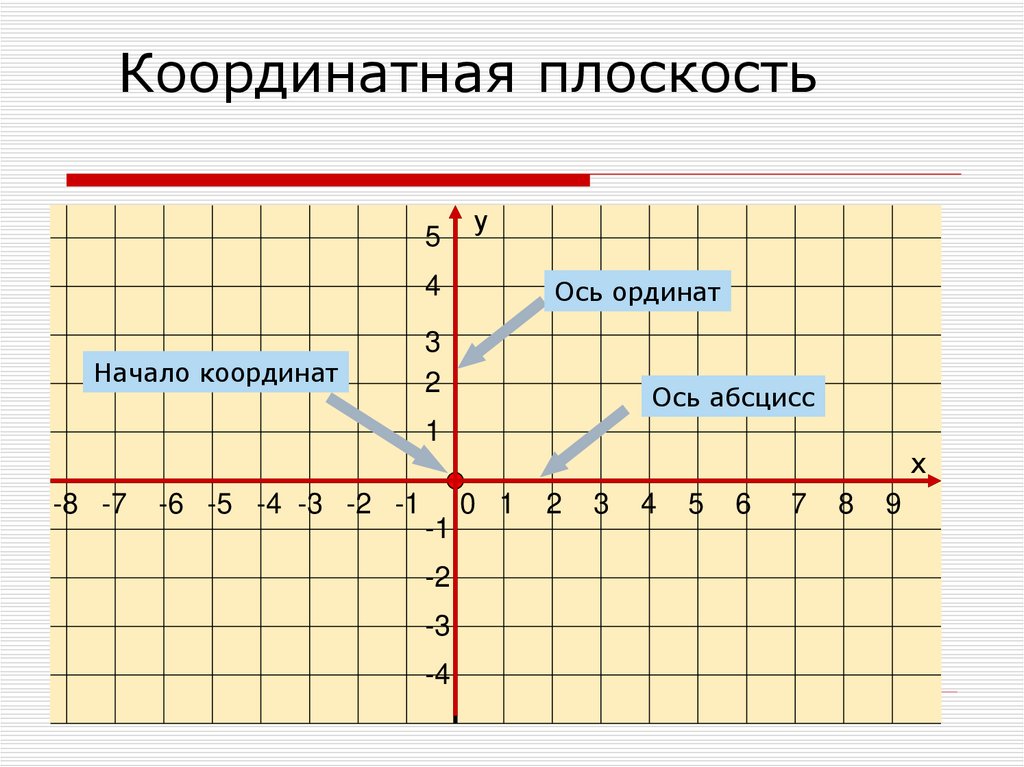

Следовательно, координаты 𝐶 в (𝐴;𝐼,𝐿) равны (2,2).

В нашем последнем примере нам нужно будет определить координаты заданной точки во вновь определенной координатной плоскости.

Пример 5. Определение типа данной координатной плоскости и координат точки на другой координатной плоскости

Рассмотрим точки 𝐴(1,1), 𝐵(−1,1) и 𝐶(−1,3) в ортонормированной координатной плоскости (𝑂;𝐼,𝐽).

1. Какой тип координатной плоскости (𝑂;𝐴,𝐵)?
2. Каковы координаты точки 𝐶 на координатной плоскости (𝑂;𝐴,𝐵)?

Ответ

Часть 1

В координатной плоскости (𝑂;𝐴,𝐵) 𝑂 — начало координат, ⃖⃗𝑂𝐴 — ось 𝑥 с 𝑂𝐴 в качестве единицы длины, а ⃖⃗𝑂𝐵 — 𝑦-ось с 𝑂𝐵 как его единица длины. К определить тип координатной плоскости, нам нужно определить

1. перпендикулярны ли ⃖⃗𝑂𝐴 и ⃖⃗𝑂𝐵,
2. являются ли 𝑂𝐴=𝑂𝐵.

Заметим, что обе 𝑂𝐴 и 𝑂𝐵 являются диагоналями квадрат сетки. Мы знаем, что диагональ квадрата является осью симметрии квадрата, а значит, 𝑚∠𝐴𝑂𝐼=𝑚∠𝐴𝑂𝐽=45∘ и 𝑚∠𝐵𝑂𝐽=45∘. Следовательно, как 𝑚∠𝐴𝑂𝐵=𝑚∠𝐴𝑂𝐽+𝑚∠𝐽𝑂𝐵, находим, что 𝑚∠𝐴𝑂𝐵=45+45=90∘.

Кроме того, поскольку диагонали квадрата имеют одинаковую длину и 𝑂𝐴 и 𝑂𝐵 — диагонали двух равных квадратов, имеем 𝑂𝐴=𝑂𝐵. Таким образом, мы можем заключить, что (𝑂;𝐴,𝐵) является ортонормированной координатной плоскостью, поскольку ее оси перпендикулярны и имеют одинаковую единичную длину.

Часть 2

Чтобы найти координаты 𝐶 в (𝑂;𝐴,𝐵), нам нужно провести две линии параллельно осям 𝑥 и 𝑦, проходящим через 𝐶.

Прямая, параллельная оси 𝑦, проходящая через 𝐶, пересекает ось 𝑥 в 𝐴, что дает 𝑥-координату 1.

Прямая, параллельная оси 𝑥, проходящая через 𝐶, пересекает ось 𝑦 в точке, которая находится на расстоянии от начала координат, вдвое превышающем длину 𝑂𝐵 (отрезок прямой от начала координат до этого точка пересечения в два раза больше диагонали квадрата сетки) и на положительной стороне оси 𝑦 (на той же сторона как 𝐵).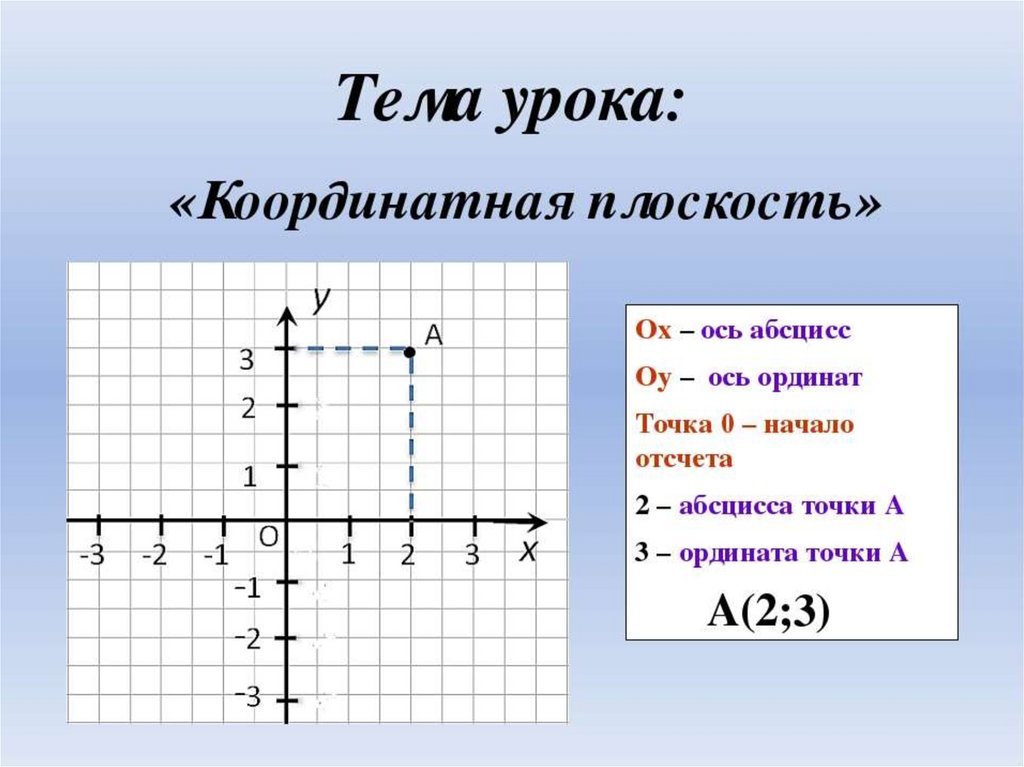 Следовательно, это соответствует 𝑦-координате 2,

Следовательно, координаты 𝐶 в (𝑂;𝐴,𝐵) равны (1,2).

Давайте закончим повторением некоторых ключевых моментов объяснения.

Ключевые точки

• Координатная плоскость образована любыми тремя неколлинеарными точками (𝑂;𝐼,𝐽), где 𝑂 начало координат, линия ⃖⃗𝑂𝐼 — ось 𝑥 с положительным направлением в направлении 𝑂𝐼, а строка ⃖⃗𝑂𝐽 — это 𝑦-ось с положительным направлением в сторону 𝑂𝐽. Длина отрезка 𝑂𝐼 — это единица длины 𝑥-ось, а 𝑂𝐽 — единичная длина 𝑦-оси.
• Стандартная система координат, которую мы используем в математике, называется ортонормированной системой координат, но есть три основных типы координатных плоскостей: косая, где 𝑂𝐼 и 𝑂𝐽 неперпендикулярны, ортогональны, где 𝑂𝐼 и 𝑂𝐽 перпендикулярны и ортонормированы, что является ортогональной плоскостью с добавленным условием, что 𝑂𝐼=𝑂𝐽.
• Учитывая координатную плоскость (𝑂;𝐼,𝐽), положение любой точки 𝑀 на плоскости описывается его координатами, отмеченными (𝑥,𝑦). 𝑥 — действительное число на 𝑥-ось точки пересечения прямой, параллельной 𝑦-оси и проходящей через 𝑀. 𝑦 — действительное число на оси 𝑦 точки пересечения прямая, параллельная оси 𝑥 и проходящая через 𝑀.

Что такое координатная плоскость? (Определение, квадранты и пример)

Написано

Malcolm McKinsey

11 января 2023 г.

Проверка по факту

Paul Mazzola

. , регулярно расположенные числовые линии, подобные рыболовной сети, разложенные на совершенно плоской поверхности, бесконечно простирающейся в ширину и длину, без толщины.

Улицы Барселоны, Торонто и Нью-Йорка расположены в соответствии с планом сетки. В них легче ориентироваться (пешком или на машине), чем в городах с беспорядочной планировкой улиц. Координатная плоскость, или декартова сетка, представляет собой план сетки. Подобно рыболовной сети, сетка координатной плоскости пропускает много вещей, но удерживает все, что попадает на сами линии. Такие вещи, как круги, наклонные линии, многоугольники и, иногда, муха.

Рене Декарт и муха

Французский математик и философ XVII века Рене Декарт изобрел систему координат, когда, лежа в постели, он заметил муху на потолке своей спальни. Ему было интересно, как он мог бы описать его движение, поэтому он использовал один угол своей спальни в качестве начала или отправной точки и представил перпендикулярные, регулярно расположенные числовые линии, образующие сетку.

Нам повезло, что потолок спальни Декарта был гладким и плоским; она создала плоскость , или совершенно плоскую поверхность, по которой ползала муха и вдохновляла одного из величайших математиков на создание одного из величайших математических инструментов.

Движение по координатной плоскости

Рене mouche domestique , живший в доме математика, имел явные математические наклонности и всегда ходил по прямым линиям.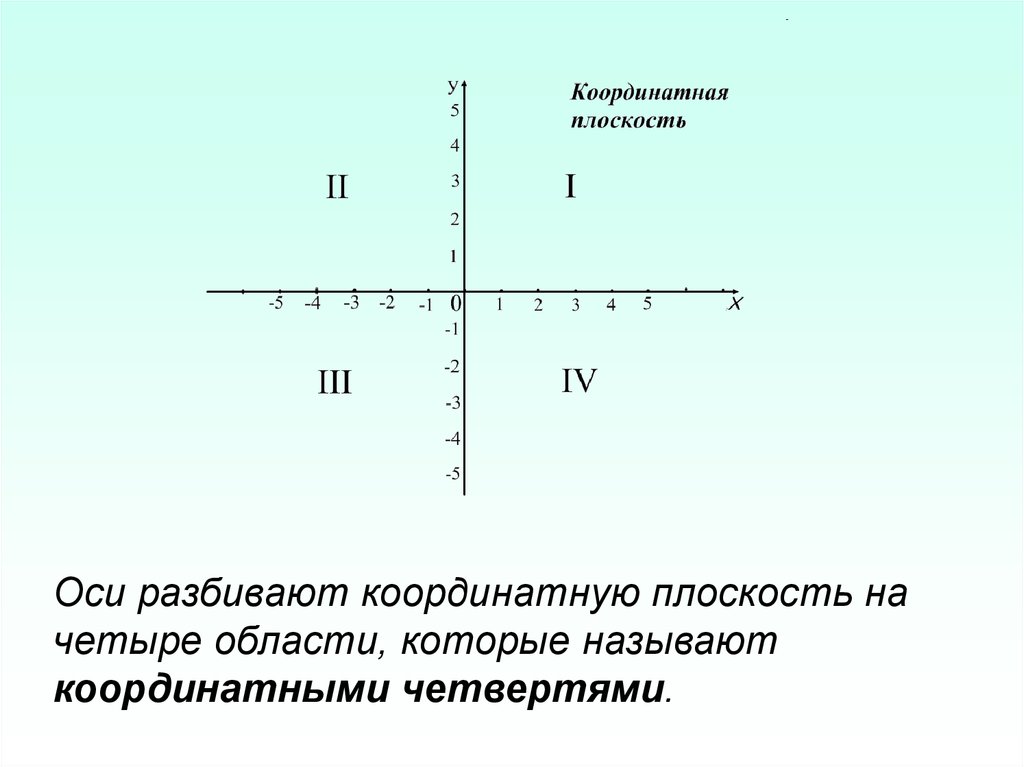 Будучи мухой, она также имела тенденцию двигаться немного хаотично, делая два шага назад на каждый шаг вперед. У него был смысл отрицательных чисел, например:

Числовая строка

La mouche de René  может начинаться с 0 , двигаться к +1 , а затем возвращаться к -1 . Следующий la petite mouche начинается с -1 , продолжается до 0 и заканчивается до -2 .

А что, если муха повернется на 90° и полетит в другом направлении? Нам нужна еще одна числовая линия, перпендикулярная нашей первой числовой линии, чтобы изобразить ее движение. Мы выстраиваем 0 на каждой числовой линии и теперь можем измерить ее движение в двух направлениях.

Две пересекающиеся числовые линии

Чтобы четко описать движение мухи, нам нужно решить, какое направление мы укажем первым, а какое вторым. Каждая числовая строка представляет собой ось , где x -ось идет слева направо, а y -ось идет вверх вниз.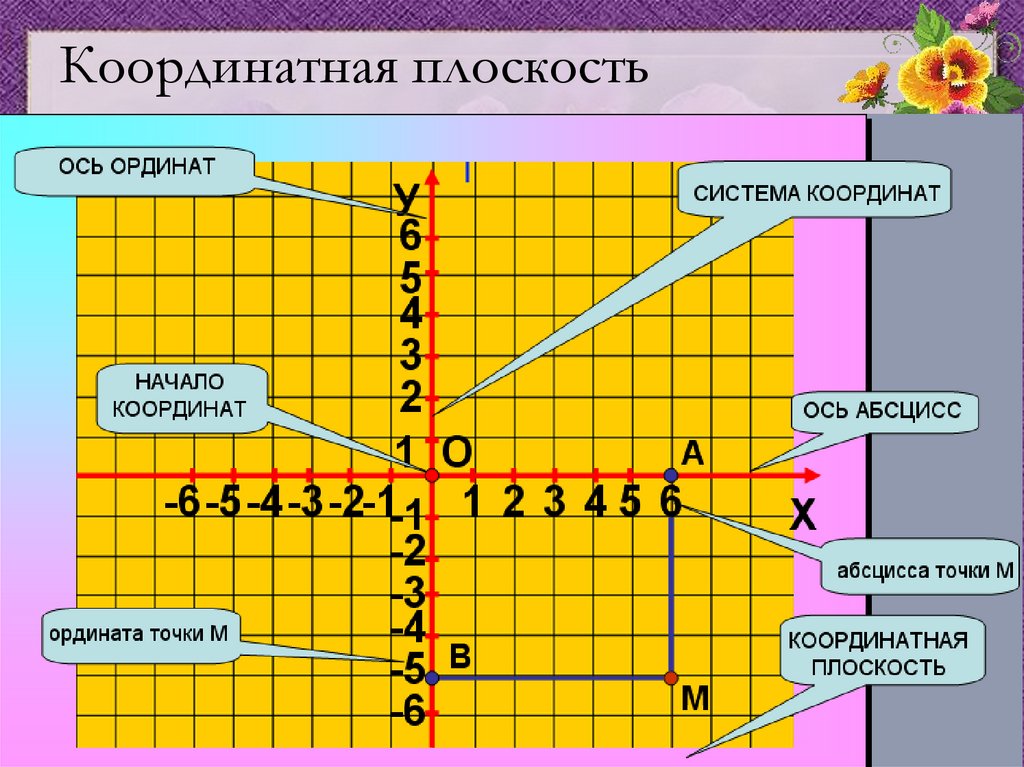

Сначала всегда указывается значение по оси x , а затем значение по оси y . Например, центр наших числовых строк — это (0, 0) , а два шага влево — это (-2, 0) . Эти значения x и y образуют пару координат, которая указывает на уникальное положение на координатной плоскости.

Если бы мы хотели быть неточными, мы могли бы приблизительно оценить движение, используя только две пересекающиеся перпендикулярные числовые линии. Однако математики не любят неточностей, поэтому мы используем несколько числовых линий в обоих направлениях:

Координатная сетка

Теперь мы можем сказать, что муха, начиная с (0, 0) , известная как начало координат , переместилась в (1, 2) . Муха переместилась на одну единицу вправо и на две единицы вверх.

Словарь координатных плоскостей

Чтобы точно говорить о расположении на координатных плоскостях, мы используем специальную лексику. Мы уже видели, что две числовые линии называются осью x (горизонтальной) и осью y (вертикальной). Мы знаем, что (0,0) называется источником. Полезно знать и другие термины.

Масштаб

Числовые строки могут содержать числа любого диапазона. У вас может быть две координатные сетки рядом, одна с осью x и ось y , начиная с -20 и далее до +20 . Другая координатная сетка может начинаться с -1000 и расширяться до +1000 . Два разных диапазона — это 90 029 масштабов 90 030 сетки.

В одной координатной плоскости ось x может иметь один масштаб (например, от -10 до +10 ), а ось y может иметь другой масштаб (например, -100 по телефону +100 ). Это позволяет отображать информацию компактно и графически, что в противном случае потребовало бы огромных сеток в основном впустую потраченного пространства.

Квадранты

Первоначальные пересекающиеся числовые линии делили координатную плоскость на четыре области, называемые квадрантами . По традиции они нумеруются римскими цифрами в направлении против часовой стрелки, начиная с верхнего правого квадранта, называемого квадрантом I.