Координаты отрезка: Найдите координаты середины отрезка AB если A(6;5) B (3;6)

Математический портал. Высшая математика. Математический анализ.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Зная координаты точек $M_1(x_1, y_1, z_1)$ и $M_2(x_2, y_2, z_2)$ и отношение $\lambda,$ в котором точка $M$ делит направленный отрезок $\overline{M_1M_2},$ найдем координаты точки $M.$

Пусть $O -$ начало координат. Обозначим $\overline{OM_1}=r_1,$ $\overline{OM_2}=r_2,$ $\overline{OM}=r.$ Так как, $$\overline{M_1M}=r-r_1, \overline{MM_2}=r_2-r,$$ то $r-r_1=\lambda(r_2-r),$ откуда (так как $\lambda\neq -1$) $$r=\frac{r_1+\lambda r_2}{1+\lambda}.$$ Полученная форма и дает решение задачи в векторной форме. Переходя в этой формуле к координатам, получим $$x=\frac{x_1+\lambda x_2}{1+\lambda}, y=\frac{y_1+\lambda y_2}{1+\lambda}, z=\frac{z_1+\lambda z_2}{1+\lambda}.$$

Примеры.

2.57. Отрезок с концами в точках $A(3, -2)$ и $B(6, 4)$ разделен на три равные части. Найти координаты точек деления.

Решение.

Пусть $C(x_C, y_C)$ и $D(x_D, y_D) -$ точки, которые делят отрезок $AB$ на три равные части. Тогда $$\lambda_1=\frac{AC}{CB}=\frac{1}{2};$$ $$x_C=\frac{x_A+\lambda_1x_B}{1+\lambda_1}=\frac{3+\frac{1}{2}\cdot 6}{1+\frac{1}{2}}=4;$$ 

$$y_C=\frac{y_A+\lambda_1y_B}{1+\lambda_1}=\frac{-2+\frac{1}{2}\cdot 4}{1+\frac{1}{2}}=0.$$ 

Далее находим координаты точки $D:$

$$\lambda_2=\frac{AD}{DB}=\frac{2}{1}=2;$$ $$x_D=\frac{x_A+\lambda_2x_B}{1+\lambda_2}=\frac{3+2\cdot 6}{1+2}=5;$$ 

$$y_D=\frac{y_A+\lambda_2y_B}{1+\lambda_2}=\frac{-2+2\cdot 4}{1+2}=2.$$ 

Ответ: $(4, 0)$ и $(5, 2).$

 

2.58.Определить координаты концов отрезка, который точками $C(2, 0, 2)$ и $D(5, -2, 0)$ разделен на три равные части.

Решение.

Пусть $A(x_A, y_A, z_A)$ и $B(x_B, y_B, z_B) -$ концы заданного отрезка.

Выпишем формулы для нахождения координат точки $C$ и подставим известные координаты:

$$\lambda_1=\frac{AC}{CB}=\frac{1}{2};$$ $$x_C=\frac{x_A+\lambda_1x_B}{1+\lambda_1}\Rightarrow 2=\frac{x_A+\frac{1}{2}\cdot x_B}{1+\frac{1}{2}}=2\frac{x_A+\frac{1}{2}\cdot x_B}{3}\Rightarrow $$ $$\Rightarrow 3=x_A+\frac{1}{2}\cdot x_B;$$ 

$$y_C=\frac{y_A+\lambda_1y_B}{1+\lambda_1}\Rightarrow 0=\frac{y_A+\frac{1}{2}\cdot y_B}{1+\frac{1}{2}}\Rightarrow 0=y_A+\frac{1}{2}\cdot y_B;$$

$$z_C=\frac{z_A+\lambda_1z_B}{1+\lambda_1}\Rightarrow 2=\frac{z_A+\frac{1}{2}\cdot z_B}{1+\frac{1}{2}}=2\frac{z_A+\frac{1}{2}\cdot z_B}{3}\Rightarrow$$ $$\Rightarrow 3=z_A+\frac{1}{2}\cdot z_B. $$ 

Аналогичные равенства запишем для точки $D:$

$$\lambda_2=\frac{AD}{DB}=\frac{2}{1}=2;$$ $$x_D=\frac{x_A+\lambda_2x_B}{1+\lambda_2}\Rightarrow 5=\frac{x_A+2\cdot x_B}{1+2}=\frac{x_A+2\cdot x_B}{3}\Rightarrow $$ $$\Rightarrow 15=x_A+2\cdot x_B;$$ 

$$y_D=\frac{y_A+\lambda_2y_B}{1+\lambda_2}\Rightarrow -2=\frac{y_A+2\cdot y_B}{1+2}\Rightarrow -6=y_A+2\cdot y_B;$$

$$z_D=\frac{z_A+\lambda_2z_B}{1+\lambda_2}\Rightarrow 0=\frac{z_A+2\cdot z_B}{1+2}\Rightarrow 0=z_A+2\cdot z_B.$$

Далее запишем полученные уравнения относительно $x_A, x_B;$ $y_A, y_B$  и $z_A, z_B$ попарно в виде систем и решим их:

$$\left\{\begin{array}{lcl}x_A+\frac{1}{2}x_B=3\\x_A+2x_B=15\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}x_A=3-0,5x_B\\3-0,5x_B+2x_B=15\end{array}\right.\Rightarrow$$ $$\Rightarrow\left\{\begin{array}{lcl}x_A=3-0,5\cdot8=-1\\x_B=\frac{12}{1,5}=8\end{array}\right.$$

$$\left\{\begin{array}{lcl}y_A+\frac{1}{2}y_B=0\\y_A+2y_B=-6\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}y_B=-2y_A\\y_A-4y_A=-6\end{array}\right. \Rightarrow$$ $$\Rightarrow\left\{\begin{array}{lcl}y_B=-4\\y_A=2\end{array}\right.$$

$$\left\{\begin{array}{lcl}z_A+\frac{1}{2}z_B=3\\z_A+2z_B=0\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}-2z_B+0,5z_B=3\\z_A=-2z_B\end{array}\right.\Rightarrow$$ $$\Rightarrow\left\{\begin{array}{lcl}z_B=-2\\z_A=4\end{array}\right.$$

Таким образом, получили координаты концов отрезка $A(-1, 2, 4)$ и $B(8, -4, -2).$ 

Ответ: $A(-1, 2, 4),$ $B(8, -4, -2).$ 

 

 

примеры, решения. Формулы деления отрезка в данном отношении Понятие деления отрезка в данном отношении

В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.

Определение 1

Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .

Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .

Определение 2

Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .

Определение 3

Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B

Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B: необходимо определить координату

x C .

Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.

| А С | = | С В | ⇔ x C — x A = x B — x C

Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)

Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).

Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):

Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.

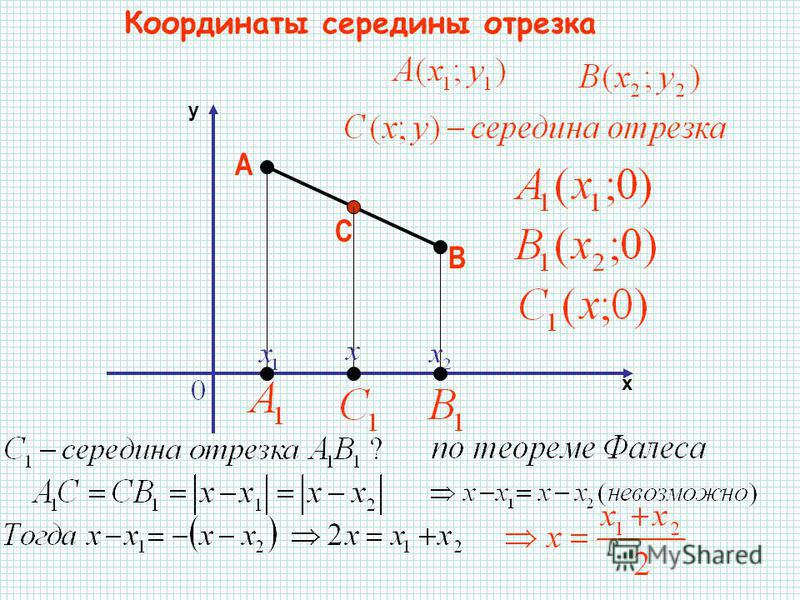
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .

Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).

Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:

x C = x A + x B 2 и y C = y A + y B 2

Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:

Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A (x A , y A) и B (x B , y B) определяются как :

(x A + x B 2 , y A + y B 2)

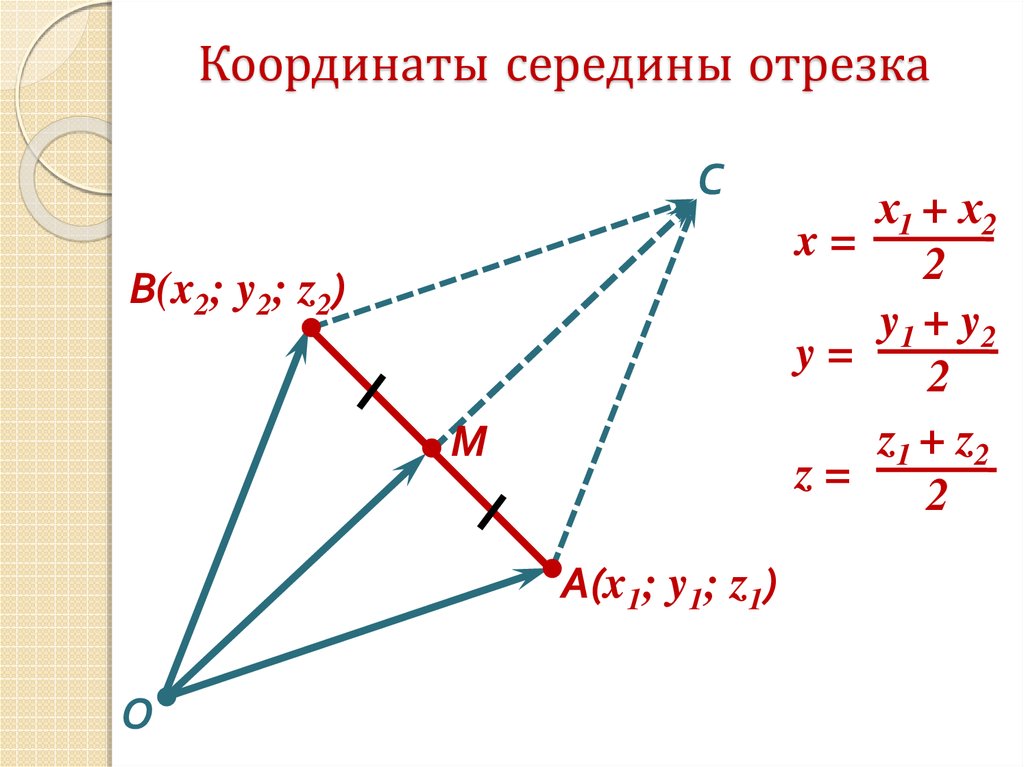
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .

A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.

Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z

Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:

x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2

Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.

Определение координат середины отрезка через координаты радиус-векторов его концов

Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.

Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .

Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:

O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2

Следовательно, точка C имеет координаты:

x A + x B 2 , y A + y B 2

По аналогии определяется формула для нахождения координат середины отрезка в пространстве:

C (x A + x B 2 , y A + y B 2 , z A + z B 2)

Примеры решения задач на нахождение координат середины отрезка

Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы.

Рассмотрим характерные примеры.

Пример 1

Исходные данные: на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.

Решение

Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .

x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2

Ответ : координаты середины отрезка А В — 5 2 , 7 2 .

Пример 2

Исходные данные: известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.

Решение

1. По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:

x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3

1. Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:

A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58

Ответ: 58

Пример 3

Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.

Решение

Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8

Ответ: координаты точки А (7 , 3 , — 8) .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Начальные геометрические сведения

Понятие отрезка, как и понятие точки, прямой, луча и угла, относится к начальным геометрическим сведениям.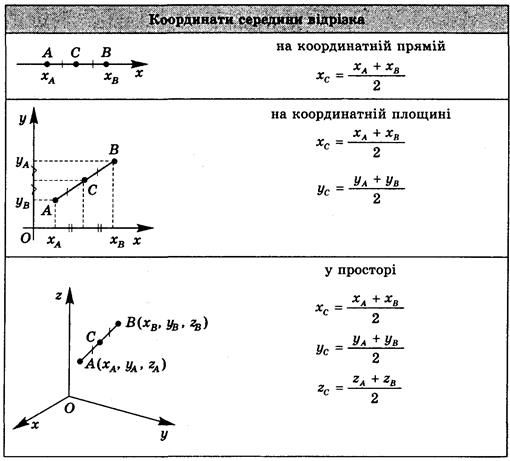 С перечисленных понятий начинается изучение геометрии.

Под «начальными сведениями» обычно понимают нечто элементарное и простое. В понимании, возможно, это так и есть. Тем не менее, такие простые понятия часто встречаются и оказываются необходимыми не только в нашей повседневной жизни, но и в производстве, строительстве и прочих сферах нашей жизнедеятельности.

Начнём с определений.

Определение 1

Отрезок — часть прямой, ограниченная двумя точками (концами).

Если концы отрезка являются точками $A$ и $B$, то образованный отрезок записывают как $AB$ или $BA$. Такому отрезку принадлежат точки $A$ и $B$, а также все точки прямой, лежащие между этими точками.

Определение 2

Середина отрезка — точка отрезка, которая делит его пополам на два равных отрезка.

Если это точка $C$, то $AC=CB$.

Измерение отрезка происходит сравнением с определённым отрезком, принятым за единицу измерения. Чаще всего используют сантиметр. Если в заданном отрезке сантиметр укладывается ровно четыре раза, то это означает, что длина данного отрезка равна $4$ см.

Введём простое наблюдение. Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих отрезков.

Формула нахождения координаты середины отрезка

Формула нахождения координаты середины отрезка относится к курсу аналитической геометрии на плоскости.

Дадим определение координатам.

Определение 3

Координаты — это определённые (или упорядоченные) числа, которые показывают положение точки на плоскости, на поверхности или в пространстве.

В нашем случае, координаты отмечаются на плоскости, определённой координатными осями.

Рисунок 3. Координатная плоскость. Автор24 — интернет-биржа студенческих работ

Опишем рисунок. На плоскости выбрана точка, называемая началом координат. Её обозначают буквой $O$. Через начало координат проведены две прямые (координатные оси), пересекающиеся под прямым углом, причём одна из них строго горизонтальная, а другая — вертикальная. Такое положение считается обычным. Горизонтальная прямая называется осью абсцисс и обозначается $OX$, вертикальная — осью ординат $OY$.

Таким образом, оси определяют плоскость $XOY$.

Координаты точек в такой системе определяются двумя числами.

Существуют разные формулы (уравнения), определяющие те или иные координаты. Обычно в курсе аналитической геометрии изучают разные формулы прямых, углов, длины отрезка и прочие.

Перейдём сразу к формуле координаты середины отрезка.

Определение 4

Если координаты точки $E(x,y)$ — это середина отрезка $M_1M_2$, то:

Рисунок 4. Формула нахождения координаты середины отрезка. Автор24 — интернет-биржа студенческих работ

Практическая часть

Примеры из школьного курса геометрии достаточно просты. Рассмотрим несколько основных.

Для лучшего понимания, рассмотрим для начала элементарный наглядный пример.

Пример 1

Имеем рисунок:

На рисунке отрезки $AC, CD, DE, EB$ равны.

1. Серединой каких отрезков является точка $D$?
2. Какая точка является серединой отрезка $DB$?

1. точка $D$ является серединой отрезков $AB$ и $CE$;
2. точка $E$.

Рассмотрим другой простой пример, в котором нужно вычислить длину.

Пример 2

Точка $B$ — середина отрезка $AC$. $AB = 9$ см. Какая длина $AC$?

Так как т. $B$ делит $AC$ пополам, то $AB = BC= 9$ см. Значит, $AC = 9+9=18$ см.

Ответ: 18 см.

Прочие подобные примеры обычно идентичны и ориентированы на умение сопоставлять значения длин и их представление с алгебраическими действиями. Нередко в задачах встречаются случаи, когда сантиметр не укладывается ровное количество раз в отрезок. Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров. Отдельно измеряют остаток, сравнивая с миллиметром. Приведём пример, демонстрирующий такой случай.

Как найти координаты середины отрезка
Для начала разберемся, что такое середина отрезка.
Серединой отрезка считают точку, которая принадлежит данному отрезку и отстоит на одинаковое расстояние от его концов.

Координаты такой точки несложно найти, если известны координаты концов этого отрезка.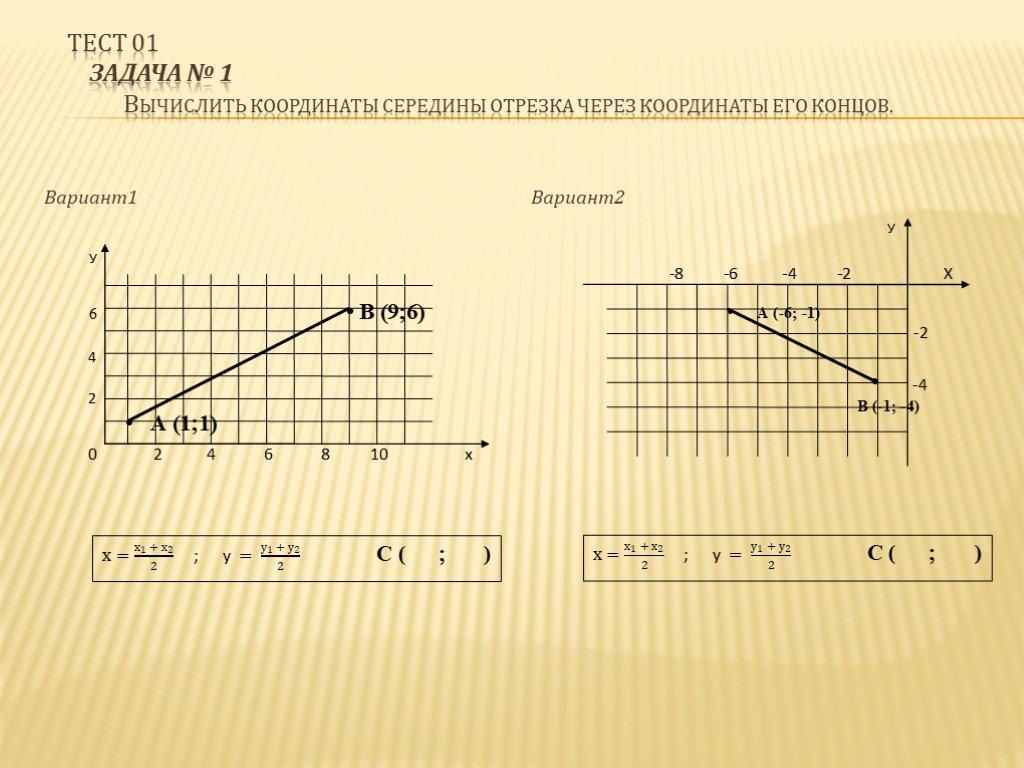 В таком случае координаты середины отрезка будут равны половине суммы соответствующих координат концов отрезка.
Координаты середины отрезка часто находят, решая задачи на медиану, среднюю линию и т.п.
Рассмотрим вычисление координат середины отрезка для двух случаев: когда отрезок задан на плоскости и задан в пространстве.
Пусть отрезок на плоскости задан двумя точками с координатами и . Тогда координаты середины отрезка РН рассчитываются по формуле:

Пусть отрезок задан в пространстве двумя точками с координатами и . Тогда координаты середины отрезка РН рассчитываются по формуле:

Пример.
Найти координаты точки К — середины МО, если М (—1; 6) и О (8; 5).

Решение.
Поскольку точки имеют две координаты, значит, отрезок задан на плоскости. Используем соответствующие формулы:

Следовательно, середина МО будет иметь координаты К (3,5; 5,5).

Ответ. К (3,5; 5,5).

Не составляет никакого труда. Для их расчета существует простое выражение, которое легко запомнить. Например, если координаты концов какого-либо отрезка соответственно равняются (х1; у1) и (х2; у2) соответственно, то координаты его середины рассчитываются как среднее арифметическое этих координат, то есть:

Вот и вся сложность.
Рассмотрим расчет координат центра одного из отрезков на конкретном примере, как Вы и просили.

Задача.
Найти координаты некоей точки М, если она является серединой (центром) отрезка КР, концов которого имеют такие координаты: (—3; 7) и (13; 21) соответственно.

Решение.
Используем рассмотренную выше формулу:

Ответ . М (5; 14).

С помощью данной формулы можно также найти не только координаты середины какого-либо отрезка, но и его концов. Рассмотрим пример.

Задача.
Даны координаты двух точек (7; 19) и (8; 27). Найти координаты одного из концов отрезка, если предыдущие две точки являются его концом и серединой.

Решение.
Обозначим концы отрезка К и Р, а его середину S. Перепишем формулу с учетом новых названий:

Подставим известные координаты и вычислим отдельные координаты:

После кропотливого труда я вдруг заметил, что размеры веб страниц достаточно велики, и если так пойдёт дальше, то можно тихо мирно озвереть =) Поэтому предлагаю вашему вниманию небольшое эссе, посвященное очень распространённой геометрической задаче – о делении отрезка в данном отношении , и, как частный случай, о делении отрезка пополам .

Данная задача по тем или иным причинам не вписалась в другие уроки, но зато сейчас есть прекрасная возможность рассмотреть её подробно и неторопливо. Приятная новость состоит в том, что мы немного отдохнём от векторов и сконцентрируем внимание на точках и отрезках.

Формулы деления отрезка в данном отношении

Понятие деления отрезка в данном отношении

Нередко обещанного вовсе ждать не приходится, сразу рассмотрим пару точек и, очевидное невероятное – отрезок :

Рассматриваемая задача справедлива, как для отрезков плоскости, так и для отрезков пространства. То есть, демонстрационный отрезок можно как угодно разместить на плоскости или в пространстве. Для удобства объяснений я нарисовал его горизонтально.

Что будем делать с данным отрезком? На этот раз пилить. Кто-то пилит бюджет, кто-то пилит супруга, кто-то пилит дрова, а мы начнём пилить отрезок на две части. Отрезок делится на две части с помощью некоторой точки , которая, понятно, расположена прямо на нём:

В данном примере точка делит отрезок ТАКИМ образом, что отрезок в два раза короче отрезка . ЕЩЁ можно сказать, что точка делит отрезок в отношении («один к двум»), считая от вершины .

На сухом математическом языке этот факт записывают следующим образом: , или чаще в виде привычной пропорции: . Отношение отрезков принято стандартно обозначать греческой буквой «лямбда», в данном случае: .

Пропорцию несложно составить и в другом порядке: – сия запись означает, что отрезок в два раза длиннее отрезка , но какого-то принципиального значения для решения задач это не имеет. Можно так, а можно так.

Разумеется, отрезок легко разделить в каком-нибудь другом отношении, и в качестве закрепления понятия второй пример:

Здесь справедливо соотношение: . Если составить пропорцию наоборот, тогда получаем: .

После того, как мы разобрались, что значит разделить отрезок в данном отношении, перейдём к рассмотрению практических задач.

Если известны две точки плоскости , то координаты точки , которая делит отрезок в отношении , выражаются формулами:

Откуда взялись данные формулы? В курсе аналитической геометрии эти формулы строго выводятся с помощью векторов (куда ж без них? =)). Кроме того, они справедливы не только для декартовой системы координат, но и для произвольной аффинной системы координат (см. урок Линейная (не) зависимость векторов. Базис векторов ). Такая вот универсальная задача.

Пример 1

Найти координаты точки , делящей отрезок в отношении , если известны точки

Решение : В данной задаче . По формулам деления отрезка в данном отношении, найдём точку :

Ответ :

Обратите внимание на технику вычислений: сначала нужно отдельно вычислить числитель и отдельно знаменатель. В результате часто (но далеко не всегда) получается трёх- или четырёхэтажная дробь. После этого избавляемся от многоэтажности дроби и проводим окончательные упрощения.

В задаче не требуется строить чертежа, но его всегда полезно выполнить на черновике:

Действительно, соотношение выполняется, то есть отрезок в три раза короче отрезка . Если пропорция не очевидна, то отрезки всегда можно тупо измерить обычной линейкой.

Равноценен второй способ решения : в нём отсчёт начинается с точки и справедливым является отношение: (человеческими словами, отрезок в три раза длиннее отрезка ). По формулам деления отрезка в данном отношении:

Ответ :

Заметьте, что в формулах необходимо переместить координаты точки на первое место, поскольку маленький триллер начинался именно с неё.

Также видно, что второй способ рациональнее ввиду более простых вычислений. Но всё-таки данную задачу чаще решают в «традиционном» порядке. Например, если по условию дан отрезок , то предполагается, что вы составите пропорцию , если дан отрезок , то «негласно» подразумевается пропорция .

А 2-ой способ я привёл по той причине, что частенько условие задачи пытаются намеренно подзапутать. Именно поэтому очень важно выполнять черновой чертёж чтобы, во-первых, правильно проанализировать условие, а, во-вторых, в целях проверки. Обидно допускать ошибки в такой простой задаче.

Пример 2

Даны точки . Найти:

а) точку , делящую отрезок в отношении ;
б) точку , делящую отрезок в отношении .

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Иногда встречаются задачи, где неизвестен один из концов отрезка:

Пример 3

Точка принадлежит отрезку . Известно, что отрезок в два раза длиннее отрезка . Найти точку , если .

Решение : Из условия следует, что точка делит отрезок в отношении , считая от вершины , то есть, справедлива пропорция: . По формулам деления отрезка в данном отношении:

Сейчас нам неизвестны координаты точки : , но это не является особой проблемой, так как их легко выразить из вышеприведённых формул. В общем виде выражать ничего не стОит, гораздо проще подставить конкретные числа и аккуратно разобраться с вычислениями:

Ответ :

Для проверки можно взять концы отрезка и, пользуясь формулами в прямом порядке, убедиться, что при соотношении действительно получится точка . И, конечно же, конечно же, не лишним будет чертёж. А чтобы окончательно убедить вас в пользе клетчатой тетради, простого карандаша да линейки, предлагаю хитрую задачу для самостоятельного решения:

Пример 4

Точка . Отрезок в полтора раза короче отрезка . Найти точку , если известны координат точек .

Решение в конце урока. Оно, кстати, не единственное, если пойдёте отличным от образца путём, то это не будет ошибкой, главное, чтобы совпали ответы.

Для пространственных отрезков всё будет точно так же, только добавится ещё одна координата.

Если известны две точки пространства , то координаты точки , которая делит отрезок в отношении , выражаются формулами:
.

Пример 5

Даны точки . Найти координаты точки , принадлежащей отрезку , если известно, что .

Решение : Из условия следует отношение: . Данный пример взят из реальной контрольной работы, и его автор позволил себе небольшую шалость (вдруг кто споткнётся) – пропорцию в условии рациональнее было записать так: .

По формулам координат середины отрезка:

Ответ :

Трёхмерные чертежи в целях проверки выполнять значительно сложнее. Однако всегда можно сделать схематический рисунок, чтобы разобраться хотя бы в условии – какие отрезки необходимо соотносить.

Что касается дробей в ответе, не удивляйтесь, обычное дело. Много раз говорил, но повторюсь: в высшей математике принято орудовать обыкновенными правильными и неправильными дробями. Ответ в виде пойдёт, но вариант с неправильными дробями более стандартен.

Разминочная задача для самостоятельного решения:

Пример 6

Даны точки . Найти координаты точки , если известно, что она делит отрезок в отношении .

Решение и ответ в конце урока. Если трудно сориентироваться в пропорциях, выполните схематический чертёж.

В самостоятельных и контрольных работах рассмотренные примеры встречаются как сами по себе, так и составной частью более крупных задач. В этом смысле типична задача нахождения центра тяжести треугольника.

Разновидность задания, где неизвестен один из концов отрезка, разбирать не вижу особого смысла, так как всё будет похоже на плоский случай, разве что вычислений чуть больше. Лучше вспомним годы школьные:

Формулы координат середины отрезка

Даже неподготовленные читатели могут помнить, как разделить отрезок пополам. Задача деления отрезка на две равные части – это частный случай деления отрезка в данном отношении. Двуручная пила работает самым демократичным образом, и каждому соседу за партой достаётся по одинаковой палке:

В этот торжественный час стучат барабаны, приветствуя знаменательную пропорцию . И общие формулы чудесным образом преображаются в нечто знакомое и простое:

Удобным моментом является тот факт, что координаты концов отрезка можно безболезненно переставить:

В общих формулах такой роскошный номер, как понимаете, не проходит. Да и здесь в нём нет особой надобности, так, приятная мелочь.

Для пространственного случая справедлива очевидная аналогия. Если даны концы отрезка , то координаты его середины выражаются формулами:

Пример 7

Параллелограмм задан координатами своих вершин . Найти точку пересечения его диагоналей.

Решение : Желающие могут выполнить чертёж. Граффити особенно рекомендую тем, кто капитально забыл школьный курс геометрии.

По известному свойству, диагонали параллелограмма своей точкой пересечения делятся пополам, поэтому задачу можно решить двумя способами.

Способ первый : Рассмотрим противоположные вершины . По формулам деления отрезка пополам найдём середину диагонали :

Объяснение урока: Разбиение отрезка на координатной плоскости

В этом объяснении мы узнаем, как найти координаты точки, которая делит отрезок на координатной плоскости с отношением, используя формула сечения.

Давайте сначала рассмотрим терминологию.

Определение: Отрезок линии

Отрезок — это часть линии, ограниченная двумя отдельными конечные точки.

Мы можем представить отрезок между двумя различными точками, 𝐴 и 𝐵, используя обозначение 𝐴𝐵. 𝐴𝐵 содержит все точки на прямая линия между 𝐴 и 𝐵.

Чтобы помочь нам понять это определение, мы можем рассмотреть отрезок линии 𝐴𝐵 нарисовано на координатной плоскости с конечные точки 𝐴(−4,5) и 𝐵(2,−3).

Середина отрезка — это средняя точка отрезка, точка равноудаленное между двумя конечными точками. Мы можем найти координаты середину 𝐴𝐵, разделив пополам каждый из горизонтальные и вертикальные расстояния между 𝐴 и 𝐵.

Резюме: середина отрезка линии

Мы можем найти середину 𝑀 отрезка между (𝑥,𝑦) и (𝑥,𝑦) с использованием 𝑀=𝑥+𝑥2,𝑦+𝑦2.

Теперь мы рассмотрим множество вопросов о делении или разбиении, отрезки линии различными способами.

Пример 1: Разделение отрезка на четыре равные части

Координаты 𝐴 и 𝐵 равны (1,9) и (9,9) соответственно. Определить координаты точек, которые делят 𝐴𝐵 на четыре равные части.

Ответ

Мы можем начать с наброска сегмента линии 𝐴𝐵 и показывая точки, которые делят его на 4 равные части. Мы можем определить эти точки как 𝑃, 𝑀 и 𝑄.

Поскольку 𝐴𝐵 делится на четыре равные части, мы можем подойти к этому вопросу, сначала найдя середину, 𝑀, из 𝐴𝐵 и затем найти середины 𝐴𝑀 и 𝑀𝐵.

Напомним, что середина 𝑀 отрезка между координатами (𝑥,𝑦) и (𝑥,𝑦) определяется выражением 𝑀=𝑥+𝑥2,𝑦+𝑦2.

Чтобы найти середину 𝑀, 𝐴𝐵, подставляем координаты 𝐴(1,9) для (𝑥,𝑦) значения и координаты 𝐵(9,9) для (𝑥,𝑦) значений, что дает 𝑀=1+92,9+92=102,182=(5,9). Таким образом, координаты 𝑀 равны (5,9).

Далее находим середину 𝑃 𝐴𝑀. Подстановка координат 𝐴(1,9) и 𝑀(5,9) для (𝑥,𝑦), и (𝑥,𝑦) соответственно, дает 𝑃=1+52,9+92=62,182=(3,9).

Наконец, мы находим середину 𝑄 𝑀𝐵. Используя координаты 𝑀(5,9) и 𝐵(9,9) дает 𝑃=5+92,9+92=142,182=(7,9).

Итак, мы нашли координаты 𝑃, 𝑀 и 𝑄, которые делят 𝐴𝐵 на 4 равные части, как (3,9),(5,9),(7,9).

Теперь мы рассмотрим пример того, как сегмент линии, который был разделен точкой можно записать в виде отношения.

Пример 2. Нахождение отношения, на которое точка делит отрезок прямой

Если 𝐶∈𝐴𝐵 и 𝐴𝐵=3𝐶𝐵, тогда 𝐶 делит 𝐵𝐴 по соотношению.

1. 2∶1
2. 1∶2
3. 1∶3
4. 3∶1

Ответ

Считаем, что у нас есть отрезок 𝐴𝐵. Где-то на этом отрезке будет точка 𝐶.

Так как нужно учитывать направление движения от 𝐴 в 𝐵 мы используем вектор 𝐴𝐵.

Движение из точки 𝐶 в точку 𝐵 равно вектор 𝐶𝐵.

Величины векторов 𝐴𝐵 и 𝐶𝐵 — их длины. Мы дано, что 𝐴𝐵=3𝐶𝐵; следовательно, мы можем написать, что длинадлины𝐴𝐵=3×𝐶𝐵.

Мы можем разделить 𝐴𝐵 на 3 равные части.

Однако нам нужно установить, в какой из этих точек 𝐶 будет лежать. Если 𝐶 ближе к 𝐴, чем 𝐵, то длина 𝐶𝐵 будет две трети длины из 𝐴𝐵.

Таким образом, было бы неверно, что 𝐴𝐵=3𝐶𝐵. Поэтому, 𝐶 должен быть в точке, которая ближе к 𝐵 чем 𝐴.

Таким образом, 𝐶𝐵=13𝐴𝐵 и 𝐴𝐵=3𝐶𝐵.

Чтобы найти коэффициент деления 𝐴𝐵 на 3 части, всего будет 2 части в 𝐴𝐶 и 1 часть в 𝐶𝐵.

Мы могли бы написать, что 𝐶 делит 𝐴𝐵 в соотношении 2∶1. Однако нас спросили, как 𝐶 делится 𝐵𝐴; поэтому решением является отношение дано в варианте ответа Б: 1∶2.

Теперь мы исследуем, как мы можем найти координаты точки на прямой. отрезок, который разбивает прямую в заданном отношении.

Векторы могут быть полезны при разделении сегментов линии в соотношении. Напомним, что векторы представляют направление и величину, а не положение по координате самолет. Учитывая две различные точки 𝐴 и 𝐵, вектор 𝐴𝐵 говорит нам относительное направление точки 𝐵 относительно точки 𝐴, а также расстояние между двумя точки. В частности, 𝐴𝐵 не обязательно должно начинаться с 𝐴 или заканчиваться на 𝐵, если они имеют то же направление и величину. Эта гибкость векторов является преимуществом, когда мы работаем с геометрическими такие проблемы, как разделение линии.

Рассмотрим, как идентифицировать координатные точки. Если точка 𝑃 разделяет 𝐴𝐵 в отношении 𝑚∶𝑛, это означает, что точка 𝑃 лежит на отрезке 𝐴𝐵 и соотношение величины векторов удовлетворяют ‖‖𝐴𝑃‖‖∶‖‖𝑃𝐵‖‖=𝑚∶𝑛.

Другими словами, если ‖‖𝐴𝑃‖‖ 𝑚 единицы длины, ‖‖𝐴𝐵‖‖ будет равно 𝑚+𝑛 единиц длины, что приводит к ‖‖𝐴𝑃‖‖=𝑚𝑚+𝑛‖‖𝐴𝐵‖‖.

В общем, было бы трудно использовать только приведенное выше уравнение, чтобы найти координаты точки разбиения 𝑃. Однако это уравнение не содержит информации о том, что 𝑃 лежит на отрезок прямой 𝐴𝐵. В частности, это означает, что 𝐴𝑃 имеет то же направление, что и 𝐴𝐵. Напомним, что два вектора имеют одинаковые направлении, если один вектор получается умножением другого вектора на некоторое положительная постоянная. Рассматривая приведенное выше уравнение, мы видим, что это положительная константа задается как 𝑚𝑚+𝑛. Это ведет к 𝐴𝑃=𝑚𝑚+𝑛𝐴𝐵.

Мы можем использовать это свойство, чтобы найти координаты точки, которая разбивает направленный отрезок в заданном отношении. Для этого сначала напишем 𝐴𝑃 и 𝐴𝐵 каждый как разность двух векторов положения: 𝐴𝑃=𝑂𝑃−𝑂𝐴, 𝐴𝐵=𝑂𝐵−𝑂𝐴.

Подстановка этих выражений в исходную формулу приводит к 𝑂𝑃−𝑂𝐴=𝑚𝑚+𝑛𝑂𝐵−𝑂𝐴.

Преобразование уравнения так, чтобы 𝑂𝑃 было предмет, получаем 𝑂𝑃 = 𝑚𝑚+𝑛𝑂𝐵— -+𝑂𝐴𝑂𝑃 = 𝑚𝑚+𝑛𝑂𝐵+ — 𝑚𝑚+𝑛+1 nather = 𝑚𝑚+𝑛𝑂𝐵+𝑛𝑚+𝑛tain𝑂𝐴.

Формула: вектор положения точки, разделяющей отрезок линии по соотношению

Пусть 𝑃 будет точкой на отрезке 𝐴𝐵, разбивая его в соотношении 𝑚∶𝑛. Тогда положение вектор 𝑂𝑃 определяется выражением 𝑂𝑃=𝑚𝑚+𝑛𝑂𝐵+𝑛𝑚+𝑛𝑂𝐴.

Давайте посмотрим, как мы можем использовать эту формулу, чтобы получить выражение для Декартовы координаты точки разбиения. Обозначим координаты точек 𝐴(𝑥,𝑦) и 𝐵(𝑥,𝑦). Тогда мы можем написать соответствующие векторы положения 𝑂𝐴=(𝑥,𝑦),𝑂𝐵=(𝑥,𝑦).

Подставляя эти выражения в приведенную выше формулу, получаем 𝑂𝑃 = 𝑚𝑚+𝑛 (𝑥, 𝑦)+𝑛𝑚+𝑛 (𝑥, 𝑦) = 𝑚𝑚+𝑛𝑥, 𝑚𝑚+𝑛𝑦+𝑛𝑚+𝑛𝑥, 𝑛𝑚+𝑛𝑦 = 𝑚𝑚+𝑛𝑥+𝑛𝑚+𝑛𝑥, 𝑚𝑚+𝑛𝑦+𝑛𝑚+𝑛𝑦 = 𝑚𝑥+𝑛𝑥𝑚+𝑛, 𝑚𝑦+𝑛𝑦𝑚+𝑛.

Мы приходим к следующей формуле.

Теорема: Формула сечения

Если у нас есть различные точки 𝐴(𝑥,𝑦) и 𝐵(𝑥,𝑦) и точка 𝑃∈𝐴𝐵 делит 𝐴𝐵 такое, что 𝐴𝑃∶𝑃𝐵=𝑚∶𝑛, то 𝑃 имеет координаты 𝑃=𝑚𝑥+𝑛𝑥𝑚+𝑛,𝑚𝑦+𝑛𝑦𝑚+𝑛. 

Теперь мы посмотрим, как мы можем применить эту формулу в нескольких примерах вопросов.

Пример 3. Нахождение координаты, разделяющей отрезок линии внутри

Если координаты 𝐴 и 𝐵 (5,5) и (−1,−4) соответственно, найдите координаты точки 𝐶, которая делит 𝐴𝐵 внутренне отношение 2∶1.

Ответ

Мы можем начертить этот направленный отрезок 𝐴𝐵 как показано.

Мы можем применить следующую формулу, чтобы найти точку 𝐶 который делит 𝐴𝐵 внутренне в отношение 2∶1. Это означает, что 𝐶∈𝐴𝐵 и соотношение будет иметь вид 𝐴𝐶∶𝐶𝐵=2∶1.

Затем мы можем применить формулу для разделения отрезка в заданном соотношении.

Если 𝐴(𝑥,𝑦) и 𝐵(𝑥,𝑦) и точка 𝑃 делит 𝐴𝐵 такое, что 𝐴𝑃∶𝑃𝐵=𝑚∶𝑛, то 𝑃 имеет координаты 𝑃=𝑚𝑥+𝑛𝑥𝑚+𝑛,𝑚𝑦+𝑛𝑦𝑚+𝑛.

Для нашей задачи 𝐴 имеет координаты (5,5) и 𝐵 имеет координаты (−1,−4). Мы можем заменить эти координаты в формулу для (𝑥,𝑦) и (𝑥,𝑦) соответственно.

Значения соотношения 2∶1 можно заменить на 𝑚 и 𝑛 соответственно.

Следовательно, мы будем иметь координаты 𝐶 как 𝐶=2(−1)+1(5)2+1,2(−4)+1(5)2+1.

Упрощая, имеем 𝐶=33,−33=(1,−1).

Таким образом, координаты точки 𝐶, которая делит 𝐴𝐵 внутренне по соотношению 2∶1 являются (1,−1).

Теперь мы увидим, как мы можем разбить линейный отрезок внешне в заданное соотношение.

До сих пор мы наблюдали, как определить координаты точки, которая делит отрезок в заданном отношении. Мы называем такие проблемы внутренними проблемы разделения, так как точка, которую мы ищем, находится внутри отрезок.

Давайте теперь рассмотрим другой тип задач, известный как внешнее деление. проблемы. В этих задачах точка, разделяющая отрезок лежит не внутри, а на продолжении отрезка, как показано на схеме ниже.

Рассматривая диаграмму выше, мы говорим, что точка 𝑃 делит 𝐴𝐵 внешне в соотношении 𝑚∶𝑛, где 𝑚>𝑛. Мы можем решить такие внешние проблемы деления, немного изменив наш предыдущий подход к проблемы с внутренним разделением. Основное отличие для этого случая состоит в том, что 𝐴𝑃, с величиной 𝑚 длины единиц, является большим вектором по сравнению с 𝐵𝑃, с величиной 𝑛 единицы длины. Вычитанием мы видим, что длина из 𝐴𝐵 равно 𝑚−𝑛 единиц. Это ведет к ‖‖𝐴𝑃‖‖=𝑚𝑚−𝑛‖‖𝐴𝐵‖‖.

Как и в предыдущем контексте, 𝐴𝑃 и 𝐴𝐵 имеют одинаковое направление, поэтому мы можем написать 𝐴𝑃=𝑚𝑚−𝑛𝐴𝐵.

Так же, как мы сделали для задачи внутреннего разделения, мы можем вычислить формула для вектора положения 𝑃: 𝑂𝑃 — — 𝑂𝐴 = 𝑚𝑚 — 𝑛𝑂𝐵 — неели 𝑂𝐴𝑂𝑃=𝑚𝑚−𝑛𝑂𝐵−𝑛𝑚−𝑛𝑂𝐴.

Отметим, что эта формула очень похожа на полученную ранее для проблемы внутреннего разделения. Заметные отличия заключаются в следующем:

• Два выражения вычитаются, а не складываются.
• Выражение 𝑚+𝑛 заменено на 𝑚−𝑛.

В правой части выше выражение 𝑚+𝑛 для внутреннего разбиения заменен на 𝑚−𝑛 для внешнего разделения. Выведем формулу для декартовых координат точки разбиения, учитывая координаты 𝐴(𝑥,𝑦) и 𝐵(𝑥,𝑦): 𝑂𝑃 = m 𝑚𝑚 — 𝑛𝑦 — 𝑛𝑚 — = 𝑚𝑥 — 𝑛𝑥𝑚 — 𝑛, 𝑚𝑦 — 𝑛𝑦𝑚 — 𝑛. 

Это приводит к следующей формуле.

Теорема: Формула сечения с внешним делением

Если у нас есть различные точки 𝐴(𝑥,𝑦) и 𝐵(𝑥,𝑦) и точка 𝑃∉𝐴𝐵 делит 𝐴𝐵 такое, что 𝐴𝑃∶𝑃𝐵=𝑚∶𝑛, тогда 𝑃 имеет координаты 𝑃=𝑚𝑥−𝑛𝑥𝑚−𝑛,𝑚𝑦−𝑛𝑦𝑚−𝑛.

Теперь мы увидим, как можно применить эту формулу в следующем примере.

Пример 4. Нахождение координат точки, разделяющей отрезок прямой Внешне в заданное соотношение

Если 𝐴(3,−2) и 𝐵(−2,4), найти в векторной форме координаты точки 𝐶, которая делит 𝐴𝐵 внешне в отношение 4∶3.

Ответ

Мы можем начать с наброска точек 𝐴 и 𝐵 и продолжение направленного отрезка 𝐴𝐵 указать 𝐶 который делит 𝐴𝐵 внешне. Мы можем написать, что 𝐴𝐶∶𝐶𝐵=4∶3.

Вспоминаем формулу раздела для внешнего деления.

Если у нас есть различные точки 𝐴(𝑥,𝑦) и 𝐵(𝑥,𝑦) и точка 𝑃∉𝐴𝐵 делит 𝐴𝐵 такое, что 𝐴𝑃∶𝑃𝐵=𝑚∶𝑛, то 𝑃 имеет координаты 𝑃=𝑚𝑥−𝑛𝑥𝑚−𝑛,𝑚𝑦−𝑛𝑦𝑚−𝑛.

Мы можем подставить значения 𝐴(3,−2) и 𝐵(−2,4) для (𝑥,𝑦) и (𝑥,𝑦) значений соответственно, и значения отношения 4∶3 для 𝑚 и 𝑛 в формулу сечения, чтобы найти координаты из 𝐶. Это дает нам 𝐶=4(−2)−3(3)4−3,4(4)−3(−2)4−3=−8−91,16+61=(−17,22).

Поскольку нас просят дать ответ в векторной форме, мы можем указать позицию вектор 𝐶 как (−17,22).

Теперь мы увидим пример того, как мы можем использовать формулу сечения, чтобы найти отношение, в котором делится отрезок.

Пример 5. Нахождение отношения, в котором ось 𝑥 делит отрезок прямой

Заполните пропуск: Учитывая, что 𝐶(−3,3) и 𝐷(4,−2), 𝑥-ось делит 𝐶𝐷 в соотношении .

1. 3∶5
2. 5∶3
3. 2∶3
4. 3∶2

Ответ

Мы можем начать с построения координат 𝐷 и рисуем вектор 𝐶𝐷.

Чтобы найти, как делится ось 𝑥 𝐶𝐷, нам сначала нужно найти точка, где 𝐶𝐷 пересекает 𝑥-ось. Учитывая координаты 𝐶 и 𝐷, мы можем найти уравнение 𝐶𝐷, начиная с нахождения наклона этой строки.

Наклон, 𝑚, линии, соединяющей две точки (𝑥,𝑦) и (𝑥,𝑦) можно найти с помощью 𝑚=𝑦−𝑦𝑥−𝑥.

Следовательно, наклон между 𝐶(−3,3) а 𝐷(4,−2) определяется выражением 𝑚=−2−34−(−3)=−57=−57.

Затем мы можем использовать форму точки-наклона линии, такую, что учитывая точку (𝑥,𝑦) и наклон, 𝑚, мы можем записать уравнение прямой как 𝑦−𝑦=𝑚(𝑥−𝑥).

Мы можем заменить координаты либо 𝐶, либо 𝐷 в эту форму, поэтому используя 𝐶(−3,3) для (𝑥,𝑦) значения и 𝑚=−57, имеем 𝑦−3=−57(𝑥−(−3))𝑦−3=−57(𝑥+3).

Затем мы можем умножить обе части на 7 и раскрыть скобки на правая сторона, дающая 7𝑦-21=-5(𝑥+3)7𝑦-21=-5𝑥-15.

Преобразование, чтобы записать это в общей форме уравнения линии, 𝑎𝑥+𝑏𝑦+𝑐=0, имеем 5𝑥+7𝑦−6=0.

Напомним, что прямая пересекает ось 𝑥, когда 𝑦=0, поэтому подставляя это в уравнение 5𝑥+7𝑦−6=0 и упрощение дает 5𝑥+7(0)−6=0,5𝑥−6=0,5𝑥=6,𝑥=65.

Теперь мы вычислили, что отрезок прямой 𝐶𝐷 пересекает 𝑥-ось в точке 65,0.

Теперь нам нужно найти отношение, в котором эта координата, 65,0, делит 𝐶𝐷.

Для этого мы можем использовать формулу сечения для внутреннего деления отрезок. Если у нас есть различные точки 𝐴(𝑥,𝑦) и 𝐵(𝑥,𝑦) и точка 𝑃∈𝐴𝐵 делит 𝐴𝐵 такое, что 𝐴𝑃∶𝑃𝐵=𝑚∶𝑛, то 𝑃 имеет координаты 𝑃=𝑚𝑥+𝑛𝑥𝑚+𝑛,𝑚𝑦+𝑛𝑦𝑚+𝑛. 

В этом вопросе мы знаем точки 𝐶(−3,3) и 𝐷(4,−2) и точку 𝑃65,0 что делит 𝐶𝐷. Нам нужно рассчитать отношение значения 𝑚 и 𝑛.

Замена 𝐶(−3,3) и 𝐷(4,−2) для (𝑥,𝑦) и (𝑥,𝑦) соответственно в секцию формула, мы имеем 𝑃=𝑚(4)+𝑛(−3)𝑚+𝑛,𝑚(−2)+𝑛(3)𝑚+𝑛=4𝑚−3𝑛𝑚+𝑛,−2𝑚+3𝑛𝑚+𝑛.

Мы знаем, что у 𝑃 есть координаты 65,0, поэтому мы можем написать 65,0=4𝑚−3𝑛𝑚+𝑛,−2𝑚+3𝑛𝑚+𝑛.

Вычисляя 𝑥-координаты, имеем 65=4𝑚−3𝑛𝑚+𝑛.

Мы можем перекрестно умножить и упростить, чтобы написать выражение для 𝑚 с точки зрения 𝑛 как 5(4𝑚−3𝑛)=6(𝑚+𝑛)20𝑚−15𝑛=6𝑚+6𝑛14𝑚=21𝑛𝑚𝑛=2114𝑚𝑛=32.

Отношение 𝐶𝑃∶𝑃𝐷=𝑚∶𝑛, поэтому 𝐶𝑃∶𝑃𝐷=3∶2.

Таким образом, мы можем дать ответ, что ось 𝑥 делит 𝐶𝐷 в соотношении 3∶2.

Для проверки нашего ответа мы могли бы найти расстояние 𝐶𝑃 и расстояние 𝑃𝐷 и найдите отношение 𝐶𝑃∶𝑃𝐷 напрямую.

Напомним, что формула расстояния для нахождения расстояния, 𝑑, между двумя точками (𝑥,𝑦) и (𝑥,𝑦) задается формулой 𝑑=(𝑥−𝑥)+(𝑦−𝑦). 

Чтобы найти длину 𝐶𝑃, ‖‖𝐶𝑃‖‖, подставляем значения 𝐶(−3,3) и 𝑃65,0 за (𝑥,𝑦) и (𝑥,𝑦) значения, чтобы дать ‖‖𝐶𝑃‖‖=65−(−3)+(0−3)=215+3=66625=3√745.

Чтобы найти длину 𝑃𝐷, ‖‖𝑃𝐷‖‖, подставляем 𝑃65,0 и 𝐷(4,−2) для (𝑥,𝑦) и (𝑥,𝑦) значений, что дает ‖‖𝑃𝐷‖‖=4−65+(−2−0)=145+(−2)=29625=2√745.

Тогда мы можем записать соотношение из 𝐶𝑃∶𝑃𝐷 как 𝐶𝑃∶𝑃𝐷=3√745∶2√745.

Умножение обеих частей отношения на 5, а затем деление на √74, дает 𝐶𝑃∶𝑃𝐷=3√74∶2√74=3∶2.

Таким образом, мы подтвердили наш ответ, что ось 𝑥 делит 𝐶𝐷 по соотношению 3∶2.

В следующем примере мы видим более сложную задачу, включающую разбиение отрезка.

Пример 6. Решение текстовой задачи путем деления отрезка

Автобус едет из города 𝐴(10,−10) в город 𝐵(−8,8). Его первая остановка находится в 𝐶, что на полпути между городами. Его вторая остановка находится в 𝐷, что составляет две трети пути от 𝐴 до 𝐵. Каковы координаты 𝐶 и 𝐷?

Ответ

Нам дано, что город 𝐴 имеет координаты (10,−10) и город 𝐵 имеет координаты (−8,8). Во-первых, нам нужно найти координаты города 𝐶, на полпути между эти.

Мы можем использовать формулу для середины прямой. Чтобы найти середина 𝑀 отрезка между двумя точками (𝑥,𝑦) и (𝑥,𝑦) мы можем использовать 𝑀=𝑥+𝑥2,𝑦+𝑦2.

Подставляя (𝑥,𝑦)=(10,−10) и (𝑥,𝑦)=(−8,8) в это формула дает среднюю точку, 𝐶, как 𝐶=10+(−8)2,−10+82=22,−22=(1,−1).

Далее нам нужно найти координаты 𝐷, т.е. две трети пути от 𝐴 до 𝐵. Направление, 𝐴 к 𝐵, важно, так как указывает на положение 𝐷. 𝐷 будет ближе к 𝐵 чем 𝐴. Мы можем думать о позицию, разделив 𝐴𝐵 на 3 равные части. Мы можем написать соотношение 𝐴𝐷∶𝐷𝐵 как 2∶1.

Формулу можно использовать для разделения отрезка в заданном соотношении. Если 𝐴(𝑥,𝑦) и 𝐵(𝑥,𝑦) и точка 𝑃 делит 𝐴𝐵 так, что 𝐴𝑃∶𝑃𝐵=𝑚∶𝑛, то 𝑃 имеет координаты 𝑃=𝑚𝑥+𝑛𝑥𝑚+𝑛,𝑚𝑦+𝑛𝑦𝑚+𝑛.

В этом вопросе имеем 𝐴(10,−10), 𝐵(−8,8) и точка 𝐷 что делит 𝐴𝐵 в соотношении 2∶1. Подставив их в формулу, найти 𝐷 дает 𝐷=2(−8)+1(10)2+1,2(8)+1(−10)2+1=−63,63=(−2,2).

В качестве полезной проверки нашего ответа мы можем рассмотреть длины 𝐴𝐵 и 𝐴𝐷, применяя формулу расстояния. Чтобы найти расстояние 𝑑 между двумя точками (𝑥,𝑦) и (𝑥,𝑦), вычисляем 𝑑=(𝑥−𝑥)+(𝑦−𝑦).

Чтобы вычислить длину 𝐴𝐷, мы можем заменить координаты 𝐴(10,−10) и 𝐷(−2,2) в формулу, чтобы дать 𝑑=(−2−10)+(2−(−10))=(−12)+12=√288=12√2.

Чтобы вычислить длину 𝐴𝐵, подставляем 𝐴(10,−10) и 𝐵(−8,8) в формулу расстояния, что дает 𝑑=(−8−10)+(8−(−10))=(−18)+18=√648=18√2.

Таким образом, мы можем записать отношение длин 𝐴𝐷 ∶𝐴𝐵 как 𝐴𝐷∶𝐴𝐵=12√2∶18√2=12∶18=2∶3.

Нам дали, что 𝐷 — это две трети пути от 𝐴 до 𝐵. Таким образом, у нас есть подтвердил, что 𝐷 имеет координаты (−2,2).

Мы можем дать ответ, что координаты 𝐶 и 𝐷 (1,−1)(−2,2) и

Ключевые точки

• Середина 𝑀 отрезка прямой между (𝑥,𝑦) и (𝑥,𝑦) определяется выражением 𝑀=𝑥+𝑥2,𝑦+𝑦2. 
• Если у нас есть различные точки 𝐴(𝑥,𝑦) и 𝐵(𝑥,𝑦) и точка 𝑃 делит 𝐴𝐵 внутренне такое, что 𝐴𝑃∶𝑃𝐵=𝑚∶𝑛, тогда 𝑃 имеет координаты 𝑃=𝑚𝑥+𝑛𝑥𝑚+𝑛,𝑚𝑦+𝑛𝑦𝑚+𝑛.
• При решении задач, связанных с разбиением отрезка, мы должны быть осторожны, чтобы установить правильный порядок соотношения. Если 𝐴𝐵 делится точкой 𝑃 в отношении 𝑚∶𝑛, то отношение 𝐴𝑃∶𝑃𝐵 будет 𝑚∶𝑛. Если 𝐵𝐴 делится точкой 𝑃 в соотношении 𝑚∶𝑛, тогда отношение 𝐴𝑃∶𝑃𝐵 вместо этого будет быть 𝑛∶𝑚.
• Если у нас есть различные точки 𝐴(𝑥,𝑦) и 𝐵(𝑥,𝑦) и точка 𝑃∉𝐴𝐵 делит 𝐴𝐵 внешне такой что 𝐴𝑃∶𝑃𝐵=𝑚∶𝑛, то 𝑃 имеет координаты 𝑃=𝑚𝑥−𝑛𝑥𝑚−𝑛,𝑚𝑦−𝑛𝑦𝑚−𝑛.

Калькулятор разделов — Калькулятор соотношений направленных отрезков

Введите точки и отношения в соответствующие поля ввода и выберите тип раздела, т.е. внутренний или внешний. Нажмите кнопку расчета, чтобы найти координаты точки с помощью калькулятора отрезков.

Формула:
Внутренне = ( mx ₂ +nx ₁ m+n , my ₂ +ny ₁ m+n ) Внешне = ( mx ₂ -nx ₁ м-н , мой ₂ -ny ₁ м-н )

Тип:

Внутри

Внешне

Пункт один:

Вторая точка:

Соотношение:

РЕКЛАМА

РЕКЛАМА

Содержание:

• Калькулятор разбиения
• Координаты точки — определение
• Формула координат деления отрезка
• Как найти отношение направленного отрезка?

Дайте нам отзыв

✎

✉

Калькулятор разбиений 

Калькулятор отношений направленных отрезков – это онлайн-инструмент, который находит координаты точки, разделяющей прямую (внутреннюю/внешнюю), соединяющую две точки A и B для заданного отношения м90 и н.

Координаты точки — определение

Координаты точки — это пара чисел, указывающая ее точное местоположение на двумерной плоскости. Координатная плоскость имеет две оси под прямым углом друг к другу, называемые x и y ось.

Formula of coordinates dividing a line segment

Coordinates dividing line internally

Coordinates dividing line externally

Where,

x ₁ , x ₂ , y ₁ , y ₂ являются конечной точкой отрезка,

m и n – внешние и внутренние коэффициенты.

Как найти отношение направленного отрезка?

Найдем координаты точек, разделяющих отрезок, соединяющий две точки, на примере.

Пример:

Найдите координаты точки, которая делит направленный отрезок внутренней линии с концами (2, 4), (3, 6) с отношением 5:6.