Координаты середины отрезка онлайн: Онлайн калькулятор. Середина отрезка

Применение метода координат в решении простейших задач 9 класс онлайн-подготовка на Ростелеком Лицей

Обзор основных сведений и формул для векторов в координатах

 

В координатной плоскости любой вектор  однозначно разлагается по векторам  и  

 

Числа  определяются единственным образом и называются координатами вектора  в данной системе координат (рис. 1).

Рис. 1. Координаты вектора

Если есть точка , то вектор с началом в начале координат, который называется радиус-вектором точки , имеет те же самые координаты: .

Основываясь на этом, мы рассмотрели 3 стандартные задачи:

Определение координат середины отрезка по координатам концов отрезка и  

Рис. 2. Иллюстрация к задаче

Определение длины вектора  с координатами .

 

Определение длины отрезка  по координатам концов  и .

Теперь применим эти сведения для решения задач.

 

Решение задач с использованием метода координат

 

 

Задача 1.

 

Рис. 3. Иллюстрация к задаче

Дан треугольник с вершинами . Найти медиану .     

Дано:

           ;

           

           

Найти: .

Решение:

Найдем координаты точки  как середины отрезка ВС:

Найдем длину отрезка :

.

Ответ: .

Задача 2.

Вершина  параллелограмма  лежит на положительной полуоси , вершина  имеет координаты ; . Найти координаты точки  сторону  диагональ .

Решение:

Построим данный параллелограмм в прямоугольной системе координат (рис. 4).

Рис. 4. Иллюстрация к задаче

Так как , то координаты точки  . Пусть координаты точки .

Так как  параллелограмм, то ;

Координаты равны, следовательно,

Итак, ;

 так как вектор  имеет те же координаты, что и точка .

 так как координаты вектора  совпадают с координатами точки

Ответ: ;

Задача 3.

Найти периметр треугольника, если известны координаты его вершин (рис. 5).

Рис. 5. Иллюстрация к задаче

Дано: 

            

            ;

 .

Найти: периметр .

Решение:

Воспользуемся формулой вычисления расстояния между точками.

Найдем длину :

Найдем длину :

Найдем длину :

Найдем периметр:

Ответ:

 

Заключение

 

 

Мы сделали обзор сведений о координатах, о простейших задачах и применили эти сведения для решения конкретных геометрических задач.

 

 

Список литературы

1. Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
2. Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
3. Погорелов А. В. Геометрия, уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. E-science. ru (Источник).
2. E-science.ru (Источник).
3. Mathematics.ru (Источник).

 

Домашнее задание

1. Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010., №№ 943, 945, 947.

 

Найти длину отрезка по координатам точек. Нахождение координат середины отрезка: примеры, решения

Если вы хорошо заточенным карандашом прикоснетесь к тетрадному листу, то останется след, который дает представление о точке. (рис. 3 ).

Отметим на листе бумаги две точки A и B. Эти точки можно соединить различными линиями (рис. 4 ). А как соединить точки A и B самой короткой линией? Это можно сделать с помощь линейки (рис. 5 ). Полученную линию называют отрезком .

Точка и отрезок − примеры геометрических фигур .

Точки A и B называют концами отрезка .

Существует единственный отрезок, концами которого являются точки A и B. Поэтому отрезок обозначают, записывая точки, которые являются его концами. Например, отрезок на рисунке 5 обозначают одним из двух способов: AB или BA. Читают: «отрезок AB» или «отрезок BA».

На рисунке 6 изображены три отрезка. Длина отрезка AB равна 1 см. Он помещается в отрезке MN ровно три раза, а в отрезке EF − ровно 4 раза. Будем говорить, что длина отрезка MN равна 3 см, а длина отрезка EF − 4 см.

Также принято говорить: «отрезок MN равен 3 см», «отрезок EF равен 4 см». Пишут: MN = 3 см, EF = 4 см.

Длины отрезков MN и EF мы измерили единичным отрезком , длина которого равна 1 см. Для измерения отрезков можно выбрать и другие единицы длины , например: 1 мм, 1 дм, 1 км. На рисунке 7 длина отрезка равна 17 мм. Он измерен единичным отрезком, длина которого равна 1 мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7 ).

Вообще, измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается .

Длина отрезка обладает следующим свойством.

Если на отрезке AB отметить точку C, то длина отрезка AB равна сумме длин отрезков AC и CB (рис. 8 ).

Пишут: AB = AC + CB.

На рисунке 9 изображены два отрезка AB и CD. Эти отрезки при наложении совпадут.

Два отрезка называют равными, если они совпадут при наложении.

Следовательно отрезки AB и CD равны. Пишут: AB = CD.

Равные отрезки имеют равные длины.

Из двух неравных отрезков бОльшим будем считать тот, у уоторого длина больше. Например, на рисунке 6 отрезок EF больше отрезка MN.

Длину отрезка AB называют расстоянием между точками A и B.

Если несколько отрезков расположить так, как показано на рисунке 10, то получится геометрическая фигура, которую называют ломаная . Заметим, что все отрезки на рисунке 11 ломаную не образуют. Считают, что отрезки, образуют ломаную, если конец первого отрезка совпадает с концом второго, а другой конец второго отрезка − с концом третьего и т.

д.

Точки A, B, C, D, E − вершины ломаной ABCDE, точки A и E − концы ломаной , а отрезки AB, BC, CD, DE − ее звенья (см. рис. 10 ).

Длиной ломаной называют сумму длин всех ее звеньев.

На рисунке 12 изображены две ломаные, концы которых совпадают. Такие ломаные называют замкнутыми .

Пример 1 . Отрезок BC на 3 см меньше отрезка AB, длина которого равна 8 см (рис. 13 ). Найдите длину отрезка AC.

Решение. Имеем: BC = 8 − 3 = 5 (см).

Воспользовавшись свойством длины отрезка, можно записать AC = AB + BC. Отсюда AC = 8 + 5 = 13 (см).

Ответ: 13 см.

Пример 2 . Известно, что MK = 24 см, NP = 32 см, MP = 50 см (рис. 14 ). Найдите длину отрезка NK.

Решение. Имеем: MN = MP − NP.

Отсюда MN = 50 − 32 = 18 (см).

Имеем: NK = MK − MN.

Отсюда NK = 24 − 18 = 6 (см).

Ответ: 6 см.

Определить длину отрезка возможно разными способами.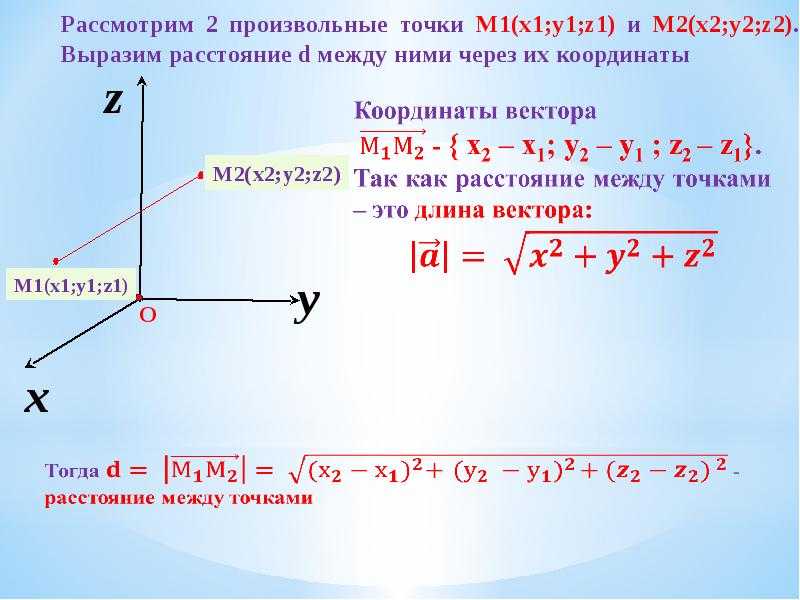 Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.

Длина отрезка с помощью линейки

Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.

Метод координат на плоскости

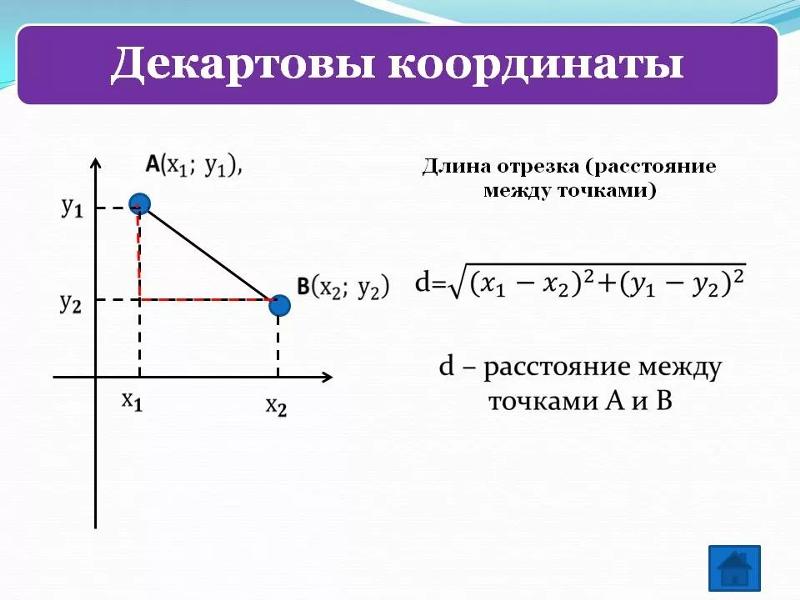
Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.

Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.

Метод координат в пространстве

Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях . Как найти длину вектора?

1. Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
2. После этого нужно возвести каждую координату вектора в квадрат.
3. Затем складываем квадраты координат.
4. Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.

Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).

Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.

Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .

Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.

Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая.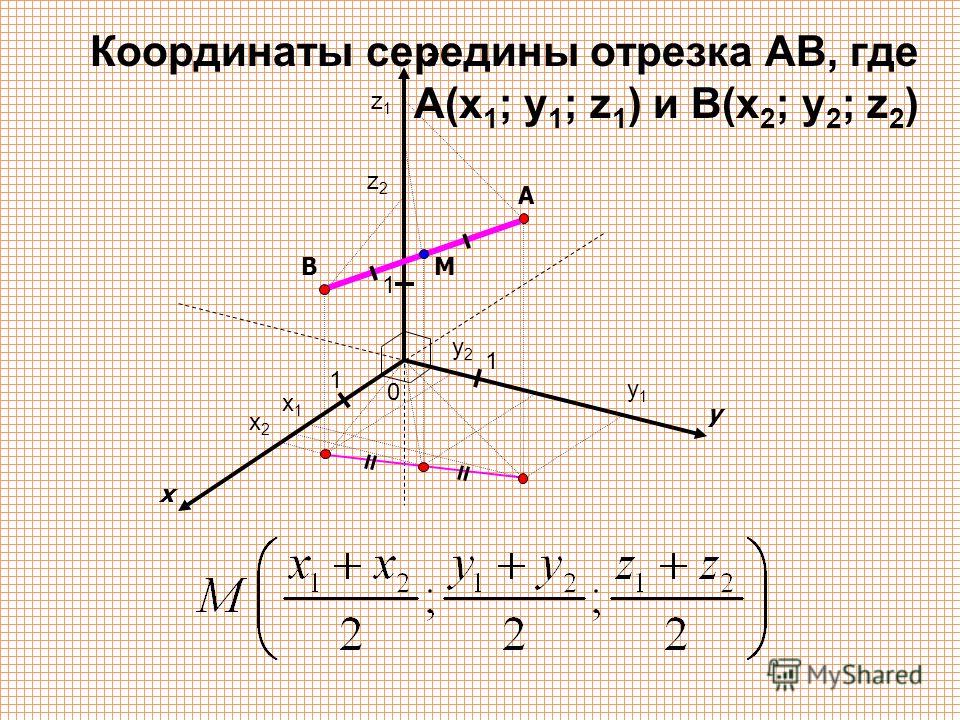 В этих системах координат вся точка имеет три координаты. Зная координаты 2-х точек, дозволено определить расстояние между этими двумя точками.

Вам понадобится

• Декартовы, полярные и сферические координаты концов отрезка

Инструкция

1. Разглядите для начала прямоугольную декартову систему координат. Расположение точки в пространстве в этой системе координат определяется

координатами x,y и z. Из начала координат к точке проводится радиус-вектор. Проекции этого радиус-вектора на координатные оси и будут координатами этой точки.Пускай у вас сейчас есть две точки с координатами x1,y1,z1 и x2,y2 и z2 соответственно. Обозначьте за r1 и r2, соответственно, радиус-векторы первой и 2-й точки. Видимо, что расстояние между этими двумя точками будет равно модулю вектора r = r1-r2, где (r1-r2) – векторная разность.Координаты вектора r, видимо, будут следующими: x1-x2, y1-y2, z1-z2. Тогда модуль вектора r либо расстояние между двумя точками будет равно: r = sqrt(((x1-x2)^2)+((y1-y2)^2)+((z1-z2)^2)). 2))

Видео по теме

Длина, как уже отмечалось, обозначается знаком модуля.

Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле

Если даны две точки пространства и , то длину отрезка можно вычислить по формуле

Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант

Пример 3

Решение: по соответствующей формуле:

Ответ:

Для наглядности выполню чертёж

Отрезок – это не вектор , и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.

Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:

Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».

Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:

Обратите внимание на важный технический приём – вынесение множителя из-под корня . В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.

Вот другие распространенные случаи:

Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.

Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.

В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.

Давайте заодно повторим возведение корней в квадрат и другие степени:

Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.

Задание для самостоятельного решения с отрезком в пространстве:

Пример 4

Даны точки и . Найти длину отрезка .

Решение и ответ в конце урока.

В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.

Yandex.RTB R-A-339285-1 Определение 1

Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .

Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .

Определение 2

Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .

Определение 3

Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B

Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B: необходимо определить координату x C .

Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.

| А С | = | С В | ⇔ x C — x A = x B — x C

Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)

Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).

Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):

Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.

Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .

Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).

Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:

x C = x A + x B 2 и y C = y A + y B 2

Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:

Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A (x A , y A) и B (x B , y B) определяются как :

(x A + x B 2 , y A + y B 2)

Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) .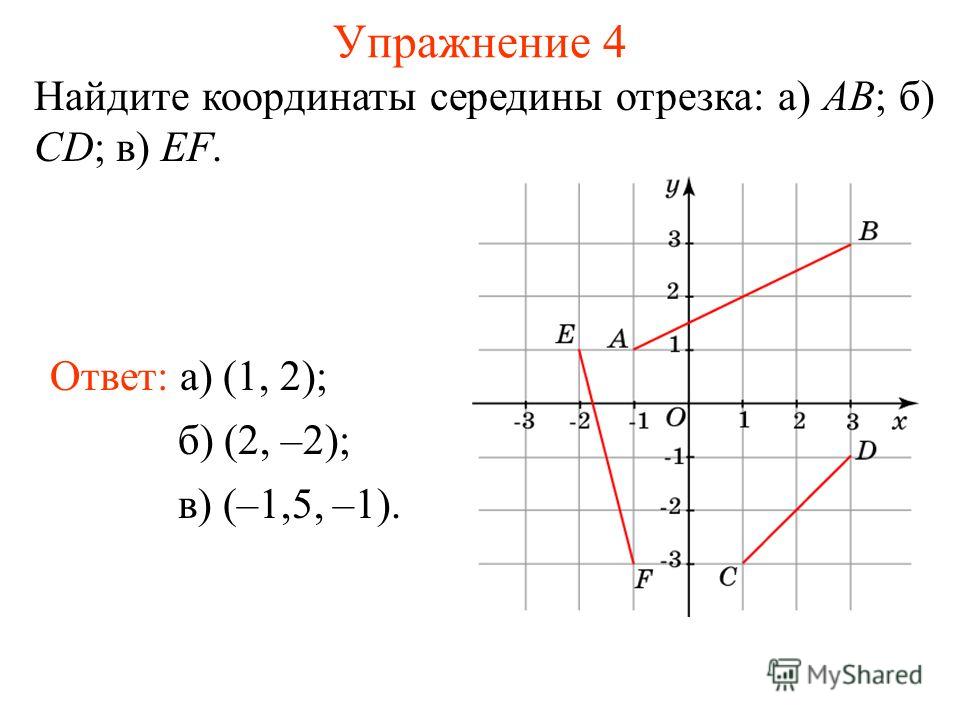 Необходимо определить координаты точки C , являющейся серединой отрезка A B .

A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.

Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z

Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:

x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2

Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.

Определение координат середины отрезка через координаты радиус-векторов его концов

Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.

Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .

Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:

O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2

Следовательно, точка C имеет координаты:

x A + x B 2 , y A + y B 2

По аналогии определяется формула для нахождения координат середины отрезка в пространстве:

C (x A + x B 2 , y A + y B 2 , z A + z B 2)

Примеры решения задач на нахождение координат середины отрезка

Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы.

Рассмотрим характерные примеры.

Пример 1

Исходные данные: на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.

Решение

Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .

x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2

Ответ : координаты середины отрезка А В — 5 2 , 7 2 .

Пример 2

Исходные данные: известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.

Решение

1. По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:

x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3

1. Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:

A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58

Ответ: 58

Пример 3

Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.

Решение

Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8

Ответ: координаты точки А (7 , 3 , — 8) .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Калькулятор средней точки

— онлайн-инструмент для нахождения средней точки

Калькулятор средней точки

— это онлайн-инструмент, который вычисляет среднюю точку для заданных точек на координатной плоскости. Середина — это точка на отрезке, которая находится на равном расстоянии от двух конечных точек. Это также центр тяжести отрезка.

Что такое калькулятор средней точки?

Калькулятор средней точки используется для вычисления средней точки отрезка прямой, если заданы координаты x и y двух конечных точек. Середина — это точка, которая делит отрезок внутри в соотношении 1:1. Чтобы использовать Калькулятор средней точки введите значения в поля ввода.

Калькулятор средней точки

Как пользоваться калькулятором средней точки?

Выполните следующие действия, чтобы с помощью онлайн-калькулятора средней точки найти среднюю точку отрезка прямой.

• Шаг 1: Перейдите к онлайн-калькулятору средней точки Cuemath.
• Шаг 2: Введите значения координат «x» и «y» для обеих точек в соответствующих полях ввода.
• Шаг 3: Нажмите « Вычислить «, чтобы найти среднюю точку.
• Шаг 4: Нажмите « Сброс », чтобы очистить поля и ввести новые значения.

Как работает калькулятор средней точки?

Формула средней точки является частным случаем формулы сечения. Формула сечения используется для определения отношения, в котором точка делит отрезок линии снаружи или внутри. Поскольку середина всегда будет делить отрезок линии в соотношении 1:1, формулу сечения можно преобразовать, чтобы получить формулу средней точки. Чтобы найти середину любого отрезка прямой, используются следующие шаги.

1. Возьмите сумму двух координат x конечных точек и разделите ее на 2.
2. Возьмите сумму двух координат Y конечных точек и разделите ее на 2.
3. Значения, полученные на шаге 1 и шаге 2, дадут координаты x и y соответственно для средней точки сегмента прямой.

Для любых двух точек, скажем, A (x ₁ , y ₁ ) и C (x ₂ , y ₂ ), середина — это точка B, расположенная посередине между точками A и C. Формула дается:

Середина = [(x ₁ + x ₂ )/2, (y ₁ + y ₂ )/2]

Хотите найти сложные математические решения за секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Записаться на бесплатный пробный урок

Решенные примеры на калькуляторе средней точки

Пример 1:

Найдите середину отрезка, соединяющего точки (-3, 2) и (1, -6). Проверьте это с помощью калькулятора средней точки.

Решение:

Пусть (x ₁ , y ₁ ) = (-3, 2) и (x ₂ , y ₂ ) = (1, -03) Середина 9002 вычисляется по формуле:

Середина = ( (x ₁ + x ₂ ) / 2 , (y ₁ + y ₂ ) / 2 )

= ((-3 + 1) / 2 , (2 + (-6)) / 2 )

= (-2/2 , -4/2)

= (-1, -2)

Следовательно, середина отрезка, соединяющего точки (-3, 2) и (1, -6) равно (-1, -2)

Пример 2:

Найдите середину отрезка, соединяющего точки (5, 10) и (3, 12). Проверьте это с помощью калькулятора средней точки

Решение:

Пусть (x ₁ , y ₁ ) = 5, 10) и (x ₂ , y ₂ 2) 0 3 (0 2) 3

Середина вычисляется по формуле:

Середина = ( (x ₁ + x ₂ ) / 2 , (y ₁ + y ₂ ) / 2 )

= ((5 +

) / 2 , (10 + 12) / 2 )

= (8/2 , 22/2)

= (4, 11)

Следовательно, середина отрезка, соединяющего точки (5, 10) и (3, 12), равна (4, 11)

Теперь используйте калькулятор средней точки, чтобы найти среднюю точку отрезка, соединяющего следующие пары точек.

• (2,3) и (4,5)
• (-4,6) и (-7,-2)

☛ Статьи по теме:

• Средняя точка
• Центроид

☛ Математические калькуляторы:

Калькулятор географической средней точки, найдите свой личный центр тяжести

Находит точную точку, которая находится посередине между двумя или более точками. Найдите свой личный центр тяжести — среднее географическое положение всех мест, в которых вы жили. Посмотрите результаты на карте Google. Использование калькулятора Часто задаваемые вопросы

Этот калькулятор в настоящее время можно использовать только с параметром широта/долгота, чтобы найти координаты средней точки. Вы можете найти широту и долготу для адресов и городов в: Поиск геокода

Geo Challenge

География мелочи

Какой остров является четвертым по величине в мире и вторым по величине производителем ванили в мире?
Ответ

Предположим, что Солнце представлено 1/2-дюймовым шариком. В этом масштабе, как далеко он будет от Солнца до трех звезд звездной системы Альфа Центавра и их планет?
Ответ

Посмотреть прошлые вопросы Geo Challenge

Инструменты GeoMidpoint

Давайте встретимся посередине

Давайте встретимся посередине находит идеальный ресторан или другую достопримечательность на полпути между двумя или более адресами. Встретьтесь с другом на полпути к обеду.

Генератор случайных точек

Генератор случайных точек генерирует одну или несколько точек в случайных местах на поверхности земли. Вы можете бросить один или несколько виртуальных дротиков на карту Google и посмотреть, где они приземлятся.

Карты Google

Для использования калькулятора и просмотра ответов на вопросы Geo Challenge требуется Javascript.

Найдите точку на полпути

Вот несколько из множества возможных применений калькулятора:

• Найдите свой личный центр тяжести. Выберите все города или адреса, где вы жили, затем просмотрите эти места на карте вместе с маркером, указывающим на ваше точное среднее местоположение.
• Найдите середину полета между двумя городами. Например, точка, которая находится на полпути между Чикаго и Лос-Анджелесом, находится в 22 милях (35 км) к юго-западу от Лимона, штат Колорадо.
• Планирование поездки — найдите центральный узел для мест, которые вы собираетесь посетить.
• Найдите центральное место для конгресса или воссоединения семьи, которое будет честным и равноправным для тех, кто путешествует.
• Найдите центральное место для нового бизнеса или объекта, который будет обслуживать близлежащие населенные пункты.
• Места средней точки можно посетить с помощью устройств GPS. Пожалуйста, прочтите эти рекомендации по использованию GPS перед тем, как отправиться в путешествие.

Использование калькулятора средней точки

Добавьте каждый из ваших адресов или других местоположений на карту. Подробные инструкции см. в справке. Используйте опцию «Адрес», чтобы ввести ваши адреса или другие местоположения один за другим. «Множественный ввод» позволяет копировать и вставлять список адресов из электронной таблицы или другой программы.

Форматы адресов

350 Пятая авеню, Нью-Йорк, NY
Даунинг-стрит, 10, Лондон, Великобритания
Атланта, Джорджия
Сидней, Австралия

Местоположение также можно указать по широте и долготе, используя один из допустимых форматов.

Вес по времени и другой вес

Вы можете использовать «Вес по времени», чтобы взвесить свои места для расчета личного центра тяжести. Введите количество времени, которое вы провели в каждом месте. Если вы оставите поля для лет, месяцев и дней пустыми, то все ваши места будут иметь одинаковый вес для расчета. В качестве альтернативы вы можете использовать «Другой вес», чтобы ввести население или другие весовые коэффициенты для каждого местоположения.

Методы расчета

Для расчета средней точки доступны три различных метода расчета, каждый из которых полезен в разных ситуациях. Есть причины предпочесть один метод другому.

Как работает калькулятор

Калькулятор вычисляет географическую среднюю точку, исходя из предположения о сферической форме Земли. Географическая середина любых двух точек на земной поверхности расположена на полпути вдоль маршрута большого круга, который является кратчайшим маршрутом, пролегающим между обеими точками, и это было бы похоже на натяжение нити между двумя точками на земном шаре, а затем нахождение середины Струна. Географическая середина трех или более точек на земной поверхности является центром тяжести (центром масс или средним положением) для всех точек.

Чтобы визуализировать концепцию центра тяжести, представьте, что небольшой груз расположен в месте расположения различных городов на земном шаре. Теперь представьте, что земному шару позволено свободно вращаться до тех пор, пока самая тяжелая часть земного шара не будет притянута силой тяжести, пока она не окажется лицом вниз. Самая низкая (и самая тяжелая) часть земного шара является центром тяжести и географической средней точкой для всех взвешенных городов. Подробное описание см. в разделе Методы расчета.

Картографические проекции

Много искажений возникает, когда земля проецируется на плоскую поверхность, например, на карту с использованием проекции Меркатора. Из-за этого искажения, если вы нанесете две точки на плоскую карту вместе с соответствующей вычисленной средней точкой, вы обнаружите, что средняя точка часто сильно отличается от двух точек. Это можно легко проиллюстрировать на примере. Если вы поместите линейку на плоской настенной карте между Фениксом, штат Аризона, и Кабулом, Афганистан, средняя точка двух городов окажется в Атлантическом океане в нескольких сотнях миль от оконечности Португалии. Однако калькулятор географической средней точки дает истинные координаты средней точки широты 88,9.300 северной долготы 171,1427 западной долготы, что составляет 72 мили (116 км) от Северного полюса. Убедиться в этом можно, протянув нить между двумя городами на глобусе.

В общем, истинная середина в Северном полушарии будет севернее, чем вы могли бы ожидать, если смотреть на плоскую карту, и, наоборот, истинная середина в Южном полушарии будет южнее, чем вы могли бы ожидать. Для городов, расположенных близко друг к другу, эта очевидная разница между сферической землей и плоской картой незначительна, но разница может быть значительной для городов с большим разнесением по долготе, например, городов на разных континентах.