SQRT и другие способы
В учебнике показано, как извлечь квадратный корень в Excel, а также как вычислить корень N из любого значения.
Возведение числа в квадрат и извлечение квадратного корня — очень распространенные операции в математике. Но как сделать квадратный корень в Excel? Либо с помощью функции SQRT, либо путем возведения числа в степень 1/2. Следующие примеры показывают полную информацию.
- Поиск квадратного корня с помощью функции Excel SQRT
- Получить квадратный корень с формулой экспоненты
- Найдите квадратный корень с помощью функции POWER
- Как вычислить корень N в Excel
Как извлечь квадратный корень в Excel с помощью функции SQRT
Самый простой способ извлечь квадратный корень в Excel — использовать специально разработанную для этого функцию: ячейка, содержащая число, для которого вы хотите найти квадратный корень.
Например, чтобы получить квадратный корень из 225, используйте следующую формулу:
=КОРЕНЬ(225)
Чтобы вычислить квадратный корень из числа в A2, используйте эту формулу:
=КОРЕНЬ(A2)
Если число отрицательное, как в строках 7 и 8 на снимке экрана выше, функция Excel SQRT возвращает #ЧИСЛО! ошибка.
), который находится над цифрой 6 на большинстве клавиатур. 9(1/2), «»)
Почему показатель степени 1/2 равен квадратному корню?
Для начала, что мы называем квадратным корнем? Это не что иное, как число, которое при умножении само на себя дает исходное число. Например, квадратный корень из 25 равен 5, потому что 5×5=25. Это кристально ясно, не так ли?
Ну, умножение 25 1/2 само по себе также дает 25:
25 ½ x 25 ½ = 25 (½+½) = 5 = 25 сказал другой способ: √25 x √25 = 25 и: 25 ½ x 25 ½ = 25 Таким образом, 25 ½ — эквивалент до √25. Функция СТЕПЕНЬ — это просто еще один способ выполнить приведенное выше вычисление, т. е. возвести число в степень 1/2. Синтаксис функции СТЕПЕНЬ Excel следующий: СТЕПЕНЬ(число, степень) Как вы можете легко догадаться, чтобы получить квадратный корень, вы добавляете 1/2 к мощность аргумент. Как показано на снимке экрана ниже, все три формулы квадратного корня дают одинаковый результат, какую из них использовать, зависит от ваших личных предпочтений: Формула экспоненты, обсуждавшаяся несколькими абзацами выше, не ограничивается нахождением только квадратного корня. Эти же приемы можно использовать для получения любого n -го -го корня — просто введите нужный корень в знаменатель дроби после знака вставки: 90,25. Обратите внимание, что дробных показателей степени
(1 )0005 Как найти квадратный корень с помощью функции СТЕПЕНЬ
Например: =СТЕПЕНЬ(A2, 1/2) Как для вычисления корня N в Excel
Те же результаты могут быть получены при использовании функции СТЕПЕНЬ:
- Кубический корень из 64: =СТЕПЕНЬ(64, 1/3)
- 4 корень из 16: =POWER(16, 1/4) 9(1/B$2)
На снимке экрана ниже показаны результаты, округленные до 2 знаков после запятой:
Совет.
Чтобы выполнить несколько вычислений с помощью одной формулы, как в приведенном выше примере, исправьте ссылку на столбец и/или строку, где это необходимо, используя знак доллара ($). Дополнительные сведения см. в разделе Зачем использовать знак доллара в формулах Excel.Вот как вы можете извлечь квадратный корень в Excel. Я благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Вас также может заинтересовать
Война в Украине!
Чтобы поддержать Украину и спасти жизни
, пожалуйста, посетите эту страницу. Значение корня 2 — квадратный корень из 2 с использованием различных методов
Что ж, ответ на этот простой вопрос: значение корня 2 (т. е. √2) равно 1,412. Чтобы понять, что такое корень 2 (√2) и расчет значения корня 2, нам сначала нужно понять концепцию мощности и корней.
Степени и корни
Степени: пусть a будет любым числом, а n будет натуральным числом, тогда
{an}= a×a×a.
……..умножить на n разГде a называется основанием, n называется показателем степени или индексом, а an называется экспоненциальным выражением. an читается как «a в степени n», или «a в степени n», или просто «степень n».
В частности, a¹ = a.
Корень: Когда число умножается само на себя, полученное произведение называется квадратом этого числа. Таким образом, само число становится корнем его кратного (результирующего).
Например: 92} = \frac{9}{5}\]является корнем \[\frac{9}{5}\].
Если а — любое число, то а2 называется квадратным числом или числом с полным квадратом.
Number
Perfect Square
Number
Perfect Square
1
1²=1
11
11²=121
2
2²=4
12
12²=144
3
3²=9
13
13²=169
4
4²=16
14
14²=196
5
5²=25
15
15²=225
6
6²=36
16
16²=256
7
7²=49
17
17²=289
8
8²=64
18
18²=324
9
9²=81
19
19²=361
10
10²=100
20
20²=400
Квадратный корень
Квадратный корень из числа — это число, которое при умножении само на себя дает исходное число.
Например:
Поскольку \[2 \times 2\]=4, квадратный корень из 4 равен 2.
Как \[\frac{3}{5} \times \frac{3}{5} = \frac{9}{{25}}\], квадратный корень из \[\frac{9}{ {25}}\]is \[\frac{3}{5}\]
Метод нахождения квадратного корня из заданного квадратного числа
Шаг 1) Выразите заданное число как произведение простых чисел.
Шаг 2) Объедините в группы пары одинаковых простых чисел.
Шаг 3) Возьмите по одному множителю из каждой пары простых чисел. Умножьте их вместе; полученный таким образом продукт представляет собой искомый квадратный корень из заданного числа.
Значение корня два (\[\sqrt 2 \])
Возьмем число «а», которое при умножении на себя дает «2». Таким образом, мы можем сказать, что a — это квадратный корень из 2.
То есть \[\sqrt 2 = a\].Чтобы найти значение a, мы сначала проверяем, является ли заданное число полным квадратом или нет. Вы также можете обратиться к приведенной выше таблице, чтобы найти квадратный корень из полного квадрата. Но так как 2 не является полным квадратом, а также является иррациональным числом, точное значение корня 2 никогда не может быть определено. Мы все еще можем найти приблизительное значение под корнем 2 методом деления в длину.
Значение корня два по «методу деления в длину»
Шаг 1) Выберите число, найдя не менее двух совершенных корней.
Шаг 2) Разделите 2 на выбранные квадратные корни
Шаг 3) Возьмите среднее значение результата деления и 2.
Шаг 4) Используйте результат и повторяйте шаги два и три, пока не получите удовлетворительный результат.
\[\textrm{Значение}\sqrt{2}=1,41421356237309504880168872420969807856967187537694\]
Деление продолжается, но мы берем приблизительное значение 2, то есть 1,414.
92} = \left( { — \frac{8}{3}} \right)\left( { — \frac{8}{3}} \right) = \frac{{64}}{9} = 7 \frac{1}{3}\]Пример 2. Найдите квадратный корень из следующих чисел:
1) 6\[\frac{1}{4}\]
2) 42,25
Решение:
1) \[\ sqrt {6 \ frac {1} {4}}\] = \[\ sqrt {\ frac {{25}} {4}} \] = \[\ frac {{\ sqrt { 5 \times 5} }}{{\sqrt {2 \times 2} }} = \frac{5}{2} = 2\frac{1}{2}\]
2) \[\sqrt {42,25 } = \sqrt {\frac{{4225}}{{100}}} \]
\[ = \sqrt {\ frac{{169}}{4}} \]
\[ = \frac{{\sqrt {13 \times 13}}}}{{\sqrt {2 \times 2}}} = \frac{{13}}{2} = \frac{{13 \times 5}}{{2 \times 5}} = \frac{{65}}{{10}} = 6,5\]
Узнайте о значении корня 2
В этой статье рассматриваются значение корня 2, а также различные методы, чтобы узнать квадратный корень из 2. Часто задаваемые вопросы в конце этой статьи могут помочь вам с вашими сомнениями, если вы столкнетесь с ними, проходя через то же самое.
Чтобы выполнить несколько вычислений с помощью одной формулы, как в приведенном выше примере, исправьте ссылку на столбец и/или строку, где это необходимо, используя знак доллара ($). Дополнительные сведения см. в разделе Зачем использовать знак доллара в формулах Excel.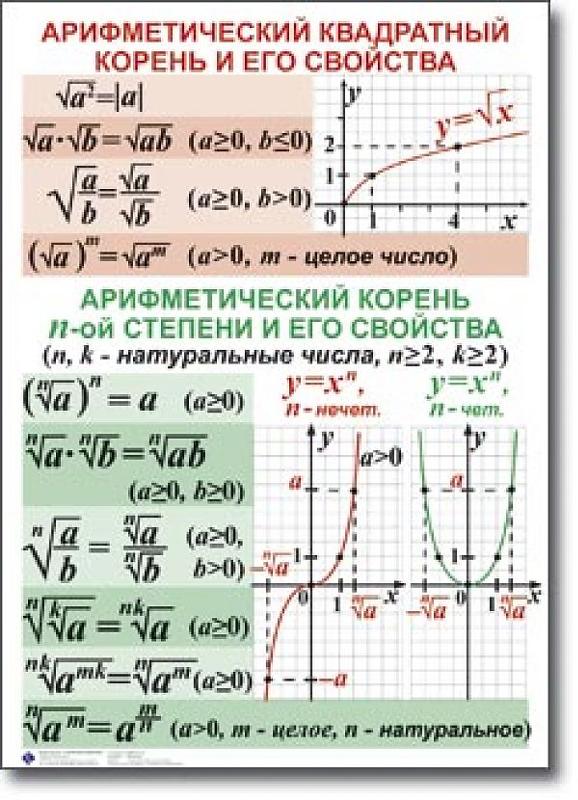
……..умножить на n раз
То есть \[\sqrt 2 = a\].
92} = \left( { — \frac{8}{3}} \right)\left( { — \frac{8}{3}} \right) = \frac{{64}}{9} = 7 \frac{1}{3}\]