ЕГЭ по математике, профильный уровень. Иррациональное уравнение
- Альфашкола
- Статьи
- ЕГЭ по математике, профильный уровень. Иррациональное уравнение
Продолжаем готовиться к экзаменам вместе с лучшими преподавателями Альфа-школы. В новой статье Андрей Алексеевич показывает подробное решение задачи из темы «Иррациональное уравнение».
Условие:
а) Решите уравнение .
б) Укажите все корни этого уравнения, принадлежащие промежутку \([-\sqrt3;\sqrt30]\).
Решение
Основным способом решения таких уравнений является возведение «в квадрат» обеих частей уравнения.
а) Начнем решать это уравнение:
Как видите, мы учли, что правая часть исходного уравнения «3 – х» больше или равна нулю. После возведения в квадрат обеих частей мы раскрыли скобки в правой части по формуле сокращенного умножения, перенесли получившееся выражение в левую часть и привели подобные. Получилось кубическое уравнение. Сгруппируем выражение в левой части:
Как видите, из получившихся трех корней только два удовлетворяют условию «3 – х» больше или равна нулю.
Первая часть задания выполнена, уравнение решено.
б) Чтобы найти корни, удовлетворяющие заданному промежутку, необходимо оценить, чему будет равен «корень из трех» и «корень из 30», относительно «-2» и «2», не забывая о «минусе» перед числами.
\(-2<-\sqrt3<2<\sqrt30\)
Отсюда видно, что заданному отрезку \([-\sqrt3;\sqrt30]\) принадлежит только число 2.
Ответ: а) {-2;2}; б) 2.
Автор — Андрей Найденов
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Вера Александровна Бондаренко
Репетитор по математике
Стаж (лет)
Образование:
Ульяновский государственный педагогический университет имени ИН Ульянова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Я считаю, что знать русский язык, грамотно писать и говорить на нём – это гражданский долг каждого человека, проживающего в Российской Федерации.
Анастасия Владимировна Федорова
Репетитор по математике
Стаж (лет)
Образование:
СпбгуКиТ
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 1-7 классы.
Математика очень интересная и важная наука. Все в нашем мире подчиняется законам математики и знания по этому предмету нужны человеку постоянно.
Мария Николаевна Тимоня
Репетитор по математике
Стаж (лет)
Образование:
ФГБОУ ВО Марийский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 5-9 классов. Готовлю к ОГЭ. Вместе разберемся со всеми сложностями, вам стоит лишь поверить в себя.
Я обожаю моменты, когда даже самые трудные задачи решаются! Эмоциональное удовлетворение, духовный подъем — вот что дарит математика
Похожие статьи
- Конус
- Сколько одно число составляет в процентах от другого?
- Факультет ПЭК (МГИМО): проходной балл, отзывы
- ЕГЭ по математике, базовый уровень. Текстовые задачи (вариант 5)
- Учимся решать текстовые задачи
- Лайфхаки для уставших родителей: как не кричать
- Что такое педикулез и как с ним бороться
- Почему дети симулируют болезнь
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Красота математики в формате бумаги A4 / Хабр
Многие удобные нам вещи — результат чьих-то расчётов.
Благодаря людям, которые заняты этими расчётами, большинство может спокойно забыть о том, что многие важные аспекты нашей жизни зависят от чисел и их свойств. К старту нашего флагманского курса по Data Science напоминаем о математической красоте формата бумаги A4.
Если вы не из США и не прогуливали большую часть учёбы и работы, вы наверняка имели дело с форматом A4. Вы не задавались вопросом, почему формат этот имеет именно такой размер? Давайте смахнём пыль со школьного учебника по математике и разберёмся во всём.
Сообщу вам формат бумаги на случай, если вы его всё-таки не знаете. Это ровно 210 на 297 мм. Можете не верить мне на слово. Проверьте. Я подожду. Если у вас в доме не завалялось ни одного листа А4, вы гораздо тщательнее делаете уборку в доме, чем я… Мерить такой лист удобно обычной 30-сантиметровой линейкой, которая наверняка найдётся в ящике вашего стола или неподалёку от него. Теперь остаётся только один вопрос:
И вслед за этим зачастую мы спрашиваем: «Вы это серьёзно? 297 миллиметров? А почему не 300?» Я знаю, что это искреннее недоумение.
Эти слова до сих пор звучат у меня в ушах с того школьного урока черчения, на котором один из моих товарищей именно в такой форме сетовал об извращённости нашего мира. Не помню, получил ли он ответ, но боюсь, что его боль по этому поводу так никто и не разделил. Давайте потратим остаток статьи на утешение страданий этого мальчика.
Поможем прокачать ваши навыки или освоить самые востребованные IT-профессии:
- Полный курс по Data Science. Получите одну из самых перспективных профессий за 24 месяца.
- «Fullstack-разработчик на Python». Станьте незаменимым специалистом и универсалом за 15 месяцев.
- «Надёжный старт в IT». Пройдите лучший курс для новичков: попробуйте 9 профессий и освойте подходящую именно вам.
Воистину — каждый, кто когда-либо хотел отмерить половину листа бумаги, испытал лёгкое негодование. Немудрено: отмерить нужно 148,5 мм, а на линейке нет полумиллиметровых делений.
Предлагаю вам взять прямоугольный лист бумаги, отличный от листа формата А4. Ведь никто не мешает вам оторвать немного бумаги формата А4, а затем аккуратно сложить ее в прямоугольник. Взяв прямоугольник, отличный от А4, попробуйте сложить его ровно пополам [сверху вниз]. Вы увидите, что теперь лист бумаги вдвое меньше по размерам и совсем другой формы. Возможно, вы начали с «почти квадратного» прямоугольника, а теперь он стал «длинным и тонким», или наоборот.
Теперь проделайте это с листом A4. Кажется, вы уже поняли, что произойдёт. Вы получите формат A5. Он составляет половину формата А4 (ещё бы: вы же пополам складывали). Более того, форма осталась той же. Строго говоря, форма осталась аналогичной, соотношение сторон сохранено. Если вы хоть немного задумаетесь об этом, вы будете поражены. Ведь обычно прямоугольники так себя не ведут.
Возможно, эта «случайность» была одной из лучших идей XVIII века. Но пример приведу из наших дней: учителя уже много лет пользуются этим, чтобы буквально ополовинить свои затраты на ксерокопирование материалов.
Первая известная дискуссия по этой теме датируется 1786 годом — как и письмо от немецкого академика Георга Кристофа Лихтенберга его не менее известному соотечественнику Иоганну Бекману[1].
Однако есть предположения, что соответствующая задача давалась на экзаменах студентам задолго до этого[2].
Тем не менее только в ХХ веке Германия — а вслед за ней и большая часть мира — отразила эту идею в стандарте. Международный стандарт для формата бумаги получил номер ISO 216[3]
На самом деле существует лишь одно соотношение сторон прямоугольника, которое даёт аналогичную форму при складывании вдвое. Как вы думаете, какое? Нет, это не «золотое сечение», но тоже весьма интересное соотношение.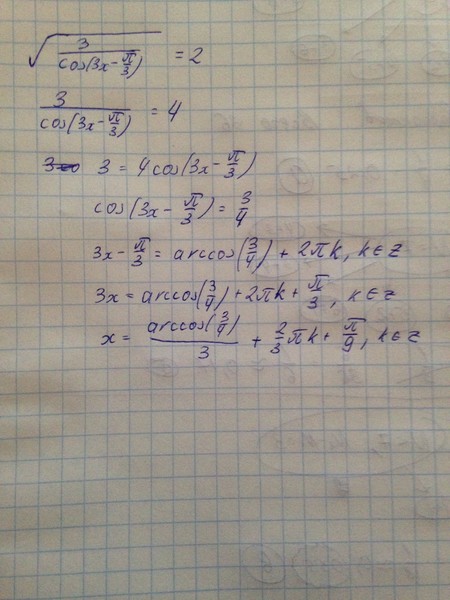
Дальше я напишу, как его рассчитали.
Построим обычный прямоугольник с соотношением сторон (длинная к короткой) :
Теперь проведём линию половинного сгиба, чтобы получить прямоугольник с соотношением сторон (длинная к короткой) .
Если мы, во имя всех упомянутых благ, хотим, чтобы два соотношения были одинаковыми, мы должны получить равные дроби
(или , об отрицательных соотношениях поговорим в другой раз).
Этим важным свойством обладает только одно соотношение. Это квадратный корень из 2, который, как известно (а в данном случае — по иронии судьбы), дробью не является. Поэтому размеры бумаги, в каких бы величинах вы их ни измеряли, не будут целочисленными и, с точки зрения многих людей, «красивыми». Поскольку ни одна пара чисел не даст отношения , приходится прибегать к приближённым значениям.
Поэтому мы должны (и смогли) отказаться от мечты о «красивой» длине сторон, что не мешает нам получать «красивые» площади. На самом деле, современная международная система форматов «А» начинается с бумаги формата А0, со сторонами в правильном соотношении , но с площадью ровно 1 м2, или настолько близкой к ней, насколько это возможно при длине сторон в целых миллиметрах (1189 х 841 мм, если быть точным).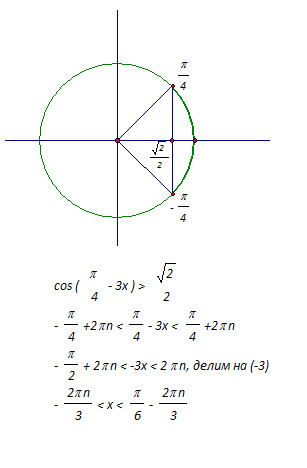
Теперь складывайте этот лист вдвое и режьте его, пока он не уместится в папку и не станет удобным для работы. Вы получите формат A4, отсюда и «4» в названии.
Кстати, если вам всё это в новинку, но помнится кое-что из школьного курса математики, вам может понравиться другой способ понять это. Помните «коэффициенты масштаба площади» и «коэффициенты масштаба длины»? Коэффициент масштаба площади тождественно равен квадрату коэффициента масштаба длины. Так вот, если вы хотите, чтобы коэффициент масштаба площади был (или ), коэффициент масштаба длины должен быть (или ). Конечно же, вы помните.
Нравится вам это или нет, но иррациональные числа полезны. Звучит отрезвляюще. А для некоторых — удручающе. Вспомним хотя бы миф о том, что сделали пифагорейцы с Гиппасом, который назвал выражение иррациональным). Но, как только мы преодолеем страх перед иррациональными величинами, мы сможем пожинать плоды. Теперь вес бумаги легко рассчитать, потому что он пропорционален площади: бумага плотностью 80 грамм на (квадратный) метр формата А0 весит ровно 80 г.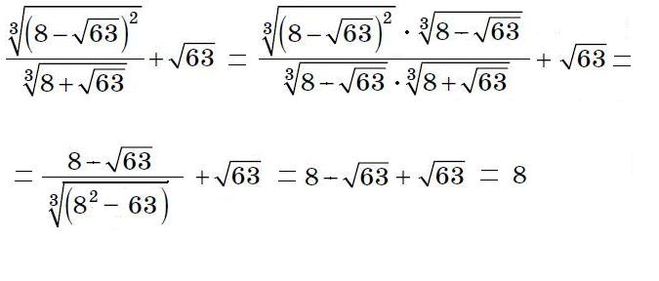
Бумага формата А4 такой плотности весит 5 г, так как её сложили пополам 4 раза [уменьшили в 24, то есть в 16 раз].
Ширина стержня линера увеличивается на коэффициент . Таким образом, следующий линер в наборе подойдёт для следующего формата бумаги. Вот так красиво всё устроено.
Чертёжные ручки с маркировкой размера (с увеличением на коэффициент 1,4). Wikimedia Commons
Какой из этого можно сделать вывод? Многие удобные нам вещи — результат чьих-то расчётов. Благодаря им мы теперь можем спокойно забыть, что многие важные аспекты нашей жизни зависят от чисел и их свойств. Благодаря тому, что кто-то об этом не забыл.
Да, обо всем этом мы можем спокойно забыть. Но прошу вас: вспомните об этом, когда кто-то снова решит отмерить пол-листа, и вы снова услышите глас вопиющего в пустыне: «Ну почему 297?» Теперь вы знаете, что ответить.
Ссылки
[1] Тот самый Лихтенберг, который дал своё имя фигурам Лихтенберга, рисункам искровых разрядов высокого напряжения.
И тот самый Бекман, который ввёл в науку термин «технология». Теперь вы это знаете.
[2] https://www.cl.cam.ac.uk/~mgk25/lichtenberg-letter.html.
[3] https://en.wikipedia.org/wiki/Paper_size.
Стать востребованным профессионалом в IT с самого начала или прокачаться помогут наши курсы. Скидка 45% по промокоду HABR:
- Профессия Data Analyst (12 месяцев)
- Профессия Data Scientist (24 месяца)
Готовый перевод Horror Camgirl / Омерзительная кэм-герл: Часть 373. Цзюньяо, почему ты такая жестокая? :: Tl.Rulate.ru
Я развернула к выходу. Дверь камеры медленно закрывалась, когда я услыхала:
— Хорошо, я скажу, тебе, но ты должна поклясться сердцем.
— Вы не в том положении, чтобы диктовать условия, — холодно сказала я.
Глава семья Жань сжал кулаки, снова заколебался и, наконец, вымолвил:
— Хорошо, на этот раз я поверю тебе…
Он рассказал, что его предок много-много лет назад отправились в горы Куньлунь, чтобы найти редкое духовное растение.
В горах он заблудился, долго плутал по лесу и, наконец, вышел к зеленому озеру. Ему очень хотелось пить, поэтому вода была кстати.
Раздевшись, он прыгнул в озеро. Искупавшись, он выбрался из воды и понял, что пейзаж изменился. Его окружала не растительность горы Куньлунь, а цветущий персиковый сад. Цветущие персиковые деревья в горах похоже на розовое пламя, а летящие на ветру лепестки, словно из сказочной страны.
Предок никогда подробно не рассказывал о жизни в Тайном Царстве Цветущего Персика, но сказал, что девять раз умирал, пока, наконец, ему удалось сбежать, захватив с собой белую флейту.
Я попросила его подробно рассказать о местонахождении Тайного Царства Цветущего Персика, после чего ушла.
Глава семьи Жань холодно смотрел на закрытую металлическую дверь, на его лице расцвела странная улыбка.
— Ты обязательно найдешь смерть в Таинственном Царстве Цветущего Персика.
Каждое слово он отчеканил, как клятву.
Переговоры с директором юго-восточного отдела Лю не заняли много времени.
За младшего отпрыска семьи Жань я отдала ему эликсиры четвертого уровня. Также я попросила его организовать ему выезд за границу. Мальчика тайно вывезли в Швецию.
Ли Музи была отравлена сильным ядом. Хотя ее организм был очищен от токсина, она не приходила в себя. Полагаю, понадобится месяц или два, чтобы она полностью пришла в себя. Я договорилась, чтобы она прошла курс лечения в госпитале при Академии людей со способностями.
Руководители Академии были рассерженными и чувствовали себя виноватыми одновременно. Они винили себя в том, что не уберегли своего человека, а сердились на того, кто посмел подобное сотворить с их студенткой.
Они предоставили Ли Музи бесплатное лечение, использовали лучшие эликсиры для восстановления функционала ее мозга, а также пообещали дать ей хорошие ресурсы для совершенствования в качестве компенсации после того, как она придет в себя.
Закончив с организационными моментами, я вернулась в Шаньчэн. Я планировала немного подождать, прежде чем оправиться в Тайное Царство Цветущего Персика.
Я решила, что искать корни нужно после того, как база совершенствования станет выше.
Проснувшись следующим утром с первыми лучами солнца, я увидела возле двери дома букет цветов. Странно! Цветы выглядели так, словно только что были собраны, на них все еще была утренняя роса.
Эти цветы были своеобразными духовными растениями, которые растут только на скалах восточных гор. Их особенность – цветение за час до рассвета. Кто же мог принести их?
Под букетом была записка, написанная красивым почерком. Тан Мингли!
«Не забудь позавтракать», — гласила надпись.
Я была слегка удивлена. Отнеся цветы к дому Тан Мингли, я вернулась к себе.
Тан Мингли открыл входную дверь. Его лицо было меланхоличным и печальным.
Мое сердце защемило, но я должна быть твердой и ожесточить сердце. Я не хочу быть катастрофой для него и Инь Шенгуа, не хочу чтобы из-за меня дрались насмерть.
С того дня каждое утро у моей двери был букет только что собранных цветов. Под букетом всегда лежала записка, полная любви и заботы.
Я не знаю, что делать. Рассказать об этом брату нелегко, старшего Инь Чаншена нет, остается только один человек, которому я могу довериться – Лорд Женгуян.
Услышав об этом, Лорд Женгуян спросил:
— Он пил твою кровь?
Я была удивлена и на долгое время замолчала, после чего, наконец, кивнула.
Лорд Женгуян вздохнул:
— Это судьба, невозможно заставить его отказаться от тебя.
— Тогда что мне делать? – я сделала паузу и продолжила. – Я слышала, что есть эликсир, который называется Ванцин Дань…
— Это лекарство от симптомов, а не первопричины, — сказал Лорд Женгуян. – Единственный способ заставить его отказаться от тебя – это забрать у него твою кровь.
Я была в шоке.
— Разве можно забрать кровь?
— Конечно, можно. – ответил он. – Его сила исходит от тебя, значит, только ты можешь забрать ее. После того, как ты заберешь ее, он вернется в свое первоначальное состояние и станет обычным человеком.
Я задумалась, разве это не гуманнее, чем убить его?
— Цзюняьо, — сказал Лорд Женгуян, — ты действительно хочешь, чтобы он забыл тебя?
Его вопрос заставил меня застыть.
Действительно ли я хочу, чтобы он забыл меня? Действительно хочу? Я не смела спросить свое сердце, так как боялась получить ужасные ответы.
Сжав кулаки, я отчетливо произнесла каждое слово:
— Старший, пожалуйста, научите меня, как заставить Инь Шенгуа и Тан Мингли забыть меня. Пусть они забудут меня, пусть забудут обо мне, и не станут убивать друг друга, и не будут страдать так сильно, как сейчас.
Глубоко вздохнув, я приняла решение.
— Ты точно решила? – спросил наставник.
— Да, — кивнула я.
— В таком случае у меня есть две бутылочки воды Ванцин из реки Ванцин, что в бессмертном мире. Она намного сильнее Ванцин Дань. После того, как они выпьют ее, ты никогда больше их не увидишь. Они навсегда забудут тебя.
Вскоре снаружи раздался голос, оповестивший о прибытии посылки. Я внесла ее в дом и открыла коробку. Внутри лежали две хрустальные бутылочки с прозрачной жидкостью без вкуса и цвета. Это вода из сказочного мира Бессмертных.
— Спасибо, старший, — я глубоко поклонилась компьютеру.
Лорд Женгуян покачав голов, глубоко вздохнул.
— Девочка, я знаю, что ты много страдала раньше и не хочешь человеческой любви, но ты не должна так сильно себя мучить.
В моих глазах застыла печаль. Опустив голову, я посмотрела на воду забвения и, наконец, так крепко сжала бутылочки, что суставы на пальцах побелели.
— Это лучше для них и для меня. – сказала я. – Когда они забудут обо мне и перестанут преследовать, то и я вскоре забуду о них.
Я еще раз поблагодарила Лорда Женгуяна, а затем пошла на кухню, чтобы приготовить роскошный ужин.
После я постучала в дверь Тан Мингли. Он радостно смотрел на меня, светясь от счастья. Мое сердце дрогнуло, но я сказала себе: «Цзюньяо, ты должна ожесточить свое сердце, чтобы помочь ему выбраться из моря страданий».
— Тан Мингли, — сказала я, слабо улыбнувшись, — я приготовила слишком много еды на ужин, боюсь, не сумею справиться с ним. Как насчет… не хочешь составить мне компанию?
— Это большая честь для меня, — улыбнулся Тан Мингли.
Он сел за обеденный стол, а я налила ему бокал вина.
— Это мое абрикосовое вино, я сделала его из свежих весенних абрикосов урожая этого года. В нем много духовных растений. Ты можешь попробовать его.
Он поднял бокал и глубоко вдохнул аромат. Его взгляд был похож на взгляд человека, выпившего много спиртного.
— Оно достойно Цзюньяо. Вино, обогащенное духовными травами, обладает крепким ароматом и высоким градусом. Думаю, достаточно выпить только один глоток…
В итоге он выпил все. В тот момент мне стало грустно, а на сердце пусто. В моих глазах застыла легкая меланхолия.
— Ты же видел в интернете статьи о семье Жань, верно? – спросила я. – Ты также нанял команду, которая своими постами подливала масло в огонь.
— Для того, чтобы создать шумиху вокруг семьи Жань не обязательно кого-то нанимать. Их деяния на слуху у многих, а теперь новости о них разлетелись со скоростью ветра.
— Это уже не важно… — я пристально посмотрела в его глаза. – Мингли, спасибо.
Я взяла его за руку, впервые проявив инициативу.
— Мингли, спасибо за заботу обо мне. Если бы тебя не было, я бы давно умерла.
Тан Мингли, казалось, что-то заметил.
— Цзюньяо, что случилось? – спросил он, нахмурившись.
Я посмотрела на него с грустными глазами. Неожиданно он что-то почувствовал. Окружающая обстановка поплыла перед его глазами, голова заболела, бокал выпал из его ослабевшей руки и, упав на пол, разбился.
— Цзюньяо? – он схватил меня за руку. – Что ты со мной сделала?
Я подошла к нему, обняла и прошептала на ухо:
— Мингли, извини. Я не хочу смотреть, как ты и Инь Шенгуа сражаются друг с другом из-за меня, не хочу видеть, как кто-то из вас умрет. Забудь меня, это лучше, что может с тобой произойти.
— Нет, Цзюньяо, ты не можешь этого сделать… — он сильнее вцепился в мою руку. – Цзюньяо, я люблю тебя. Не дай мне забыть тебя. Если тебя не будет в моей оставшейся жизни, я не знаю, что буду делать, как буду жить.
Я крепко обняла его сзади.
Слезы текли по моим щекам.
— Мингли, в будущем ты встретишь хорошую девушку, которая будет любить тебя и родит тебе детей. Ты заслуживаешь лучшего. А я… возможно, таким как я не суждено испытать в этой жизни счастье.
Я тихо вздохнула и погладила его по голове.
— До свидания, Мингли.
— Цзюньяо, почему ты… такая жестокая…
Блеск в глазах Тан Мингли постепенно угас, он закрыл глаза.
— Мингли, ты не понимаешь, это величайшая доброта. – я продолжала молча плакать. – Я не хорошая девушка, я не знаю, как ответить на твои чувства… Я не хочу, чтобы из-за меня проливалась кровь. Надеюсь, ты будешь счастлив.
Вытерев слезы с щек, я осторожно подняла его и перенесла в сад на его вилле. Затем собрала свои вещи и покинула горный город, решив спрятаться в северном городе Аньлинь.
http://tl.rulate.ru/book/27460/1259908
(Ctrl + влево) Предыдущая глава | Оглавление | Следующая глава (Ctrl + вправо)
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Квадраты и квадратные корни
Сначала узнайте о квадратах, затем получите квадратные корни.
Как возвести число в квадрат
Чтобы возвести число в квадрат: умножьте его само на себя .
Пример: Сколько будет 3 в квадрате?
| 3 В квадрате | = | = 3 × 3 = 9 |
«Квадрат» часто записывается как маленькая двойка, например:
.
Здесь написано «4 в квадрате равно 16»
(маленькая двойка говорит
число появляется дважды при умножении)
Квадраты От 0
2 до 6 2| 0 В квадрате | = | 0 2 | = | 0 × 0 | = | 0 |
| 1 В квадрате | = | 1 2 | = | 1 × 1 | = | 1 |
| 2 В квадрате | = | 2 2 | = | 2 × 2 | = | 4 |
| 3 В квадрате | = | 3 2 | = | 3 × 3 | = | 9 |
| 4 В квадрате | = | 4 2 | = | 4 × 4 | = | 16 |
| 5 В квадрате | = | 5 2 | = | 5 × 5 | = | 25 |
| 6 В квадрате | = | 6 2 | = | 6 × 6 | = | 36 |
| Квадраты также в таблице умножения: |
Отрицательные числа
Мы также можем возвести в квадрат отрицательных чисел .
Пример. Что произойдет, если возвести в квадрат (−5) ?
Ответ:
(−5) × (−5) = 25
(поскольку отрицательное значение, умноженное на отрицательное, дает положительное значение)
Было интересно!
Когда мы возводим в квадрат отрицательное число , мы получаем положительный результат .
Точно так же, как возведение в квадрат положительного числа:
.(Подробнее читайте Квадраты и квадратные корни в алгебре)
Квадратные корни
квадратный корень из идет в другую сторону:
3 в квадрате равно 9, поэтому квадратный корень из из 9 это 3
Квадратный корень из числа равен …
… значение, которое может быть , умноженным само на , чтобы получить исходное число.
Квадратный корень из 9 равен …
… 3 , потому что при умножении 3 на само получается 9 .
Это все равно, что спросить:
Что мы можем умножить само на себя, чтобы получить это?
Чтобы помочь вам вспомнить , подумайте о корне дерева: «Я знаю дерево , но какой корень его создал? » В данном случае дерево «9», а корень «3». |
Вот еще несколько квадратов и квадратных корней:
| 4 | 16 | |
| 5 | 25 | |
6 | 36 | |
7 | 49 | |
Десятичные числа
Это также работает для десятичных чисел.
Попробуйте ползунки ниже (примечание: «…» означает, что десятичные дроби продолжаются бесконечно):
Использование ползунков:
- Чему равен квадратный корень из 8 ?
- Чему равен квадратный корень из 9 ?
- Чему равен квадратный корень из 10 ?
- Сколько будет 1 в квадрате?
- Что такое 1,1 в квадрате?
- Что такое 2,6 в квадрате?
Негативы
Ранее мы обнаружили, что можем возводить в квадрат отрицательные числа:
Пример: (−3) в квадрате
(−3) × (−3) = 9
И, конечно же, 3 × 3 = 9 .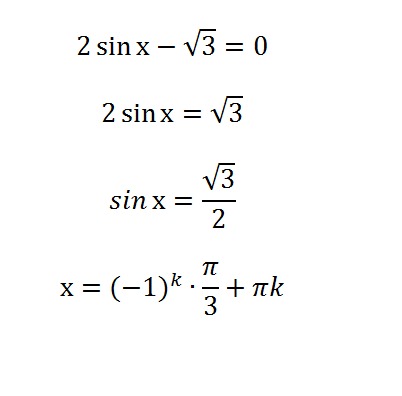
Таким образом, квадратный корень из 9 может быть −3 или +3
.Пример: Чему равен квадратный корень из 25?
(−5) × (−5) = 25
5 × 5 = 25
Таким образом, квадратные корни из 25 равны −5 и +5
.Символ квадратного корня
| Это специальный символ, означающий «квадратный корень». это вроде как галочка, и на самом деле начались сотни лет назад в виде точки с движением вверх. Он называется радикальным , и всегда делает математику важной! |
Мы используем его так:
и мы говорим «квадратный корень из 9 равен 3»
Пример: Что такое √25?
25 = 5 × 5, другими словами, когда мы умножаем 5 само по себе (5 × 5) мы получаем 25
Таким образом, ответ:
√25 = 5
Но подождите! Разве квадратный корень из не может также быть −5 ? Потому что (−5) × (−5) = 25 тоже.
- Ну, квадратный корень из 25 может быть -5 или +5.
- Но когда мы используем радикальный символ √ , мы даем только положительный (или нулевой) результат .
Пример: Что такое √36 ?
Ответ: 6 × 6 = 36, поэтому √36 = 6
Идеальные квадраты
Идеальные квадраты (также называемые «квадратными числами») — это квадраты целых чисел:
.| Совершенный Квадраты | |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
| 11 | 121 |
| 12 | 144 |
| 13 | 169 |
| 14 | 196 |
| 15 | 225 |
| и т. д… |
Постарайтесь запомнить их до 12.
Вычисление квадратных корней
Легко извлечь квадратный корень из полного квадрата, но действительно сложно из вычислить другие квадратные корни.
Пример: что такое √10?
Итак, 3 × 3 = 9 и 4 × 4 = 16, поэтому мы можем предположить, что ответ находится между 3 и 4.
- Попробуем 3,5: 3,5 × 3,5 = 12,25
- Попробуем 3,2: 3,2 × 3,2 = 10,24
- Попробуем 3,1: 3,1 × 3,1 = 9,61
- …
Приближаемся к 10, но для получения хорошего ответа потребуется много времени!
В этот момент я достаю свой калькулятор, и он показывает: 3,1622776601683793319988935444327 Но цифры продолжаются и продолжаются без какой-либо закономерности. Так даже ответ калькулятора только приближение ! |
Примечание: подобные числа называются иррациональными числами, если вы хотите узнать больше.
Самый простой способ вычисления квадратного корня
| Используйте кнопку квадратного корня вашего калькулятора! |
А также используйте свой здравый смысл, чтобы убедиться, что у вас есть правильный ответ.
Увлекательный способ вычисления квадратного корня
Существует забавный метод вычисления квадратного корня, который с каждым разом становится все более и более точным:
| а) начните с предположения (допустим, 4 — это квадратный корень из 10) | |
| b) разделить на предположение (10/4 = 2,5) c) добавить это к предположению (4 + 2,5 = 6,5) d) затем разделить результат на 2, другими словами разделить его пополам. (6,5/2 = 3,25) e) теперь установите это как новое предположение и начните с b) снова |
- Наша первая попытка увеличила число с 4 до 3,25
- Повторный переход (от b до e ) дает нам: 3,163
- Повторный переход (от b до e ) дает нам: 3,1623
Итак, после 3-х раз вокруг ответ 3,1623, что довольно хорошо, потому что:
3,1623 х 3,1623 = 10,00014
Теперь. .. почему бы вам не попробовать вычислить квадратный корень из 2 таким образом?
Как угадать
Что, если нам нужно угадать квадратный корень из такого сложного числа, как «82 163″… ?
В этом случае мы могли бы подумать, что «82 163» состоит из 5 цифр, поэтому квадратный корень может состоять из 3 цифр (100×100=10 000), а квадратный корень из 8 (первая цифра) равен примерно 3 (3×3=9).), так что 300 — хорошее начало.
День квадратного корня
4 апреля 2016 года — День квадратного корня, потому что дата выглядит так: 4/4/16
Следующим после этого является 5 мая 2025 года (5/5/25)
309 310 315, 1082, 1083, 2040, 3156, 2041, 2042, 3154
Квадратный корень из 3 — Как найти квадратный корень из 3?
LearnPracticeDownload
Квадратный корень из 3 выражается как √3 в радикальной форме и как (3) ½ или (3) 0,5 в экспоненциальной форме. Квадратный корень из 3, округленный до 7 знаков после запятой, равен 1,7320508.
Это положительное решение уравнения x 2 = 3.
- Корень квадратный из 3: 1,7320508075688772
- Квадратный корень из 3 в экспоненциальной форме: (3) ½ или (3) 0,5
- Квадратный корень из 3 в подкоренной форме: √3
| 1. | Что такое квадратный корень из 3? |
| 2. | Является ли квадратный корень из 3 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 3? |
| 4. | Важные примечания |
| 5. | Часто задаваемые вопросы о квадратном корне из 3 |
| 6. | Сложные вопросы |
Что такое квадратный корень из 3?
Квадратный корень из числа — это число, которое при умножении само на себя дает исходное число.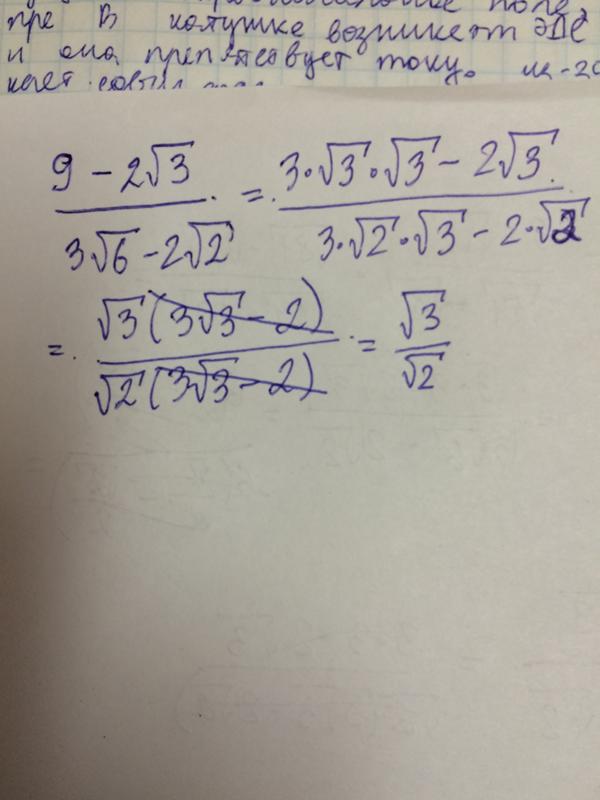
Например, квадратный корень из 25 равен 5, так как 5 умножить на 5 дает 25. Однако у вас также могут быть квадратные корни некоторых чисел, которые не дают целых чисел, например 3. Мы можем выразить квадратный корень из 3 разными способами
- Десятичная форма: 1,732.
- Радикальная форма: √3
- Экспоненциальная форма: 3 1/2
Является ли квадратный корень из 3 рациональным или иррациональным?
- Десятичная часть квадратного корня из 3 не является конечной. Это определение иррационального числа.
- Глядя на десятичную форму корня 3, мы видим, что она бесконечна —
√3 = 1,732050807……. - Следовательно, мы можем заключить, что Квадратный корень из 3 является иррациональным
Как найти квадратный корень из 3?
Поскольку мы пришли к выводу, что квадратный корень из 3 не является конечным, мы можем использовать только метод длинного деления для вычисления его значения.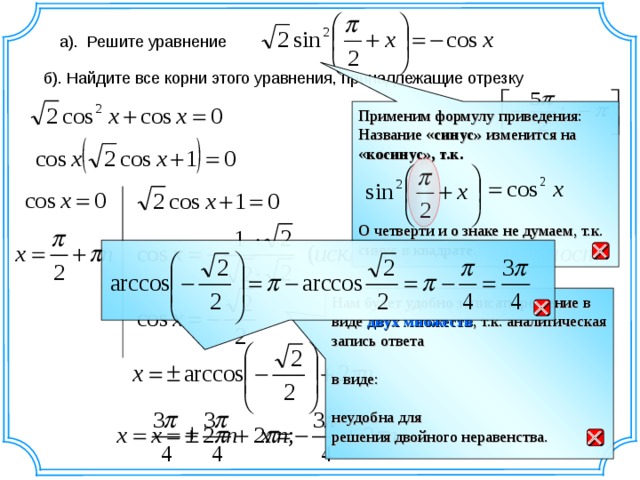
- Шаг 1: Для начала запишем 3 как 3.000000 и сгруппируем нули после запятой в пары по 2 слева направо, как показано ниже. (для цифр слева от запятой соединяйте их справа налево)
- Шаг 2: Подумайте о числе, которое при умножении само на себя меньше или равно 3. В этом случае это число будет 1.
- Шаг 3: Разделив 3 на 1 с частным, равным 1, мы получим остаток 2.
- Шаг 4: Перетащите пару нулей вниз и закрасьте ее рядом с 2 , чтобы получить делимое 200.
- Шаг 5: Делитель, который здесь равен 1, добавляется к самому себе и записывается ниже. Теперь у нас есть 2X в качестве нового делителя, и нам нужно найти значение X, которое делает произведение 2X × X меньше или равным 200. В этом случае 27 — это искомое значение 9.1255
- Шаг 6: Число 7 ставится в частном после запятой. Новый делитель для следующего деления будет 2X + X, что в данном случае равно 34.
Действуя таким же образом и повторяя с шага 4, мы можем вычислить остальные десятичные дроби.
Изучение квадратных корней с помощью иллюстраций и интерактивных примеров
- Квадратный корень из 4
- Квадратный корень из 2
- Квадратный корень из 5
- Квадратный корень из 9
- Квадратный корень из 15
Важные примечания
- Действительные корни √3 равны ± 1,732.
- Квадратный корень из полного квадрата — это всегда рациональное целое число, а корень других чисел — всегда иррациональный. Например, √16 = 4, а √17 = 4,1231… .
Загадочные вопросы
- Найдите значение √√3.
- Какова длина стороны квадрата площадью 10? (Подсказка: используйте метод длинного деления)
- Найдите квадратный корень из 33.
Пример 1
Джон интересовался, совпадает ли значение -√3 с √-3.
Что вы думаете?Решение
Отрицательные квадратные корни не могут быть действительными числами.
-√3 — действительное число.
Но √-3 — мнимое число.
Следовательно, они не совпадают, а -√3 не совпадает с √-3.Пример 2
Майкл едет по шоссе со средней скоростью 50√3 км/ч ровно 1 час. Какое расстояние он преодолевает?
Решение
Нам нужно использовать формулу Расстояние = Скорость * Время
Скорость = 50√3 = 86,603 км/ч
Время = 1 час
Используя формулу, Расстояние = 86,603 * 1 = 86,603Следовательно, Майкл преодолевает расстояние 86,603 км
Пример: Если площадь круга равна 3π в 2 . Найдите радиус окружности.
Решение:
Пусть ‘r’ будет радиусом окружности.
⇒ Площадь круга = πr 2 = 3π в 2
⇒ г = ±√3 в 90 937 Так как радиус не может быть отрицательным,
⇒ г = √3
Квадратный корень из 3 равен 1,732.
⇒ г = 1,732 в
Что вы думаете?
перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу для изучения математики?
Выйдите за рамки заучивания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы о квадратном корне из 3
Каково значение квадратного корня из 3?
Квадратный корень из 3 равен 1,73205.
Почему квадратный корень из 3 является иррациональным числом?
Число 3 простое. Отсюда следует, что число 3 беспарное и не находится в степени двойки. Следовательно, квадратный корень из 3 иррационален.
Если квадратный корень из 3 равен 1,732. Найдите значение квадратного корня из 0,03.
Представим √0,03 в форме p/q, т. е. √(3/100) = 0,03/10 = 0,173. Следовательно, значение √0,03 = 0,173
Вычислить 14 плюс 16 квадратный корень 3
Данное выражение равно 14 + 16 √3.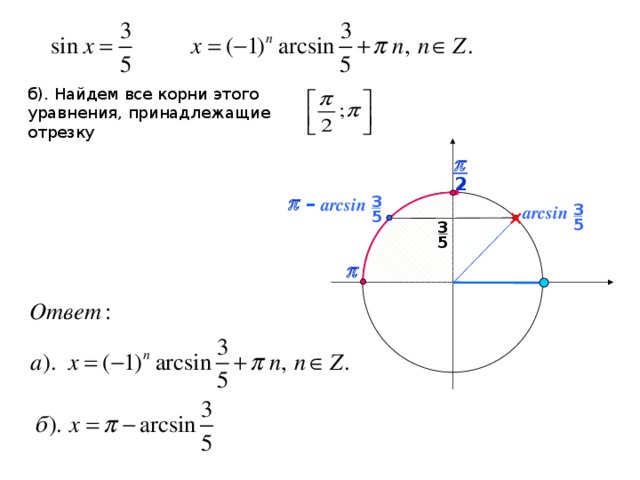
Мы знаем, что квадратный корень из 3 равен 1,732. Следовательно, 14 + 16 √3 = 14 + 16 × 1,732 = 14 + 27,713 = 41,713
Является ли число 3 идеальным квадратом?
Число 3 простое. Это означает, что квадратный корень из 3 не может быть выражен как произведение двух равных целых чисел. Следовательно, число 3 не является полным квадратом.
Что такое квадратный корень из 3 в простейшей радикальной форме?
Число 3 — простое число. Это означает, что число 3 беспарное и не находится в степени 2. Следовательно, радикальная форма квадратного корня из 3 не может быть дополнительно упрощена.
Рабочие листы по математике и
наглядная учебная программа
Калькулятор дробей
Этот калькулятор выполняет основные и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями.
Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Math Symbols
| Symbol | Symbol name | Symbol Meaning | Example | |||||
|---|---|---|---|---|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 | |||||
| — | знак минус | вычитание | 1 1/2 — 2/3 | |||||
| * | asterisk | multiplication | 2/3 * 3/4 | |||||
| × | times sign | multiplication | 2 /3 × 5/6 | |||||
| : | Знак дивизии | Дивизион | 1/2: 3 | |||||
| / | Строш | Дивизион | 1/3 | 12 | Дивизион | 1/3 | 12 | 41/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
more math problems »
Почему мы используем плюс или минус в квадратном корне? Арифметическое значение, которое используется для представления количества и используется при выполнении расчетов, определяется как Числа. Такой символ, как «4,5,6», который представляет число, известен как цифра. Без чисел мы не можем вести подсчет вещей, даты, времени, денег и т. Свойства чисел делают их полезными при выполнении над ними арифметических операций. Эти числа могут быть записаны в числовой форме, а также в словах. Например, 3 записывается словами три, 35 записывается словами тридцать пять и т. д. Учащиеся могут написать числа от 1 до 100 словами, чтобы узнать больше. Существуют разные типы чисел, которые мы можем выучить. Это целые и натуральные числа, нечетные и четные числа, рациональные и иррациональные числа и т. д. Что такое система счисления? Система счисления — это метод записи чисел, представляющий собой математический способ представления чисел данного набора с использованием чисел или символов математическим способом. Система записи для обозначения чисел с использованием цифр или символов логическим образом определяется как система счисления. Мы можем использовать цифры от 0 до 9, чтобы составить все числа. Например, 156, 3907, 3456, 1298, 784859 и т. д. Что такое квадратный корень?Значение числа квадратных корней, которое при умножении само на себя дает исходное число. Предположим, что a — это квадратный корень из b, тогда он представляется как a = √b, или мы можем выразить то же уравнение как a 2 = b. Здесь ‘√’ этот символ, который мы использовали для обозначения корня чисел, называется радикалом. Положительное число, когда его нужно умножить само на себя, представляет собой квадрат числа. Квадратный корень из квадрата любого положительного числа дает исходное число. Например, квадрат 4 равен 16, 4 2 = 16, а квадратный корень из 16, √16 = ±4. Так как 4 — совершенный квадрат, то найти квадратный корень из таких чисел несложно, но для неполного квадрата это действительно сложно. Квадратный корень представлен как «√». Число здесь под подкоренным символом называется подкоренным. Например, квадратный корень из 4 также представлен как радикал 4. Оба представляют одно и то же значение. Формула для нахождения квадратного корня: a = √b Свойства квадратных корней Она определяется как функция «один к одному», которая принимает положительное число в качестве входных данных и возвращает квадрат корень заданного входного числа. f(x) = √x Например, здесь, если x = 9, функция возвращает выходное значение как 3. Свойства квадратного корня следующие:
Легко найти квадратный корень из числа, которое является полным квадратом. Совершенные квадраты — это положительные числа, которые можно записать как произведение числа на себя, или вы можете сказать, что совершенный квадрат — это число, равное степени 2 любого целого числа. Число, которое можно представить как произведение двух равных целых чисел. Например, 16 — это совершенный квадрат, потому что это произведение двух равных целых чисел, 4 × 4 = 16. Однако 24 не является идеальным квадратом, потому что его нельзя выразить как произведение двух равных целых чисел. (8 × 3 = 24).
С помощью квадратных корней мы можем определить, является ли число полным квадратом или нет, если мы вычислим квадратный корень данного числа. Если квадратный корень представляет собой целое число, то данное число будет полным квадратом, а если значение квадратного корня не является целым числом, то данное число не является полным квадратом.
Возьмем другой пример
Почему мы используем плюс или минус в квадратном корне?Ответ:
Примеры задачВопрос 1: Чему равны два квадратных корня из 100? Решение:
Вопрос 2: Каковы квадратные корни из 12? Решение:
Вопрос 3: Чему равны два квадратных корня из 144? Решение:
Функция квадратного корня в Python — Real PythonСмотреть сейчас Это руководство содержит соответствующий видеокурс, созданный командой Real Python. Посмотрите его вместе с письменным руководством, чтобы углубить свое понимание: Функция квадратного корня в Python Вы пытаетесь решить квадратное уравнение? Возможно, вам нужно вычислить длину одной стороны прямоугольного треугольника. Для этих и других типов уравнений функция квадратного корня Python, К концу этой статьи вы узнаете:
Начинаем! Python Pit Stop: Это руководство представляет собой быстрый и практический способ найти нужную информацию, так что вы вернетесь к своему проекту в кратчайшие сроки! Бесплатный бонус: Нажмите здесь, чтобы получить нашу бесплатную памятку по Python, которая покажет вам основы Python 3, такие как работа с типами данных, словарями, списками и функциями Python. Квадратные корни в математикеВ алгебре квадрат , x , является результатом числа, n , умноженного на себя: x = n² Вы можете вычислять квадраты с помощью Python: >>> >>> n = 5 >>> х = п ** 2 >>> х 25 Оператор Python Таким образом, квадратный корень — это число n , которое при умножении само на себя дает квадрат x . В этом примере n , квадратный корень равен 5. 25 является примером идеального квадрата . Совершенные квадраты — это квадраты целых чисел: .>>> >>> 1 ** 2 1 >>> 2 ** 2 4 >>> 3 ** 2 9 Возможно, вы запомнили некоторые из этих правильных квадратов, когда изучали таблицу умножения на уроке элементарной алгебры. Если вам дан маленький идеальный квадрат, может быть достаточно просто вычислить или запомнить его квадратный корень. Но для большинства других квадратов этот расчет может стать немного более утомительным. Часто оценка достаточно хороша, когда у вас нет калькулятора. К счастью, у вас как у разработчика Python есть калькулятор, а именно интерпретатор Python! Удалить рекламу Функция извлечения квадратного корня Python Модуль Python Вы начнете с импорта >>> >>> импорт математики Это все, что нужно! Теперь вы можете использовать Он принимает один параметр, Возвращаемое значение Давайте рассмотрим несколько примеров того, как (и как не следует) использовать Квадратный корень из положительного числа Один тип аргумента, который вы можете передать Например, вы можете найти квадратный корень из >>> >>> math. Возвращаемое значение — Наряду с целыми числами вы также можете передать >>> >>> math.sqrt(70.5) 8.396427811873332 Вы можете проверить точность этого квадратного корня, вычислив его обратную величину: >>> >>> 8.396427811873332 ** 2 70,5 Квадратный корень из нуля Даже >>> >>> math.sqrt(0) 0,0 Хотя вам, вероятно, не придется часто вычислять квадратный корень из нуля, вы можете передавать переменную в Удалить рекламу Квадратный корень из отрицательных чиселКвадрат любого действительного числа не может быть отрицательным. Это связано с тем, что отрицательный продукт возможен только в том случае, если один фактор положительный, а другой отрицательный. Квадрат по определению является произведением числа и самого себя, поэтому отрицательный действительный квадрат невозможен: .>>> >>> math.sqrt(-25) Traceback (последний последний вызов): Файл " Если вы попытаетесь передать отрицательное число в Квадратные корни в реальном миреЧтобы увидеть реальное применение функции квадратного корня Python, давайте обратимся к теннису. Представьте, что Рафаэль Надаль, один из самых быстрых игроков в мире, только что нанес удар справа из дальнего угла, где базовая линия встречается с боковой линией теннисного корта: Теперь предположим, что его противник нанес ответный удар (тот, при котором мяч будет коротким с небольшим импульсом вперед) в противоположный угол, где другая боковая линия встречается с сеткой: Какое расстояние должен пробежать Надаль, чтобы достать мяч? По нормативным размерам теннисного корта вы можете определить, что длина базовой линии составляет 27 футов, а боковой линии (с одной стороны сетки) — 39 футов.ноги длинные. Итак, по сути, это сводится к нахождению гипотенузы прямоугольного треугольника: . Используя ценное уравнение из геометрии, теорему Пифагора, мы знаем, что a² + b² = c² , где a и b — катеты прямоугольного треугольника, а c — гипотенуза. Таким образом, мы можем рассчитать расстояние, которое должен пробежать Надаль, переставив уравнение для решения c : .Вы можете решить это уравнение, используя функцию квадратного корня Python: >>> >>> а = 27 >>> б = 39 >>> math.sqrt(a ** 2 + b ** 2) 47.434164 | 569
Наиболее распространенные мнемоники для запоминания этого порядка операций: 
6 детей — девочки. Какую часть детей составляют девочки?
д., эти числа также используются для измерения и используются для маркировки.
С помощью этих цифр любой может составить бесконечное число.
Называется подкоренным символом. Чтобы представить число «а» в виде квадратного корня, с помощью этого символа можно записать как: «√a», где a — это число.
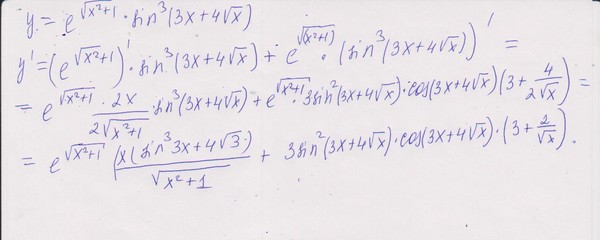
sqrt() 
sqrt(49)
7,0
