Что такое квадратный корень. Таблица квадратных корней
В данной статье разберем понятие “квадратный корень” и приведем таблицу квадратных корней от 1 до 10000.
Чтобы возвести в квадрат число нужно умножить число на само себя. Кратко запись числа в квадрате выглядит следующим образом:
3 · 3 = 32 = 9
Но как быть, если нам нужно получить обратный результат? Например, узнать, какое число при возведении в квадрат дало бы число «9»?
Нужно запомнить, что:
- Нахождение исходного числа, которое в квадрате дало бы требуемое, называется извлечением квадратного корня.
- Извлечение квадратного корня — это действие, обратное возведению в квадрат.
У квадратного корня есть специальный знак. Исходя из вычислений выше, нетрудно догадаться, что число, которое в квадрате дает «9», это число «3». Запись извлечения квадратного корня из числа «9» выглядит так:
√9 = 3
Читаем запись: «Арифметический квадратный корень из девяти».
Квадратный корень из нуля равен нулю: √0 = 0
В таблице приведены квадратные корни натуральных чисел от 1 до 100.
| √1 = 1 √4 = 2 √9 = 3 √16 = 4 √25 = 5 √36 = 6 √49 = 7 √64 = 8 √81 = 9 √100 = 10 | √121 = 11 √144 = 12 √169 = 13 √196 = 14 √225 = 15 √256 = 16 √289 = 17 √324 = 18 √361 = 19 √400 = 20 | √441 = 21 √484 = 22 √529 = 23 √576 = 24 √625 = 25 √676 = 26 √729 = 27 √784 = 28 √841 = 29 √900 = 30 | √961 = 31 √1024 = 32 √1089 = 33 √1156 = 34 √1225 = 35 √1296 = 36 √1369 = 37 √1444 = 38 √1521 = 39 √1600 = 40 | √1681 = 41 √1764 = 42 √1849 = 43 √1936 = 44 √2025 = 45 √2116 = 46 √2209 = 47 √2304 = 48 √2401 = 49 √2500 = 50 |
| √2601 = 51 √2704 = 52 √2809 = 53 √2916 = 54 √3025 = 55 √3136 = 56 √3249 = 57 √3364 = 58 √3481 = 59 √3600 = 60 | √3721 = 61 √3844 = 62 √3969 = 63 √4096 = 64 √4225 = 65 √4356 = 66 √4489 = 67 √4624 = 68 √4761 = 69 √4900 = 70 | √5041 = 71 √5184 = 72 √5329 = 73 √5476 = 74 √5625 = 75 √5776 = 76 √5929 = 77 √6084 = 78 √6241 = 79 √6400 = 80 | √6561 = 81 √6724 = 82 √6889 = 83 √7056 = 84 √7225 = 85 √7396 = 86 √7569 = 87 √7744 = 88 √7921 = 89 √8100 = 90 | √8281 = 91 √8464 = 92 √8649 = 93 √8836 = 94 √9025 = 95 √9216 = 96 √9409 = 97 √9604 = 98 √9801 = 99 √10000 = 100 |
Последние материалы
-
Що таке Scratch і як його використовувати
-
Що дає і чого не може дати дітям “Ментальна арифметика”
-
Лайфхаки возведения в квадрат некоторых двузначных чисел
Категорії
- Айкидо для детей
- Английский язык
- Важливі звички, які обов’язково потрібно розвинути у дитини
- Дети и родители
- Информатика, основы программирования
- Йога для детей
- Логопедия
- Математика, логика, мышление
- Музыка для детей
- Оборудование для занятий в клубе
- Обучение без стресса
- Обучение ребенка
- Онлайн обучение (e-learning)
- Подготовка ребенка к школе
- Развитие ребенка 1-3 лет
- Развитие ребенка 3-7 лет
- Развитие ребенка 7-17 лет
- Развитие ребенка до 1 года
- Рисование, лепка, оригами
- Театральная студия
- Учебные программы
- Фитнес для детей
- Що робити, якщо…
- Эмоциональный интеллект ребенка
- Языки, чтение, письмо
Добро пожаловать в детский клуб Kokoro
Мечтаете об успешном будущем для Вашего ребенка? Хотите дать детям навыки, которые обязательно пригодятся им в будущем? Хотите, чтобы Ваш ребенок всесторонне развивался на увлекательных занятиях? Тогда детский клуб Kokoro – это то, что Вам нужно!
Запишитесь на бесплатное пробное занятие уже сегодня по тел. 095-65-38-165, 097-497-28-68
095-65-38-165, 097-497-28-68
Читать далее
Наш Facebook
Таблица корней
В данной статье мы с вами разберем такое понятие как квадратный корень, какие бывают виды корней, а так же рассмотрим таблицу корней и то как ей пользоваться.
Итак, что же такое квадратный корень. Для того чтобы это понять воспользуемся примерами из школьного курса и рассмотрим простое уравнение, типа: х2 = 4. Что бы его решить нужно понять какое число нужно возводить в квадрат для получения 4. Это не так уж и сложно так как таблица умножения подсказывает нам что это 2 либо -2. с целью упрощения математического решения и ввели понятие квадратного корня с присвоением ему специального символа ?.
Квадратным корнем положительного числа а, будет только положительное число квадрат от которого равняется а.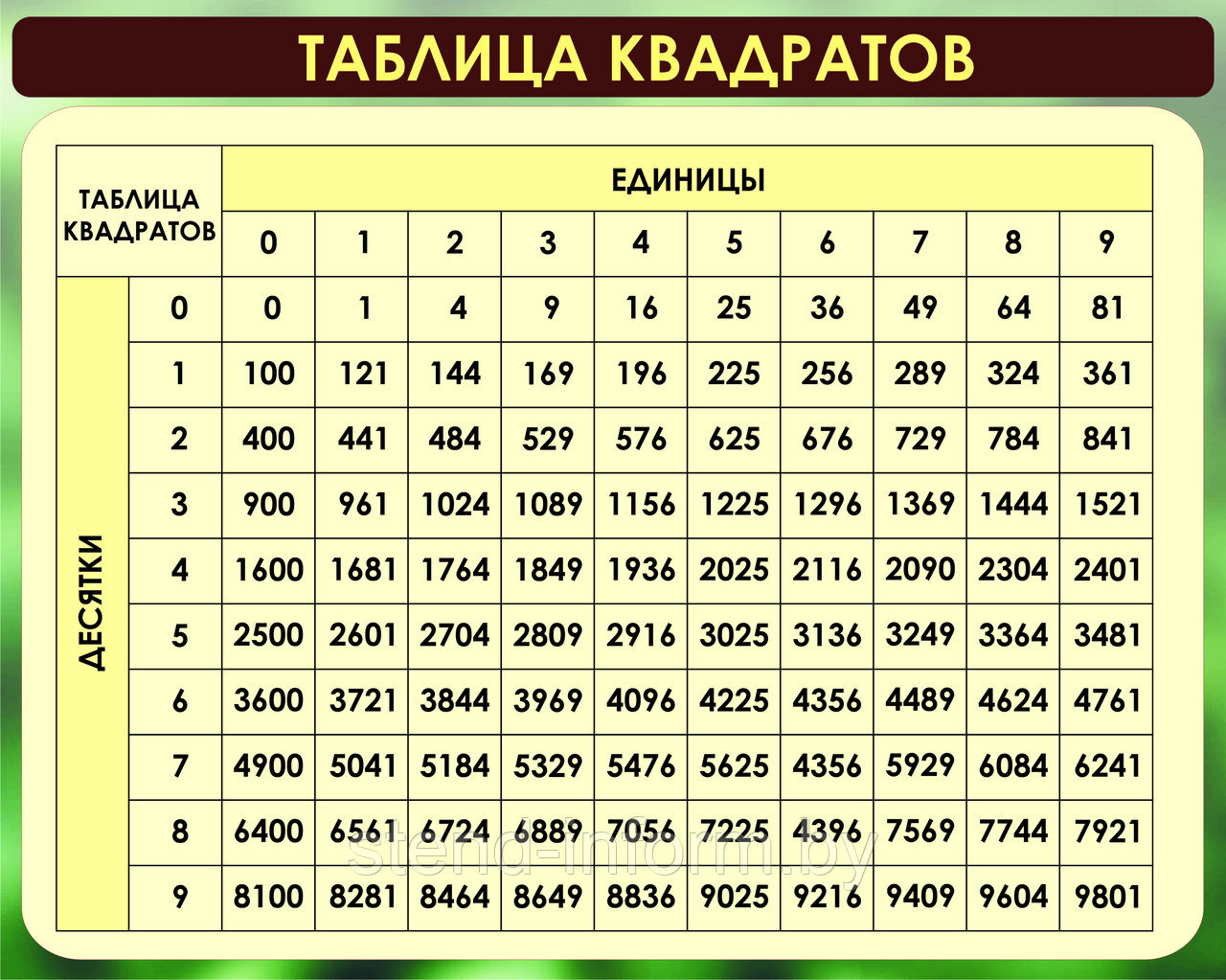
Как вы думаете почему а может быть только положительное число. Опять обратимся к примеру и найдем корень для ?(-9). И это будет 32 = 9, но не — 9, а если возьмем -3. Проверим (-3)2 = 9. Опять не получается и все это из-за того что не существует таких чисел, которые в квадрате давали бы число со знаком минус.
Можно заметить что квадратный корень в решении, может быть только положительным числом, но почему тогда в первом уравнении упоминалось как 2 так и -2? Объясняю, есть квадратные уравнения и арифметические квадратные корни от числа и это разные вещи. Например х2=4 не тоже самое что х=?4.
Да, в этом легко запутаться, но когда нужно только извлечь корень от какого либо числа, то в ответе получим исключительно положительный ответ.
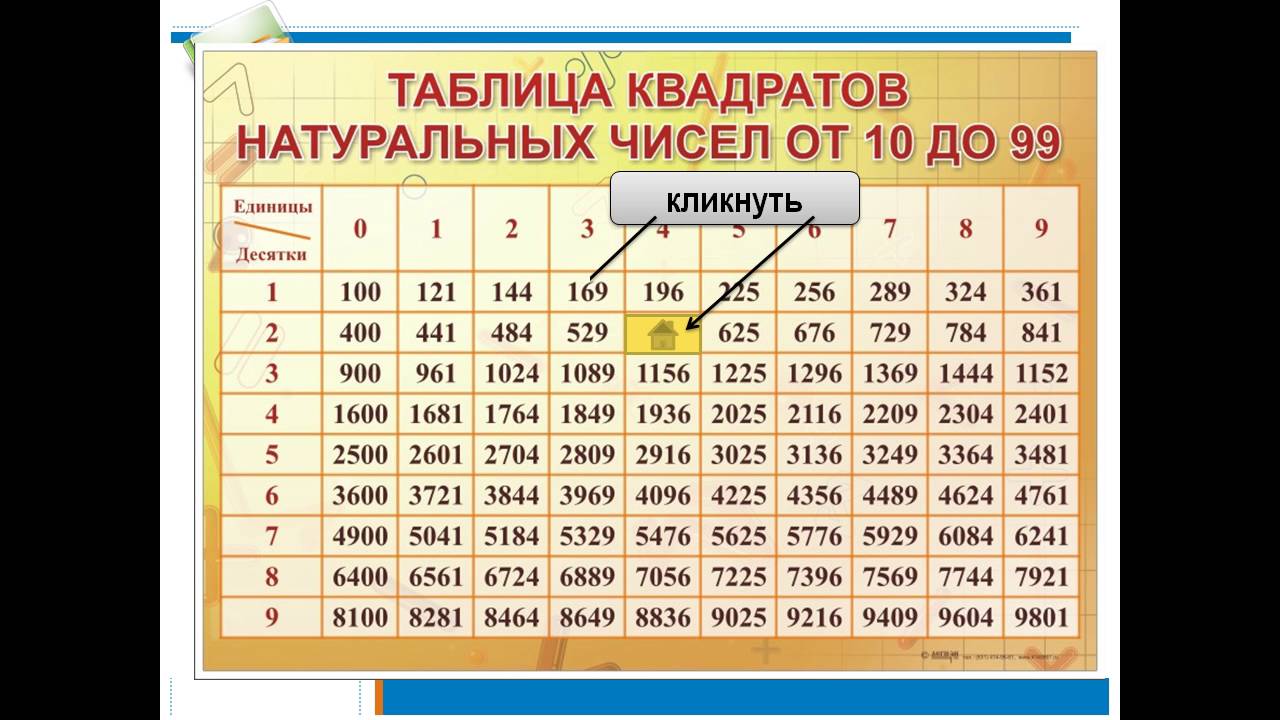
Для удобства и быстроты нахождения решений, существует таблица корней, которая содержит в себе уже готовые извлеченные корни. Пользуйтесь!
Верхняя строка содержит единицы, а левый столбец десятки.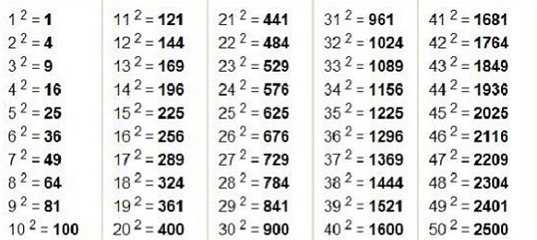 К примеру вам необходимо узнать квадратный корень числа 54. Ищем десятки с левой стороны (это будет цифра 5), а единицы с верху (это будет цифра 4). При пересечении этих значений и находится нужный нам ответ который равен 6,7082.
К примеру вам необходимо узнать квадратный корень числа 54. Ищем десятки с левой стороны (это будет цифра 5), а единицы с верху (это будет цифра 4). При пересечении этих значений и находится нужный нам ответ который равен 6,7082.
Также есть таблица квадратов, не путайте с таблицей корней. Выглядит она так:
Она удобно если вам нужно сразу получить значение двухзначного числа в квадрате. К примеру, нужно возвести 89 в квадрат. Находим 8 слева, 9 сверху, на пересечении значение квадрата — 7921.
Чем больше вы будите работать с корнями, тем реже будите пользоваться данной таблицей. Так как все значения со временем запоминаются. Это как таблица умножения, которой мы пользуемся только для изучения и запоминания.
С корнями возможно производить только три действия и это:
— умножать,
— делить,
-возводить в степень.
Свойства и Примеры объединены и показаны в таблице.
Когда срочно нужна курсовая работа, а времени на её написание практически нет. Стоит обратиться за помощью, которая находиться на сайте http://zakazat-kursovuyu.ru/index.php/zakaz-kursovoj. Ценой и качеством Вы будите приятно удивленны.
Квадратный корень от 1 до 100
Квадратный корень от 1 до 100 — это список квадратных корней всех чисел от 1 до 100. Квадратный корень может иметь как отрицательные, так и положительные значения. Положительные значения квадратных корней от 1 до 100 находятся в диапазоне от 1 до 10.
В квадратных корнях от 1 до 100 числа 1, 4, 9, 16, 25, 36, 49, 64, 81 и 100 являются полными квадратами. а остальные числа являются несовершенными квадратами, т.е. их квадратный корень будет иррациональным. Квадратный корень от 1 до 100 в радикальной форме выражается как √x, а в экспоненциальной форме он выражается как (x) ½ .
Квадратный корень от 1 до 100 в радикальной форме выражается как √x, а в экспоненциальной форме он выражается как (x) ½ .
Изучение квадратного корня от 1 до 100 поможет вам быстро упростить длинные уравнения, занимающие много времени. Значение квадратных корней от 1 до 100 до 3 знаков после запятой указано в таблице ниже.
Ученикам рекомендуется тщательно запомнить эти значения квадратного корня от 1 до 100 для более быстрого выполнения математических вычислений. Нажмите на кнопку загрузки, чтобы сохранить копию в формате PDF.
В таблице ниже показаны значения квадратных корней от 1 до 100 для идеальных квадратов.
В таблице ниже показаны значения от 1 до 100 квадратных корней для неполных квадратов.
Каково значение квадратного корня от 1 до 100?
Значение квадратного корня от 1 до 100 представляет собой число (x 1/2 ), умноженное само на себя дает исходное число. Он может иметь как отрицательные, так и положительные значения. В диапазоне от 1 до 100 квадратные корни из 1, 4, 9, 16, 25, 36, 49, 64, 81 и 100 являются целыми числами (рациональными), а квадратные корни из 2, 3, 5, 6, 7 , 8, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20, 21, 22, 23, 24, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35 , 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 82, 83, 84, 85, 86 , 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98 и 99 — десятичные числа, которые не являются ни конечными, ни повторяющимися (иррациональными).
В диапазоне от 1 до 100 квадратные корни из 1, 4, 9, 16, 25, 36, 49, 64, 81 и 100 являются целыми числами (рациональными), а квадратные корни из 2, 3, 5, 6, 7 , 8, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20, 21, 22, 23, 24, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35 , 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 82, 83, 84, 85, 86 , 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98 и 99 — десятичные числа, которые не являются ни конечными, ни повторяющимися (иррациональными).
Какие существуют методы вычисления квадратных корней от 1 до 100?
Существует два метода, обычно используемых для вычисления значения квадратного корня от 1 до 100. Для идеальных квадратов (1, 4, 9, 16, 25, 36, 49, 64, 81 и 100) мы можем использовать простые числа. методом факторизации и для неполных квадратов (2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 18, 19)., 20, 21, 22, 23, 24, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46 , 47, 48, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 65, 66, 67, 68, 69, 70, 71, 72, 73 , 74, 75, 76, 77, 78, 79, 80, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98 и 99) можно использовать метод длинного деления.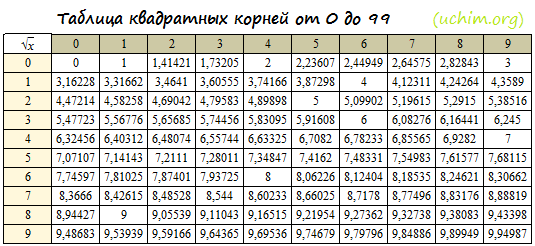
Если извлечь квадратный корень от 1 до 100, сколько из них будет иррациональным?
Цифры 2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20, 21, 22, 23, 24, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46 , 47, 48, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 65, 66, 67, 68, 69, 70, 71, 72, 73 , 74, 75, 76, 77, 78, 79, 80, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98 и 99 — несовершенные квадраты. Следовательно, их квадратный корень будет иррациональным числом (не может быть выражено в виде p/q, где q ≠ 0).
Каково значение 21 плюс 2 квадратного корня 784?
Значение √784 равно 28. Итак, 21 + 2 × √784 = 21 + 2 × 28 = 77. Следовательно, значение 21 плюс 2 квадратного корня из 784 равно 77.
Сколько чисел в квадратных корнях от 1 до 100 рациональны?
Числа 1, 4, 9, 16, 25, 36, 49, 64, 81 и 100 являются полными квадратами, поэтому их квадратные корни будут целыми числами, т. е. могут быть выражены в виде p/q, где q ≠ 0 , Следовательно, квадратный корень из чисел 1, 4, 9, 16, 25, 36, 49, 64, 81 и 100 являются рациональными числами.
е. могут быть выражены в виде p/q, где q ≠ 0 , Следовательно, квадратный корень из чисел 1, 4, 9, 16, 25, 36, 49, 64, 81 и 100 являются рациональными числами.
Какие значения квадратных корней от 1 до 100 находятся между 2 и 3 включительно?
Значения квадратных корней от 1 до 100 между 2 и 3 составляют √4 (2), √5 (2,236), √6 (2,449), √7 (2,646), √8 (2,828) и √9 (3 ).
Квадратный корень от 1 до 20
Квадратный корень от 1 до 20 — это список квадратных корней из всех чисел от 1 до 20. Квадратный корень может иметь как положительные, так и отрицательные значения. Положительные значения квадратных корней от 1 до 20 находятся в диапазоне от 1 до 4,47214.
В квадратных корнях от 1 до 20 числа 1, 4, 9 и 16 являются полными квадратами, а остальные числа являются неполными квадратами, т.е. их квадратный корень будет иррациональным. Квадратный корень от 1 до 20 в радикальной форме выражается как √x, а в экспоненциальной форме он выражается как (x) ½ .
Квадратные корни от 1 до 20:
- В подкоренной форме: √x
- В экспоненциальной форме: (x) ½
- Наибольший квадратный корень: √20 = 4,4721
Где x — любое число от 1 до 20.
| 1. | Квадратный корень от 1 до 20 |
| 2. | Квадратный корень от 1 до 20 PDF |
| 3. | Как вычислить квадратный корень от 1 до 20? |
| 4. | Часто задаваемые вопросы |
Квадратный корень от 1 до 20 Таблица
Квадратный корень от 1 до 20
Изучение квадратного корня от 1 до 20 поможет вам быстро упростить длинные уравнения, занимающие много времени. Значение квадратных корней от 1 до 20 до 3 знаков после запятой указано в таблице ниже.
Квадратный корень от 1 до 20 с округлением до 3 знаков после запятой | |
√1 = 1 | √2 = 1,414 |
√3 = 1,732 | √4 = 2 |
√5 = 2,236 | √6 = 2,449 |
√7 = 2,646 | √8 = 2,828 |
√9 = 3 | √10 = 3,162 |
√11 = 3,317 | √12 = 3,464 |
√13 = 3,606 | √14 = 3,742 |
√15 = 3,873 | √16 = 4 |
√17 = 4,123 | √18 = 4,243 |
√19 = 4,359 | √20 = 4,472 |
Ученикам рекомендуется тщательно запомнить значения квадратного корня от 1 до 20 для более быстрого выполнения математических вычислений. Нажмите на кнопку загрузки, чтобы сохранить копию в формате PDF.
Нажмите на кнопку загрузки, чтобы сохранить копию в формате PDF.
Квадратный корень от 1 до 20 для идеальных квадратов
В таблице ниже показаны значения квадратных корней от 1 до 20 для идеальных квадратов.
√1 = 1 | √4 = 2 |
√9 = 3 | √16 = 4 |
Квадратный корень от 1 до 20 для неидеальных квадратов
В таблице ниже показаны значения квадратного корня от 1 до 20 для неидеальных квадратов.
√2 = 1,414 | √3 = 1,732 |
√5 = 2,236 | √6 = 2,449 |
√7 = 2,646 | √8 = 2,828 |
√10 = 3,162 | √11 = 3,317 |
√12 = 3,464 | √13 = 3,606 |
√14 = 3,742 | √15 = 3,873 |
√17 = 4,123 | √18 = 4,243 |
√19 = 4,359 | √20 = 4,472 |
☛ Проверка: Калькулятор квадратного корня
Как вычислить квадратный корень от 1 до 20?
Метод 1: Факторизация простых чисел
Пример: Значение √4
- Факторизация простых чисел 4 равна 2 × 2
- Парные простые множители: 2
Следовательно, значение √4 = 2
Метод 2: метод длинного деления
Квадратные корни чисел от 1 до 20
Решенные примеры на квадратный корень от 1 до 20
Пример 1: Квадратный металлический лист имеет площадь 11 кв.
 дюймов. Найдите длину стороны металлического листа.
дюймов. Найдите длину стороны металлического листа.Решение:
Пусть «a» будет длиной стороны металлического листа
Площадь квадратного металлического листа = 11 дюймов 2 = a 2
т.е. 2 = 11
a = √11 = 3,317 дюйма
Следовательно, длина стороны металлического листа составляет 3,317 дюйма.
Пример 2: Если круглая столешница имеет площадь 15π кв. дюймов. Найдите радиус столешницы в дюймах?
Решение:
Площадь круглой столешницы = 15π в 2 = πr 2
т. е. 15 = r 2 . Следовательно, радиус = √15
Используя значения от 1 до 20 таблицы квадратного корня, радиус столешницы = √15 дюймов = 3,873 дюйма
Пример 3: Найдите значение 9√15 + 6√13
Решение:
9√15 + 6√13 = 9 × (3,873) + 6 × (3,606) [значение √15 = 3,873 и √13 = 3,606]
Следовательно, 9√15 + 6√13 = 34,857 + 21,636 = 56,493
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы по квадратному корню от 1 до 20
Каково значение квадратного корня от 1 до 20?
Значение квадратного корня от 1 до 20 представляет собой число (x 1/2 ), умноженное само на себя дает исходное число. Он может иметь как отрицательные, так и положительные значения. В диапазоне от 1 до 20 квадратные корни из 1, 4, 9 и 16 являются целыми числами (рациональными), а квадратные корни из 2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14 , 15, 17, 18, 19 и 20 — десятичные числа, которые не являются ни конечными, ни повторяющимися (иррациональными).
Если взять квадратные корни от 1 до 20, сколько из них окажутся иррациональными?
Числа 2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 18, 19 и 20 — неполные квадраты. Следовательно, их квадратный корень будет иррациональным числом (не может быть выражено в виде p/q, где q ≠ 0).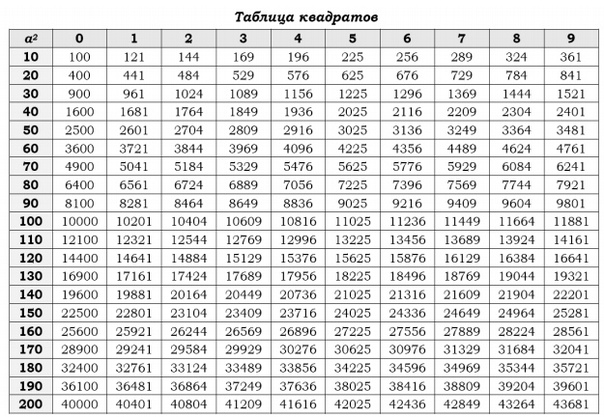

 дюймов. Найдите длину стороны металлического листа.
дюймов. Найдите длину стороны металлического листа.