Формулы Байеса
Формула Байеса:Вероятности P(Hi) гипотез Hi называют априорными вероятностями — вероятности до проведения опытов.
Вероятности P(A/Hi) называют апостериорными вероятностями – вероятности гипотез Hi, уточненных в результате опыта.
Для решения задач можно использовать этот калькулятор
Пример №1. Прибор может собираться из высококачественных деталей и из деталей обычного качества. Около 40% приборов собираются из высококачественных деталей. Если прибор собран из высококачественных деталей, его надежность (вероятность безотказной работы) за время t равна 0,95; если из деталей обычного качества — его надежность равна 0,7. Прибор испытывался в течение времени t и работал безотказно. Найдите вероятность того, что он собран из высококачественных деталей.
Решение. Возможны две гипотезы: H1 — прибор собран из высококачественных деталей; H Вероятности этих гипотез до опыта: P(H1) = 0,4, P(H2) = 0,6. В результате опыта наблюдалось событие A — прибор безотказно работал время t. Условные вероятности этого события при гипотезах H1 и H2 равны: P(A|H1) = 0,95; P(A|H2) = 0,7. По формуле (12) находим вероятность гипотезы H1 после опыта:
Вероятности этих гипотез до опыта: P(H1) = 0,4, P(H2) = 0,6. В результате опыта наблюдалось событие A — прибор безотказно работал время t. Условные вероятности этого события при гипотезах H1 и H2 равны: P(A|H1) = 0,95; P(A|H2) = 0,7. По формуле (12) находим вероятность гипотезы H1 после опыта:
Пример №2. Два стрелка независимо один от другого стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка 0,8, для второго 0,4. После стрельбы в мишени обнаружена одна пробоина. Предполагая, что два стрелка не могут попасть в одну и ту же точку, найдите вероятность того, что в мишень попал первый стрелок.
Решение. Пусть событие A — после стрельбы в мишени обнаружена одна пробоина. До начала стрельбы возможны гипотезы:
H 1 — ни первый, ни второй стрелок не попадет, вероятность этой гипотезы: P(H1) = 0,2 · 0,6 = 0,12.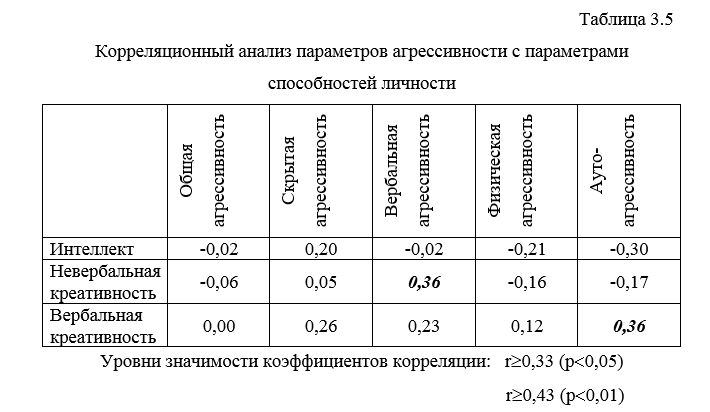
H2 — оба стрелка попадут, P(H2) = 0,8 · 0,4 = 0,32.
H3 — первый стрелок попадет, а второй не попадет, P(H3) = 0,8 · 0,6 = 0,48.
H4 — первый стрелок не попадет, а второй попадет, P (H4) = 0,2 · 0,4 = 0,08.
Условные вероятности события A при этих гипотезах равны:
P(A|H1)=0; P(A|H2)=0; P(A|H3)=1; P(A|H4)=1.
После опыта гипотезы H1 и H2 становятся невозможными, а вероятности гипотез H3 и H4
будут равны:
Итак, вероятнее всего, что мишень поражена первым стрелком.
Пример №3. В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами-изготовителями. На складе имеются электродвигатели названных заводов соответственно в количестве 19,6 и 11 шт., которые могут безотказно работать до конца гарантийного срока соответственно с вероятностями 0,85, 0,76 и 0,71.
Решение. Первым испытанием является выбор электродвигателя, вторым — работа электродвигателя во время гарантийного срока. Рассмотрим следующие события:
A — электродвигатель работает безотказно до конца гарантийного срока;
H1 — монтер возьмет двигатель из продукции первого завода;
H2 — монтер возьмет двигатель из продукции второго завода;
H3 — монтер возьмет двигатель из продукции третьего завода.
Вероятность события A вычисляем по формуле полной вероятности:
P(A)=P(A|H1)·H1 + P(A|H2)·H2 + P(A|H3)·H3
Условные вероятности заданы в условии задачи:
P(A|H1)=0.
 85; P(A|H2)=0.76; P(A|H3)=0.71
85; P(A|H2)=0.76; P(A|H3)=0.71
Найдем вероятности P(H1)=19/36 ≈ 0,528; P(H2)=6/36 ≈ 0,167; P(H3)=11/36 ≈ 0,306;
P(A)=0,85·19/36+0,76·6/36+0,71·11/36 ≈ 0,792
По формулам Бейеса (12) вычисляем условные вероятности гипотез Hi:
Пример №4. Вероятности того, что во время работы системы, которая состоит из трех элементов, откажут элементы с номерами 1, 2 и 3, относятся как 3: 2: 5. Вероятности выявления отказов этих элементов равны соответственно 0,95; 0,9 и 0,6.
б) В условиях данной задачи во время работы системы обнаружен отказ. Какой из элементов вероятнее всего отказал?
Решение.
Пусть А – событие отказа. Введем систему гипотез h2 – отказ первого элемента, h3 – отказ второго элемента, h4 – отказ третьего элемента.
Находим вероятности гипотез:
P(h2) = 3/(3+2+5) = 0. 3
3
P(h3) = 2/(3+2+5) = 0.2
P(h4) = 5/(3+2+5) = 0.5
Согласно условию задачи условные вероятности события А равны:
P(A|h2) = 0.95, P(A|h3) = 0.9, P(A|h4) = 0.6
а) Найдите вероятность обнаружения отказа в работе системы.
P(A) = P(h2)*P(A|h2) + P(h3)*P(A|h3) + P(h4)*P(A|h4) = 0.3*0.95 + 0.2*0.9 + 0.5*0.6 = 0.765
б) В условиях данной задачи во время работы системы обнаружен отказ. Какой из элементов вероятнее всего отказал?
P1 = P(h2)*P(A|h2)/ P(A) = 0.3*0.95 / 0.765 = 0.373
P2 = P(h3)*P(A|h3)/ P(A) = 0.2*0.9 / 0.765 = 0.235
P3 = P(h4)*P(A|h4)/ P(A) = 0.5*0.6 / 0.765 = 0.392
Максимальная вероятность у третьего элемента.
4.3. Корреляционная таблица
При большом числе
наблюдений одно и то же значение случайной
величины Х может встретиться
раз, одно и то же значение случайной
величиныY может встретиться
раз, а одна и та же пара чисел (х, у)
может наблюдаться
раз.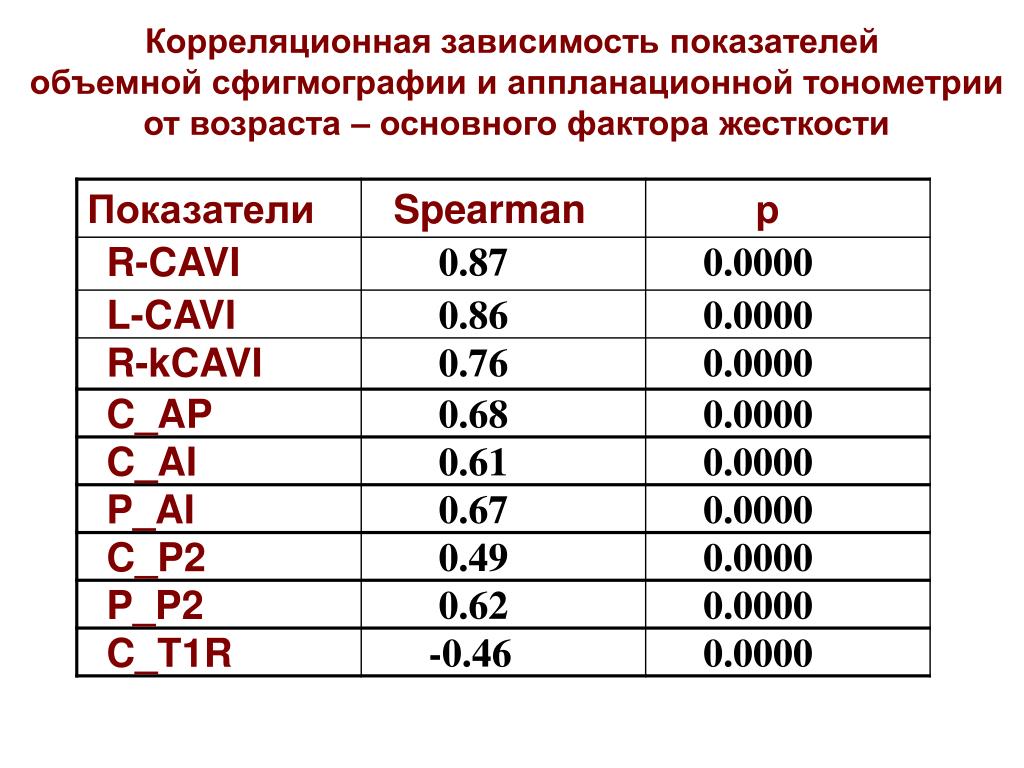 Поэтому данные наблюдений группируют,
т.е. подсчитывают частоты,,. Все сгруппированные данные за-писывают
в виде таблицы, которую называют корреляционной.
Поэтому данные наблюдений группируют,
т.е. подсчитывают частоты,,. Все сгруппированные данные за-писывают
в виде таблицы, которую называют корреляционной.
Поясним ее строение на простом примере. Имеем таблицу:
Y X | 1 | 2 | 3 | 4 | 5 | |
1 | 6 | 4 | 10 | |||
0 | 1 | 4 | 6 | 11 | ||
1 | 5 | 9 | 5 | 19 | ||
2 | 3 | 7 | 10 | |||
3 | 12 | 10 | 15 | 10 |
В
первой строке указаны наблюдаемые
значения (1,
2, 3, 4, 5)
слу-чайной величины Х,
а в первом столбце таблицы – наблюдаемые
значения (1,
0,
1,
2)
случайной величины Y.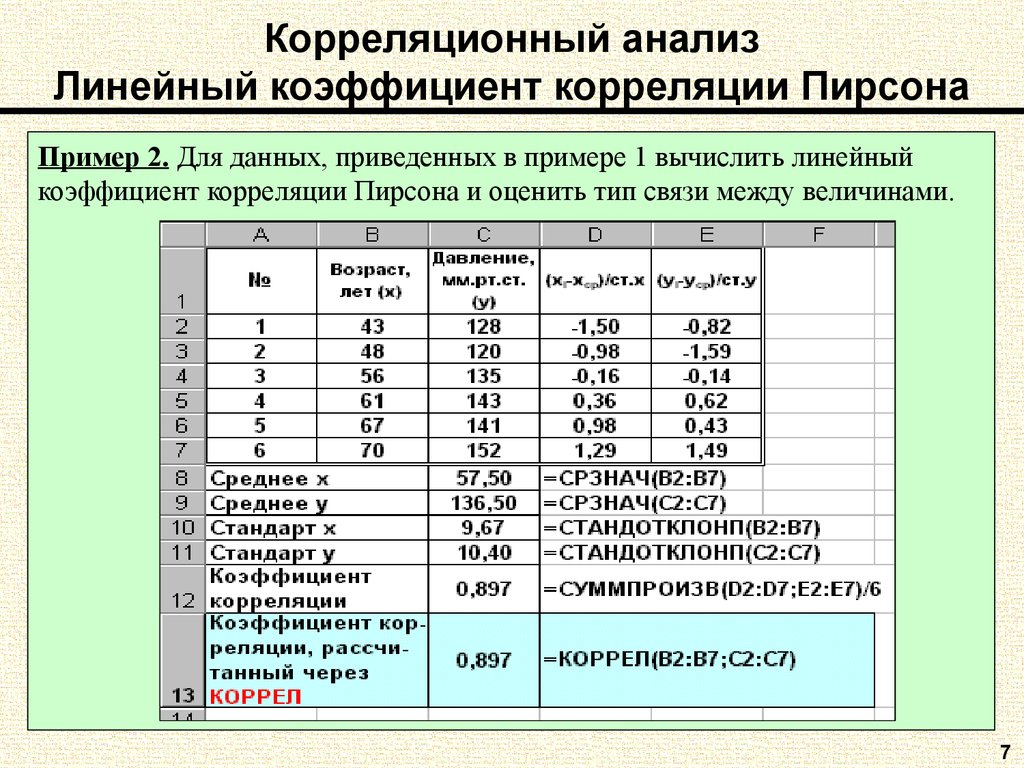 На пересечении строк и столбцов находятся
частоты
наблюдаемых
пар значений случайных величин
На пересечении строк и столбцов находятся
частоты
наблюдаемых
пар значений случайных величин
В последнем столбце записаны суммы частот строк. Например, сумма частот второй строки равна — это число указывает, что значение случайной величины Y, равное 0 (в сочетании с различными значениями случайной величины Х ), наблюдалось 11 раз.
В последней строке записаны суммы частот столбцов. Например, сумма частот четвертого столбца равна — это число указывает, что значение случайной величины Х, равное 4 (в сочетании с различными значениями случайной величины Y ), наблюдалось 15 раз.
Общее число наблюдений
Ранее мы полагали, что значения Х и соответствующие им значения Y
наблюдались по одному разу. На практике,
безусловно, одна пара случайных величин
(х, у)
может наблюдаться любое число раз.
На практике,
безусловно, одна пара случайных величин
(х, у)
может наблюдаться любое число раз.Поэтому формула для коэффициента регрессии (4.4) примет вид
(4.5)
где в сумме учтено, что пара (х, у) наблюдалась раз, а и выборочные средние квадратические отклонения случайных величин Х и Y.
Умножим обе части равенства (4.5) на дробь и назовем это выражение выборочным коэффициентом корреляции
Тогда уравнение линейной регрессии Y на Х будет иметь вид
Замечание 2. Выборочный коэффициент корреляции является безраз-мерной оценкой коэффициента регрессии
Таким образом, основная задача корреляционного анализа состоит в оценке степени линейной связи между случайными величинами Х и Y, которая устанавливается при помощи выборочного коэффициента корре-ляции
Если выборочный
коэффициент корреляции
мал, то линейная связь считается слабой
и ее можно не принимать во внимание. Если же выборочный коэффициент корреляцииблизок к1,
то линейная связь сильная и к ней следует
относиться практически как к функциональной.
В противном случае, связь принято считать
статистической. И, наконец, при
связь между случайными величинамиХ и Y имеет строго линейный характер.
Если же выборочный коэффициент корреляцииблизок к1,
то линейная связь сильная и к ней следует
относиться практически как к функциональной.
В противном случае, связь принято считать
статистической. И, наконец, при
связь между случайными величинамиХ и Y имеет строго линейный характер.
Замечание. Выборочный коэффициент корреляции является лишь оценкой теоретического коэффициента корреляциигенеральной сово-купности, поэтому возникает необходимость проверить гипотезу о значи-мости выборочного коэффициента корреляции. Однако, если выборка имеет достаточно большой объем и хорошо представляет генеральную совокупность, т.е. является репрезентативной, то вывод (гипотезу) о ли-нейной зависимости между случайными величинами Х и Y , полученный по данным выборки, можно распространить и на всю генеральную сово-купность.
Например, для оценки теоретического коэффициента корреляции генеральной совокупности (если она распределена нормально) можно воспользоваться формулой
Таблица корреляции
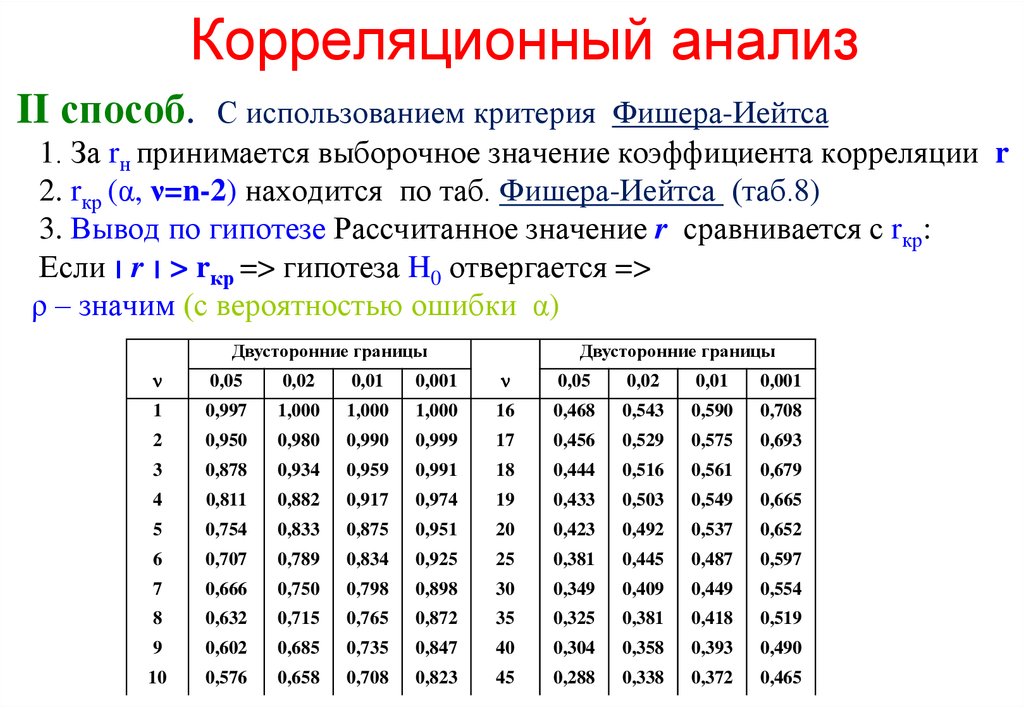
В таблице корреляций представлены критические значения коэффициента корреляции r-Пирсона и коэффициента корреляции r-Спирмена
Критические значения коэффициентов корреляции
| n | p | |||
| 0,1 | 0,05 | 0,01 | 0,001 | |
| 5 | 0,805 | 0,878 | 0,959 | 0,991 |
| 6 | 0,729 | 0,811 | 0,917 | 0,974 |
| 7 | 0,669 | 0,754 | 0,875 | 0,951 |
| 8 | 0,621 | 0,707 | 0,834 | 0,925 |
| 9 | 0,582 | 0,666 | 0,798 | 0,898 |
| 10 | 0,549 | 0,632 | 0,765 | 0,872 |
| 11 | 0,521 | 0,602 | 0,735 | 0,847 |
| 12 | 0,497 | 0,576 | 0,708 | 0,823 |
| 13 | 0,476 | 0,553 | 0,684 | 0,801 |
| 14 | 0,458 | 0,532 | 0,661 | 0,780 |
| 15 | 0,441 | 0,514 | 0,641 | 0,760 |
| 16 | 0,426 | 0,497 | 0,623 | 0,742 |
| 17 | 0,412 | 0,482 | 0,606 | 0,725 |
| 18 | 0,400 | 0,468 | 0,590 | 0,708 |
| 19 | 0,389 | 0,456 | 0,575 | 0,693 |
| 20 | 0,378 | 0,444 | 0,561 | 0,679 |
| 21 | 0,369 | 0,433 | 0,549 | 0,665 |
| 22 | 0,360 | 0,423 | 0,537 | 0,652 |
| 23 | 0,352 | 0,413 | 0,526 | 0,640 |
| 24 | 0,344 | 0,404 | 0,515 | 0,629 |
| 25 | 0,337 | 0,396 | 0,505 | 0,618 |
| 26 | 0,330 | 0,388 | 0,496 | 0,607 |
| 27 | 0,323 | 0,381 | 0,487 | 0,597 |
| 28 | 0,317 | 0,374 | 0,479 | 0,588 |
| 29 | 0,311 | 0,367 | 0,471 | 0,579 |
| 30 | 0,306 | 0,361 | 0,463 | 0,570 |
| 31 | 0,301 | 0355 | 0,456 | 0,562 |
| 32 | 0,296 | 0,349 | 0,449 | 0,554 |
| 33 | 0,291 | 0,344 | 0,442 | 0,547 |
| 34 | 0,287 | 0,339 | 0,436 | 0,539 |
| 35 | 0,283 | 0,334 | 0,430 | 0,532 |
| 36 | 0,279 | 0,329 | 0,424 | 0,525 |
| 37 | 0,275 | 0,325 | 0,418 | 0,519 |
| 38 | 0,271 | 0,320 | 0,413 | 0,513 |
| 39 | 0,267 | 0,316 | 0,408 | 0,507 |
| 40 | 0,264 | 0,312 | 0,403 | 0,501 |
| 41 | 0,260 | 0,308 | 0,398 | 0,495 |
| 42 | 0,257 | 0,304 | 0,393 | 0,490 |
| 43 | 0,254 | 0,301 | 0,389 | 0,484 |
| 44 | 0,251 | 0,297 | 0,384 | 0,479 |
| 45 | 0,248 | 0,294 | 0,380 | 0474 |
| 46 | 0,246 | 0,291 | 0,376 | 0,469 |
| 47 | 0,243 | 0,288 | 0,372 | 0,465 |
| 48 | 0,240 | 0,285 | 0,368 | 0,460 |
| 49 | 0,238 | 0,282 | 0,365 | 0,456 |
| 50 | 0,235 | 0,279 | 0,361 | 0,451 |
| 51 | 0,233 | 0,276 | 0,358 | 0,447 |
| 52 | 0,231 | 0,273 | 0,354 | 0,443 |
| 53 | 0,228 | 0,271 | 0,351 | 0,439 |
| 54 | 0,226 | 0,268 | 0,348 | 0,435 |
| 55 | 0,224 | 0,266 | 0,345 | 0,432 |
| 56 | 0,222 | 0,263 | 0,341 | 0,428 |
| 57 | 0,220 | 0,261 | 0,339 | 0,424 |
| 58 | 0,218 | 0,259 | 0,336 | 0,421 |
| 59 | 0,216 | 0,256 | 0,333 | 0,418 |
| 60 | 0,214 | 0,254 | 0,330 | 0,414 |
| 61 | 0,213 | 0,252 | 0,327 | 0,411 |
| 62 | 0,211 | 0,250 | 0,325 | 0,408 |
| 63 | 0,209 | 0,248 | 0,322 | 0,405 |
| 64 | 0,207 | 0,246 | 0,320 | 0,402 |
| 65 | 0,206 | 0,244 | 0,317 | 0,399 |
| 66 | 0,204 | 0,242 | 0,315 | 0,396 |
| 67 | 0,203 | 0,240 | 0,313 | 0,393 |
| 68 | 0,201 | 0,239 | 0,310 | 0,390 |
| 69 | 0,200 | 0,237 | 0,308 | 0,388 |
| 70 | 0,198 | 0,235 | 0,306 | 0,385 |
| 80 | 0,185 | 0,220 | 0,286 | 0,361 |
| 90 | 0,174 | 0,207 | 0,270 | 0,341 |
| 100 | 0,165 | 0,197 | 0,256 | 0,324 |
| 110 | 0,158 | 0,187 | 0,245 | 0,310 |
| 120 | 0,151 | 0,179 | 0,234 | 0,297 |
| 130 | 0,145 | 0,172 | 0,225 | 0,285 |
| 140 | 0,140 | 0,166 | 0,217 | 0,275 |
| 150 | 0,135 | 0,160 | 0,210 | 0,266 |
| 200 | 0,117 | 0,139 | 0,182 | 0,231 |
| 250 | 0,104 | 0,124 | 0,163 | 0,207 |
| 300 | 0,095 | 0,113 | 0,149 | 0,189 |
| 350 | 0,088 | 0,105 | 0,138 | 0,175 |
| 400 | 0,082 | 0,098 | 0,129 | 0,164 |
| 450 | 0,078 | 0,092 | 0,121 | 0,155 |
| 500 | 0,074 | 0,088 | 0,115 | 0,147 |
| 600 | 0,067 | 0,080 | 0,105 | 0,134 |
| Коэффициент корреляции Пирсона | Расчет коэффициента корреляции Пирсона |
| Коэффициент корреляции Спирмена | Расчет коэффициента корреляции Спирмена |
| Коэффициент корреляции Кендалла | Расчет коэффициента корреляции Кендалла |
Автор Заказ работ по математической статистикеРубрики Корреляционный анализ, Корреляция Пирсона, Корреляция Спирмена
2.
 12. Парная корреляция
12. Парная корреляцияНачнем с наиболее простого случая. Пусть с помощью выборки объемом N изучались объекты генеральной совокупности, каждый из которых характеризуется двумя (парой) Количественных признаков X И Y. Подчеркиваем: Количественных, ибо если эти признаки качественные, то исследование их взаимозависимости – это задача дисперсионного анализа. Например, если объектами генеральной совокупности являются изделия некоторого массового производства, то их количественными признаками X И Y могут быть, например, каких-то два их контролируемых размера; или размер и вес; или затраты на производство и выручка от продажи, и т. д. Выборочные данные оформляют в виде таблицы (5.1):
Xi Yj | X1 | X2 | … | Xn | (5. | |
Y1 | N11 | N21 | … | Nn1 | M1 | |
Y2 | N12 | N22 | … | Nn2 | M2 | |
… | … | … | … | … | … | |
Ym | N1m | N2m | … | Nnm | Mm | |
N1 | N2 | … | Nn |
Эта таблица называется Корреляционной.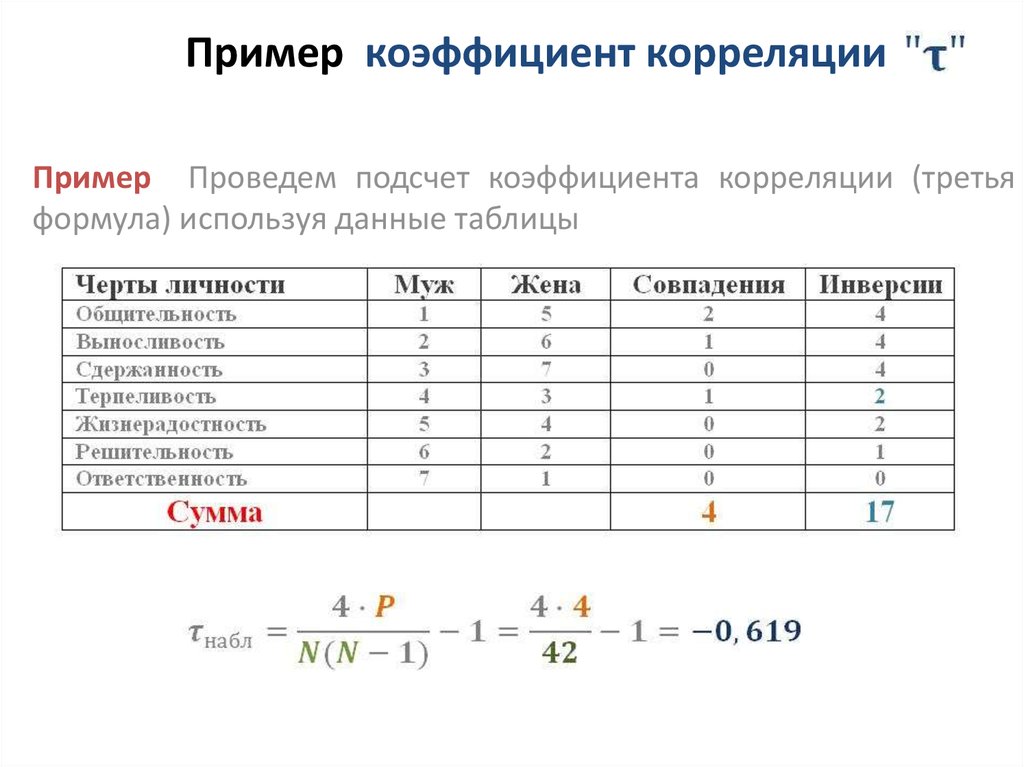 Из нее видно, что признак Х у объектов выборки принимал значения Xi = (X1 ; X2 ; … Xn ), а признак Y – значения Yj = (Y1 ; Y2 ; … Ym ), причем пара значений (X1; Y1) встретилась у N11 Объектов, пара (X2; Y1) – у N21 Объектов, и т. д. Числа Ni = (N1 ; N2 ; … Nn ) определяют общее количество объектов выборки со значениями признака Х, равными (X1 ; X2 ; … Xn ) Соответственно, а числа (M1; M2; … Mm ) – общее количество объектов со значениями (Y1 ; Y2 ; … ; Ym ) признака Y соответственно.
Из нее видно, что признак Х у объектов выборки принимал значения Xi = (X1 ; X2 ; … Xn ), а признак Y – значения Yj = (Y1 ; Y2 ; … Ym ), причем пара значений (X1; Y1) встретилась у N11 Объектов, пара (X2; Y1) – у N21 Объектов, и т. д. Числа Ni = (N1 ; N2 ; … Nn ) определяют общее количество объектов выборки со значениями признака Х, равными (X1 ; X2 ; … Xn ) Соответственно, а числа (M1; M2; … Mm ) – общее количество объектов со значениями (Y1 ; Y2 ; … ; Ym ) признака Y соответственно.2012/37/1.png) При этом ясно, что
При этом ясно, что
(5.2) |
Корреляционная таблица (5.1) фактически является статистическим распределением выборки при исследовании двумерного (двухпараметрического) признака Z=(X, Y) объектов генеральной совокупности.
Данные корреляционной таблицы для наглядности удобно изобразить и в виде так называемого Корреляционного поля. Корреляционное поле – это нанесенное на плоскость Xoy множество всех N экспериментальных точек с координатами (Xi; Yj) с учетом их кратности Nij. Это значит, что при построении корреляционного поля нужно показать, что в точке (Xi; Yj) плоскости Xoy содержится не одна, а Nij точек. Чтобы это было видно на корреляционном поле, нужно эти точки немного отделить друг от друга. Они тогда образуют видимую компактную кучку из Nij точек, окружающих точку (Xi; Yj )(рис.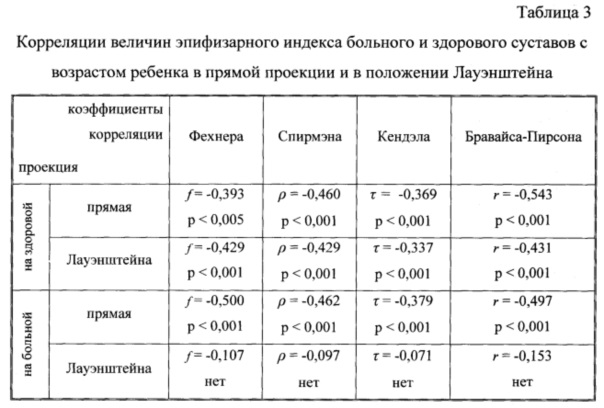 3.11).
3.11).
Рис. 3.11
Как мы знаем из части I (§6, глава 2), корреляционную зависимость (зависимость в среднем) величины Y от величины X характеризует так называемое Уравнение регрессии величины Y на величину X. А график этого уравнения называется Линией регрессии Y на Х. Примерный (оценочный) вид этой линии мы получим, если по данным корреляционной таблицы (5.1) для каждого выборочного значения X=Xi Найдем среднее значение величины Y
(5.3) |
И затем нанесем на корреляционное поле ломаную, соединяющую точки с координатами – рис. 3.11. Эта ломаная называется Выборочной линией регрессии Y на X. Построив эту линию, визуально можем оценить и наличие, и тесноту корреляционной зависимости Y От Х: чем меньше разброс точек корреляционного поля вокруг выборочной линии регрессии Y на Х, тем эта зависимость теснее.
Задачи корреляционно-регрессионного анализа в математической статистике аналогичны тем, что были поставлены в теории вероятностей (§6, глава 2). Этих задач две.
Задача 1. Дать оценку истинного (генерального) уравнения регрессии величины Y на величину Х. А следовательно, дать и оценку истинной (генеральной) линии регрессии Y на Х. Мы говорим лишь об оценке, ибо найти точно по выборочным данным и генеральное уравнение регрессии, и генеральную линию регрессии, очевидно, невозможно.
Задача 2. Оценить степень тесноты корреляционной зависимости Y от Х.
Начнем с рассмотрения первой из этих задач. Идея ее решения состоит в подборе возможно простого уравнения
(5.4) |
График которого тем не менее будет достаточно близким к выборочной линии (ломаной) регрессии. То есть будет достаточно хорошим приближением этой ломаной, сглаживающим эту ломаную. Такое уравнение называется Выравнивающим (или Сглаживающим) выборочным уравнением регрессии. Именно оно и принимается за оценку истинного (генерального) уравнения регрессии , то есть за решение первой задачи корреляционно-регрессионного анализа.
Такое уравнение называется Выравнивающим (или Сглаживающим) выборочным уравнением регрессии. Именно оно и принимается за оценку истинного (генерального) уравнения регрессии , то есть за решение первой задачи корреляционно-регрессионного анализа.
Отметим, однако, что два указанных выше требования: а) простота сглаживающего уравнения регрессии (5.4), а значит, и простота сглаживающей линии регрессии, и б) близость сглаживающей линии регрессии к реальной ломаной регрессии, вообще говоря, противоречивы, ибо повысить указанную близость можно лишь за счет усложнения сглаживающего уравнения. Поэтому на практике стараются добиться некоей золотой середины: и чтобы сглаживающее уравнение регрессии (5.4) было не слишком сложным, и чтобы соответствующая ему сглаживающая линия регрессии тем не менее в целом была достаточно близкой к выборочной ломаной регрессии. Как из многих возможных вариантов выбрать лучший (найти эту золотую середину) – об этом будет сказано ниже.
В качестве наиболее простых форм сглаживающего уравнения (5. 4) чаще всего принимаются следующие его формы:
4) чаще всего принимаются следующие его формы:
1) Уравнение прямой
(5.5) |
2) Уравнение гиперболы
(5.6) |
3) Уравнение параболы
(5.7) |
Напомним, что эти линии в принципе имеют следующий вид:
Линейная зависимость (5.5) наиболее проста по форме, ее параметры K И B Легко интерпретируются. В частности, коэффициент K указывает, на сколько в среднем увеличится (при K>0) или уменьшится (при K<0) величина Y, если значение Х величины Х увеличится на единицу. А параметр B указывает среднее значение величины Y при Х = 0. Благодаря этим преимуществам, а также благодаря простоте вычисления параметров K И B уравнение (5. 5) используется в качестве приближенного (сглаживающего) уравнения регрессии даже в тех случаях, когда более логичным представляется использование уравнение кривой.
5) используется в качестве приближенного (сглаживающего) уравнения регрессии даже в тех случаях, когда более логичным представляется использование уравнение кривой.
Гиперболы (5.6) – это либо монотонно возрастающая, либо монотонно убывающая кривая. Однако, в отличие от прямой, рост или убывание гиперболы имеет тенденцию к затуханию, практически сходя на нет при больших значениях Х величины Х. Параметр B при этом представляет собой предельное значение при X ® ¥. Убывающей гиперболой, например, хорошо выражается зависимость себестоимости продукции растениеводства от урожайности, а возрастающей – зависимость продуктивности животных от расхода кормов.
Парабола (5.7) имеет вершину или впадину и применяется для приближенной описания зависимостей, в которых с изменением Х убывание может меняться на возрастание, и наоборот. Примером параболической зависимости является, например, зависимость средней урожайности от дозы удобрений, когда начальные дозы удобрений приводят к значительному увеличению урожая, последующие – к постепенно уменьшающимся прибавкам, а чрезмерные – к снижению урожая и даже к его гибели. Иногда график параболы используется только частично (только восходящая или только нисходящая ветвь). Параметры параболы, за исключением А0, интерпретировать сложно. Ну, а параметр А0 является, очевидно, оценкой среднего значения величины Y при Х = 0.
Иногда график параболы используется только частично (только восходящая или только нисходящая ветвь). Параметры параболы, за исключением А0, интерпретировать сложно. Ну, а параметр А0 является, очевидно, оценкой среднего значения величины Y при Х = 0.
Подходящую форму сглаживающего уравнения регрессии выбирают, исходя из общих теоретических соображений или, что чаще, по виду корреляционного поля (рис. 3.11). При этом, как уже говорилось выше, наиболее часто уравнение регрессии выбирается в одной из форм (5.5) – (5.7). А для нахождения параметров выбранного уравнения используется универсальный стандартный метод, называемый Методом наименьших квадратов.
Суть этого метода в следующем. Из корреляционной таблицы (5.1) для каждого Х = хI По формуле (5.3) находим выборочное среднее значение величины Y. Далее, для выбранной формы уравнения регрессии записываем сглаживающие средние . В итоге получаем следующую таблицу соответствий экспериментальных и сглаживающих средних значений величины Х, принимающей значения ХI с частотами Ni (I = 1, 2, … N):
ХI | X1 | X2 | … | Xn | (5. |
Ni | N1 | N2 | … | Nn | |
… | |||||
… |
Параметры выбранного сглаживающего уравнения регрессии считаются наилучшими, если они обеспечивают минимально возможные отклонения выборочных средних от подсчитанных по уравнению регрессии сглаживающих средних . В методе наименьших квадратов за меру отклонений от принимается сумма квадратов их разностей. При этом должно быть учтено, что в образовании каждого участвуют Ni точек корреляционного поля. То есть в средней как бы сливаются Ni значений величины Y. C Учетом сказанного указанная сумма принимает вид:
(5. |
В эту сумму входят параметры выбранной функции . И эти параметры подбираются таким образом, чтобы сумма Q была минимально возможной. А это – стандартная задача математического анализа об исследовании функции нескольких переменных на экстремум (минимум или максимум), где Q – функция, а ее переменные – параметры функции . Решая эту задачу, находим наилучшие параметры функции, а вместе с ними получаем и искомое наилучшее (для выбранной формы) сглаживающее уравнение регрессии (5.4), являющееся оценкой истинного (генерального) уравнения регрессии .
Заметим что и реальные выборочные средние , и сглаживающие средние имеют одно и тоже среднее значение – общую выборочную среднюю величины Y. То есть
(5.10) |
Первое из этих равенств следует из выражения (5.3):
А второе равенство получим, рассудив следующим образом. Так как сглаживающая кривая получена методом наименьших квадратов в процессе минимизации суммы (5. 9), то она наилучшим способом вписывается в выборочную линию регрессии, то есть имеет от нее в целом минимальное отклонение. Поэтому если эту сглаживающую линию поднять или опустить, то есть если заменить на линию , где С – некоторая константа, то взамен функции (5.9) получим функцию
9), то она наилучшим способом вписывается в выборочную линию регрессии, то есть имеет от нее в целом минимальное отклонение. Поэтому если эту сглаживающую линию поднять или опустить, то есть если заменить на линию , где С – некоторая константа, то взамен функции (5.9) получим функцию
Значения которой при всех С больше величины (5.9). А свое наименьшее значение (экстремум) функция Q(C) должна иметь при С = 0. Но это значит, что
При
Отсюда следует:
То есть и второе равенство (5.10) доказано.
Равенства (5.10) можно использовать для контроля правильности подсчета и реальных выборочных средних , и сглаживающих выборочных средних
Рассмотрим, в частности, приложение метода наименьших квадратов к случаю, когда теоретические соображения или конфигурация корреляционного поля позволяют в качестве сглаживающего уравнения регрессии использовать уравнение прямой (5.5). Сформируем для этого случая сумму Q:
Вспоминая, что необходимым условием минимума (или максимума) функции нескольких переменных является равенство нулю всех ее частных производных первого порядка, получим следующую систему уравнений (так называемую Нормальную систему) для нахождения параметров K и B Функции (5.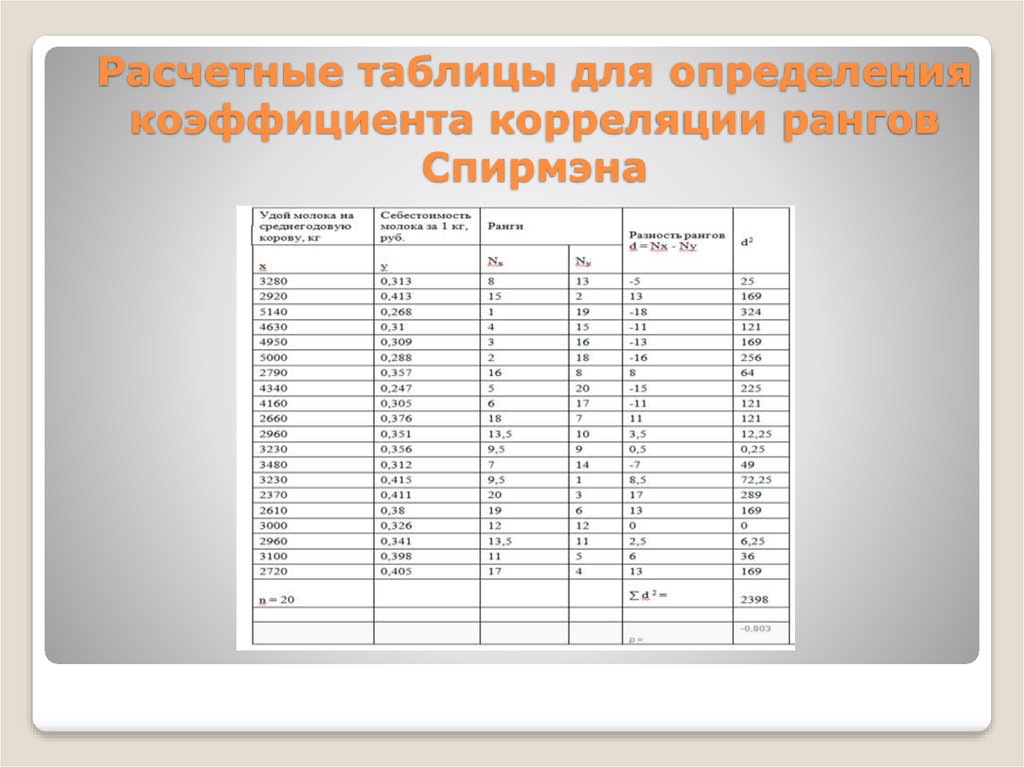 5):
5):
(5.11) |
Сократив на (-2) и разделив затем обе части каждого уравнения на N, получим:
(5.12) |
Учтем, что
(5.13) |
Тогда система (5.12) примет вид:
(5.14) |
Решая ее, находим K И B:
(5.15) |
Подставляя найденные значения K И B в уравнение (5.5), получим искомое сглаживающее линейное уравнение регрессии Y На X:
(5.16) |
Отметим, что по своей форме оно точно такое же, как и уравнение (6. 22) (часть I, глава 2, §6), полученное нами ранее в теории вероятностей. Совпадают эти уравнения не только по форме, но и по существу.
22) (часть I, глава 2, §6), полученное нами ранее в теории вероятностей. Совпадают эти уравнения не только по форме, но и по существу.
Действительно, в уравнении (6.22), согласно (6.23), (6.7) и (6.5) главы 2 фигурируют
(5.17) |
Сравнивая эти выражения с теми выражениями (5.13) и (5.15), что используются в только что полученном уравнении (5.16), видим, что разница между ними состоит лишь в том, что выражения (5.17) дают истинные (генеральные) значения параметров , а выражения (5.13) и (5.15) дают выборочные значения этих же параметров.
Кстати, выборочный коэффициент линейной корреляции RXy, являющийся выборочным значением истинного (генерального) коэффициента линейной корреляции R(X, Y) случайных величин X И Y, находится по формуле:
(5.18) |
Или, что то же самое, по формуле, связывающей его с параметром K уравнения (5. 16):
16):
(5.19) |
При этом
(5.20) |
– выборочные значения среднеквадратических отклонений S(Х) и S(Y) величин X И Y соответственно, а
(5.21) |
– выборочное значение корреляционного момента (ковариации) M(X,Y) величин X И Y.
Значение RXy выборочного коэффициента линейной корреляции используется, в соответствии с §6 (часть I, глава 2), для оценки степени тесноты и линейности корреляционной связи между случайными величинами X И Y. Степень же тесноты Любой (а не только линейной) корреляционной зависимости Y от X определяет, как мы знаем (§ 6, глава 2, часть I) Корреляционное отношение η(Y, X), чье выборочное значение ηYx, с учетом формулы (6. 40) главы 2, находится по формуле:
40) главы 2, находится по формуле:
(5.22) |
Оно показывает долю, которую составляет по отношение к . То есть показывает, какую часть составляет средний разброс выборочных средних вокруг общей средней величины Y в выборке по отношению к среднему разбросу значений Yj величины Y в выборке вокруг той же общей средней .
Минимально возможное значение (HYx)Min = 0 указывает на то, что . То есть что разброс выборочных средних вокруг общей средней отсутствует. А это значит, что для всех Xi (I = 1, 2, …, N). Выборочная ломаная регрессии (рис. 3.11) становится в этом случае горизонтальной прямой. Выборочные средние не меняются с изменением X , а значит, они от Х не зависят. Тогда выборка свидетельствует о том, что, скорее всего, величина Y корреляционно (в среднем) не зависит от величины Х. Мы говорим «скорее всего», потому что никаких окончательных выводов относительно генеральной совокупности исследование выборки дать не может — другая выборка может привести и к другим выводам.
Мы говорим «скорее всего», потому что никаких окончательных выводов относительно генеральной совокупности исследование выборки дать не может — другая выборка может привести и к другим выводам.
Максимально же возможное значение (HYx)Max = 1 указывает на отсутствие разброса значений величины Y относительно их средних значений для каждого ХI (I = 1, 2, …, N). Это означает отсутствие разброса точек корреляционного поля вокруг выборочной линии регрессии (рис. 3.11). То есть в этом случае каждому Xi соответствует лишь одно значение . Иначе говоря, в этом случае выборочные данные свидетельствуют в пользу того, что величина Y жестко (функционально) зависит от величины X.
Если в формуле (5.22) заменить реальные условные средние на сглаживающие условные средние и возвести полученное выражение в квадрат, то получим так называемый Выборочный коэффициент детерминации
(5. |
Он показывает долю, которую составляет дисперсия сглаживающих средних по отношению к общей дисперсии выборочных значений Yj Исследуемого признака Y. То есть он показывает долю общего изменения (вариации) величины Y, объясняемую подобранным сглаживающим уравнением регрессии . Его обычно выражают в процентах.
Выборочное корреляционное отношение HYx не зависит, очевидно, от формы выбранного сглаживающего уравнения регрессии , ибо его величина определяется исключительно выборочными данными. А вот выборочный коэффициент детерминации Dyx От этой формы зависит. Как можно доказать,
(5.24) |
И чем больше Dyx (чем ближе он к ), тем лучше построенное сглаживающее уравнение регрессии объясняет вариацию (изменение) зависимой величины Y. А следовательно, тем удачнее это уравнение построено. При сглаживающая линия регрессии точно пройдет через все экспериментальные точки корреляционного поля, то есть через все узлы ломаной, изображенной на рис. 3.11. Это – идеальный вариант для сглаживающей линии. Правда, уравнение такой идеальной сглаживающей линии при большом числе узлов выборочной ломаной линии регрессии, как правило, слишком сложно. Поэтому на практике идут на существенное упрощение подбираемого сглаживающего уравнения регрессии, жертвуя при этом неизбежным снижением коэффициента детерминации. Если же усложнение сглаживающего уравнения регрессии не пугает, то среди различных подобранных сглаживающих уравнений лучшим считается то, которое обеспечивает наибольший коэффициент детерминации. На вычислительных машинах, кстати, и построение сглаживающих уравнений регрессии в различных формах, и выбор из них наилучшего (по коэффициенту детерминации) делается по специальной стандартной программе.
При сглаживающая линия регрессии точно пройдет через все экспериментальные точки корреляционного поля, то есть через все узлы ломаной, изображенной на рис. 3.11. Это – идеальный вариант для сглаживающей линии. Правда, уравнение такой идеальной сглаживающей линии при большом числе узлов выборочной ломаной линии регрессии, как правило, слишком сложно. Поэтому на практике идут на существенное упрощение подбираемого сглаживающего уравнения регрессии, жертвуя при этом неизбежным снижением коэффициента детерминации. Если же усложнение сглаживающего уравнения регрессии не пугает, то среди различных подобранных сглаживающих уравнений лучшим считается то, которое обеспечивает наибольший коэффициент детерминации. На вычислительных машинах, кстати, и построение сглаживающих уравнений регрессии в различных формах, и выбор из них наилучшего (по коэффициенту детерминации) делается по специальной стандартной программе.
Кстати, если сглаживающее уравнение регрессии строить в линейной (наиболее простой) форме (5. 5), то будем иметь:
5), то будем иметь:
(5.25) |
Действительно, для этого случая на основании (5.16) имеем:
(5.26) |
Если сглаживающее уравнение регрессии строится в нелинейной и достаточно сложной форме, то такое построение трудно произвести вручную, и его лучше поручить машине. Если же возможности воспользоваться машиной (персональным компьютером) нет, то для несложных нелинейных случаев, в частности для уравнений вида (5.6) и (5.7) все можно сделать и вручную. Делается это с помощью метода наименьших квадратов совершенно аналогично тому, как это было проделано выше при построении сглаживающего линейного уравнения (5.5), принявшего итоговую форму (5.16).
Пусть, например, сглаживающее уравнение регрессии строится в гиперболической форме (5.6). Заметим, что такое уравнение – это фактически уравнение (5.5), если в последнем заменить X На . Поэтому для параметров K И B Уравнения (5.6) мы можем воспользоваться формулами (5.15), заменив в них X На :
Поэтому для параметров K И B Уравнения (5.6) мы можем воспользоваться формулами (5.15), заменив в них X На :
(5.27) |
Здесь
(5.28) |
Наконец, рассмотрим еще построение сглаживающего уравнения регрессии в параболической форме (5.7). Формируя для этого случая сумму (5.9)
(5.29) |
И отыскивая ее минимум, приходим к аналогичной (5.12) нормальной системе для нахождения параметров (A0; A1; A2) сглаживающего уравнения регрессии (5.7). Приведём окончательный вид этой системы:
(5.30) |
Решая эту систему, находим (A0; A1; A2), а вместе с ними – и искомое параболическое уравнение регрессии (5. 7).
7).
Построив сглаживающее уравнение регрессии В нескольких различных формах (линейное, гиперболическое, параболическое и т. д.) и выбрав из них лучшее, мы тем не менее еще не можем быть уверены в пригодности такого уравнения для приближения им истинного (генерального) уравнения регрессии . Дело в том, что построенная сглаживающая линия регрессии может на некоторых своих участках выходить за пределы корреляционного поля, особенно если полоса точек этого поля узкая (корреляционная зависимость Y От X близка к функциональной). Тогда на этих участках сглаживающая линия не будет соответствовать корреляционному полю (будем неадекватна ему), а значит, будет неадекватно ему и уравнение этой сглаживающей линии. Такое уравнение не может быть использовано для всех Х, входящих в корреляционную таблицу, а значит, его применение чревато грубыми ошибками, если им мы будем приближать генеральное уравнение регрессии . В этом случае уравнение считается Неадекватным выборочным данным И применяться не должно.
Таким образом, после построения сглаживающего уравнения регрессии его еще нужно проверить на адекватность выборочным данным. Адекватность этого уравнения будет тем выше, чем лучше будет соответствующая ему сглаживающая линия регрессии вписываться в полосу точек корреляционного поля. То есть чем меньше будет разброс этих точек вокруг указанной линии.
Оценим величину этого разброса. Для этого подсчитаем сумму квадратов отклонений ординат Yi Всех точек корреляционного поля от сглаживающей линии регрессии :
(5.31) |
Проведем следующее преобразование этой суммы:
Учитывая, согласно (5.2) и (5.3), что
Получим окончательно:
Q0 = QПовт + QАдекв (5.32) |
Здесь
(5. |
Сумма QПовт характеризует разброс выборочных значений вокруг выборочных средних при проведении повторных опытов для различных Xi, поэтому она так и обозначена: QПовт. Она определяет степень влияния на величину Y различных неучтенных факторов (помех), не связанных с величиной Х. Кстати, сумма QПовт Не зависит, очевидно, от сглаживающего уравнения регрессии , так что уменьшить или увеличить ее нельзя – она определяется исключительно выборочными данными. А вот вторая сумма QАдекв зависит от вида уравнения . Она характеризует меру отклонений сглаживающих средних от реальных (выборочных) средний . И чем эта сумма меньше, тем более адекватным будет, очевидно, сглаживающее уравнение регрессии . Поэтому эта сумма так и обозначена: QАдекв. Кстати, сумма QАдекв – это как раз та сумма Q (см. (5.9)), на минимизации которой основано построение сглаживающего уравнения регрессии.
Естественно, что если QАдекв = 0, то сглаживающее уравнение регрессии полностью адекватно выборочным данным (корреляционной таблице (5.1)). А если QАдекв ¹ 0, что обычно и бывает на самом деле, то сравнивая QАдекв С QПовт выясняют, достаточно ли мала сумма QАдекв, чтобы для данного уровня значимости A можно было бы принять нулевую гипотезу Н0 об адекватности сглаживающего уравнения регрессии при альтернативной гипотезе Н1 Об его неадекватности. Это можно сделать по критерию Фишера-Снедекора, если заведомо известно (или подтверждено экспериментально), что зависимая случайная величина Y при любом значении Х величины Х распределена по нормальному закону и имеет не зависящую от Х постоянную дисперсию.
Для этого делением сумм QПовт И QАдекв. на соответствующие им числа степеней свободы KПовт = N – N и KАдекв. = N – Q (Q – число коэффициентов уравнения регрессии) находят дисперсию повторности и дисперсию адекватности
= N – Q (Q – число коэффициентов уравнения регрессии) находят дисперсию повторности и дисперсию адекватности
(5.34) |
После этого находят выборочное значение критерия F Фишера-Снедекора
(5.35) |
И сравнивают его с критическим значением
, (5.36)
взятом из таблицы 5 Приложения. И если FВыб > FКр, то при данном уровне значимости A гипотезу Н0 об адекватности сглаживающего уравнения регрессии отвергают. То есть считают подобранное уравнение непригодным для приближения истинного (генерального) уравнения регрессии . А если окажется, что FВыб < FКр, то нет оснований отвергать гипотезу Н0. И только такое (адекватное) уравнение регрессии можно использовать в дальнейшем.
Кстати, если для имеющихся выборочных данных построено несколько различных сглаживающих выборочных уравнений регрессии, и все они адекватны выборочным данным, то лучшим среди них считается то, которое, не являясь заметно сложнее прочих, обеспечивает наибольший коэффициент детерминации .
Наряду с проверкой адекватности сглаживающего уравнения регрессии имеется возможность проверить и Значимость каждого его коэффициента в отдельности. Это значит – имеется возможность установить, достаточно ли подсчитанное значение интересующего нас коэффициента для статистически обоснованного вывода а том, что он отличен от нуля. И если окажется, что коэффициент не значим, то его можно положить равным нулю. Это приведет к упрощению сглаживающего уравнения регрессии без существенного ущерба для его качества. Но на этом мы не останавливаемся. Отметим лишь, что такое исследование производится автоматически, если сглаживающее уравнение регрессии строится с помощью стандартной программы корреляционно-регрессионного анализа на ЭВМ. В сглаживающем уравнении регрессии, выдаваемом машиной, фигурируют лишь значимые коэффициенты, а заодно и указывается, адекватно ли все уравнение в целом.
В сглаживающем уравнении регрессии, выдаваемом машиной, фигурируют лишь значимые коэффициенты, а заодно и указывается, адекватно ли все уравнение в целом.
Пример 1. На некотором предприятии исследовалась зависимость себестоимости Y единицы продукции (в условных единицах) от объема Х Произведенной за день продукции. Статистическое распределение выборки за 30 рабочих дней приведено в следующей таблице:
Xi yj | 5 | 10 | 15 | 20 | 25 | (5.37) | |
10 | – | – | – | 1 | 4 | 5 | |
11 | – | 3 | 6 | 4 | 1 | 14 | |
12 | 1 | 3 | 2 | – | 1 | 7 | |
13 | 3 | – | 1 | – | – | 4 | |
4 | 6 | 9 | 5 | 6 | N = 30 |
Требуется подобрать подходящую форму сглаживающего уравнения регрессии , оценивающего корреляционную зависимость себестоимости Y единицы продукции от объема Х продукции, произведенной за день, и построить это уравнение. Оценить степень тесноты указанной корреляционной зависимости, а также качество и адекватность построенного сглаживающего уравнения регрессии.
Оценить степень тесноты указанной корреляционной зависимости, а также качество и адекватность построенного сглаживающего уравнения регрессии.
Решение. Сначала по данным корреляционной таблицы (5.37) построим
Корреляционное поле (рис. 3.13.).
Рис. 3.13
Используя формулу (5.3), вычислим для каждого выборочную среднюю :
По точкам () строим на корреляционном поле выборочную линию регрессии – ломанную L (ее узлы на рис. 3.13 обозначены квадратиками).
Теперь встает очередная задача – в какой форме искать сглаживающее равнение этой выборочной линии регрессии?
Обратим внимание на то, что с увеличением X выборочные средние убывают, причем это убывание затухает. Так и должно быть (по смыслу рассматриваемых величин X и Y). Это дает основание строить сглаживающее выборочное уравнение регрессии в гиперболической форме (5. 6). Коэффициенты K и B этого уравнения находятся по данным корреляционной таблицы (5.37) с помощью формул (5.27) и (5.28):
6). Коэффициенты K и B этого уравнения находятся по данным корреляционной таблицы (5.37) с помощью формул (5.27) и (5.28):
(5.39)
Итак, сглаживающее выборочное уравнение регрессии в гиперболической форме (5.6) таково:
(5.40)
Вычислим сглаживающие средние для всех Xi и сравним их с реальными выборочными средними :
Xi | 5 | 10 | 15 | 20 | 25 | (5.41) |
Ni | 4 | 6 | 9 | 5 | 6 | |
12,75 | 11,50 | 11,44 | 10,80 | 10,50 | ||
12,85 | 11,55 | 11,12 | 10,90 | 10,77 |
Впрочем, сначала убедимся, что и те, и другие средние подсчитаны правильно. Используя в качестве контроля формулы (5.10) убеждаемся, что обе суммы (5.10) дают один и тот же результат – общую среднюю =11,33. То есть и реальные, и сглаживающие средние подсчитаны верно. И они весьма близки друг к другу. Это демонстрирует и рис. 3.13, где изображена гипербола (5.40) с указанием на ней точек , помеченных треугольниками.
Используя в качестве контроля формулы (5.10) убеждаемся, что обе суммы (5.10) дают один и тот же результат – общую среднюю =11,33. То есть и реальные, и сглаживающие средние подсчитаны верно. И они весьма близки друг к другу. Это демонстрирует и рис. 3.13, где изображена гипербола (5.40) с указанием на ней точек , помеченных треугольниками.
А теперь перейдем к получению ответов на остальные вопросы – о степени тесноты корреляционной зависимости Y от X и о качестве построенного уравнения (5.40).
Степень тесноты корреляционной зависимости Y от X оценивает выборочное корреляционное отношение . Подсчитывая его по формуле (5.22), получим: . Величина Оказалась весьма значительной (гораздо ближе к 1, чем нулю), что указывает на определенную и достаточно тесную корреляционную зависимость Y от X.
Подсчитаем еще, используя формулу (5.23), выборочный коэффициент детерминации . При этом, согласно (5.24),
(5.42)
Значение указывает, что построенное сглаживающее выборочное уравнение регрессии (5. 40) объясняет 52% общего объема вариации (изменения) величины Y в выборке и лишь немного не дотягивает до своего максимально возможного значения в 56,25 %. И это имеет место при весьма простом виде уравнения (5.40). Чтобы окончательно убедиться в высоком качестве этого уравнения, следует проверить его на адекватность выборочным данным. Для этого, используя формулы (5.33) – (5.35), подсчитаем выборочное значение критерия Фишера – Снедекора:
40) объясняет 52% общего объема вариации (изменения) величины Y в выборке и лишь немного не дотягивает до своего максимально возможного значения в 56,25 %. И это имеет место при весьма простом виде уравнения (5.40). Чтобы окончательно убедиться в высоком качестве этого уравнения, следует проверить его на адекватность выборочным данным. Для этого, используя формулы (5.33) – (5.35), подсчитаем выборочное значение критерия Фишера – Снедекора:
(5.43)
Далее задаем уровень значимости (например =0,05) и по таблице критических точек распределения Фишера – Снедекора находим:
(5.44)
И так как оказалось, что , то у нас нет оснований отвергать гипотезу Н0 об адекватности уравнения (5.40) выборочным данным. В пользу этого свидетельствует и рис. 3.13: гипербола L* нигде не выходит за пределы корреляционного поля.
Все задания примера 1 выполнены.
Кстати, если бы мы искали сглаживающее выборочное уравнение регрессии в линейной форме (5. 5), то, используя (5.13) и (5.15), получили бы:
5), то, используя (5.13) и (5.15), получили бы:
И тогда вместо гиперболического (5.40) мы бы получили линейное уравнение
(5.46)
Если подсчитать по этому уравнению сглаживающие средние и сравнить их с реальными выборочными средними , то получим следующую таблицу:
Xi | 5 | 10 | 15 | 20 | 25 | (5.47) |
Ni | 4 | 6 | 9 | 5 | 6 | |
12,75 | 11,50 | 11,44 | 10,80 | 10,50 | ||
12,37 | 11,87 | 11,38 | 10,89 | 10,40 |
Если для полученных сглаживающих средних провести, на основе формулы (5. 10), контроль, то он (проверьте это) сходится — опять получаем общую среднюю .
10), контроль, то он (проверьте это) сходится — опять получаем общую среднюю .
Как видим, в таблице (5.47), как и в таблице (5.41), расхождение средних И невелико. То есть линейное уравнение (5.46), как и гиперболическое уравнение (5.40), тоже достаточно качественное.
Выясним все же, какое из них лучше. Для этого подсчитаем выборочный коэффициент детерминации DyХ и для линейного уравнения (5.46) . Используя формулу (5.23) получим: DyХ=50%. Впрочем, в линейном случае его можно было бы найти и по формуле (5.26), если предварительно найти выборочный коэффициент линейной корреляции :
Итак, линейное сглаживающее уравнение регрессии (5.46) объясняет примерно 50% всей вариации зависимой величины Y. Гиперболическое же уравнение (5.40) объясняло чуть больше – 52% этой вариации. То есть по этому показателю гиперболическое уравнение несколько лучше линейного. И оно, по существу, так же просто, как и линейное.
Выше мы показали, что гиперболическое уравнение адекватно выборочным данным. Покажем, что и линейное уравнение им адекватно. Используя опять формулы (5.33) – (5.35), получаем:
Покажем, что и линейное уравнение им адекватно. Используя опять формулы (5.33) – (5.35), получаем:
(см. (5.43)
(5.49)
При том же уровне значимости =0,05, который был принят при проверке гипотезы об адекватности гиперболического уравнения регрессии, в соответствии с (5.36) получаем для линейного уравнения (5.46) то же самое критическое значение критерия Фишера – Снедекора, что было указано в (5.44): . И так как опять , то у нас нет оснований отвергать гипотезу Н0 И об адекватности линейного сглаживания уравнения регрессии (5.46) выборочным данным.
В общем, оба сглаживающие выборочные уравнения регрессии – гиперболическое (5.40) и линейное (5.46) – адекватны выборочным данным и оба достаточно хороши. Из них несколько лучшим является гиперболическое уравнение (5.40).
| < Предыдущая | Следующая > |
|---|
Как сделать корреляционный анализ зависимости данных в Excel
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel. ru Уроки Excel Пример выполнения корреляционного анализа в Excel
ru Уроки Excel Пример выполнения корреляционного анализа в Excel
Одним из самых распространенных методов, применяемых в статистике для изучения данных, является корреляционный анализ, с помощью которого можно определить влияние одной величины на другую. Давайте разберемся, каким образом данный анализ можно выполнить в Экселе.
- Назначение корреляционного анализа
- Выполняем корреляционный анализ
- Метод 1: применяем функцию КОРРЕЛ
- Метод 2: используем “Пакет анализа”
- Заключение
Назначение корреляционного анализа
Смотрите также: “Как сделать регрессионный анализ в Excel: пример, анализ результатов”
Корреляционный анализ позволяет найти зависимость одного показателя от другого, и в случае ее обнаружения – вычислить коэффициент корреляции (степень взаимосвязи), который может принимать значения от -1 до +1:
- если коэффициент отрицательный – зависимость обратная, т.
 е. увеличение одной величины приводит к уменьшению второй и наоборот.
е. увеличение одной величины приводит к уменьшению второй и наоборот. - если коэффициент положительный – зависимость прямая, т.е. увеличение одного показателя приводит к увеличению второго и наоборот.
Сила зависимости определяется по модулю коэффициента корреляции. Чем больше значение, тем сильнее изменение одной величины влияет на другую. Исходя из этого, при нулевом коэффициенте можно утверждать, что взаимосвязь отсутствует.
Выполняем корреляционный анализ
Для изучения и лучшего понимания корреляционного анализа, давайте попробуем его выполнить для таблицы ниже.
Здесь указаны данные по среднесуточной температуре и средней влажности по месяцам года. Наша задача – выяснить, существует ли связь между этими параметрами и, если да, то насколько сильная.
Метод 1: применяем функцию КОРРЕЛ
В Excel предусмотрена специальная функция, позволяющая сделать корреляционный анализ – КОРРЕЛ. Ее синтаксис выглядит следующим образом:
КОРРЕЛ(массив1;массив2).
Порядок действий при работе с данным инструментом следующий:
- Встаем в свободную ячейку таблицы, в которой планируем рассчитать коэффициент корреляции. Затем щелкаем по значку “fx (Вставить функцию)” слева от строки формул.
- В открывшемся окне вставки функции выбираем категорию “Статистические” (или “Полный алфавитный перечень”), среди предложенных вариантов отмечаем “КОРРЕЛ” и щелкаем OK.
- На экране отобразится окно аргументов функции с установленным курсором в первом поле напротив “Массив 1”. Здесь мы указываем координаты ячеек первого столбца (без шапки таблицы), данные которого требуется проанализировать (в нашем случае – B2:B13). Сделать это можно вручную, напечатав нужные символы с помощью клавиатуры. Также выделить требуемый диапазон можно непосредственно в самой таблице с помощью зажатой левой кнопки мыши. Затем переходим ко второму аргументу “Массив 2”, просто щелкнув внутри соответствующего поля либо нажав клавишу Tab.
 Здесь указываем координаты диапазона ячеек второго анализируемого столбца (в нашей таблице – это C2:C13). По готовности щелкаем OK.
Здесь указываем координаты диапазона ячеек второго анализируемого столбца (в нашей таблице – это C2:C13). По готовности щелкаем OK. - Получаем коэффициент корреляции в ячейке с функцией. Значение “-0,63” свидетельствует об умеренно-сильной обратной зависимости между анализируемыми данными.
Метод 2: используем “Пакет анализа”
Смотрите также: “Поиск решения в Excel: пример использования функции”
Альтернативным способом выполнения корреляционного анализа является использование “Пакета анализа”, который предварительно нужно включить. Для этого:
- Заходим в меню “Файл”.
- В перечне слева выбираем пункт “Параметры”.
- В появившемся окне кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу для параметра “Управление” выбираем “Надстройки Excel” и щелкаем “Перейти”.
- В открывшемся окошке отмечаем “Пакет анализа” и подтверждаем действие нажатием кнопки OK.

Все готово, “Пакет анализа” активирован. Теперь можно перейти к выполнению нашей основной задачи:
- Нажимаем кнопку “Анализ данных”, которая находится во вкладке “Данные”.
- Появится окно, в котором представлен перечень доступных вариантов анализа. Отмечаем “Корреляцию” и щелкаем OK.
- На экране отобразится окно, в котором необходимо указать следующие параметры:
- “Входной интервал”. Выделяем весь диапазон анализируемых ячеек (т.е. сразу оба столбца, а не по одному, как это было в описанном выше методе).
- “Группирование”. На выбор предложено два варианта: по столбцам и строкам. В нашем случае подходит первый вариант, т.к. именно подобным образом расположены анализируемые данные в таблице. Если в выделенный диапазон включены заголовки, следует поставить галочку напротив пункта “Метки в первой строке”.
- “Параметры вывода”. Можно выбрать вариант “Выходной интервал”, в этом случае результаты анализа будут вставлены на текущем листе (потребуется указать адрес ячейки, начиная с которой будут выведены итоги).
 Также предлагается вывод результатов на новом листе или в новой книге (данные будут вставлены в самом начале, т.е. начиная с ячейки A1). В качестве примера оставляем “Новый рабочий лист” (выбран по умолчанию).
Также предлагается вывод результатов на новом листе или в новой книге (данные будут вставлены в самом начале, т.е. начиная с ячейки A1). В качестве примера оставляем “Новый рабочий лист” (выбран по умолчанию). - Когда все готово, щелкаем OK.
- Получаем тот же самый коэффициент корреляции, что и в первом методе. Это говорит о том, что в обоих случаях мы все сделали верно.
Заключение
Смотрите также: “Основные статистические функции в Excel: использование, формулы”
Таким образом, выполнение корреляционного анализа в Excel – достаточно автоматизированная и простая в освоении процедура. Все что нужно знать – где найти и как настроить необходимый инструмент, а в случае с “Пакетом решения”, как его активировать, если до этого он уже не был включен в параметрах программы.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Корреляционная зависимость.
 Коэффициент парной корреляции
Коэффициент парной корреляции- Понятие корреляционной зависимости
- Коэффициент парной корреляции и теснота корреляционной зависисмости
- Основы корреляционного анализа
Корреляционная зависимость — это вероятностная зависимость между величинами, которая возникает тогда, когда одна из величин зависит не только от данной второй, но и от ряда случайных факторов, или когда среди условий, от которых зависят та и другая величины, имеются общие для них обоих условия.
То есть корреляционная зависимость отличается от функциональной зависимости, при которой одна
величина зависит только от второй и возникает взаимно-однозначное соответствие: значению одной величины
соответствует строго определённое значение второй величины. Поэтому, хотя и при корреляционной зависимости
результаты наблюдения находятся на некотором приближении к прямой линии, они не лежат на прямой, а лишь
приближаются к ней (рисунок внизу). Для увеличения рисунка
нужно щёлкнуть по нему левой кнопкой мыши.
Для увеличения рисунка
нужно щёлкнуть по нему левой кнопкой мыши.
Понятие корреляционной зависимости проиллюстрируем на примере из так любимой многоми темы цен на недвижимость. По некоторой выборке обобщены данные об общей площади квартир и ценах на квартиры. На оси Ox задана общая площадь квартир, а на оси Oy — цены на квартиры. Точки на графике (рис. выше) — результаты выборочного наблюдения.
На графике видно, что результаты наблюдения находятся на некотором приближении к
прямой. Поэтому можно утверждать, что между признаками (общей площадью квартиры и ценой квартиры)
существует зависимость. А именно: чем больше общая площадь квартиры, тем выше цена. Но результаты
наблюдения располагаются не строго на прямой, поэтому нельзя утверждать, что каждой определённой
величине площади квартиры в квадратных метрах соответствует строго определённая величина цены. Значит,
мы говорим, что зависимость между признаками — корреляционная.
Пусть обобщены и данные о площади кухни квартир и ценами квартир. На оси Ox задана площадь кухни, а на оси Oy — цены на квартиры (рис. внизу). Для увеличения рисунка нужно щёлкнуть по нему левой кнопкой мыши.
Видим, что результаты наблюдений также выстраиваются на некотором приближении к прямой. Но в случае с площадью кухни отклонения результатов наблюдения от прямой несколько больше, чем в случае с общей площадью. Между тем здесь мы также наблюдаем корреляционную зависимость и можно утверждать, что чем больше площадь кухни, тем выше цена квартиры.
В этих двух случаях мы наблюдаем корреляционные зависимости разной интенсивности или тесноты. В случае общей площади квартиры зависимости более интенсивная (тесная), а в случае с площадью кухни — менее интенсивная (тесная).
В описанных случаях случайная величина Y (цена квартиры) — зависимая переменная,
а случайна величина X (общая площадь квартиры или площадь кухни) — независимая переменная.
Статистика — не Ваша специализация? Закажите статистическую обработку данных
Тесноту линейной зависимости характеризует коэффициент парной линейной корреляции. Коэффициент корреляции рассчитывается следующим образом:
.
Для более предметного изложения следует заметить, что здесь идёт речь о коэффициенте
парной корреляции Пирсона. Существуют и другие виды коэффициентов корреляции, например, коэффициент корреляции
Спирмена, коэффициент корреляции Кендалла и другие. Кроме того, коэффициент корреляции Пирсона не
применяется, когда исследуются качественные переменные, что нередко в исследованиях поведения человека. Но коэффициент корреляции Пирсона применяется в
большинстве случаев, поскольку чаще всего предполагается, что распределение переменных нормальное или
несущественно отличается от нормального, и исследуются количественные факторы. Именно такое распределение является условием применения
коэффициента корреляции Пирсона.
Значения коэффициента корреляции находится в пределах от -1 до 1.
Ниже приведена таблица значений коэффициента корреляции и соответствующих им характеристик тесноты связи между переменными.
Значение коэффициента корреляции | Линейная зависимость |
-1 | функциональная отрицательная |
0 | не существует |
1 | функциональная положительная |
слабая | |
средней тесноты | |
тесная |
Пример. В таблице – данные о валовом внутреннем продукте (ВВП) и частным потреблением (в средних ценах 1995 года), в условных единицах. Найти коэффициент корреляции между этими величинами.
В таблице – данные о валовом внутреннем продукте (ВВП) и частным потреблением (в средних ценах 1995 года), в условных единицах. Найти коэффициент корреляции между этими величинами.
Квартал, год | ВВП | Частное потребление |
I, 1995 | 652,870 | 357,191 |
II, 1995 | 601,893 | 356,533 |
III, 1995 | 590,792 | 376,951 |
IV, 1995 | 593,667 | 379,866 |
I, 1996 | 580,435 | 385,749 |
II, 1996 | 612,063 | 392,194 |
III, 1996 | 620,847 | 417,342 |
IV, 1996 | 614,360 | 426,991 |
I, 1997 | 609,708 | 394,661 |
II, 1997 | 664,246 | 416,367 |
III, 1997 | 682,696 | 428,103 |
IV, 1997 | 680,104 | 464,410 |
I, 1998 | 667,513 | 412,133 |
II, 1998 | 704,317 | 450,606 |
III, 1998 | 698,793 | 469,775 |
IV, 1998 | 668,498 | 477,421 |
I, 1999 | 663,786 | 415,650 |
II, 1999 | 703,213 | 477,013 |
III, 1999 | 707,238 | 498,525 |
IV, 1999 | 694,329 | 510,171 |
I, 2000 | 704,055 | 447,272 |
II, 2000 | 738,637 | 504,100 |
III, 2000 | 753,565 | 522,277 |
IV, 2000 | 754,459 | 533,585 |
Решение. Результативным признаком Y является частное потребление, а факториальным признаком X – валовой внутренний продукт.
Результативным признаком Y является частное потребление, а факториальным признаком X – валовой внутренний продукт.
Для расчёта коэффициента корреляции создадим рабочую таблицу:
| X | Y | XY | ||
I, 1995 | 562,870 | 357,191 | 201052,098 | 316822,637 | 127585,410 |
II, 1995 | 601,893 | 356,533 | 214594,717 | 362275,183 | 127115,780 |
. | … | … | … | … | … |
III, 2000 | 753,565 | 522,277 | 393569,668 | 567860,209 | 272773,265 |
IV, 2000 | 754,459 | 533,585 | 402568,006 | 569208,383 | 284712,952 |
Всего | 15872,084 | 10514,886 | 7015990,600 | 10569153,153 | 4670555,076 |
Используя первоначальные данные и производя расчёты, находим коэффициент корреляции:
Статистика — не Ваша специализация? Закажите статистическую обработку данных
Пройти тест по теме Теория вероятностей и математическая статистика
Корреляционный анализ — совокупность основанных на теории
корреляции методов обнаружения корреляционной зависимости между случайными величинами или признаками. Корреляционный анализ экспериментальных данных для двух случайных величин предлагает следующие основные
практические приёмы:
Корреляционный анализ экспериментальных данных для двух случайных величин предлагает следующие основные
практические приёмы:
- построение корреляционного поля и составление корреляционной таблицы;
- вычисление выборочных коэффициентов корреляции;
- проверка статистической гипотезы значимости корреляционной связи.
Корреляционное поле и корреляционная таблица являются вспомогательными средствами
при анализе выборочных данных. При нанесении на координатную плоскость двумерных выборочных точек
получают корреляционное поле. По характеру расположения точек поля можно составить предварительное
мнение о форме зависимости случайных величин (например, о том, что одна величина в среднем возрастает
или убывает при возрастании другой). Для численной обработки результаты обычно группируют и представляют
в форме корреляционной таблицы. В каждой клетке корреляционной таблицы приводятся численности тех пар,
компоненты которых попадают в соответствующие интервалы группировки по каждой переменной. Предполагая
длины интервалов группировки равными между собой, выбирают центры интервалов и численность пар в качестве
основы для расчётов.
Предполагая
длины интервалов группировки равными между собой, выбирают центры интервалов и численность пар в качестве
основы для расчётов.
При корреляционном анализе обычно не указываают, какой из факторов является зависимым, а какой — независимым. Также в задачи корреляционного анализа не входит уставления формы зависимости между переменными и, соответственно, составления формулы, отражающей форму зависимости. Это входит в задачи регрессионного анализа.
Статистика — не Ваша специализация? Закажите статистическую обработку данных
Пройти тест по теме Теория вероятностей и математическая статистика
К началу страницы
| Назад | Листать | Вперёд>>> |
Всё по теме «Математическая статистика»
Характеристики выборки и генеральной совокупности: среднее значение, дисперсия, погрешности выборки
Доверительный интервал для математического ожидания
Распределение Стьюдента и малые выборки
Проверка статистических гипотез
Парная линейная регрессия. Задачи регрессионного анализа
Задачи регрессионного анализа
Множественная корреляция, её коэффициент. Частная корреляция
Множественная линейная регрессия. Улучшение модели регрессии
Дисперсионный анализ: соединение теории и практики
Как читать корреляционную матрицу
В статистике нас часто интересует взаимосвязь между двумя переменными.
Например, мы можем захотеть понять взаимосвязь между количеством часов, отработанных студентом, и полученными им экзаменационными баллами.
Один из способов количественной оценки этой взаимосвязи заключается в использовании коэффициента корреляции Пирсона, который является мерой линейной связи между двумя переменными . Имеет значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными
- 0 указывает на отсутствие линейной корреляции между двумя переменными
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными
Чем дальше коэффициент корреляции от нуля, тем сильнее связь между двумя переменными.
Связанный: Что считается «сильной» корреляцией?
Но в некоторых случаях мы хотим понять корреляцию между более чем одной парой переменных. В этих случаях мы можем создать корреляционная матрица , представляющая собой квадратную таблицу, которая показывает коэффициенты корреляции между несколькими переменными.
Пример матрицы корреляцииВ приведенной ниже матрице корреляции показаны коэффициенты корреляции между несколькими переменными, связанными с образованием:
Каждая ячейка в таблице показывает корреляцию между двумя конкретными переменными. Например, выделенная ячейка ниже показывает, что корреляция между количеством часов, потраченных на учебу, и оценкой за экзамен – 9.0022 0,82 , что указывает на сильную положительную корреляцию. Больше часов, потраченных на учебу, тесно связано с более высокими баллами на экзаменах.
В выделенной ячейке ниже показано, что корреляция между «часами учебы» и «часами сна» составляет -0,22 , что указывает на слабую отрицательную корреляцию. Больше часов, потраченных на учебу, связано с меньшим количеством часов, потраченных на сон.
Больше часов, потраченных на учебу, связано с меньшим количеством часов, потраченных на сон.
А выделенная ячейка ниже показывает, что корреляция между «количеством часов, проведенных во сне» и «показателем IQ» составляет 9.0022 0,06 , что указывает на то, что они в основном не коррелированы. Существует очень небольшая связь между количеством часов, которые студент спит, и его показателем IQ.
Также обратите внимание, что все коэффициенты корреляции по диагонали таблицы равны 1, потому что каждая переменная идеально коррелирует сама с собой. Эти клетки бесполезны для интерпретации.
Варианты корреляционной матрицыОбратите внимание, что корреляционная матрица совершенно симметрична. Например, в верхней правой ячейке отображается то же значение, что и в нижней левой ячейке: 9.0004
Это связано с тем, что обе ячейки измеряют корреляцию между «часами, потраченными на учебу» и «рейтингом школы».
Поскольку матрица корреляции симметрична, половина коэффициентов корреляции, показанных в матрице, являются избыточными и ненужными. Таким образом, иногда будет отображаться только половина матрицы корреляции:
А иногда матрица корреляции будет раскрашена как тепловая карта, чтобы сделать коэффициенты корреляции еще более удобными для чтения:
Когда использовать матрицу корреляцииНа практике матрица корреляции обычно используется по трем причинам:
1. Матрица корреляции удобно обобщает набор данных.
Матрица корреляции — это простой способ суммировать корреляции между всеми переменными в наборе данных. Например, предположим, что у нас есть следующий набор данных, содержащий следующую информацию для 1000 учащихся:
Было бы очень сложно понять взаимосвязь между каждой переменной, просто глядя на необработанные данные. К счастью, корреляционная матрица может помочь нам быстро понять корреляции между каждой парой переменных.
2. Корреляционная матрица служит диагностическим признаком регрессии.
Одним из ключевых допущений множественной линейной регрессии является то, что ни одна независимая переменная в модели не имеет сильной корреляции с другой переменной в модели.
Когда две независимые переменные сильно коррелированы, это приводит к проблеме, известной как мультиколлинеарность, и может затруднить интерпретацию результатов регрессии.
Один из самых простых способов обнаружить потенциальную проблему мультиколлинеарности — посмотреть на матрицу корреляции и визуально проверить, сильно ли коррелируют какие-либо переменные друг с другом.
3. Корреляционную матрицу можно использовать в качестве исходных данных для других анализов.
Корреляционная матрица используется в качестве исходных данных для других сложных анализов, таких как исследовательский факторный анализ и модели структурных уравнений.
Дополнительные ресурсыВ следующих учебных пособиях объясняется, как создать матрицу корреляции с помощью различных статистических программ:
Как создать матрицу корреляции в Excel
Как создать матрицу корреляции в SPSS
Как создать матрицу корреляции в Stata
Как создать матрицу корреляции в Python
Как создать матрицу корреляции в Matlab
Опубликовано Заком
Просмотреть все сообщения Зака
Корреляция | Аннотированный вывод SPSS
На этой странице показан пример корреляции со сносками, объясняющими
выход. Эти данные были собраны по 200 учащимся средних школ и
баллы по различным тестам, в том числе по естественным наукам, математике, чтению и общественным наукам ( сост ).
Переменная женщина является дихотомической переменной, кодируемой 1, если студент был
женщина и 0, если мужчина.
Эти данные были собраны по 200 учащимся средних школ и
баллы по различным тестам, в том числе по естественным наукам, математике, чтению и общественным наукам ( сост ).
Переменная женщина является дихотомической переменной, кодируемой 1, если студент был
женщина и 0, если мужчина.
В приведенном ниже синтаксисе команда get file используется для загрузки данных hsb2. в СПСС. В кавычках нужно указать где находится файл данных на твоем компьютере. Помните, что вам нужно использовать расширение .sav и что вам нужно закончить команду точкой. По умолчанию SPSS выполняет попарное удаление пропущенных значений. Это означает, что пока оба переменные в корреляции имеют действительные значения для случая, этот случай включен в корреляции. 9Подкоманда 0130 /print используется для отмечены статистически значимые корреляции.
получить файл "c:\data\hsb2.sav". корреляции /variables = чтение, запись, математика, наука, женщина /print = носичка.
а. Корреляция Пирсона — эти числа измеряют силу и
направление линейной зависимости между двумя переменными.
коэффициент корреляции может варьироваться от -1 до +1, где -1 указывает на идеальное
отрицательная корреляция, +1 указывает на идеальную положительную корреляцию и 0
указывает на полное отсутствие корреляции. (Переменная, коррелирующая сама с собой, будет
всегда имеют коэффициент корреляции, равный 1.) Вы можете подумать о
коэффициент корреляции, который говорит вам, в какой степени вы можете угадать
значение одной переменной при заданном значении другой переменной. От
диаграмма рассеяния переменных читать и писать ниже,
мы можем видеть, что точки стремятся вдоль линии, идущей от нижнего левого угла к
вверху справа, что равносильно утверждению, что корреляция положительная.
0,597 — числовое описание того, насколько плотно вокруг воображаемой линии
точки лежат. Если бы корреляция была выше, точки, как правило, были бы ближе к
линия; если бы он был меньше, они, как правило, были бы дальше от линии. Также обратите внимание, что по определению любая переменная, коррелирующая сама с собой, имеет
соотношение 1,
Также обратите внимание, что по определению любая переменная, коррелирующая сама с собой, имеет
соотношение 1,
б. Сиг. (2-стороннее) — это значение p, связанное с корреляция. В сноске под таблицей корреляции поясняется, что одиночные и двойные звездочки означают.
в. N — это количество случаев, которые использовались в корреляции. Поскольку у нас нет недостающих данных в этом наборе данных, все корреляции были основаны на все 200 случаев в наборе данных. Однако, если некоторые переменные отсутствовали значений, N будут разными для разных корреляций.
Диаграмма рассеяния
График /scatterplot(bivar) = запись с чтением.
Корреляция с использованием списочного удаления недостающих данных
Корреляции в таблице ниже интерпретируются так же, как и
выше. Единственная разница заключается в том, как обрабатываются пропущенные значения.
Когда вы выполняете удаление по списку, как мы делаем с /missing = listwise подкоманда, если в случае отсутствует значение какой-либо из переменных, перечисленных в /variables подкоманда, этот регистр исключается из всех корреляций,
даже если есть допустимые значения для двух переменных в текущем
корреляция. Например, если отсутствовало значение переменной читать , случай все равно будет исключен из расчета
корреляция между записью и математикой .
Например, если отсутствовало значение переменной читать , случай все равно будет исключен из расчета
корреляция между записью и математикой .
На самом деле нет правил, определяющих, когда вы должны использовать парный или список удаление. Это зависит от вашей цели и от того, важно ли это для точно такие же случаи должны использоваться во всех корреляциях. Если у вас есть много недостающих данных, некоторые корреляции могут быть основаны на многих случаях, которые не входит в другие корреляции. С другой стороны, если вы используете удаления по списку, у вас может остаться не так много случаев, которые можно было бы использовать в расчет.
Обратите внимание, что SPSS иногда включает сноски как часть вывода. Мы оставили их нетронутыми и начали свои со следующей буквы алфавит.
корреляции /variables = чтение, запись, математика, наука, женщина /print = носик /отсутствует = по списку.
б. Корреляция Пирсона — это корреляция между двумя
переменные (одна указана в строке, другая в столбце). это
интерпретируются так же, как корреляции в предыдущем примере.
это
интерпретируются так же, как корреляции в предыдущем примере.
в. Сиг. (2-стороннее) — это значение p, связанное с корреляция. В сноске под таблицей корреляции поясняется, что одиночные и двойные звездочки означают.
Нажмите здесь, чтобы сообщить об ошибке на этой странице или оставить комментарий
Ваше имя (обязательно)
Ваш адрес электронной почты (должен быть действительным, чтобы мы могли получить отчет!)
Комментарий/отчет об ошибке (обязательно)
Как цитировать эту страницу
Вычисление и построение корреляционной матрицы в Python и Pandas • datagy
В этом руководстве вы узнаете, как рассчитать корреляционную матрицу в Python и как построить ее в виде тепловой карты. Вы узнаете, что такое корреляционная матрица и как ее интерпретировать, а также краткий обзор того, что такое коэффициент корреляции.
Затем вы узнаете, как рассчитать корреляционную матрицу с помощью библиотеки pandas. Затем вы узнаете, как построить матрицу корреляции тепловой карты с помощью Seaborn. Наконец, вы узнаете, как настроить эти тепловые карты для включения определенных значений.
Быстрый ответ: используйте df.corr() Pandas для расчета матрицы корреляции в Python
# Расчет матрицы корреляции с Pandas импортировать панд как pd матрица = df.corr() печать (матрица) # Возвращает: # b_len b_dep f_len f_dep # b_len 1.000000 -0.235053 0.656181 0.595110 # b_dep -0,235053 1,000000 -0,583851 -0,471916 # f_len 0,656181 -0,583851 1,000000 0,871202 # f_dep 0,595110 -0,471916 0,871202 1,000000
Содержание
Что такое матрица корреляции и как ее интерпретировать
Матрица корреляции — это распространенный инструмент, используемый для сравнения коэффициентов корреляции между различными функциями (или атрибутами) в наборе данных . Это позволяет нам визуализировать, насколько сильно (или как мало) существует корреляция между различными переменными.
Это позволяет нам визуализировать, насколько сильно (или как мало) существует корреляция между различными переменными.
Это важный этап предварительной обработки конвейеров машинного обучения. Поскольку матрица корреляции позволяет нам идентифицировать переменные с высокой степенью корреляции, они позволяют нам уменьшить количество признаков, которые мы можем иметь в наборе данных.
Это часто называют уменьшением размерности и может использоваться для улучшения времени выполнения и эффективности наших моделей.
Это теория нашей корреляционной матрицы. Но как на самом деле выглядит как ? Матрица корреляции имеет такое же количество строк и столбцов, сколько столбцов в нашем наборе данных.
Это означает, что если у нас есть набор данных с 10 столбцами, то наша матрица будет состоять из десяти строк и десяти столбцов. Каждая строка и столбец представляют переменную (или столбец) в нашем наборе данных, а значение в матрице — это коэффициент корреляции между соответствующей строкой и столбцом.
Что такое коэффициент корреляции? Коэффициент корреляции представляет собой значение между -1 и +1 , которое обозначает как силу , так и направленность отношения между двумя переменными.
- Чем ближе значение к 1 (или -1), тем сильнее связь.
- Чем ближе число к 0, тем слабее связь.
Отрицательный коэффициент говорит нам об отрицательной связи, т. е. о том, что при увеличении одного значения другое уменьшается. Точно так же положительный коэффициент указывает на то, что по мере увеличения одного значения увеличивается и другое.
Давайте посмотрим, как выглядит корреляционная матрица, когда мы отображаем ее как тепловую карту. Здесь у нас есть простая матрица 4 × 4, что означает, что у нас есть 4 столбца и 4 строки.
Пример матрицы корреляции, визуализированный в виде тепловой карты Значения в нашей матрице — это коэффициенты корреляции между парами признаков. Мы видим, что у нас есть диагональная линия значений 1. Это потому, что эти значения представляют корреляцию между столбцом и самим собой. Поскольку эти значения, конечно, всегда одинаковы, они всегда будут равны 1,9.0004
Мы видим, что у нас есть диагональная линия значений 1. Это потому, что эти значения представляют корреляцию между столбцом и самим собой. Поскольку эти значения, конечно, всегда одинаковы, они всегда будут равны 1,9.0004
Если у вас острый глаз, вы заметите, что значения в правом верхнем углу являются зеркальным отображением нижнего левого угла матрицы. Это связано с тем, что отношение между двумя переменными в парах столбец-строка всегда будет одинаковым. Обычной практикой является удаление их из матрицы тепловой карты, чтобы лучше визуализировать данные. Это то, чему вы научитесь в следующих разделах руководства.
Вычисление матрицы корреляции в Python с помощью Pandas
Pandas позволяет невероятно легко создать матрицу корреляции с использованием метода DataFrame, .корр() . Метод принимает ряд параметров. Давайте рассмотрим их перед тем, как перейти к примеру:
matrix = df.corr(
method = 'pearson', # Метод корреляции
min_periods = 1 # Минимальное количество требуемых наблюдений
) По умолчанию метод corr будет использовать коэффициент корреляции Пирсона, хотя вы также можете выбрать методы Кендалла или Спирмена. Точно так же вы можете ограничить количество наблюдений, необходимых для получения результата.
Точно так же вы можете ограничить количество наблюдений, необходимых для получения результата.
Загрузка образца кадра данных Pandas
Теперь, когда вы понимаете, как работает метод, давайте загрузим образец кадра данных Pandas. Для этого мы будем использовать функцию Seaborn load_dataset , которая позволяет нам генерировать некоторые наборы данных на основе реальных данных. Мы загрузим набор данных пингвинов . Seaborn позволяет нам создавать очень полезные визуализации Python, предоставляя простую в использовании высокоуровневую оболочку для Matplotlib.
# Загрузка образца фрейма данных Pandas
импортировать панд как pd
импортировать Seaborn как sns
df = sns.load_dataset('пингвины')
# Мы переименовываем столбцы, чтобы они лучше печатались
df.columns = ['виды', 'остров', 'b_len', 'b_dep', 'f_len', 'f_dep', 'sex']
печать (df.head())
# Возвращает:
# вид остров b_len b_dep f_len f_dep пол
# 0 Адели Торгерсен 39.1 18,7 181,0 3750,0 Самец
# 1 Адели Торгерсен 39,5 17,4 186,0 3800,0 Жен. # 2 Адели Торгерсен 40,3 18,0 195,0 3250,0 Жен.
# 3 Адели Торгерсен NaN NaN NaN NaN NaN
# 4 Адели Торгерсен 36,7 19,3 193,0 3450,0 Женщина
# 2 Адели Торгерсен 40,3 18,0 195,0 3250,0 Жен.
# 3 Адели Торгерсен NaN NaN NaN NaN NaN
# 4 Адели Торгерсен 36,7 19,3 193,0 3450,0 Женщина Давайте разберем, что мы здесь сделали:
- Мы загрузили библиотеку Pandas, используя псевдоним pd . Мы также загрузили библиотеку Seaborn, используя псевдоним sns .
- Затем мы создали DataFrame,
df, используя функцию load_dataset и передавая'пингвинов'в качестве аргумента. - Наконец, мы напечатали первые пять строк DataFrame, используя метод
.head()
Мы видим, что наш DataFrame имеет 7 столбцов. Некоторые из этих столбцов являются числовыми, а другие — строковыми.
Вычисление матрицы корреляции с помощью Pandas
Теперь, когда наш Pandas DataFrame загружен, давайте воспользуемся методом corr для расчета нашей матрицы корреляции. Мы просто применим метод непосредственно ко всему DataFrame:
# Расчет корреляционной матрицы с Pandas матрица = df.corr() печать (матрица) # Возвращает: # b_len b_dep f_len f_dep # b_len 1.000000 -0.235053 0.656181 0.595110 # b_dep -0,235053 1,000000 -0,583851 -0,471916 # f_len 0,656181 -0,583851 1,000000 0,871202 # f_dep 0.595110 -0.471916 0.871202 1.000000
Мы можем видеть, что, хотя наш исходный фрейм данных имел семь столбцов, Pandas вычислял матрицу только с использованием числовых столбцов. Мы видим, что четыре наших столбца были превращены в пары столбцов-строк, обозначающие отношения между двумя столбцами.
Например, мы можем видеть, что коэффициент корреляции между переменными body_mass_g и flipper_length_mm равен 0,87. Это указывает на то, что существует относительно сильная положительная связь между двумя переменными.
Округление значений нашей матрицы корреляции с помощью Pandas
Мы можем округлить значения в нашей матрице до двух цифр, чтобы их было легче читать. Возвращаемая матрица на самом деле является фреймом данных Pandas. Это означает, что мы можем применять различные методы обработки данных к самой матрице. Мы можем использовать Pandas
Это означает, что мы можем применять различные методы обработки данных к самой матрице. Мы можем использовать Pandas round метод для округления наших значений.
матрица = df.corr().round(2) печать (матрица) # Возвращает: # b_len b_dep f_len f_dep # b_len 1,00 -0,24 0,66 0,60 # b_dep -0,24 1,00 -0,58 -0,47 # f_len 0,66 -0,58 1,00 0,87 # f_dep 0.60 -0.47 0.87 1.00
Хотя при этом мы немного теряем точность, это упрощает чтение отношений.
В следующем разделе вы узнаете, как использовать библиотеку Seaborn для построения тепловой карты на основе матрицы.
Как построить матрицу корреляции тепловой карты с помощью Seaborn
Во многих случаях вам потребуется визуализировать матрицу корреляции. Это легко сделать в формате тепловой карты, где мы можем отображать значения, которые мы можем лучше понять визуально. Библиотека Seaborn позволяет очень легко создать тепловую карту с помощью функции тепловой карты .
Теперь давайте импортируем pyplot из matplotlib, чтобы визуализировать наши данные. Хотя на самом деле мы будем использовать Seaborn для визуализации данных, Seaborn в значительной степени полагается на matplotlib для визуализации.
Хотя на самом деле мы будем использовать Seaborn для визуализации данных, Seaborn в значительной степени полагается на matplotlib для визуализации.
# Визуализация корреляционной матрицы Pandas с помощью Seaborn
импортировать панд как pd
импортировать Seaborn как sns
импортировать matplotlib.pyplot как plt
df = sns.load_dataset('пингвины')
матрица = df.corr().round(2)
sns.heatmap(matrix, annot=True)
plt.show() Здесь мы импортировали библиотеку pyplot как plt , что позволяет нам отображать наши данные. Затем мы использовали функцию sns.heatmap() , передав нашу матрицу и попросив библиотеку аннотировать нашу тепловую карту со значениями, используя annot= параметр. Это вернуло следующий график:
Мы видим, что здесь произошло несколько странных вещей. Во-первых, мы знаем, что коэффициент корреляции может принимать значения от -1 до +1. В настоящее время наш график показывает только значения примерно от -0,5 до +1. Из-за этого, если мы не будем осторожны, мы можем сделать вывод, что негативные отношения сильнее, чем они есть на самом деле.
В настоящее время наш график показывает только значения примерно от -0,5 до +1. Из-за этого, если мы не будем осторожны, мы можем сделать вывод, что негативные отношения сильнее, чем они есть на самом деле.
Кроме того, данные не отображаются по-разному. Мы хотим, чтобы наши цвета были сильными, когда отношения становятся крепкими. Скорее, цвета ослабевают, когда значения приближаются к +1.
Здесь мы можем изменить несколько дополнительных параметров:
-
vmin=,vmax=используются для привязки цветовой карты. Если ничего не передается, значения выводятся, что приводит к тому, что отрицательные значения не превышают 0,5. Поскольку мы знаем, что коэффициенты или корреляция должны быть привязаны к +1 и -1, мы можем передать их. Поскольку мы хотим, чтобы цвета отличались от 0, мы должны указать здесь 0 в качестве аргумента. - cmap= позволяет нам передать карту другого цвета. Поскольку мы хотим, чтобы цвета были ярче на обоих концах дивергенции, мы можем передать vlag в качестве аргумента, чтобы показать, что цвета меняются от синего к красному.

Давайте попробуем еще раз, передав эти три новых аргумента:
# Визуализация корреляционной матрицы Pandas с помощью Seaborn
импортировать панд как pd
импортировать Seaborn как sns
импортировать matplotlib.pyplot как plt
df = sns.load_dataset('пингвины')
матрица = df.corr().round(2)
sns.heatmap(matrix, annot=True, vmax=1, vmin=-1, center=0, cmap='vlag')
plt.show() Возвращает следующую матрицу. Он расходится от -1 до +1, и цвета удобно темнеют на любом полюсе.
Правильно отформатированная тепловая карта с расходящимися цветамиВ этом разделе вы узнали, как форматировать тепловую карту, созданную с помощью Seaborn, чтобы лучше визуализировать отношения между столбцами.
Постройте только нижнюю половину корреляционной матрицы с помощью Seaborn
Одна вещь, которую вы заметите, это то, насколько избыточно показывать верхнюю и нижнюю половины корреляционной матрицы. Наш разум может интерпретировать только ограниченное количество вещей, поэтому может быть полезно показывать только нижнюю половину нашей визуализации. Точно так же может иметь смысл удалить диагональную линию из единиц, поскольку она не имеет реального значения.
Точно так же может иметь смысл удалить диагональную линию из единиц, поскольку она не имеет реального значения.
Для этого мы можем использовать функцию numpy triu , которая создает треугольник матрицы. Давайте начнем с импорта numpy и добавления переменной mask в нашу функцию. Затем мы можем передать эту маску в нашу функцию Seaborn, попросив тепловую карту маскировать только те значения, которые мы хотим видеть:
# Отображаем только нижнюю половину нашей корреляционной матрицы.
импортировать панд как pd
импортировать Seaborn как sns
импортировать matplotlib.pyplot как plt
импортировать numpy как np
df = sns.load_dataset('пингвины')
матрица = df.corr().round(2)
маска = np.triu(np.ones_like(матрица, dtype=bool))
sns.heatmap(matrix, annot=True, vmax=1, vmin=-1, center=0, cmap='vlag', mask=mask)
plt.show() Это возвращает следующее изображение:
Отображение только нижней половины матрицы с использованием маски numpy Мы видим, насколько здесь проще понять силу отношений нашего набора данных. Поскольку мы удалили значительное количество визуального беспорядка (более половины!), мы можем гораздо лучше интерпретировать смысл визуализации.
Поскольку мы удалили значительное количество визуального беспорядка (более половины!), мы можем гораздо лучше интерпретировать смысл визуализации.
Как сохранить матрицу корреляции в файл в Python
Иногда может потребоваться сохранить матрицу корреляции программно. До сих пор мы использовали plt.show() для отображения нашего графика. Затем вы можете, конечно, вручную сохранить результат на свой компьютер. Но matplotlib упрощает простое программное сохранение графика с помощью функции savefig() для сохранения нашего файла.
Файл позволяет нам передать путь к файлу, чтобы указать, где мы хотим сохранить файл. Скажем, мы хотели сохранить его в каталоге, где запущен скрипт, мы можем указать относительный путь, как показано ниже:
# Сохранение тепловой карты
plt.savefig('тепловая карта.png') В коде, показанном выше, мы сохраним файл как файл png с именем тепловой карты . Файл будет сохранен в каталоге, где запущен скрипт.
Выбор только сильных корреляций в матрице корреляций
В некоторых случаях может потребоваться выбрать только сильные корреляции в матрице. Как правило, корреляция считается сильной, когда абсолютное значение больше или равно 0,7. Поскольку возвращаемая матрица представляет собой кадр данных Pandas, мы можем использовать методы фильтрации Pandas для фильтрации нашего кадра данных.
Поскольку мы хотим выбрать сильные взаимосвязи, мы должны иметь возможность выбирать значения больше или равные 0,7 и меньше или равные -0,7 Поскольку это сделало бы наш оператор выбора более сложным, мы можем просто отфильтровать значение нашего коэффициента корреляции .
Давайте посмотрим, как это сделать:
matrix = df.corr() матрица = матрица.unstack() матрица = матрица [абс (матрица) >= 0,7] печать (матрица) # Возвращает: # bill_length_mm bill_length_mm 1.000000 # bill_depth_mm bill_depth_mm 1.000000 # flipper_length_mm flipper_length_mm 1.000000 # body_mass_g 0.871202 # body_mass_g flipper_length_mm 0,871202 # body_mass_g 1.000000
Здесь мы сначала берем нашу матрицу и применяем метод unstack , который преобразует матрицу в одномерный ряд значений с мультииндексом. Это означает, что каждый индекс указывает и на строку, и на столбец, или на предыдущую матрицу. Затем мы можем отфильтровать серию на основе абсолютного значения.
Выбор только положительных/отрицательных корреляций в матрице корреляций
В некоторых случаях может потребоваться выбрать только положительные корреляции в наборе данных или только отрицательные корреляции. Мы можем, опять же, сделать это, сначала разложив фрейм данных, а затем выбрав только положительные или отрицательные отношения.
Давайте сначала посмотрим, как мы можем выбрать только положительные отношения:
matrix = df.corr() матрица = матрица.unstack() матрица = матрица[матрица > 0] печать (матрица) # Возвращает: # bill_length_mm bill_length_mm 1.000000 # длина_плавника_мм 0,656181 # body_mass_g 0,595110 # bill_depth_mm bill_depth_mm 1.000000 # flipper_length_mm bill_length_mm 0,656181 # длина_плавника_мм 1.000000 # body_mass_g 0.871202 # body_mass_g bill_length_mm 0,595110 # длина_плавника_мм 0,871202 # body_mass_g 1.000000
Здесь мы видим, что этот процесс почти аналогичен выбору только сильных отношений. Мы просто меняем наш фильтр ряда, чтобы он включал только отношения, где коэффициент больше нуля.
Точно так же, если мы хотим выбрать отрицательные отношения, нам нужно изменить только один символ. Мы можем изменить сравнение > на < :
матрица = матрица[матрица < 0]
Это полезный инструмент, позволяющий нам увидеть, какие отношения имеют какое-либо направление. Мы можем даже комбинировать их и выбирать только сильные положительные отношения или сильные отрицательные отношения.
Заключение
В этом руководстве вы узнали, как использовать Python и Pandas для расчета матрицы корреляции. Вы вкратце узнали, что такое корреляционная матрица и как ее интерпретировать. Затем вы узнали, как использовать Pandas
Затем вы узнали, как использовать Pandas corr 9.0239 для расчета корреляционной матрицы и ее фильтрации на основе различных критериев. Вы также узнали, как использовать библиотеку Seaborn для визуализации матрицы с помощью функции тепловой карты , позволяющей лучше визуализировать и понимать данные с первого взгляда.
Чтобы узнать больше о методе кадра данных Pandas .corr() , ознакомьтесь с официальной документацией здесь.
Дополнительные ресурсы
Чтобы узнать о связанных темах, ознакомьтесь со статьями, перечисленными ниже:
- Pandas Variance: расчет дисперсии столбца фрейма данных Pandas
- Pandas Describe: описательная статистика вашего фрейма данных
- Quantile Pandas: расчет процентилей фрейма данных
- Среднее значение Pandas: расчет среднего значения Pandas для одного или нескольких столбцов Диаграмма в Excel - GeeksforGeeks
Корреляция в основном означает взаимную связь между двумя или более наборами данных.
 В статистике двумерные данные или две случайные величины используются для нахождения корреляции между ними. Коэффициент корреляции обычно представляет собой измерение корреляции между двумерными данными, которое в основном обозначает, насколько две случайные величины коррелируют друг с другом.
В статистике двумерные данные или две случайные величины используются для нахождения корреляции между ними. Коэффициент корреляции обычно представляет собой измерение корреляции между двумерными данными, которое в основном обозначает, насколько две случайные величины коррелируют друг с другом.Если коэффициент корреляции равен 0, двумерные данные не коррелируют друг с другом.
Если коэффициент корреляции равен -1 или +1, двумерные данные сильно коррелируют друг с другом.
r=-1 означает сильную отрицательную связь, а r=1 означает сильную положительную связь.
В целом, если коэффициент корреляции близок к -1 или +1, то мы можем сказать, что двумерные данные сильно коррелируют друг с другом.
Коэффициент корреляции рассчитывается с использованием коэффициента корреляции Пирсона, который определяется как:
где,
r : Коэффициент корреляции : значения переменной x. : значения переменной y. n : количество выборок, взятых в наборе данных.
 Числитель: Ковариация x и y.
Знаменатель: Произведение стандартного отклонения x и стандартного отклонения y.
Числитель: Ковариация x и y.
Знаменатель: Произведение стандартного отклонения x и стандартного отклонения y. В этой статье мы обсудим, как сделать корреляционные диаграммы в Excel на подходящих примерах.
Пример 1: Рассмотрим следующий набор данных:
ПОИСК КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ В EXCEL
В Excel для нахождения коэффициента корреляции используйте формулу:
=КОРРЕЛ(массив1,массив2) array1 : массив переменной x массив2: массив переменной y
Чтобы вставить массив1 и массив2, просто выберите диапазон ячеек для обоих.
1. Найдем коэффициент корреляции переменных и X и Y1.
array1 : Набор значений X. Диапазон ячеек от A2 до A6.
массив2 : Набор значений Y1. Диапазон ячеек от B2 до B6.
Точно так же вы можете найти коэффициенты корреляции для (X , Y2) и (X , Y3), используя формулу Excel.
Наконец, коэффициенты корреляции следующие:
Из приведенной выше таблицы мы можем сделать вывод, что:
X и Y1 имеют отрицательный коэффициент корреляции.

X и Y2 имеют положительный коэффициент корреляции.
X и Y3 не коррелированы, так как коэффициент корреляции почти равен нулю.
Диаграмма рассеяния в основном используется для анализа двумерных данных. Диаграмма состоит из двух переменных X и Y, одна из которых независима, а вторая зависит от предыдущей. Диаграмма представляет собой графическое представление того, как эти два данных коррелируют друг с другом. Возможны три случая на основе значения коэффициента корреляции , R , как показано ниже:
Типы диаграммы корреляции
Пример 2: Рассмотрим следующий набор данных:
Коэффициенты корреляции для приведенного выше набора данных:
Шаги построения диаграммы корреляции: Лист Excel.
- Перейти к Вставить вкладку в верхней части окна Excel.
- Выберите Вставить Точечная или пузырьковая диаграмма .
 Появится всплывающее меню.
Появится всплывающее меню. - Теперь выберите точечную диаграмму.
- Теперь нам нужно добавить линейную линию тренда на точечную диаграмму, чтобы показать корреляцию между двумерными данными. Для этого выберите график и в правом верхнем углу нажмите кнопку «+» , а затем установите флажок Trendline .
- Теперь линия тренда добавлена, и наша корреляционная диаграмма готова.
Диаграмма отрицательного отношения
- Теперь вы можете отформатировать линию тренда, выбрав и нажав кнопку «9».0022 Формат Trendline ”опция. Откроется диалоговое окно, в котором вы можете изменить тип и цвет линии тренда, а также отобразить значение на диаграмме.
Вы можете дополнительно отформатировать приведенную выше диаграмму, сделав ее более интерактивной, изменив «Стили диаграммы», добавив подходящие «Названия осей», «Название диаграммы», «Метки данных», изменив «Тип диаграммы» и т. д. Это можно сделать с помощью кнопки «+» в правом верхнем углу диаграммы Excel.
д. Это можно сделать с помощью кнопки «+» в правом верхнем углу диаграммы Excel.
Наконец, после всех модификаций графики выглядят так:
Диаграмма корреляции 1
Поскольку коэффициент корреляции равен R=-0,79, мы получили отрицательно коррелированную диаграмму. Линейная линия тренда будет расти вниз.
Диаграмма корреляции 2
Поскольку коэффициент корреляции равен R=0,89, мы получили положительно коррелированную диаграмму. Линейная линия тренда будет расти вверх.
Диаграмма корреляции 3
Поскольку коэффициент корреляции равен R = 0,01, , что приблизительно равно 0, поэтому мы получили график с нулевой корреляцией. Линейная линия тренда будет прямой линией, параллельной оси X, и это означает, что двумерные данные X и Y3 не коррелируют друг с другом.
Матрица корреляции в программировании на R
Корреляция относится к взаимосвязи между двумя переменными. Это относится к степени линейной корреляции между любыми двумя случайными величинами. Это отношение может быть выражено в виде диапазона значений, выраженных в интервале [-1, 1]. Значение -1 указывает на идеальную нелинейную (отрицательную) зависимость, 1 — на идеальную положительную линейную зависимость, а 0 — на промежуточное значение между ни положительной, ни отрицательной линейной взаимозависимостью. Однако значение 0 не означает, что переменные полностью независимы друг от друга. Матрицы корреляции вычисляют степень линейной связи между набором случайных величин, беря по одной паре за раз и выполняя для каждого набора пар в данных.
Это относится к степени линейной корреляции между любыми двумя случайными величинами. Это отношение может быть выражено в виде диапазона значений, выраженных в интервале [-1, 1]. Значение -1 указывает на идеальную нелинейную (отрицательную) зависимость, 1 — на идеальную положительную линейную зависимость, а 0 — на промежуточное значение между ни положительной, ни отрицательной линейной взаимозависимостью. Однако значение 0 не означает, что переменные полностью независимы друг от друга. Матрицы корреляции вычисляют степень линейной связи между набором случайных величин, беря по одной паре за раз и выполняя для каждого набора пар в данных.
- Все диагональные элементы корреляционной матрицы должны быть равны 1, потому что корреляция переменной сама с собой всегда идеальна, c ii =1.
- Должно быть симметрично c ij =c ji .
В программировании R матрица корреляции может быть заполнена с помощью функции cor(), которая имеет следующий синтаксис:
Синтаксис: cor (x, use = , method = )
Параметры:
x: Это числовая матрица или фрейм данных.

использование: Работа с отсутствующими данными.
- all.obs: значение этого параметра предполагает, что фрейм данных не имеет пропущенных значений и выдает ошибку в случае нарушения.
- complete.obs: удаление по списку.
- попарно.полные.наблюдения: попарное удаление.
метод: Сделки с типом отношений. Для вычислений можно использовать либо Пирсона, либо Спирмена, либо Кендалла. По умолчанию используется метод Пирсона.
Корреляция на языке программирования R
Матрица корреляции может быть вычислена в R после загрузки данных. В следующем фрагменте кода показано использование функции cor() :
R
|
Output:
[1] "Original Data"
Год Пробег..тыс. Цена
1 1998 27 9991
2 1997 17 9925
3 1998 28 10491
4 1998 5 10990
5 1997 38 9493
6 1997 36 9991
[1] «Корреляционная матрица»
Год Пробег. .тыс. Цена
Год 1.0000000 -0.7480982 0.9343679
Пробег..тыс. -0,7480982 1,0000000 -0,8113807
Price 0,9343679 -0,8113807 1,0000000
.тыс. Цена
Год 1.0000000 -0.7480982 0.9343679
Пробег..тыс. -0,7480982 1,0000000 -0,8113807
Price 0,9343679 -0,8113807 1,0000000 Вычисление коэффициентов корреляции R содержит встроенную функцию rcorr() , которая генерирует коэффициенты корреляции и таблицу p-значений для всех возможных пар столбцов фрейма данных. Эта функция в основном вычисляет уровни значимости для Корреляции Пирсона и Спирмена .
Синтаксис: rcorr (x, type = c("pearson", "spearman"))
Чтобы запустить эту функцию в R, нам нужно скачать и загрузить пакет « Hmisc » в окружение. Это можно сделать следующим образом:
install.packages("Hmisc")
library("Hmisc")
Следующий фрагмент кода показывает вычисление коэффициентов корреляции в R:
R
|
Output:
[1] "Original Data" Год Пробег..тыс. Цена 1 1998 27 9991 2 1997 17 9925 3 1998 28 10491 4 1998 5 10990 5 1997 38 9493 6 1997 36 9991 Год Пробег..тыс. Цена Год 1,00 -0,75 0,93 Пробег..тыс. -0,75 1,00 -0,81 Цена 0,93 -0,81 1,00 п = 23 п Год Пробег..тыс. Цена Год 0 0 Пробег..тыс. 0 0 Цена 0 0
В R мы будем использовать пакет «corrplot» для реализации коррелограммы. Следовательно, чтобы установить пакет из консоли R, мы должны выполнить следующую команду:
install.packages("corrplot") После того, как мы правильно установили пакет, мы загрузим пакет в наш скрипт R, используя библиотеку( ) следующим образом:
library("corrplot") Мы воспользуемся функцией corrplot() и упомянем фигуру в аргументах ее метода.
Р
9000
|
Результат:
Создание корреляционной матрицы в Python с помощью NumPy и Pandas
16 Акции
- Более
В этом посте мы рассмотрим, как рассчитать корреляционную матрицу в Python с помощью NumPy и Pandas. Теперь в этом руководстве будет несколько примеров корреляционной матрицы Python. Во-первых, мы прочитаем данные из файла CSV, чтобы мы могли простым способом взглянуть на методы numpy. corrcoef и Pandas DataFrame.corr.
corrcoef и Pandas DataFrame.corr.
Теперь полезно построить корреляционную таблицу (матрицу), особенно если в наших данных много переменных (см. еще три причины, читая дальше). В конце поста есть ссылка на Jupyter Notebook с примерами кода.
Содержание
Предварительные условия
Теперь, прежде чем мы продолжим использовать NumPy и Pandas для создания корреляционной матрицы в Python, нам нужно убедиться, что у нас установлены эти пакеты Python. Если на используемом нами компьютере установлен научный дистрибутив Python, такой как Anaconda или ActivePython, нам, скорее всего, не нужно устанавливать пакеты Python. В других случаях NumPy и Pandas можно установить с помощью conda (Anaconda/Miniconda) или pip.
Установка пакетов Python с помощью pip и conda
Дополнительные примеры по установке пакетов Python см. в этом посте. Тем не менее, откройте окно терминала или приглашение Anaconda и введите: pip install pandas numpy (pip) или Чтобы установить этот пакет с помощью conda, выполните: conda install -c anaconda numpy . Обратите внимание, что при необходимости обновление pip также можно выполнить с помощью pip.
Обратите внимание, что при необходимости обновление pip также можно выполнить с помощью pip.
Что такое корреляционная матрица?
Матрица корреляции используется для одновременного изучения взаимосвязи между несколькими переменными. Когда мы делаем этот расчет, мы получаем таблицу, содержащую коэффициенты корреляции между каждой переменной и другими. Теперь коэффициент показывает нам как силу связи, так и ее направление (положительные или отрицательные корреляции). В Python корреляционную матрицу можно создать, например, с помощью пакетов Python Pandas и NumPy.
Как сделать матрицу корреляции в Python?
Теперь, когда мы знаем, что такое корреляционная матрица, мы рассмотрим самый простой способ сделать корреляционную матрицу с Python: с Pandas.
импортировать панды как pd
df = pd.read_csv('datafile.csv')df.cor()
Приведенный выше код даст вам корреляционную матрицу, напечатанную, например, в Блокнот Юпитер. Прочтите сообщение для получения дополнительной информации.
Прочтите сообщение для получения дополнительной информации.
Перед тем, как взглянуть на применение корреляционной матрицы, я также хочу упомянуть, что pip можно использовать для установки определенной версии пакета Python, если это необходимо.
Применение корреляционной матрицыТеперь, прежде чем мы перейдем к коду Python, вот три основные причины для создания корреляционной матрицы:
- Если у нас есть большой набор данных, и мы намерены исследовать закономерности.
- Для использования в других статистических методах. Например, корреляционные матрицы можно использовать в качестве данных при проведении исследовательского факторного анализа, подтверждающего факторного анализа, моделей структурных уравнений.
- Матрицы корреляции также можно использовать в качестве диагностики при проверке предположений, например, для регрессионный анализ.
Метод корреляции
В настоящее время в большинстве корреляционных матриц используется корреляция продукта-момента Пирсона (r ) . В зависимости от типа данных наших переменных или от того, соответствуют ли данные предположениям о корреляции, обычно используются другие методы, такие как корреляция Спирмена (ро) и Тау Кендалла.
В зависимости от типа данных наших переменных или от того, соответствуют ли данные предположениям о корреляции, обычно используются другие методы, такие как корреляция Спирмена (ро) и Тау Кендалла.
В следующем разделе мы рассмотрим общий синтаксис двух методов вычисления корреляционной матрицы в Python.
Синтаксис corrcoef и cor
Здесь мы найдем общий синтаксис для вычисления корреляционных матриц с помощью Python с использованием 1) NumPy и 2) Pandas.
Матрица корреляции с NumPy
Общий синтаксис для создания корреляционной таблицы в Python с использованием NumPy: в этом случае x — это одномерный или двумерный массив с переменными и наблюдениями, для которых мы хотим получить коэффициенты корреляции. Кроме того, каждая строка размером x представляет одну из наших переменных, тогда как каждый столбец представляет собой одно наблюдение всех наших переменных. Не волнуйтесь, мы рассмотрим, как использовать np.corrcoef позже. Небольшое примечание: если вам нужно, вы можете преобразовать массив NumPy в целое число в Python.
Не волнуйтесь, мы рассмотрим, как использовать np.corrcoef позже. Небольшое примечание: если вам нужно, вы можете преобразовать массив NumPy в целое число в Python.
Корреляционная матрица с использованием Pandas
Для создания корреляционной таблицы в Python с Pandas используется общий синтаксис:
Язык кода: Python (python)
df.corr()
Здесь, df. — это DataFrame, который у нас есть, а cor() — это метод получения коэффициентов корреляции. Конечно, позже в этом посте мы рассмотрим, как использовать Pandas и метод corr.
Вычисление корреляционной матрицы в Python с помощью NumPy
Теперь мы рассмотрим некоторые детали метода corrcoef в NumPy. Обратите внимание, что это будет простой пример, и обратитесь к документации, указанной в начале поста, для более подробного объяснения.
Сначала мы загрузим данные с помощью метода numpy.loadtxt . Во-вторых, мы будем использовать метод corrcoeff для создания корреляционной таблицы.
Матрица корреляции (массив NumPy)Язык кода: Python (python)
импортировать numpy как np данные = './SimData/correlationMatrixPython.csv' x = np.loadtxt (данные, skiprows = 1, разделитель = ',', распаковать = верно) np.corrcoef(x)
Обратите внимание, мы использовали аргумент skiprows , чтобы пропустить первую строку, содержащую имена переменных, и аргумент разделителя , поскольку столбцы разделены запятая. Наконец, мы использовали аргумент unpack , чтобы наши данные соответствовали требованиям corrcoef. В качестве последнего примечания; используя NumPy, мы не можем вычислить Rho Спирмена или Tau Кендалла. То есть метод corrcoef будет только обратная корреляция Коэффициенты R лиц.
То есть метод corrcoef будет только обратная корреляция Коэффициенты R лиц.
3 шага к созданию корреляционной матрицы в Python с Pandas
В этом разделе мы узнаем, как создать корреляционную таблицу в Python с Pandas за 3 простых шага.
1. Импорт Pandas
В сценарии или Jupyter Notebook нам нужно начать с импорта Pandas:
.9010 в Import Data Python с пандамиЯзык кода: Python (python)
import pandas as pd
Импортируйте данные в кадр данных Pandas следующим образом:
Язык кода: Python (python)
data = './SimData/correlationMatrixPython.csv' df = pd.read_csv (данные) df.head()
Теперь помните, что файл данных должен находиться в подпапке относительно Jupyter Notebook, называемой SimData.
На изображении ниже мы видим значения четырех переменных в наборе данных:
Первые 5 строкКонечно, важно указать полный путь к файлу данных. Обратите внимание, что есть, конечно, и другие способы создания фрейма данных Pandas. Например, мы можем создать фрейм данных из словаря Python. Кроме того, также можно считывать данные из файла Excel с помощью Pandas или очищать данные из таблицы HTML в фрейм данных, и это лишь некоторые из них.
3. Рассчитайте матрицу корреляции с помощью Pandas:
Теперь мы находимся на последнем этапе создания корреляционной таблицы в Python с помощью Pandas:
Язык кода: Python (python)
df.corr()
Используя данные примера, мы получаем следующий вывод, когда распечатываем его в блокноте Jupyter:
Корреляционная таблица, созданная с помощью Python Pandas метод ='Копейщик' аргумент метода corr. См. изображение ниже. Вот ссылка на пример набора данных.
См. изображение ниже. Вот ссылка на пример набора данных.
Верхние и нижние треугольные корреляционные таблицы с Pandas
В этом разделе мы собираемся использовать NumPy и Pandas вместе с нашей корреляционной матрицей (мы сохранили ее как cormat : cormat = df.corr () ).
Язык кода: Python (python)
импортировать numpy как np def triang(cormat, triang='нижний'): если треугольник == 'верхний': rstri = pd.DataFrame(np.triu(cormat.values), индекс=cormat.index, столбцы = cormat.columns).round (3) rstri = rstri.iloc[:,1:] rstri.drop(rstri.tail(1).index, inplace=True) если треугольник == 'ниже': rstri = pd.DataFrame(np.tril(cormat.values), индекс=cormat.index, столбцы = cormat.columns).round (3) rstri = rstri.iloc[:,:-1] rstri.drop(rstri.head(1).index, inplace=True) rstri.replace(to_replace=[0,1], значение='', inplace=Истина) возврат(рстри)
Теперь эту функцию можно запустить с треугольником аргументов («верхний» или «нижний»). Например, если мы хотим иметь верхний треугольник, мы делаем следующее.
Корреляционная таблица Pandas Верхний треугольныйЯзык кода: JavaScript (javascript)
triang(cormat, 'upper')
Разумеется, существуют и другие способы передачи корреляционной матрицы. Например, мы можем исследовать взаимосвязь между каждой переменной (если их не слишком много), используя метод Pandas scatter_matrix для создания парного графика. Другие варианты — например, создать коррелограмму или тепловую карту (см. пост под названием 9Методы визуализации данных в Python, которые вам нужно знать, для получения дополнительной информации об этих двух методах).
Другие варианты — например, создать коррелограмму или тепловую карту (см. пост под названием 9Методы визуализации данных в Python, которые вам нужно знать, для получения дополнительной информации об этих двух методах).
Приведенную выше тепловую карту можно воспроизвести с помощью кода, найденного в Jupyter Notebook здесь.
Заключение
В этом посте мы создали корреляционную матрицу, используя Python и пакеты NumPy и Pandas. В целом, оба метода довольно просты в использовании. Однако, если нам нужно использовать другие методы корреляции, мы не можем использовать corrcoef. Как мы видели, с помощью метода Pandas corr это возможно (просто используйте аргумент метода). Наконец, мы также создали корреляционные таблицы с Pandas и NumPy (т. е. верхние и нижние треугольные).
Если есть что-то, что нужно исправить, или что-то, что следует добавить в эту корреляционную матрицу в учебнике по Python, оставьте комментарий ниже.

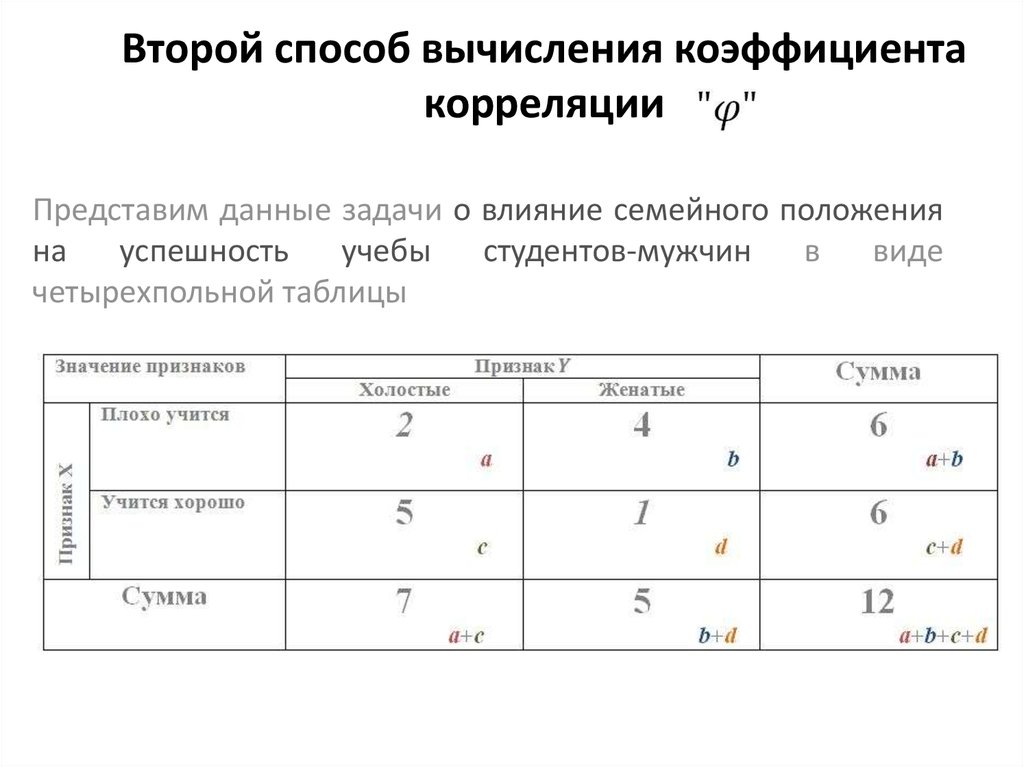 1)
1)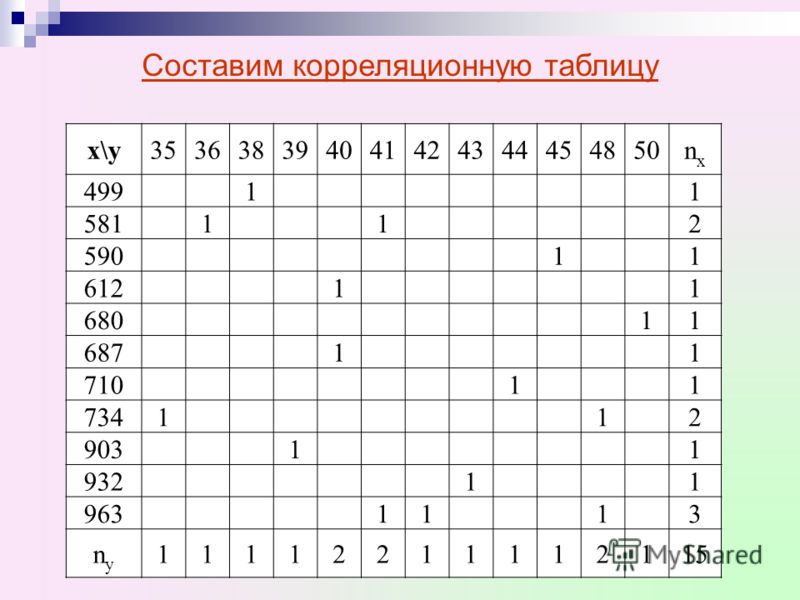 8)
8)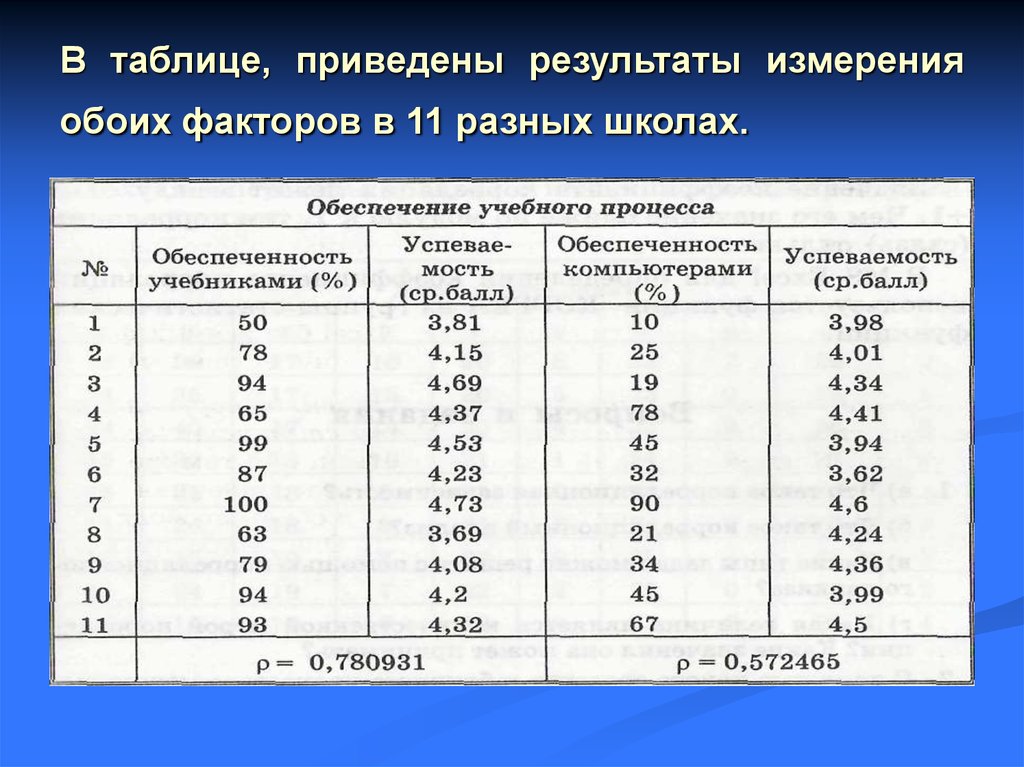 9)
9)