Урок 36. формулы половинного аргумента — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №36. Формулы половинного аргумента.
Перечень вопросов, рассматриваемых в теме
1) Формулы синуса, косинуса, тангенса и котангенса половинного аргумента;
2) Преобразовывать тригонометрические выражений на основе использования формулы синуса, косинуса, тангенса и котангенса половинного аргумента;
3) Решение уравнения с использованием формулы синуса, косинуса половинного аргумента.
Глоссарий по теме
Формулы половинного угла (аргумента) представляют собой противоположность формулам двойного угла, так как они выражают синус, косинус, тангенс и котангенс угла при помощи тригонометрических функций угла α.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.
Теоретический материал для самостоятельного изучения
Сегодня мы узнаем формулы, позволяющие нам по известным значениям ; находить ; ; . Их называют формулы половинного аргумента.
Повторим формулу косинуса двойного аргумента .
А если учесть, что и , то получим ещё две формулы, которые нам сегодня понадобятся:
и
Пример. а) Найти , если .
Вычислим по формуле
б) Найти , если .
Вычислим по формуле .
- Запишем формулу косинуса двойного аргумента в виде и заменим х на . Тогда получим:, учтём, что
, получаем
(1) формула синуса половинного аргумента.
Запишем формулу косинуса двойного угла, где в виде
(2) формула косинуса половинного угла.
По формулам (1) и (2) можно найти или , если известны значения и положение угла , т. е. в какой координатной четверти он находится, чтобы определить знак выражения или .
е. в какой координатной четверти он находится, чтобы определить знак выражения или .
Эти формулы ещё имеют название «формулы понижения степени», так как в левой части находится вторая степень синуса и косинуса, а в правой – первая, т.е. степень понизилась. Но будьте внимательны: степень понижается, а аргумент удваивается.
Например, .
Пример. Известно, что . Найдите ; ;
1) найдём по формуле: ; .
По условию . Разделив обе части неравенства на 2, получаем , значит угол во второй четверти, здесь синус положительный. .
2) ; найдём по формуле ,
Мы уже выяснили, что угол во второй четверти, косинус отрицательный.
3) Так как тангенс это отношение синуса на косинус, то
- Выведем формулу для тангенса половинного аргумента. Для этого разделим левую часть формулы (1) на левую часть формулы (2) и правую часть формулы (1) на правую часть формулы (2).
сократим на 2 , и учитывая, что , получим:
формула тангенса половинного аргумента (3).
Так как котангенс это число, взаимообратное тангенсу, то
Пример. Найти и , если известно, что и .
По формуле (3) находим , а Найдём положение угла
По условию ,( разделим на 2)
, угол в первой четверти, тангенс положительный, , а .
- Выведем формулу, по которой можно найти через .
Для этого используем формулу синуса двойного угла , заменив в ней х на . Получаем , учтём, что , то
, разделим числитель и знаменатель на , получаем:
(4)
(5)
Пример. Найти , если .
По формуле (5) .
С помощью доказанных на этом уроке формул можно не только вычислять значения выражений, но и упрощать выражения, доказывать тождества и решать тригонометрических уравнений.
Пример. Доказать тождество .
Представим , а , преобразуем левую часть тождества
, но , то
Левая часть равна правой части, тождество доказано.
Примеры и разбор решения заданий тренировочного модуля
№1. Известно, что и . Найдите ; ;
Известно, что и . Найдите ; ;
Установите соответствие между множествами значений А и В:
А В
а) 1)
б) cos 2)
в) tg 3)
г) ctg 4)3
5)
Ответ:
Подсказка: используйте формулы половинного аргумента и определение тангенса и котангенса.
№2. Известно, что . Найти ;
Установите соответствие между множествами значений А и В:
А В
а) 1)
б) ; 2)
в) 3)
г) ; 4)
Ответ:
Подсказка: используйте формулы половинного аргумента.
№3.Вычислите
Ответ:12.
Подсказка: используйте формулу синуса двойного угла, где .
№4. Известно, что , Найти ;
Установите соответствие между множествами значений А и В:
А В
а) 1)
б) ; 2)
в) 3)
г) ; 4)
Ответ:
Подсказка: используйте формулы половинного аргумента, зависимость синуса от косинуса, определения тангенса и котангенса.
№5.Вычислите .
Ответ: 0,5.
Подсказка: используйте формулу половинного аргумента.
№6. Известно, что. Найти ;
Установите соответствие между множествами значений А и В:
А В
а) 1)
б) ; 2)
в) 3)-
г) ; 4)
Ответ:
Подсказка: используйте формулы половинного аргумента, определения тангенса и котангенса.
№7. Вычислите и установите соответствие между множествами значений А и В:
А В
а) ; 1)
б) ; 2)
в) ; 3) 0,25
Ответ:
Подсказка: используйте формулу синуса и косинуса двойного угла, где .
№8.Упростите выражения и установите соответствие между множествами выражений А и В:
А В
а); 1)
б); 2)
в) ; 3)
Ответ:
Подсказка: используйте формулу синуса и косинуса двойного угла, где и определение тангенса.
№9*. Упростите выражение .
Выберите правильный ответ:1)2)3)2.
Ответ:2)
Подсказка: используйте формулу синуса двойного угла, где .
№10*. Известно, что . Найти ;
Установите соответствие между множествами значений А и В:
А В
а) 1)
б) ; 2)
в) 3)
г) ; 4)
Ответ:
Подсказка: используйте формулы половинного аргумента, зависимость синуса от косинуса, определения тангенса и котангенса.
№11*.Вычислите .
Ответ:1,5.
Подсказка: используйте формулы синуса двойного угла, где ; квадрата суммы и основное тригонометрическое тождество.
№12*.Известно, что , Найти ;
Установите соответствие между множествами значений А и В:
А В
а) 1)
б) ; 2)
в) 3)
г) ; 4)
Ответ:
Подсказка: используйте формулы половинного аргумента, зависимость синуса от косинуса, определения тангенса и котангенса.
№13*.Вычислите. Установите соответствие между множествами значений А и В:
А В
а) 1)
б) ; 2)
в) 3)
г) ; 4)
Ответ:
Подсказка: используйте формулу синуса и косинуса двойного угла, где и определение тангенса и котангенса.
№14*.Решите уравнения и выберите верный ответ:
1); 2);3)
Ответ: 2)
Подсказка: используйте формулу половинного аргумента, разделив предварительно обе части уравнения на 2.
Проверочная работа:
№1.
а) Известно, что , ,
Вычислите и установите соответствие между множествами А и В:
А В
а) ; 1)
б) cos; 2)
в) ; 3)
г) ; 4)
5)2
Ответ:
Подсказка: используй формулы половинного аргумента и определение тангенса и котангенса.
б) Известно, что , ,
Вычислите и установите соответствие между множествами А и В:
А В
а) ; 1)
б) cos; 2)
в) ; 3)
г) ; 4)
5)
Ответ:
Подсказка: используй формулы половинного аргумента и определение тангенса и котангенса.
№2.Вычислите: а); б)
Ответ: а) 5; б) 6
Подсказка: используйте формулу тангенса двойного угла, где .
№3.
а)Упростите выражение:
Выберите верный ответ:1)
Ответ: 1)
б) Упростите выражение:
Выберите верный ответ:1)
Ответ: 1)
Подсказка: используйте определение тангенса и котангенса, основное тригонометрическое тождество, формулу синуса и косинуса двойного угла, где .
Формулы половинного угла в тригонометрии
Формулы половинного угла (аргумента) представляют собой противоположность формулам двойного угла , так как они выражают синус, косинус, тангенс и котангенс угла α2 при помощи тригонометрических функций угла α. В статье раскрыты формулы половинного угла и добавлены их доказательства с примерами решений.
В статье раскрыты формулы половинного угла и добавлены их доказательства с примерами решений.
Список формул половинного угла
Стандартные формулы половинного угла:
sin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα
Формулы для sin и cos половинного угла справедливы при любом значении заданного угла α. Формулу для tg любого угла αопределяет tgα2, значение угла α≠π+2π·z при z равном любому целому числу ( выражение 1+cosα с таким же значением α не должно принимать значение 0). Формула ctg угла считается справедливой для любого угла α, где половинный угол имеет место быть, α≠2π·z.
Самые значимые формулы половинного угла для квадратов тригонометрических функций выводятся через положительное или отрицательное значение арифметического квадратного корня. Имеем формулы половинного угла:
sinα2=±1-cosα2, cosα2=±1+cosα2, tgα2=±1-cosα1+cosα, ctgα2=±1+cosα1-cosα
Знак «-» указывает, что тригонометрическая функция принадлежит определенной четверти угла α2.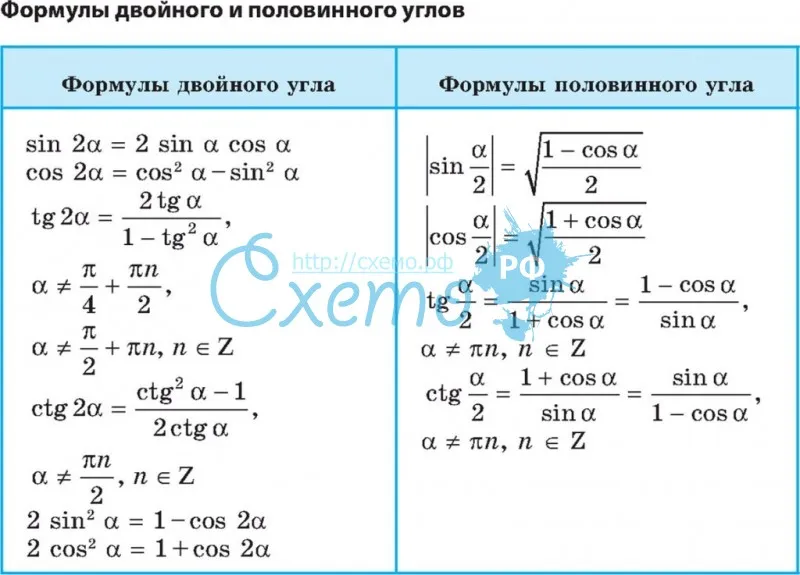
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеПрименим формулы на практике.
Доказательство формул половинного угла
Доказательство формул половинного угла основывается на формулах cos двойного угла cosα=1-2·sin2α2 и cosα=2·cos2α2-1. Упростив первое выражение по sin2α2, получим саму формулу половинного угла sin2α2=1-cosα2, второе выражение по cos2α2 получим cos2α2=1+cosα2.
Чтобы доказать формулы половинного угла для tg и ctg угла α2, необходимо применить основные тригонометрические тождества tgα2=sinα2cosα2 и ctgα2=cosα2sinα2, к ним необходимо добавить формулы половинного угла cos и sin, которые доказали выше. При подстановке получим выражения, имеющие вид:
tg2α2=sin2α2cos2α2=1-cosα21+cosα2=1-cosα1+cosα;ctg2α2=cos2α2sin2α2=1-cosα21+cosα2=1+cosα1-cosα;
Все формулы половинного угла были доказаны.
Примеры использования
Покажем применение формул половинного угла при решении примера.
Известно, что cos30°=32. Необходимо вычислить значение cos 15 градусов, используя формулы половинного угла.
Решение
Данный пример рассматривает применение формулы половинного угла для косинуса, имеющей вид cos2α2=1+cosα2.
Следуя из условия, подставляем числовые значения и получаем: cos215°=1+cos30°2=1+322=2+34. После получения значения косинуса 15 градусов, необходимо найти само значение косинуса. Для этого вспомним, что угол в 15 градусов принадлежит первой четверти. Там косинус угла имеет положительное значение ( чтобы вспомнить знаки тригонометрических функций, необходимо повторить теорию знаков синуса, косинуса, тангенса и котангенса по четвертям). Следуя из вышесказанного, имеем cos215°=2+34, тогда cos 15°=2+34=2+32. Ответ: cos 15°=2+32.
Применяя формулу половинного угла, стоит учитывать тот факт, что угол может быть не явного вида α2 и α, а потребует дальнейшего приведения к стандартному виду. Главное условие – нахождение аргумента в правой части формул половинного угла было в 2 раза больше, чем в левой. Иначе применение формулы будет невозможно.
Иначе применение формулы будет невозможно.
Если формула позволит записывать данное равенство таким образом sin27α=1-cos14α2 или sin2 5α17=1-cos10α172, то формула будет применима.
Для правильного преобразования и применения формул половинного аргумента необходимо досконально изучить свойства тригонометрических функций. Не любое выражение поддается такому преобразованию в тригонометрии. Необходимо внимательно следить за значениями углов тригонометрических функций и их нахождение в четвертях для определения знака для выражения.
Все формулы половинного угла в тригонометрии:
Формулы половинного угла: доказательства (вывод) и примеры
Формулы половинного угла (половинного аргумента) – это часть от всех основных тригонометрических формул. Они выражают функции синус, косинус, тангенс, котангенс угла `\frac{\alpha}2` через эти ж функции аргумента `\alpha`.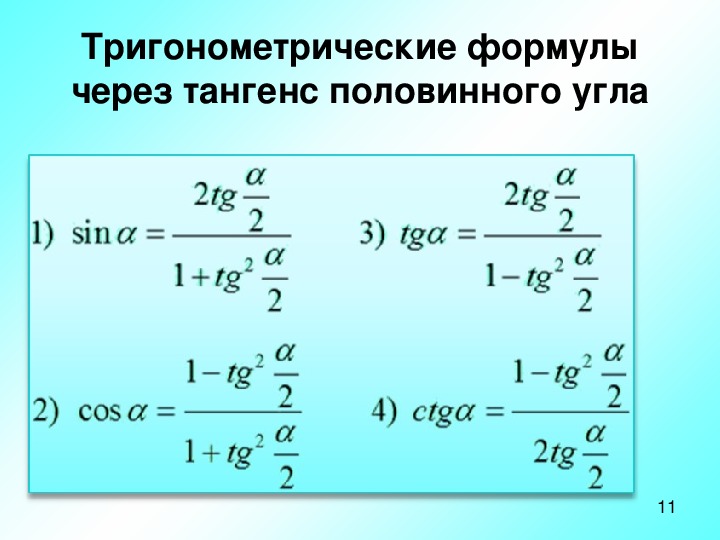 Они, можно сказать, противоположны формулам двойного угла. Ниже приведены все формулы половинных углов, их вывод, а также примеры решения задач с их использованием.
Они, можно сказать, противоположны формулам двойного угла. Ниже приведены все формулы половинных углов, их вывод, а также примеры решения задач с их использованием.
Содержание статьи:
Список всех формул половинного угла
Их можно встретить записанными в двух видах. В первом каждая из тригонометрических функций выражается через радикал:
`sin \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}2}`
`cos \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}2}`
`tg \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}{1+cos \ \alpha}}=` `\frac {sin \ \alpha}{1+cos \ \alpha}=\frac {1-cos \ \alpha}{sin \ \alpha}`
`ctg \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}{1-cos \ \alpha}}=` `\frac {sin \ \alpha}{1-cos \ \alpha}=\frac {1+cos \ \alpha}{sin \ \alpha}`
Знак «+» или «-» перед корнями зависит от того, в какую из координатных четвертей попадает угол `\frac{\alpha}2`.
Во втором варианте имеем дело с квадратами тригонометрических функций половинного угла:
`sin^2 \ \frac \alpha 2=\frac {1-cos \ \alpha}2`
`cos^2 \ \frac \alpha 2=\frac {1+cos \ \alpha}2`
`tg^2 \ \frac \alpha 2=\frac {1-cos \ \alpha}{1+cos \ \alpha}`
`ctg^2 \ \frac \alpha 2=\frac {1+cos \ \alpha}{1-cos \ \alpha}`
Формула синуса и косинуса половинного угла имеет место при любом угле `\alpha`.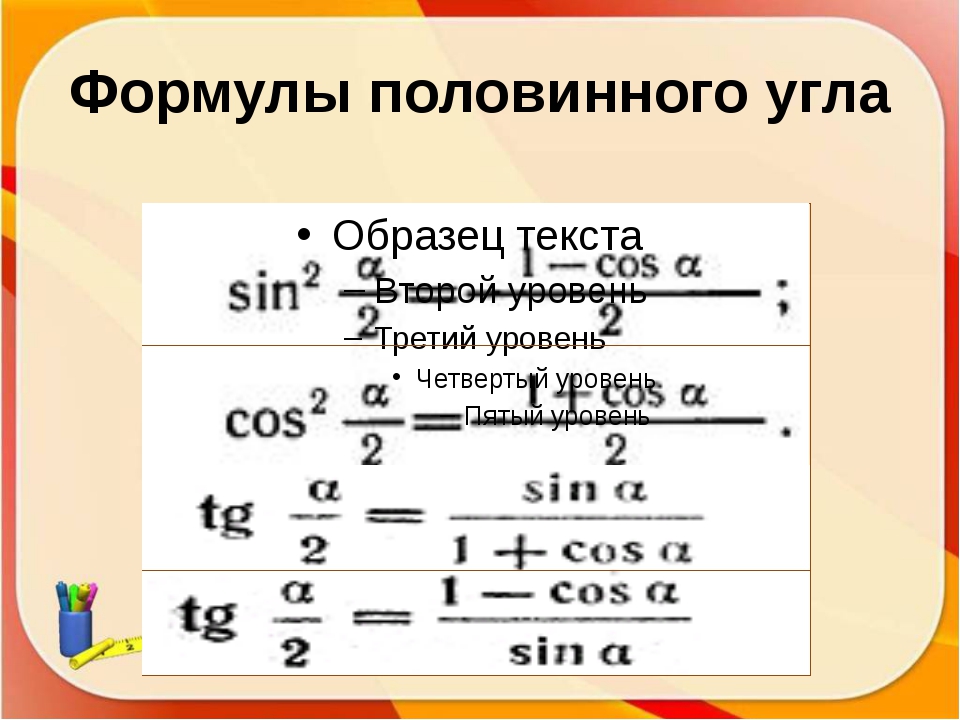 2 \frac \alpha 2-1`. Выразив из первого равенства ` sin \frac \alpha 2` получим `sin \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}2}`. Аналогично разрешив второе равенство относительно ` cos \frac \alpha 2` в результате будем иметь `cos \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}2}`.
2 \frac \alpha 2-1`. Выразив из первого равенства ` sin \frac \alpha 2` получим `sin \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}2}`. Аналогично разрешив второе равенство относительно ` cos \frac \alpha 2` в результате будем иметь `cos \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}2}`.
Формулы тангенса и котангенса половинного угла можно вывести, используя определения этих функций в виде `tg \frac \alpha 2=\frac{sin\frac \alpha 2}{cos \frac \alpha 2}` и `ctg \frac \alpha 2=\frac{cos \frac \alpha 2}{sin \frac \alpha 2}`, а также две уже доказанные выше формулы для синуса и косинуса.
В результате будем иметь: `tg \frac \alpha 2=\frac{sin\frac \alpha 2}{cos \frac \alpha 2}=` `\frac{\pm \sqrt{\frac {1-cos \ \alpha}2}}{\pm \sqrt{\frac {1+cos \ \alpha}2}}=` `\pm \sqrt{\frac {1-cos \ \alpha}{1+cos \ \alpha}}` и `ctg \frac \alpha 2=\frac{cos\frac \alpha 2}{sin \frac \alpha 2}=` `\frac{\pm \sqrt{\frac {1+cos \ \alpha}2}}{\pm \sqrt{\frac {1-cos \ \alpha}2}}=` `\pm \sqrt{\frac {1+cos \ \alpha}{1-cos \ \alpha}}`. \circ=\frac{\sqrt{2+\sqrt3}}2`.
\circ=\frac{\sqrt{2+\sqrt3}}2`.
Пример 2. Вычислить значение выражения `4cos \frac {\alpha}2+2cos \alpha+5`, если `cos \alpha=\frac {1}8`.
Решение. Используя ту же формулу, что и в первом примере (`cos \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}2}`) и известное значение косинуса, упростим выражение: `4\sqrt{\frac {1+cos \ \alpha}2}+2cos \alpha+5=4\sqrt{\frac {1+\frac {1}8}2}+2 \cdot \frac {1}8+5=` `4\sqrt{\frac {9}16}+\frac{1}4+5=8\frac{1}4`.
Ответ. `4cos \frac {\alpha}2+2cos \alpha+5=8\frac{1}4`.
Еще несколько примеров с подробным объяснением посмотрите на видео:
В большинстве случаев формулы половинного угла используются при преобразовании тригонометрических выражений.
Материалы по теме:
Поделиться с друзьями:
Загрузка…Конспект урока на тему «Формулы половинного угла» (10 класс)
Урок 82 (18) Дата: 12. 02.2018 Алгебра и начала анализа — 10 класс
02.2018 Алгебра и начала анализа — 10 класс
Тема урока: «Формулы тригонометрических функций половинного угла»
Цели урока: Показать как с помощью основного тригонометрического тождества и формул двойного угла выводится формулы для половинного угла; сформировать умения применять полученные формулы при упрощении и вычислении тригонометрических выражений.
Развивать алгоритмическое мышление, память, умение излагать мысли, делать выводы, обобщения; содействовать рациональной организации труда.
Воспитать внимательность, наблюдательность, трудолюбие и заинтересованность учащихся новым материалом
Тип урока: урок формирования новых умений и навыков
Методы обучения: проблемное изложение, дифференцированный метод.
Форма: фронтальная, индивидуальная, групповая.
Оборудование: компьютер, презентация, интерактивная доска, учебники, тетради
Ход урока:
Организационный момент: приветствие, проверка готовности к уроку.
 (1 мин)
(1 мин)
Мотивация деятельности учащихся (3 мин)
Эпиграф к уроку.
Нельзя математику изучить,
наблюдая, как это делает другой.
Айвен Нивен
(канадско-американский математик)
Учитель. На предыдущих уроках мы говори о формулах сложения синуса, косинуса, тангенса двух углов, а также выучили формулы двойных углов. То есть мы увидели с вами законы, по которым необходимо работать в тригонометрии. Сегодня же мы продолжим разговор о тригонометрических формулах и с помощью предыдущего материала получим еще несколько новых формул. А также научимся применять вновь изученные формулы при решении упражнений.
Оглашается тема урока (учащиеся записывают ее в тетрадь)
Учитель. Давайте вместе поставим перед собой цели урока – чего в течении урока мы должны достичь? (учащиеся называют цели урока)
Цели урока для учащихся: получить формулы половинного угла;
научиться их применять при работе с тригонометрическими выражениями.
Учитель. Итак наша сегодняшняя задача познакомится с новым блоком формул, названными формулами половинного аргумента. Но перед тем как приступить к новой теме, давайте мы свами проверим качество наших уже имеющиеся знаний, т.е. вспомним пройденный материал по элементам тригонометрии.
Актуализация опорных знаний (12 мин)
Индивидуальная работа.
Учащиеся выполняют самостоятельную работу по вариантам (карточки)
Самостоятельная работа на тему
«Формулы сложения и двойного угла»
Вариант 1
Вычислите:
а) б)
Вычислите:
а) ;
б)
Упростите выражение:
Самостоятельная работа на тему
«Формулы сложения и двойного угла»
Вариант 2
Вычислите:
а) б)
Вычислите:
а) ;
б) ;
Упростите выражение:
Обмен тетрадями и взаимопроверка решений и ответов по готовым решениям на слайдах.
Усвоение новых знаний и умений (10 мин)
Учитель. Вот и настало время для ознакомления с темой сегодняшнего нашего урока «Формулы для половинных углов». Вспомним эпиграф нашего урока и постараемся сами вывести формулы половинного аргумента.
Групповая дифференцированная работа
Учащиеся класса объединяются в четыре группы – 2 группы с сильными учениками и 2 группы с учениками послабее.
Задача первых двух групп фактически раскрыть тему урока – получить формулы половинного угла, а других двух групп – подготовить себя к восприятию нового материала и с помощью карточек-инструкторов также получить новые формулы.
Группам необходимо решить проблемное задание. Одни учащиеся самостоятельно способны найти решение, а другим предлагаются подсказки в виде наводящих вопросов-действий, которые по очереди высвечиваются на слайдах на доске.
Вопросы на карточках-инструкторах
Запишите основное тригонометрическое тождество ()
Запишите формулу косинуса двойного угла ()
Запишите данные формулы для половинных углов ()
Сложите формулы основного тригонометрического тождества и формулу косинуса двойного угла записанные для половинных углов ()
Вычтите основное тригонометрическое тождество и формулу косинуса двойного угла записанные для половинных углов ()
Выразите синус и косинус половинного аргумента
А как получить тангенс половинного угла? (поделить квадрат синуса на квадрат косинуса)
Поделите формулу квадрата синуса половинного угла на квадрат косинуса половинного угла ()
Выпишите формулы, которые соответствуют сегодняшней теме урока
Итак, мы получили формулы половинного угла или формулы понижения степени
Формирование навыков применения полученных формул при решении упражнений (10 мин)
Решение примеров по учебнику
Учебник Алимов Ш. А. стр 155 №514 — №518 – нечетные
А. стр 155 №514 — №518 – нечетные
Класс работает в тетради, а у доски 2 человека: первый решает с объяснением, а второй сначала самостоятельно, а потом комментирует свое решение.
Учитель отмечает самостоятельную работу учащихся на местах
Рефлексия (3 мин)
Возвращаясь к эпиграфу урока, хочется, чтобы учащиеся отметили свою самостоятельность по выводу формул на уроке:
Я сам догадался и самостоятельно получил новые знания.
Мне подсказали, но большую часть информации я получил самостоятельно.
Я действовал по инструкции и мне все понятно.
Я действовал по инструкции, но некоторые моменты остались не понятны.
Мне сегодня все было сложным и непонятным
Оценивание учащихся (3 мин): учащиеся получат оценку за выполнение самостоятельной работы и за работу в группах с учетом количества практических заданий выполненных самостоятельно.
 2\frac{23π}{12}-\sqrt{27}=\sqrt{108}\)\( \frac{1+\cos\frac{2\cdot 23π}{12}}{2}\)\(-\sqrt{27}=\sqrt{108}\)\(\frac{1+\cos\frac{23π}{6}}{2}\)\(-\sqrt{27}=\)…
2\frac{23π}{12}-\sqrt{27}=\sqrt{108}\)\( \frac{1+\cos\frac{2\cdot 23π}{12}}{2}\)\(-\sqrt{27}=\sqrt{108}\)\(\frac{1+\cos\frac{23π}{6}}{2}\)\(-\sqrt{27}=\)…
\(\frac{23π}{6}=\frac{24π-π}{6}=\frac{24π}{6}-\frac{π}{6}=4π-\frac{π}{6}\).Попали в самое большое из трех стандартных значений косинуса: \(\frac{1}{2}\), \(\frac{\sqrt{2}}{2}\), \(\frac{\sqrt{3}}{2}\). Значит \(\cos\frac{23π}{6}=\frac{\sqrt{3}}{2}\).
…\(=\sqrt{108}\)\(\frac{1+\frac{\sqrt{3}}{2}}{2}\)\(-\sqrt{27}=\sqrt{27\cdot 4}\)\(\frac{1+\frac{\sqrt{3}}{2}}{2}\)\(-\sqrt{27}=2\sqrt{27}\cdot\)\(\frac{1+\frac{\sqrt{3}}{2}}{2}\)\(-\sqrt{27}=\sqrt{27}(1+\frac{\sqrt{3}}{2})-\sqrt{27}=\)
\(=\sqrt{27}+\frac{\sqrt{27\cdot 3}}{2}-\sqrt{27}=\frac{\sqrt{81}}{2}=\frac{9}{2}=4,5\).Это решение не самое простое из всех возможных (наиболее легкое приведено в статье «формулы двойного угла»), но до него легче всего догадаться, если знаешь формулу половинного угла.
 2\frac{7π}{8}\).
2\frac{7π}{8}\).
\(=\sqrt{32}-\sqrt{128}\)\(\frac{1-\cos\frac{7π}{4}}{2}\)\(=\)
Вычислим косинус с помощью формулы приведения. Для этого сначала преобразуем \(\frac{7π}{4}\):
\(\frac{7π}{4}=\frac{8π-π}{4}=\frac{8π}{4}-\frac{π}{4}=2π-\frac{π}{4}\)
\(=\sqrt{32}-\sqrt{128}\)\(\frac{1-\cos(2π-\frac{π}{4})}{2}\)\(=\)
Теперь применим к косинусу формулу приведения:
-
\((2π-\frac{π}{4})\) – это четвертая четверть, косинус в ней положителен. Значит, знак перед косинусом останется прежним.
-
\(2π\) — находится на «горизонтали» — функция остается прежней.

\(\cos(2π-\frac{π}{4})=\cos\frac{π}{4}\).
\(=\sqrt{32}-\sqrt{128}\)\(\frac{1-\cos\frac{π}{4}}{2}\)\(=\)
\(\cos\frac{π}{4}=\frac{\sqrt{2}}{2}\).
\(=\sqrt{32}-\sqrt{128}\)\(\frac{1-\frac{\sqrt{2}}{2}}{2}\)\(=\)
Домножим числитель и знаменатель дроби на \(2\), чтоб избавиться от «трехэтажности».
\(=\sqrt{32}-\sqrt{128}\)\(\frac{2-\sqrt{2}}{4}\)\(=\)
Игнорировать корни больше невозможно. Вынесем из \(\sqrt{128}\) четверку, чтоб она сократилась со знаменателем:
\(\sqrt{128}=\sqrt{16\cdot 8}=4\sqrt{8}\)
\(=\sqrt{32}-4\sqrt{8}\)\(\frac{2-\sqrt{2}}{4}\)\(=\)
Сократим четверки.

\(=\sqrt{32}-\sqrt{8}(2-\sqrt{2})=\)
Раскроем скобки.
\(=\sqrt{32}-2\sqrt{8}+\sqrt{16}=\)
Занесем \(2\) под корень и вычислим \(\sqrt{16}\).
\(=\sqrt{32}-\sqrt{32}+4=4\).
Ответ: \(4\).
Смотрите также:
Формулы тригонометрии с примерамиКонспект | План-конспект урока по алгебре (10 класс):
№
Этапы уроки
Задачи урока
Деятельность учителя
Деятельность ученика
УУД
1
Организационный
Создать благоприятный психологический настрой на работу
Приветствие, проверка подготовленности к учебному занятию (собрать индивидуальные РНО у учащихся), организация внимания детей.

Чем мы занимались на прошлом уроке?
Сегодня мы применим наши навыки приведения подобных слагаемых для изучения новой темы.
Включаются в деловой ритм урока.
Приводили подобные слагаемые
Да — Нет
Личностные: самоопределение. Регулятивные: целеполагание. Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.
2
Постановка формируемых результатов и задач урока. Мотивация учебной деятельности учащихся.
Эпиграф к уроку: «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно.»
(А. Эйнштейн)
Догадались какую тему мы будем сегодня изучать?
3
Актуализация знаний.

Развитие исследовательских навыков, дифференцированного подхода в обучении
Учитель: Новые знания нам будет очень трудно осваивать без умения быстро и верно считать, поэтому, как всегда, начнем урок с устного счета:
1.Раскройте скобки: №1 с. 245
2. Открываем тетради, записываем число, классная работа.
3.Обратите внимание на записи.
На доске:
5(x-3) = 20;
a-4+b;
x+8=-15;
4b;
7,5-3k;
5x=2x+6;
6m -1.
Внимательно их изучите и ответьте на вопросы.
— На какие две группы можно разделить написанное?
— Как можно назвать каждую из групп?
— Интересна ли для нас 1 группа: выражения?
— А вторая? Почему?
4. Итак, еще раз. Кто теперь догадался, а кто убедился какая тема сегодняшнего урока?
5. Исходя из названия темы, давайте сформулируем цель нашего урока.
6. Для того, чтобы достичь цели урока, какие задачи нам надо поставить?
1.
 Решают в уме, один из учеников проговаривает ответ
Решают в уме, один из учеников проговаривает ответ2. Делают записи в тетради.
3.Учащиеся внимательно смотрят на записи, отвечая на вопросы:
- 2) На уравнения и выражения
- Нет
- Да, потому что уравнения можно решить.
4. Ребята объявляют тему урока и записывают в тетради:
«Решение уравнений».
5. Формулируют цель: познакомиться с разными видами уравнений; научиться их решать.
6. Формулируют задачи:
1)вспомнить основные понятия, свойства, которые можно отнести к уравнениям;
2)изучить материал учебника по этой теме;
3)внимательно слушать учителя;
4)делать необходимые записи в тетрадях.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстником. Логические- анализ объектов с целью выделения признаков.
4.
Изучение нового материала.
Овладеть приемами решения уравнений.

Работа с текстом. Обеспечение восприятия, осмысления и первичного запоминания детьми способов решения уравнений.
1.Подготовительный этап.
– А что значит «решить уравнение»?
– Итак, уравнение – это равенство. А в жизни мы
встречаемся с понятием равенство?
Актуализация и постановка проблемы.
– Давайте посмотрим. Весы находятся в равновесии. Что произойдет, если с одной чаши весов убрать
груз?
– А что надо сделать, чтобы весы снова оказались в
равновесии?
– Это свойство «весов» нам еще пригодится.
— Давайте вернемся к началу нашего урока. В тетрадях запишем 1 уравнение и решим его. Какие существуют способы решения данного уравнения?
— Хорошо! Давайте сначала решим уравнение, применив распределительное свойство умножения:
1 способ
5(x-3) = 20
5x-15=20
5x=20+15
5x=35
x=35:5
x=7
— А сейчас по правилу отыскания неизвестных компонентов
2 способ
5(x-3) = 20
— Что неизвестно в уравнении?
— Как найти неизвестный множитель?
x-3=20:5
x-3=4
x=4+3
x=7
-Что мы получили в итоге?
— Что называется корнем уравнения?
-Число 7 является корнем уравнения x-3=4
и уравнения 5(x-3) = 20, так как 7-3=4 и 5(7-3) = 20.

— Как из первого уравнения можно получить второе?
Мы с вами убедились, что корнем этих двух уравнений является одно и то же число. Поэтому:
Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и тоже число, не равное нулю.
2. Снова вернемся к началу урока и теперь рассмотрим второе уравнение: x+8= — 15. Как его можно решить?
Это уравнение решается с использованием зависимостей между компонентами и результатами математических действий. Но изучение отрицательных чисел дает возможность решить эти уравнения иначе.
— Вспомним, чему равна сумма противоположных чисел?
— Как можно получить в левой части уравнения только с x?
— Рассмотрим решение этих уравнений.
x+8= — 15
x= -15-8
x=-23
— Мы видим, что слагаемые без переменной перешли из левой части уравнения в правую с противоположным знаком.
— А сейчас рассмотрим третье уравнение и решим его:5х=2х+6
— Чем данное уравнение отличается от предыдущего?
— Как его можно решить?
— Нужно получить такое уравнение, чтобы слагаемые с x были только слева.
 Что для этого необходимо сделать?
Что для этого необходимо сделать?5х=2х+6
5x+ (-2x) = 6
3x=6
x=6:3
x=2
— Хорошо! Давайте рассмотрим такой вопрос: Вы собираетесь за границу. О чем в первую очередь вы должны подумать, когда пересечете границу?
— Правильно, пересекая границу, вам обязательно надо поменять паспорт.
— Давайте представим, что знак «=» — это граница, а знак числа – это ваш паспорт. Когда мы пересекаем границу, меняем паспорт, то есть, если число переносим из одной части в другую, мы должны поменять знак.
Корни уравнения не изменяются, если любое слагаемое перенести из одной части уравнения в другую, изменив при этом его знак.
1. Отвечают на вопросы:
1)Найти все значения
неизвестных, при которых оно обращается в верное равенство или установить, что таких значений нет.
2) Называют возможные варианты, например, при взвешивании
3) Чаша с гирями перевесит.
4) Убрать гири.
5)Записывают уравнение в тетрадях, предлагают варианты решения.

6)Вспоминают распределительное свойство умножения и решают уравнение в тетрадях, комментируя вместе с учителем ход решения.
7)Отвечают на вопросы: Множитель
8)Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель
9) Корень уравнения x=7
Корнем уравнения называют то значение неизвестного, при котором это уравнение обращается в верное равенство
10) Это уравнение можно получить, разделив обе части данного уравнения на 5 или умножив обе части на 1\5.
11) Записывают в тетрадях вывод.
1)Записывают уравнение в тетрадях, предлагают возможные варианты, решая уравнение
2) Нулю
3)Прибавить или отнять противоположные числам в правой части.
4) Неизвестное есть и в правой и в левой части уравнения.
5) Предлагают варианты решения уравнения
6) Для этого надо неизвестное число из правой части перенести в левую часть
7) Слушают, отвечают на вопросы.
8) Записывают в тетрадях вывод.

5
Этап первичное осмысление и закрепление знаний
Установление правильности и осознанности изучения темы.
1. Принято при решении уравнений переносить слагаемые так, чтобы в левой части уравнения были неизвестные числа, а в правой — известные числа.
Решить №1151(1-4) и 1153(1,2), 1155 с комментированием попарно.
— Решают в тетрадях, один из учеников комментирует решение с места
Регулятивные: контроль, Познавательные: умение сделать правильный выбор, Коммуникативные: управление поведением партнера, контроль
6
Повторение. Этап Закрепления изученного материала.
Выявление качества и уровня усвоения знаний и способов
действий, а также выявление недостатков в знаниях и способах действий, установление причин выявленных недостатков.

«Если вы хотите научиться плавать, то смело входите в воду
а если хотите научиться решать уравнения, РЕШАЙТЕ ИХ!»
Решить №1174 и 1175.
После самостоятельного решения (некоторые ребята, назначенные учителем решают в парах), проверяем результаты, учитель выводит верное оформление и решение на интерактивную доску.
Самостоятельное выполнение заданий с применением новых
свойств уравнений, проверяем результаты, какие получили ответы? Выясняют правильный ответ, сверяя с интерактивной доской.
Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения; Личностные: самоопределение.
7
Подведение итогов урока.
Дать качественную оценку работы класса и отдельных обучаемых
Что изучили сегодня на уроке? Вопросы 1-3 с.
 244
244Называют правила: перенос слагаемых и умножение обеих частей уравнения на одно и тоже число.
Регулятивные: оценка, осознание уровня и качества усвоения; контроль
8
Информация о домашнем задании
Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания.
Наш урок подходит к концу, с начала запишем домашнее задание, затем подведем итоги.
— На доске: Домашнее задание: §41, вопросы 1-3, № 1152(1-3), 1154(1,2), 1156
— Ваши вопросы по домашнему заданию.
Записывают домашнее задание задают вопросы если есть вопросы по заданию.
Коммуникативные: умение организовать свою работу.
9
Рефлексия
Рефлексия, мотивации их собственной деятельности и взаимодействия с учителем и другими детьми в классе.

— А теперь подведем итоги:
Что мы хотели узнать?
Что мы узнали?
На все ли вопросы мы получили ответы?
— Давайте еще раз вспомним определение уравнения, корня уравнения.
— Итог урока каждый из вас подведет с помощью телеграммы; то есть в виде одного краткого предложения, которое выразит ваше отношение к уроку.
Ученики оценивают свою работу.
1) Проводят самоанализ, отвечают на вопросы; вспоминают правила; определение уравнения, корня уравнения.
2) В конце своей работы каждый ученик пишет телеграмму. По желанию зачитывают на весь класс
Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли; Познавательные: рефлексия
Тригонометрические формулы — список всех формул: sin, cos, tg, ctg
В этой статье приведены все тригонометрические формулы и тождества (сложения, приведения, двойного угла, половинного угла, разности функций и др.
 ), при помощи которых решается наибольшая часть задач по тригонометрии. Сгруппируем эти формулы по назначению.
), при помощи которых решается наибольшая часть задач по тригонометрии. Сгруппируем эти формулы по назначению.Основные тригонометрические формулы
Тригонометрические формулы – это самые незаменимые математические выражения, необходимые для тригонометрических функций. Они выполняются для всех значений аргумента.
Для начала напомним, что синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg) – неразрывно связаны с понятием угла.
Синусом угла называется отношение противолежащего катета к гипотенузе. Следуя из этого правило, легко запомнить, что косинус угла – отношение близкого катета (прилежащего) к гипотенузе.
А вот тангенс отличается от первых двух понятиях. Это отношение дальнего к близкому катету. Котангенс с точностью да наоборот от тангенса. Котангенс – отношение близкого к дальнему катету.
Теперь перейдём непосредственно к самим формулам.
Основные формулы Эти формулы связывают синус, косинус, тангенс, котангенс одного угла. Каждая из них является следствием каких-то определений.
Эти формулы связывают синус, косинус, тангенс, котангенс одного угла. Каждая из них является следствием каких-то определений.У вышеперечисленных тождеств соотношение между синусом, косинусом, тангенсом и котангенсом одного и того же угла. Благодаря им можно выразить одну тригонометрическую функцию через любую другую.
Нужна работа? Есть решение!
Более 70 000 экспертов: преподавателей и доцентов вузов готовы помочь вам в написании работы прямо сейчас.
Подробнее Гарантии Отзывы
Формулы приведения
Формулы приведения – это формулы, при помощи которых значения тригонометрических функций аргументов выражаются через значения синуса, косинуса, тангенса и котангенса.
Формулы приведенияЛюбая из семи формул приведения может быть записана и для градусной меры угла. Чтобы использовать эти формулы, не заучивая их, нужно помнить всего лишь два правила формул приведения:
- Правило знака: с правой части формулы ставится тот знак, который имеет значение выражения в левой части при условии, что угол принадлежит I четверти.

- Правило названий: это тогда, когда в левой части формулы угол равен или . В этом случае синус меняется на косинус, а тангенс на котангенс. Так же и наоборот. Когда же угол равен или , тогда названия выражения сохраняется.
Формулы сложения для синуса, косинуса, тангенса и котангенса
Формулы сложения нужны для того, чтобы выражать функции разности или же суммы двух углов при помощи тригонометрических функций этих углов.
Формулы сложенияСинус суммы – .
Синус разности двух углов – .
Косинус суммы – .
Косинус разности – .
Тангенс суммы – .
Тангенс разности – .
Котангенс суммы – .
Котангенс разности –
Благодаря тригонометрическим формулам сложения мы можем понять, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов.
Формулы двойного угла
Формулы двойного угла – это такие формулы, которые связывают тригонометрические функции угла (синус, косинус, тангенс, котангенс) с тригонометрическими функциями угла .
Формулы двойного угла
Из формулы сложения для синуса при получим и после приведения подобных слагаемых получается первое тождество . Второе тождество получается аналогичным путём. Что касается двух последних тождеств (3 и 4), они получаются при , соответственно из формул:
Формулы половинного угла
Формулы половинного угла даны для квадратов тригонометрических функций.
Формулы половинного углаПервые две формулы (синус и косинус) справедливы любому углу . Третья формула (тангенс) предназначается для любых углов , при которых определён . И четвёртая, формула котангенса половинного угла справедлива для всех углов альфа, но при которых определён котангенс половинного угла (
Формулы понижения степени
Формулы понижения степени – это такие тригонометрические формулы, которые позволяют перейти от степеней тригонометрических функций к функциям первой степени. Однако от кратного аргумента.
Формулы понижения степениФормулы суммы и разности тригонометрических функций
Благодаря формулам суммы и разности можно легко упрощать тригонометрические выражения.
Формулы суммы и разности Кроме того, они часто используются при решении тригонометрических уравнений. Рассмотрим формулы суммы и разности.
Кроме того, они часто используются при решении тригонометрических уравнений. Рассмотрим формулы суммы и разности.Формулы произведения косинусов, синусов и синуса на косинуса
При помощи этих формул можно перейти от произведения тригонометрических функций к разности или сумме.
Формулы произведенияВсе формулы, которые переходят от произведения к сумме или разности осуществляется при помощи вышеописанных формул произведения косинусов, синусов и синус на косинус.
Универсальная тригонометрическая подстановка
Основные тригонометрические формулы завершаются такими формулами, которые выражают функции тригонометрии через тангенс половинного угла.Такая замена называется – универсальная тригонометрическая подстановка. Она очень удобно тем, что любая тригонометрическая функция выражается рационально через тангенс половинного угла без корней.
Универсальная тригонометрическая подстановкаЭти формулы выражаются через тангенс половинного угла.

Итак, мы написали самые простые и самые основные формулы, которые необходимо знать каждому учащемуся. Ведь именно при их помощи изучается тригонометрия. Кроме того, многие формулы необходимо знать для более эффективной подготовки к ЕГЭ.
Все тригонометрические формулы обновлено: 16 апреля, 2020 автором: Научные Статьи.Ру
7.3 Формулы двойного угла, полуугла и редукции — предварительное вычисление
Цели обучения
В этом разделе вы:
- Используйте формулы двойного угла, чтобы найти точные значения.
- Используйте формулы двойного угла для проверки идентичности.
- Используйте формулы сокращения, чтобы упростить выражение.
- Используйте формулы половинного угла, чтобы найти точные значения.
Рис. 1 Велосипедные пандусы для опытных райдеров имеют более крутой уклон, чем пандусы, предназначенные для новичков.
Велосипедные пандусы, изготовленные для соревнований (см.
 Рисунок 1), должны различаться по высоте в зависимости от уровня навыков участников. Для опытных спортсменов угол между рампой и землей должен составлять θθ так, чтобы tanθ = 53.tanθ = 53. Для новичков угол делится пополам. Какая крутизна ската для новичков? В этом разделе мы исследуем три дополнительные категории идентичностей, которые мы можем использовать, чтобы ответить на такие вопросы, как этот.
Рисунок 1), должны различаться по высоте в зависимости от уровня навыков участников. Для опытных спортсменов угол между рампой и землей должен составлять θθ так, чтобы tanθ = 53.tanθ = 53. Для новичков угол делится пополам. Какая крутизна ската для новичков? В этом разделе мы исследуем три дополнительные категории идентичностей, которые мы можем использовать, чтобы ответить на такие вопросы, как этот.Использование формул двойного угла для нахождения точных значений
В предыдущем разделе мы использовали формулы сложения и вычитания для тригонометрических функций.Теперь мы еще раз посмотрим на те же формулы. Формулы двойного угла являются частным случаем формул суммы, где α = β.α = β. Вывод формулы двойного угла для синуса начинается с формулы суммы
sin (α + β) = sinαcosβ + cosαsinβsin (α + β) = sinαcosβ + cosαsinβЕсли положить α = β = θ, α = β = θ, то имеем
sin (θ + θ) = sinθcosθ + cosθsinθ sin (2θ) = 2sinθcosθsin (θ + θ) = sinθcosθ + cosθsinθ sin (2θ) = 2sinθcosθПолучение двойного угла для косинуса дает нам три варианта.
cos (θ + θ) = cosθcosθ − sinθsinθ cos (2θ) = cos2θ − sin2θcos (θ + θ) = cosθcosθ − sinθsinθ cos (2θ) = cos2θ − sin2θ Во-первых, исходя из формулы суммы, cos (α + β) = cosαcosβ − sinαsinβ, cos (α + β) = cosαcosβ − sinαsinβ, и полагая α = β = θ, α = β = θ, имеем
Во-первых, исходя из формулы суммы, cos (α + β) = cosαcosβ − sinαsinβ, cos (α + β) = cosαcosβ − sinαsinβ, и полагая α = β = θ, α = β = θ, имеемИспользуя свойства Пифагора, мы можем расширить эту формулу двойного угла для косинуса и получить еще две интерпретации.Первый:
cos (2θ) = cos2θ − sin2θ = (1 − sin2θ) −sin2θ = 1−2sin2θcos (2θ) = cos2θ − sin2θ = (1 − sin2θ) −sin2θ = 1−2sin2θВторая интерпретация:
cos (2θ) = cos2θ − sin2θ = cos2θ− (1 − cos2θ) = 2cos2θ − 1cos (2θ) = cos2θ − sin2θ = cos2θ− (1 − cos2θ) = 2cos2θ − 1Аналогичным образом, чтобы вывести формулу двойного угла для касательной, замена α = β = θα = β = θ в формуле суммы дает
tan (α + β) = tanα + tanβ1 − tanαtanβtan (θ + θ) = tanθ + tanθ1 − tanθtanθtan (2θ) = 2tanθ1 − tan2θtan (α + β) = tanα + tanβ1 − tanαtanβtan (θ + θ) = tanθ + tanθ1 −tanθtanθtan (2θ) = 2tanθ1 − tan2θФормулы двойного угла
Формулы двойного угла резюмируются следующим образом:
sin (2θ) = 2sinθcosθsin (2θ) = 2sinθcosθ
cos (2θ) = cos2θ − sin2θ = 1−2sin2θ = 2cos2θ − 1cos (2θ) = cos2θ − sin2θ = 1−2sin2θ = 2cos2θ − 1
tan (2θ) = 2tanθ1 − tan2θtan (2θ) = 2tanθ1 − tan2θКак сделать
Зная тангенс угла и квадрант, в котором он расположен, используйте формулы двойного угла, чтобы найти точное значение.

- Нарисуйте треугольник, чтобы отразить данную информацию.
- Определите правильную формулу двойного угла.
- Подставить значения в формулу на основе треугольника.
- Упростить.
Пример 1
Использование формулы двойного угла для нахождения точного значения с учетом тангенса
Учитывая, что tanθ = −34tanθ = −34 и θθ находится в квадранте II, найдите следующее:
- ⓐ грех (2θ) грех (2θ)
- ⓑ cos (2θ) cos (2θ)
- ⓒ тангенс (2θ) тангенс (2θ)
Решение
Если мы нарисуем треугольник, чтобы отразить данную информацию, мы сможем найти значения, необходимые для решения проблем на изображении.Нам даны tanθ = −34, tanθ = −34, такие, что θθ находится в квадранте II. Тангенс угла равен противоположной стороне по соседней стороне, и поскольку θθ находится во втором квадранте, соседняя сторона находится на оси x и является отрицательной.
(−4) 2+ (3) 2 = c216 + 9 = c225 = c2c = 5 (−4) 2+ (3) 2 = c216 + 9 = c225 = c2c = 5 Используйте теорему Пифагора, чтобы найти длину гипотенузы:
Используйте теорему Пифагора, чтобы найти длину гипотенузы:Теперь мы можем нарисовать треугольник, похожий на один показан на рисунке 2.
Рисунок 2
- ⓐ Начнем с написания формулы двойного угла для синуса.sin (2θ) = 2sinθcosθsin (2θ) = 2sinθcosθ
Мы видим, что нам нужно найти sinθsinθ и cosθ.cosθ. Из рисунка 2 видно, что гипотенуза равна 5, поэтому sinθ = 35, sinθ = 35 и cosθ = -45. Cosθ = -45. Подставьте эти значения в уравнение и упростите.
Таким образом,
sin (2θ) = 2 (35) (- 45) = −2425 sin (2θ) = 2 (35) (- 45) = −2425 - ⓑ Напишите формулу двойного угла для косинуса.
cos (2θ) = cos2θ − sin2θcos (2θ) = cos2θ − sin2θ
Снова подставьте значения синуса и косинуса в уравнение и упростите.
cos (2θ) = (- 45) 2− (35) 2 = 1625−925 = 725 cos (2θ) = (- 45) 2− (35) 2 = 1625−925 = 725 - ⓒ Напишите формулу двойного угла для касательной.
 tan (2θ) = 2tanθ1 − tan2θtan (2θ) = 2tanθ1 − tan2θ
tan (2θ) = 2tanθ1 − tan2θtan (2θ) = 2tanθ1 − tan2θВ этой формуле нам нужен тангенс, который мы получили как tanθ = −34.tanθ = −34. Подставьте это значение в уравнение и упростите.
tan (2θ) = 2 (−34) 1 — (- 34) 2 = −321−916 = −32 (167) = −247tan (2θ) = 2 (−34) 1 — (- 34) 2 = −321 −916 = −32 (167) = −247
Попробуй # 1
Даны sinα = 58, sinα = 58, θθ в квадранте I, найти cos (2α).cos (2α).
Пример 2
Использование формулы двойного угла для косинуса без точных значений
Используйте формулу двойного угла для косинуса, чтобы записать cos (6x) cos (6x) через cos (3x) .cos (3x).
Решение
cos (6x) = cos (2 (3x + 3x)) = cos2 (3x) −sin2 (3x) = 2cos2 (3x) −1cos (6x) = cos (2 (3x + 3x)) = cos2 (3x) — sin2 (3x) = 2 cos2 (3x) −1Анализ
Этот пример показывает, что мы можем использовать формулу двойного угла, не имея точных значений.
 Он подчеркивает, что образец — это то, что нам нужно запомнить, и что идентичности верны для всех значений в области определения тригонометрической функции.
Он подчеркивает, что образец — это то, что нам нужно запомнить, и что идентичности верны для всех значений в области определения тригонометрической функции.Использование формул двойного угла для проверки идентичности
Установление тождеств с использованием формул двойного угла выполняется с использованием тех же шагов, которые мы использовали для вывода формул суммы и разности. Выберите более сложную часть уравнения и переписывайте ее, пока она не совпадет с другой стороной.
Пример 3
Использование формул двойного угла для установления идентичности
Определите следующую идентичность, используя формулы двойного угла:
1 + sin (2θ) = (sinθ + cosθ) 21 + sin (2θ) = (sinθ + cosθ) 2Решение
Мы будем работать с правой частью знака равенства и перепишем выражение, пока оно не совпадет с левой частью.
(sinθ + cosθ) 2 = sin2θ + 2sinθcosθ + cos2θ = (sin2θ + cos2θ) + 2sinθcosθ = 1 + 2sinθcosθ = 1 + sin (2θ) (sinθ + cosθ) 2 = sin2θ + 2sinθcosθ + cos2θ = (sin2θ + cos2θ) + 2sinθcosθ = 1 + 2sinθcosθ = 1 + sin (2θ)
Анализ
Этот процесс несложен, если мы вспомним формулу полного квадрата из алгебры:
(a ± b) 2 = a2 ± 2ab + b2 (a ± b) 2 = a2 ± 2ab + b2, где a = sinθa = sinθ и b = cosθ.б = cosθ. Часть успеха в математике — это способность распознавать закономерности. Хотя термины или символы могут меняться, алгебра остается непротиворечивой.
Попробуй # 2
Установите тождество: cos4θ − sin4θ = cos (2θ) .cos4θ − sin4θ = cos (2θ).
Пример 4
Проверка идентичности двойного угла по касательной
Подтвердите личность:
tan (2θ) = 2cotθ − tanθtan (2θ) = 2cotθ − tanθРешение
В этом случае мы будем работать с левой частью уравнения и упрощать или переписывать, пока она не станет равной правой части уравнения.
tan (2θ) = 2tanθ1 − tan2θ Формула двойного угла = 2tanθ (1tanθ) (1 − tan2θ) (1tanθ) Умножьте на член, который дает желаемый числитель. = 21tanθ − tan2θtanθ = 2cotθ − tanθ Используйте обратное тождество для 1tanθ.tan (2θ) = 2tanθ1 − tan2θ Формула двойного угла = 2tanθ (1tanθ) (1 − tan2θ) (1tanθ) Умножьте на член, который дает желаемый числитель. = 21tanθ − tan2θtanθ = 2cotθ − tanθ Используйте обратное тождество для 1tanθ.
Анализ
Вот случай, когда более сложная часть исходного уравнения появилась справа, но мы решили работать с левой стороной.Однако, если бы мы выбрали левую сторону для переписывания, мы бы работали в обратном направлении, чтобы прийти к эквивалентности. Например, предположим, что мы хотим показать
2tanθ1 − tan2θ = 2cotθ − tanθ2tanθ1 − tan2θ = 2cotθ − tanθДавайте работать над правой стороной.
2cotθ − tanθ = 21tanθ − tanθ (tanθtanθ) = 2tanθ1tanθ (tanθ) −tanθ (tanθ) = 2tanθ1 − tan2θ2cotθ − tanθ = 21tanθ − tanθ (tanθtanθ) = 2tanθ1tanθ (tanθ) −tanθ (tanθ) = 2tanθ1 − tan2θПри использовании тождеств для упрощения тригонометрического выражения или решения тригонометрического уравнения обычно существует несколько путей к желаемому результату.
 Не существует установленного правила относительно того, какой стороной следует манипулировать. Однако начать следует с изложенных ранее рекомендаций.
Не существует установленного правила относительно того, какой стороной следует манипулировать. Однако начать следует с изложенных ранее рекомендаций.Попробуй # 3
Проверьте тождество: cos (2θ) cosθ = cos3θ − cosθsin2θ.cos (2θ) cosθ = cos3θ − cosθsin2θ.
Использование формул сокращения для упрощения выражения
Формулы двойного угла можно использовать для вывода формул редукции, которые представляют собой формулы, которые мы можем использовать для уменьшения мощности данного выражения, включающего четные степени синуса или косинуса.Они позволяют нам переписать четные степени синуса или косинуса в терминах первой степени косинуса. Эти формулы особенно важны на курсах математики более высокого уровня, в частности, в математическом анализе. Также называемые формулами уменьшения мощности, включены три тождества, которые легко выводятся из формул двойного угла.
Мы можем использовать две из трех формул двойного угла для косинуса, чтобы получить формулы приведения для синуса и косинуса.
cos (2θ) = 1−2sin2θ2sin2θ = 1 − cos (2θ) sin2θ = 1 − cos (2θ) 2cos (2θ) = 1−2sin2θ2sin2θ = 1 − cos (2θ) sin2θ = 1 − cos (2θ) 2 Начнем с cos (2θ) = 1−2sin2θ.cos (2θ) = 1−2sin2θ.Решить относительно sin2θ: sin2θ:
Начнем с cos (2θ) = 1−2sin2θ.cos (2θ) = 1−2sin2θ.Решить относительно sin2θ: sin2θ:Далее мы используем формулу cos (2θ) = 2cos2θ − 1.cos (2θ) = 2cos2θ − 1. Решить относительно cos2θ: cos2θ:
cos (2θ) = 2cos2θ − 11 + cos (2θ) = 2cos2θ1 + cos (2θ) 2 = cos2θ cos (2θ) = 2cos2θ − 11 + cos (2θ) = 2cos2θ1 + cos (2θ) 2 = cos2θПоследняя формула редукции получается записью тангенса через синус и косинус:
tan2θ = sin2θcos2θ = 1 − cos (2θ) 21 + cos (2θ) 2 Подставим формулы редукции.= (1 − cos (2θ) 2) (21 + cos (2θ)) = 1 − cos (2θ) 1 + cos (2θ) tan2θ = sin2θcos2θ = 1 − cos (2θ) 21 + cos (2θ) 2 Подставим сокращение формулы. = (1 − cos (2θ) 2) (21 + cos (2θ)) = 1 − cos (2θ) 1 + cos (2θ)Формулы приведения
Краткое изложение формул сокращения:
sin2θ = 1 − cos (2θ) 2 sin2θ = 1 − cos (2θ) 2 cos2θ = 1 + cos (2θ) 2cos2θ = 1 + cos (2θ) 2 tan2θ = 1 − cos (2θ) 1 + cos (2θ) tan2θ = 1 − cos (2θ) 1 + cos (2θ)Пример 5
Написание эквивалентного выражения, не содержащего степени больше 1
Напишите эквивалентное выражение для cos4xcos4x, которое не включает никакие степени синуса или косинуса больше 1.

Решение
Мы применим формулу приведения косинуса дважды.
cos4x = (cos2x) 2 = (1 + cos (2x) 2) 2 Формула сокращения для cos2x. = 14 (1 + 2cos (2x) + cos2 (2x)) = 14 + 12cos (2x) +14 (1 + cos2 (2x) 2) Подставляем формулу сокращения для cos2x. = 14 + 12cos (2x) + 18 + 18cos (4x) = 38 + 12cos (2x) + 18cos (4x) cos4x = (cos2x) 2 = (1 + cos (2x) 2) 2 Подставляем формулу сокращения для cos2x. = 14 (1 + 2cos (2x) + cos2 (2x)) = 14 + 12cos (2x) +14 (1 + cos2 (2x) 2) Подставляем формулу сокращения для cos2x.= 14 + 12cos (2x) + 18 + 18cos (4x) = 38 + 12cos (2x) + 18cos (4x)Анализ
Решение находится путем использования формулы редукции дважды, как уже отмечалось, и формулы полного квадрата из алгебры.
Пример 6
Использование формул уменьшения мощности для подтверждения личности
Используйте формулы уменьшения мощности, чтобы доказать
sin3 (2x) = [12sin (2x)] [1 − cos (4x)] sin3 (2x) = [12sin (2x)] [1 − cos (4x)]Решение
Мы будем работать над упрощением левой части уравнения:
sin3 (2x) = [sin (2x)] [sin2 (2x)] = sin (2x) [1 − cos (4x) 2] Подставьте формулу уменьшения мощности. = sin (2x) (12) [1 − cos (4x)] = 12 [sin (2x)] [1 − cos (4x)] sin3 (2x) = [sin (2x)] [sin2 (2x)] = sin (2x) [1 − cos (4x) 2] Подставим формулу уменьшения мощности. = sin (2x) (12) [1 − cos (4x)] = 12 [sin (2x)] [1 − cos (4x)]
= sin (2x) (12) [1 − cos (4x)] = 12 [sin (2x)] [1 − cos (4x)] sin3 (2x) = [sin (2x)] [sin2 (2x)] = sin (2x) [1 − cos (4x) 2] Подставим формулу уменьшения мощности. = sin (2x) (12) [1 − cos (4x)] = 12 [sin (2x)] [1 − cos (4x)]Анализ
Обратите внимание, что в этом примере мы заменили
для sin2 (2x) .sin2 (2x). В формуле указано
sin2θ = 1 − cos (2θ) 2 sin2θ = 1 − cos (2θ) 2Положим θ = 2x, θ = 2x, поэтому 2θ = 4x.2θ = 4x.
Попробуй # 4
Используйте формулы уменьшения мощности, чтобы доказать, что 10cos4x = 154 + 5cos (2x) + 54cos (4x). 10cos4x = 154 + 5cos (2x) + 54cos (4x).
Использование формул полуугла для нахождения точных значений
Следующий набор тождеств — это набор формул половинного угла, который может быть получен из формул редукции и мы можем использовать, когда у нас есть угол, который составляет половину размера специального угла.
 Если мы заменим θθ на α2, α2, формула половинного угла для синуса будет найдена путем упрощения уравнения и решения для sin (α2).грех (α2). Обратите внимание, что перед формулами полуугла стоит знак ± ±. Это не означает, что допустимы как положительные, так и отрицательные выражения. Скорее, это зависит от квадранта, в котором заканчивается α2α2.
Если мы заменим θθ на α2, α2, формула половинного угла для синуса будет найдена путем упрощения уравнения и решения для sin (α2).грех (α2). Обратите внимание, что перед формулами полуугла стоит знак ± ±. Это не означает, что допустимы как положительные, так и отрицательные выражения. Скорее, это зависит от квадранта, в котором заканчивается α2α2.Формула половинного угла для синуса получается следующим образом:
sin2θ = 1 − cos (2θ) 2sin2 (α2) = 1 − cos (2⋅α2) 2 = 1 − cosα2sin (α2) = ± 1 − cosα2 sin2θ = 1 − cos (2θ) 2sin2 (α2) = 1 − cos (2⋅α2) 2 = 1 − cosα2sin (α2) = ± 1 − cosα2Чтобы вывести формулу половинного угла для косинуса, мы имеем
cos2θ = 1 + cos (2θ) 2cos2 (α2) = 1 + cos (2⋅α2) 2 = 1 + cosα2 cos (α2) = ± 1 + cosα2 cos2θ = 1 + cos (2θ) 2cos2 (α2) = 1 + cos (2⋅α2) 2 = 1 + cosα2 cos (α2) = ± 1 + cosα2Для касательной идентичности имеем
tan2θ = 1 − cos (2θ) 1 + cos (2θ) tan2 (α2) = 1 − cos (2⋅α2) 1 + cos (2⋅α2) = 1 − cosα1 + cosα tan (α2) = ± 1 − cosα1 + cosα tan2θ = 1 − cos (2θ) 1 + cos (2θ) tan2 (α2) = 1 − cos (2⋅α2) 1 + cos (2⋅α2) = 1 − cosα1 + cosα tan (α2) = ± 1 −cosα1 + cosαФормулы полуугловых
Формулы половинного угла следующие:
sin (α2) = ± 1 − cosα2sin (α2) = ± 1 − cosα2 cos (α2) = ± 1 + cosα2cos (α2) = ± 1 + cosα2 tan (α2) = ± 1 − cosα1 + cosα = sinα1 + cosα = 1 − cosαsinαtan (α2) = ± 1 − cosα1 + cosα = sinα1 + cosα = 1 − cosαsinαПример 7
Использование формулы полуугла для нахождения точного значения синусоидальной функции
Найдите sin (15∘) sin (15∘) по формуле половинного угла.

Решение
Так как 15∘ = 30∘2,15∘ = 30∘2, мы используем формулу полуугла для синуса:
sin30∘2 = 1 − cos30∘2 = 1−322 = 2−322 = 2−34 = 2−32sin30∘2 = 1 − cos30∘2 = 1−322 = 2−322 = 2−34 = 2−32Анализ
Обратите внимание, что мы использовали только положительный корень, потому что sin (15o) sin (15o) положительный.
Как к
Зная тангенс угла и квадрант, в котором находится угол, найдите точные значения тригонометрических функций половины угла.
- Нарисуйте треугольник для представления данной информации.
- Определите правильную формулу полуугла.
- Подставить значения в формулу на основе треугольника.
- Упростить.
Пример 8
Нахождение точных значений с использованием идентичностей половинных углов
Учитывая, что tanα = 815tanα = 815 и αα лежит в квадранте III, найдите точное значение следующего:
- ⓐ sin (α2) sin (α2)
- ⓑ cos (α2) cos (α2)
- ⓒ тангенс (α2) загар (α2)
Решение
Используя данную информацию, мы можем нарисовать треугольник, показанный на рисунке 3.
 Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить sinα = −817sinα = −817 и cosα = −1517.cosα = −1517.
Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить sinα = −817sinα = −817 и cosα = −1517.cosα = −1517.Рисунок 3
- ⓐПрежде чем мы начнем, мы должны помнить, что если αα находится в квадранте III, то 180 ° <α <270 °, 180 ° <α <270 °, поэтому 180 ° 2 <α2 <270 ° 2,180 ° 2 <α2 <270 ° 2. Это означает, что конечная сторона α2α2 находится во втором квадранте, поскольку 90 ° <α2 <135 ° .90 ° <α2 <135 °.
Чтобы найти sinα2, sinα2, мы начнем с написания формулы половинного угла для синуса.Затем мы подставляем значение косинуса, которое мы нашли из треугольника на рисунке 3, и упрощаем.
sinα2 = ± 1 − cosα2 = ± 1 — (- 1517) 2 = ± 32172 = ± 3217⋅12 = ± 1617 = ± 417 = 41717 sinα2 = ± 1 − cosα2 = ± 1 — (- 1517) 2 = ± 32172 = ± 3217⋅12 = ± 1617 = ± 417 = 41717Мы выбираем положительное значение sinα2sinα2, потому что угол заканчивается во втором квадранте, а синус положительный во втором квадранте.

- ⓑ Чтобы найти cosα2, cosα2, мы напишем формулу половинного угла для косинуса, подставим значение косинуса, которое мы нашли из треугольника на рисунке 3, и упростим.cosα2 = ± 1 + cosα2 = ± 1 + (- 1517) 2 = ± 2172 = ± 217⋅12 = ± 117 = −1717 cosα2 = ± 1 + cosα2 = ± 1 + (- 1517) 2 = ± 2172 = ± 217⋅ 12 = ± 117 = −1717
Мы выбираем отрицательное значение cosα2cosα2, потому что угол находится в квадранте II, потому что косинус отрицателен в квадранте II.
- ⓒ Чтобы найти tanα2, tanα2, запишем формулу полуугла для тангенса. Опять же, мы подставляем значение косинуса, которое мы нашли из треугольника на рисунке 3, и упрощаем.tanα2 = ± 1 − cosα1 + cosα = ± 1 — (- 1517) 1 + (- 1517) = ± 3217217 = ± 322 = −16 = −4tanα2 = ± 1 − cosα1 + cosα = ± 1 — (- 1517) 1 + (- 1517) = ± 3217217 = ± 322 = −16 = −4
Мы выбрали отрицательное значение tanα2tanα2, потому что α2α2 лежит в квадранте II, а касательная отрицательна в квадранте II.
Попробуй # 5
Учитывая, что sinα = −45sinα = −45 и αα лежит в квадранте IV, найдите точное значение cos (α2) .
 cos (α2).
cos (α2).Пример 9
Определение размера половины угла
Теперь вернемся к задаче, поставленной в начале раздела. Велосипедная рампа сконструирована для соревнований высокого уровня с углом θθ, образованным рампой и землей. Другой пандус будет построен наполовину крутым для соревнований новичков. Если tanθ = 53tanθ = 53 для соревнований более высокого уровня, каков угол для соревнований новичков?
Решение
Поскольку угол для соревнований новичков измеряет половину крутизны угла для соревнований высокого уровня, а tanθ = 53tanθ = 53 для соревнований высокого уровня, мы можем найти cosθcosθ из прямоугольного треугольника и теоремы Пифагора, чтобы мы могли использовать полуугловые тождества.См. Рисунок 4.
32 + 52 = 34 c = 3432 + 52 = 34 c = 34Рисунок 4
Мы видим, что cosθ = 334 = 33434.
tanθ2 = 1−334341 + 33434 = 34−3343434 + 33434 = 34−33434 + 334 ≈0,57tanθ2 = 1−334341 + 33434 = 34−3343434 + 33434 = 34−33434 + 334 ≈0,57 cosθ = 334 = 33434. Мы можем использовать формулу половинного угла для касательной: tanθ2 = 1 − cosθ1 + cosθ.tanθ2 = 1 − cosθ1 + cosθ. Поскольку tanθtanθ находится в первом квадранте, tanθ2.tanθ2 тоже. Таким образом,
cosθ = 334 = 33434. Мы можем использовать формулу половинного угла для касательной: tanθ2 = 1 − cosθ1 + cosθ.tanθ2 = 1 − cosθ1 + cosθ. Поскольку tanθtanθ находится в первом квадранте, tanθ2.tanθ2 тоже. Таким образом,. найти угол: tan − 1 (0.57) ≈29,7∘.tan − 1 (0,57) ≈29,7∘. Таким образом, угол наклона рампы для соревнований новичков составляет ≈29,7∘.≈29,7∘.
7.3 Упражнения по разделам
Устные
1.Объясните, как определить тождества редукции из тождества с двойным углом cos (2x) = cos2x − sin2x.cos (2x) = cos2x − sin2x.
2.Объясните, как определить формулу двойного угла для tan (2x) tan (2x), используя формулы двойного угла для cos (2x) cos (2x) и sin (2x) .sin (2x).
3.Мы можем определить формулу полуугла для tan (x2) = 1 − cosx1 + cosxtan (x2) = 1 − cosx1 + cosx, разделив формулу для sin (x2) sin (x2) на cos (x2).
4. соз (х2). Объясните, как определить две формулы для tan (x2) tan (x2)
которые не содержат квадратных корней.
соз (х2). Объясните, как определить две формулы для tan (x2) tan (x2)
которые не содержат квадратных корней.Для формулы половинного угла, приведенной в предыдущем упражнении для tan (x2), tan (x2), объясните, почему деление на 0 не имеет значения. (Подсказка: проверьте значения cosxcosx, необходимые для того, чтобы знаменатель был равен 0.)
Алгебраический
Для следующих упражнений найдите точные значения a) sin (2x), sin (2x), b) cos (2x), cos (2x) и c) tan (2x) tan (2x) без решение для xx
5.Если sinx = 18, sinx = 18 и xx находится в квадранте I.
6.Если cosx = 23, cosx = 23 и xx находится в квадранте I.
7.Если cosx = −12, cosx = −12 и xx находится в квадранте III.
8.Если tanx = −8, tanx = −8 и xx находится в квадранте IV.
Для следующих упражнений найдите значения шести тригонометрических функций, если указанные условия выполнены.
9.
cos (2θ) = 35cos (2θ) = 35 и 90∘≤θ≤180∘90∘≤θ≤180∘
10.cos (2θ) = 12cos (2θ) = 12 и 180∘≤θ≤270∘180∘≤θ≤270∘
Упростите следующие упражнения до одного тригонометрического выражения.
11.2sin (π4) 2cos (π4) 2sin (π4) 2cos (π4)
12.4sin (π8) cos (π8) 4sin (π8) cos (π8)
Для следующих упражнений найдите точное значение, используя формулы половинного угла.
14.cos (−11π12) cos (−11π12)
18.тангенс (-3π12) тангенс (-3π12)
Для следующих упражнений найдите точные значения a) sin (x2), sin (x2), b) cos (x2), cos (x2) и c) tan (x2) tan (x2) без решения относительно x. ,Икс, когда 0∘≤x≤360∘0∘≤x≤360∘
20.Если tanx = −43, tanx = −43, а xx находится в квадранте IV.
21.Если sinx = −1213, sinx = −1213 и xx находится в квадранте III.
22.
Если cscx = 7, cscx = 7, а xx находится в квадранте II.
23.Если secx = −4, secx = −4 и xx находится в квадранте II.
Для следующих упражнений используйте Рисунок 5, чтобы найти требуемые половинные и двойные углы.
Рисунок 5
24.Найдите sin (2θ), cos (2θ), sin (2θ), cos (2θ) и tan (2θ) .tan (2θ).
25.Найдите sin (2α), cos (2α), sin (2α), cos (2α) и tan (2α) .tan (2α).
26.Найдите sin (θ2), cos (θ2), sin (θ2), cos (θ2) и tan (θ2) .tan (θ2).
27.Найдите sin (α2), cos (α2), sin (α2), cos (α2) и tan (α2) .tan (α2).
Для следующих упражнений упростите каждое выражение. Не оценивайте.
28.cos2 (28∘) −sin2 (28∘) cos2 (28∘) −sin2 (28∘)
29.2cos2 (37∘) −12cos2 (37∘) −1
30.1−2sin2 (17∘) 1−2sin2 (17∘)
31.cos2 (9x) −sin2 (9x) cos2 (9x) −sin2 (9x)
32.
4sin (8x) cos (8x) 4sin (8x) cos (8x)
33.6sin (5x) cos (5x) 6sin (5x) cos (5x)
Для следующих упражнений подтвердите свою личность.
34.(sint − cost) 2 = 1 − sin (2t) (sint − cost) 2 = 1 − sin (2t)
35.sin (2x) = — 2sin (−x) cos (−x) sin (2x) = — 2sin (−x) cos (−x)
36.cotx − tanx = 2cot (2x) cotx − tanx = 2cot (2x)
37.1 + cos (2θ) sin (2θ) tan2θ = tanθ1 + cos (2θ) sin (2θ) tan2θ = tanθ
Для следующих упражнений перепишите выражение с показателем степени не выше 1.
Технологии
Для следующих упражнений сократите уравнения до степени единицы, а затем проверьте ответ графически.
Для следующих упражнений алгебраически найдите эквивалентную функцию только в терминах sinxsinx и / или cosx, cosx, а затем проверьте ответ, построив графики обоих уравнений.

Расширения
Для следующих упражнений подтвердите личность.
55.sin (2x) = 2tanx1 + tan2xsin (2x) = 2tanx1 + tan2x
56.cos (2α) = 1 − tan2α1 + tan2αcos (2α) = 1 − tan2α1 + tan2α
57.tan (2x) = 2sinxcosx2cos2x − 1tan (2x) = 2sinxcosx2cos2x − 1
58.(sin2x − 1) 2 = cos (2x) + sin4x (sin2x − 1) 2 = cos (2x) + sin4x.
59.sin (3x) = 3sinxcos2x − sin3xsin (3x) = 3sinxcos2x − sin3x
60.cos (3x) = cos3x − 3sin2xcosxcos (3x) = cos3x − 3sin2xcosx
61.1 + cos (2t) sin (2t) −cost = 2cost2sint − 11 + cos (2t) sin (2t) −cost = 2cost2sint − 1
62.sin (16x) = 16sinxcosxcos (2x) cos (4x) cos (8x) sin (16x) = 16sinxcosxcos (2x) cos (4x) cos (8x)
63.cos (16x) = (cos2 (4x) −sin2 (4x) −sin (8x)) (cos2 (4x) −sin2 (4x) + sin (8x)) cos (16x) = (cos2 (4x) −sin2 (4x) −sin (8x)) (cos2 (4x) −sin2 (4x) + sin (8x))
4.
 2 (α / 2) = (1 — cos α) / 2`
2 (α / 2) = (1 — cos α) / 2`Решение дает нам следующий синус для тождества полуугла :
`sin (альфа / 2) = + — sqrt ((1-cos alpha) / 2`
Знак (положительный или отрицательный) sin (alpha / 2) зависит от квадранта. в котором лежит `α / 2`.
Если «α / 2» находится в первом или втором квадранте , формула использует положительный случай:
`sin (alpha / 2) = sqrt (1-cos alpha) / 2`
Если α / 2 находится в третьем или четвертом квадранте , в формуле используется отрицательный регистр:
`sin (alpha / 2) = — sqrt (1-cos alpha) / 2`
Формула полуугла — косинус
Используя аналогичный процесс, с той же заменой `theta = alpha / 2` (таким образом, 2 θ = α ) мы подставляем в тождество
cos 2 θ = 2cos 2 θ — 1 (см.
 2 (альфа / 2) = (1 + cos alpha) / 2`
2 (альфа / 2) = (1 + cos alpha) / 2`Решая относительно cos (α / 2), получаем:
`cos (альфа / 2) = + — sqrt ((1 + cos alpha) / 2`
Как и раньше, нужный нам знак зависит от квадранта.
Если α / 2 находится в первом или четвертом квадранте , формула использует положительный случай:
`cos (альфа / 2) = sqrt ((1 + cos alpha) / 2`
Если α / 2 находится во втором или третьем квадранте , в формуле используется отрицательный регистр:
`cos (альфа / 2) = — sqrt ((1 + cos alpha) / 2`
Формула полуугла — касательная
Тангенс половины угла определяется по формуле:
`tan (alpha / 2) = (1-cos alpha) / (sin alpha)`
Проба
Сначала напомним `tan x = (sin x) / (cos x)`.2а)) `
Затем находим квадратный корень:
`= (1-cos a) / (sin a)`
Конечно, нам нужно будет делать поправку на положительные и отрицательные знаки, в зависимости от рассматриваемого квадранта.
 @`, используя соотношение половинного угла синуса, приведенное выше.(текст (o))) / 2) `
@`, используя соотношение половинного угла синуса, приведенное выше.(текст (o))) / 2) ``= + — sqrt (((1 + 0.866)) / 2)`
`= 0,9659`
Первый квадрант, значит, это положительный результат.
2. Найдите значение sin (alpha / 2), если cos alpha = 12/13, где 0 ° < α <90 °.
Ответ
`sin (альфа / 2) = + — sqrt ((1-cos alpha) / 2)`
`= sqrt ((1-12 / 13) / 2)`
`= sqrt ((1/13) / 2)`
`= sqrt (1/26)`
`= 0,1961`
Мы выбираем позитив, потому что находимся в первом квадранте.2сек \ theta`
`= (1 + cos theta) sec \ theta`
`= (1 + cos theta) 1 / (cos theta)`
`= сек \ тета + 1`
`=» RHS «`
9.3: Формулы двойного, полууглового и редукционного
Цели обучения
- Используйте формулы двойного угла, чтобы найти точные значения
- Используйте формулы двойного угла для проверки идентичности
- Использование формул сокращения для упрощения выражения
- Используйте формулы половинного угла, чтобы найти точные значения
Велосипедные пандусы, изготовленные для соревнований (см.
Рисунок \ (\ PageIndex {1} \): Велосипедные пандусы для опытных райдеров имеют более крутой уклон, чем те, что предназначены для новичков. Рисунок \ (\ PageIndex {1} \)), должны различаться по высоте в зависимости от уровня навыков участников.Для опытных участников угол между рампой и землей должен быть \ (\ theta \) таким, чтобы \ (\ tan \ theta = \ dfrac {5} {3} \). Для новичков угол делится пополам. Какая крутизна ската для новичков? В этом разделе мы исследуем три дополнительные категории идентичностей, которые мы можем использовать, чтобы ответить на такие вопросы, как этот.
Рисунок \ (\ PageIndex {1} \)), должны различаться по высоте в зависимости от уровня навыков участников.Для опытных участников угол между рампой и землей должен быть \ (\ theta \) таким, чтобы \ (\ tan \ theta = \ dfrac {5} {3} \). Для новичков угол делится пополам. Какая крутизна ската для новичков? В этом разделе мы исследуем три дополнительные категории идентичностей, которые мы можем использовать, чтобы ответить на такие вопросы, как этот.Использование формул двойного угла для поиска точных значений
В предыдущем разделе мы использовали формулы сложения и вычитания для тригонометрических функций.Теперь мы еще раз посмотрим на те же формулы. Формулы двойного угла являются частным случаем формул суммы, где \ (\ alpha = \ beta \). Вывод формулы двойного угла для синуса начинается с формулы суммы
\ [\ sin (\ alpha + \ beta) = \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta \]
Если мы положим \ (\ alpha = \ beta = \ theta \), то у нас будет
\ [\ begin {align *} \ sin (\ theta + \ theta) & = \ sin \ theta \ cos \ theta + \ cos \ theta \ sin \ theta \\ [4pt] \ sin (2 \ theta) & = 2 \ sin \ theta \ cos \ theta \ end {align *} \]
Получение двойного угла для косинуса дает нам три варианта.
 2 \ theta} \ end {align} \]
2 \ theta} \ end {align} \]Как сделать: учитывая тангенс угла и квадрант, в котором он расположен, используйте формулы двойного угла, чтобы найти точное значение
- Нарисуйте треугольник, чтобы отразить данную информацию.
- Определите правильную формулу двойного угла.
- Подставить значения в формулу на основе треугольника.
- Упростить.
Пример \ (\ PageIndex {1} \): Использование формулы двойного угла для нахождения точного значения с использованием тангенса
Учитывая, что \ (\ tan \ theta = — \ dfrac {3} {4} \) и \ (\ theta \) находится в квадранте II, найдите следующее:
- \ (\ sin (2 \ theta) \)
- \ (\ соз (2 \ тета) \)
- \ (\ загар (2 \ тета) \)
Решение
Если мы нарисуем треугольник, чтобы отразить данную информацию, мы сможем найти значения, необходимые для решения проблем на изображении.
 2 \\ [4pt] c & = 5 \ end {align *} \]
2 \\ [4pt] c & = 5 \ end {align *} \]Теперь мы можем нарисовать треугольник, подобный показанному на рисунке \ (\ PageIndex {2} \).
Рисунок \ (\ PageIndex {2} \)- Начнем с написания формулы двойного угла для синуса.
\ (\ sin (2 \ theta) = 2 \ sin \ theta \ cos \ theta \)
Мы видим, что нам нужно найти \ (\ sin \ theta \) и \ (\ cos \ theta \). Основываясь на рисунке \ (\ PageIndex {2} \), мы видим, что гипотенуза равна \ (5 \), поэтому \ (\ sin θ = 35 \), \ (\ sin θ = 35 \) и \ (\ cos θ = −45 \).2} \\ [4pt]
& = \ dfrac {- \ dfrac {3} {2}} {1- \ dfrac {9} {16}} \\ [4pt]
& = — \ dfrac {3} { 2} \ left (\ dfrac {16} {7} \ right) \\ [4pt]
& = — \ dfrac {24} {7}
\ end {align *} \]
Упражнение \ (\ PageIndex {1} \)
Учитывая \ (\ sin \ alpha = \ dfrac {5} {8} \), с \ (\ theta \) в квадранте I, найдите \ (\ cos (2 \ alpha) \).
- Ответ
\ (\ cos (2 \ alpha) = \ dfrac {7} {32} \)
Пример \ (\ PageIndex {2} \): использование формулы двойного угла для косинуса без точных значений
Используйте формулу двойного угла для косинуса, чтобы записать \ (\ cos (6x) \) через \ (cos (3x) \).
 2 3x \ end {align *} \]
2 3x \ end {align *} \]Анализ
Этот пример показывает, что мы можем использовать формулу двойного угла, не имея точных значений. Он подчеркивает, что образец — это то, что нам нужно запомнить, и что идентичности верны для всех значений в области определения тригонометрической функции.
Использование формул двойного угла для проверки личности
Установление тождеств с использованием формул двойного угла выполняется с использованием тех же шагов, которые мы использовали для вывода формул суммы и разности.2 \ theta} {\ tan \ theta}} \\ [4pt] & = \ dfrac {2} {\ cot \ theta- \ tan \ theta} \ qquad \ text {Используйте обратную идентичность для} \ dfrac {1} { \ tan \ theta} \ end {align *} \]
Анализ
Вот случай, когда более сложная часть исходного уравнения появилась справа, но мы решили работать с левой стороной. Однако, если бы мы выбрали левую сторону для переписывания, мы бы работали в обратном направлении, чтобы прийти к эквивалентности.
 2 \ theta} \ end {align *} \]
2 \ theta} \ end {align *} \]При использовании тождеств для упрощения тригонометрического выражения или решения тригонометрического уравнения обычно существует несколько путей к желаемому результату.2 \ тета \)
Использование формул сокращения для упрощения выражения
Формулы двойного угла можно использовать для получения формул редукции , , которые являются формулами, которые мы можем использовать для уменьшения степени данного выражения, включающего четные степени синуса или косинуса. Они позволяют нам переписать четные степени синуса или косинуса в терминах первой степени косинуса. Эти формулы особенно важны на курсах математики более высокого уровня, в частности, в математическом анализе. Также называемые формулами уменьшения мощности, включены три тождества, которые легко выводятся из формул двойного угла.2 x \\ [4pt]
& = \ dfrac {1} {4} + \ dfrac {1} {2} \ cos (2x) + \ dfrac {1} {8} + \ dfrac {1} {8} \ cos (4x) \\ [4pt]
& = \ dfrac {3} {8} + \ dfrac {1} {2} \ cos (2x) + \ dfrac {1} {8} \ cos (4x)
\ end {align *} \]Анализ
Решение находится путем использования формулы редукции дважды, как уже отмечалось, и формулы полного квадрата из алгебры. 2 (2x)] \\ [4pt] & = \ sin (2x) \ left [\ dfrac {1- \ cos (4x)} {2} \ right] \ qquad \ text {Подставьте формулу уменьшения мощности.2 x \\ [4pt] & = \ dfrac {10} {4} + \ dfrac {10} {2} \ cos (2x) + \ dfrac {10} {8} + \ dfrac {10} {8} \ cos (4x) \\ [4pt] & = \ dfrac {30} {8} +5 \ cos (2x) + \ dfrac {10} {8} \ cos (4x) \\ [4pt] & = \ dfrac { 15} {4} +5 \ cos (2x) + \ dfrac {5} {4} \ cos (4x) \ end {align *} \]
Использование формул полуугла для нахождения точных значений
Следующий набор идентичностей — это набор формул полууглов , которые могут быть получены из формул редукции и мы можем использовать, когда у нас есть угол, который составляет половину размера специального угла.Если мы заменим \ (\ theta \) на \ (\ dfrac {\ alpha} {2} \), формула полуугла для синуса будет найдена путем упрощения уравнения и решения для \ (\ sin \ left (\ dfrac { \ alpha} {2} \ right) \). Обратите внимание, что перед формулами полуугла стоит знак \ (\ pm \). 2 \ left (\ dfrac {\ alpha} {2} \ right) & = \ dfrac {1- \ cos \ left (2 \ cdot \ dfrac {\ alpha} {2} \ right)} {1+ \ cos \ left (2 \ cdot \ dfrac {\ alpha} {2} \ right)} \\ [4pt] \ tan \ left (\ dfrac {\ alpha} {2} \ right) & = \ pm \ sqrt {\ dfrac {1- \ cos \ alpha} {1+ \ cos \ alpha}} \ end {align *} \]
ПОЛУУГОЛЬНЫЕ ФОРМУЛЫ
Формулы полуугла следующие:
\ [\ begin {align} \ sin \ left (\ dfrac {\ alpha} {2} \ right) & = \ pm \ sqrt {\ dfrac {1- \ cos \ alpha} {2}} \ label {полусинус } \\ [4pt] \ cos \ left (\ dfrac {\ alpha} {2} \ right) & = \ pm \ sqrt {\ dfrac {1+ \ cos \ alpha} {2}} \\ [4pt] \ загар \ left (\ dfrac {\ alpha} {2} \ right) & = \ pm \ sqrt {\ dfrac {1- \ cos \ alpha} {1+ \ cos \ alpha}} = \ dfrac {\ sin \ alpha } {1+ \ cos \ alpha} = \ dfrac {1- \ cos \ alpha} {\ sin \ alpha} \ end {align} \]
Пример \ (\ PageIndex {7} \)
Использование формулы полуугла для нахождения точного значения синусоидальной функции.{\ circ}} {2}} \\ [4pt]
& = \ sqrt {\ dfrac {1- \ dfrac {\ sqrt {3}} {2}} {2}} \\ [4pt]
& = \ sqrt {\ dfrac {\ dfrac {2- \ sqrt {3}} {2}} {2}} \\ [4pt]
& = \ sqrt {\ dfrac {2- \ sqrt {3}} {4} } \\ [4pt]
& = \ dfrac {\ sqrt {2- \ sqrt {3}}} {2}
\ end {align *} \]Помните, что мы можем проверить ответ с помощью графического калькулятора.
Анализ
Обратите внимание, что мы использовали только положительный корень, потому что \ (\ sin (15 °) \) положительный.
Howto: Зная тангенс угла и квадрант, в котором находится угол, найдите точные значения тригонометрических функций половины угла.
- Нарисуйте треугольник для представления данной информации.
- Определите правильную формулу полуугла.
- Подставить значения в формулу на основе треугольника.
- Упростить.
Пример \ (\ PageIndex {8} \): поиск точных значений с использованием половинных углов
Учитывая, что \ (\ tan \ alpha = \ dfrac {8} {15} \) и \ (α \) лежит в квадранте III, найдите точное значение следующего:
- \ (\ sin \ left (\ dfrac {\ alpha} {2} \ right) \)
- \ (\ cos \ left (\ dfrac {\ alpha} {2} \ right) \)
- \ (\ tan \ left (\ dfrac {\ alpha} {2} \ right) \)
Решение
Используя данную информацию, мы можем нарисовать треугольник, показанный на рисунке \ (\ PageIndex {3} \).Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить \ (\ sin \ alpha = — \ dfrac {8} {17} \) и \ (\ cos \ alpha = — \ dfrac {15} {17} \).
Рисунок \ (\ PageIndex {3} \)- Прежде чем мы начнем, мы должны помнить, что если \ (α \) находится в квадранте III, то \ (180 ° <\ alpha <270 ° \), поэтому \ (\ dfrac {180 °} {2} <\ dfrac {\ alpha} {2} <\ dfrac {270 °} {2} \). Это означает, что конечная сторона \ (\ dfrac {\ alpha} {2} \) находится в квадранте II, поскольку \ (90 ° <\ dfrac {\ alpha} {2} <135 ° \). Чтобы найти \ (\ sin \ dfrac {\ alpha} {2} \), мы начнем с написания формулы половинного угла для синуса.Затем мы подставляем значение косинуса, которое мы нашли из треугольника на рисунке \ (\ PageIndex {3} \), и упрощаем. \ [\ begin {align *} \ sin \ dfrac {\ alpha} {2} & = \ pm \ sqrt {\ dfrac {1- \ cos \ alpha} {2}} \\ [4pt] & = \ pm \ sqrt {\ dfrac {1 - (- \ dfrac {15} {17})} {2}} \\ [4pt] & = \ pm \ sqrt {\ dfrac {\ dfrac {32} {17}} {2} } \\ [4pt] & = \ pm \ sqrt {\ dfrac {32} {17} \ cdot \ dfrac {1} {2}} \\ [4pt] & = \ pm \ sqrt {\ dfrac {16} { 17}} \\ [4pt] & = \ pm \ dfrac {4} {\ sqrt {17}} \\ [4pt] & = \ dfrac {4 \ sqrt {17}} {17} \ end {align *} \] Мы выбираем положительное значение \ (\ sin \ dfrac {\ alpha} {2} \), потому что угол заканчивается в квадранте II, а синус положительный в квадранте II.
- Чтобы найти \ (\ cos \ dfrac {\ alpha} {2} \), мы напишем формулу половинного угла для косинуса, подставив значение косинуса, которое мы нашли из треугольника на рисунке \ (\ PageIndex {3} \) и упростить. \ [\ begin {align *} \ cos \ dfrac {\ alpha} {2} & = \ pm \ sqrt {\ dfrac {1+ \ cos \ alpha} {2}} \\ [4pt] & = \ pm \ sqrt {\ dfrac {1+ \ left (- \ dfrac {15} {17} \ right)} {2}} \\ [4pt] & = \ pm \ sqrt {\ dfrac {\ dfrac {2} {17} } {2}} \\ [4pt] & = \ pm \ sqrt {\ dfrac {2} {17} \ cdot \ dfrac {1} {2}} \\ [4pt] & = \ pm \ sqrt {\ dfrac {1} {17}} \\ [4pt] & = — \ dfrac {\ sqrt {17}} {17} \ end {align *} \] Выбираем отрицательное значение \ (\ cos \ dfrac {\ alpha } {2} \), потому что угол находится в квадранте II, потому что косинус отрицателен в квадранте II.
- Чтобы найти \ (\ tan \ dfrac {\ alpha} {2} \), мы записываем формулу полуугла для касательной. Опять же, мы подставляем значение косинуса, которое мы нашли из треугольника на рисунке \ (\ PageIndex {3} \), и упрощаем. \ [\ begin {align *} \ tan \ dfrac {\ alpha} {2} & = \ pm \ sqrt {\ dfrac {1- \ cos \ alpha} {1+ \ cos \ alpha}} \\ [4pt] & = \ pm \ sqrt {\ dfrac {1- \ left (- \ dfrac {15} {17} \ right)} {1+ \ left (- \ dfrac {15} {17} \ right)}} \\ [4pt] & = \ pm \ sqrt {\ dfrac {\ dfrac {32} {17}} {\ dfrac {2} {17}}} \\ [4pt] & = \ pm \ sqrt {\ dfrac {32} {2}} \\ [4pt] & = — \ sqrt {16} \\ [4pt] & = -4 \ end {align *} \] Выбираем отрицательное значение \ (\ tan \ dfrac {\ alpha} {2} \), потому что \ (\ dfrac {\ alpha} {2} \) лежит в квадранте II, а касательная отрицательна в квадранте II.
Упражнение \ (\ PageIndex {5} \)
Учитывая, что \ (\ sin \ alpha = — \ dfrac {4} {5} \) и \ (\ alpha \) лежит в квадранте IV, найдите точное значение \ (\ cos \ left (\ dfrac {\ alpha } {2} \ right) \).
- Ответ
\ (- \ dfrac {2} {\ sqrt {5}} \)
Пример \ (\ PageIndex {9} \): определение размера половины угла
Теперь вернемся к задаче, поставленной в начале раздела. Велосипедная рампа построена для соревнований высокого уровня с углом \ (θ \), образованным рампой и землей.Другой пандус будет построен наполовину крутым для соревнований новичков. Если \ (tan θ = 53 \) для соревнований более высокого уровня, каков угол для соревнований новичков?
Решение
Поскольку угол для соревнований новичков измеряет половину крутизны угла для соревнований высокого уровня и \ (\ tan \ theta = \ dfrac {5} {3} \) для соревнований высокого уровня, мы можем найти \ (\ cos \ theta \) из прямоугольного треугольника и теоремы Пифагора, так что мы можем использовать тождества полууглов.2 & = 34 \\ [4pt] c & = \ sqrt {34} \ end {align *} \]
Рисунок \ (\ PageIndex {4} \)Мы видим, что \ (\ cos \ theta = \ dfrac {3} {\ sqrt {34}} = \ dfrac {3 \ sqrt {34}} {34} \). Мы можем использовать формулу половинного угла для касательной: \ (\ tan \ dfrac {\ theta} {2} = \ sqrt {\ dfrac {1− \ cos \ theta} {1+ \ cos \ theta}} \). Поскольку \ (\ tan \ theta \) находится в первом квадранте, то же самое и \ (\ tan \ dfrac {\ theta} {2} \).
\ [\ begin {align *}
\ tan \ dfrac {\ theta} {2} & = \ sqrt {\ dfrac {1- \ dfrac {3 \ sqrt {34}} {34}} {1+ \ dfrac {3 \ sqrt {34}} {34}}} \\ [4pt]
& = \ sqrt {\ dfrac {\ dfrac {34-3 \ sqrt {34}} {34}} {\ dfrac {34 + 3 \ sqrt {34}} {34}}} \\ [4pt]
& = \ sqrt {\ dfrac {34-3 \ sqrt {34}} {34 + 3 \ sqrt {34}}} \\ [4pt]
& \ около 0.{−1} (0,57) ≈29,7 ° \). Таким образом, угол пандуса для соревнований новичков равен \ (≈29,7 ° \).СМИ
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с формулами двойного угла, половинного угла и редукции.
- Двойные углы идентификации
- Полуугловые идентичности
Ключевые уравнения
Формулы двойного угла
\ (\ sin (2 \ theta) = 2 \ sin \ theta \ cos \ theta \)
\ (\ cos (2 \ theta) = {\ cos} ^ 2 \ theta — {\ sin} ^ 2 \ theta \)
\ (= 1-2 {\ sin} ^ 2 \ theta \)
\ (= 2 {\ cos} ^ 2 \ theta − 1 \)
\ (\ tan (2 \ theta) = \ dfrac {2 \ tan \ theta} {1 — {\ tan} ^ 2 \ theta} \)
Формулы приведения
\ ({\ sin} ^ 2 \ theta = \ dfrac {1- \ cos (2 \ theta)} {2} \)
\ ({\ cos} ^ 2 \ theta = \ dfrac {1+ \ cos (2 \ theta)} {2} \)
\ ({\ tan} ^ 2 \ theta = \ dfrac {1- \ cos (2 \ theta)} {1+ \ cos (2 \ theta)} \)
Формулы полууглов
\ (\ sin \ dfrac {\ alpha} {2} = \ pm \ sqrt {\ dfrac {1− \ cos \ alpha} {2}} \)
\ (\ cos \ dfrac {\ alpha} {2} = \ pm \ sqrt {\ dfrac {1+ \ cos \ alpha} {2}} \)
\ (\ tan \ dfrac {\ alpha} {2} = \ pm \ sqrt {\ dfrac {1− \ cos \ alpha} {1+ \ cos \ alpha}} \)
\ (= \ dfrac {\ sin \ alpha} {1+ \ cos \ alpha} \)
\ (= \ dfrac {1− \ cos \ alpha} {\ sin \ alpha} \)
Ключевые понятия
- Двойные угловые тождества выводятся из формул суммы основных тригонометрических функций: синуса, косинуса и тангенса.См. Пример \ (\ PageIndex {1} \), Пример \ (\ PageIndex {2} \), Пример \ (\ PageIndex {3} \) и Пример \ (\ PageIndex {4} \).
- Формулы редукции особенно полезны в исчислении, поскольку они позволяют уменьшить степень тригонометрического члена. См. Пример \ (\ PageIndex {5} \) и Пример \ (\ PageIndex {6} \).
- Формулы полууглов позволяют нам найти значение тригонометрических функций, включающих полууглы, независимо от того, известен ли исходный угол или нет. См. Пример \ (\ PageIndex {7} \), Пример \ (\ PageIndex {8} \) и Пример \ (\ PageIndex {9} \).
Авторы и авторство
Тригонометрические идентичности полууглов — Формулы и вывод тригонометрических полууглов
Идентификаторы половинного угла триггера или функции, фактически участвующие в тех тригонометрических функциях, которые содержат в себе половинные углы. Квадратный корень из первых двух функций синуса и косинуса, отрицательного или положительного, полностью зависит от наличия угла в квадранте. Узнайте больше о Trig Identities в trigidentities.Информация.
А вот и исчерпывающая таблица, которая ясно показывает тождества половинного угла всех основных тригонометрических тождеств. Узнайте больше о Идентификаторы обратного триггера .
Вывод тождеств полуугловых триггеров
Сегодня мы выведем следующие тригонометрические формулы полуугла.
Формула полуугла — синус- cos 2 θ = 1− 2sin2 θ
Теперь, если допустим
, затем 2 θ = α и наша формула принимает следующий вид:
Теперь решаем
- Sin (α / 2)
- 2 sin 2 ( 2 α ) = 1 − cos α
- sin ˆ 2 (2 α ) = 1 — cos α
Решение дает нам следующий синус для тождества полуугла :
Теперь поговорим о положительном или отрицательном знаке Sin (α / 2).
- Если угол лежит в первом квадранте, то все положительные значения означают, что идентичность синусоидального полуугла будет положительной.
- И если он находится в квадранте 3 rd или 4 rd , мы введем отрицательный знак с тождеством половины угла синуса.
Просто используя аналогичный процесс, с теми же заменами, что и выше. Теперь мы должны подставить эти значения в следующий идентификатор Trig.
- cos 2 θ = 2cos 2 θ — 1
После подстановки значений We
- Cos α = 2 cosˆ2 (α / 2) -1 —– (1)
Теперь вам нужно перевернуть уравнение.
Обратное уравнение:
- 2 cosˆ2 (α / 2) -1 = Cos α —– (2)
Сложите уравнение (1) и (2)
Разделить на 2 с обеих сторон
Взяв квадратный корень с обеих сторон, мы получили формулу половинного угла косинуса теперь
давайте поговорим о положительном или отрицательном знаке косинуса (α / 2).
- Если угол лежит в первом или четвертом квадранте, то косинус (α / 2) будет положительным
- И если он находится в квадранте 2 nd или 3 rd , мы введем отрицательный знак с тождеством половины угла косинуса.
Сводка тригонометрических отождествлений
За последние несколько страниц вы видели довольно много тригонометрических отождествлений. Для справки удобно иметь их краткое изложение. Эти тождества в основном относятся к одному углу, обозначенному θ , но есть некоторые, которые включают два угла, и для них два угла обозначены α и β . Более важные личности.
Необязательно знать все личности с головы до ног. Но вы должны это сделать.Определение соотношений для тангенса, котангенса, секанса и косеканса в терминах синуса и косинуса. Формула Пифагора для синусов и косинусов. Это, наверное, самая важная триггерная идентичность. Тождества, выражающие триггерные функции в терминах их дополнений. В этом нет ничего особенного. Каждая из шести триггерных функций равна своей совместной функции, оцениваемой под дополнительным углом. Периодичность триггерных функций. Синус, косинус, секанс и косеканс имеют период 2 π , а тангенс и котангенс имеют период π . Обозначения для отрицательных углов. Синус, тангенс, котангенс и косеканс являются нечетными функциями, а косинус и секанс — четными функциями. Тождества Птолемея, формулы суммы и разности для синуса и косинуса. Формулы двойного угла для синуса и косинуса. Обратите внимание, что существует три формы формулы двойного угла для косинуса. Вам нужно знать только одно, но уметь вывести два других из формулы Пифагора. Менее важные личности.
Вы должны знать, что эти личности есть, но они не так важны, как упомянутые выше. Все они могут быть получены из вышеперечисленных, но иногда для этого требуется немного поработать.Формула Пифагора для касательных и секущих. Есть еще один для котангенсов и косекансов, но поскольку котангенсы и косекансы нужны редко, в нем нет необходимости. Тождества, выражающие триггерные функции в терминах их дополнений. Формулы суммы, разности и двойного угла для касательной. Формулы половинных углов. Для синуса и косинуса берут положительный или отрицательный квадратный корень в зависимости от квадранта угла θ /2. Например, если θ /2 — острый угол, тогда будет использоваться положительный корень. Действительно неясные личности.
Они здесь как раз для извращенности. Нет, не совсем. У них есть несколько приложений, но обычно это узкие приложения, и о них также можно забыть, пока они не понадобятся.Идентификаторы продукта-суммы. Эта группа идентичностей позволяет вам преобразовать сумму или разность синусов или косинусов в произведение синусов и косинусов. Идентификационные данные продукта. Кроме того: как ни странно, эти идентификаторы продуктов использовались до изобретения логарифмов для выполнения умножения. Вот как можно использовать второй. Если вы хотите умножить x на y, используйте таблицу, чтобы найти угол α , косинус которого равен x , и угол β , косинус которого равен y . Найдите косинусы суммы α + β .а разность α — β . Усредните эти два косинуса. Вы получаете товар xy ! Три просмотра таблиц и вычисление суммы, разницы и среднего, а не одно умножение. Тихо Браге (1546–1601), среди прочих, использовал этот алгоритм, известный как простафаэрез . Формулы тройного угла. Вы можете легко восстановить их по формулам сложения и двойного угла. Еще формулы полууглов. Они описывают основные триггерные функции в терминах тангенса половины угла. Они используются в исчислении для особого вида подстановки в интегралах, иногда называемой подстановкой Вейерштрасса t . Двойной угол, половина угла и формулы редукции
Использование формул двойного угла для поиска точных значений
В предыдущем разделе мы использовали формулы сложения и вычитания для тригонометрических функций.Теперь мы еще раз посмотрим на те же формулы. Формулы двойного угла являются частным случаем формул суммы, где [latex] \ alpha = \ beta [/ latex]. Вывод формулы двойного угла для синуса начинается с формулы суммы
[латекс] \ sin \ left (\ alpha + \ beta \ right) = \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta [/ latex]
Если мы допустим [latex] \ alpha = \ beta = \ theta [/ latex], то у нас будет
[латекс] \ begin {array} {l} \ sin \ left (\ theta + \ theta \ right) = \ sin \ theta \ cos \ theta + \ cos \ theta \ sin \ theta \ hfill \\ \ text { } \ sin \ left (2 \ theta \ right) = 2 \ sin \ theta \ cos \ theta \ hfill \ end {array} [/ latex]
Получение двойного угла для косинуса дает нам три варианта.{2} \ theta} [/ латекс]
Как сделать: учитывая тангенс угла и квадрант, в котором он расположен, используйте формулы двойного угла, чтобы найти точное значение.
- Нарисуйте треугольник, чтобы отразить данную информацию.
- Определите правильную формулу двойного угла.
- Подставить значения в формулу на основе треугольника.
- Упростить.
Пример 1: Использование формулы двойного угла для нахождения точного значения с использованием тангенса
Учитывая, что [латекс] \ tan \ theta = — \ frac {3} {4} [/ latex] и [latex] \ theta [/ latex] находится во втором квадранте, найдите следующее:
- [латекс] \ sin \ left (2 \ theta \ right) [/ latex]
- [латекс] \ cos \ left (2 \ theta \ right) [/ латекс]
- [латекс] \ загар \ влево (2 \ тета \ вправо) [/ латекс]
Решение
Если мы нарисуем треугольник, чтобы отразить данную информацию, мы сможем найти значения, необходимые для решения проблем на изображении.{2} \\ \ hfill c = 5 \ text {} \ end {array} [/ latex]
Теперь мы можем нарисовать треугольник, подобный изображенному на рисунке 2.
Рисунок 2
- Начнем с написания формулы двойного угла для синуса.
[латекс] \ sin \ left (2 \ theta \ right) = 2 \ sin \ theta \ cos \ theta [/ latex]
Мы видим, что нам нужно найти [латекс] \ sin \ theta [/ latex] и [latex] \ cos \ theta [/ latex]. Из рисунка 2 видно, что гипотенуза равна 5, поэтому [latex] \ sin \ theta = \ frac {3} {5} [/ latex] и [latex] \ cos \ theta = — \ frac {4} {5} [/ латекс].{2}} \ hfill \\ \ text {} = \ frac {- \ frac {3} {2}} {1- \ frac {9} {16}} \ hfill \\ \ text {} = — \ frac {3} {2} \ left (\ frac {16} {7} \ right) \ hfill \\ \ text {} = — \ frac {24} {7} \ hfill \ end {array} [/ latex]
Попробуйте 1
Учитывая [латекс] \ sin \ alpha = \ frac {5} {8} [/ latex], с [latex] \ theta [/ latex] в квадранте I, найдите [latex] \ cos \ left (2 \ alpha \ справа) [/ латекс].
Решение
Пример 2: Использование формулы двойного угла для косинуса без точных значений
Используйте формулу двойного угла для косинуса, чтобы записать [латекс] \ cos \ left (6x \ right) [/ latex] в терминах [latex] \ cos \ left (3x \ right) [/ latex].{2} 3x \ hfill \ end {array} [/ latex]
Анализ решения
Этот пример показывает, что мы можем использовать формулу двойного угла, не имея точных значений. Он подчеркивает, что образец — это то, что нам нужно запомнить, и что идентичности верны для всех значений в области определения тригонометрической функции.
Использование формул двойного угла для проверки личности
Установление тождеств с использованием формул двойного угла выполняется с использованием тех же шагов, которые мы использовали для вывода формул суммы и разности.{4} \ theta = \ cos \ left (2 \ theta \ right) [/ latex].
Решение
Пример 4: Проверка идентичности двойного угла для касательной
Подтвердите личность:
[латекс] \ tan \ left (2 \ theta \ right) = \ frac {2} {\ cot \ theta — \ tan \ theta} [/ latex]
Решение
В этом случае мы будем работать с левой частью уравнения и упрощать или переписывать, пока она не станет равной правой части уравнения. {2} \ theta} = \ frac {2} {\ cot \ theta — \ tan \ theta} [/ latex]
Давайте работать над правой стороной.{2} \ theta [/ латекс].
Решение
Использование формул сокращения для упрощения выражения
Формулы двойного угла могут использоваться для вывода формул редукции , которые представляют собой формулы, которые мы можем использовать для уменьшения степени данного выражения, включающего четные степени синуса или косинуса. Они позволяют нам переписать четные степени синуса или косинуса в терминах первой степени косинуса. Эти формулы особенно важны на курсах математики более высокого уровня, в частности, в математическом анализе.{2} \ theta} \ hfill & \ hfill \\ \ text {} = \ frac {\ frac {1- \ cos \ left (2 \ theta \ right)} {2}} {\ frac {1+ \ cos \ left (2 \ theta \ right)} {2}} \ hfill & \ text {Подставьте формулы редукции.} \ hfill \\ \ text {} = \ left (\ frac {1- \ cos \ left (2 \ theta \ right)} {2} \ right) \ left (\ frac {2} {1+ \ cos \ left (2 \ theta \ right)} \ right) \ begin {array} {cccc} & & & \ end {массив} \ hfill & \ hfill \\ \ text {} = \ frac {1- \ cos \ left (2 \ theta \ right)} {1+ \ cos \ left (2 \ theta \ right)} \ hfill & \ hfill \ end {array} [/ latex]
A Общее примечание: формулы приведения
Формулы редукции резюмируются следующим образом:
[латекс] {\ sin} ^ {2} \ theta = \ frac {1- \ cos \ left (2 \ theta \ right)} {2} [/ latex]
[латекс] {\ cos} ^ {2} \ theta = \ frac {1+ \ cos \ left (2 \ theta \ right)} {2} [/ latex]
[латекс] {\ tan} ^ {2} \ theta = \ frac {1- \ cos \ left (2 \ theta \ right)} {1+ \ cos \ left (2 \ theta \ right)} [/ латекс ]
Пример 5: Написание эквивалентного выражения, не содержащего степени больше 1
Напишите эквивалентное выражение для [latex] {\ cos} ^ {4} x [/ latex], которое не включает никаких степеней синуса или косинуса больше 1. {2} \ left (2x \ right) \ right] \ hfill & \ hfill \\ \ text {} = \ sin \ left (2x \ right) \ left [\ frac {1- \ cos \ left (4x \ right)} {2} \ right] \ hfill & \ text {Подставить формулу уменьшения мощности}.{4} x = \ frac {15} {4} +5 \ cos \ left (2x \ right) + \ frac {5} {4} \ cos \ left (4x \ right) [/ latex].
Решение
Использование формул полуугла для нахождения точных значений
Следующий набор идентичностей — это набор формул полууглов , которые могут быть получены из формул редукции и мы можем использовать, когда у нас есть угол, который составляет половину размера специального угла. Если мы заменим [latex] \ theta [/ latex] на [latex] \ frac {\ alpha} {2} [/ latex], формула половинного угла для синуса будет найдена путем упрощения уравнения и решения для [latex] \ sin \ left (\ frac {\ alpha} {2} \ right) [/ latex].{2} \ left (\ frac {\ alpha} {2} \ right) = \ frac {1- \ cos \ left (2 \ cdot \ frac {\ alpha} {2} \ right)} {1+ \ cos \ left (2 \ cdot \ frac {\ alpha} {2} \ right)} \ hfill \\ \ text {} = \ frac {1- \ cos \ alpha} {1+ \ cos \ alpha} \ hfill \\ \ text {} \ tan \ left (\ frac {\ alpha} {2} \ right) = \ pm \ sqrt {\ frac {1- \ cos \ alpha} {1+ \ cos \ alpha}} \ hfill \ end {array} [/ latex]
A Общее примечание: формулы полуугловых
Формулы полуугла следующие:
[латекс] \ sin \ left (\ frac {\ alpha} {2} \ right) = \ pm \ sqrt {\ frac {1- \ cos \ alpha} {2}} [/ latex]
[латекс] \ cos \ left (\ frac {\ alpha} {2} \ right) = \ pm \ sqrt {\ frac {1+ \ cos \ alpha} {2}} [/ latex]
[латекс] \ begin {array} {l} \ tan \ left (\ frac {\ alpha} {2} \ right) = \ pm \ sqrt {\ frac {1- \ cos \ alpha} {1+ \ cos \ alpha}} \ hfill \\ = \ frac {\ sin \ alpha} {1+ \ cos \ alpha} \ hfill \\ = \ frac {1- \ cos \ alpha} {\ sin \ alpha} \ hfill \ end {array} [/ latex]
Пример 7: Использование формулы полуугла для нахождения точного значения синусоидальной функции
Найдите [латекс] \ sin \ left ({15} ^ {\ circ} \ right) [/ latex] по формуле половинного угла.{\ text {o}} \ right) [/ latex] положительный.
Как: по тангенсу угла и квадранту, в котором находится угол, найдите точные значения тригонометрических функций половины угла.
- Нарисуйте треугольник для представления данной информации.
- Определите правильную формулу полуугла.
- Подставить значения в формулу на основе треугольника.
- Упростить.
Пример 8: Нахождение точных значений с использованием идентичностей половинных углов
Учитывая, что [latex] \ tan \ alpha = \ frac {8} {15} [/ latex] и [latex] \ alpha [/ latex] находится в квадранте III, найдите точное значение следующего:
- [латекс] \ sin \ left (\ frac {\ alpha} {2} \ right) [/ latex]
- [латекс] \ cos \ left (\ frac {\ alpha} {2} \ right) [/ latex]
- [латекс] \ tan \ left (\ frac {\ alpha} {2} \ right) [/ latex]
Решение
Используя данную информацию, мы можем нарисовать треугольник, показанный на рисунке 3.\ circ [/latex]. Чтобы найти [latex] \ sin \ frac {\ alpha} {2} [/ latex], мы начинаем с написания формулы половинного угла для синуса. Затем мы подставляем значение косинуса, которое мы нашли из треугольника на рисунке 3, и упрощаем.
[латекс] \ begin {массив} {l} \ begin {array} {l} \\ \ sin \ frac {\ alpha} {2} = \ pm \ sqrt {\ frac {1- \ cos \ alpha} { 2}} \ end {array} \ hfill \\ \ text {} = \ pm \ sqrt {\ frac {1- \ left (- \ frac {15} {17} \ right)} {2}} \ hfill \ \ \ text {} = \ pm \ sqrt {\ frac {\ frac {32} {17}} {2}} \ hfill \\ \ text {} = \ pm \ sqrt {\ frac {32} {17} \ cdot \ frac {1} {2}} \ hfill \\ \ text {} = \ pm \ sqrt {\ frac {16} {17}} \ hfill \\ \ text {} = \ pm \ frac {4} { \ sqrt {17}} \ hfill \\ \ text {} = \ frac {4 \ sqrt {17}} {17} \ hfill \ end {array} [/ latex]
Мы выбираем положительное значение [latex] \ sin \ frac {\ alpha} {2} [/ latex], потому что угол заканчивается в квадранте II, а синус положительный в квадранте II.
-
- Чтобы найти [latex] \ cos \ frac {\ alpha} {2} [/ latex], мы напишем формулу половинного угла для косинуса, подставим значение косинуса, которое мы нашли из треугольника на рисунке 3, и упростим .
[латекс] \ begin {массив} {l} \ begin {array} {l} \ hfill \\ \ hfill \\ \ cos \ frac {\ alpha} {2} = \ pm \ sqrt {\ frac {1+ \ cos \ alpha} {2}} \ hfill \ end {array} \ hfill \\ \ text {} = \ pm \ sqrt {\ frac {1+ \ left (- \ frac {15} {17} \ right) } {2}} \ hfill \\ \ text {} = \ pm \ sqrt {\ frac {\ frac {2} {17}} {2}} \ hfill \\ \ text {} = \ pm \ sqrt {\ frac {2} {17} \ cdot \ frac {1} {2}} \ hfill \\ \ text {} = \ pm \ sqrt {\ frac {1} {17}} \ hfill \\ \ text {} = — \ frac {\ sqrt {17}} {17} \ hfill \ end {array} [/ latex]
Мы выбираем отрицательное значение [latex] \ cos \ frac {\ alpha} {2} [/ latex], потому что угол находится в квадранте II, потому что косинус отрицателен в квадранте II.
- Чтобы найти [latex] \ tan \ frac {\ alpha} {2} [/ latex], мы записываем формулу половинного угла для касательной. Опять же, мы подставляем значение косинуса, которое мы нашли из треугольника на рисунке 3, и упрощаем.
[латекс] \ begin {массив} {l} \ begin {array} {l} \ hfill \\ \ tan \ frac {\ alpha} {2} = \ pm \ sqrt {\ frac {1- \ cos \ alpha } {1+ \ cos \ alpha}} \ hfill \ end {array} \ hfill \\ \ text {} = \ pm \ sqrt {\ frac {1- \ left (- \ frac {15} {17} \ right )} {1+ \ left (- \ frac {15} {17} \ right)}} \ hfill \\ \ text {} = \ pm \ sqrt {\ frac {\ frac {32} {17}} {\ frac {2} {17}}} \ hfill \\ \ text {} = \ pm \ sqrt {\ frac {32} {2}} \ hfill \\ \ text {} = — \ sqrt {16} \ hfill \ \ \ text {} = — 4 \ hfill \ end {array} [/ latex]
Мы выбираем отрицательное значение [latex] \ tan \ frac {\ alpha} {2} [/ latex], потому что [latex] \ frac {\ alpha} {2} [/ latex] лежит в квадранте II, а касательная отрицательный в квадранте II.
Попробовать 5
Учитывая, что [latex] \ sin \ alpha = — \ frac {4} {5} [/ latex] и [latex] \ alpha [/ latex] находится в квадранте IV, найдите точное значение [latex] \ cos \ left (\ frac {\ alpha} {2} \ right) [/ latex].
Решение
Пример 9: Определение размера половины угла
Теперь вернемся к задаче, поставленной в начале раздела. Велосипедная рампа предназначена для соревнований высокого уровня с углом [латекс] \ тета [/ латекс], образованным рампой и землей.Другой пандус будет построен наполовину крутым для соревнований новичков. Если [latex] \ tan \ theta = \ frac {5} {3} [/ latex] для соревнований более высокого уровня, каков угол для соревнований новичков?
Решение
Поскольку угол для соревнований новичков измеряет половину крутизны угла для соревнований высокого уровня и [латекс] \ tan \ theta = \ frac {5} {3} [/ latex] для соревнований высокого уровня, мы можем найти [латекс ] \ cos \ theta [/ latex] из прямоугольного треугольника и теоремы Пифагора, так что мы можем использовать тождества половинного угла.{2} = 34 \ hfill \\ \ text {} c = \ sqrt {34} \ hfill \ end {array} [/ latex]
Рисунок 4
Мы видим, что [latex] \ cos \ theta = \ frac {3} {\ sqrt {34}} = \ frac {3 \ sqrt {34}} {34} [/ latex]. Мы можем использовать формулу половинного угла для касательной: [латекс] \ tan \ frac {\ theta} {2} = \ sqrt {\ frac {1- \ cos \ theta} {1+ \ cos \ theta}} [/ латекс]. Поскольку [latex] \ tan \ theta [/ latex] находится в первом квадранте, то же самое и [latex] \ tan \ frac {\ theta} {2} [/ latex]. Таким образом,
[латекс] \ begin {массив} {l} \ begin {array} {l} \ hfill \\ \ hfill \\ \ tan \ frac {\ theta} {2} = \ sqrt {\ frac {1- \ frac {3 \ sqrt {34}} {34}} {1+ \ frac {3 \ sqrt {34}} {34}}} \ hfill \ end {array} \ hfill \\ \ text {} = \ sqrt {\ frac {\ frac {34 — 3 \ sqrt {34}} {34}} {\ frac {34 + 3 \ sqrt {34}} {34}}} \ hfill \\ \ text {} = \ sqrt {\ frac {34 — 3 \ sqrt {34}} {34 + 3 \ sqrt {34}}} \ hfill \\ \ text {} \ приблизительно 0.{2} \ theta = \ frac {1- \ cos \ left (2 \ theta \ right)} {1+ \ cos \ left (2 \ theta \ right)} \ end {array} [/ latex]
Ключевые понятия
- Двойные угловые тождества выводятся из формул суммы основных тригонометрических функций: синуса, косинуса и тангенса.
- Формулы редукции особенно полезны в исчислении, поскольку они позволяют уменьшить степень тригонометрического члена.
- Формулы полууглов позволяют нам найти значение тригонометрических функций, включающих полууглы, независимо от того, известен ли исходный угол или нет.
Глоссарий
- формулы двойного угла
- тождеств, полученных из формул суммы для синуса, косинуса и тангенса, в которых углы равны
- формулы половинного угла
- тождеств, полученных из формул приведения и используемых для определения значений половинного угла тригонометрических функций
- формулы восстановления
- тождеств, полученных из формул двойного угла и используемых для уменьшения мощности тригонометрической функции
Упражнения по разделам
1.{2} х [/ латекс].
2. Объясните, как определить формулу двойного угла для [латекса] \ tan \ left (2x \ right) [/ latex], используя формулы двойного угла для [latex] \ cos \ left (2x \ right) [/ латекс] и [латекс] \ sin \ left (2x \ right) [/ latex].
3. Мы можем определить формулу половинного угла для [латекс] \ tan \ left (\ frac {x} {2} \ right) = \ frac {\ sqrt {1- \ cos x}} {\ sqrt {1 + \ cos x}} [/ latex], разделив формулу для [latex] \ sin \ left (\ frac {x} {2} \ right) [/ latex] на [latex] \ cos \ left (\ frac { x} {2} \ right) [/ latex].Объясните, как определить две формулы для [latex] \ tan \ left (\ frac {x} {2} \ right) [/ latex], которые не содержат квадратных корней.
4. Для формулы половинного угла, приведенной в предыдущем упражнении для [latex] \ tan \ left (\ frac {x} {2} \ right) [/ latex], объясните, почему деление на 0 не имеет значения. (Подсказка: проверьте значения [латекс] \ cos x [/ latex], необходимые для того, чтобы знаменатель был равен 0.)
Для следующих упражнений найдите точные значения a) [латекс] \ sin \ left (2x \ right) [/ latex], b) [latex] \ cos \ left (2x \ right) [/ latex] и c) [latex] \ tan \ left (2x \ right) [/ latex] без решения для [latex] x [/ latex].
5. Если [латекс] \ sin x = \ frac {1} {8} [/ latex], а [latex] x [/ latex] находится в квадранте I.
6. Если [латекс] \ cos x = \ frac {2} {3} [/ latex], а [latex] x [/ latex] находится в квадранте I.
7. Если [латекс] \ cos x = — \ frac {1} {2} [/ latex], а [latex] x [/ latex] находится в квадранте III.
8. Если [латекс] \ tan x = -8 [/ latex], а [latex] x [/ latex] находится в квадранте IV.
Для следующих упражнений найдите значения шести тригонометрических функций, если указанные условия выполнены.
9.{\ circ} [/ латекс]
Упростите следующие упражнения до одного тригонометрического выражения.
11. [латекс] 2 \ sin \ left (\ frac {\ pi} {4} \ right) 2 \ cos \ left (\ frac {\ pi} {4} \ right) [/ latex]
12. [латекс] 4 \ sin \ left (\ frac {\ pi} {8} \ right) \ cos \ left (\ frac {\ pi} {8} \ right) [/ latex]
Для следующих упражнений найдите точное значение, используя формулы половинного угла.
13. [латекс] \ sin \ left (\ frac {\ pi} {8} \ right) [/ latex]
14. [латекс] \ cos \ left (- \ frac {11 \ pi} {12} \ right) [/ latex]
15.[латекс] \ sin \ left (\ frac {11 \ pi} {12} \ right) [/ latex]
16. [латекс] \ cos \ left (\ frac {7 \ pi} {8} \ right) [/ latex]
17. [латекс] \ tan \ left (\ frac {5 \ pi} {12} \ right) [/ latex]
18. [латекс] \ tan \ left (- \ frac {3 \ pi} {12} \ right) [/ latex]
19. [латекс] \ tan \ left (- \ frac {3 \ pi} {8} \ right) [/ latex]
Для следующих упражнений найдите точные значения a) [latex] \ sin \ left (\ frac {x} {2} \ right) [/ latex], b) [latex] \ cos \ left (\ frac { x} {2} \ right) [/ latex] и c) [latex] \ tan \ left (\ frac {x} {2} \ right) [/ latex] без решения для [latex] x [/ latex] .
20. Если [латекс] \ tan x = — \ frac {4} {3} [/ latex], а [latex] x [/ latex] находится в квадранте IV.
21. Если [латекс] \ sin x = — \ frac {12} {13} [/ latex], а [latex] x [/ latex] находится в квадранте III.
22. Если [латекс] \ csc x = 7 [/ latex], а [latex] x [/ latex] находится в квадранте II.
23. Если [латекс] \ sec x = -4 [/ latex], а [latex] x [/ latex] находится в квадранте II.
Для следующих упражнений используйте Рисунок 5, чтобы найти требуемые половинные и двойные углы.
Рисунок 5
24.Найдите [латекс] \ sin \ left (2 \ theta \ right), \ cos \ left (2 \ theta \ right) [/ latex] и [latex] \ tan \ left (2 \ theta \ right) [/ latex ].
25. Найдите [латекс] \ sin \ left (2 \ alpha \ right), \ cos \ left (2 \ alpha \ right) [/ latex] и [latex] \ tan \ left (2 \ alpha \ right). [/латекс].
26. Найдите [латекс] \ sin \ left (\ frac {\ theta} {2} \ right), \ cos \ left (\ frac {\ theta} {2} \ right) [/ latex] и [латекс ] \ tan \ left (\ frac {\ theta} {2} \ right) [/ latex].
27. Найдите [латекс] \ sin \ left (\ frac {\ alpha} {2} \ right), \ cos \ left (\ frac {\ alpha} {2} \ right) [/ latex] и [латекс ] \ tan \ left (\ frac {\ alpha} {2} \ right) [/ latex].2} \ frac {\ alpha} {2} = \ frac {{1 — \ cos \ alpha}} {2},} \; \; \ Rightarrow {\ left | {\ sin \ frac {\ alpha} {2}} \ right | = \ sqrt {\ frac {{1 — \ cos \ alpha}} {2}},} \; \; \ Rightarrow {\ sin \ frac {\ alpha} {2} = \ pm \ sqrt {\ frac {{1 — \ cos \ alpha}} {2}}.} \]
Мы вывели тождество синусоидального полуугла:
Знак \ (\ pm \) в начале правой части означает, что квадратный корень может быть положительным или отрицательным — в зависимости от квадранта, в котором угол \ (\ large {\ frac {\ alpha} {2 }} \ normalsize \) лежит.2} \ frac {\ alpha} {2} = \ frac {{1 + \ cos \ alpha}} {2},} \; \; \ Rightarrow {\ left | {\ cos \ frac {\ alpha} {2}} \ right | = \ sqrt {\ frac {{1 + \ cos \ alpha}} {2}},} \; \; \ Rightarrow {\ cos \ frac {\ alpha} {2} = \ pm \ sqrt {\ frac {{1 + \ cos \ alpha}} {2}}.} \]
Следовательно,
Знак зависит от квадранта, в котором лежит \ (\ large {\ frac {\ alpha} {2}} \ normalsize \).
Касательная половина угла
Теперь мы можем вывести формулу для вычисления \ (\ tan \ large {\ frac {\ alpha} {2}} \ normalsize.2} \ frac {\ alpha} {2}}}} = {\ frac {{1 — \ cos \ alpha}} {{1 + \ cos \ alpha}}.} \]
Следовательно,
, где знак \ (\ pm \) зависит от того, в какие квадранты круга попадает угол \ (\ large {\ frac {\ alpha} {2}} \ normalsize \). 2} \ frac {\ alpha} {2}}} {{\ sin \ alpha}}} = {\ frac {{1 — \ cos \ alpha}} {{\ sin \ alpha}},} \]
или
Котангенс половины угла
По определению,
\ [\ cot \ frac {\ alpha} {2} = \ frac {1} {{\ tan \ frac {\ alpha} {2}}}.\]
Следовательно, мы имеем следующие тождества полууглов для котангенса:
Решенные проблемы
Щелкните или коснитесь проблемы, чтобы увидеть решение.
Пример 1
Найдите \ (\ sin \ large {\ frac {\ alpha} {2}} \ normalsize, \) \ (\ cos \ large {\ frac {\ alpha} {2}} \ normalsize, \) и \ (\ tan \ large {\ frac {\ alpha} {2}} \ normalsize \), если \ (\ alpha = \ large {\ frac {\ pi} {3}} \ normalsize. \)Пример 2
Найдите \ (\ sin \ large {\ frac {\ beta} {2}} \ normalsize, \) \ (\ cos \ large {\ frac {\ beta} {2}} \ normalsize, \) и \ (\ tan \ large {\ frac {\ beta} {2}} \ normalsize \), если \ (\ tan \ beta = \ large {\ frac {{24}} {7}} \ normalsize \) и \ (\ pi \ lt \ beta \ lt \ large {\ frac {{3 \ pi}} {2}} \ normalsize.2} \ left ({\ frac {\ pi} {4} — \ frac {\ alpha} {2}} \ right). \]Пример 1.
Найдите \ (\ sin \ large {\ frac {\ alpha} {2}} \ normalsize, \) \ (\ cos \ large {\ frac {\ alpha} {2}} \ normalsize, \) и \ (\ tan \ large {\ frac {\ alpha} {2}} \ normalsize \), если \ (\ alpha = \ large {\ frac {\ pi} {3}} \ normalsize. \)Решение.
Угол \ (\ large {\ frac {\ alpha} {2}} \ normalsize = \ large {\ frac {\ pi} {6}} \ normalsize \) лежит в \ (1 \ text {st} \ ) квадрант, в котором все функции имеют положительный знак.Следовательно,
\ [{\ sin \ frac {\ alpha} {2} = \ sqrt {\ frac {{1 — \ cos \ alpha}} {2}}} = {\ sqrt {\ frac {{1 — \ cos \ frac {\ pi} {3}}} {2}}} = {\ sqrt {\ frac {{1 — \ frac {1} {2}}} {2}}} = {\ sqrt {\ frac {1 } {4}}} = {\ frac {1} {2};} \]
\ [{\ cos \ frac {\ alpha} {2} = \ sqrt {\ frac {{1 + \ cos \ alpha}} {2}}} = {\ sqrt {\ frac {{1 + \ cos \ гидроразрыв {\ pi} {3}}} {2}}} = {\ sqrt {\ frac {{1 + \ frac {1} {2}}} {2}}} = {\ sqrt {\ frac {3 } {4}}} = {\ frac {{\ sqrt 3}} {2};} \]
\ [{\ tan \ frac {\ alpha} {2} = \ frac {{\ sin \ frac {\ alpha} {2}}} {{\ cos \ frac {\ alpha} {2}}}} = {\ frac {{\ frac {1} {2}}} {{\ frac {{\ sqrt 3}} {2}}}} = {\ frac {1} {{\ sqrt 3}}.2} + 1}}}} = {- \ sqrt {\ frac {1} {{\ frac {{576}} {{49}} + 1}}}} = {- \ sqrt {\ frac {{49 }} {{625}}}} = {- \ frac {7} {{25}}.} \]
Обратите внимание, что
\ [{\ pi \ lt \ beta \ lt \ frac {{3 \ pi}} {2},} \; \; \ Rightarrow {\ frac {\ pi} {2} \ lt \ frac {\ beta} {2} \ lt \ frac {{3 \ pi}} {4},} \]
, то есть угол \ (\ large {\ frac {\ beta} {2}} \ normalsize \) попадает в квадрант \ (2 \ text {nd} \). В этом квадранте синус положительный, а косинус и тангенс отрицательны. Следовательно,
\ [{\ sin \ frac {\ beta} {2} = \ sqrt {\ frac {{1 — \ cos \ beta}} {2}}} = {\ sqrt {\ frac {{1 — \ left ( {- \ frac {7} {{25}}} \ right)}} {2}}} = {\ sqrt {\ frac {{16}} {{25}}}} = {\ frac {4} { 5};} \]
\ [{\ cos \ frac {\ beta} {2} = — \ sqrt {\ frac {{1 + \ cos \ beta}} {2}}} = {- \ sqrt {\ frac {{1 + \ left ({- \ frac {7} {{25}}} \ right)}} {2}}} = {- \ sqrt {\ frac {9} {{25}}}} = {- \ frac {3 } {5};} \]
\ [{\ tan \ frac {\ beta} {2} = \ frac {{\ sin \ frac {\ beta} {2}}} {{\ cos \ frac {\ beta} {2}}}} = {\ frac {{\ frac {4} {5}}} {{- \ frac {3} {5}}}} = {- \ frac {4} {3}.2} \ frac {\ beta} {2}}}} = {\ frac {{1 — \ frac {{1 — \ cos \ beta}} {{1 + \ cos \ beta}}}} {{1 + \ frac {{1 — \ cos \ beta}} {{1 + \ cos \ beta}}}}} = {\ frac {{\ frac {{1 + \ cos \ beta — \ left ({1 — \ cos \ beta} \ right)}} {{1 + \ cos \ beta}}}} {{\ frac {{1 + \ cos \ beta + 1 — \ cos \ beta}} {{1 + \ cos \ beta}} }}}} = {\ frac {{\ cancel {1} + \ cos \ beta — \ cancel {1} + \ cos \ beta}} {{1 + \ cancel {\ cos \ beta} + 1 — \ cancel {\ cos \ beta}}}} = {\ frac {{\ cancel {2} \ cos \ beta}} {\ cancel {2}}} = {\ cos \ beta.} \]
Пример 6.\ cancel {2}} \ alpha}} {\ cancel {\ sin \ alpha}}} = {\ sin \ alpha.} \]
Пример 7.
Подтвердите личность \ [\ cot \ frac {\ alpha} {2} — \ tan \ frac {\ alpha} {2} = 2 \ cot \ alpha. \]Решение.
Подставляем выражения для тангенса и котангенса половинного угла:
\ [{\ cot \ frac {\ alpha} {2} = \ frac {{1 + \ cos \ alpha}} {{\ sin \ alpha}}, \; \;} \ kern0pt {\ tan \ frac { \ alpha} {2} = \ frac {{1 — \ cos \ alpha}} {{\ sin \ alpha}}.} \]
Это дает:
\ [{\ cot \ frac {\ alpha} {2} — \ tan \ frac {\ alpha} {2}} = {\ frac {{1 + \ cos \ alpha}} {{\ sin \ alpha}} — \ frac {{1 — \ cos \ alpha}} {{\ sin \ alpha}}} = {\ frac {{1 + \ cos \ alpha — \ left ({1 — \ cos \ alpha} \ right)} } {{\ sin \ alpha}}} = {\ frac {{\ cancel {1} + \ cos \ alpha — \ cancel {1} + \ cos \ alpha}} {{\ sin \ alpha}}} = { \ frac {{2 \ cos \ alpha}} {{\ sin \ alpha}}} = {2 \ cot \ alpha.2} \ left ({\ frac {\ pi} {4} — \ frac {\ alpha} {2}} \ right)} = {1 — \ cos \ left ({\ frac {\ pi} {2} — \ alpha} \ right)} = {1 — \ sin \ alpha} = {LHS.} \]
.
 (1 мин)
(1 мин) 2\frac{23π}{12}-\sqrt{27}=\sqrt{108}\)\( \frac{1+\cos\frac{2\cdot 23π}{12}}{2}\)\(-\sqrt{27}=\sqrt{108}\)\(\frac{1+\cos\frac{23π}{6}}{2}\)\(-\sqrt{27}=\)…
2\frac{23π}{12}-\sqrt{27}=\sqrt{108}\)\( \frac{1+\cos\frac{2\cdot 23π}{12}}{2}\)\(-\sqrt{27}=\sqrt{108}\)\(\frac{1+\cos\frac{23π}{6}}{2}\)\(-\sqrt{27}=\)… 2\frac{7π}{8}\).
2\frac{7π}{8}\).
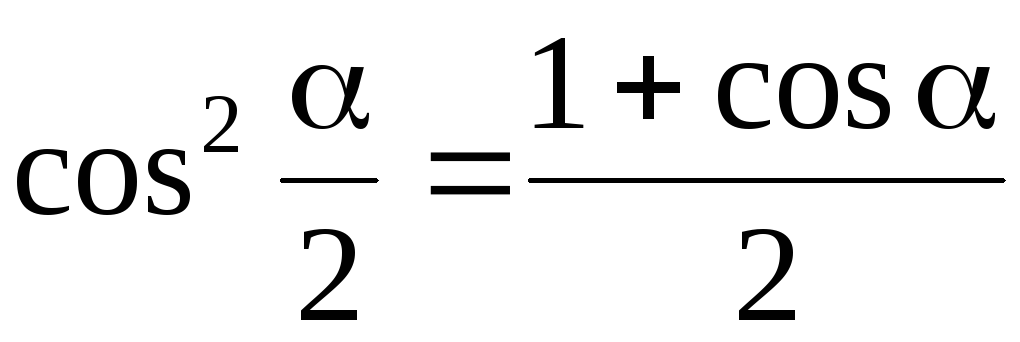



 Решают в уме, один из учеников проговаривает ответ
Решают в уме, один из учеников проговаривает ответ
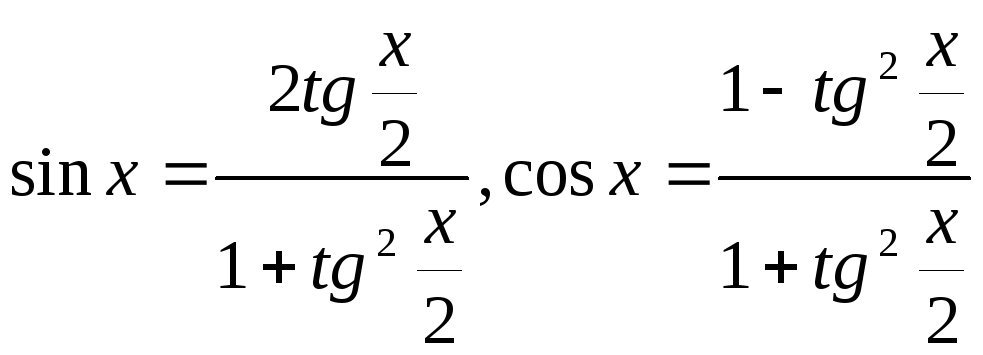
 Что для этого необходимо сделать?
Что для этого необходимо сделать?

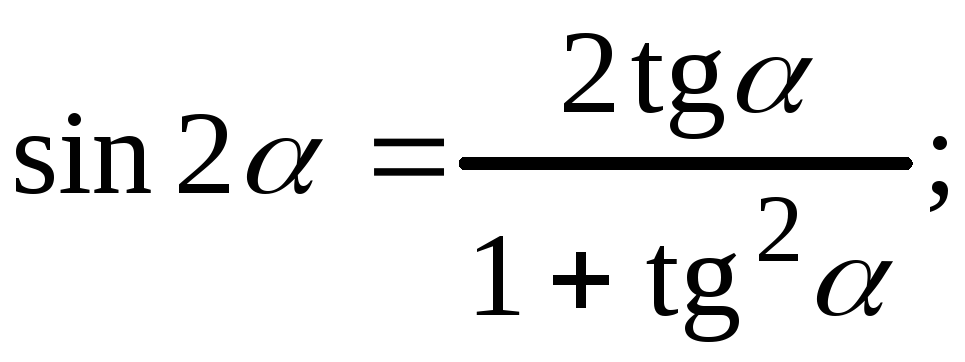
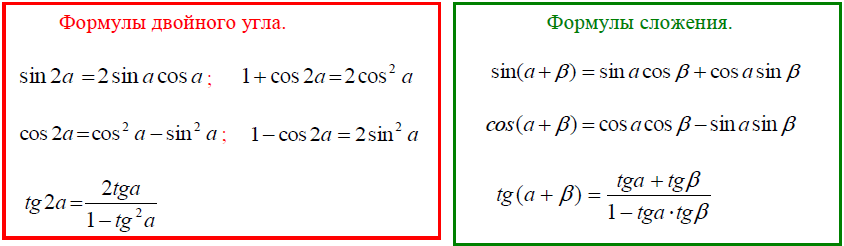 244
244
 ), при помощи которых решается наибольшая часть задач по тригонометрии. Сгруппируем эти формулы по назначению.
), при помощи которых решается наибольшая часть задач по тригонометрии. Сгруппируем эти формулы по назначению. Эти формулы связывают синус, косинус, тангенс, котангенс одного угла. Каждая из них является следствием каких-то определений.
Эти формулы связывают синус, косинус, тангенс, котангенс одного угла. Каждая из них является следствием каких-то определений.

 Кроме того, они часто используются при решении тригонометрических уравнений. Рассмотрим формулы суммы и разности.
Кроме того, они часто используются при решении тригонометрических уравнений. Рассмотрим формулы суммы и разности.
 Рисунок 1), должны различаться по высоте в зависимости от уровня навыков участников. Для опытных спортсменов угол между рампой и землей должен составлять θθ так, чтобы tanθ = 53.tanθ = 53. Для новичков угол делится пополам. Какая крутизна ската для новичков? В этом разделе мы исследуем три дополнительные категории идентичностей, которые мы можем использовать, чтобы ответить на такие вопросы, как этот.
Рисунок 1), должны различаться по высоте в зависимости от уровня навыков участников. Для опытных спортсменов угол между рампой и землей должен составлять θθ так, чтобы tanθ = 53.tanθ = 53. Для новичков угол делится пополам. Какая крутизна ската для новичков? В этом разделе мы исследуем три дополнительные категории идентичностей, которые мы можем использовать, чтобы ответить на такие вопросы, как этот. Во-первых, исходя из формулы суммы, cos (α + β) = cosαcosβ − sinαsinβ, cos (α + β) = cosαcosβ − sinαsinβ, и полагая α = β = θ, α = β = θ, имеем
Во-первых, исходя из формулы суммы, cos (α + β) = cosαcosβ − sinαsinβ, cos (α + β) = cosαcosβ − sinαsinβ, и полагая α = β = θ, α = β = θ, имеем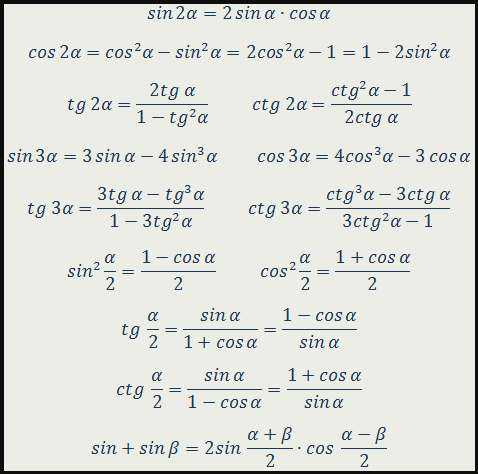
 Используйте теорему Пифагора, чтобы найти длину гипотенузы:
Используйте теорему Пифагора, чтобы найти длину гипотенузы: tan (2θ) = 2tanθ1 − tan2θtan (2θ) = 2tanθ1 − tan2θ
tan (2θ) = 2tanθ1 − tan2θtan (2θ) = 2tanθ1 − tan2θ Он подчеркивает, что образец — это то, что нам нужно запомнить, и что идентичности верны для всех значений в области определения тригонометрической функции.
Он подчеркивает, что образец — это то, что нам нужно запомнить, и что идентичности верны для всех значений в области определения тригонометрической функции.
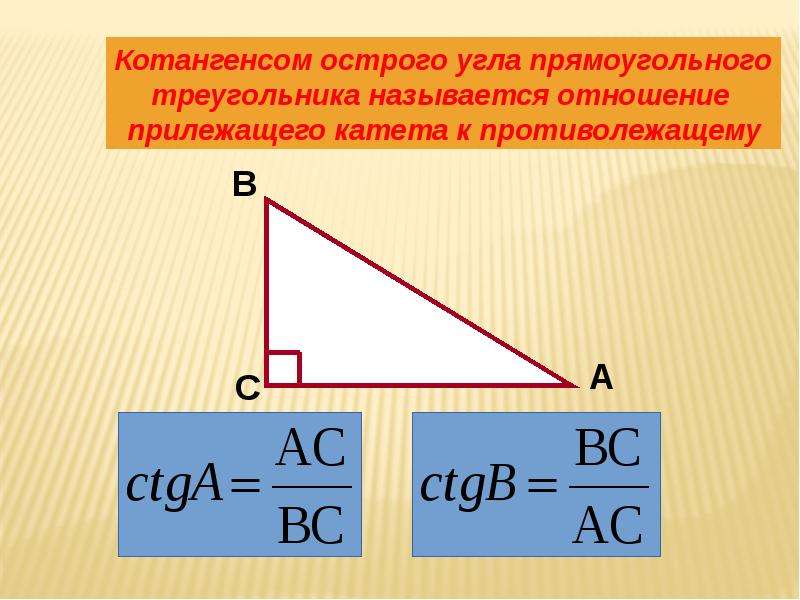
 Не существует установленного правила относительно того, какой стороной следует манипулировать. Однако начать следует с изложенных ранее рекомендаций.
Не существует установленного правила относительно того, какой стороной следует манипулировать. Однако начать следует с изложенных ранее рекомендаций. Начнем с cos (2θ) = 1−2sin2θ.cos (2θ) = 1−2sin2θ.Решить относительно sin2θ: sin2θ:
Начнем с cos (2θ) = 1−2sin2θ.cos (2θ) = 1−2sin2θ.Решить относительно sin2θ: sin2θ:
 = sin (2x) (12) [1 − cos (4x)] = 12 [sin (2x)] [1 − cos (4x)] sin3 (2x) = [sin (2x)] [sin2 (2x)] = sin (2x) [1 − cos (4x) 2] Подставим формулу уменьшения мощности. = sin (2x) (12) [1 − cos (4x)] = 12 [sin (2x)] [1 − cos (4x)]
= sin (2x) (12) [1 − cos (4x)] = 12 [sin (2x)] [1 − cos (4x)] sin3 (2x) = [sin (2x)] [sin2 (2x)] = sin (2x) [1 − cos (4x) 2] Подставим формулу уменьшения мощности. = sin (2x) (12) [1 − cos (4x)] = 12 [sin (2x)] [1 − cos (4x)] Если мы заменим θθ на α2, α2, формула половинного угла для синуса будет найдена путем упрощения уравнения и решения для sin (α2).грех (α2). Обратите внимание, что перед формулами полуугла стоит знак ± ±. Это не означает, что допустимы как положительные, так и отрицательные выражения. Скорее, это зависит от квадранта, в котором заканчивается α2α2.
Если мы заменим θθ на α2, α2, формула половинного угла для синуса будет найдена путем упрощения уравнения и решения для sin (α2).грех (α2). Обратите внимание, что перед формулами полуугла стоит знак ± ±. Это не означает, что допустимы как положительные, так и отрицательные выражения. Скорее, это зависит от квадранта, в котором заканчивается α2α2.
 Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить sinα = −817sinα = −817 и cosα = −1517.cosα = −1517.
Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить sinα = −817sinα = −817 и cosα = −1517.cosα = −1517.
 cos (α2).
cos (α2). cosθ = 334 = 33434. Мы можем использовать формулу половинного угла для касательной: tanθ2 = 1 − cosθ1 + cosθ.tanθ2 = 1 − cosθ1 + cosθ. Поскольку tanθtanθ находится в первом квадранте, tanθ2.tanθ2 тоже. Таким образом,
cosθ = 334 = 33434. Мы можем использовать формулу половинного угла для касательной: tanθ2 = 1 − cosθ1 + cosθ.tanθ2 = 1 − cosθ1 + cosθ. Поскольку tanθtanθ находится в первом квадранте, tanθ2.tanθ2 тоже. Таким образом, соз (х2). Объясните, как определить две формулы для tan (x2) tan (x2)
которые не содержат квадратных корней.
соз (х2). Объясните, как определить две формулы для tan (x2) tan (x2)
которые не содержат квадратных корней.



 2 (α / 2) = (1 — cos α) / 2`
2 (α / 2) = (1 — cos α) / 2` 2 (альфа / 2) = (1 + cos alpha) / 2`
2 (альфа / 2) = (1 + cos alpha) / 2` @`, используя соотношение половинного угла синуса, приведенное выше.(текст (o))) / 2) `
@`, используя соотношение половинного угла синуса, приведенное выше.(текст (o))) / 2) ` Рисунок \ (\ PageIndex {1} \)), должны различаться по высоте в зависимости от уровня навыков участников.Для опытных участников угол между рампой и землей должен быть \ (\ theta \) таким, чтобы \ (\ tan \ theta = \ dfrac {5} {3} \). Для новичков угол делится пополам. Какая крутизна ската для новичков? В этом разделе мы исследуем три дополнительные категории идентичностей, которые мы можем использовать, чтобы ответить на такие вопросы, как этот.
Рисунок \ (\ PageIndex {1} \)), должны различаться по высоте в зависимости от уровня навыков участников.Для опытных участников угол между рампой и землей должен быть \ (\ theta \) таким, чтобы \ (\ tan \ theta = \ dfrac {5} {3} \). Для новичков угол делится пополам. Какая крутизна ската для новичков? В этом разделе мы исследуем три дополнительные категории идентичностей, которые мы можем использовать, чтобы ответить на такие вопросы, как этот. 2 \ theta} \ end {align} \]
2 \ theta} \ end {align} \]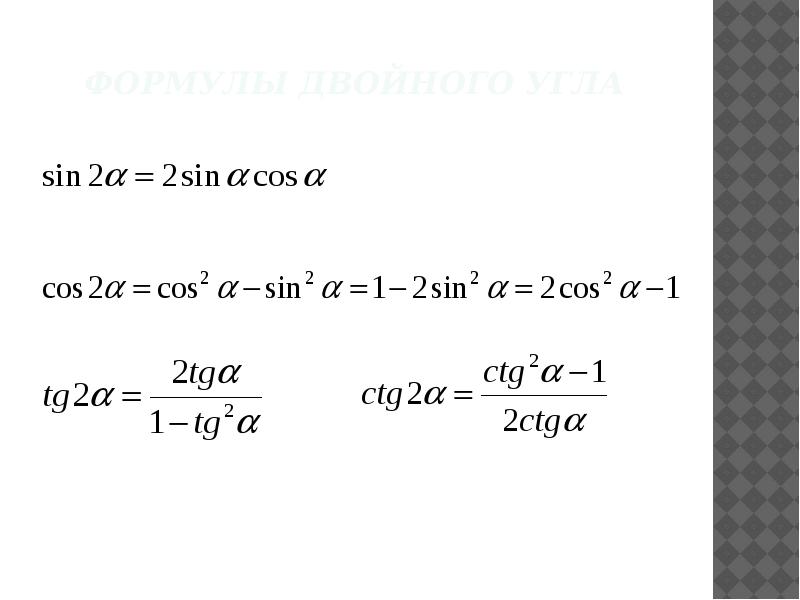 2 \\ [4pt] c & = 5 \ end {align *} \]
2 \\ [4pt] c & = 5 \ end {align *} \] 2 3x \ end {align *} \]
2 3x \ end {align *} \] 2 \ theta} \ end {align *} \]
2 \ theta} \ end {align *} \]