| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |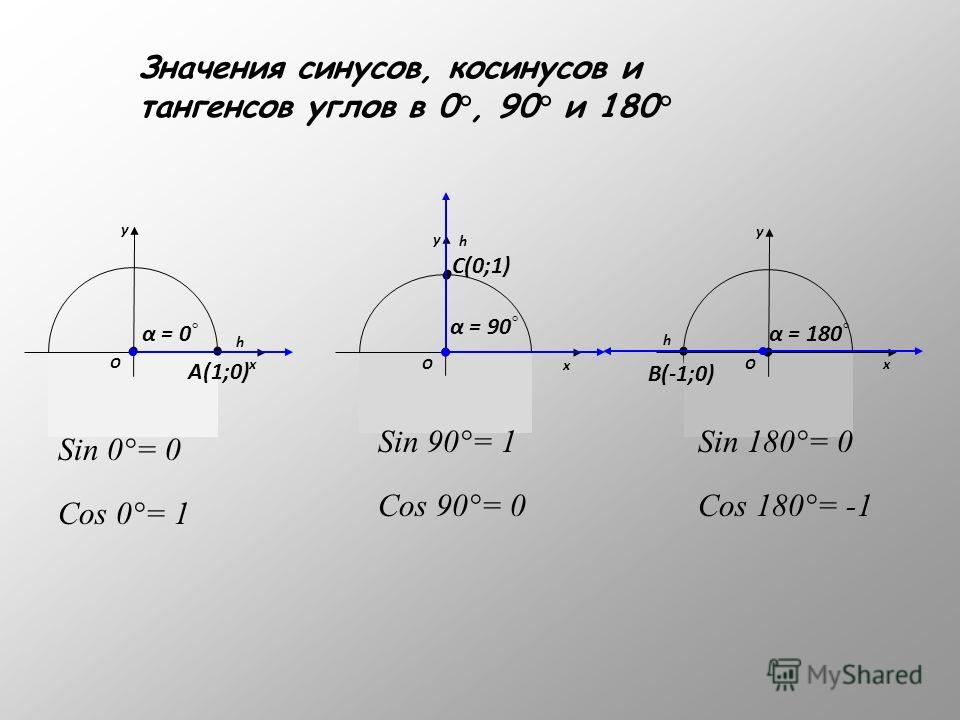
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |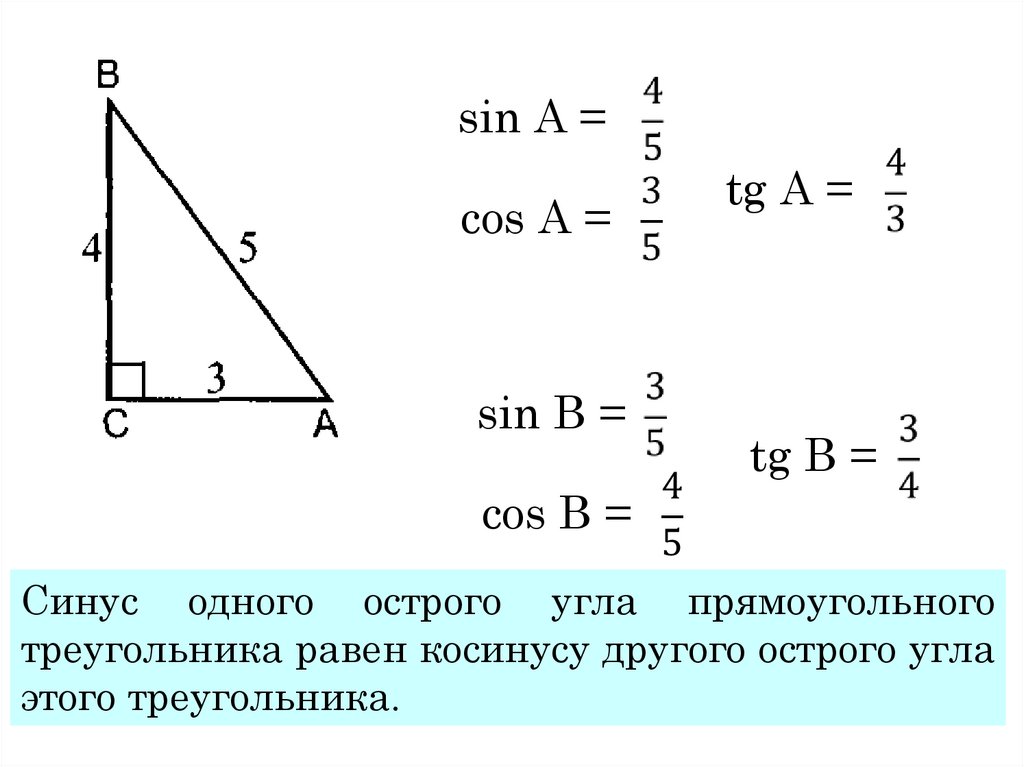
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | sin(120 град. ) | ||
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Синус, косинус, тангенс угла. Основное тригонометрическое тождество. Формулы приведения 9 класс онлайн-подготовка на
Тема 30.
Синус, косинус, тангенс угла.
Основное тригонометрическое тождество. Формулы приведения.
Введем прямоугольную систему координат Oxy и построим полуокружность радиуса 1 с центром в начале координат, расположенную в первом и втором квадрантах. Назовем ее единичной полуокружностью. Из точки O проведем луч h, пересекающий единичную полуокружность в точке M(x;y).
Обозначим буквой α угол между лучом hи положительной полуосью абсцисс (если луч h совпадает с положительной полуосью абсцисс, то будем считать, что α = 0°).
Если угол α острый, то из прямоугольного ∆DOM:
имеем sinα=MDOM , cosα=ODOM. Но OM = 1, MD
Итак, синус острого угла α равен ординате у точки М, а косинус угла α — абсцисса x точки M.
Если угол α прямой, тупой или развернутый или α = 0°, то синус и косинус угла α также определим по этим формулам.
Таким образом, для любого угла α из промежутка 0° ≤ α ≤ 180° синусом угла α называется ордината y точки М, а косинусом угла α — абсцисса x точки М. Так как координаты (x; y) точек единичной полуокружности заключены в промежутках 0 ≤ y ≤ 1, -1 ≤ x ≤ 1, то для любого α из промежутка 0° ≤ α ≤ 180° справедливы неравенства 0 ≤ sin α ≤ 1, -1 ≤ cos α ≤ 1.
Найдем значения синуса и косинуса для углов 0°, 90°, 180°. Для этого рассмотрим лучи OA, OC и OB, соответствующие этим углам. Так как точки А, С и В имеют координаты А(1; 0), С(0; 1), В(-1; 0), то
sin 0° = 0, sin 90° = 0, sin 180° = 0
cos 0° = 1, cos 90° = 0, cos 180° = -1.
Тангенсом угла α(α ≠ 90°) называется отношение sinαcosα, т.е. tgα=sinαcosα
При α = 90° tg α не определен, поскольку cos 90° = 0, и знаменатель обращается в ноль.
tg 90° = 0, tg 180° = 0.
Котангенсом угла α(α ≠ 0°,α ≠ 180°) называется отношение cosαsinα, т.е. ctgα=cosαsinα
При α = 0° и α = 180° сtg α не определен, поскольку
sin 0° = 0 sin 180° = 0
ctg 90° = 0
Вернемся к нашей единичной полуокружности АСВ с центром О. Эта полуокружность является дугой окружности, уравнение которой имеет вид x2 + y2 = 1. Подставив сюда выражения для х и у получим равенство sin2α + cos2α = 1, которое выполняется для любого α из промежутка 0° ≤ α ≤ 180°.
Это равенство называется основным тригонометрическим тождеством.
Справедливы также следующие тождества:
sin 90° — α = cos α, cos 90° — α = sin α при 0° ≤ α ≤90°
sin 180° — α = sin α, cos 180° — α = — cos α при 0° ≤ a ≤ 180°.
Они называются формулами приведения.
Рассмотрим примеры:
-
Найти cos α если sinα=32.
sin2α + cos2α = 1
322+cos2α=1
34+cos2α=1
cos2α=1-34
cos2α=14
cosα=±12
Ответ: ±12
-
Найти sin 120°, cos 120°, tg 120°
sin120°=sin180°-60°=sin60°=32
cos120°=cos180°-60°=-cos60°=-12
tg120°=sin120°cos120°=32÷-12=-3
Cos 180 градусов — Найти значение Cos 180 градусов
LearnPracticeDownload
Значение cos 180 градусов равно -1 .
Cos 180 градусов в радианах записывается как cos (180° × π/180°), т. е. cos (π) или cos (3,141592…). В этой статье мы обсудим способы нахождения значения cos 180 градусов на примерах.
- Cos 180°: -1
- Cos (-180 градусов): -1
- Cos 180° в радианах: cos (π) или cos (3,1415926 . . . .)
Каково значение Cos 180 градусов?
Значение cos 180 градусов равно -1. Cos 180 градусов также можно выразить с помощью эквивалента данного угла (180 градусов) в радианах (3,14159 . . .)
Мы знаем, используя преобразование градусов в радианы, что θ в радианах = θ в градусах × (pi/180° )
⇒ 180 градусов = 180° × (π/180°) рад = π или 3,1415 . . .
∴ cos 180° = cos(3.1415) = -1
Объяснение:
Для cos 180 градусов угол 180° лежит на отрицательной оси x. Таким образом, значение cos 180° = -1
Поскольку функция косинуса является периодической функцией, мы можем представить cos 180° как cos 180 градусов = cos(180° + n × 360°), n ∈ Z.
⇒ cos 180° = cos 540° = cos 900° и так далее.
Примечание: Поскольку косинус является четной функцией, значение cos(-180°) = cos(180°).
Методы определения значения cos 180 градусов
Значение cos 180° принимается равным -1. Мы можем найти значение cos 180 градусов по:
- Использование единичного круга
- Использование тригонометрических функций
Cos 180 градусов с использованием единичной окружности
Чтобы найти значение cos 180 градусов с помощью единичной окружности:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 180° с положительной осью x.
- Космос 180 градусов равен x-координате (-1) точки пересечения (-1, 0) единичной окружности и r.
Отсюда значение cos 180° = x = -1
Cos 180° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить cos 180 градусов как:
- ± √(1-sin²(180°))
- ± 1/√(1 + tan²(180°))
- ± кроватка 180°/√(1 + кроватка²(180°))
- ±√(косек²(180°) — 1)/косек 180°
- 1/сек 180°
Примечание.
Поскольку 180° лежит на отрицательной оси x, конечное значение cos 180° будет отрицательным.
Мы можем использовать тригонометрические тождества для представления cos 180° как
- -cos(180° — 180°) = -cos 0°
- -cos(180° + 180°) = -cos 360°
- sin(90° + 180°) = sin 270°
- sin(90° — 180°) = sin(-90°)
☛ Также проверьте:
- cos 53 градуса
- потому что 90 градусов
- потому что 180 градусов
- потому что 217 градусов
- потому что 345 градусов
- потому что 540 градусов
Примеры использования Cos 180 градусов
Пример 1. Найдите значение 2 cos(180°)/3 sin(-90°).
Решение:
Используя тригонометрические тождества, мы знаем, что cos(180°) = sin(90° — 180°) = sin(-90°).
⇒ cos(180°) = sin(-90°)
⇒ Значение 2 cos(180°)/3 sin(-90°) = 2/3Пример 2: Используя значение cos 180°, решите: (1-sin²(180°)).
Решение:
Мы знаем, (1-sin²(180°)) = (cos²(180°)) = 1
⇒ (1-sin²(180°)) = 1Пример 3: Найдите значение (cos² 90° — sin² 90°). [Подсказка: используйте cos 180° = -1]
Решение:
Используя формулу cos 2a,
(cos² 90° — sin² 90°) = cos(2 × 90°) = cos 180°
∵ cos 180° = -1
⇒ (cos² 90° — sin² 90°) = -1
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы о Cos 180 Degrees
Что такое Cos 180 Degrees?
Cos 180 градусов — значение тригонометрической функции косинуса для угла, равного 180 градусам.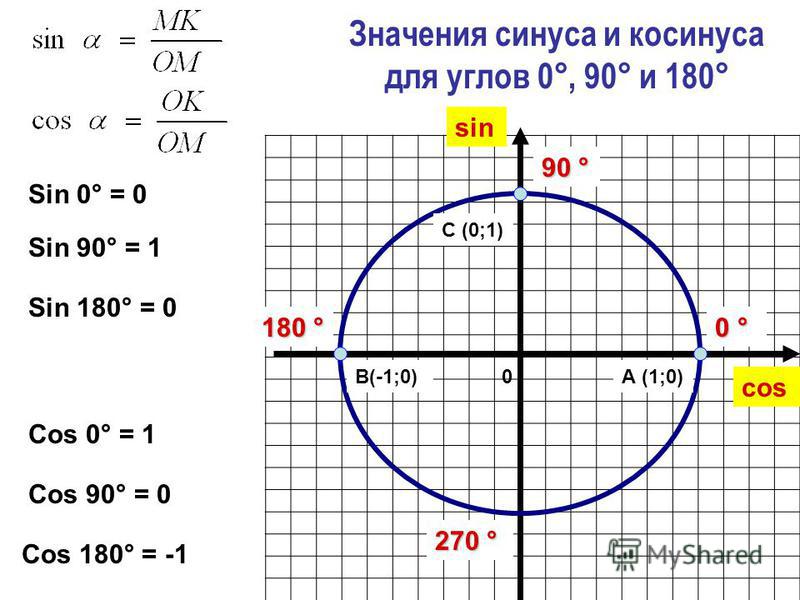
Значение cos 180° равно -1
Каково значение Cos 180 градусов относительно Cot 180°?
Мы можем представить функцию косинуса в терминах функции котангенса, используя тригонометрические тождества, cos 180° можно записать как -cot 180°/√(1 + cot²(180°)).
Как найти значение Cos 180 градусов?
Значение cos 180 градусов можно рассчитать, построив угол 180° с осью x и затем найдя координаты соответствующей точки (-1, 0) на единичной окружности. Значение cos 180° равно координате x (-1). ∴ cos 180° = -1.
Каково точное значение cos 180 градусов?
Точное значение для cos 180 градусов равно -1.
Как найти косинус 180° с точки зрения других тригонометрических функций?
Используя формулу тригонометрии, значение cos 180° может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-sin²(180°))
- ± 1/√(1 + tan²(180°))
- ± кроватка 180°/√(1 + кроватка²(180°))
- ± √(косек²(180°) — 1)/косек 180°
- 1/сек 180°
☛ Также проверьте: таблицу тригонометрии
Скачать БЕСПЛАТНО учебные материалы
Тригонометрия
Рабочие листы по математике и визуальный учебный план
Значение Cos 180° | Изучение и решение вопросов
Введение в Cos Angle
Дата последнего обновления: 16 апреля 2023 г.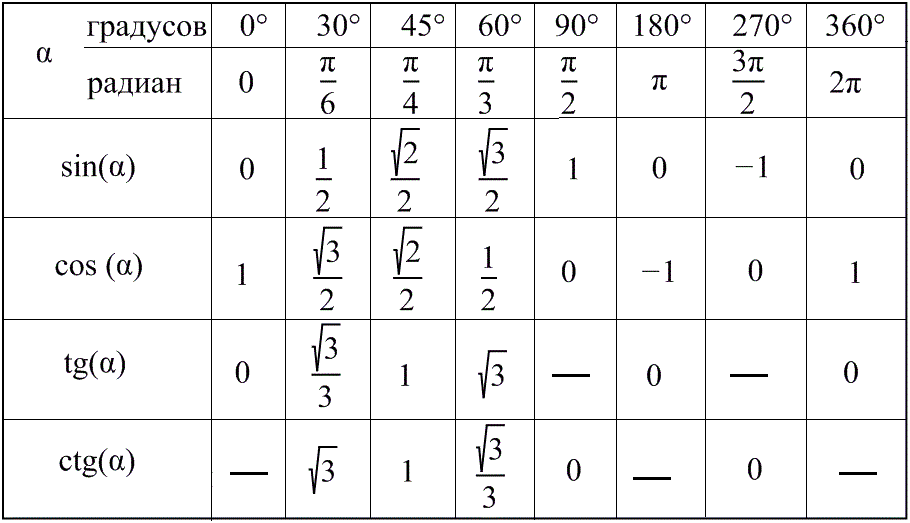
8 Тригонометрические функции (также известные как круговые функции, угловые функции или гониометрические функции) — это реальные функции, которые связывают угол прямоугольного треугольника с отношениями длин двух сторон в математике. Тригонометрия — это исследование измерений треугольника, сосредоточенное на длине, высоте и углах треугольника. Они широко используются во всех геодезических исследованиях, включая навигацию, механику твердого тела, небесную механику, геодезию и многие другие. Они относятся к простейшим периодическим функциям, поэтому их часто используют в анализе Фурье для анализа периодических событий.
В реальном мире тригонометрические функции весьма полезны. Инженерное дело, архитектура, спутниковая навигация, медицинская визуализация и создание звуковых волн — вот лишь несколько примеров. Инженеры, архитекторы и астронавты используют тригонометрические функции для вычисления различных показателей, на которые влияют характеристики треугольника. Он генерирует звуковые и световые волны, используя волновую картину тригонометрических функций в различных приложениях.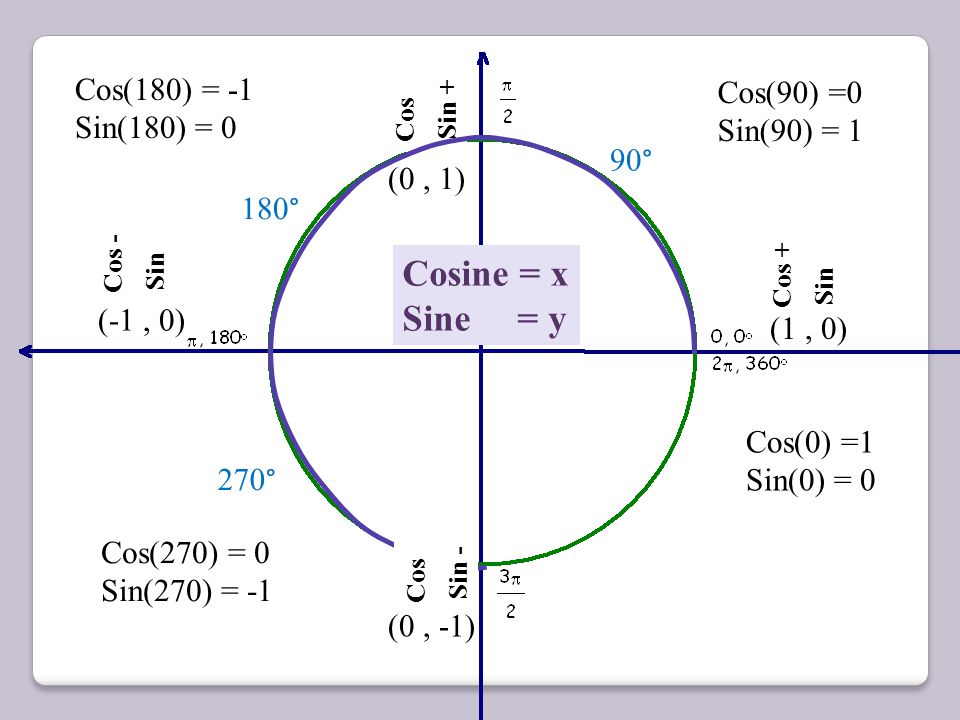
Паттерны синусоидальных и косинусоидальных волн используются при разработке компьютерной музыки.
В этой статье мы собираемся обсудить значения косинуса, как их получить, забавные факты, связанные с тригонометрическими отношениями, решенные проблемы, а также будут даны ответы на несколько наиболее важных вопросов, связанных с косинусом.
Формула угла Cos
В тригонометрии существует множество формул, но когда речь идет о прямоугольном треугольнике, есть всего несколько основных формул. Отношение соседней стороны к гипотенузе, являющейся одним из острых углов, известно как cos theta или cos. Ниже приведена формула косинуса:
Cos θ = $\left(\frac{Adjacent ~ side}{Гипотенуза~Side}\right)$
На изображении выше показан прямоугольный треугольник.
Значение cos 1800
Значение Cos 180° (π) равно -1
Как получить значение Cos 180°?
Значение cos 180 градусов или cos pi может быть выражено через несколько углов, таких как 0°, 90° и 270°.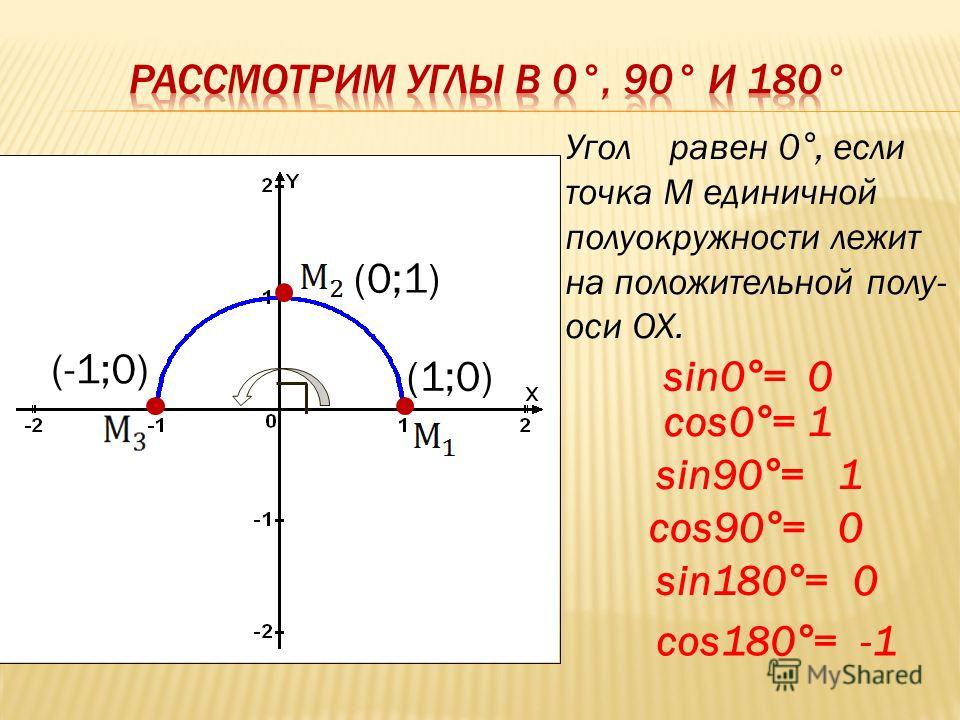
Рассмотрим единичный круг, который в декартовой плоскости делится на четыре квадранта. Значение cos 180 градусов от декартовой плоскости рассчитывается с использованием значения 180 градусов во втором квадранте. Потому что значения косинуса второго квадранта всегда отрицательные.
Из значения cos, равного 0, мы получим значение cos 180°.
Точное значение cos 0 градусов равно 1, как мы знаем.
В результате, cos 180 градусов равен -(cos 0), что равно — (1)
Следовательно, cos 180 градусов равен -1.
Радианы также используются для его представления.
Итак, значение cos = -1, когда значение = 180.
Есть еще несколько способов вывода косинуса. Для определения значения из таблицы тригонометрии получают несколько степенных значений функций синуса и косинуса.
Как известно,
180° – 0° = 180° ——— (A)
270° – 90° = 180° ——— (B)
Метод A: 180-градусное вычисление косинуса
Теперь используем приведенное выше представление в косинусной функции, тогда мы получаем,
Значение cos pi = Cos 180° = cos(180° – 0°) = – cos 0° = – (1) = – 1
Следовательно, значение cos pi = -1
Метод B: вычисление значения косинуса π
Согласно приведенному выше уравнению B,
Значение Cos 180°= cos(270° – 90°)
Cos 180°= – sin 90° (Мы знаем, что данная связь с sin, cos ( 270° – a ) = – sin a)
Sin 90 градусов имеет значение 1.
Когда заменяем значение в приведенном выше уравнении, получаем
Значение Cos 180° = – (1) = -1
Следовательно, значение cos 180° равно -1.
Ниже приведены значения тригонометрических соотношений для различных углов:
Углы (в градусах) 325
45°
60°
90°
180°
270°
360°
Углы (в радианах)
π/6
π/4
π/3
π/2
π
308 3π/2
2π
sin
0
1/2
1/√2
√3/2
1
0328
-1
0
соз
1
√3/2
1/√2
1/2
-1
0
1
желтовато-коричневый
0
1/√3
1
∞
0
∞
0
косек
∞
2
2/√3
1
∞
-1
∞
сек.
38 √2
2
∞
-1
∞
1
детская кроватка
√3
1
1/√3
0
∞
0
∞
а) Cos 180 минус x
т. е. cos (1800 — x) = -cos x
Объяснение:
Одним из самых простых способов может быть использование формулы
⇒ cos(A-B) = cosA cosB +sinAsinB
Следовательно, cos(1800-x) = cos 1800 cosx + sin 1800sinx
⇒ (-1)cosx + 0$\times$sinx
⇒s 8 Следовательно, это решено
b) Cos 180 Plus x
cos (1800+x) = -cosx
Используйте метод суммирования в тождестве косинуса,
⇒ cos(A+B) = cosA cosB — sinA sin B
⇒ cos(1800)cosx-sin(1800)sinx = -cosx
⇒ -1(cosx) — 0(sinx) = -cosx
⇒ -cosx = -cosx
⇒ LHS = RHS
Следовательно, проблема решена.
Забавный факт
Использование тригонометрических функций в реальной жизни:
Они используются в океанографии для определения высоты морских приливов.
Функции синуса и косинуса необходимы при изучении периодических функций, включая звуковые и световые волны.
Тригонометрия и алгебра составляют исчисление.
Тригонометрия может использоваться, помимо прочего, для кровли дома, придания наклонной крыше (в случае бунгало на одну семью) и расчета высоты крыши здания.
Часто используется в морской и авиационной отраслях.
Используется для формирования картографии (создания карт).
Спутниковые навигационные системы также используют тригонометрию.
Многие реальные события могут быть представлены с помощью функций синуса и косинуса, например, радиоволны, приливы, музыкальные тона и электрические токи.
Примеры задач с пошаговым решением:
1 .Если a = 18, b = 24 и c = 30, то найдите значение Cos A
Ответ: По определению мы знаем, что в прямоугольном треугольнике с длиной стороны, противоположной углу θ, перпендикулярной (P), основанием (B) и гипотенузой (H):
Sinθ =$\ влево(\frac{{P}}{H}\right)$, Cosθ =$\left(\frac{{B}}{H}\right)$, tanθ=$\left(\frac{{P} {B}\right)$,
Даны стороны треугольника a = 18, b = 24 и c = 30,
Теперь, используя тригонометрические соотношения, мы получаем значение cos θ as,
Cosθ = $\left(\frac{{B}}{H}\right)=\left(\frac{{24}}{30}\right)=\left(\frac{{4}}{5 }\справа)$
2.