Синус, косинус, тангенс угла. Основное тригонометрическое тождество. Формулы приведения 9 класс онлайн-подготовка на
Тема 30.
Синус, косинус, тангенс угла. Основное тригонометрическое тождество. Формулы приведения.
Введем прямоугольную систему координат Oxy и построим полуокружность радиуса 1 с центром в начале координат, расположенную в первом и втором квадрантах. Назовем ее единичной полуокружностью. Из точки O проведем луч h, пересекающий единичную полуокружность в точке M(x;y).
Обозначим буквой α угол между лучом hи положительной полуосью абсцисс (если луч h совпадает с положительной полуосью абсцисс, то будем считать, что α = 0°).
Если угол α острый, то из прямоугольного ∆DOM:
имеем sinα=MDOM , cosα=ODOM. Но OM = 1, MD = x, OD = y, поэтому sin α = y, cos α = x

Итак, синус острого угла α равен ординате у точки М, а косинус угла α — абсцисса x точки M. Если угол α прямой, тупой или развернутый или α = 0°, то синус и косинус угла α также определим по этим формулам.
Таким образом, для любого угла α из промежутка 0° ≤ α ≤ 180° синусом угла α называется ордината y точки М, а косинусом угла α — абсцисса x точки М. Так как координаты (x; y) точек единичной полуокружности заключены в промежутках 0 ≤ y ≤ 1, -1 ≤ x ≤ 1, то для любого α из промежутка 0° ≤ α ≤ 180° справедливы неравенства 0 ≤ sin α ≤ 1, -1 ≤ cos α ≤ 1.
Найдем значения синуса и косинуса для углов 0°, 90°, 180°. Для этого рассмотрим лучи OA, OC и OB, соответствующие этим углам. Так как точки А, С и В имеют координаты А(1; 0), С(0; 1), В(-1; 0), то
sin 0° = 0, sin 90° = 0, sin 180° = 0
cos 0° = 1, cos 90° = 0, cos 180° = -1.
Тангенсом угла α(α ≠ 90°) называется отношение sinαcosα, т.е. tgα=sinαcosα
При α = 90° tg α не определен, поскольку cos 90° = 0, и знаменатель обращается в ноль.
tg 90° = 0, tg 180° = 0.
Котангенсом угла α(α ≠ 0°,α ≠ 180°) называется отношение cosαsinα, т.е. ctgα=cosαsinα
При α = 0° и α = 180° сtg α не определен, поскольку
ctg 90° = 0
Вернемся к нашей единичной полуокружности АСВ с центром О. Эта полуокружность является дугой окружности, уравнение которой имеет вид x2 + y2 = 1. Подставив сюда выражения для х и у получим равенство sin2α + cos2α = 1, которое выполняется для любого α из промежутка 0° ≤ α ≤ 180°. Это равенство называется основным тригонометрическим тождеством.
Это равенство называется основным тригонометрическим тождеством.
Справедливы также следующие тождества:
sin 90° — α = cos α, cos 90° — α = sin α при 0° ≤ α ≤90°
sin 180° — α = sin α, cos 180° — α = — cos α при 0° ≤ a ≤ 180°.
Они называются формулами приведения.
Рассмотрим примеры:
-
Найти cos α если sinα=32.
sin2α + cos2α = 1
322+cos2α=1
34+cos2α=1
cos2α=1-34
cos2α=14
cosα=±12
Ответ: ±12
-
Найти sin 120°, cos 120°, tg 120°
sin120°=sin180°-60°=sin60°=32
cos120°=cos180°-60°=-cos60°=-12
tg120°=sin120°cos120°=32÷-12=-3
Синус и косинус угла — matematika
w3.org/1999/xhtml» align=»left»>
Синус и косинус угла
|
Определения синуса и косинуса — Концепция
Определения синуса и косинуса прямоугольного треугольника применимы только к острым углам, поэтому необходимо более полное определение. Точка, в которой крайняя сторона пересекает единичную окружность (x, y), является основой для этого определения.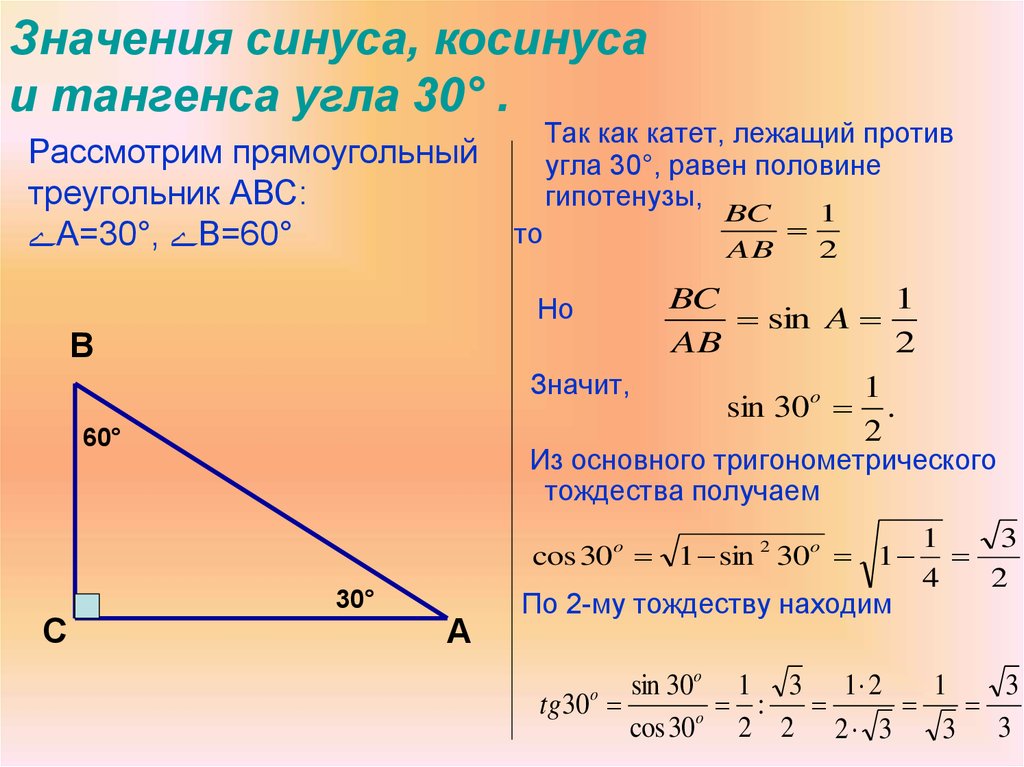 Поскольку радиус (и, следовательно, гипотенуза прямоугольного треугольника) равен 1, знаменатели косинус = соседний / гипотенуза и синус = противоположный / гипотенуза также равны 1. Таким образом, определение синуса — это y = синус и x = косинус.
Поскольку радиус (и, следовательно, гипотенуза прямоугольного треугольника) равен 1, знаменатели косинус = соседний / гипотенуза и синус = противоположный / гипотенуза также равны 1. Таким образом, определение синуса — это y = синус и x = косинус.
синус косинус определение синуса и косинуса прямоугольного треугольника углы в стандартном положении единица круг определения синуса и косинуса
Я хочу поговорить о чем-то действительно важном определении синуса и косинуса. Теперь вы, возможно, помните из геометрии определение синуса и косинуса прямоугольного треугольника, которое начинается с прямоугольного треугольника, и мы обозначим 3 стороны x, y и z, острый угол здесь — тета, а это прямой угол. Мы определили косинус теты как сторону, примыкающую к тете, деленную на гипотенузу. И под соседним мы подразумеваем сторону, которая находится рядом с тета, это гипотенуза, длинная сторона прямоугольного треугольника, и поэтому это означает, что x больше z. Синус определяется как сторона, противоположная тете y относительно гипотенузы, поэтому y больше z.
И под соседним мы подразумеваем сторону, которая находится рядом с тета, это гипотенуза, длинная сторона прямоугольного треугольника, и поэтому это означает, что x больше z. Синус определяется как сторона, противоположная тете y относительно гипотенузы, поэтому y больше z.
Теперь прибавьте к этому углу в стандартном положении единичную окружность, окружность с радиусом 1 x в квадрате плюс у в квадрате равно 1, здесь это окружность.
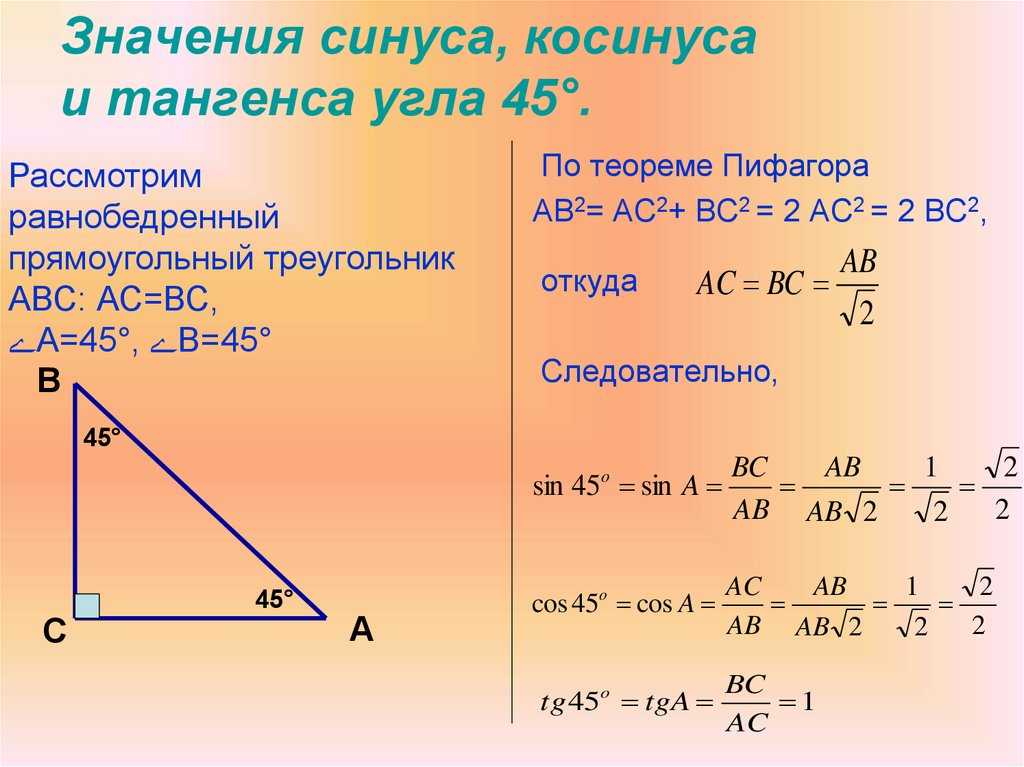
Это будет работать для 0 градусов, 90 градусов и любого другого угла, так что сила определений единичного круга заключается в том, что они работают для всех углов, которые мы будем использовать для остальной части курса тригонометрии.
тригонометрия — Почему синус/косинус угла равен его дополнению?
спросил
Изменено 3 года, 5 месяцев назад
Просмотрено 3к раз
$\begingroup$
Я только что получил тригонометрический текст и изучал закон синусов и косинусов, чтобы решать треугольники, отличные от прямоугольных. Что-то, что я нашел странным при изучении доказательств этих теорем, — это утверждения о том, что синус / косинус угла равен его дополнению. Это не кажется мне интуитивным, и мне трудно понять, как синус угла 45 градусов может равняться синусу угла 135 градусов. Может кто-нибудь объяснить мне эту концепцию?
Что-то, что я нашел странным при изучении доказательств этих теорем, — это утверждения о том, что синус / косинус угла равен его дополнению. Это не кажется мне интуитивным, и мне трудно понять, как синус угла 45 градусов может равняться синусу угла 135 градусов. Может кто-нибудь объяснить мне эту концепцию?
Спасибо
- тригонометрия
$\endgroup$
3
$\begingroup$
Не верно для косинуса.
$\cos (\theta) = -\cos (180-\theta)$
Самый простой способ изучить эти функции — начать с единичного круга. Нарисуйте окружность радиусом 1 с центром в начале координат. Рисовать в радиусе. $\theta$ — это угол между положительной осью x и вашим радиусом, измеренный против часовой стрелки от положительной оси x.
Координата Y, где этот радиус пересекает окружность, равна $\sin\theta$, координата x равна $\cos\theta$.
Начиная с этой структуры, должно быть немного яснее, что $\sin(180-\theta)=\sin(\theta)$.
Если вы исходите из закона синусов. Если у вас есть $\треугольник ABC$, то площадь $\треугольника ABC = (mAB)(mAC)\sin A$
Если построить точку D так, что $\угол DAC$ является дополнительным к $\углу BAC $ и $mAD = mAB$, то DB параллелен AC и площадь $\треугольника DAC$ = площадь $\треугольника BAC$.
площадь $\треугольника ABC = (mAB)(mAC)\sin A$ = площадь $\треугольника ADC = (mAD)(mAC)\sin \sup A$
$\sin A = \sin \sup
австралийских долларов$\endgroup$
$\begingroup$
Как и многие вещи в тригонометрии, здесь есть несколько подходов. Я не знаю вашего триггерного фона, поэтому буду максимально простым.
Подход к единичной окружности
Единичная окружность — это окружность с центром $(0,0)$ и радиусом $1$. комментарий мечтателя к вашему исходному вопросу содержит хорошую картинку.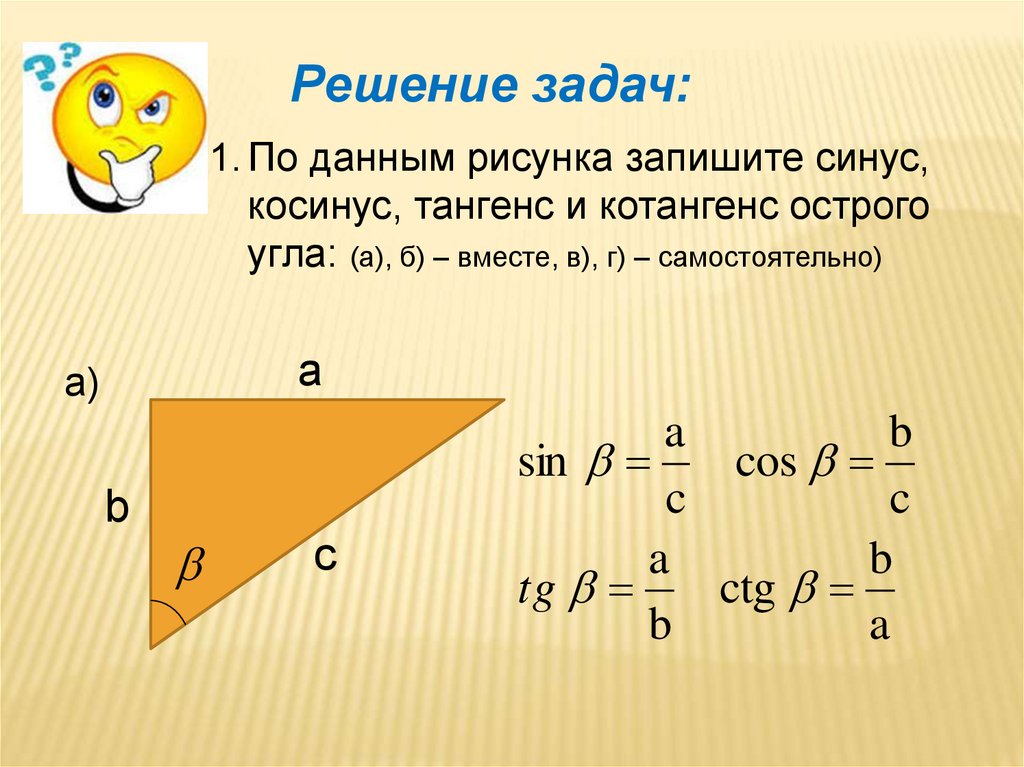

 Произведение синусов
вычисляется именно таким методом и полезно для упрощения той или иной
функции.
Произведение синусов
вычисляется именно таким методом и полезно для упрощения той или иной
функции. Произведение синусов с тангенсами и котангенсами одного угла
удачно вписываются в формулы, выражающие соотношения этих функций с
синусом и косинусом.
Произведение синусов с тангенсами и котангенсами одного угла
удачно вписываются в формулы, выражающие соотношения этих функций с
синусом и косинусом.