Косинус угла между векторами онлайн: Онлайн калькулятор. Вычисление угла между векторами

Почему мы узнаем об угле между двумя векторами?

Скалярные произведения векторов и углов между ними могут быть полезными строительными блоками не только для понимания теоретических взаимосвязей между векторами, но и для понимания того, как эти взаимосвязи коррелируют с нашей жизнью практическим или материальным образом.

А что может быть более осязаемым, чем сесть в автомобиль для катания на американских горках и рухнуть вниз с крутого обрыва?

Допустим, мы разрабатываем новые американские горки и хотим получить общее представление о некоторых характеристиках аттракциона, исходя из профиля трассы и веса транспортного средства. В этом случае мы хотим получить оценку работы, выполняемой транспортным средством под действием силы тяжести, когда оно ускоряется вниз по линейному склону.

Зная вес транспортного средства, пройденное линейное расстояние и угол гусеницы, мы можем использовать концепцию скалярных произведений и угол между векторами для оценки работы, проделанной над транспортным средством. к тому времени, когда он достигнет дна капли. Это полезная информация, потому что мы можем предсказать, сколько энергии потребуется тормозной системе, чтобы остановить транспортное средство в конце падения.

Теперь давайте посмотрим на уравнение работы и сравним его с уравнением, используемым для связи угла между двумя векторами с скалярным произведением двух векторов:

$$\begin{align} & \text{Work } = F \cdot d = |F| |д| \: cos \: \theta \\ \\ & cos \: \theta = \frac{\textbf{u} \cdot \textbf{v}}{\left| \textbf{и} \право| \влево| \textbf{v} \right|} \end{align}$$

Как видите, второе уравнение представляет собой перестроенную версию первого.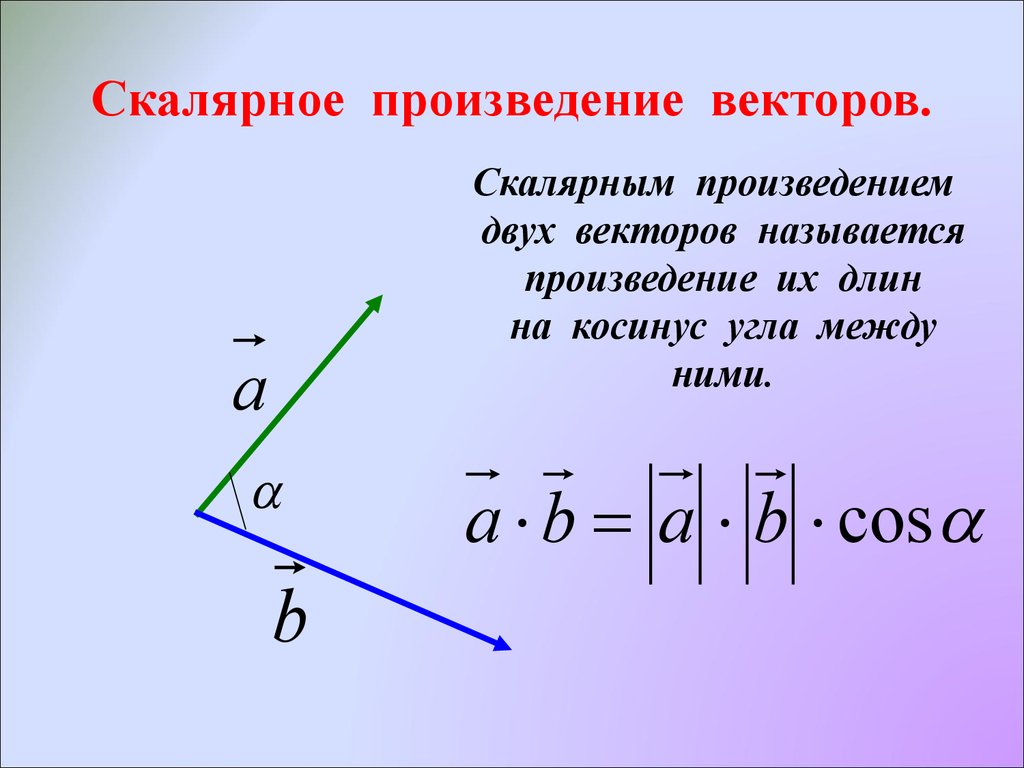 Теперь, если мы применим уравнение работы к нашему примеру, мы получим следующее:

$$\begin{align} & \text{Work } = W \cdot d = |W| |д| \: cos \: \theta \end{align}$$

Это помогает нам понять потребности в энергии для нашей тормозной системы, чтобы транспортное средство можно было безопасно остановить в конце падения.

Как вычислить угол между двумя векторами

Мы можем вычислить угол между двумя векторами, используя следующее уравнение:

$$\begin{align}& cos \: \theta = \frac{\textbf{ u} \cdot \textbf{v}}{\left| \textbf{и} \право| \влево| \textbf{v} \right|} \hspace{10ex} \textbf{ (1) } \end{align}$$

Где u · v — скалярное произведение векторов u и v , | и | величина вектора u , | против | — величина вектора v , а θ — угол между векторами u и v .

Шаги для определения угла между двумя векторами следующие:

1. Вычислить скалярное произведение u · v .
2. Найти | и | (величина вектора и ).
3. Найти | против | (модуль вектора v ).
4. Заглушка u · v , | и |, и | против | в уравнение для нахождения угла между двумя векторами (уравнение 1) и решить для θ.
5. (Необязательно) При необходимости преобразуйте ответ в градусы из радианов.

Пример задачи

$$\begin{align}& \text{Дано:} \\ \\ & \textbf{u} = \langle 1, 2, 3\rangle \text{ и } \textbf {v} = \langle 4, 5, 6\rangle \\ \\ & \text{Найти угол между векторами } \textbf{u} \text{ и } \textbf{v} \text{.}\\ \ \ & \text{1.) Уравнение для нахождения угла } \theta \text{ между двумя векторами имеет вид:} \\ \\ & \hspace{3ex} cos \: \theta = \frac{\textbf{ u} \cdot \textbf{v}}{\left| \textbf{и} \право| \влево| \textbf{v} \right|} \\ \\ & \hspace{3ex} \text{Где: } \\ & \hspace{3ex} \textbf{u} \cdot \textbf{v} \text{ скалярное произведение векторов } \textbf{u} \text{ и } \textbf{v} \text{, } \left| \textbf{и} \право| \text{ является величиной } \\ & \hspace{3ex} \text{vector} \textbf{u} \text{, } \left| \textbf{v} \право| \text{ — величина вектора } \textbf{v} \text{, а } \theta \text{ — угол между} \\ & \hspace{3ex} \text{vectors} \textbf{u} \text { и } \textbf{v} \text{. }\\ \\ & \text{2.) Начнем с поиска } \textbf{u} \cdot \textbf{v} \: \text{:}\\ \\ & \hspace{4ex} \text{2.1) } \textbf{u} \cdot \textbf{v} = \langle1, 2, 3\rangle \cdot \langle 4, 5, 6\rangle = (1) (4) + (2)(5) + (3)(6) \\ \\ & \hspace{8ex} \Longrightarrow (4) + (10) + (18) = 32\\ \\ & \hspace{ 8ex} \Longrightarrow \textbf{u} \cdot \textbf{v} = 32\\ \\ & \text{3.) Далее найдем} \left| \textbf{и} \право| \text{ и} \left| \textbf{v} \право| \: \text{:}\\ \\ & \hspace{4ex} \text{3.1) } \left| \textbf{и} \право| = \ sqrt {\ textbf {u} \ cdot \ textbf {u}} = \ sqrt {\ langle1, 2, 3 \ rangle \ cdot \ langle1, 2, 3 \ rangle} = \ sqrt {(1) (1) + (2)(2) + (3)(3)} \\ \\ & \hspace{8ex} \Longrightarrow \sqrt{(1) + (4) + (9)} = \sqrt{(14)} = 3.74166\\ \\ & \hspace{8ex} \Longrightarrow \left| \textbf{и} \право| = 3.74166\\ \\ & \hspace{4ex} \text{3.2) } \left| \textbf{v} \право| = \ sqrt {\ textbf {v} \ cdot \ textbf {v}} = \ sqrt {\ langle4, 5, 6 \ rangle \ cdot \ langle4, 5, 6 \ rangle} = \ sqrt {(4) (4) + (5)(5) + (6)(6)} \\ \\ & \hspace{8ex} \Longrightarrow \sqrt{(16) + (25) + (36)} = \sqrt{(77)} = 8. 77496\\ \\ & \hspace{8ex} \Longrightarrow \left| \textbf{v} \право| = 8.77496\\ \\ & \text{4.) Теперь давайте подставим значения для } \textbf{u} \cdot \textbf{v} \text{, } \left| \textbf{и} \право| \text{, и} \left| \textbf{v} \право| \text{ в данное уравнение} \\ & \hspace{3ex} \text{из шага 1 и решить для } \theta \: \text{:}\\ \\ & \hspace{4ex} \text{4.1) } потому что \: \ theta = \ frac {\ textbf {u} \ cdot \ textbf {v}} {\ left | \textbf{и} \право| \влево| \textbf{v} \right|} \Longrightarrow cos \: \theta = \frac{(32)}{(3,74166)(8,7749{\circ} \text{.}\end{align}$$

Как работает калькулятор

Калькулятор угла между двумя векторами состоит из нескольких языков программирования. Эти языки включают HTML (язык гипертекстовой разметки), CSS (каскадные таблицы стилей) и JS (JavaScript).

HTML используется для создания базовой структуры полей калькулятора и решения. Этим полям присваиваются специальные идентификаторы, на которые ссылаются при стилизации элементов калькулятора, при выполнении специальных операций во время расчета и при использовании выпадающего меню для выбора единицы ответа.

CSS используется для применения характеристик стиля к упомянутым выше элементам HTML. Это включает, помимо прочего, форму, размер и цвет полей калькулятора и решения.

JS — это то, что дает калькулятору его настоящую функциональность. Когда вы нажимаете кнопку на калькуляторе или нажимаете «рассчитать», код JS начинает обозначать действия, которые приводят к желаемому конечному результату. Например, когда вы нажимаете кнопку «+» на клавиатуре, JS сообщает калькулятору добавить символ «+» в нужное поле ввода для вас. Точно так же, когда вы нажимаете «Вычислить», JS сообщает калькулятору, что он должен выполнить предписанный набор операций, который приводит к пользовательскому ответу и набору шагов решения на основе вашего вопроса.

Все эти разные языки объединяются, чтобы обеспечить простое в использовании, эффективное и приятное обучение.

Угол между двумя векторами — Криста Кинг Математика

Формула для угла между векторами

Чтобы найти угол между двумя векторами, мы будем использовать формулу

???\cos{\theta}=\frac{a\cdot b}{|a||b| }???

где ???а??? и ???б??? данные векторы, ???a\cdot{b}??? скалярное произведение векторов, ???|a|??? длина ???a???, а ???|b|??? длина ???b???. Чтобы найти длину векторов, мы будем использовать формулу расстояния 92}???

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Как вычислить угол между двумя векторами

Пройти курс

Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂

Учить больше

Нахождение угла между двумя векторами в трех измерениях

Пример

Нахождение угла между векторами.

???a=\langle4,-2,3\rangle???

???b=\langle1,3,-1\rangle???

Начнем с нахождения скалярного произведения ???a??? и ???b???, ???a\cdot b???.

???a\cdot{b}=(4)(1)+(-2)(3)+(3)(-1)???

???a\cdot{b}=4-6-3???

???a\cdot{b}=-5???

Формула для угла между векторами также требует формулы для расстояния между двумя точками 9\циркуляр???

Получите доступ к полному курсу Calculus 3

Начать

Учиться математикеКриста Кинг 13 мая 2020 г.