Косинус в квадрате плюс синус в квадрате: Cos в квадрате 15 градусов — sin в квадрате 15 градусов

Содержание

Тангенс 45 градусов плюс синус в квадрате 17 градусов плюс косинус в квадрате 17 градусов .

Геометрия, 15.09.2019 08:20, ТИТАНИТ

Показать ответы

Другие вопросы по: Геометрия

Твір на тему на якій вулиці ти живеш…

Опубликовано: 28.02.2019 05:10

Ответов: 2

Распространите предложение второстепенными членами. включите в предложения эпитеты. наступает зима. закружились снежинки. повалил снег…

Опубликовано: 02.03.2019 13:40

Ответов: 3

Вкаких областях деятельности человека могут использоваться электронные таблицы?…

Опубликовано: 03.03.2019 19:30

Ответов: 1

Кролик за день сьедает 3 кг 500 г корма, из них трава составляет 7/10, а зерно — 7/100 всех кормов. сколько вместе травы и зерна сьедает кролик за день?…

Опубликовано: 04.03.2019 05:00

Ответов: 2

Один з гострих кутів прямокутного трикутника у 4 рази більший за другий…

Опубликовано: 04.03.2019 08:40

Ответов: 1

Театр деониса. представления в таких театрах начинались часов в 7 утра и продолжались до захода солнца: ставили подряд несколько спектаклей. чем объяснить, что театральные постанов…

Опубликовано: 04.03.2019 09:10

Ответов: 1

Знаешь правильный ответ?

Тангенс 45 градусов плюс синус в квадрате 17 градусов плюс косинус в квадрате 17 градусов ….

Видео-урок: вычисление тригонометрических функций с помощью тождеств Пифагора

Стенограмма видео

В этом видео мы научимся использовать тождества Пифагора, чтобы найти значения тригонометрических функций. Мы начнем с напоминания некоторых ключевых формулы и определения.

Мы знаем, что триггерные функции периодичны и имеют бесконечное число решений. Однако в этом видео мы сосредоточьтесь на решениях от нуля до 360 градусов, используя диаграмму CAST. 𝑥- и 𝑦-оси создают четыре квадранты, как показано. В первом квадранте положительные 𝑥- и положительные 𝑦-значения; второй квадрант имеет отрицательные 𝑥- и положительные 𝑦-значения; квадрант три, отрицательный 𝑥 и отрицательный 𝑦; и четвертый квадрант, положительный 𝑥 и отрицательный 𝑦.

При работе с нашим триггером функции, мы измеряем против часовой стрелки от положительной оси 𝑥. Это означает, что первый квадрант содержит углы от нуля до 90 градусов; квадрант два, между 90 и 180 степени; и так далее. Мы можем обозначить квадранты с помощью аббревиатура CAST, как показано. В первом квадранте, обозначенном буквой А, грех угла 𝜃, cos угла 𝜃 и тангенс угла 𝜃 все положительны. Во втором квадранте грех угла 𝜃 положительный. Однако, cos угла 𝜃 и тангенс угла 𝜃 оба отрицательны. В третьем квадранте, когда 𝜃 лежит между 180 и 270 градусами тангенс 𝜃 положителен, тогда как грех 𝜃 и cos 𝜃 оба отрицательны. Наконец, в четвертом квадранте cos 𝜃 положительна, а sin и тангенс 𝜃 отрицательны.

В этом видео нам также нужно будет вспомните три взаимных триггерных тождества. csc угла 𝜃 равна единице над грехом угла 𝜃.

Секунда угла 𝜃 равна единице над косой угла 𝜃. А койка угла 𝜃 равна один над загаром угла 𝜃. Если функции sin 𝜃, cos 𝜃, и tan 𝜃 положительны или отрицательны, то их обратная величина также будет положительной или отрицательный. Это означает, что все шесть функций положительны в первом квадранте. Во втором квадранте между 90 и 180 градусов, синус 𝜃 и csc 𝜃 будут положительными, тогда как все четыре остальные функции будут отрицательными. Этот шаблон продолжается в квадранте три и четыре.

В вопросах, следующих за это видео, нам нужно будет использовать эту информацию, чтобы решить, являются ли наши ответы положительным или отрицательным.

Теперь рассмотрим три Пифагорейские тождества. Во-первых, у нас есть грех в квадрате 𝜃 плюс cos в квадрате 𝜃 равен единице. Наша вторая идентичность тан в квадрате 𝜃 плюс один равно сек в квадрате 𝜃.

Пока нам не нужно рассматривать доказательства личности в этом видео, мы можем получить от первой личности до второе тождество путем деления каждого члена на косинус в квадрате 𝜃. sin в квадрате 𝜃 разделить на cos квадрат 𝜃 равен тангенсу в квадрате 𝜃, так как грех 𝜃 над соз 𝜃 равен тангенсу 𝜃. Деление квадрата косина 𝜃 на косинус квадрат 𝜃 дает нам единицу. Из взаимных тождеств мы известно, что единица, деленная на кос в квадрате 𝜃, равна сек в квадрате 𝜃. Третье пифагорейское тождество один плюс детская кроватка в квадрате 𝜃 равна csc в квадрате 𝜃. Это можно получить, разделив каждый член первого тождества квадратом греха 𝜃.

грех в квадрате 𝜃 разделить на грех квадрат 𝜃 равен единице. cos в квадрате 𝜃 разделить на sin квадрат 𝜃 равен единице на тангенс в квадрате 𝜃. А это равно раскладушке в квадрате 𝜃. Наконец, один разделить на грех в квадрате 𝜃 равно csc в квадрате 𝜃.

Теперь мы будем использовать эти три тождества вместе с диаграммой CAST для решения некоторых триггерных уравнений.

Найти cos 𝜃 при данном sin 𝜃 равно до отрицательных трех пятых, где 𝜃 больше или равно 270 градусам и меньше чем 360 градусов.

Есть много способов решить Эта проблема. В этом видео мы будем использовать Пифагорейское тождество: sin в квадрате 𝜃 плюс cos в квадрате 𝜃 равно единице. Прежде чем подставить в наше значение sin 𝜃, стоит отметить, что 𝜃 должно быть больше или равно 270 градусам и менее 360 градусов. Используя наши знания о CAST диаграмме это означает, что 𝜃 должно лежать в четвертом квадранте. В этом квадранте косис угла 𝜃 положительно, тогда как грех 𝜃 и тангенс 𝜃 отрицательны. Это связано с тем, что мы говорят, что грех 𝜃 отрицателен на три пятых. Мы знаем, что наш ответ для cos of 𝜃 должен быть положительным.

Теперь мы можем заменить значение sin 𝜃 в нашу пифагорейскую идентичность. Это дает нам отрицательные три пятых квадрат плюс кос в квадрате 𝜃 равен единице. Возведение в квадрат отрицательного числа дает положительный ответ. Следовательно, отрицательные три пятых квадрат равен девяти двадцать пятым. Затем мы можем вычесть это из обоих стороны нашего уравнения. потому что квадрат 𝜃 равен 16 больше 25 или шестнадцать двадцать пятых. Квадратный корень с обеих сторон этого уравнения, мы видим, что cos из 𝜃 равен положительному или отрицательному квадратному корню из 16 на 25. Извлекая квадратный корень из дроби, мы просто квадратный корень из числителя и знаменателя отдельно. Квадратный корень из 16 равен четырем, а квадратный корень из 25 равен пяти. Поскольку cos 𝜃 должен быть положительным, мы можем заключить, что cos 𝜃 составляет четыре пятых.

В нашем следующем вопросе нам нужно оценить функцию синуса, учитывая функцию косинуса и квадрант угол.

Найдите значение sin 𝜃, учитывая cos 𝜃 равно минусу 21 на 29, где 𝜃 больше 90 градусов и меньше чем 180 градусов.

Чтобы ответить на этот вопрос, мы будем использовать тождество Пифагора: sin в квадрате 𝜃 плюс cos в квадрате 𝜃 равно один. Нам говорят, что 𝜃 лежит между 90 и 180 градусов, поэтому стоит рассмотреть нашу диаграмму CAST. Угол лежит во втором квадрант, что означает, что грех угла 𝜃 должен быть положительным. Кос угла 𝜃 и тангенса угла угол 𝜃 должен быть отрицательным. Это связано с тем, что мы говорят, что cos 𝜃 равен минус 21 на 29. Это также помогает нам в том, что мы знаем ответ на грех 𝜃 должен быть положительным.

Мы можем заменить значение cos 𝜃 в пифагорейское тождество. Возведение в квадрат отрицательного 21 на 29дает нам 441 на 841. Затем мы можем вычесть это из обоих стороны нашего уравнения такие, что квадрат греха 𝜃 равен единице минус 441 в течение 841. Правая часть упрощается до 400 на 841. Затем мы можем извлечь квадратный корень из обеих сторон нашего уравнения так, чтобы грех 𝜃 был равен положительному или отрицательному квадратному корню из 400 на 841.

Квадратный корень числителя дает нас 20 и знаменатель 29. Поскольку грех 𝜃 должен быть положительным, если потому что 𝜃 отрицателен 21 больше 29, а 𝜃 лежит между 90 и 180 градусами, тогда грех 𝜃 равен 20 на 29.

В нашем следующем вопросе мы будем использовать тождества Пифагора для вычисления выражения.

Найдите значение sin 𝜃 cos 𝜃 данный sin 𝜃 плюс cos 𝜃 равно пяти четвертям.

Чтобы решить эту проблему, мы нужно будет вспомнить пифагорейские тождества. Начнем с уравнения sin 𝜃 плюс cos 𝜃 равно пяти больше четырех. Мы можем возвести в квадрат обе стороны этого уравнение. Левая сторона становится грехом 𝜃 плюс cos 𝜃 умножить на sin 𝜃 плюс cos 𝜃. Правая часть равна 25 больше 16, поскольку мы просто возводим в квадрат числитель и знаменатель отдельно.

Распределение скобок или расширяя скобки с помощью методов FOIL, мы получаем sin в квадрате 𝜃 plus sin 𝜃 cos 𝜃 плюс грех 𝜃 кос 𝜃 плюс кос в квадрате 𝜃. Мы можем сгруппировать или собрать середину термины. грех в квадрате 𝜃 плюс два греха 𝜃 потому что 𝜃 плюс cos в квадрате 𝜃 равно 25 на 16. Одно из пифагорейских тождеств утверждает, что квадрат греха 𝜃 плюс квадрат квадрата 𝜃 равен единице. Это означает, что мы можем переписать левая часть нашего уравнения как два sin 𝜃 cos 𝜃 плюс один. Затем мы можем вычесть единицу из обоих стороны этого уравнения.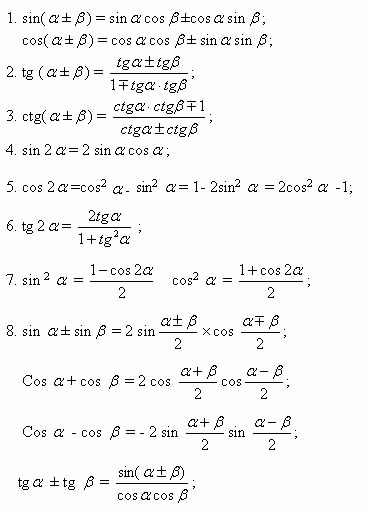 25 на 16 минус один равно девять больше 16.

Затем мы можем разделить обе стороны это новое уравнение на два, что дает нам sin 𝜃 cos 𝜃 равно девяти больше 32. Если sin 𝜃 плюс cos 𝜃 равно пять на четыре, тогда sin 𝜃, умноженный на cos 𝜃, равно девяти на 32.

В нашем последнем вопросе нам понадобится использовать другую пифагорейскую идентичность.

Найти секунду 𝜃 минус тангенс 𝜃 учитывая сек 𝜃 плюс тангенс 𝜃 равно минус 14 на 27.

Напомним, что разница Два квадрата утверждают, что 𝑥 в квадрате минус 𝑦 в квадрате равно 𝑥 плюс 𝑦 умножить на 𝑥 минус 𝑦. Это означает, что сек 𝜃 плюс загар 𝜃 умноженное на сек 𝜃 минус тангенс 𝜃 равно сек в квадрате 𝜃 минус тангенс в квадрате 𝜃. Нам говорят в вопросе значение секунды 𝜃 плюс тангенс 𝜃. Он равен минус 14 больше 27. И нам нужно рассчитать значение сек 𝜃 минус загар 𝜃.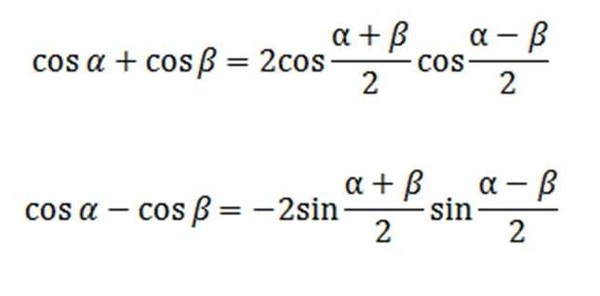

Одно из пифагорейских тождеств утверждает, что тангенс в квадрате 𝜃 плюс один равен сек в квадрате 𝜃. Если мы вычтем тангенс в квадрате 𝜃 из обе части этого уравнения, у нас есть сек в квадрате 𝜃 минус тангенс в квадрате 𝜃 равно один. Это эквивалентно правая часть нашего уравнения. Минус 14 на 27 умножить на сек 𝜃 минус тангенс 𝜃 равно единице. Затем мы можем разделить обе части это уравнение на минус 14 на 27. Мы знаем, что деление на дробь равносильно умножению на обратную дробь. Следовательно, правая часть равна равно единице, умноженной на минус 27 на 14,

Если секунда 𝜃 плюс тангенс 𝜃 равно отрицательному значению 14 на 27, то секунда 𝜃 минус тангенс 𝜃 равна отрицательное 27 на 14. Эти значения являются обратными величинами друг друга.

Теперь мы суммируем ключ очки из этого видео. Три пифагорейских тождества следующие. грех в квадрате 𝜃 плюс кос в квадрате 𝜃 равен единице. тангенс в квадрате 𝜃 плюс один равно сек в квадрате 𝜃. Один плюс детская кроватка в квадрате 𝜃 равна csc в квадрате 𝜃. В этом видео мы увидели, что можно использовать эти тождества, чтобы найти значения триггерных функций. При решении любых триггерных уравнений Также важно вспомнить, какие из функций положительны, а какие отрицательны в каждом квадрант. Один из способов сделать это — использовать Диаграмма CAST, как показано на рисунке.

Фундаментальные триггерные тождества — Magoosh ACT

Фундаментальные триггерные тождества. До сих пор мы говорили о трех основных тригонометрических функциях: синусе, косинусе и тангенсе. Эти три соотношения. Но технически из трех сторон треугольника СОХКАТОА на самом деле можно создать шесть соотношений. Итак, каждая из шести — это отдельная триггерная функция.

И действительно важно знать все шесть. Итак, мы знаем уже троих из них. Итак, давайте взглянем на этот треугольник SOHCATOA. Вот наш знакомый треугольник SOHCATOA, угол которого равен 41 градусу. Есть противолежащая, смежная гипотенуза. Итак, три соотношения, которые мы можем создать, — это знакомые соотношения СОХКАТОА.

Но мы можем создать еще три соотношения. И вот они. Котангенс смежный над противоположным. Секанс — это гипотенуза над соседней. А косеканс — это гипотенуза относительно противоположного. И это шесть коэффициентов в целом.

Подождите секунду. Что это за имена? Давайте посмотрим на эти имена очень внимательно. Вот полные имена. Итак, мы уже говорили о синусе, косинусе и тангенсе. А теперь мы говорим о котангенсе, секансе и косекансе.

И обратите внимание, как они перечислены здесь. Если вы помните, три слева, то три справа — это одно и то же имя с ко перед ним. Так что, по крайней мере, некоторые из этих названий происходят от геометрических соотношений. Давайте поговорим об этом минуту. Итак, теперь давайте посмотрим на круг.

Может быть единичным кругом радиуса 1 с центром в начале координат. Таким образом, AB и CD параллельны оси Y. Итак, у нас есть два вертикальных сегмента, AB и CD. И похоже, что B — это точка, где эта радиусная линия пересекает окружность, она продолжается. И D выглядит так, как будто она касается окружности, где она пересекает ось x.

Итак, обратите внимание на несколько вещей. Что в треугольнике OAB треугольник внутри круга, OB, радиус, равен 1. И, конечно же, OA — это косинус, а AB — это синус. Итак, это знакомое соотношение SOHCATOA. Теперь посмотрите на треугольник, немного больший треугольник, ОКР. Итак, это тот, который приходит, начинается в О, проходит через В до С.

Опускается в D и возвращается по оси X. Что ж, в этом треугольнике OD равно 1. Таким образом, это будет означать, что противоположное CD больше 1 равно касательной. Таким образом, тангенс равен CD. А это значит, что гипотенуза над соседней, ОС над 1, секущая.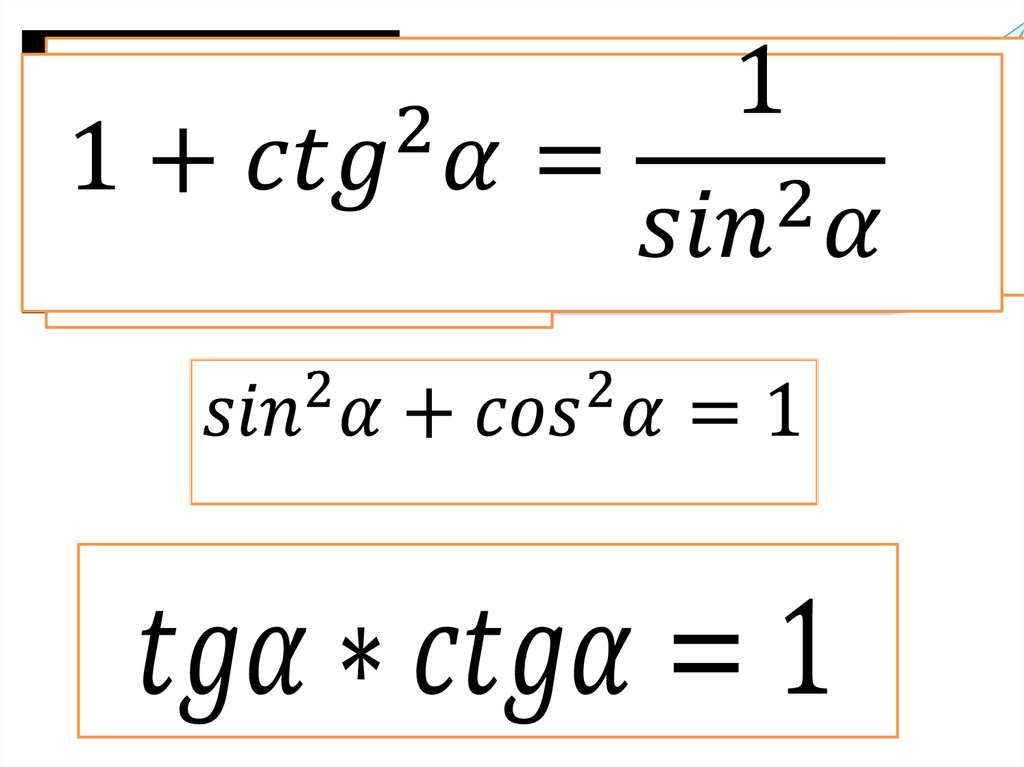

Итак, OC равен секансу. Но вот что действительно здорово в этой диаграмме. Обратите внимание, что CD, отрезок, длина которого равна касательной, на самом деле касается окружности. он проходит круг и касается его в одной точке. Это, по сути, касательная линия.

Обратите внимание, что OC, который является секущей, на самом деле пересекает окружность. И это то, что известно в геометрии как секущая линия. Вот почему эти две функции имеют такие имена, потому что одна из них представляет длину касательного сегмента. И один представляет длину секущего сегмента. Итак, если вы очень визуальный человек, это может помочь вам немного запомнить эти вещи.

Итак, синус и косинус — самые элементарные триггерные функции. И мы можем выразить остальные четыре через них. И это действительно важные формулы, которые нужно знать. Тангенс мы можем записать как синус над косинусом. Котангенс мы можем записать как косинус над синусом. Так что обратите внимание, что эти два являются взаимными.

Тангенс и котангенс обратны. Секанс обратен косинусу, а косеканс обратен синусу. Обратите внимание, что люди иногда путаются, потому что думают, что «с» и «с» должны идти вместе. С и с должны идти вместе, они не идут. Секанс является обратной величиной косинуса.

Косеканс является величиной, обратной синусу. Таким образом, тест может дать вам один из них, если он вам понадобится в задаче. Но он может ожидать, что вы тоже его запомните. Так что действительно хорошо запомнить эти четыре. На первом уроке по тригонометрии мы упомянули фундаментальное тождество Пифагора: косинус в квадрате плюс синус в квадрате равняется единице.

Теперь, когда у нас есть еще две функции, мы можем также выразить другие тождества Пифагора. Один из них равен тангенсу в квадрате плюс 1 равно секансу в квадрате. Один из них равен квадрату котангенса плюс 1 равно косекансу в квадрате. Таким образом, тест, скорее всего, даст вам эти уравнения, если они потребуются для решения задачи.

Но они могут служить кратчайшим путем или способом подтверждения ответа. Еще одна вещь, которую я скажу, это то, что если вы планируете заняться исчислением, я гарантирую, я абсолютно гарантирую, что вам нужно знать все три из этих уравнений, как только вы начнете исчисление. Так что я скажу несколько вещей о них. Конечно, вы можете запоминать их вслепую, но мы этого не рекомендуем.

Что мы действительно рекомендуем, так это понимать их. Итак, если вы начнете с того, что вверху, косинус в квадрате плюс синус в квадрате равно 1, вы можете разделить все с обеих сторон на косинус в квадрате. Вы получите верхнюю пифагорейскую идентичность по нижней касательной и секущей. Или вы можете разделить все на косинус в квадрате плюс синус в квадрате равно 1 на синус в квадрате.

И затем вы получаете нижний, котангенс в квадрате и косеканс. В качестве альтернативы вы можете вернуться к исходному треугольнику SOHCATOA с ABC и начать с теоремы Пифагора. а в квадрате плюс б в квадрате равно с в квадрате. Возможно, вы помните, что мы получили это верхнее тождество Пифагора: косинус в квадрате плюс синус в квадрате равно 1,9. 0005

Мы получили это, взяв в квадрате a плюс b в квадрате плюс c в квадрате и разделив все три члена на c в квадрате. Что ж, вместо деления на c в квадрате мы можем разделить все три члена либо на a в квадрате, либо на b в квадрате. И если вы сделаете это, а затем подставите из соотношений триггерные функции, вы получите эти два пифагорейских тождества.

Поэтому я настоятельно рекомендую сделать это самостоятельно. Покажите несколькими способами, что вы можете составить все эти уравнения, потому что тогда вы действительно их поймете. Хорошо, теперь мы можем перейти к практической задаче. Поставьте видео на паузу, и мы поговорим об этом. Хорошо, в треугольнике справа, с точки зрения b и c, что из следующего является значением тангенса тета?

Хорошо, давайте подумаем об этом. У нас там две стороны, нам даны b и c. И, конечно же, с — это гипотенуза. b противоположен, а тангенс противоположен соседнему. У нас наоборот, у нас нет соседнего. Итак, нам понадобится третья сторона.

Косинус в квадрате плюс синус в квадрате: Cos в квадрате 15 градусов — sin в квадрате 15 градусов

Тангенс 45 градусов плюс синус в квадрате 17 градусов плюс косинус в квадрате 17 градусов .

Другие вопросы по: Геометрия

Популярные вопросы

Популярные вопросы

Видео-урок: вычисление тригонометрических функций с помощью тождеств Пифагора

Стенограмма видео

Фундаментальные триггерные тождества — Magoosh ACT

Добавить комментарий Отменить ответ