Таблица котангенсов | Главный механик
Таблица котангенсов Брадиса – тесно связана с таблицей тангенсов. Это естественно, так как приставка “ко” прямо указывает нам на то, что он является обратным значением от тангенса. Это выражается и в тригонометрической формуле нахождения котангенса:
Котангенсы и тригонометрические функции, знакомство
В геометрии важную роль играют тригонометрические функции, которые объясняют, как относятся между собой углы и стороны треугольника с прямым углом. Наука не стоит на месте и развивается, так же как и тригонометрия. Есть новые решения дифференцированных уравнений, которые выражают тригонометрические функции и о которых Евклид не мог знать.
В основном, используются для вычислений значений тригонометрических функций, причем только первые из двух могут определяться только с помощью геометрии.
Синус (sin):
Косинус (cos):
Котангенс (ctg):
Тангенс (tg):
Секанс (sec):
Косеканс (cosec):
.
Рассматривая прямоугольный треугольник, нужно учесть, что все справочные материалы дают одинаковое обозначение всех его параметров, таких как углы и стороны.
Три угла в нем обозначаются α, β, γ, причем угол 90° всегда обозначается γ. Сторона, лежащая напротив прямого угла, называется гипотенуза и обозначается всегда с. Альфа это первая буква греческого алфавита и угол, с которого начинаются все расчёты, также называется α. Сторона, или катет, лежащая напротив этого угла, называется противолежащей и называется а или ВС от названия вершин. Сторона, которая лежит рядом с углом или катет, называется прилежащей и обозначается b или АС.
По теории Евклида, который довел её раз и навсегда, сумма всех углов этого треугольника, который лежит в одной плоскости, равна 180°или числу π. И значения каждого угла будут находиться в промежутке между 0 и π /2.
Тогда тригонометрические функции можно выразить через размеры сторон этого треугольника. Так как угол α является первым и в греческом алфавите и в нашем треугольнике, начинаем знакомство с функциями через этот угол.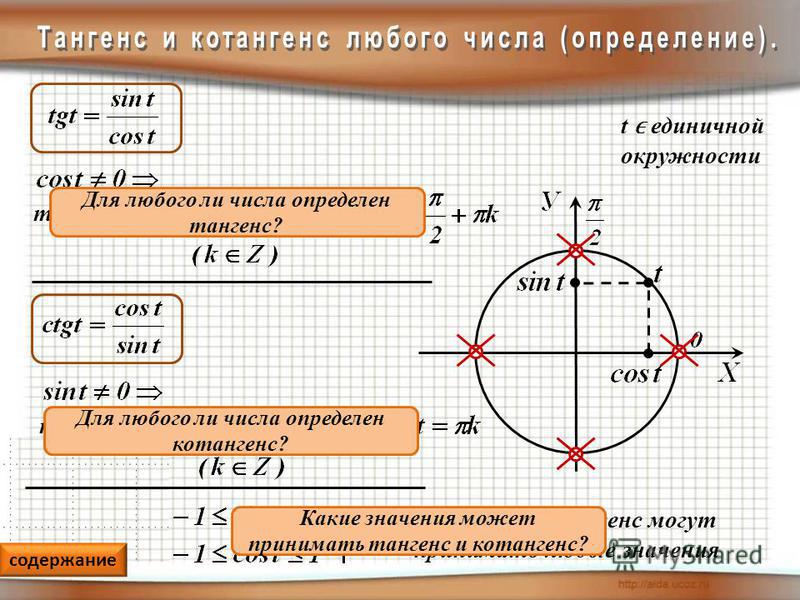
Синус α можно выразить через отношение катета, который противолежит углу α к гипотенузе нашего треугольника, то есть через формулу sin α = а: с.
Косинус α выражаем, соответственно, выражается через отношение катета, который лежит напротив этого угла, к гипотенузе нашего треугольника, то есть через формулу sin α = а: с. Также нужно помнить, что sin β = α: с, что позволяет принять то, что sin α равен cos β и следовательно sin β равен cos α, что помогает при решении задач.
Тангенс α равен частному от отношения противолежащего катета а к катету прилежащему b: tg α = а : b.
Соответственно, котангенс мы выражаем аналогичным способом ctg α = b : а.
Секанс угла α составляет отношение гипотенузы треугольника к катету, прилежащему к этому углу sec α = c : b, а косеканс по угла α той же теории как отношение гипотенузы треугольника к катету, который противостоит углу, cosec α = с : a.
Если задать систему координат с центром в точке О, а точка А, которая будет двигаться по окружности, образует радиус ОА.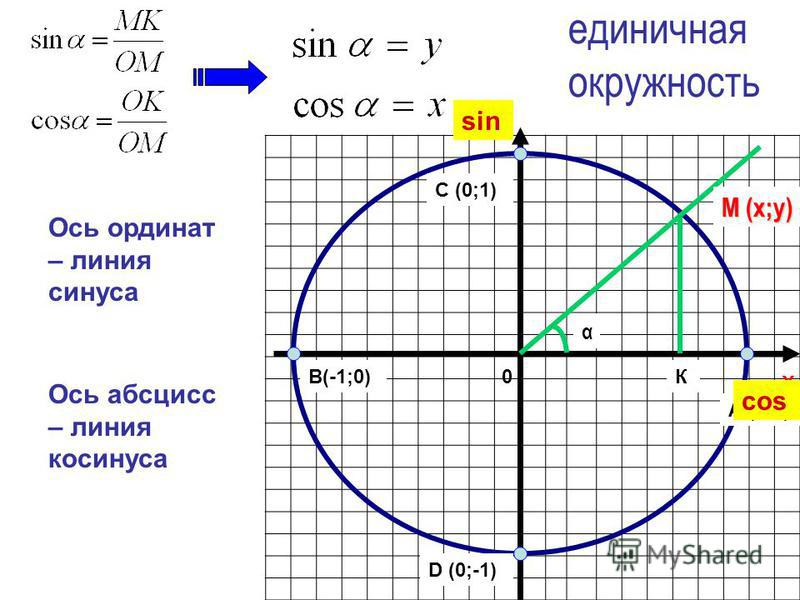 Это наглядно видно на чертеже.
Это наглядно видно на чертеже.
Угол поворота можно считать произвольным и, согласно принятым обозначениям, называется θ. Через эту окружность можно выражать вышеназванные функции.
Например, тангенсом этого угла θсчитается отношение ординаты точки А на окружности к её абсциссе. Тогда если ctg α = b : а, а АС = sin θ, ОС = cos θ, то tgθ = sin θ : cos θ. Аналогично получаем ctg θ = cos θ : sin θ или 1 : tgθ.
Калькулятор расчета котангенса угла
Применение функции котангенса для решения задач по тригонометрии
Для понимания того, как пользоваться тригонометрическими функциями, нужно практически решить задачу с применением этих функций.
Пример: прямоугольный треугольник АВС, катет ВС = а = 8 см, катет АС = b = 13 см. Нужно найти все недостающие размеры в треугольнике.
Первая формула, которую мы применяем, это ctg α = b : а. Тогда ctg α = 13 : 8=1, 625. Затем по таблице Брадиса для функций тангенсов и котангенсов ищем наше значение котангенса.
Котангенсы углов смотрим, начиная с правой стороны таблицы. Находим значение 1,6255, которое равно 30 ° 30′, но оно больше нашего на 0,0005. Можем принять его таким, а можем отнять от найденного значения поправку в 1′. Тогда угол α = 30 ° 29′. Угол β, согласно Эвклиду, будет равен: β = 90° – 30 ° 29′ = 59° 21′.Затем ищем гипотенузу с. Гипотенузу лучше искать через функцию синуса, то есть через sin α, который равен а: с, тогда с = а : sin α.
Обращаемся к таблице Брадиса, но уже не к значению тангенсов и котангенсов, а там, где указаны значения синуса и косинуса угла.
Ближайшее значение 30° 36′, будет 0,5060, тогда не хватает 3′, Что по полям поправок равно 0,0008. Добавляем это число к найденному: 0, 5060 + 0,0008 = 0,5068. Подставляем это значение в формулу, с = 8 : 0,5068, с = 15,8 см. Задачу мы успешно решили.
Можно искать значение углов через значение числа π, которое равно 180°. Тогда наиболее популярные углы, такие, как котангенс 30 градусов, котангенс 0 градусов, котангенс 60 градусов, котангенс 90 градусов, котангенс 45 градусов, котангенс 15 градусов, котангенс 75 градусов можно рассматривать намного проще. Нужно знать, что котангенс 0 градусов не существует, а котангенс 90 градусов равен 0.
Нужно знать, что котангенс 0 градусов не существует, а котангенс 90 градусов равен 0.
Можно найти котангенс угла 5 градусов, который равен 11,83 и находится в таблице Брадиса котангенсов для малых углов и добавлять или отнимать от наиболее часто встречающихся углов. Например, угол 45 градусов, его котангенс равен 1, тогда котангенс угла 50 градусов будет равен 1+11,83 = 12,83. Котангенс 35 градусов можно рассчитать путем добавления к котангенсу 30 градусов угол 5 градусов.
Для удобства есть рассчитанная таблица основных углов через значение π, которое уже рассчитано. Ниже показана таблица котангенсов и тангенсов основных углов.
| Значение угла α (градусов) | Значение угла α в радианах | ctg (Котангенс) |
|---|---|---|
| Котангенс 0 | 0 | — |
| Котангенс 15 | π/12 | 3.7321 |
| Котангенс 30 | π/6 | 1.7321 |
| Котангенс 45 | π/4 | 1 |
| Котангенс 50 | 5π/18 | 0.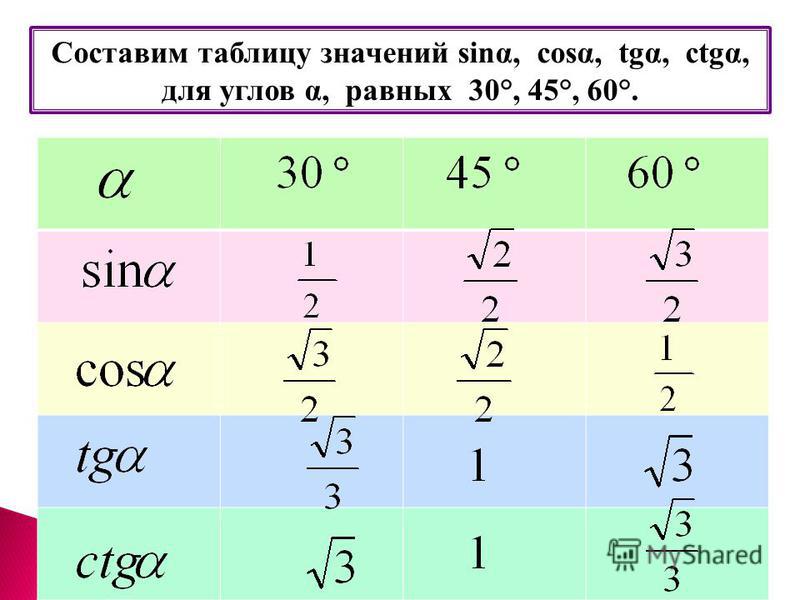 8391 8391 |
| Котангенс 60 | π/3 | 0.5774 |
| Котангенс 65 | 13π/36 | 0.4663 |
| Котангенс 70 | 7π/18 | 0.364 |
| Котангенс 75 | 5π/12 | 0.2679 |
| Котангенс 90 | π/2 | 0 |
| Котангенс 105 | 5π/12 | |
| Котангенс 120 | 2π/3 | -0.5774 |
| Котангенс 135 | 3π/4 | -1 |
| Котангенс 140 | 7π/9 | -1.1918 |
| Котангенс 150 | 5π/6 | -1.7321 |
| Котангенс 180 | π | — |
| Котангенс 270 | 3π/2 | 0 |
| Котангенс 360 | 2π |
Если угол больше 90 градусов, нужно помнить, что функции имеют свойство повторяться, поэтому, если ищем тангенс 145 градусов, тогда 180 – 145 = 35 градусов, но уже со знаком «минус», это можно понять по чертежу окружности, где положительное или отрицательное значение абсциссы и ординаты.
Научиться быстро пользоваться таблицами Брадиса и рассчитывать значения треугольника совсем не сложно, главное, уловить суть процесса. Но можно, если это не экзамен по математике, рассчитать функцию котангенса и онлайн на сайте.
Таблица котангенсов Брадиса для углов до 75 градусов
| ctg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ctg | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | 1′ | 2′ | 3′ |
| 0 | 90° | |||||||||||||
| 89° | 0 | 17 | 35 | 52 | 70 | 87 | 105 | 122 | 140 | 157 | 175 | 3 | 6 | 9 |
| 88° | 175 | 192 | 209 | 227 | 244 | 262 | 279 | 297 | 314 | 332 | 349 | 3 | 6 | 9 |
| 87° | 349 | 384 | 402 | 419 | 437 | 454 | 472 | 489 | 507 | 524 | 3 | 6 | 9 | |
| 86° | 524 | 542 | 559 | 577 | 594 | 612 | 629 | 647 | 664 | 682 | 699 | 3 | 6 | 9 |
| 85° | 699 | 717 | 734 | 752 | 769 | 787 | 805 | 822 | 840 | 857 | 0. 0875 0875 | 3 | 6 | 9 |
| 84° | 0.0875 | 892 | 910 | 928 | 945 | 963 | 981 | 998 | 1016 | 1033 | 1051 | 3 | 6 | 9 |
| 83° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 3 | 6 | 9 |
| 82° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 3 | 6 | 9 |
| 81° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 3 | 6 | 9 |
| 80° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0.1763 | 3 | 6 | 9 |
| 79° | 0. 1763 1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 3 | 6 | 9 |
| 78° | 1944 | 1962 | 1980 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 3 | 6 | 9 | |
| 77° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 3 | 6 | 9 |
| 76° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 3 | 6 | 9 |
| 75° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0.2679 | 3 | 6 | 9 |
| 74° | 0.2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 3 | 6 | 9 |
| 73° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 3 | 6 | 9 |
| 72° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 3 | 6 | 10 |
| 71° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 3 | 6 | 10 |
| 70° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0.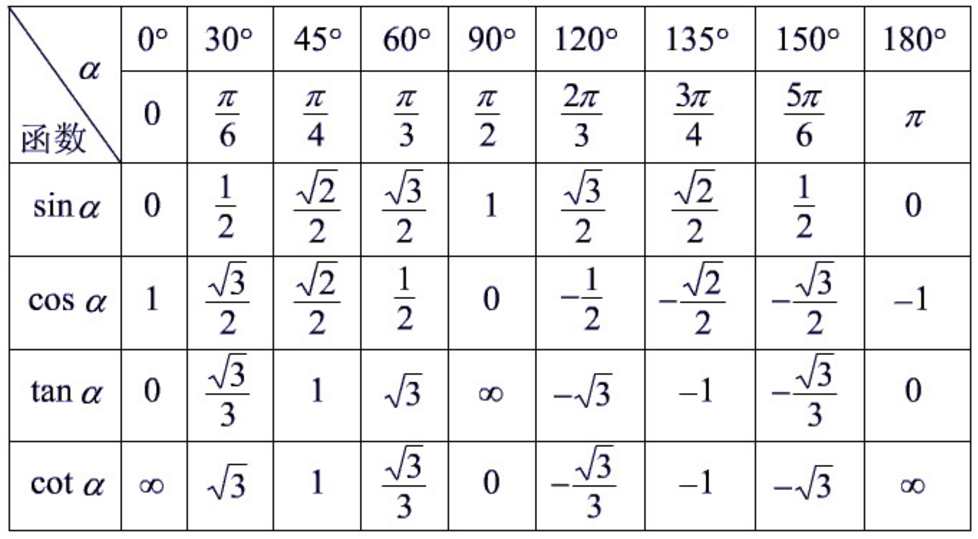 364 364 | 3 | 7 | 10 |
| 69° | 0.364 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 3 | 7 | 10 |
| 68° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 3 | 7 | 10 |
| 67° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 3 | 7 | 10 |
| 66° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 3 | 7 | 10 |
| 65° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0.4663 | 4 | 7 | 11 |
| 64° | 0. 4663 4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 4 | 7 | 11 |
| 63° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 4 | 7 | 11 |
| 62° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 4 | 7 | 11 |
| 61° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 4 | 8 | 11 |
| 60° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0.5774 | 4 | 8 | 12 |
| 59° | 0.5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 4 | 8 | 12 |
| 58° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 4 | 8 | 12 |
| 57° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 4 | 8 | 12 |
| 56° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 4 | 8 | 13 |
| 55° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0. 7002 7002 | 4 | 9 | 13 |
| 54° | 0.7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 4 | 8 | 13 |
| 53° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 5 | 9 | 14° |
| 52° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 5 | 9 | 14 |
| 51° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 5 | 9 | 14 |
| 50° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0.8391 | 5 | 10 | 15 |
| 49° | 0. 8391 8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0.8693 | 5 | 10 | 15 |
| 48° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 5 | 10 | 16 |
| 47° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 6 | 11 | 16 |
| 46° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0.9657 | 6 | 11 | 17 |
| 45° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 1 | 6 | 11 | 17 |
| 44° | 1 | 35 | 70 | 105 | 141 | 176 | 212 | 247 | 283 | 319 | 355 | 6 | 12 | 18 |
| 43° | 355 | 392 | 428 | 464 | 501 | 538 | 575 | 612 | 649 | 686 | 724 | 6 | 12 | 18 |
| 42° | 724 | 761 | 799 | 837 | 875 | 913 | 951 | 990 | 1028 | 1067 | 1106 | 6 | 13 | 19 |
| 41° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 7 | 13 | 20 |
| 40° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1. 1918 1918 | 7 | 14 | 21 |
| 39° | 1.1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 7 | 14 | 22 |
| 38° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 8 | 15 | 23 |
| 37° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 8 | 16 | 24 |
| 36° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 8 | 16 | 25 |
| 35° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1.4281 | 9 | 17 | 26 |
| 34° | 1. 4281 4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 9 | 18 | 27 |
| 33° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 10 | 19 | 29 |
| 32° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 10 | 20 | 30 |
| 31° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 11 | 21 | 32 |
| 30° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1.7321 | 11 | 23 | 34 |
| 29° | 1.732 | 1. 739 739 | 1.746 | 1.753 | 1.76 | 1.767 | 1.775 | 1.782 | 1.789 | 1.797 | 1.804 | 1 | 2 | 4 |
| 28° | 1.804 | 1.811 | 1.819 | 1.827 | 1.834 | 1.842 | 1.849 | 1.857 | 1.865 | 1.873 | 1.881 | 1 | 3 | 4 |
| 27° | 1.881 | 1.889 | 1.897 | 1.905 | 1.913 | 1.921 | 1.929 | 1.937 | 1.946 | 1.954 | 1.963 | 1 | 3 | 4 |
| 26° | 1.963 | 1.971 | 1.98 | 1.988 | 1.997 | 2.006 | 2.014 | 2.023 | 2.032 | 2.041 | 2.05 | 1 | 3 | 4 |
| 25° | 2.05 | 2.059 | 2.069 | 2.078 | 2.087 | 2.097 | 2.106 | 2.116 | 2.125 | 2.135 | 2.145 | 2 | 3 | 5 |
| 24° | 2. 145 145 | 2.154 | 2.164 | 2.174 | 2.184 | 2.194 | 2.204 | 2.215 | 2.225 | 2.236 | 2.246 | 2 | 3 | 5 |
| 23° | 2.246 | 2.257 | 2.267 | 2.278 | 2.289 | 2.3 | 2.311 | 2.322 | 2.333 | 2.344 | 2.356 | 2 | 4 | 5 |
| 22° | 2.356 | 2.367 | 2.379 | 2.391 | 2.402 | 2.414 | 2.426 | 2.438 | 2.45 | 2.463 | 2.475 | 2 | 4 | 6 |
| 21° | 2.475 | 2.488 | 2.5 | 2.513 | 2.526 | 2.539 | 2.552 | 2.565 | 2.578 | 2.592 | 2.605 | 2 | 4 | 6 |
| 20° | 2.605 | 2.619 | 2.633 | 2.646 | 2.66 | 2.675 | 2.689 | 2.703 | 2.718 | 2.733 | 2.747 | 2 | 5 | 7 |
| 19° | 2. 747 747 | 2.762 | 2.778 | 2.793 | 2.808 | 2.824 | 2.84 | 2.856 | 2.872 | 2.888 | 2.904 | 3 | 5 | 8 |
| 18° | 2.904 | 2.921 | 2.937 | 2.954 | 2.971 | 2.989 | 3.006 | 3.024 | 3.042 | 3.06 | 3.078 | 3 | 6 | 9 |
| 17° | 3.078 | 3.096 | 3.115 | 3.133 | 3.152 | 3.172 | 3.191 | 3.211 | 3.23 | 3.251 | 3.271 | 3 | 6 | 10 |
| 16° | 3.271 | 3.291 | 3.312 | 3.333 | 3.354 | 3.376 | 3 | 7 | 10 | |||||
| 3.398 | 3.42 | 3.442 | 3.465 | 3.487 | 4 | 7 | 11 | |||||||
| 15° | 3.487 | 3.511 | 3.534 | 3.558 | 3.582 | 3.606 | 4 | 8 | 12 | |||||
3. 63 63 | 3.655 | 3.681 | 3.706 | 3.732 | 4 | 8 | 13 | |||||||
| 14° | 3.732 | 3.758 | 3.785 | 3.812 | 3.839 | 3.867 | 4 | 9 | 13 | |||||
| 3.895 | 3.923 | 3.952 | 3.981 | 4.011 | 5 | 10 | 14 |
Таблица котангенсов Брадиса для углов, близких к 90 градусам
| ctg | 0′ | 1′ | 2′ | 3′ | 4′ | 5′ | 6′ | 7′ | 8′ | 9′ | 10′ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ctg | 10′ | 9′ | 8′ | 7′ | 6′ | 5′ | 4′ | 3′ | 2′ | 1′ | 0′ |
| 50′ | 4.011 | 4.016 | 4.021 | 4.026 | 4.031 | 4.036 | 4.041 | 4.046 | 4.051 | 4.056 | 4.061 |
| 40′ | 4.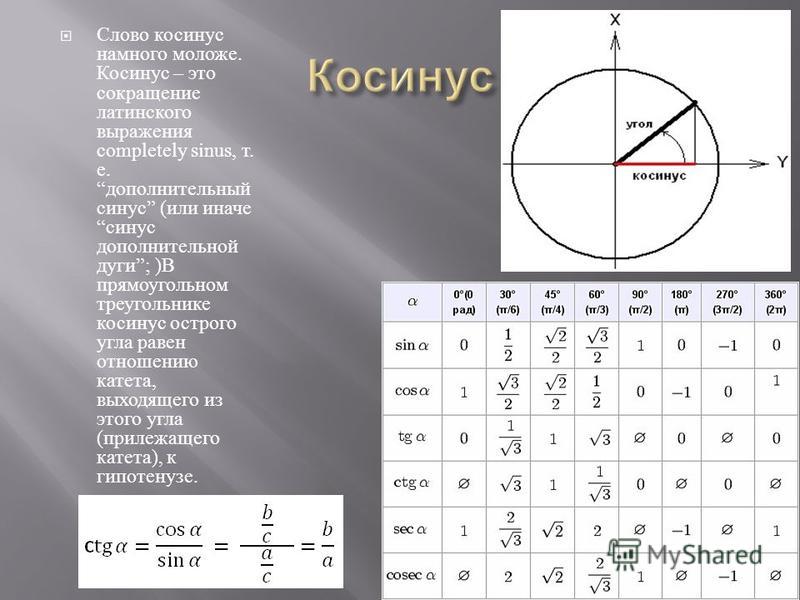 061 061 | 4.066 | 4.071 | 4.076 | 4.082 | 4.087 | 4.092 | 4.097 | 4.102 | 4.107 | 4.113 |
| 30′ | 4.113 | 4.118 | 4.123 | 4.128 | 4.134 | 4.139 | 4.144 | 4.149 | 4.155 | 4.16 | 4.165 |
| 20′ | 4.165 | 4.171 | 4.176 | 4.181 | 4.187 | 4.192 | 4.198 | 4.203 | 4.208 | 4.214 | 4.219 |
| 10′ | 4.219 | 4.225 | 4.23 | 4.236 | 4.241 | 4.247 | 4.252 | 4.258 | 4.264 | 4.269 | 4.275 |
| 13°00′ | 4.275 | 4.28 | 4.286 | 4.292 | 4.297 | 4.303 | 4.309 | 4.314 | 4.32 | 4.326 | 4.331 |
| 50′ | 4.331 | 4.337 | 4.343 | 4.349 | 4.355 | 4.36 | 4.366 | 4.372 | 4.378 | 4. 384 384 | 4.39 |
| 40′ | 4.39 | 4.396 | 4.402 | 4.407 | 4.413 | 4.419 | 4.425 | 4.431 | 4.437 | 4.443 | 4.449 |
| 30′ | 4.449 | 4.455 | 4.462 | 4.468 | 4.474 | 4.48 | 4.486 | 4.492 | 4.498 | 4.505 | 4.511 |
| 20′ | 4.511 | 4.517 | 4.523 | 4.529 | 4.536 | 4.542 | 4.548 | 4.555 | 4.561 | 4.567 | 4.574 |
| 10′ | 4.574 | 4.58 | 4.586 | 4.593 | 4.599 | 4.606 | 4.612 | 4.619 | 4.625 | 4.632 | 4.638 |
| 12°00′ | 4.638 | 4.645 | 4.651 | 4.658 | 4.665 | 4.671 | 4.678 | 4.685 | 4.691 | 4.698 | 4.705 |
| 50′ | 4.705 | 4.711 | 4.718 | 4.725 | 4.732 | 4.739 | 4. 745 745 | 4.752 | 4.759 | 4.766 | 4.773 |
| 40′ | 4.773 | 4.78 | 4.787 | 4.794 | 4.801 | 4.808 | 4.815 | 4.822 | 4.829 | 4.836 | 4.843 |
| 30′ | 4.843 | 4.85 | 4.857 | 4.864 | 4.872 | 4.879 | 4.886 | 4.893 | 4.901 | 4.908 | 4.915 |
| 20′ | 4.915 | 4.922 | 4.93 | 4.937 | 4.945 | 4.952 | 4.959 | 4.967 | 4.974 | 4.982 | 4.989 |
| 10′ | 4.989 | 4.997 | 5.005 | 5.012 | 5.02 | 5.027 | 5.035 | 5.043 | 5.05 | 5.058 | 5.066 |
| 11°00′ | 5.066 | 5.074 | 5.081 | 5.089 | 5.097 | 5.105 | 5.113 | 5.121 | 5.129 | 5.137 | 5.145 |
| 50′ | 5.145 | 5.153 | 5.161 | 5. 169 169 | 5.177 | 5.185 | 5.193 | 5.201 | 5.209 | 5.217 | 5.226 |
| 40′ | 5.226 | 5.234 | 5.242 | 5.25 | 5.259 | 5.267 | 5.276 | 5.284 | 5.292 | 5.301 | 5.309 |
| 30′ | 5.309 | 5.318 | 5.326 | 5.335 | 5.343 | 5.352 | 5.361 | 5.369 | 5.378 | 5.387 | 5.396 |
| 20′ | 5.396 | 5.404 | 5.413 | 5.422 | 5.431 | 5.44 | 5.449 | 5.458 | 5.466 | 5.475 | 5.485 |
| 10′ | 5.485 | 5.494 | 5.503 | 5.512 | 5.521 | 5.53 | 5.539 | 5.549 | 5.558 | 5.567 | 5.576 |
| 10°00′ | 5.576 | 5.586 | 5.595 | 5.605 | 5.614 | 5.623 | 5.633 | 5.642 | 5.652 | 5.662 | 5.671 |
| 50′ | 5. 671 671 | 5.681 | 5.691 | 5.7 | 5.71 | 5.72 | 5.73 | 5.74 | 5.749 | 5.759 | 5.769 |
| 40′ | 5.769 | 5.779 | 5.789 | 5.799 | 5.81 | 5.82 | 5.83 | 5.84 | 5.85 | 5.861 | 5.871 |
| 30′ | 5.871 | 5.881 | 5.892 | 5.902 | 5.912 | 5.923 | 5.933 | 5.944 | 5.954 | 5.965 | 5.976 |
| 20′ | 5.976 | 5.986 | 5.997 | 6.008 | 6.019 | 6.03 | 6.041 | 6.051 | 6.062 | 6.073 | 6.084 |
| 10′ | 6.084 | 6.096 | 6.107 | 6.118 | 6.129 | 6.14 | 6.152 | 6.163 | 6.174 | 6.186 | 6.197 |
| 9°00′ | 6.197 | 6.209 | 6.22 | 6.232 | 6.243 | 6.255 | 6.267 | 6.278 | 6.29 | 6.302 | 6.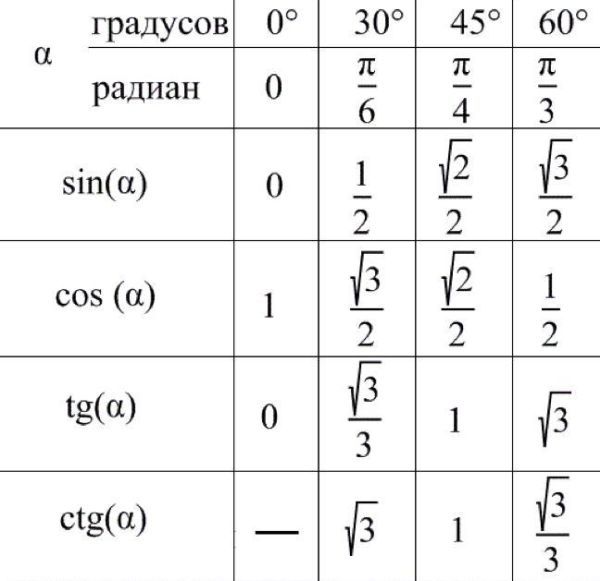 314 314 |
| 50′ | 6.314 | 6.326 | 6.338 | 6.35 | 6.362 | 6.374 | 6.386 | 6.398 | 6.41 | 6.423 | 6.435 |
| 40′ | 6.435 | 6.447 | 6.46 | 6.472 | 6.485 | 6.497 | 6.51 | 6.522 | 6.535 | 6.548 | 6.561 |
| 30′ | 6.561 | 6.573 | 6.586 | 6.599 | 6.612 | 6.625 | 6.638 | 6.651 | 6.665 | 6.678 | 6.691 |
| 20′ | 6.691 | 6.704 | 6.718 | 6.731 | 6.745 | 6.758 | 6.772 | 6.786 | 6.799 | 6.813 | 6.827 |
| 10′ | 6.827 | 6.841 | 6.855 | 6.869 | 6.883 | 6.897 | 6.911 | 6.925 | 6.94 | 6.954 | 6.968 |
| 8°00′ | 6.968 | 6.983 | 6.997 | 7.012 | 7.026 | 7.041 | 7.056 | 7. 071 071 | 7.085 | 7.1 | 7.115 |
| 50′ | 7.115 | 7.13 | 7.146 | 7.161 | 7.176 | 7.191 | 7.207 | 7.222 | 7.238 | 7.253 | 7.269 |
| 40′ | 7.269 | 7.284 | 7.3 | 7.316 | 7.332 | 7.348 | 7.363 | 7.38 | 7.396 | 7.412 | 7.429 |
| 30′ | 7.429 | 7.445 | 7.462 | 7.478 | 7.495 | 7.511 | 7.528 | 7.545 | 7.562 | 7.579 | 7.596 |
| 20′ | 7.596 | 7.613 | 7.63 | 7.647 | 7.665 | 7.682 | 7.7 | 7.717 | 7.735 | 7.753 | 7.77 |
| 10′ | 7.77 | 7.788 | 7.806 | 7.824 | 7.842 | 7.861 | 7.879 | 7.897 | 7.916 | 7.934 | 7.953 |
| 7°00′ | 7.953 | 7.972 | 7.991 | 8.009 | 8.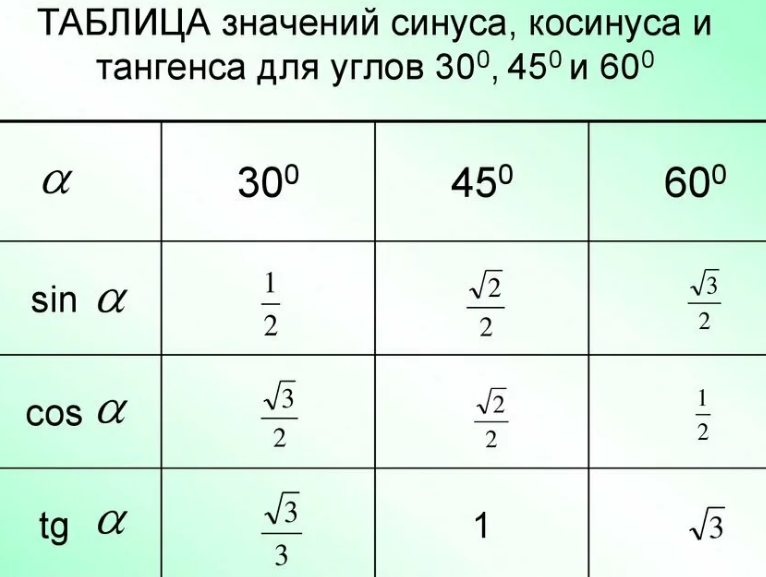 028 028 | 8.048 | 8.067 | 8.086 | 8.105 | 8.125 | 8.144 |
| 50′ | 8.144 | 8.164 | 8.184 | 8.204 | 8.223 | 8.243 | 8.264 | 8.284 | 8.304 | 8.324 | 8.345 |
| 40′ | 8.345 | 8.366 | 8.386 | 8.407 | 8.428 | 8.449 | 8.47 | 8.491 | 8.513 | 8.534 | 8.556 |
| 30′ | 8.556 | 8.577 | 8.599 | 8.621 | 8.643 | 8.665 | 8.687 | 8.709 | 8.732 | 8.754 | 8.777 |
| 20′ | 8.777 | 8.8 | 8.823 | 8.846 | 8.869 | 8.892 | 8.915 | 8.939 | 8.962 | 8.986 | 9.01 |
| 10′ | 9.01 | 9.034 | 9.058 | 9.082 | 9.106 | 9.131 | 9.156 | 9.18 | 9.205 | 9.23 | 9.255 |
| 6°00′ | 9.255 | 9. 281 281 | 9.306 | 9.332 | 9.357 | 9.383 | 9.409 | 9.435 | 9.461 | 9.488 | 9.514 |
| 50′ | 9.514 | 9.541 | 9.568 | 9.595 | 9.622 | 9.649 | 9.677 | 9.704 | 9.732 | 9.76 | 9.788 |
| 40′ | 9.788 | 9.816 | 9.845 | 9.873 | 9.902 | 9.931 | 9.96 | 9.989 | 10.02 | 10.05 | 10.08 |
| 30′ | 10.08 | 10.11 | 10.14 | 10.17 | 10.2 | 10.23 | 10.26 | 10.29 | 10.32 | 10.35 | 10.39 |
| 20′ | 10.39 | 10.42 | 10.45 | 10.48 | 10.51 | 10.55 | 10.58 | 10.61 | 10.64 | 10.68 | 10.71 |
| 10′ | 10.71 | 10.75 | 10.78 | 10.81 | 10.85 | 10.88 | 10.92 | 10.95 | 10.99 | 11.02 | 11. 06 06 |
| 5°00′ | 11.06 | 11.1 | 11.13 | 11.17 | 11.2 | 11.24 | 11.28 | 11.32 | 11.35 | 11.39 | 11.43 |
| 50′ | 11.43 | 11.47 | 11.51 | 11.55 | 11.59 | 11.62 | 11.66 | 11.7 | 11.74 | 11.79 | 11.83 |
| 40′ | 11.83 | 11.87 | 11.91 | 11.95 | 11.99 | 12.03 | 12.08 | 12.12 | 12.16 | 12.21 | 12.25 |
| 30′ | 12.25 | 12.29 | 12.34 | 12.38 | 12.43 | 12.47 | 12.52 | 12.57 | 12.61 | 12.66 | 12.71 |
| 20′ | 12.71 | 12.75 | 12.8 | 12.85 | 12.9 | 12.95 | 13 | 13.05 | 13.1 | 13.15 | 13.2 |
| 10′ | 13.2 | 13.25 | 13.3 | 13.35 | 13.4 | 13.46 | 13.51 | 13. 56 56 | 13.62 | 13.67 | 13.73 |
| 4°00′ | 13.73 | 13.78 | 13.84 | 13.89 | 13.95 | 14.01 | 14.07 | 14.12 | 14.18 | 14.24 | 14.3 |
| 50′ | 14.3 | 14.36 | 14.42 | 14.48 | 14.54 | 14.61 | 14.67 | 14.73 | 14.8 | 14.86 | 14.92 |
| 40′ | 14.92 | 14.99 | 15.06 | 15.12 | 15.19 | 15.26 | 15.33 | 15.39 | 15.46 | 15.53 | 15.6 |
| 30′ | 15.6 | 15.68 | 15.75 | 15.82 | 15.89 | 15.97 | 16.04 | 16.12 | 16.2 | 16.27 | 16.35 |
| 20′ | 16.35 | 16.43 | 16.51 | 16.59 | 16.67 | 16.75 | 16.83 | 16.92 | 17 | 17.08 | 17.17 |
| 10′ | 17.17 | 17.26 | 17.34 | 17.43 | 17. 52 52 | 17.61 | 17.7 | 17.79 | 17.89 | 17.98 | 18.07 |
| 3°00′ | 18.07 | 18.17 | 18.27 | 18.37 | 18.46 | 18.56 | 18.67 | 18.77 | 18.87 | 18.98 | 19.08 |
| 50′ | 19.08 | 19.19 | 19.3 | 19.41 | 19.52 | 19.63 | 19.74 | 19.85 | 19.97 | 20.09 | 20.21 |
| 40′ | 20.21 | 20.33 | 20.45 | 20.57 | 20.69 | 20.82 | 20.95 | 21.07 | 21.2 | 21.34 | 21.47 |
| 30′ | 21.47 | 21.61 | 21.74 | 21.88 | 22.02 | 22.16 | 22.31 | 22.45 | 22.6 | 22.75 | 22.9 |
| 20′ | 22.9 | 23.06 | 23.21 | 23.37 | 23.53 | 23.69 | 23.86 | 24.03 | 24.2 | 24.37 | 24.54 |
| 10′ | 24.54 | 24. 72 72 | 24.9 | 25.08 | 25.26 | 25.45 | 25.64 | 25.83 | 26.03 | 26.23 | 26.43 |
| 2°00′ | 26.43 | 26.64 | 26.84 | 27.06 | 27.27 | 27.49 | 27.71 | 27.94 | 28.17 | 28.4 | 28.64 |
| 50′ | 28.64 | 28.88 | 29.12 | 29.37 | 29.62 | 29.88 | 30.14 | 30.41 | 30.68 | 30.96 | 31.24 |
| 40′ | 31.24 | 31.53 | 31.82 | 32.12 | 32.42 | 32.73 | 33.05 | 33.37 | 33.69 | 34.03 | 34.37 |
| 30′ | 34.37 | 34.72 | 35.07 | 35.43 | 35.8 | 36.18 | 36.56 | 36.96 | 37.36 | 37.77 | 38.19 |
| 20′ | 38.19 | 38.62 | 39.06 | 39.51 | 39.97 | 40.44 | 40.92 | 41.41 | 41.92 | 42.43 | 42.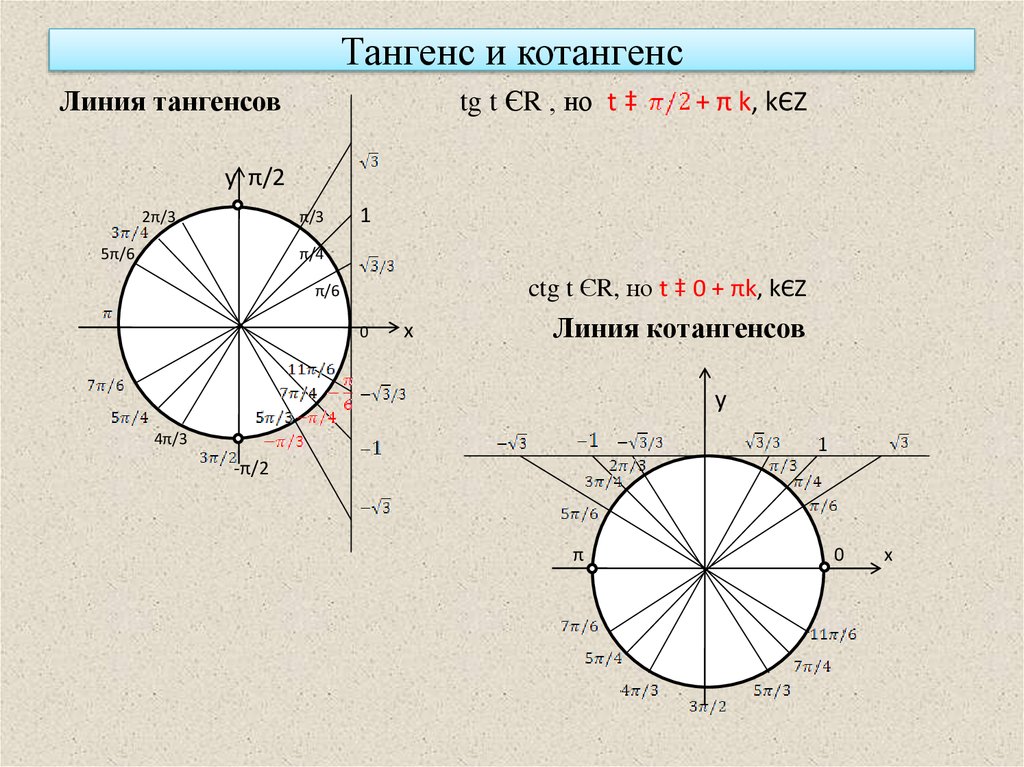 96 96 |
| 10′ | 42.96 | 43.51 | 44.07 | 44.64 | 45.23 | 45.83 | 46.45 | 47.09 | 47.74 | 48.41 | 49.1 |
| 1°00′ | 49.1 | 49.82 | 50.55 | 51.3 | 52.08 | 52.88 | 53.71 | 54.56 | 55.44 | 56.35 | 57.29 |
| 50′ | 57.29 | 58.26 | 59.27 | 60.31 | 61.38 | 62.5 | 63.66 | 64.86 | 66.11 | 67.4 | 68.75 |
| 40′ | 68.75 | 70.15 | 71.62 | 73.14 | 74.73 | 76.39 | 78.13 | 79.94 | 81.85 | 83.84 | 85.94 |
| 30′ | 85.94 | 88.14 | 90.46 | 92.91 | 95.49 | 98.22 | 101.1 | 104.2 | 107.4 | 110.9 | 114.6 |
| 20′ | 114.6 | 118.5 | 122.8 | 127.3 | 132.2 | 137.5 | 143.2 | 149. 5 5 | 156.3 | 163.7 | 171.9 |
| 10′ | 171.9 | 180.9 | 191 | 202.2 | 214.9 | 229.2 | 245.6 | 264.4 | 286.5 | 312.5 | 343.8 |
| 0°00′ | 343.8 | 382 | 429.7 | 491.1 | 573 | 687.5 | 859.4 | 1146 | 1719 | 3438 |
Интересные статьи
Таблица котангенс угла
Котангенс угла
Определение 1
Котангенсом угла называют отношение катета, являющегося образующим лучом рассматриваемого угла и не являющегося гипотенузой, к стороне, лежащей напротив данного угла и называемой противолежащим катетом.
Котангенс является обратной функцией тангенса, то есть, котангенс, кратко обозначаемый как ctg, равен: $\mathrm{ctg}α=\frac{1}{\mathrm{tg} α}$.
Если под рукой имеется таблица Брадиса для синусов и косинусов, то для того чтобы узнать значение котангенса, можно воспользоваться его определением через эти тригонометрические функции:
$\mathrm{ctg} α=\frac{\cos α}{\sin α}$.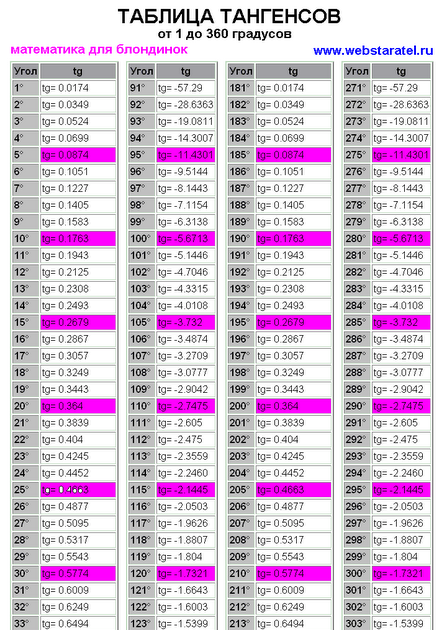
Для треугольника с гипотенузой, равной радиусу единичной окружности, для ctg также будет соблюдаться соотношение:
$\mathrm{ctg} α=\frac{x_B}{y_B}$, где $x_B, y_B$ — проекции гипотенузы на оси абсцисс и ординат соответственно.
Для того чтобы узнать значение котангенса, также можно воспользоваться приведённой ниже таблицей значений. Ниже приведены значения от $0$ до $180$ градусов, но данную таблицу можно использовать и для $α > 180°$, для этого нужно найти разность $α-180°$ и затем уже искать котангенс для неё.
Таблица значений котангенса от $0$ до $180$ градусов
котангенс (1) ° ≈ 57,28996
котангенс (2) ° ≈ 28,63625
котангенс (3) ° ≈ 19,08114
котангенс (4) ° ≈ 14,30067
котангенс (5) ° ≈ 11,43005
котангенс (6) ° ≈ 9,51436
котангенс (7) ° ≈ 8,14435
котангенс (8) ° ≈ 7,11537
котангенс (9) ° ≈ 6,31375
котангенс (10) ° ≈ 5,67128
котангенс (11) ° ≈ 5,14455
котангенс (12) ° ≈ 4,70463
котангенс (13) ° ≈ 4,33148
котангенс (14) ° ≈ 4,01078
котангенс (15) ° ≈ 3,73205
котангенс (16) ° ≈ 3,48741
котангенс (17) ° ≈ 3,27085
котангенс (18) ° ≈ 3,07768
котангенс (19) ° ≈ 2,90421
котангенс (20) ° ≈ 2,74748
котангенс (21) ° ≈ 2,60509
котангенс (22) ° ≈ 2,47509
котангенс (23) ° ≈ 2,35585
котангенс (24) ° ≈ 2,24604
котангенс (25) ° ≈ 2,14451
котангенс (26) ° ≈ 2,0503
котангенс (27) ° ≈ 1,96261
котангенс (28) ° ≈ 1,88073
котангенс (29) ° ≈ 1,80405
котангенс (30) ° ≈ 1,73205
котангенс (31) ° ≈ 1,66428
котангенс (32) ° ≈ 1,60033
котангенс (33) ° ≈ 1,53986
котангенс (34) ° ≈ 1,48256
котангенс (35) ° ≈ 1,42815
котангенс (36) ° ≈ 1,37638
котангенс (37) ° ≈ 1,32704
котангенс (38) ° ≈ 1,27994
котангенс (39) ° ≈ 1,2349
котангенс (40) ° ≈ 1,19175
котангенс (41) ° ≈ 1,15037
котангенс (42) ° ≈ 1,11061
котангенс (43) ° ≈ 1,07237
котангенс (44) ° ≈ 1,03553
котангенс (45) ° = 1
котангенс (46) ° ≈ 0,96569
котангенс (47) ° ≈ 0,93252
котангенс (48) ° ≈ 0,9004
котангенс (49) ° ≈ 0,86929
котангенс (50) ° ≈ 0,8391
котангенс (51) ° ≈ 0,80978
котангенс (52) ° ≈ 0,78129
котангенс (53) ° ≈ 0,75355
котангенс (54) ° ≈ 0,72654
котангенс (55) ° ≈ 0,70021
котангенс (56) ° ≈ 0,67451
котангенс (57) ° ≈ 0,64941
котангенс (58) ° ≈ 0,62487
котангенс (59) ° ≈ 0,60086
котангенс (60) ° ≈ 0,57735
котангенс (61) ° ≈ 0,55431
котангенс (62) ° ≈ 0,53171
котангенс (63) ° ≈ 0,50953
котангенс (64) ° ≈ 0,48773
котангенс (65) ° ≈ 0,46631
котангенс (66) ° ≈ 0,44523
котангенс (67) ° ≈ 0,42447
котангенс (68) ° ≈ 0,40403
котангенс (69) ° ≈ 0,38386
котангенс (70) ° ≈ 0,36397
котангенс (71) ° ≈ 0,34433
котангенс (72) ° ≈ 0,32492
котангенс (73) ° ≈ 0,30573
котангенс (74) ° ≈ 0,28675
котангенс (75) ° ≈ 0,26795
котангенс (76) ° ≈ 0,24933
котангенс (77) ° ≈ 0,23087
котангенс (78) ° ≈ 0,21256
котангенс (79) ° ≈ 0,19438
котангенс (80) ° ≈ 0,17633
котангенс (81) ° ≈ 0,15838
котангенс (82) ° ≈ 0,14054
котангенс (83) ° ≈ 0,12278
котангенс (84) ° ≈ 0,1051
котангенс (85) ° ≈ 0,08749
котангенс (86) ° ≈ 0,06993
котангенс (87) ° ≈ 0,05241
котангенс (88) ° ≈ 0,03492
котангенс (89) ° ≈ 0,01746
котангенс (90) ° = 0
котангенс (91) ° ≈ -0,01746
котангенс (92) ° ≈ -0,03492
котангенс (93) ° ≈ -0,05241
котангенс (94) ° ≈ -0,06993
котангенс (95) ° ≈ -0,08749
котангенс (96) ° ≈ -0,1051
котангенс (97) ° ≈ -0,12278
котангенс (98) ° ≈ -0,14054
котангенс (99) ° ≈ -0,15838
котангенс (100) ° ≈ -0,17633
котангенс (101) ° ≈ -0,19438
котангенс (102) ° ≈ -0,21256
котангенс (103) ° ≈ -0,23087
котангенс (104) ° ≈ -0,24933
котангенс (105) ° ≈ -0,26795
котангенс (106) ° ≈ -0,28675
котангенс (107) ° ≈ -0,30573
котангенс (108) ° ≈ -0,32492
котангенс (109) ° ≈ -0,34433
котангенс (110) ° ≈ -0,36397
котангенс (111) ° ≈ -0,38386
котангенс (112) ° ≈ -0,40403
котангенс (113) ° ≈ -0,42447
котангенс (114) ° ≈ -0,44523
котангенс (115) ° ≈ -0,46631
котангенс (116) ° ≈ -0,48773
котангенс (117) ° ≈ -0,50953
котангенс (118) ° ≈ -0,53171
котангенс (119) ° ≈ -0,55431
котангенс (120) ° ≈ -0,57735
котангенс (121) ° ≈ -0,60086
котангенс (122) ° ≈ -0,62487
котангенс (123) ° ≈ -0,64941
котангенс (124) ° ≈ -0,67451
котангенс (125) ° ≈ -0,70021
котангенс (126) ° ≈ -0,72654
котангенс (127) ° ≈ -0,75355
котангенс (128) ° ≈ -0,78129
котангенс (129) ° ≈ -0,80978
котангенс (130) ° ≈ -0,8391
котангенс (131) ° ≈ -0,86929
котангенс (132) ° ≈ -0,9004
котангенс (133) ° ≈ -0,93252
котангенс (134) ° ≈ -0,96569
котангенс (135) ° = -1
котангенс (136) ° ≈ -1,03553
котангенс (137) ° ≈ -1,07237
котангенс (138) ° ≈ -1,11061
котангенс (139) ° ≈ -1,15037
котангенс (140) ° ≈ -1,19175
котангенс (141) ° ≈ -1,2349
котангенс (142) ° ≈ -1,27994
котангенс (143) ° ≈ -1,32704
котангенс (144) ° ≈ -1,37638
котангенс (145) ° ≈ -1,42815
котангенс (146) ° ≈ -1,48256
котангенс (147) ° ≈ -1,53986
котангенс (148) ° ≈ -1,60033
котангенс (149) ° ≈ -1,66428
котангенс (150) ° ≈ -1,73205
котангенс (151) ° ≈ -1,80405
котангенс (152) ° ≈ -1,88073
котангенс (153) ° ≈ -1,96261
котангенс (154) ° ≈ -2,0503
котангенс (155) ° ≈ -2,14451
котангенс (156) ° ≈ -2,24604
котангенс (157) ° ≈ -2,35585
котангенс (158) ° ≈ -2,47509
котангенс (159) ° ≈ -2,60509
котангенс (160) ° ≈ -2,74748
котангенс (161) ° ≈ -2,90421
котангенс (162) ° ≈ -3,07768
котангенс (163) ° ≈ -3,27085
котангенс (164) ° ≈ -3,48741
котангенс (165) ° ≈ -3,73205
котангенс (166) ° ≈ -4,01078
котангенс (167) ° ≈ -4,33148
котангенс (168) ° ≈ -4,70463
котангенс (169) ° ≈ -5,14455
котангенс (170) ° ≈ -5,67128
котангенс (171) ° ≈ -6,31375
котангенс (172) ° ≈ -7,11537
котангенс (173) ° ≈ -8,14435
котангенс (174) ° ≈ -9,51436
котангенс (175) ° ≈ -11,43005
котангенс (176) ° ≈ -14,30067
котангенс (177) ° ≈ -19,08114
котангенс (178) ° ≈ -28,63625
котангенс (179) ° ≈ -57,28996
котангенс (180) ° = -$\infty$
404 Cтраница не найдена
Размер:
AAA
Цвет: C C C
Изображения
Вкл. Выкл.
Выкл.
Обычная версия сайта
Найти ближайший филиал Версия для слабовидящих Версия для слабовидящих
КАМЕНСК-УРАЛЬСКИЙ
АГРОПРОМЫШЛЕННЫЙ ТЕХНИКУМ
Сохраняя традиции, вместе создаем будущее!
Не хватает прав доступа к веб-форме.
Выше сщщбщение успешно отправлено.
-
Сведения об ОО
- Основные сведения
- Структура и органы управления
- Документы
- Образование
- Образовательные стандарты
- Руководство. Педагогический состав
- Педагогический состав
- МТО и оснащенность ОП
- Стипендия и иные виды материальной поддержки
- Платные образовательные услуги
- Финансово-хозяйственная деятельность
- Вакантные места для приёма (перевода)
- Противодействие коррупции
- Бесплатная юридическая помощь
- Награды, достижения ОО
- Инновационная деятельность
- Доступная среда
- Международное сотрудничество
-
Летопись техникума
- Страницы летописи
- Руководители
- Нам есть у кого учиться
- Педагоги техникума
- Наша гордость — выпускники
- Достижения
- СМИ о техникуме
- Хранители нашей истории
-
Абитуриентам
- Прием 2022
- Дни открытых дверей
- Специальности/профессии
- Общежитие
- Правила и условия приема
- Документы для поступления
- Подать заявление онлайн
- Студенческая жизнь
- Приемная комиссия
- Мониторинг подачи заявлений и документов
- Зачисление
- Фото-экскурсия
- Инклюзивное образование
- Целевое обучение
-
Студентам
- Расписание
- Заочное отделение
- Документы
- Студенческая жизнь
- Государственная итоговая аттестация
- Центр профориентологии
- Стипендия и иные виды материальной поддержки
- Спорт
- Конференции и олимпиады
- Советы психолога
- Сайты преподавателей
- ЕГЭ для студентов учреждений СПО
- Воспитательная работа
- Целевое обучение
- Выпускникам
-
Сотрудникам
- Документы
- Методическая служба
-
Родителям
- Телефонный справочник
- Информация для Родителей
- Специальности / профессии
- Главная
- ›
- uploads
- ›
- about_the_university
- ›
- 14_sistema-distantsionnogo-obucheniya
- ›
- raspisanie-zanyatiy-na-09-11-14-11
Детская кроватка 0 градусов — Найдите значение детской кроватки 0 градусов
LearnPracticeDownload
Значение детской кроватки 0 градусов не определено (∞) . Раскладушка 0 градусов в радианах записывается как раскладушка (0° × π/180°), то есть раскладушка (0π) или раскладушка (0). В этой статье мы обсудим способы нахождения значения cot 0 градусов на примерах.
Раскладушка 0 градусов в радианах записывается как раскладушка (0° × π/180°), то есть раскладушка (0π) или раскладушка (0). В этой статье мы обсудим способы нахождения значения cot 0 градусов на примерах.
- Детская кроватка 0°: не определено(∞)
- Cot 0° в радианах: cot (0π) или cot (0 . . .)
Каково значение детской кроватки 0 градусов?
Значение кроватки 0 градусов равно ∞. Cot 0 градусов также можно выразить с помощью эквивалента данного угла (0 градусов) в радианах (0 . . .)
Мы знаем, используя преобразование градусов в радианы, что θ в радианах = θ в градусах × (pi/180° )
⇒ 0 градусов = 0° × (π/180°) рад = 0π или 0 . . .
∴ кроватка 0° = кроватка(0) = не определено(∞)
Объяснение:
Для кроватки 0 градусов угол 0° лежит на положительной оси x. Таким образом, значение кроватки 0° = undefined(∞)
Поскольку функция котангенса является периодической функцией, мы можем представить cot 0° как cot 0 градусов = cot(0° + n × 180°), n ∈ Z.
⇒ раскладушка 0° = раскладушка 180° = раскладушка 360° и так далее.
Методы определения значения кроватки 0 градусов
Значение кроватки 0° задано как undefined(∞). Мы можем найти значение кроватки 0 градусов по:
- Используя Unit Circle
- Использование тригонометрических функций
Детская кроватка 0 градусов с использованием единичного круга
Чтобы найти значение кроватки 0 градусов с помощью единичного круга:
- Нарисуйте единичный радиус окружности ‘r’, образующий угол 0° с положительной осью x.
- Раскладушка 0 градусов равна x-координате(1), деленной на y-координату(0) точки пересечения (1, 0) единичной окружности и r.
Следовательно, значение кроватки 0° = x/y = undefined(∞).
Cot 0° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить cot 0 градусов как:
- cos(0°)/sin(0°)
- ± cos 0°/√(1 — cos²(0°))
- ± √(1 — sin²(0°))/sin 0°
- ± 1/√(сек²(0°) — 1)
- ± √(cosec²(0°) — 1)
- 1/тангенс 0°
Мы можем использовать тригонометрические тождества для представления cot 0° как
- tan (90° — 0°) = tan 90°
- -тангенс (90° + 0°) = -тангенс 90°
- -кроватка (180° — 0°) = -кроватка 180°
Примечание. Поскольку 0° лежит на положительной оси x, конечное значение cot 0° будет неопределенным (∞).
Поскольку 0° лежит на положительной оси x, конечное значение cot 0° будет неопределенным (∞).
☛ Также проверьте:
- кроватка 34 градуса
- кроватка 75 градусов
- кроватка 1 градус
- кроватка 10 градусов
- кроватка 0 градусов
- кроватка 53 градуса
Примеры использования детской кроватки 0 градусов
Пример 1: Упрощение: 4 (cot 0°/tan 45°)
Решение:
Мы знаем cot 0° = ∞ и tan 45° = 1
⇒ 4 (кот 0°/тангенс 45°) = ∞Пример 2. Найдите значение cot 0°, используя cos 0° и sin 0°.
Решение:
Мы знаем, cot 0° = cos 0°/sin 0°
= 1/0 = не определено (∞)Пример 3: Найдите значение (cos (0°) cosec (0°) sec (0°))/2. [Подсказка: используйте cot 0° = ∞]
Решение:
Используя формулы тригонометрии,
(cos (0°) cosec (0°) sec (0°))/2 = cos (0°)/(2 sin (0°) cos (0°))
Используя формулу sin 2a,
2 sin (0°) cos (0°) = sin (2 × 0°) = sin 0°
⇒ cos (0°) / sin (0°) = кроватка 0°
⇒ (cos (0°) cosec (0°) sec (0°))/2 = ∞
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы о детской кроватке 0 градусов
Что такое детская кроватка 0 градусов?
Cot 0 градусов — значение котангенса тригонометрической функции для угла, равного 0 градусов. Значение кроватки 0° не определено или ∞.
Каково значение Cot 0 градусов в терминах Sin 0°?
Используя тригонометрические тождества, мы можем записать кроватку 0° через sin 0° как кроватку(0°) = √(1 — sin²(0°))/sin 0° . Здесь значение sin 0° равно 0,
Как найти 0° с помощью других тригонометрических функций?
Используя формулу тригонометрии, значение cot 0° может быть выражено через другие тригонометрические функции следующим образом:
- cos(0°)/sin(0°)
- ± cos 0°/√(1 — cos²(0°))
- ± √(1 — sin²(0°))/sin 0°
- ± 1/√(сек²(0°) — 1)
- ± √(cosec²(0°) — 1)
- 1/тангенс 0°
☛ Также проверьте: таблицу тригонометрии
Как найти значение 0 градусов?
Значение cot 0 градусов можно рассчитать, построив угол 0° с осью x и затем найдя координаты соответствующей точки (1, 0) на единичной окружности. Значение кроватки 0° равно координате x(1), деленной на координату y (0). ∴ кроватка 0° = undefined(∞)
Значение кроватки 0° равно координате x(1), деленной на координату y (0). ∴ кроватка 0° = undefined(∞)
Каково значение кроватки 0° в терминах сек 0°?
Мы можем представить функцию котангенса через функцию секанса, используя тригонометрические тождества, cot 0° можно записать как 1/√(sec²(0°) — 1). Здесь значение sec 0° равно 1,
Скачать БЕСПЛАТНЫЕ учебные материалы
Тригонометрия
Рабочие листы по математике и
визуальные учебные программы
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар(30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктический(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc (45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | кос(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар(45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек (45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | кос(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найдите точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы | 45 | |
| 33 | Найти точное значение | кос(45) | |
| 34 | Упростить | 92||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | рыжевато-коричневый (пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | кос(30) | |
| 47 | Найдите точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | кос(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | кос(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех (300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найдите точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | желтовато-коричневый ((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-(квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найдите точное значение | КСК(45) | |
| 83 | Упростить | арктангел (квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | желтовато-коричневый ((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | кос(270) | |
| 98 | Найдите точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Cot Theta — определение, формулы, значения и примеры
Функция котангенса «или» cot theta является одной из тригонометрических функций помимо синуса, косинуса, тангенса, секанса и косеканса.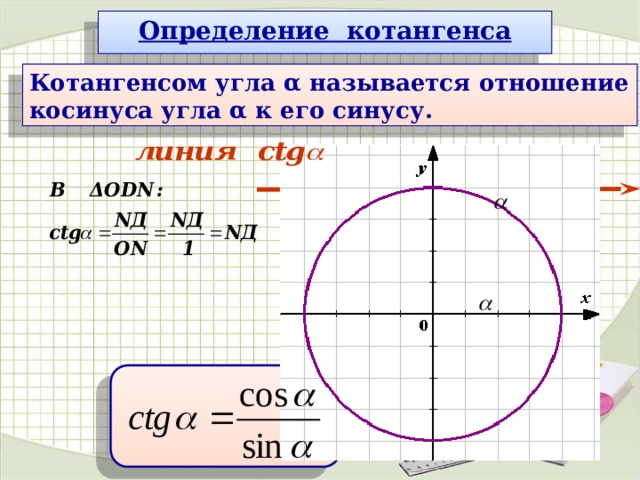 Функция котангенса в тригонометрии прямоугольного треугольника определяется как отношение прилежащей стороны к противолежащей стороне.
Функция котангенса в тригонометрии прямоугольного треугольника определяется как отношение прилежащей стороны к противолежащей стороне.
Математическое обозначение котангенса:
\(\ cot(\ theta) = \frac{\text{Смежная сторона}}{\text{Противоположная сторона}}\)
Подробнее о Cot ThetaCot theta также можно рассчитать из отношения косинуса угла к синусу угла. 92(\theta)\), а его интеграл равен \(\ln|\sin(\theta)|\). Обратная величина \(\cot(\theta)\) равна \(\tan(\theta)\).
График тета-функции cotНиже приведена таблица значений котангенса для различных градусов и радиан.
| Radians | Degree | Cotangent Value |
| 0 | 0° | \(\infty\) |
| \(\frac{\pi}{6 }\) | 30° | \(\frac{3}{\sqrt{3}}\) |
| \(\frac{\pi}{4}\) | 45° | 1 |
| \(\frac{ \pi}{3}\) | 60° | \(\frac{1}{\sqrt{3}}\) |
| \(\frac{\pi}{2}\) | 90 ° | 0 |
| \(\pi\) | 180° | \(\infty\) |
| \(\frac{3\pi} 17 19 9 1 0 | ||
| \(2\pi\) | 360° | \(\infty\) 92(x) = 1 – \frac{16}{25} = \frac{9}{25}\) \(\cos(x) = \frac{3}{5}\) Теперь, \(\tan(x) = \frac{\sin(x)}{\cos(x)} = \frac{\frac{4}{5}}{\frac{3}{5}}\ ) \(\tan(x) = \frac{4}{3}\) Как известно, \(\cot(x) = \frac{1}{\tan(x)}\ ) \(∴ \cot(x) = \frac{3}{4}\) Вопрос 2. Раствор. Использование тригонометрического тождества, 92 – 1 = \frac{25}{64} – 1 = -\frac{39}{64}\) \(∴ \tan(x) = \sqrt{-\frac{39}{64}} \) Вопрос 3. Джон стоит на земле и смотрит на вершину башни с углом возвышения 60°. Расстояние между Джоном и башней 15 футов. Вычислите высоту башни. Раствор. Как известно, \(\tan(\theta) = \frac{\text{Противоположный}}{\text{Смежный}}\) \(\tan(60°) = \frac{\text {Напротив}}{\text{15}}\) \(\sqrt{3} = \frac{\text{Наоборот}}{\text{15}}\) \(\text{Напротив} = 15 \sqrt{3}\) ∴ высота башни \(15 \sqrt{3}\) футов. Часто задаваемые вопросыОбъясните, как кроватка(-х) = -кроватка(х). Как мы знаем, \(\cot(x) = \frac{\sin(x)}{\cos(x)}\). |


 Если \(\sec(x) = \frac{5}{8}\), вычислить значение \(\tan(x)\).
Если \(\sec(x) = \frac{5}{8}\), вычислить значение \(\tan(x)\). 