Таблица котангенсов, прочитать полную таблицу котангенсов
Содержание:
Котангенс — равен отношению косинуса к синусу (ctg(x) = Cos(x)/Sin(x)), тоесть таблицу котангенсов можно получить просто поделив значения из таблицы косинусов на значения из таблицы синусов. Тангенс и котангенс находятся в прямой зависимости, так как tg(x) = Sin(x)/Cos(x), а ctg(x) = Cos(x)/Sin(x), то ctg(x) = 1/tg(x). Таким образом таблицу котангенсов можно получить из таблицы тангенсов (Надо только подставить нужное Вам значение в предыдущую формулу). Пользуйтесь таблицей котангенсов на здоровье.
Таблица котангенсов 0° — 180°
|
|
|
Таблица котангенсов 180° — 360°
|
|
|
Слишком сложно?
Таблица котангенсов, таблица значений котангенсов не по зубам? Тебе ответит эксперт через 10 минут!
Новости за 7 дней.
Сколько предметов домашнего обихода должно быть под рукой в ванной комнате?
Их десятки.
И что с ними делать?
Как правило, они не отличаются выдающимся дизайном.
Основой набора мебели для ванной комнаты Step стали популярные накладные раковины, устанавливаемые на столешницу, для которых предусмот.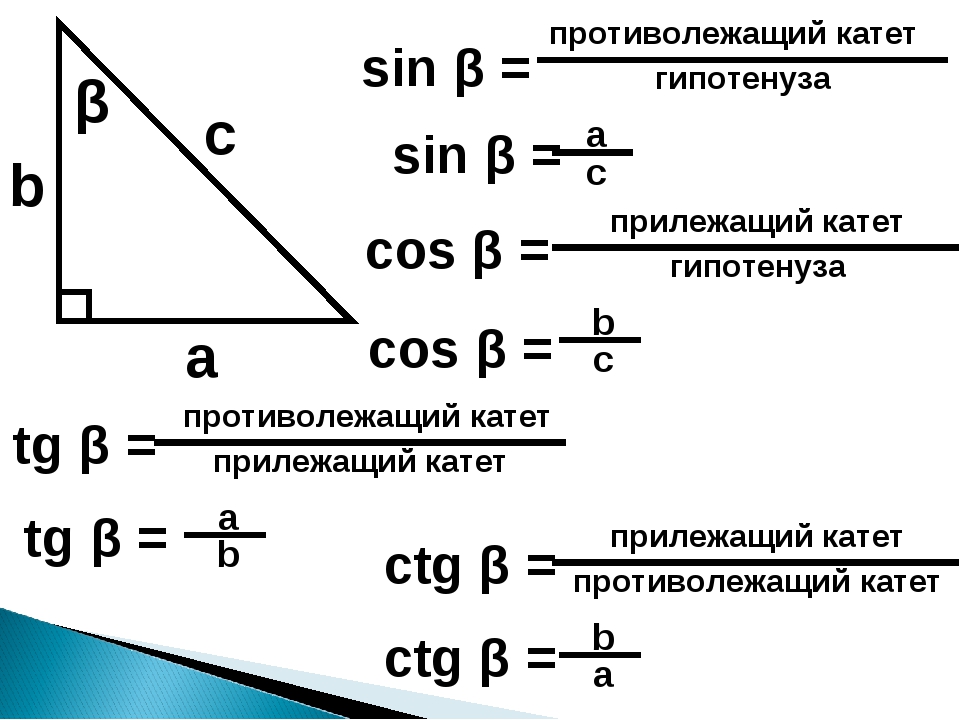 …
…
Ассортимент гофрированных труб из нержавеющей стали торговой марки Stahlmann пополнился новыми диаметрами: 40А и 50А. Компания «Электросистемы и технологии» (входит в ГК «ССТ), официальный дистрибьютор бренда Stahlmann, по многочисленным просьбам клиентов расширила ассортимент гибких гофрированны….
Компания группы PORCELANOSA Grupo представляет свои новые коллекции напольного покрытия для наружного применения и самые инновационные технические решения для ванных комнат и систем гидроизоляции в официальных магазинах Испании и Португалии. Butech расширяет свой каталог продукции и технических реш….
В ассортименте EKF появилась эргономичная розетка для кухни со встраиваемой техникой. Новинка c разъёмами типа РШ-ВШ позволяет удобно и эстетично подключить сразу два прибора – варочную панель и духовку. Преимущества нового изделия: привлекательная цена – можно сэкономить до 20 % бюджета; ла….
Серия MPT включает четыре модели носимых видеорегистраторов Dahua со встроенными видеокамерами для ведения аудио- и видеозаписи непосредственно на месте события и формирования в случае происшествия доказательной базы. Эти мобильные устройства предназначены для использования в сфере обеспечения обще….
Эти мобильные устройства предназначены для использования в сфере обеспечения обще….
Одноабонентская вызывная панель IP-видеодомофона VTO2211G-WP обладает элегантным дизайном и тонкой легкой конструкцией. При этом она оснащена всем необходимым для быстрой установки и удобства эксплуатации. Помимо проводного интерфейса Ethernet, который также поддерживает подачу питания PoE, вызывн….
Стремительное развитие технологий и рост современных городов значительно влияют на наш образ жизни, дизайн и архитектуру. В интерьерах стиль лофт лучше всего отражает урбанистический дух, предоставляя простор для творчества и самовыражения. Новая коллекция мебели AQUATON ЛОФТ Урбан объединяет ос….
Решить проблему размещения на плоских кровлях дополнительного оборудования призваны два инновационных технических решения, разработанных Группой компаний fischer, мировым лидером в разработке и производстве современных крепежных изделий.
Новые кровельные опоры — FFRB и FFRBH — призваны сделать эксп. …
…
За изысканным интерьером всегда стоит качественный крепёж, который позволяет надёжно фиксировать полки, картины, люстры и другие аксессуары. Именно эту задачу решает серия пластиковых дюбелей с крюком EasyHook — новинка компании fischer, мирового лидера в сфере инновационных крепёжных решений. В с….
Качественная краска для деревянного пола – эффективное решение при реставрации старого или обустройстве нового напольного покрытия. Правильно подобранный ЛКМ защитит дерево от истирания, исцарапывания, влаги, ультрафиолета, сохранит красивую фактуру дерева, придаст нужный оттенок, а также продлит с….
Представляем НОВИНКУ – клей SUPERFLEX K77 Белый для керамической плитки и керамогранита. SUPERFLEX K77 Белый – высокоэластичный плиточный клей на основе белого цемента для укладки любого типа плитки из керамогранита, клинкера, керамики и натурального камня, в том числе крупного формата. Свойства….
Динамики подавляющего большинства телевизоров хорошо справляются лишь с воспроизведением голосов дикторов новостей, а вот для музыки и спецэффектов в кино требуется более серьезное решение. Вот только большие колонки полноформатного домашнего кинотеатра — далеко не самый удобный и комфортный выход ….
Вот только большие колонки полноформатного домашнего кинотеатра — далеко не самый удобный и комфортный выход ….
Устройства ввода — это та часть компьютера, с которой мы напрямую контактируем каждый день. И именно от них часто зависит, насколько удобно нам будет работать, учиться или играть. Поэтому компания SVEN постоянно расширяет ассортимент компьютерных мышей и клавиатур, предлагая все новые решения. Ко….
Выбирайте паровую станцию, чтобы почувствовать себя обладателем профессиональной техники для домашнего использования. По сравнению с классическими паровыми утюгами, паровая станция VT-2430 позволит Вам гладить белье в несколько раз быстрее и качественнее. Отгладить костюм, брюки, платье, плащ или ….
Новый цвет — море сочетаний.
За поисками этого оттенка мы отправились в Северную Европу.
Нам нужен был серый, который вызывает ассоциацию с природой, а не бетонными джунглями.
Глядя на пейзажи Исландии, мы поняли: «Вот он.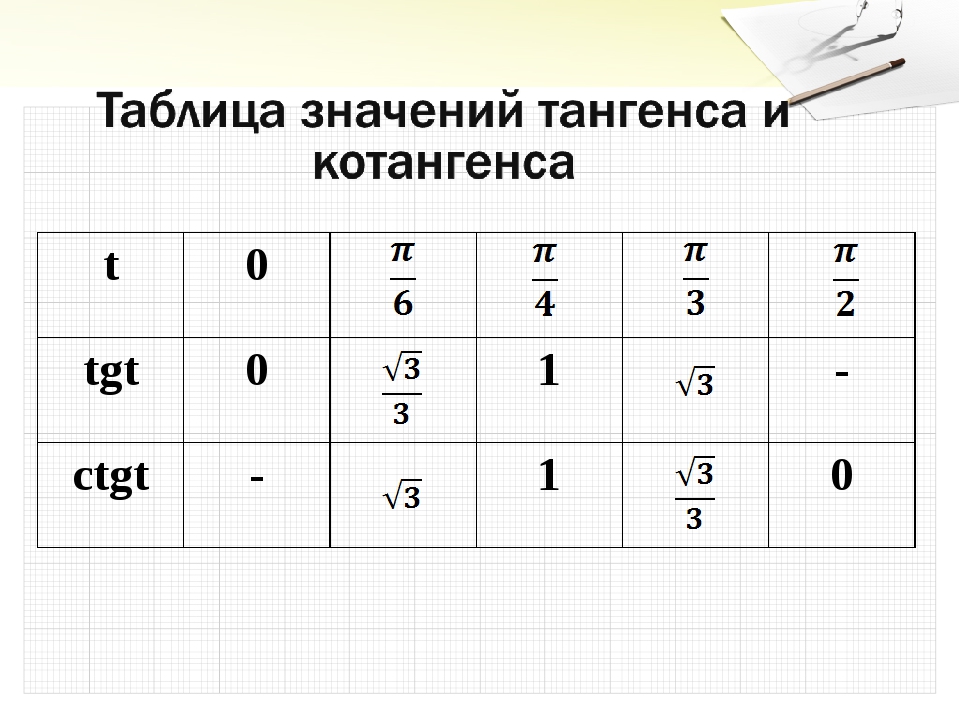 Тот самый цвет».
Спокойный, насыщенный, с теплым коричневым подтоном.
….
Тот самый цвет».
Спокойный, насыщенный, с теплым коричневым подтоном.
….
Компания dormakaba рада предложить Вам бесшумные решения для межкомнатных дверей — защёлки DORMA со смещённым магнитным ригелем серии 940-М WC и 940-М PZ. Товар на складе. Цвет исполнения торцевой планки замка: АВ – античная бронза и SN – матовый никель. Магнитные замки рекомендуются для установ….
Стилизованный рисунок натюрморта с кофе в обрамлении кофейных зернышек и сегменты с надписями на кофейную тематику чередуются с плитками, воспроизводящими фактуру шероховатого камня. Баланс между акцентными и фоновыми элементами решен в пользу фона, что создает воздушность композиции, но при этом с….
Нежный узор из стилизованных полевых цветов.
Плавными каллиграфическими росчерками он заполняет пространство, создавая легкий, вальсирующий ритм композиции.
Отдельные элементы узора не объединены в сетку или колонны, традиционные для ритмики обойных принтов, а соединены в V-образные пересечения со.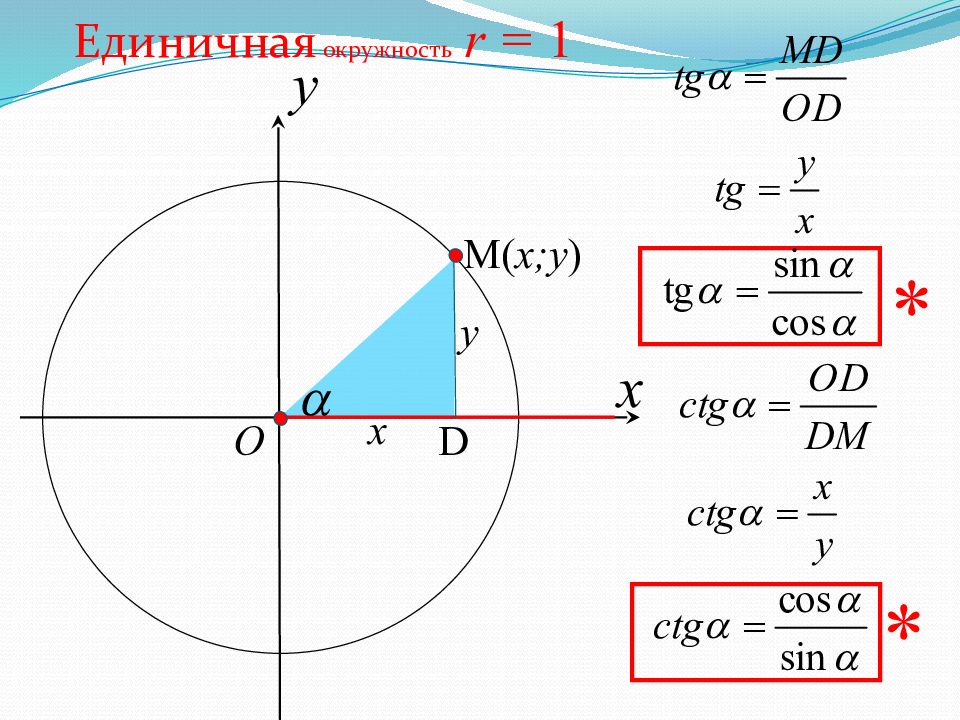 …
…
Ветки, усыпанные некрупными цветами, застилают все полотно. Цельность композиции и наполненность пространства дизайна создают умиротворяющую обстановку и успокаивающий ритм. Тонкие веточки почти полностью укрыты цветами, присутствуют в узоре минимально. Переходы между элементами сглажены, отсутст….
Компактная вилка PPG16-42-201 с заземлением имеют разборную конструкцию и выполнена из ABS пластика и латунных токоведущих контактов. Заземляющие стальные контакты, предусмотренные в конструкции, позволяют безопасно эксплуатировать электроприборы. Применение: Вилки разборные STEKKER серии PPG п….
Коробка «Express» 53800R теперь выпускаются в обновленном конструктиве. 8 герметичных вводов расположены по периметру коробки с максимальным размером вводов до 25 мм, а 2 дополнительных отверстия – на торцевой части коробки (их размер до 20 мм). Теперь есть возможность использовать c ответвительны….
Ассортимент шкафов из фибергласа пополнился новинками – в линейке появились цельнолитые навесные шкафы. Корпуса, изготовленные по этой технологии, имеют более высокую степень пыле- и влагозащиты и меньшую стоимость.
При этом в новых моделях реализуются и все преимущества фибергласа: абсолютная кор….
Корпуса, изготовленные по этой технологии, имеют более высокую степень пыле- и влагозащиты и меньшую стоимость.
При этом в новых моделях реализуются и все преимущества фибергласа: абсолютная кор….
Беспроводная технология LoRa – отличное решение для управления уличным освещением как для целых районов или дорог, так и для ограниченных участков – парковок ТЦ, дворов ЖК, парков и скверов. Достаточно «защелкнуть» в светильник «умный» LoRa контроллер через стандартный NEMA разъем и освещение управ….
Ассортимент Werkel™ пополнился розетками с подсветкой в новых цветах: серебряный и слоновая кость. Кроме своей основной функции — питания электроприборов, розетка с помощью подсветки помогает обозначить себя в темное время суток. Подсветка создает равномерное рассеянное свечение, подходящее для ….
“Освещение придает пространству индивидуальный шарм.
Важно, чтобы оно было отражением владельцев, подчеркивало многогранность дизайнерской идеи, даже в сдержанном и минималистичном интерьере. ”
— Добрый день! Меня зовут Заблодская Камилия, дизайнер студии «Time» с пятилетним опытом, и сегодня я под….
”
— Добрый день! Меня зовут Заблодская Камилия, дизайнер студии «Time» с пятилетним опытом, и сегодня я под….
Идеально вписываются в любой интерьер и экономят средства на электроэнергии! ЭРА обновила ассортимент светодиодных ламп со штырьковым цоколем G4-G9, созданных для прямой замены предшественника – галогенной лампы. Капсульный светодиод мощностью 3-6 Вт излучает столько же света, сколько галогенная л….
К летнему сезону сформирован хороший товарных запас по силовым удлинителям ЭРА для дачных и строительных работ. Второй квартал это самое горячее время для данной товарной группы, предлагаем обратить внимание на ассортимент. Серия ЭРА RPx — удлинители на пластиковой катушке; Серия ЭРА RMx — уд….
Компания ФОКУС представляет новый светильник ЖКХ 10, разработанный для освещения подъездов, лестничных площадок, коридоров и вспомогательных помещений.
Благодаря степени защиты IP 65, обеспечивающей достаточную защиту от влаги и пыли, светильник так же можно размещать в помещениях с повышенной вл. …
…
Компания представляет новую мебель для ванных комнат и спален, а также инновационную линейку кухонных гарнитуров, изготовленных из дерева и XTONE, для организации функциональных пространств. Компания Gamadecor делает выбор в пользу бесконечных и функциональных пространств за счет использования див….
Таблица котангенсов | umath.ru
Котангенсом угла называется отношение косинуса этого угла к синусу:
Таблица котангенсов — таблица, содержащая значения котангенсов углов. В нашей таблице вычислены котангенсы углов от 1° до 180°.
Таблицы котангенсов удобно использовать при отсутствии калькулятора с тригонометрическими функциями.
См. также: таблица синусов, таблица косинусов, таблица тангенсов.
Таблица котангенсов углов 0°, 30°, 45°, 60°, 90°
Замечание: котангенс 0° не определён, так как .
Таблица котангенсов углов от 1° до 90°
| ctg(1°) = 57.289962 ctg(2°) = 28.  636253 636253ctg(3°) = 19.081137 ctg(4°) = 14.300666 ctg(5°) = 11.430052 ctg(6°) = 9.514364 ctg(7°) = 8.144346 ctg(8°) = 7.115370 ctg(9°) = 6.313752 ctg(10°) = 5.671282 ctg(11°) = 5.144554 ctg(12°) = 4.704630 ctg(13°) = 4.331476 ctg(14°) = 4.010781 ctg(15°) = 3.732051 ctg(16°) = 3.487414 ctg(17°) = 3.270853 ctg(18°) = 3.077684 ctg(19°) = 2.904211 ctg(20°) = 2.747477 ctg(21°) = 2.605089 ctg(22°) = 2.475087 ctg(23°) = 2.355852 ctg(24°) = 2.246037 ctg(25°) = 2.144507 ctg(26°) = 2.050304 ctg(27°) = 1.962611 ctg(28°) = 1.880726 ctg(29°) = 1.804048 ctg(30°) = 1.732051 | ctg(31°) = 1.664279 ctg(32°) = 1.600335 ctg(33°) = 1.539865 ctg(34°) = 1.482561 ctg(35°) = 1.428148 ctg(36°) = 1.376382 ctg(37°) = 1.327045 ctg(38°) = 1.279942 ctg(39°) = 1.234897 ctg(40°) = 1.191754 ctg(41°) = 1.150368 ctg(42°) = 1.110613 ctg(43°) = 1.072369 ctg(44°) = 1. 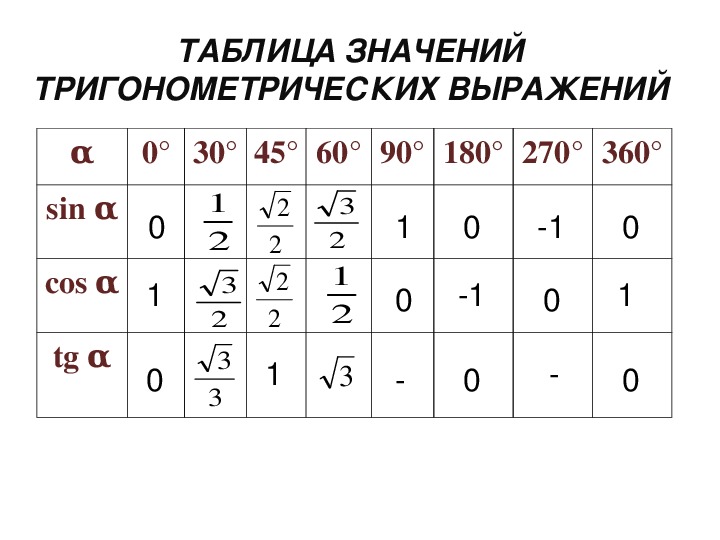 035530 035530ctg(45°) = 1 ctg(46°) = 0.965689 ctg(47°) = 0.932515 ctg(48°) = 0.900404 ctg(49°) = 0.869287 ctg(50°) = 0.839100 ctg(51°) = 0.809784 ctg(52°) = 0.781286 ctg(53°) = 0.753554 ctg(54°) = 0.726543 ctg(55°) = 0.700208 ctg(56°) = 0.674509 ctg(57°) = 0.649408 ctg(58°) = 0.624869 ctg(59°) = 0.600861 ctg(60°) = 0.577350 | ctg(61°) = 0.554309 ctg(62°) = 0.531709 ctg(63°) = 0.509525 ctg(64°) = 0.487733 ctg(65°) = 0.466308 ctg(66°) = 0.445229 ctg(67°) = 0.424475 ctg(68°) = 0.404026 ctg(69°) = 0.383864 ctg(70°) = 0.363970 ctg(71°) = 0.344328 ctg(72°) = 0.324920 ctg(73°) = 0.305731 ctg(74°) = 0.286745 ctg(75°) = 0.267949 ctg(76°) = 0.249328 ctg(77°) = 0.230868 ctg(78°) = 0.212557 ctg(79°) = 0.194380 ctg(80°) = 0.176327 ctg(81°) = 0.158384 ctg(82°) = 0.140541 ctg(83°) = 0.122785 ctg(84°) = 0.105104 ctg(85°) = 0.087489 ctg(86°) = 0. 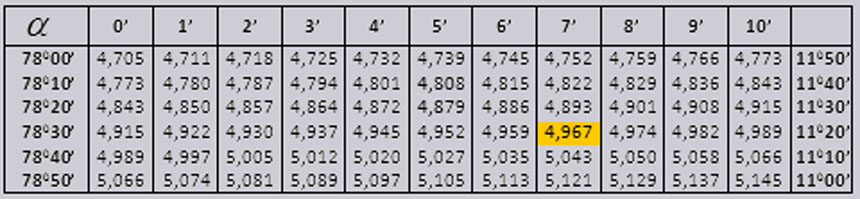 069927 069927ctg(87°) = 0.052408 ctg(88°) = 0.034921 ctg(89°) = 0.017455 ctg(90°) = 0 |
Таблица котангенсов углов от 91° до 180°
| ctg(91°) = -0.017455 ctg(92°) = -0.034921 ctg(93°) = -0.052408 ctg(94°) = -0.069927 ctg(95°) = -0.087489 ctg(96°) = -0.105104 ctg(97°) = -0.122785 ctg(98°) = -0.140541 ctg(99°) = -0.158384 ctg(100°) = -0.176327 ctg(101°) = -0.194380 ctg(102°) = -0.212557 ctg(103°) = -0.230868 ctg(104°) = -0.249328 ctg(105°) = -0.267949 ctg(106°) = -0.286745 ctg(107°) = -0.305731 ctg(108°) = -0.324920 ctg(109°) = -0.344328 ctg(110°) = -0.363970 ctg(111°) = -0.383864 ctg(112°) = -0.404026 ctg(113°) = -0.424475 ctg(114°) = -0.445229 ctg(115°) = -0.466308 ctg(116°) = -0.487733 ctg(117°) = -0.509525 ctg(118°) = -0.531709 ctg(119°) = -0.554309 ctg(120°) = -0.577350 | ctg(121°) = -0.600861 ctg(122°) = -0. 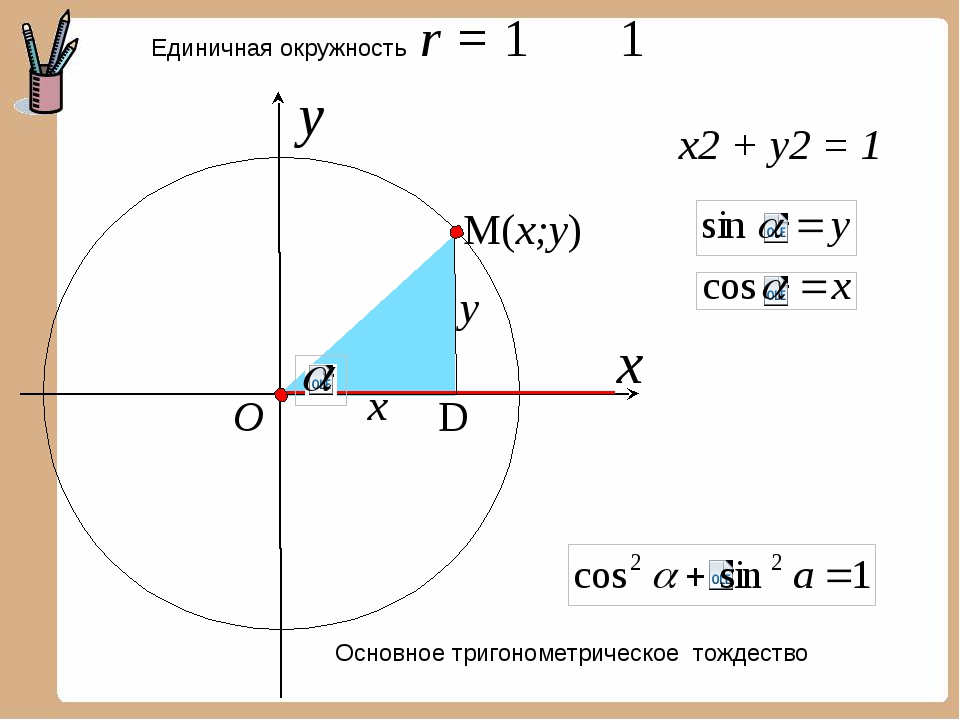 624869 624869ctg(123°) = -0.649408 ctg(124°) = -0.674509 ctg(125°) = -0.700208 ctg(126°) = -0.726543 ctg(127°) = -0.753554 ctg(128°) = -0.781286 ctg(129°) = -0.809784 ctg(130°) = -0.839100 ctg(131°) = -0.869287 ctg(132°) = -0.900404 ctg(133°) = -0.932515 ctg(134°) = -0.965689 ctg(135°) = -1 ctg(136°) = -1.035530 ctg(137°) = -1.072369 ctg(138°) = -1.110613 ctg(139°) = -1.150368 ctg(140°) = -1.191754 ctg(141°) = -1.234897 ctg(142°) = -1.279942 ctg(143°) = -1.327045 ctg(144°) = -1.376382 ctg(145°) = -1.428148 ctg(146°) = -1.482561 ctg(147°) = -1.539865 ctg(148°) = -1.600335 ctg(149°) = -1.664279 ctg(150°) = -1.732051 | ctg(151°) = -1.804048 ctg(152°) = -1.880726 ctg(153°) = -1.962611 ctg(154°) = -2.050304 ctg(155°) = -2.144507 ctg(156°) = -2.246037 ctg(157°) = -2.355852 ctg(158°) = -2.475087 ctg(159°) = -2.605089 ctg(160°) = -2.747477 ctg(161°) = -2.  904211 904211ctg(162°) = -3.077684 ctg(163°) = -3.270853 ctg(164°) = -3.487414 ctg(165°) = -3.732051 ctg(166°) = -4.010781 ctg(167°) = -4.331476 ctg(168°) = -4.704630 ctg(169°) = -5.144554 ctg(170°) = -5.671282 ctg(171°) = -6.313752 ctg(172°) = -7.115370 ctg(173°) = -8.144346 ctg(174°) = -9.514364 ctg(175°) = -11.430052 ctg(176°) = -14.300666 ctg(177°) = -19.081137 ctg(178°) = -28.636253 ctg(179°) = -57.289962 ctg(180°) не определено |
Таблица котангенсов.
Таблица котангенсов — это записанные в таблицу посчитанные значения котангенсов углов от 0° до 360°. Используя таблицу котангенсов Вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение котангенса от нужного Вам угла достаточно найти его в таблице.
Таблица котангенсов в радианах
| α | 0 | π6 | π4 | π3 | π2 | π | 3π2 | 2π |
| сtg α | ∞ | √3 | 1 | √33 | 0 | ∞ | 0 | ∞ |
Таблица котангенсов углов от 0° до 180°
| ctg(0°) = ∞ ctg(1°) = 57.  28996 28996ctg(2°) = 28.63625 ctg(3°) = 19.08114 ctg(4°) = 14.30067 ctg(5°) = 11.43005 ctg(6°) = 9.51436 ctg(7°) = 8.14435 ctg(8°) = 7.11537 ctg(9°) = 6.31375 ctg(10°) = 5.67128 ctg(11°) = 5.14455 ctg(12°) = 4.70463 ctg(13°) = 4.33148 ctg(14°) = 4.01078 ctg(15°) = 3.73205 ctg(16°) = 3.48741 ctg(17°) = 3.27085 ctg(18°) = 3.07768 ctg(19°) = 2.90421 ctg(20°) = 2.74748 ctg(21°) = 2.60509 ctg(22°) = 2.47509 ctg(23°) = 2.35585 ctg(24°) = 2.24604 ctg(25°) = 2.14451 ctg(26°) = 2.0503 ctg(27°) = 1.96261 ctg(28°) = 1.88073 ctg(29°) = 1.80405 ctg(30°) = 1.73205 ctg(31°) = 1.66428 ctg(32°) = 1.60033 ctg(33°) = 1.53986 ctg(34°) = 1.48256 ctg(35°) = 1.42815 ctg(36°) = 1.37638 ctg(37°) = 1.32704 ctg(38°) = 1.27994 ctg(39°) = 1.2349 ctg(40°) = 1.19175 ctg(41°) = 1.15037 ctg(42°) = 1.11061 ctg(43°) = 1.07237 ctg(44°) = 1.03553 ctg(45°) = 1 ctg(46°) = 0.  96569 96569ctg(47°) = 0.93252 ctg(48°) = 0.9004 ctg(49°) = 0.86929 ctg(50°) = 0.8391 ctg(51°) = 0.80978 ctg(52°) = 0.78129 ctg(53°) = 0.75355 ctg(54°) = 0.72654 ctg(55°) = 0.70021 ctg(56°) = 0.67451 ctg(57°) = 0.64941 ctg(58°) = 0.62487 ctg(59°) = 0.60086 ctg(60°) = 0.57735 | ctg(61°) = 0.55431 ctg(62°) = 0.53171 ctg(63°) = 0.50953 ctg(64°) = 0.48773 ctg(65°) = 0.46631 ctg(66°) = 0.44523 ctg(67°) = 0.42447 ctg(68°) = 0.40403 ctg(69°) = 0.38386 ctg(70°) = 0.36397 ctg(71°) = 0.34433 ctg(72°) = 0.32492 ctg(73°) = 0.30573 ctg(74°) = 0.28675 ctg(75°) = 0.26795 ctg(76°) = 0.24933 ctg(77°) = 0.23087 ctg(78°) = 0.21256 ctg(79°) = 0.19438 ctg(80°) = 0.17633 ctg(81°) = 0.15838 ctg(82°) = 0.14054 ctg(83°) = 0.12278 ctg(84°) = 0.1051 ctg(85°) = 0.08749 ctg(86°) = 0.06993 ctg(87°) = 0.05241 ctg(88°) = 0.03492 ctg(89°) = 0.01746 ctg(90°) = 0 ctg(91°) = -0.  01746 01746ctg(92°) = -0.03492 ctg(93°) = -0.05241 ctg(94°) = -0.06993 ctg(95°) = -0.08749 ctg(96°) = -0.1051 ctg(97°) = -0.12278 ctg(98°) = -0.14054 ctg(99°) = -0.15838 ctg(100°) = -0.17633 ctg(101°) = -0.19438 ctg(102°) = -0.21256 ctg(103°) = -0.23087 ctg(104°) = -0.24933 ctg(105°) = -0.26795 ctg(106°) = -0.28675 ctg(107°) = -0.30573 ctg(108°) = -0.32492 ctg(109°) = -0.34433 ctg(110°) = -0.36397 ctg(111°) = -0.38386 ctg(112°) = -0.40403 ctg(113°) = -0.42447 ctg(114°) = -0.44523 ctg(115°) = -0.46631 ctg(116°) = -0.48773 ctg(117°) = -0.50953 ctg(118°) = -0.53171 ctg(119°) = -0.55431 ctg(120°) = -0.57735 | ctg(121°) = -0.60086 ctg(122°) = -0.62487 ctg(123°) = -0.64941 ctg(124°) = -0.67451 ctg(125°) = -0.70021 ctg(126°) = -0.72654 ctg(127°) = -0.75355 ctg(128°) = -0.78129 ctg(129°) = -0.80978 ctg(130°) = -0.8391 ctg(131°) = -0.86929 ctg(132°) = -0.  9004 9004ctg(133°) = -0.93252 ctg(134°) = -0.96569 ctg(135°) = -1 ctg(136°) = -1.03553 ctg(137°) = -1.07237 ctg(138°) = -1.11061 ctg(139°) = -1.15037 ctg(140°) = -1.19175 ctg(141°) = -1.2349 ctg(142°) = -1.27994 ctg(143°) = -1.32704 ctg(144°) = -1.37638 ctg(145°) = -1.42815 ctg(146°) = -1.48256 ctg(147°) = -1.53986 ctg(148°) = -1.60033 ctg(149°) = -1.66428 ctg(150°) = -1.73205 ctg(151°) = -1.80405 ctg(152°) = -1.88073 ctg(153°) = -1.96261 ctg(154°) = -2.0503 ctg(155°) = -2.14451 ctg(156°) = -2.24604 ctg(157°) = -2.35585 ctg(158°) = -2.47509 ctg(159°) = -2.60509 ctg(160°) = -2.74748 ctg(161°) = -2.90421 ctg(162°) = -3.07768 ctg(163°) = -3.27085 ctg(164°) = -3.48741 ctg(165°) = -3.73205 ctg(166°) = -4.01078 ctg(167°) = -4.33148 ctg(168°) = -4.70463 ctg(169°) = -5.14455 ctg(170°) = -5.67128 ctg(171°) = -6.31375 ctg(172°) = -7.11537 ctg(173°) = -8.  14435 14435ctg(174°) = -9.51436 ctg(175°) = -11.43005 ctg(176°) = -14.30067 ctg(177°) = -19.08114 ctg(178°) = -28.63625 ctg(179°) = -57.28996 ctg(180°) = ∞ |
Таблица котангенсов углов от 181° до 360°
| ctg(181°) = 57.28996 ctg(182°) = 28.63625 ctg(183°) = 19.08114 ctg(184°) = 14.30067 ctg(185°) = 11.43005 ctg(186°) = 9.51436 ctg(187°) = 8.14435 ctg(188°) = 7.11537 ctg(189°) = 6.31375 ctg(190°) = 5.67128 ctg(191°) = 5.14455 ctg(192°) = 4.70463 ctg(193°) = 4.33148 ctg(194°) = 4.01078 ctg(195°) = 3.73205 ctg(196°) = 3.48741 ctg(197°) = 3.27085 ctg(198°) = 3.07768 ctg(199°) = 2.90421 ctg(200°) = 2.74748 ctg(201°) = 2.60509 ctg(202°) = 2.47509 ctg(203°) = 2.35585 ctg(204°) = 2.24604 ctg(205°) = 2.14451 ctg(206°) = 2.0503 ctg(207°) = 1.96261 ctg(208°) = 1.88073 ctg(209°) = 1.80405 ctg(210°) = 1.73205 ctg(211°) = 1.  66428 66428ctg(212°) = 1.60033 ctg(213°) = 1.53986 ctg(214°) = 1.48256 ctg(215°) = 1.42815 ctg(216°) = 1.37638 ctg(217°) = 1.32704 ctg(218°) = 1.27994 ctg(219°) = 1.2349 ctg(220°) = 1.19175 ctg(221°) = 1.15037 ctg(222°) = 1.11061 ctg(223°) = 1.07237 ctg(224°) = 1.03553 ctg(225°) = 1 ctg(226°) = 0.96569 ctg(227°) = 0.93252 ctg(228°) = 0.9004 ctg(229°) = 0.86929 ctg(230°) = 0.8391 ctg(231°) = 0.80978 ctg(232°) = 0.78129 ctg(233°) = 0.75355 ctg(234°) = 0.72654 ctg(235°) = 0.70021 ctg(236°) = 0.67451 ctg(237°) = 0.64941 ctg(238°) = 0.62487 ctg(239°) = 0.60086 ctg(240°) = 0.57735 | ctg(241°) = 0.55431 ctg(242°) = 0.53171 ctg(243°) = 0.50953 ctg(244°) = 0.48773 ctg(245°) = 0.46631 ctg(246°) = 0.44523 ctg(247°) = 0.42447 ctg(248°) = 0.40403 ctg(249°) = 0.38386 ctg(250°) = 0.36397 ctg(251°) = 0.34433 ctg(252°) = 0.32492 ctg(253°) = 0.  30573 30573ctg(254°) = 0.28675 ctg(255°) = 0.26795 ctg(256°) = 0.24933 ctg(257°) = 0.23087 ctg(258°) = 0.21256 ctg(259°) = 0.19438 ctg(260°) = 0.17633 ctg(261°) = 0.15838 ctg(262°) = 0.14054 ctg(263°) = 0.12278 ctg(264°) = 0.1051 ctg(265°) = 0.08749 ctg(266°) = 0.06993 ctg(267°) = 0.05241 ctg(268°) = 0.03492 ctg(269°) = 0.01746 ctg(270°) = 0 ctg(271°) = -0.01746 ctg(272°) = -0.03492 ctg(273°) = -0.05241 ctg(274°) = -0.06993 ctg(275°) = -0.08749 ctg(276°) = -0.1051 ctg(277°) = -0.12278 ctg(278°) = -0.14054 ctg(279°) = -0.15838 ctg(280°) = -0.17633 ctg(281°) = -0.19438 ctg(282°) = -0.21256 ctg(283°) = -0.23087 ctg(284°) = -0.24933 ctg(285°) = -0.26795 ctg(286°) = -0.28675 ctg(287°) = -0.30573 ctg(288°) = -0.32492 ctg(289°) = -0.34433 ctg(290°) = -0.36397 ctg(291°) = -0.38386 ctg(292°) = -0.40403 ctg(293°) = -0.42447 ctg(294°) = -0.44523 ctg(295°) = -0.  46631 46631ctg(296°) = -0.48773 ctg(297°) = -0.50953 ctg(298°) = -0.53171 ctg(299°) = -0.55431 ctg(300°) = -0.57735 | ctg(301°) = -0.60086 ctg(302°) = -0.62487 ctg(303°) = -0.64941 ctg(304°) = -0.67451 ctg(305°) = -0.70021 ctg(306°) = -0.72654 ctg(307°) = -0.75355 ctg(308°) = -0.78129 ctg(309°) = -0.80978 ctg(310°) = -0.8391 ctg(311°) = -0.86929 ctg(312°) = -0.9004 ctg(313°) = -0.93252 ctg(314°) = -0.96569 ctg(315°) = -1 ctg(316°) = -1.03553 ctg(317°) = -1.07237 ctg(318°) = -1.11061 ctg(319°) = -1.15037 ctg(320°) = -1.19175 ctg(321°) = -1.2349 ctg(322°) = -1.27994 ctg(323°) = -1.32704 ctg(324°) = -1.37638 ctg(325°) = -1.42815 ctg(326°) = -1.48256 ctg(327°) = -1.53986 ctg(328°) = -1.60033 ctg(329°) = -1.66428 ctg(330°) = -1.73205 ctg(331°) = -1.80405 ctg(332°) = -1.88073 ctg(333°) = -1.96261 ctg(334°) = -2.0503 ctg(335°) = -2.14451 ctg(336°) = -2.  24604 24604ctg(337°) = -2.35585 ctg(338°) = -2.47509 ctg(339°) = -2.60509 ctg(340°) = -2.74748 ctg(341°) = -2.90421 ctg(342°) = -3.07768 ctg(343°) = -3.27085 ctg(344°) = -3.48741 ctg(345°) = -3.73205 ctg(346°) = -4.01078 ctg(347°) = -4.33148 ctg(348°) = -4.70463 ctg(349°) = -5.14455 ctg(350°) = -5.67128 ctg(351°) = -6.31375 ctg(352°) = -7.11537 ctg(353°) = -8.14435 ctg(354°) = -9.51436 ctg(355°) = -11.43005 ctg(356°) = -14.30067 ctg(357°) = -19.08114 ctg(358°) = -28.63625 ctg(359°) = -57.28996 ctg(360°) = ∞ |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
|
|
|
Таблица котангенсов, найти котангенс угла
Тригонометрические функции – это соотношение катетов и гипотенузы угла в прямоугольном треугольнике. Это очень важно. Длина сторон может изменяться, но соотношение останется прежним. На этом основании были созданы таблицы Брадиса, в котором указаны синус, косинус, тангенс и котангенс угла.
Котангенс – это соотношение катетов угла прямоугольного треугольника. Записывается следующим образом: ctg (А) = АС/ВС, где АС – ближний к углу катет, ВС – противолежащий катет.
Все данные есть в таблице котангенсов угла. Зная угол и одну из сторон, можно получить остальные данные. Производить расчеты можно на сайте посредством онлайн-калькулятора. Утверждение: знаю угол – знаю его тригонометрические функции, верно во все времена.
Таблица котангенсов от 0° — 360°
|
|
|
|
|
|
|
|
|
|
Смотрите также
Таблица котангенсов для школьников и студентов
Таблица котангенсов необходима для вычислений, связанных со значениями тригонометрических функций.
Легко запомнить, что значения ctg 0° = ctg 180° = ctg 360° = ∞,
а ctg 90° = ctg 270° = 0.
ctg 1° — ctg 90°
ctg 1° = 57.28996ctg 2° = 28.63625
ctg 3° = 19.08114
ctg 4° = 14.30067
ctg 5° = 11.43005
ctg 6° = 9.51436
ctg 7° = 8.14435
ctg 8° = 7.11537
ctg 9° = 6.31375
ctg 10° = 5.67128
ctg 11° = 5.14455
ctg 12° = 4.70463
ctg 13° = 4.33148
ctg 14° = 4.01078
ctg 15° = 3.73205
ctg 16° = 3.48741
ctg 17° = 3.27085
ctg 18° = 3.07768
ctg 19° = 2.90421
ctg 20° = 2.74748
ctg 21° = 2.60509
ctg 22° = 2.47509
ctg 23° = 2.35585
ctg 24° = 2.24604
ctg 25° = 2.14451
ctg 26° = 2.05030
ctg 27° = 1.96261
ctg 28° = 1.88073
ctg 29° = 1.80405
ctg 30° = 1.73205
ctg 31° = 1.66428
ctg 32° = 1.60033
ctg 33° = 1.53986
ctg 34° = 1.48256
ctg 35° = 1.42815
ctg 36° = 1.37638
ctg 37° = 1.32704
ctg 38° = 1.27994
ctg 39° = 1.23490
ctg 40° = 1.19175
ctg 41° = 1.15037
ctg 42° = 1.11061
ctg 43° = 1.07237
ctg 44° = 1.03553
ctg 45° = 1.00000
ctg 46° = 0.96569
ctg 47° = 0.93252
ctg 48° = 0.90040
ctg 49° = 0.86929
ctg 50° = 0.83910
ctg 51° = 0.80978
ctg 52° = 0.78129
ctg 53° = 0.75355
ctg 54° = 0.72654
ctg 55° = 0.70021
ctg 56° = 0.67451
ctg 57° = 0.64941
ctg 58° = 0.62487
ctg 59° = 0.60086
ctg 60° = 0.57735
ctg 61° = 0.55431
ctg 62° = 0.53171
ctg 63° = 0.50953
ctg 64° = 0.48773
ctg 65° = 0.46631
ctg 66° = 0.44523
ctg 67° = 0.42447
ctg 68° = 0.40403
ctg 69° = 0.38386
ctg 70° = 0.36397
ctg 71° = 0.34433
ctg 72° = 0.32492
ctg 73° = 0.30573
ctg 74° = 0.28675
ctg 75° = 0.26795
ctg 76° = 0.24933
ctg 77° = 0.23087
ctg 78° = 0.21256
ctg 79° = 0.19438
ctg 80° = 0.17633
ctg 81° = 0.15838
ctg 82° = 0.14054
ctg 83° = 0.12278
ctg 84° = 0.10510
ctg 85° = 0.08749
ctg 86° = 0.06993
ctg 87° = 0.05241
ctg 88° = 0.03492
ctg 89° = 0.01746
ctg 90° = 0.00000
ctg 91° — ctg 180°
ctg 91° = -0.01746ctg 92° = -0.03492
ctg 93° = -0.05241
ctg 94° = -0.06993
ctg 95° = -0.08749
ctg 96° = -0.10510
ctg 97° = -0.12278
ctg 98° = -0.14054
ctg 99° = -0.15838
ctg 100° = -0.17633
ctg 101° = -0.19438
ctg 102° = -0.21256
ctg 103° = -0.23087
ctg 104° = -0.24933
ctg 105° = -0.26795
ctg 106° = -0.28675
ctg 107° = -0.30573
ctg 108° = -0.32492
ctg 109° = -0.34433
ctg 110° = -0.36397
ctg 111° = -0.38386
ctg 112° = -0.40403
ctg 113° = -0.42447
ctg 114° = -0.44523
ctg 115° = -0.46631
ctg 116° = -0.48773
ctg 117° = -0.50953
ctg 118° = -0.53171
ctg 119° = -0.55431
ctg 120° = -0.57735
ctg 121° = -0.60086
ctg 122° = -0.62487
ctg 123° = -0.64941
ctg 124° = -0.67451
ctg 125° = -0.70021
ctg 126° = -0.72654
ctg 127° = -0.75355
ctg 128° = -0.78129
ctg 129° = -0.80978
ctg 130° = -0.83910
ctg 131° = -0.86929
ctg 132° = -0.90040
ctg 133° = -0.93252
ctg 134° = -0.96569
ctg 135° = -1.00000
ctg 136° = -1.03553
ctg 137° = -1.07237
ctg 138° = -1.11061
ctg 139° = -1.15037
ctg 140° = -1.19175
ctg 141° = -1.23490
ctg 142° = -1.27994
ctg 143° = -1.32704
ctg 144° = -1.37638
ctg 145° = -1.42815
ctg 146° = -1.48256
ctg 147° = -1.53986
ctg 148° = -1.60033
ctg 149° = -1.66428
ctg 150° = -1.73205
ctg 151° = -1.80405
ctg 152° = -1.88073
ctg 153° = -1.96261
ctg 154° = -2.05030
ctg 155° = -2.14451
ctg 156° = -2.24604
ctg 157° = -2.35585
ctg 158° = -2.47509
ctg 159° = -2.60509
ctg 160° = -2.74748
ctg 161° = -2.90421
ctg 162° = -3.07768
ctg 163° = -3.27085
ctg 164° = -3.48741
ctg 165° = -3.73205
ctg 166° = -4.01078
ctg 167° = -4.33148
ctg 168° = -4.70463
ctg 169° = -5.14455
ctg 170° = -5.67128
ctg 171° = -6.31375
ctg 172° = -7.11537
ctg 173° = -8.14435
ctg 174° = -9.51436
ctg 175° = -11.43005
ctg 176° = -14.30067
ctg 177° = -19.08114
ctg 178° = -28.63625
ctg 179° = -57.28996
ctg 180° = ∞
ctg 181° — ctg 270°
ctg 181° = 57.28996ctg 182° = 28.63625
ctg 183° = 19.08114
ctg 184° = 14.30067
ctg 185° = 11.43005
ctg 186° = 9.51436
ctg 187° = 8.14435
ctg 188° = 7.11537
ctg 189° = 6.31375
ctg 190° = 5.67128
ctg 191° = 5.14455
ctg 192° = 4.70463
ctg 193° = 4.33148
ctg 194° = 4.01078
ctg 195° = 3.73205
ctg 196° = 3.48741
ctg 197° = 3.27085
ctg 198° = 3.07768
ctg 199° = 2.90421
ctg 200° = 2.74748
ctg 201° = 2.60509
ctg 202° = 2.47509
ctg 203° = 2.35585
ctg 204° = 2.24604
ctg 205° = 2.14451
ctg 206° = 2.05030
ctg 207° = 1.96261
ctg 208° = 1.88073
ctg 209° = 1.80405
ctg 210° = 1.73205
ctg 211° = 1.66428
ctg 212° = 1.60033
ctg 213° = 1.53986
ctg 214° = 1.48256
ctg 215° = 1.42815
ctg 216° = 1.37638
ctg 217° = 1.32704
ctg 218° = 1.27994
ctg 219° = 1.23490
ctg 220° = 1.19175
ctg 221° = 1.15037
ctg 222° = 1.11061
ctg 223° = 1.07237
ctg 224° = 1.03553
ctg 225° = 1.00000
ctg 226° = 0.96569
ctg 227° = 0.93252
ctg 228° = 0.90040
ctg 229° = 0.86929
ctg 230° = 0.83910
ctg 231° = 0.80978
ctg 232° = 0.78129
ctg 233° = 0.75355
ctg 234° = 0.72654
ctg 235° = 0.70021
ctg 236° = 0.67451
ctg 237° = 0.64941
ctg 238° = 0.62487
ctg 239° = 0.60086
ctg 240° = 0.57735
ctg 241° = 0.55431
ctg 242° = 0.53171
ctg 243° = 0.50953
ctg 244° = 0.48773
ctg 245° = 0.46631
ctg 246° = 0.44523
ctg 247° = 0.42447
ctg 248° = 0.40403
ctg 249° = 0.38386
ctg 250° = 0.36397
ctg 251° = 0.34433
ctg 252° = 0.32492
ctg 253° = 0.30573
ctg 254° = 0.28675
ctg 255° = 0.26795
ctg 256° = 0.24933
ctg 257° = 0.23087
ctg 258° = 0.21256
ctg 259° = 0.19438
ctg 260° = 0.17633
ctg 261° = 0.15838
ctg 262° = 0.14054
ctg 263° = 0.12278
ctg 264° = 0.10510
ctg 265° = 0.08749
ctg 266° = 0.06993
ctg 267° = 0.05241
ctg 268° = 0.03492
ctg 269° = 0.01746
ctg 270° = 0.00000
ctg 271° — ctg 360°
ctg 271° = -0.01746ctg 272° = -0.03492
ctg 273° = -0.05241
ctg 274° = -0.06993
ctg 275° = -0.08749
ctg 276° = -0.10510
ctg 277° = -0.12278
ctg 278° = -0.14054
ctg 279° = -0.15838
ctg 280° = -0.17633
ctg 281° = -0.19438
ctg 282° = -0.21256
ctg 283° = -0.23087
ctg 284° = -0.24933
ctg 285° = -0.26795
ctg 286° = -0.28675
ctg 287° = -0.30573
ctg 288° = -0.32492
ctg 289° = -0.34433
ctg 290° = -0.36397
ctg 291° = -0.38386
ctg 292° = -0.40403
ctg 293° = -0.42447
ctg 294° = -0.44523
ctg 295° = -0.46631
ctg 296° = -0.48773
ctg 297° = -0.50953
ctg 298° = -0.53171
ctg 299° = -0.55431
ctg 300° = -0.57735
ctg 301° = -0.60086
ctg 302° = -0.62487
ctg 303° = -0.64941
ctg 304° = -0.67451
ctg 305° = -0.70021
ctg 306° = -0.72654
ctg 307° = -0.75355
ctg 308° = -0.78129
ctg 309° = -0.80978
ctg 310° = -0.83910
ctg 311° = -0.86929
ctg 312° = -0.90040
ctg 313° = -0.93252
ctg 314° = -0.96569
ctg 315° = -1.00000
ctg 316° = -1.03553
ctg 317° = -1.07237
ctg 318° = -1.11061
ctg 319° = -1.15037
ctg 320° = -1.19175
ctg 321° = -1.23490
ctg 322° = -1.27994
ctg 323° = -1.32704
ctg 324° = -1.37638
ctg 325° = -1.42815
ctg 326° = -1.48256
ctg 327° = -1.53986
ctg 328° = -1.60033
ctg 329° = -1.66428
ctg 330° = -1.73205
ctg 331° = -1.80405
ctg 332° = -1.88073
ctg 333° = -1.96261
ctg 334° = -2.05030
ctg 335° = -2.14451
ctg 336° = -2.24604
ctg 337° = -2.35585
ctg 338° = -2.47509
ctg 339° = -2.60509
ctg 340° = -2.74748
ctg 341° = -2.90421
ctg 342° = -3.07768
ctg 343° = -3.27085
ctg 344° = -3.48741
ctg 345° = -3.73205
ctg 346° = -4.01078
ctg 347° = -4.33148
ctg 348° = -4.70463
ctg 349° = -5.14455
ctg 350° = -5.67128
ctg 351° = -6.31375
ctg 352° = -7.11537
ctg 353° = -8.14435
ctg 354° = -9.51436
ctg 355° = -11.43005
ctg 356° = -14.30067
ctg 357° = -19.08114
ctg 358° = -28.63625
ctg 359° = -57.28996
ctg 360° = ∞
- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике
- Табличные значения синуса 30, 45, 60 градусов.
- Подготовка к контрольной работе по геометрии 8 класса.
- Теорема о вписанном угле.
- Таблица умножения (от 1 до 10).
- Расширенная таблица умножения (от 1 до 20).
- Таблица квадратов (от 1 до 10).
- Таблица кубов (от 1 до 10).
- Таблица степеней (от 1 до 10).
- Таблица факториалов (от 1 до 10).
- Таблица Брадиса (с уточнениями).
- Таблица синусов.
- Таблица косинусов.
- Таблица тангенсов.
- Таблица котангенсов.
- Таблица тригонометрических функций.
- Таблица натуральных логарифмов.
- Таблица десятичных логарифмов.
- Таблица логарифмов по основанию.
- Формулы сокращённого умножения (2, 3, 4 и n-ой степеней).
- Формулы и свойства степеней.
- Формулы и свойства корней.
- Формулы и свойства логарифмов.
- Формулы и свойства арифметической прогрессии.
- Формулы и свойства геометрической прогрессии.
- Тригонометрические формулы.
- Обратные тригонометрические функции.
- Площади фигур.
- Объёмы фигур.
- Периметры фигур.
- Площади поверхностей фигур.
- Правильный многоугольник.
- Треугольник.
- Теорема Пифагора.
- Натуральные числа.
| детская кроватка (0 °) = ∞ детская кроватка (1 °) = 57,28996 детская кроватка (2 °) = 28,63625 детская кроватка (3 °) = 19,08114 детская кроватка (4 °) = 14,30067 детская кроватка (5 °) = 11,43005 детская кроватка (6 °) = 9,51436 детская кроватка (7 °) = 8,14435 детская кроватка (8 °) = 7,11537 детская кроватка (9 °) = 6,31375 детская кроватка (10 °) = 5,67128 детская кроватка (11 °) = 5,14455 детская кроватка ( 12 °) = 4,70463 детская кроватка (13 °) = 4,33148 детская кроватка (14 °) = 4,01078 детская кроватка (15 °) = 3,73205 детская кроватка (16 °) = 3,48741 детская кроватка (17 °) = 3,27085 детская кроватка (18 ° ) = 3,07768 детская кроватка (19 °) = 2. | детская кроватка (61 °) = 0.55431 детская кроватка (62 °) = 0,53171 детская кроватка (63 °) = 0,50953 детская кроватка (64 °) = 0,48773 детская кроватка (65 °) = 0,46631 детская кроватка (66 °) = 0,44523 детская кроватка (67 °) = 0,42447 детская кроватка (68 °) = 0,40403 детская кроватка (69 °) = 0,38386 детская кроватка (70 °) = 0,36397 детская кроватка (71 °) = 0,34433 детская кроватка (72 °) = 0,32492 детская кроватка (73 °) = 0,30573 детская кроватка ( 74 °) = 0,28675 детская кроватка (75 °) = 0,26795 детская кроватка (76 °) = 0,24933 детская кроватка (77 °) = 0,23087 детская кроватка (78 °) = 0,21256 детская кроватка (79 °) = 0,19438 детская кроватка (80 ° ) = 0,17633 детская кроватка (81 °) = 0,15838 детская кроватка (82 °) = 0.14054 детская кроватка (83 °) = 0,12278 детская кроватка (84 °) = 0,1051 детская кроватка (85 °) = 0,08749 детская кроватка (86 °) = 0,06993 детская кроватка (87 °) = 0,05241 детская кроватка (88 °) = 0,03492 детская кроватка (89 °) = 0,01746 детская кроватка (90 °) = 0 детская кроватка (91 °) = -0,01746 детская кроватка (92 °) = -0,03492 детская кроватка (93 °) = -0,05241 детская кроватка (94 °) = — 0,06993 детская кроватка (95 °) = -0,08749 детская кроватка (96 °) = -0,1051 детская кроватка (97 °) = -0,12278 детская кроватка (98 °) = -0,14054 детская кроватка (99 °) = -0,15838 детская кроватка (100 °) = -0,17633 детская кроватка (101 °) = -0,19438 детская кроватка (102 °) = -0.21256 детская кроватка (103 °) = -0,23087 детская кроватка (104 °) = -0,24933 детская кроватка (105 °) = -0,26795 детская кроватка (106 °) = -0,28675 детская кроватка (107 °) = -0,30573 детская кроватка (108 °) = -0,32492 детская кроватка (109 °) = -0,34433 детская кроватка (110 °) = -0,36397 детская кроватка (111 °) = -0,38386 детская кроватка (112 °) = -0,40403 детская кроватка (113 °) = -0,42447 детская кроватка (114 °) = -0,44523 детская кроватка (115 °) = -0,46631 детская кроватка (116 °) = -0,48773 детская кроватка (117 °) = -0,50953 детская кроватка (118 °) = -0,53171 детская кроватка (119 ° ) = -0,55431 детская кроватка (120 °) = -0,57735 | детская кроватка (121 °) = -0.60086 детская кроватка (122 °) = -0,62487 детская кроватка (123 °) = -0,64941 детская кроватка (124 °) = -0,67451 детская кроватка (125 °) = -0,70021 детская кроватка (126 °) = -0,72654 детская кроватка (127 °) = -0,75355 детская кроватка (128 °) = -0,78129 детская кроватка (129 °) = -0,80978 детская кроватка (130 °) = -0,8391 детская кроватка (131 °) = -0,86929 детская кроватка (132 °) = -0,9004 детская кроватка (133 °) = -0, детская кроватка (134 °) = -0,96569 детская кроватка (135 °) = -1 детская кроватка (136 °) = -1,03553 детская кроватка (137 °) = -1,07237 детская кроватка (138 ° ) = -1,11061 детская кроватка (139 °) = -1,15037 детская кроватка (140 °) = -1.19175 детская кроватка (141 °) = -1,2349 детская кроватка (142 °) = -1,27994 детская кроватка (143 °) = -1,32704 детская кроватка (144 °) = -1,37638 детская кроватка (145 °) = -1,42815 детская кроватка (146 °) = -1,48256 детская кроватка (147 °) = -1,53986 детская кроватка (148 °) = -1,60033 детская кроватка (149 °) = -1,66428 детская кроватка (150 °) = -1,73205 детская кроватка (151 °) = -1,80405 детская кроватка (152 °) = -1,88073 детская кроватка (153 °) = -1,96261 детская кроватка (154 °) = -2,0503 детская кроватка (155 °) = -2,14451 детская кроватка (156 °) = -2,24604 детская кроватка (157 ° ) = -2,35585 детская кроватка (158 °) = -2,47509 детская кроватка (159 °) = -2.60509 детская кроватка (160 °) = -2,74748 детская кроватка (161 °) = -2, |
PI = 3.141592 … (примерно 22/7 = 3,1428)
|
Калькулятор Arctan. Найти арктангенс
Воспользуйтесь этим калькулятором арктангенса, чтобы быстро найти арктангенс. Ищете ли вы простой ответ на вопрос «что такое арктан?» или вам интересно узнать об интегральном или производном от arctan, вы попали в нужное место.Ниже вы также найдете график arctan, а также аккуратную таблицу с часто используемыми значениями, такими как arctan (1) и arctan (0). Кроме того, вы можете просто ввести интересующее значение в этот инструмент, и вы найдете ответ в мгновение ока.
Заинтересованы в более продвинутой тригонометрии? Ознакомьтесь с нашими калькуляторами закона синусов и закона косинусов, если вам нужно решить треугольники.
Что такое арктан?
Арктангенс — это функция, обратная касательной. Проще говоря, мы используем arctan, когда хотим найти угол, для которого нам известно значение тангенса.
Однако, в самом строгом смысле, поскольку касательная является периодической тригонометрической функцией, у нее нет обратной функции. Тем не менее, мы можем определить обратную функцию, если ограничим область до интервала, в котором функция является монотонной. Обычно выбираемый интервал -π / 2 Использование условного обозначения tan -1 x может привести к путанице в отношении разницы между арктангенсом и котангенсом.Оказывается, арктан и детская кроватка — разные вещи: Надеемся, что теперь вы не сомневаетесь в том, что арктан и котан разные. Чтобы избежать дальнейших недоразумений, вы можете использовать арктангенс (x), а не загар -1 x нотацию . Ограничивая область определения главной касательной функции, мы получаем арктангенс, который изменяется исключительно от −π / 2 до π / 2 радиан.Однако область определения функции арктангенса — это все действительные числа. Тогда график выглядит следующим образом: Как создается этот арктановый граф? Отражая tan (x) в диапазоне (-π / 2 π / 2) через линию y = x.Вы также можете посмотреть на это как на замену горизонтальной и вертикальной осей: Отношения в тригонометрии имеют решающее значение для более глубокого понимания этой темы. Изучение прямоугольного треугольника с длинами сторон 1 и x является хорошей отправной точкой, если вы хотите найти отношения между arctan и основными тригонометрическими функциями: Другие полезные отношения с арктангенсом: Первое уравнение легко доказать, исходя из свойств прямоугольного треугольника с длинами сторон 1 и x, поскольку мы прекрасно знаем, что сумма углов в треугольнике равна 180 °.Вычитая прямой угол, равный 90 °, мы получаем два непрямых угла, которые в сумме должны составлять 90 °. Таким образом, мы можем записать углы как arctan (x) и arctan (1 / x). Это действительно один из самых простых в использовании калькуляторов! Просто введите номер , по которому вы хотите найти арктан . Поскольку домен arctan — это все вещественные числа, вам не о чем беспокоиться. Допустим, мы хотим найти арктангенс 1. Просто введите число, и калькулятор арктангенса отобразит результат .Как мы и ожидали, арктангенс 1 равен 45 °. Этот калькулятор арктангенса работает и в обратном направлении, то есть как стандартный калькулятор тангенса — введите угол во второе поле, и появится тангенс этого угла. Значение Cos 65 градусов = 0,4226182617407 Значение Cos 65 радиан = -0,56245385123817 Значение 65 градусов в радианах = 1,1344640137963 Значение 65 радиан в градусах = 3724.2256683504 Вычислить точное значение косинуса 65 градусов Cosh 65 градусов = 8,4744462220517E + 27. Примечание: Cosh означает гиперболический косинус. acosh 65 градусов = 4,8674752736053. Примечание: acosh означает обратный гиперболический косинус. acos 65 градусов = NAN.Примечание: acos означает арккосинус. косинус 30 дробь косинус 65 к синусу косинус 65 к котангенсу При вычислении точного значения косинуса 65 в радианах или точного значения косинуса 65 градусов вы используете инструмент вычисления выше, чтобы получить преобразование, или вы используете предоставленные формулы, чтобы вычислить себя математически. Вы также можете вычислить другие числовые значения углов, используя калькулятор выше, и ввести любое значение, которое хотите вычислить. что такое Cosh Ответ: Cosh — это гиперболический косинус, математическая функция с обозначением cosh (x).cosh числа можно рассчитать с помощью вышеуказанного инструмента. Как вычислить cosh (x) без вычисления? Ответ: Вы вычисляете cosh (x), используя эту формулу cosh (x) = (e x + e -x ) / 2, чтобы решить это самостоятельно, или легко используйте инструмент выше что такое ACosh? Ответ: ACosh — это обратный гиперболический косинус, математическая функция с обозначением acosh (x). Акошу числа можно рассчитать с помощью инструмента, описанного выше. Как рассчитать acosh (x) по формуле Ответ: Расчет ACosh (x) по формуле выполняется путем получения обратной величины cosh, которая равна ACosh (x) = 1 / ((e x + e -x ) / 2) Как рассчитать acos (x) по формуле Ответ: Расчет acos (x) по формуле выполняется с использованием формулы Арккосинуса, которая равна acos (x) = Арккосинус x в радианах, 2 * pi / 3 Формула и уравнение для радианов с точностью до градуса Ответ: 1 радиан >> 1 радиан = 180 / пи Формула и уравнение для градусов в радианах Ответ: 1 градус >> 1 градус = пи / 180.Например, 200 градусов до радиана = 200 x пи / 180 >> 10pi / 9 >> = 3,49 радиана Что такое радианы? Ответ: Радиан — стандартная единица измерения угла, используемая в различных областях математики. Длина дуги окружности равна измеренному в радианах углу, который она окружает; один радиан составляет чуть менее 57,3 градуса (когда длина дуги равна радиусу; расширение в OEIS A072097). Единица радиан ранее была дополнительной единицей СИ.но это было отменено в 1995 году, и теперь радиан считается производной единицей СИ. 2 радиана равны 360 градусам. Это означает, что 1 радиан = 180 / градус, а 1 градус = / 180 радиан Что такое степень? Градус, который обозначается полностью как градус дуги, градус дуги или градус дуги, обычно обозначаемый символом °, представляет собой измерение плоского угла, определяемого таким образом, что полный поворот составляет 360 градусов. Это не единица СИ, потому что единицей измерения угла СИ является радиан, но она используется в брошюре СИ как единица измерения, поскольку полный оборот равен 2π радиан, один градус эквивалентен π / 180 радиан. Если вы обнаружите ошибку на этом сайте, мы будем благодарны, если вы сообщите нам об этом, используя предоставленный контактный адрес электронной почты. отправьте электронное письмо в контакт на нашем сайте. Далее Назад В предыдущих разделах мы использовали единичный круг для определения тригонометрических функций . В этом разделе мы расширим эти определения, чтобы применить их к прямоугольным треугольникам. Значение функции синуса или косинуса [latex] t [/ latex] — это его значение в [latex] t [/ latex] радианах.Во-первых, нам нужно создать наш прямоугольный треугольник. На рисунке 1 показана точка на единичной окружности радиуса 1. Если мы опустим вертикальный отрезок из точки [latex] \ left (x, y \ right) \\ [/ latex] на ось x , у нас есть прямоугольный треугольник, вертикальная сторона которого имеет длину [латекс] y [/ латекс], а горизонтальная сторона имеет длину [латекс] x [/ латекс]. Мы можем использовать этот прямоугольный треугольник, чтобы переопределить синус, косинус и другие тригонометрические функции как отношения сторон прямоугольного треугольника. Рисунок 1 Мы знаем [латекс] \ cos t = \ frac {x} {1} = x [/ латекс] Точно так же мы знаем [латекс] \ sin t = \ frac {y} {1} = y [/ латекс] Эти соотношения по-прежнему применяются к сторонам прямоугольного треугольника, когда не используется единичный круг, и когда треугольник находится не в стандартном положении и не отображается на графике с использованием координат [латекс] \ left (x, y \ right) [/ latex] .Чтобы иметь возможность свободно использовать эти соотношения, мы дадим сторонам более общие имена: вместо [latex] x [/ latex] мы будем называть сторону между заданным углом и прямым углом смежной стороной к углу [ латекс] т [/ латекс]. (Соседний означает «рядом с.») Вместо [латекс] y [/ латекс] мы будем называть сторону, наиболее удаленную от данного угла, противоположной стороной под углом [латекс] t [/ латекс]. И вместо [latex] 1 [/ latex] назовем сторону прямоугольного треугольника, противоположную прямому углу, гипотенузой .Эти стороны обозначены на Рисунке 2. Рисунок 2. Стороны прямоугольного треугольника относительно угла [латекс] t [/ латекс]. Дан прямоугольный треугольник с острым углом [латекс] т [/ латекс], [латекс] \ begin {align} & \ sin \ left (t \ right) = \ frac {\ text {напротив}} {\ text {hypotenuse}} & \ csc \ left (t \ right) = \ frac { \ text {гипотенуза}} {\ text {напротив}} \\ & \ cos \ left (t \ right) = \ frac {\ text {смежный}} {\ text {hypotenuse}} & \ sec \ left (t \ справа) = \ frac {\ text {hypotenuse}} {\ text {смежный}} \\ & \ tan \ left (t \ right) = \ frac {\ text {противоположный}} {\ text {смежный}} & \ cot \ left (t \ right) = \ frac {\ text {смежный}} {\ text {противоположный}} \ end {align} [/ latex] Распространенным мнемоническим символом для запоминания этих отношений является SohCahToa, образованный из первых букв « S ine is o pposite over h ypotenuse, C osine a djacent over h ypotenuse, ypotenuse, angent — o pposite over a djacent.” Дайте треугольнику, показанному на рисунке 3, найдите значение [latex] \ cos \ alpha [/ latex]. Рисунок 3 Сторона, прилегающая к углу, равна 15, а гипотенуза треугольника равна 17, поэтому: [латекс] \ begin {align} \ cos \ left (\ alpha \ right) = \ frac {\ text {смежный}} {\ text {hypotenuse}} = \ frac {15} {17} \ end {align} [/ латекс] Для треугольника, показанного на рисунке 4, найдите значение [latex] \ text {sin} t [/ latex]. Рисунок 4 [латекс] \ frac {7} {25} [/ латекс] При работе с прямоугольными треугольниками применяются одни и те же правила независимо от ориентации треугольника.Фактически, мы можем оценить шесть тригонометрических функций любого из двух острых углов в треугольнике на рисунке 5. Сторона, противоположная одному острому углу, является стороной, смежной с другим острым углом, и наоборот. Рис. 5. Сторона, прилегающая к одному углу, противоположна другой. Нас попросят найти все шесть тригонометрических функций для заданного угла в треугольнике. Наша стратегия — сначала найти синус, косинус и тангенс углов. Затем мы можем легко найти другие тригонометрические функции, потому что мы знаем, что величина, обратная синусу, является косекансной, обратная величина косинуса — секущей, а обратная величина касательной — котангенсом. Используя треугольник, показанный на рисунке 6, оцените [latex] \ sin \ alpha [/ latex], [latex] \ cos \ alpha [/ latex], [latex] \ tan \ alpha [/ latex], [latex] \ sec \ alpha [/ latex], [latex] \ csc \ alpha [/ latex] и [latex] \ cot \ alpha [/ latex]. Рисунок 6 [латекс] \ begin {align} & \ sin \ alpha = \ frac {\ text {напротив} \ alpha} {\ text {hypotenuse}} = \ frac {4} {5} \\ & \ cos \ alpha = \ frac {\ text {примыкает к} \ alpha} {\ text {hypotenuse}} = \ frac {3} {5} \\ & \ tan \ alpha = \ frac {\ text {напротив} \ alpha} {\ text {примыкает к} \ alpha} = \ frac {4} {3} \\ & \ sec \ alpha = \ frac {\ text {hypotenuse}} {\ text {примыкает к} \ alpha} = \ frac {5} { 3} \\ & \ csc \ alpha = \ frac {\ text {hypotenuse}} {\ text {напротив} \ alpha} = \ frac {5} {4} \\ & \ cot \ alpha = \ frac {\ text {примыкает к} \ alpha} {\ text {напротив} \ alpha} = \ frac {3} {4} \ end {align} [/ latex] Используя треугольник, показанный на рисунке 7, оцените [latex] \ sin t [/ latex], [latex] \ cos t [/ latex], [latex] \ tan t [/ latex], [latex] \ sec t [ / latex], [латекс] \ csc t [/ latex] и [латекс] \ cot t [/ latex]. Рисунок 7 [латекс] \ begin {align} & \ sin t = \ frac {33} {65}, \ cos t = \ frac {56} {65}, \ tan t = \ frac {33} {56}, \ \ & \ sec t = \ frac {65} {56}, \ csc t = \ frac {65} {33}, \ cot t = \ frac {56} {33} \ end {align} [/ latex] Мы уже обсуждали тригонометрические функции в связи с особыми углами на единичной окружности. Теперь мы можем использовать эти отношения для оценки треугольников, содержащих эти особые углы.\ circ [/ latex] треугольник, который также можно описать как [latex] \ frac {\ pi} {4}, \ frac {\ pi} {4}, \ frac {\ pi} {2} [/ latex ] треугольник, имеют длины в соотношении [latex] s, s, \ sqrt {2} s [/ latex]. Эти отношения показаны на рисунке 8. Рисунок 8. Длины сторон специальных треугольников Затем мы можем использовать отношения длин сторон для оценки тригонометрических функций специальных углов. Найдите точное значение тригонометрических функций [latex] \ frac {\ pi} {3} [/ latex], используя длины сторон. [латекс] \ begin {align} & \ sin \ left (\ frac {\ pi} {3} \ right) = \ frac {\ text {opp}} {\ text {hyp}} = \ frac {\ sqrt {3} s} {2s} = \ frac {\ sqrt {3}} {2} \\ & \ cos \ left (\ frac {\ pi} {3} \ right) = \ frac {\ text {adj} } {\ text {hyp}} = \ frac {s} {2s} = \ frac {1} {2} \\ & \ tan \ left (\ frac {\ pi} {3} \ right) = \ frac { \ text {opp}} {\ text {adj}} = \ frac {\ sqrt {3} s} {s} = \ sqrt {3} \\ & \ sec \ left (\ frac {\ pi} {3} \ right) = \ frac {\ text {hyp}} {\ text {adj}} = \ frac {2s} {s} = 2 \\ & \ csc \ left (\ frac {\ pi} {3} \ right ) = \ frac {\ text {hyp}} {\ text {opp}} = \ frac {2s} {\ sqrt {3} s} = \ frac {2} {\ sqrt {3}} = \ frac {2 \ sqrt {3}} {3} \\ & \ cot \ left (\ frac {\ pi} {3} \ right) = \ frac {\ text {adj}} {\ text {opp}} = \ frac { s} {\ sqrt {3} s} = \ frac {1} {\ sqrt {3}} = \ frac {\ sqrt {3}} {3} \ end {align} [/ latex] Найдите точное значение тригонометрических функций [latex] \ frac {\ pi} {4} [/ latex], используя длины сторон. {\ circ} [/ latex] Теперь, когда у нас есть эта таблица, мы можем использовать ее для нахождения точных значений тригонометрических выражений. \ circ \ right) [/ latex], используя таблица выше. Если мы посмотрим на таблицу выше, мы заметим закономерность. В прямоугольном треугольнике с углами [latex] \ frac {\ pi} {6} [/ latex] и [latex] \ frac {\ pi} {3} [/ latex] мы видим, что синус [latex] \ frac {\ pi} {3} [/ latex], а именно [latex] \ frac {\ sqrt {3}} {2} [/ latex], также является косинусом [latex] \ frac {\ pi} { 6} [/ latex], в то время как синус [latex] \ frac {\ pi} {6} [/ latex], а именно [latex] \ frac {1} {2} [/ latex], также является косинусом [латекс] \ frac {\ pi} {3} [/ латекс]. [латекс] \ begin {align} & \ sin \ frac {\ pi} {3} = \ cos \ frac {\ pi} {6} = \ frac {\ sqrt {3} s} {2s} = \ frac {\ sqrt {3}} {2} \\ & \ sin \ frac {\ pi} {6} = \ cos \ frac {\ pi} {3} = \ frac {s} {2s} = \ frac {1 } {2} \ end {align} [/ latex] Рис. 9. Синус [latex] \ frac {\ pi} {3} [/ latex] равен косинусу [latex] \ frac {\ pi} {6} [/ latex] и наоборот. Этот результат не должен вызывать удивления, потому что, как мы видим на Рисунке 9, сторона, противоположная углу [latex] \ frac {\ pi} {3} [/ latex], также является стороной, смежной с [latex] \ frac { \ pi} {6} [/ latex], поэтому [latex] \ sin \ left (\ frac {\ pi} {3} \ right) [/ latex] и [latex] \ cos \ left (\ frac {\ pi } {6} \ right) [/ latex] — это точно такое же соотношение тех же двух сторон, [latex] \ sqrt {3} s [/ latex] и [latex] 2s [/ latex].Аналогично, [latex] \ cos \ left (\ frac {\ pi} {3} \ right) [/ latex] и [latex] \ sin \ left (\ frac {\ pi} {6} \ right) [/ latex ] также имеют такое же соотношение с использованием тех же двух сторон, [латекс] [/ латекс] и [латекс] 2 [/ латекс]. Взаимосвязь между синусами и косинусами [latex] \ frac {\ pi} {6} [/ latex] и [latex] \ frac {\ pi} {3} [/ latex] также сохраняется для двух острых углов в любой прямоугольный треугольник, так как в любом случае отношение одних и тех же двух сторон будет составлять синус одного угла и косинус другого.Поскольку три угла треугольника складываются в [латекс] \ pi [/ latex], а прямой угол равен [latex] \ frac {\ pi} {2} [/ latex], оставшиеся два угла также должны составлять [латекс] \ frac {\ pi} {2} [/ латекс]. Это означает, что прямоугольный треугольник может быть образован любыми двумя углами, которые складываются с [latex] \ frac {\ pi} {2} [/ latex] — другими словами, любыми двумя дополнительными углами. Таким образом, мы можем сформулировать тождество совместной функции : Если любые два угла дополняют друг друга, синус одного является косинусом другого, и наоборот.Эта идентичность проиллюстрирована на рисунке 10. Рис. 10. Идентичность совместных функций синуса и косинуса дополнительных углов Используя это тождество, мы можем утверждать, не вычисляя, например, что синус [latex] \ frac {\ pi} {12} [/ latex] равен косинусу [latex] \ frac {5 \ pi} {12 } [/ latex], и что синус [latex] \ frac {5 \ pi} {12} [/ latex] равен косинусу [latex] \ frac {\ pi} {12} [/ latex]. Мы также можем заявить, что если для определенного угла [латекс] t [/ латекс], [латекс] \ cos \ text {} t = \ frac {5} {13} [/ latex], то [латекс] \ sin \ left (\ frac {\ pi} {2} -t \ right) = \ frac {5} {13} [/ latex]. Идентификаторы совместных функций в радианах перечислены в таблице ниже. Запишите следующее как эквивалентное выражение косинуса: [latex] \ sin \ left (\ frac {5 \ pi} {12} \ right) [/ latex]. Согласно тождествам совместных функций для синуса и косинуса, [латекс] \ sin t = \ cos \ left (\ frac {\ pi} {2} -t \ right) [/ latex].\ circ \ right) [/ латекс] В предыдущих примерах мы вычисляли синус и косинус в треугольниках, где мы знали все три стороны. Но настоящая сила тригонометрии прямоугольного треугольника проявляется, когда мы смотрим на треугольники, в которых мы знаем угол, но не знаем всех сторон. Найдите неизвестные стороны треугольника на рисунке 11. Рисунок 11 Нам известны угол и противоположная сторона, поэтому мы можем использовать касательную, чтобы найти прилегающую сторону.\ circ \ right)} \\ & = 14 \ end {align} [/ latex] Прямоугольный треугольник имеет один угол [латекс] \ frac {\ pi} {3} [/ latex] и гипотенузу 20. Найдите неизвестные стороны и угол треугольника. [латекс] \ text {смежный} = 10 [/ латекс]; [латекс] \ текст {напротив} = 10 \ sqrt {3} [/ латекс]; отсутствующий угол [латекс] \ frac {\ pi} {6} [/ latex] Тригонометрия прямоугольного треугольника имеет множество практических приложений. Например, способность вычислять длины сторон треугольника позволяет определить высоту высокого объекта, не взбираясь на вершину и не протягивая рулетку по его высоте.Мы делаем это, измеряя расстояние от основания объекта до точки на земле на некотором расстоянии, откуда мы можем смотреть на вершину высокого объекта под углом. Угол подъема объекта над наблюдателем относительно наблюдателя — это угол между горизонталью и линией от объекта до глаза наблюдателя. Правый треугольник, создаваемый этим положением, имеет стороны, которые представляют неизвестную высоту, измеренное расстояние от основания и наклонную линию обзора от земли до вершины объекта.Зная измеренное расстояние до основания объекта и угол прямой видимости, мы можем использовать тригонометрические функции для вычисления неизвестной высоты. Точно так же мы можем сформировать треугольник из вершины высокого объекта, глядя вниз. Угол наклона объекта под наблюдателем относительно наблюдателя — это угол между горизонталью и линией от объекта до глаза наблюдателя. На рисунке ниже [latex] \ alpha [/ latex] представляет угол возвышения , а [latex] \ beta [/ latex] представляет угол возвышения . Рисунок 12 Сокращение Определение Домен арктана x Диапазон обычных
основных значений arctan (x)
tan -1 x,
atan х = загар (у) все действительные числа рэнд -π / 2 cot (x) = 1 / tan (x) , поэтому котангенс в основном является обратной величиной тангенса или, другими словами, мультипликативной обратной величиной График Arctan
График Обычно используемые значения x арктан (х) рад ° -∞ -π / 2 -90 ° -3 -1.2490 -71,565 ° -2 -1,1071 -63,435 ° -√3 -π / 3 -60 ° -1 -π / 4 -45 ° -√3 / 3 -π / 6 -30 ° 0 0 0 ° √3 / 3 π / 6 30 ° 1 π / 4 45 ° √3 π / 3 60 ° 2 1.1071 63,435 ° 3 1,2490 71,565 ° ∞ π / 2 90 ° Свойства Arctan, отношения с тригонометрическими функциями, интеграл и производная от arctan
sin (arctan (x)) = x / √ (1 + x²) cos (arctan (x)) = 1 / √ (1 + x²) tan (arctan (x)) = x arctan (x) = π / 2 - arccot (x) арктан (-x) = -арктан (x) = arctan (x / √ (1 - x²)) arctan (x) dx = x arctan (x) - (1/2) ln (1 + x²) + C d / dx arctan (x) = 1 / (1 + x²) , где x ≠ -i, i arctan (x) + arctan (1 / x) = π / 2 , для x> 0 и arctan (x) + arctan (1 / x) = -π / 2 , для x <0 Калькулятор Arctan — как пользоваться
cos 65 | cos 65 градусов
Что такое cos 65?
Что такое cos Другие преобразования косинусов
= 0,0073760132620899
= 0,007376213
Тангенс к котангенсу эквивалентен делению 1 на тангенс.
Следовательно,
0,00737621365 касательная к котангенсу = 1 / 0,00737621365
= 135.570951 Как вычислить косинус 65 в радианах или точное значение косинуса 65 градусов
Раздел 4.3: Тригонометрия прямоугольного треугольника
Результаты обучения
Использование прямоугольных треугольников для вычисления тригонометрических функций
Понимание отношений правого треугольника
Как сделать: учитывая длины сторон прямоугольного треугольника и один из острых углов, найдите синус, косинус и тангенс этого угла.
Пример 1: Вычисление тригонометрической функции прямоугольного треугольника
Попробуйте
Взаимосвязь углов и их функций
Как сделать: учитывая длины сторон прямоугольного треугольника, вычислите шесть тригонометрических функций одного из острых углов.
Пример 2: Оценка тригонометрических функций углов, отличных от стандартного положения
Попробуйте
Нахождение тригонометрических функций специальных углов по длинам сторон
Как сделать: даны тригонометрические функции специального угла, оцените, используя длины сторон.
Пример 3: Оценка тригонометрических функций специальных углов с использованием длин сторон
Попробуйте
Косинус 1 [латекс] \ frac {\ sqrt {3}} {2} [/ латекс] [латекс] \ frac {\ sqrt {2}} {2} [/ латекс] [латекс] \ frac {1} {2} [/ латекс] 0 Синус 0 [латекс] \ frac {1} {2} [/ латекс] [латекс] \ frac {\ sqrt {2}} {2} [/ латекс] [латекс] \ frac {\ sqrt {3}} {2} [/ латекс] 1 Касательная 0 [латекс] \ frac {\ sqrt {3}} {3} [/ латекс] 1 [латекс] \ sqrt {3} [/ латекс] Неопределенный Секант 1 [латекс] \ frac {2 \ sqrt {3}} {3} [/ латекс] [латекс] \ sqrt {2} [/ латекс] 2 Неопределенный Косеканс Неопределенный 2 [латекс] \ sqrt {2} [/ латекс] [латекс] \ frac {2 \ sqrt {3}} {3} [/ латекс] 1 Котангенс Неопределенный [латекс] \ sqrt {3} [/ латекс] 1 [латекс] \ frac {\ sqrt {3}} {3} [/ латекс] 0 Использование равных функций дополнений
Общее примечание: идентификационные данные совместных функций
[латекс] \ cos t = \ sin \ left (\ frac {\ pi} {2} -t \ right) [/ latex] [латекс] \ sin t = \ cos \ left (\ frac {\ pi} {2} -t \ right) [/ latex] [латекс] \ tan t = \ cot \ left (\ frac {\ pi} {2} -t \ right) [/ latex] [латекс] \ cot t = \ tan \ left (\ frac {\ pi} {2} -t \ right) [/ latex] [латекс] \ sec t = \ csc \ left (\ frac {\ pi} {2} -t \ right) [/ latex] [латекс] \ csc t = \ sec \ left (\ frac {\ pi} {2} -t \ right) [/ latex] Как сделать: учитывая синус и косинус угла, найдите синус или косинус его дополнения.
Пример 5: Использование идентификаторов совместных функций
Использование тригонометрических функций
Как: для прямоугольного треугольника, длины одной стороны и меры одного острого угла найдите оставшиеся стороны.
Пример 7: Нахождение недостающих длин сторон с использованием тригонометрических соотношений
Попробуйте
Практическое руководство. Для высокого объекта измерьте его высоту косвенно.
Дерево примерно 46 футов в высоту.
Попробуйте
Какова длина лестницы, чтобы добраться до подоконника на высоте 50 футов над землей, если лестница упирается в здание под углом [латекс] \ frac {5 \ pi} {12} [/ latex]? Округлите до ближайшего фута.
Обратная тригонометрическая функция на калькуляторе
Если заданы две стороны прямоугольного треугольника, обратная тригонометрическая функция может использоваться для нахождения острого угла в треугольнике.{-1} [/ латекс]. Калькулятор вернет угол в радианах или градусах, в зависимости от того, в каком режиме находится ваш калькулятор. Нам понадобится функция арктангенса для пеленга.
Подшипник
Пеленг — это направление, в котором вы движетесь по компасу. На большинстве карт N вверху, S внизу, W слева, а E справа. Подшипники записываются в такой форме: (N или S) (Острый угол) (E или W). Угол измеряется либо от севера, либо от юга, в зависимости от того, какая буква идет первой в вашем азимуте.\ circ E [/ latex] означает, что вы пойдете на север, а затем на 20 градусов на восток или вправо. На рисунке ниже показан пример рисования подшипников. Как видите, каждый угол измеряется от N или S в зависимости от первой буквы подшипника. Подшипники НЕ рисуются в стандартном положении, что означает, что НЕ отрисовываются от положительной оси x.
Теперь мы рассмотрим некоторые прикладные задачи, связанные с пеленгами и прямоугольными треугольниками.
Пример 9: Найти подшипник
Полуавтоматический самолет едет на восток на 8 миль, делает поворот направо, а затем едет на юг еще на 11 миль.\ circ E [/ latex] на 5 миль. Как далеко на восток и как далеко на юг бегун от исходной точки? Округлите ответы до ближайшей мили.
Показать решение4 мили на восток, 3 мили на юг
Преобразовать процентную оценку в градусы
Процентный уклон часто встречается на дорогах или тропах, и это показатель крутизны. Например, если дорога имеет уклон 6%, это означает, что дорога поднимается на 6 футов на горизонтальное расстояние (пробег) в 100 футов. Процентное уклонение определяется путем деления прибавки за пробег, как показано на Рисунке 14.Подъем и бег — это тоже противоположные и смежные стороны. Мы можем найти [latex] \ theta [/ latex], взяв арктангенс.
Рисунок 14
Чтобы вычислить градусное измерение степени в процентах, сначала измените процент на десятичное число, разделив его на 100. Затем возьмите арктангенс этого десятичного числа, и это даст угол в градусах. На самом деле это угол возвышения , который мы изучали ранее в этом разделе!
Как преобразовать процентную оценку в градусы
Убедитесь, что ваш калькулятор работает в градусном режиме. {- 1} \ left (\ dfrac {\ text {процентная оценка}} {100} \ right) [/ latex]
Ключевые понятия
- Мы можем определить тригонометрические функции как отношения длин сторон прямоугольного треугольника.
- Можно использовать одинаковые длины сторон для оценки тригонометрических функций любого острого угла в прямоугольном треугольнике.
- Мы можем оценить тригонометрические функции особых углов, зная длины сторон треугольников, в которых они встречаются.
- Любые два дополнительных угла могут быть двумя острыми углами прямоугольного треугольника.
- Если два угла дополняют друг друга, тождества совместных функций утверждают, что синус одного равен косинусу другого и наоборот.
- Мы можем использовать тригонометрические функции угла, чтобы найти неизвестные длины сторон.
- Выберите тригонометрическую функцию, представляющую отношение неизвестной стороны к известной стороне.
- Тригонометрия прямоугольного треугольника позволяет измерять недоступные высоты и расстояния.
- Неизвестную высоту или расстояние можно найти, создав прямоугольный треугольник, в котором неизвестная высота или расстояние являются одной из сторон, а другая сторона и угол известны.
- Подшипники измеряются от N или S, в зависимости от первой буквы подшипника.
- Процент уклона можно выразить в градусе, который представляет собой угол подъема.
Глоссарий
- смежная сторона
- в прямоугольном треугольнике, сторона между заданным углом и прямым углом
- угол наклона
- угол между горизонталью и линией от объекта до глаза наблюдателя, предполагая, что объект расположен ниже, чем наблюдатель
- угол возвышения
- угол между горизонталью и линией от объекта до глаза наблюдателя, предполагая, что объект расположен выше, чем наблюдатель
- противоположная сторона
- в прямоугольном треугольнике со стороной, наиболее удаленной от заданного угла
- гипотенуза
- сторона прямоугольного треугольника напротив прямого угла
- процентная оценка
- Коэффициент роста за пробег, выраженный в процентах.Это мера крутизны.
Раздел 4.3 Домашние упражнения
1. Для данного прямоугольного треугольника отметьте прилегающую сторону, противоположную сторону и гипотенузу для указанного угла.
2. Когда прямоугольный треугольник с гипотенузой 1 помещается в единичный круг, какие стороны треугольника соответствуют координатам x и y?
3. Тангенс угла сравнивает стороны прямоугольного треугольника?
4. Как соотносятся два острых угла в прямоугольном треугольнике?
5.\ circ \ right) [/ латекс]
13. [латекс] \ tan \ left (\ frac {\ pi} {4} \ right) = \ cot \ left (\ text {__} \ right) [/ latex]
Для следующих упражнений найдите длины недостающих сторон, если сторона [латекс] a [/ латекс] находится под противоположным углом [латекс] A [/ латекс], сторона [латекс] b [/ латекс] находится под противоположным углом [латекс] B [/ latex], а side [latex] c [/ latex] — гипотенуза.
14. [латекс] \ cos B = \ frac {4} {5}, a = 10 [/ латекс]
15. [латекс] \ sin B = \ frac {1} {2}, a = 20 [/ латекс]
16. [латекс] \ tan A = \ frac {5} {12}, b = 6 [/ latex]
17.{\ circ} [/ латекс]
Для следующих упражнений используйте Рис. 14, чтобы оценить каждую тригонометрическую функцию угла [латекс] A [/ латекс].
Рисунок 14
21. [латекс] \ sin A [/ латекс]
22. [латекс] \ cos A [/ латекс]
23. [латекс] \ tan A [/ латекс]
24. [латекс] \ csc A [/ латекс]
25. [латекс] \ сек A [/ латекс]
26. [латекс] \ cot A [/ латекс]
Для следующих упражнений используйте Рис. 15, чтобы оценить каждую тригонометрическую функцию угла [латекс] A [/ латекс].
Рисунок 15
27. [латекс] \ sin A [/ латекс]
28. [латекс] \ cos A [/ латекс]
29. [латекс] \ tan A [/ латекс]
30. [латекс] \ csc A [/ латекс]
31. [латекс] \ сек A [/ латекс]
32. [латекс] \ cot A [/ latex]
Для следующих упражнений решите неизвестные стороны данного треугольника.
33.
34.
35.
Для следующих упражнений используйте калькулятор, чтобы найти длину каждой стороны с точностью до четырех знаков после запятой.\ circ [/ латекс]. Насколько высоко лестница поднимается к стене здания?
58. Угол подъема к верху здания в Нью-Йорке составляет 9 градусов от земли на расстоянии 1 мили от основания здания. Используя эту информацию, найдите высоту здания.
59. Угол подъема к вершине здания в Сиэтле составляет 2 градуса от земли на расстоянии 2 миль от основания здания. Используя эту информацию, найдите высоту здания.\ circ [/ latex], как далеко я от основания дерева?
61. Автомобиль едет на запад 5 миль, поворачивает налево и затем 9 миль на юг. Каков пеленг от исходного положения автомобиля до его текущего положения? Округлите ответ до двух десятичных знаков.
62. Грузовик едет на восток 4 мили, поворачивает налево, а затем едет на север 6 миль. Каков подшипник от исходного положения грузовика до его текущего положения? Округлите ответ до двух десятичных знаков.
63.\ circ W [/ latex] на 20 дюймов. Как далеко на запад и как далеко на юг находится паук от начальной точки? Округлите ответы до двух десятичных знаков.
65. Построен в 1901 году полковником Дж. У. Эдди, компания Angels Flight в Лос-Анджелесе, как говорят, является самой короткой в мире железной дорогой с внутренним доступом. Машины с противовесом, управляемые тросами, преодолевают уклон 33% на расстояние 315 футов. Какой угол образует дорожка с горизонтальной линией, округленной до одного десятичного знака?
66. Saluda Grade — это самый крутой уклон магистральной железной дороги стандартной колеи в Соединенных Штатах.Между Мелроузом и Салудой, Северная Каролина, максимальный уклон составляет 4,9% на расстоянии около 300 футов. Какой угол образует дорожка с горизонтальной линией, округленной до одного десятичного знака?
Темы | Дом Для углов до 45 ° используйте левый столбец и обозначения функций синего цвета. Для углов больше 45 ° используйте правый столбец и обозначения функций красного цвета. Например, sin 5 ° = 0,087 грех 85 ° = 0,996
Темы | Дом Авторские права © 2021 Лоуренс Спектор Вопросы или комментарии? Эл. Почта: themathpage @ яндекс.com |
Периодичность тригонометрических функций
Периодические процессы и функции
Мы часто сталкиваемся с периодическими явлениями в природе, технологиях и человеческом обществе. Вспомните \ (24 \ text {-hour} \) цикл день-ночь или приливные циклы, вызванные вращением Луны вокруг Земли.
Рисунок 1.Другой пример — маятник. Когда маятник совершает один полный оборот вперед и назад за \ (T \) секунд, отклонение маятника от положения равновесия будет таким же временами \ (t, \) \ (t + T, \) \ (t + 2T, \) и т. Д.
Периодические процессы описываются с помощью периодических функций.
Положительное действительное число \ (T \) называется периодом функции \ (f \), если
для всех значений \ (t \) из области \ (f. \)
Если \ (T \) — период функции \ (f, \), то произведение \ (nT, \), где \ (n \ in \ mathbb {Z}, \) также является периодом функции \ (ж: \)
\ [f \ left (t \ right) = f \ left ({t + nT} \ right). \]
В частности, для \ (n = -1, \) мы имеем
\ [е \ влево ({т — Т} \ вправо) = е \ влево (т \ вправо).\]
Наименьший положительный период функции называется основным периодом или просто периодом функции.
Период функций синуса и косинуса
Функции синуса и косинуса периодические с периодом \ (2 \ pi. \)
Действительно, рассмотрим две точки \ (M \ left (\ theta \ right) \) и \ (N \ left ({\ theta + 2 \ pi} \ right) \), лежащие на единичной окружности.
Рис. 2.Эти точки совпадают и имеют одинаковые координаты. Поскольку точка \ (M \ left (\ theta \ right) \) имеет координаты \ (\ cos \ theta \) и \ (\ sin \ theta, \), мы можем написать
Эти отношения показывают, что \ (2 \ pi \) является одним из периодов синуса и косинуса.
Докажите, что \ (2 \ pi \) — наименьший период для этих функций. От противного, предположим, что для функции косинуса существует период \ (T \) меньше \ (2 \ pi \). Тогда у нас
\ [\ cos \ left ({\ theta + T} \ right) = \ cos \ theta. \]
Это тождество верно для любого \ (\ theta, \), поэтому пусть \ (\ theta = 0: \)
\ [\ cos T = \ cos 0 = 1 \]
Уравнение \ (\ cos T = 1 \) имеет следующие решения: \ (T = 0, 2 \ pi, 4 \ pi, 6 \ pi, \ ldots \) Однако по нашему предположению \ (0 \ lt T \ lt 2 \ pi.\) Получили противоречие. Следовательно, уравнение \ (\ cos T = 1 \) ложно, и функция косинуса не имеет положительных периодов меньше, чем \ (2 \ pi. \)
Доказательство для синусоидальной функции проводится таким же образом.
Период других тригонометрических функций
Касательная функция имеет период \ (\ pi: \)
Функция касательной определяется для любых углов \ (\ theta \), кроме значений, где \ (\ cos \ theta = 0, \), то есть значений \ (\ large {\ frac {\ pi} {2}} \ normalsize + \ pi n, \) \ (n \ in \ mathbb {Z}.\)
Аналогично, период функции котангенса также равен \ (\ pi: \)
Функция котангенса — это отношение косинуса к синусу. Его область определения содержит все углы \ (\ theta \), кроме точек \ (\ pi n, n \ in \ mathbb {Z}, \), где синусоидальная функция равна нулю.
Секанс и косеканс являются обратными функциями косинуса и синуса соответственно. Следовательно, секущая функция периодическая с периодом \ (2 \ pi: \)
Он определен для всех действительных чисел \ (\ theta \), кроме точек \ (\ large {\ frac {\ pi} {2}} \ normalsize + \ pi n, \) \ (n \ in \ mathbb {Z }. \ circ} \ right) \)
Решение.\ circ}} = {- 1.} \]
Пример 2.
Вычислить точные значения тригонометрических функций:- \ (\ sin \ large {\ frac {{17 \ pi}} {3}} \ normalsize \)
- \ (\ cos \ left ({- \ large {\ frac {{38 \ pi}} {3}} \ normalsize} \ right) \)
- \ (\ sec {\ large {\ frac {{43 \ pi}} {6}} \ normalsize} \)
- \ (\ csc \ left ({- \ large {\ frac {{27 \ pi}} {4}} \ normalsize} \ right) \)
Решение.
- Выразим угол \ (\ large {\ frac {{17 \ pi}} {3}} \ normalsize \) в виде \ [{\ frac {{17 \ pi}} {3} = \ frac {{5 \ pi}} {3} + \ frac {{12 \ pi}} {3}} = {\ frac {{5 \ pi}} {3} + 4 \ pi} = {\ frac {{5 \ pi}} {3} + 2 \ pi \ times 2.} \] Учитывая, что синус — периодическая функция, с периодом \ (2 \ pi, \) получаем \ [{\ sin \ frac {{17 \ pi}} {3} = \ sin \ left ({\ frac {{5 \ pi}} {3} + 2 \ pi \ times 2} \ right)} = { \ sin \ frac {{5 \ pi}} {3}.} \] Угол \ (\ large {\ frac {{5 \ pi}} {3}} \ normalsize \) лежит в квадранте \ (4 \ text {th} \) и имеет опорный угол \ (\ large {\ frac {{\ pi}} {3}} \ normalsize. \) Синус-функция отрицательна в этом квадранте. потом \ [{\ sin \ frac {{17 \ pi}} {3} = \ sin \ frac {{5 \ pi}} {3}} = {- \ sin \ frac {\ pi} {3}} = { — \ frac {{\ sqrt 3}} {2}.} \]
- Представим отрицательный угол \ ({- \ large {\ frac {{38 \ pi}} {3}} \ normalsize} \) следующим образом: \ [{- \ frac {{38 \ pi}} {3}} = {\ frac {{4 \ pi}} {3} — \ frac {{42 \ pi}} {3}} = {\ frac { {4 \ pi}} {3} — 14 \ pi} = {\ frac {{4 \ pi}} {3} — 2 \ pi \ times 7.} \] Период косинуса равен \ (2 \ pi. \) Тогда \ [{\ cos \ left ({- \ frac {{38 \ pi}} {3}} \ right)} = {\ cos \ left ({\ frac {{4 \ pi}} {3} — 2 \ pi \ times 7} \ right)} = {\ cos \ frac {{4 \ pi}} {3}.} \] Угол \ (\ large {\ frac {{4 \ pi}} {3}} \ normalsize \) находится в квадранте \ (3 \ text {rd} \), в котором косинус имеет отрицательные значения.Базовый угол для \ (\ large {\ frac {{4 \ pi}} {3}} \ normalsize \) равен \ (\ large {\ frac {{\ pi}} {3}} \ normalsize. \) Таким образом , \ [{\ cos \ left ({- \ frac {{38 \ pi}} {3}} \ right)} = {\ cos \ frac {{4 \ pi}} {3}} = {- \ cos \ frac {\ pi} {3}} = {- \ frac {1} {2}.} \]
- Здесь имеем: \ [{\ frac {{43 \ pi}} {6} = \ frac {{7 \ pi}} {6} + \ frac {{36 \ pi}} {6}} = {\ frac {{7 \ pi}} {6} + 6 \ pi} = {\ frac {{7 \ pi}} {6} + 2 \ pi \ times 3.} \] Период секанса равен \ (2 \ pi. \), Поэтому уменьшаем значение угла: \ [{\ sec \ frac {{43 \ pi}} {6} = \ sec \ left ({\ frac {{7 \ pi}} {6} + 2 \ pi \ times 3} \ right)} = { \ sec \ frac {{7 \ pi}} {6}.} \] Угол \ ({\ large {\ frac {{7 \ pi}} {6}} \ normalsize} \) лежит в квадранте \ (3 \ text {rd} \), где секущая отрицательна. Его опорный угол равен \ ({\ large {\ frac {{\ pi}} {6}} \ normalsize}, \), поэтому мы имеем \ [{\ sec \ frac {{43 \ pi}} {6} = \ sec \ frac {{7 \ pi}} {6}} = {- \ sec \ frac {\ pi} {6}} = { — \ frac {2} {{\ sqrt 3}}.} \]
- Угол \ (\ left ({- \ large {\ frac {{27 \ pi}} {4}} \ normalsize} \ right) \) можно записать как
\ [{- \ frac {{27 \ pi}} {4} = \ frac {{5 \ pi}} {4} — \ frac {{32 \ pi}} {4}} = {\ frac {{5 \ pi}} {4} — 8 \ pi} = {\ frac {{5 \ pi}} {4} — 2 \ pi \ times 4.} \]
Учитывая, что период косеканса равен \ (2 \ pi, \), получаем
\ [{\ csc \ left ({- \ frac {{27 \ pi}} {4}} \ right)} = {\ csc \ left ({\ frac {{5 \ pi}} {4} — 2 \ pi \ times 4} \ right)} = {\ csc \ frac {{5 \ pi}} {4}.} \]
Угол \ ({\ large {\ frac {{5 \ pi}} {4}} \ normalsize} \) находится в квадранте \ (3 \ text {rd} \), в котором косеканс отрицательный. Базовый угол \ ({\ large {\ frac {{5 \ pi}} {4}} \ normalsize} \) равен \ ({\ large {\ frac {{\ pi}} {4}} \ normalsize} . \) Тогда имеем
\ [{\ csc \ left ({- \ frac {{27 \ pi}} {4}} \ right)} = {\ csc \ frac {{5 \ pi}} {4}} = {- \ csc \ frac {\ pi} {4}} = {- \ sqrt 2.\ circ}} = {0 — \ frac {{\ sqrt 2}} {2} — \ frac {{\ sqrt 2}} {2}} = {- \ sqrt 2.} \]
Пример 5.
Упростите выражение \ [\ frac {{\ sin \ left ({- \ frac {{13 \ pi}} {2}} \ right) + \ tan \ left ({- 7 \ pi} \ right)}} {{\ cos \ left ({- 7 \ pi} \ right) + \ cot \ left ({- \ frac {{65 \ pi}} {4}} \ right)}}. \]Решение.
Рассчитываем каждый член отдельно:
\ [{\ sin \ left ({- \ frac {{13 \ pi}} {2}} \ right)} = {\ sin \ left ({\ frac {{3 \ pi}} {2} — \ frac {{16 \ pi}} {2}} \ right)} = {\ sin \ left ({\ frac {{3 \ pi}} {2} — 8 \ pi} \ right)} = {\ sin \ left ({\ frac {{3 \ pi}} {2} — 2 \ pi \ times 4} \ right)} = {\ sin \ frac {{3 \ pi}} {2}} = {- 1,} \]
\ [{\ tan \ left ({- 7 \ pi} \ right)} = {\ tan \ left ({0 — \ pi \ times 7} \ right)} = {\ tan 0} = {0,} \]
\ [{\ cos \ left ({- 7 \ pi} \ right) = \ cos \ left ({\ pi — 8 \ pi} \ right)} = {\ cos \ left ({\ pi — 2 \ pi \ times 4} \ right)} = {\ cos \ pi} = {- 1,} \]
\ [{\ cot \ left ({- \ frac {{65 \ pi}} {4}} \ right)} = {\ cot \ left ({\ frac {{3 \ pi}} {4} — \ frac {{68 \ pi}} {4}} \ right)} = {\ cot \ left ({\ frac {{3 \ pi}} {4} — 17 \ pi} \ right)} = {\ cot \ гидроразрыв {{3 \ pi}} {4}.} \]
Угол \ (\ large {\ frac {{3 \ pi}} {4}} \ normalsize \) лежит в квадранте \ (2 \ text {nd} \), в котором котангенс отрицательный. Базовый угол \ (\ large {\ frac {{3 \ pi}} {4}} \ normalsize \) равен \ (\ large {\ frac {{\ pi}} {4}} \ normalsize, \ ) так
\ [{\ cot \ left ({- \ frac {{65 \ pi}} {4}} \ right)} = {\ cot \ frac {{3 \ pi}} {4}} = {- \ cot \ frac {\ pi} {4}} = {- 1.} \]
Следовательно,
\ [{\ frac {{\ sin \ left ({- \ frac {{13 \ pi}} {2}} \ right) + \ tan \ left ({- 7 \ pi} \ right)}} {{ \ cos \ left ({- 7 \ pi} \ right) + \ cot \ left ({- \ frac {{65 \ pi}} {4}} \ right)}}} = {\ frac {{- 1 + 0}} {{- 1 — 1}}} = {\ frac {1} {2}.} \]
Пример 6.
Упростите выражение \ [\ frac {{\ cos \ left ({- 3 \ pi} \ right) + \ sin {\ frac {{8 \ pi}} {3}}}} {{\ tan {\ frac {{9 \ pi}} {4}} + \ cot {\ frac {{13 \ pi}} {6}}}}. \]Решение.
Найдите значение каждого члена:
\ [{\ cos \ left ({- 3 \ pi} \ right) = \ cos \ left ({\ pi — 4 \ pi} \ right)} = {\ cos \ left ({\ pi — 2 \ pi \ times 2} \ right)} = {\ cos \ pi} = {- 1,} \]
\ [{\ sin \ frac {{8 \ pi}} {3}} = {\ sin \ left ({\ frac {{2 \ pi}} {3} + \ frac {{6 \ pi}} { 3}} \ right)} = {\ sin \ left ({\ frac {{2 \ pi}} {3} + 2 \ pi} \ right)} = {\ sin \ frac {{2 \ pi}} { 3}.} \]
Базовый угол для \ (\ large {\ frac {{2 \ pi}} {3}} \ normalsize \) равен \ (\ large {\ frac {{\ pi}} {3}} \ normalsize. \) Тогда
\ [{\ sin \ frac {{8 \ pi}} {3} = \ sin \ frac {{2 \ pi}} {3}} = {\ sin \ frac {\ pi} {3}} = { \ frac {{\ sqrt 3}} {2}.} \]
Остальные термины даны в
\ [{\ tan \ frac {{9 \ pi}} {4}} = {\ tan \ left ({\ frac {\ pi} {4} + \ frac {{8 \ pi}} {4}}) \ right)} = {\ tan \ left ({\ frac {\ pi} {4} + 2 \ pi} \ right)} = {\ tan \ frac {\ pi} {4}} = {1,} \ ]
\ [{\ cot \ frac {{13 \ pi}} {6}} = {\ cot \ left ({\ frac {\ pi} {6} + \ frac {{12 \ pi}} {6}}) \ right)} = {\ cot \ left ({\ frac {\ pi} {6} + 2 \ pi} \ right)} = {\ cot \ frac {\ pi} {6}} = {\ sqrt 3.} \]
Подставляем найденные значения:
\ [{\ frac {{\ cos \ left ({- 3 \ pi} \ right) + \ sin \ left ({\ frac {{8 \ pi}} {3}} \ right)}} {{\ загар \ left ({\ frac {{9 \ pi}} {4}} \ right) + \ cot \ left ({\ frac {{13 \ pi}} {6}} \ right)}}} = {\ frac {{- 1 + \ frac {{\ sqrt 3}} {2}}} {{1 + \ sqrt 3}}} = {\ frac {{- 2 + \ sqrt 3}} {{2 \ left ( {1 + \ sqrt 3} \ right)}}} = {\ frac {{\ left ({- 2 + \ sqrt 3} \ right) \ left ({1 — \ sqrt 3} \ right)}} {{ 2 \ left ({1 + \ sqrt 3} \ right) \ left ({1 — \ sqrt 3} \ right)}}} = {\ frac {{- 2 + \ sqrt 3 + 2 \ sqrt 3 — 3} } {{2 \ left ({{1 ^ 2} — {{\ left ({\ sqrt 3} \ right)} ^ 2}} \ right)}}} = {\ frac {{3 \ sqrt 3 — 5 }} {{2 \ left ({1 — 3} \ right)}}} = {\ frac {{5 — 3 \ sqrt 3}} {4}.

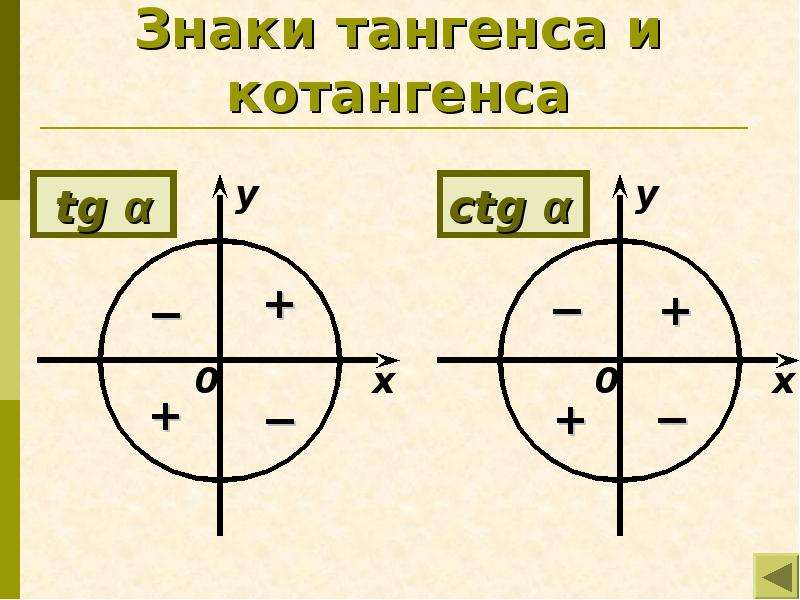 6643
6643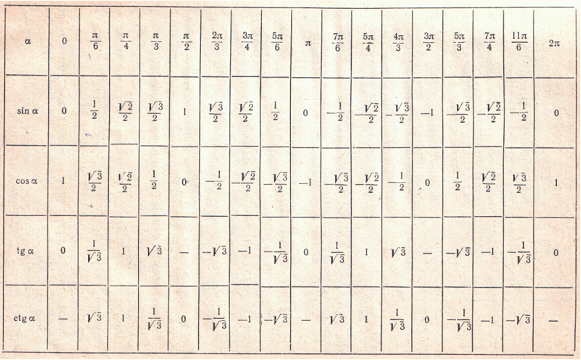 7002
7002 2126
2126 2126
2126 6745
6745 5399
5399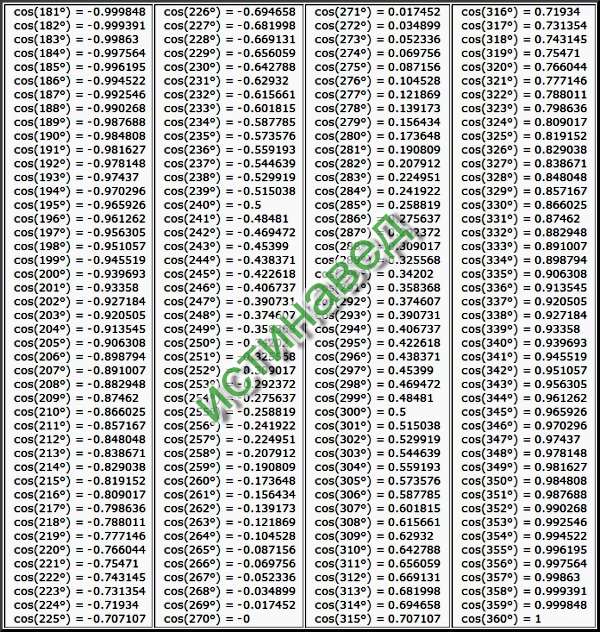 6713
6713 6713
6713 5399
5399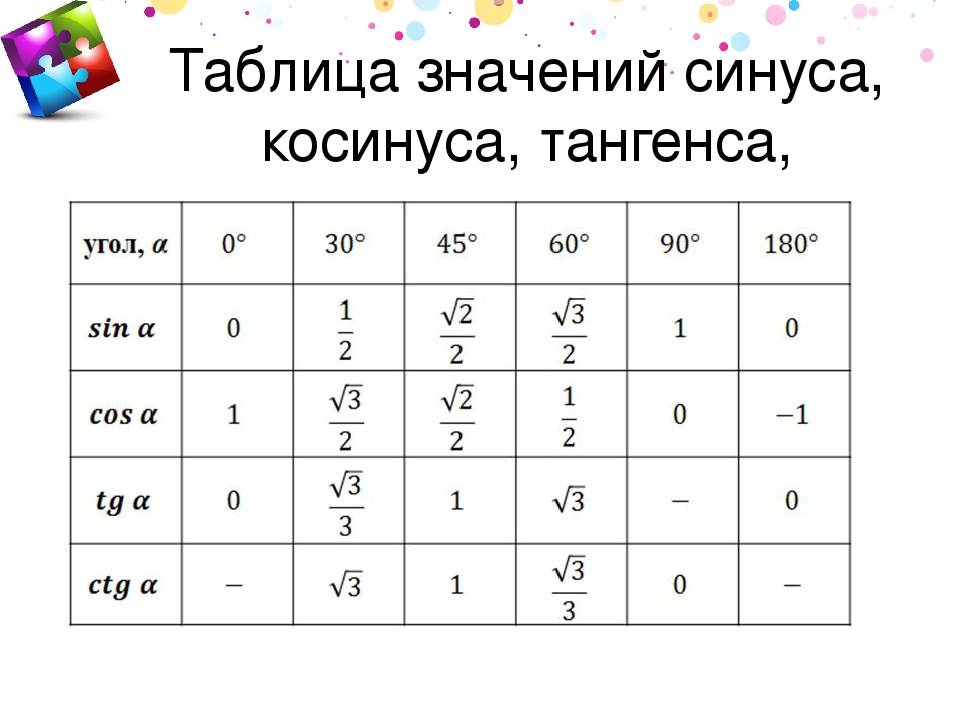 6745
6745 2126
2126 6494
6494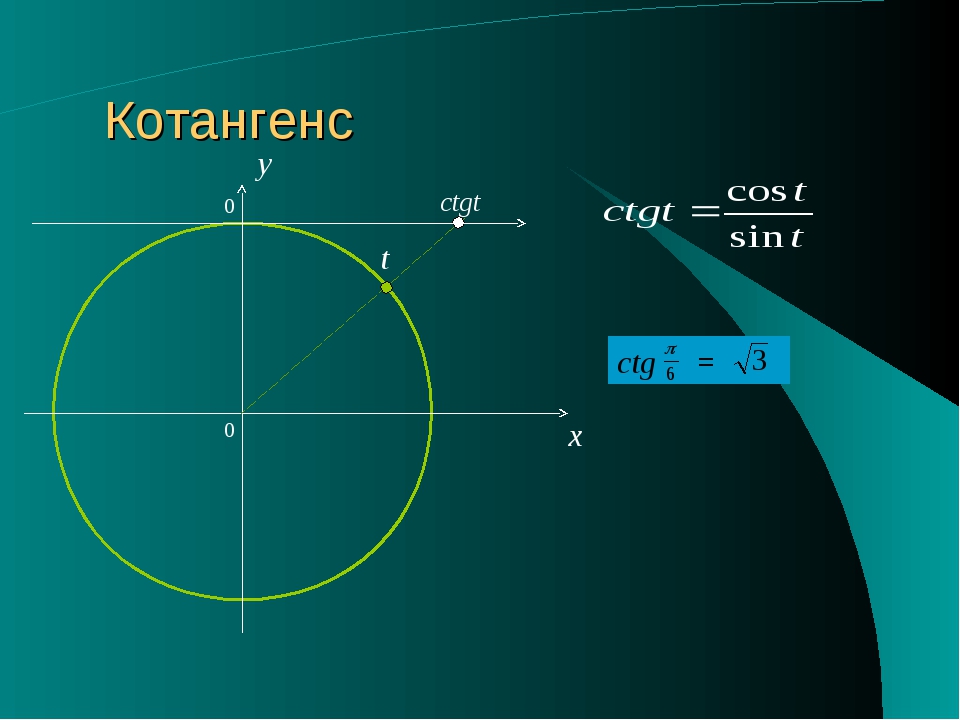 4826
4826 1446
1446 3007
3007 3559
3559 1106
1106 5543
5543