а) все делители числа 27; б) три числа, кратных 27. А.П. Ершова 6 класс Математика. СП-1 Вариант Б-2 – Рамблер/класс
2. Назовите: а) все делители числа 27; б) три числа, кратных 27. А.П. Ершова 6 класс Математика. СП-1 Вариант Б-2 – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
2.
Назовите:
б) три числа, кратных 27.
ответы
1.
а) 1, 3, 9, 27;
б) 54, 81, 108.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Психология
3 класс
5 класс
Репетитор
похожие вопросы 5
ЕГЭ Математика 11 класс. Ященко И. В. Тренировочная работа 18 Вопрос 1 Определите, какого числа цена платины была наименьшей за указанный период.
Привет…Не могу справиться с ответом на такой вопрос…может кто поможет, а?
На рисунке 26 жирными точками показана цена платины, (Подробнее…)
ЕГЭМатематикаЯщенко И.В.Семенов А.В.11 класс
ЕГЭ Математика 11 класс. Ященко И. В. Тренировочная работа 18 Вопрос 2 Найдите значение выражения.
Привет пользователи! Окажите пожалуйста услугу…ответить помогите….
Найдите значение выражения (542 — 282) : 41.
(Подробнее…)
ЕГЭМатематикаЯщенко И.В.11 классСеменов А.В.
Выпишите № 391 ГДЗ Русский язык 6 класс Ладыженская Т.А. Часть 2
Прочитайте и озаглавьте текст. Сначала выпишите вместе
с существительными прилагательные с пропущенными буквами. Укажи-
те (Подробнее…)
ГДЗРусский язык6 классЛадыженская Т.А.
Помогите рассказать о братьях. П. П. Ершов «Конек-горбунок». Вопрос 3. ГДЗ Литература 4 класс Климанова.
Что в произведении говорится о братьях и как раскрывается каждый из них в поступках? Герои поступают так:
• из (Подробнее…)
ГДЗЛитература4 классКлиманова Л.Ф.
3.
Найдите все значения х, которые
кратны 15 и удовлетворяют неравенству х < 75.
ГДЗЕршова А.П.6 классМатематика
Что такое кратное число? Ответ на webmath.ru
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Содержание:
- Определение кратного числа
- Некоторые признаки делимости натуральных чисел
- Наименьшее общее кратное (НОК)
Определение кратного числа
Определение
Число $n$ называется кратным некоторому натуральному числу $p$, если оно нацело делится на $p$. При этом говорят что $n$ кратно $p$ .
Некоторые признаки делимости натуральных чисел
Признак делимости на 2.
Число делится на 2, если его последняя цифра есть число четное (то есть 2, 4, 6, 8) или 0.
Признак делимости на 3.
Число делится на 3, если сумма его цифр делится на 3.
Признак делимости на 4.
Число делится на 4, если две его последние цифры — нули или образуют число, делящееся на 4.
Признак делимости на 5.
Число делится на 5, если оно заканчивается либо на 0, либо на 5.
Признак делимости на 8.
Число делится на 8, если три его последние цифры — нули или образуют число, делящееся на 8.
Признак делимости на 9.
Число делится на 9, если сумма его цифр делится на 9.
Признак делимости на 11.
Число делится на 11, если сумма цифр, стоящих на четных местах либо равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на число, делящееся на 11.
Признак делимости на 25.
Число делится на 5, если две его последние цифры — нули или образуют число, делящееся на 25.
Пример
Задание. Среди ниже перечисленных чисел выбрать числа кратные 3:
$$27: 36 ; 58 ; 1119 ; 2345 ; 12354$$
Решение. Будем использовать признак делимости на 3, для этого найдем сумму цифр для каждого числа:
; ;
;
Таким образом, на 3 делятся числа:
$$27 ; 36 ; 1119: 12354$$
Ответ.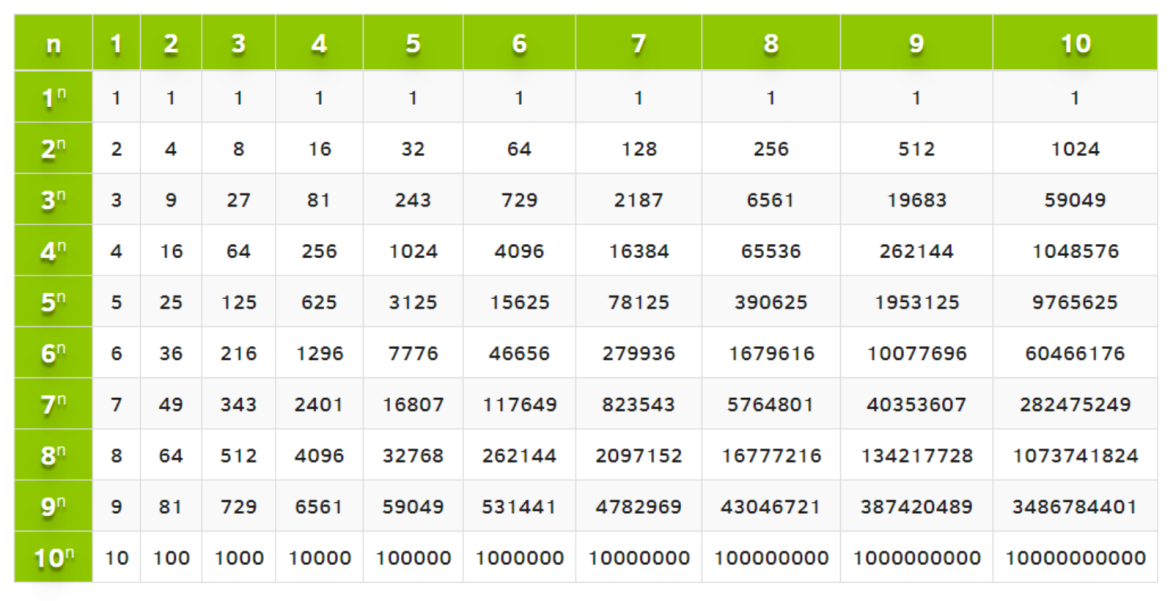
$27 ; 36 ; 1119: 12354$
Наименьшее общее кратное (НОК)
Определение
Общим кратным нескольких натуральных чисел называется натуральное число, являющееся кратным для каждого из них. Наименьшее из всех кратных называется наименьшим общим кратным (НОК).
Алгоритм нахождения наименьшего общего кратного нескольких чисел:
- выписать каноническое разложение данных чисел;
- перечислить все простые множители, входящие в канонические разложения данных чисел;
- возвести каждый множитель в наибольшую степень, с которой он входит в каноническое разложение данных чисел.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти НОК(360; 420)
Решение. Запишем каноническое разложение заданных чисел:
$360 = 2^3 \cdot 3^2 \cdot 5$ и $420 = 2^2 \cdot 3 \cdot 5 \cdot 7$
Выпишем все простые множители, которые входят в каноническое разложение заданных чисел:
$2; 3; 5; 7$ .
{2} \cdot 5 \cdot 7=2520$
Ответ. НОК(360; 420) $=2520$
Нахождение НОК онлайн Разложение чисел онлайн
Читать дальше: что такое степень числа.
Калькулятор кратных чисел
Калькулятор кратных чисел найдет 100 кратных положительному целому числу. Например, числа, кратные 3, вычисляются как 3×1, 3×2, 3×3, 3×4, 3×5 и т. д., что равно 3, 6, 9, 12, 15 и т. д. Вы можете указать минимальное значение для создания кратных, превышающих число. Например, чтобы найти 100 кратных 36, которые больше 1000, вы получите: 1008, 1044, 1080, 1116, 1152, 1188, 1224, 1260, 1296, 1332, 1368, 1404 и т. д.
Вот список из первых 20 кратных целых чисел от 1 до 20.
Кратность 1 : 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
Кратность 2 : 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40
Кратность 3 : 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60
Кратно 4 : 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80
Кратность 5 : 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100
Кратность 6 : 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96, 102, 108, 114, 120
Кратность 7 : 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126, 133, 140
Кратность 8 : 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128, 136, 144, 152, 160
Кратность 9 : 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126, 135, 144, 153, 162, 171, 180
Кратность 10 : 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 160, 170, 180, 190, 200
Кратность 11 : 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132, 143, 154, 165, 176, 187, 198, 209, 220
Кратность 12 : 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 156, 168, 180, 192, 204, 216, 228, 240
кратно 13 : 13, 26, 39, 52, 65, 78, 91, 104, 117, 130, 143, 156, 169, 182, 195, 208, 221, 234, 247, 260
Кратность 14 : 14, 28, 42, 56, 70, 84, 98, 112, 126, 140, 154, 168, 182, 196, 210, 224, 238, 252, 266, 280
Кратность 15 : 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255, 270, 285, 300
кратно 16 : 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, 176, 192, 208, 224, 240, 256, 272, 288, 304, 320
Кратность 17 : 17, 34, 51, 68, 85, 102, 119, 136, 153, 170, 187, 204, 221, 238, 255, 272, 289, 306, 323, 340
Кратность 18 : 18, 36, 54, 72, 90, 108, 126, 144, 162, 180, 198, 216, 234, 252, 270, 288, 306, 324, 342, 360
Кратность 19 : 19, 38, 57, 76, 95, 114, 133, 152, 171, 190, 209, 228, 247, 266, 285, 304, 323, 342, 361, 380
Кратность 20 : 20, 40, 60, 80, 100, 120, 140, 160, 180, 200, 220, 240, 260, 280, 300, 320, 340, 360, 380, 400
Кратность 9 — Математика с мамой
Что такое кратность 9?
К кратным 9 относятся любые числа, которые можно разделить точно на 9 без остатка.
Первые десять кратны 9равны 9, 18, 27, 36, 45, 54, 63, 72, 81 и 90. Мы можем продолжать находить другие числа, кратные 9, каждый раз прибавляя 9. Существует бесконечное число кратных 9.
Вот таблица умножения на 9, которая составляет первые 12 кратных 9:
Все числа, кратные 9, имеют разность между ними, равную 9. Прибавьте 9 к одному кратному 9, чтобы получить следующее кратное 9.
Образцы, кратные 9
Кратность 9у всех есть цифры, которые в сумме дают еще одно кратное 9. Существует также диагональный узор, созданный путем затенения чисел, кратных 9, на сетке чисел.
Вот числа, кратные 9, показаны заштрихованными на числовой сетке.
Мы можем видеть, что существует четкий диагональный шаблон, показанный в числах, кратных 9. Этот шаблон может помочь нам вычислить следующее число, кратное 9.
При обучении числам, кратным 9, может быть полезно показать числовую сетку, где показан диагональный узор.
Мы можем увидеть дальнейшие закономерности в числах, кратных 9, читая их цифры.
Цифра в конце числа уменьшается на 1 по мере перехода от одного числа, кратного 9, к следующему. Например, 9 оканчивается на 9, 18 оканчивается на 8, а 27 оканчивается на 7.
Другая закономерность заключается в том, что число в столбце десятков уменьшается на 1 при переходе от одного числа, кратного 9, к следующему. Например, в 9 цифра десятков равна 0, в 18 — 1, в 27 — 2 и так далее.
Интересный узор в числах кратных 9заключается в том, что сумма цифр в сумме кратна 9. Первые 10 кратных 9 имеют цифры, сумма которых всегда дает 9, что облегчает их запоминание.
Например, глядя на числа 9, 18, 27 и 36, мы имеем 9 = 9, 1 + 8 = 9, 2 + 7 = 9 и 3 + 6 = 9. Эта закономерность продолжается до 90. , что имеет 9 + 0 = 9.
С большими числами, кратными 9, существует закономерность добавления цифр к любому числу, кратному 9.
Например, если 12 × 9 = 108, мы видим, что сумма цифр равна 9.
. 1 + 0 + 8 = 9.
Сумма цифр составляет 9 или любое другое число, кратное 9.
Вот пример 21 × 9 = 189.
Здесь мы видим, что 1 + 8 + 9 = 18. Опять же, сумма цифр этого кратного 9 дает еще одно кратное 9. 18 равно 2 × 9.
Как определить число, кратное 9
Все числа, кратные 9, должны иметь цифры, сумма которых дает меньшее число, кратное 9. Например, 5976 кратно 9, потому что 5 + 9 + 7 + 6 = 27, а 27 равно 3 × 9. 3299 не кратно 9, потому что 3 + 2 + 9 + 9 = 23, что не кратно 9.
Чтобы решить, является ли число кратным 9, выполните следующие действия:
- Сложите цифры числа.
- Если результат кратен 9, то исходное число кратно 9.
- Если результат не кратен 9, то исходное число не кратно 9.
- Если вы не уверены, что результат кратен 9, добавьте цифры этого числа и используйте описанные выше шаги для принятия решения.
Например, вот 5976.
Первым шагом является добавление цифр.
5 + 9 + 7 + 6 = 27.
27 кратно 9, потому что 3 × 9 = 27.
Если вы не уверены, что 27 кратно 9, вы можете добавить цифры этого числа. 2 + 7 = 9, значит, 27 кратно 9.
Поскольку сумма цифр числа 5976 кратна 9, мы знаем, что 5976 тоже кратно 9.
Вот пример числа, не кратного 9. Воспользуемся правилом, чтобы показать, что 3299 не кратно 9.
Первым шагом является добавление цифр.
3 + 2 + 9 + 9 = 23.
23 не кратно 9, значит, 3299 не кратно 9.
Мы знаем, что 23 не кратно 9, потому что 2 + 3 = 5, а это не число в таблице умножения на 9.
Правило определения числа, кратного 9работает для всех чисел, независимо от их размера.
Вот еще один пример, проверяющий, является ли число 7635 кратным 9 или нет.
7 + 6 + 3 + 5 = 21. 21 не кратно 9, поэтому 7635 не кратно 9. Мы знаем, что 21 не кратно 9, потому что 2 + 1 = 3, чего нет в 9.