Дэвид Ди Анджело — Критические точки и мосты читать онлайн
Дэвид Ди Анджело
Критические точки и мосты
Как попасть из одной точки в другую с женщиной – от знакомства до постели.
Когда я только начинал учиться тому, как знакомится с женщиной, я осознал, что существует несколько «проблемных территорий», с которыми мне прийдется иметь дело.После того как я научился бороться с ними самостоятельно, я осознал, что почти ВСЕ мужчины спотыкаются о те же самые камни. Поэтому в этой книге я постараюсь помочь эти территории и улучшить те, в которых ты нуждаешься в помощи.Перед тем, как начать, позволь объяснить, что такое «критическая точка». Это моменты времени, когда ты должен сделать что-то заранее для перехода на следующий уровень. Например, если ты сидишь с женщиной и у вас прекрасно завязывается разговор, тебе, возможно, захочется завязать с ней отношения на физическом уровне. Большинство мужчин, насколько я знаю, не знают точно, как сделать «переход» на следующий уровень.
Или представь, что ты видишь женщину, с которой тебе хотелось бы познакомиться, и ты должен решить, подойти ли к ней и сказать «привет» или нет. Это критическая точка. Если ты этого не сделаешь, возможно, тебе не предоставится другого шанса.
Я знаю одного парня, который знакомится со многими девчонками. Он действительно нравится женщинам, когда видят его в первый раз. Он может заставить прийти девчонку на свидание и потом пойти с ним домой. Но каждый раз, когда он пытается перейти к физическому контакту, она решает, что пора идти домой. Я знаю и другого парня, который знакомится с женщинами, где бы он ни был. Женщины просто любят его. Они смеются с его шуток, но он никогда не спрашивает их номер телефона, поэтому он не ходит с ними на свидания.
Проблема с Критической Точкой заключается в том, что они почти ВСЕГДА хотят, чтобы мужчина проявлял инициативу и сделать то, что не может сделать женщина. Например, проходя мимо, сказать «привет», позвать на свидание, поцеловать ее.
Все эти ситуации мужчина должен преодолевать не смотря на возможность отказа.
Это удерживает большинство мужчин даже от попытки. И у большинства парней существует как минимум одна-две «территории» в которых он чувствует себя неуверенно.
Если ты чувствуешь себя неуверенно и знаешь точно, где ты можешь допустить ошибку, сказать что-то не то, то думаешь, что девчонка откажет тебе в самый ответственный момент. Опасность, конечно, в том, что мужчина может сделать ошибку в один из ключевых моментов и женщина решит уйти. Любые отношения – это как сложная мозаика. Ты можешь пройти через несколько ступеней, затем сделать ошибку и потерпеть неудачу. Ты со мной?
Вот список «критических точек»:
1. Попытка установить контакт (проходя мимо, сказать «привет»)
2. Цифры (взять номер телефона)
3. Набить стрелку (собственно, может быть сделано при знакомстве)
4. Стрелка (собственно, время, которое вы проводите вместе)
5. Подержаться за ручки (первый длительный физический контакт)
6. Поцелуи (первый физический контакт)
7. Наедине (доверие)
8.
Ласки (сексуально возбудить)
9. Раздевание (сильно возбудить)
10. Секс (очень-очень сильно возбудить)
Насколько я знаю, если человеку требуется что-то улучшить в своей жизни, он обычно учится на своем ОПЫТЕ. Многие люди делают ошибку, думая, что с ними что-то не так и они никогда не будут способны преодолеть это препятствие. Итак, я взял каждую из этих критических точек и создал то, что я называю «мостами». Позволь мне объяснить, что такое «Мост». Кое-что случается перед каждой Критической точкой. Это образовывает то, после чего следует Критическая точка. Например, если ты разговариваешь с женщиной по телефону и хочешь пригласить ее на чашечку кофе. Получается, что этот телефонный разговор решает, встретишься ты с ней или нет. Или если вы на свидании, и ты бы хотел поцеловать ее, то ее настроение и уровень удовольствия, которое она получает, общаясь с тобой, решает, захочет ли она, чтобы ты ее поцеловал. Время «между» Критическими точками – это Мосты. Если ты точно определил Критические Точки (КТ), то у тебя гораздо больше шансов достигнуть успеха, нежели если бы ты этого не сделал.
Если ты изучишь все мои «Стратегии Мостов», то это поможет тебе более плавно переходить от одной КТ к другой. И самое лучшее в моих Мост-техниках то, что они ЗАСТАВЛЯЮТ ЕЕ брать на себя инициативу и переходить на следующий уровень. Например, если ты уже наедине с девчонкой, которую ты уже целовал и собираешься облапать ее, используй мою технику «обнюхивания».
Когда ты обнюхиваешь несколько минут ее шею и плечи, она обычно заводится так, что хватает тебя и вы начинаете облапывать друг друга прямо там! (Конечно, ты захочешь отстранить ее немножко, потому что это только усилит ее желание, а так же это будет забавно для вас обоих). Возможно, самый важный мост между разговором и началом физического контакта. Большинство мужчин не знают, как перейти на «физический» уровень. Но я преуспел в этом деле. Но об этом позже.
Мост к №1, Попытка установить контакт. Возможно, самая важная концепция, это то, как ты себя чувствуешь внутри. Сегодня женщины очень чувствительны к вещам, которые звучат консервативно и банально.
Способ познакомиться с женщиной, это подойти к ней на улице и начать обычный разговор. Если ты читал мою книгу, то ты уже знаешь, что я считаю не самой лучшей идеей раздачу горы комплиментов сразу. Но это нормально сказать, «ты знаешь, я только хотел сказать… что у тебя прикольные туфельки» и т п. и потом начинай говорить.
Ключ в том, что нужно сделать что-то НОРМАЛЬНОЕ. Это напоминает мне кино «Butch Cassidy And The Sundance Kid» с Полом Ньюманом. В один момент они говорят «ОК, мы собираемся поступить честно с мошенником?» Большинство женщин мечтают о прекрасном прынце из бакалейной лавки или блокбастера. Женщину отталкивают милые, банальные парни. Не будь таким.
Так как же быть невозмутимым и нормальным? Ключ – уверенность и манера держать себя. Ты должен научиться быть уверенным в таких ситуациях. Я был удивлен, когда узнал, что большинство женщин достаточно приятные, когда познакомишься с ними поближе. Особенно, когда ты не ведешь себя как охотник или парень, который не был с женщиной 10 лет.
В книге «Double your dating» я объяснял, откуда взять эту уверенность, и что говорить женщине. Но в данный момент осознай, что это КТ и тебе нужно научиться справляться с этим. Если ты не научишься этого делать, все остальное не имеет значения.
Мост к №2, Получение номера телефона. Ключ к этому мосту – это знать, как быть интересным и забавным. В Double your dating ты прочитаешь о концепции „cocky and funny“, которой я научился у одного моего друга. Это делает разговор интересным для женщины. Следующая часть, это ТОЧНО знать, что ты собираешься сказать и как ты собираешься это сказать. Я говорю: „у тебя есть e-mail?“. Если они говорят „Да“, то я беру это да, как соглас дать его мне и тогда, ПОКА ОНИ ДОПИСАЛИ ДО СЕРЕДИНЫ, я говорю: „И выше напиши свой номер телефона“. Это проходит естественно и гладко. Но тебе придется выучить эти слова и повторить их несколько раз, чтобы они прозвучали идеально. Так что займись этим.
Читать дальше
Калькулятор критических точек| Лучшие шаги полного решения
Калькулятор критических точек
f(x) =
Как пользоваться этим калькулятором
Решение
Вернуться к калькулятору
Заполните поля ввода для вычисления решения.
Хотите неограниченный доступ к калькуляторам, ответам и шагам решения?
Присоединяйтесь сейчас
100% без риска. Отменить в любое время.
Критические точки Урок
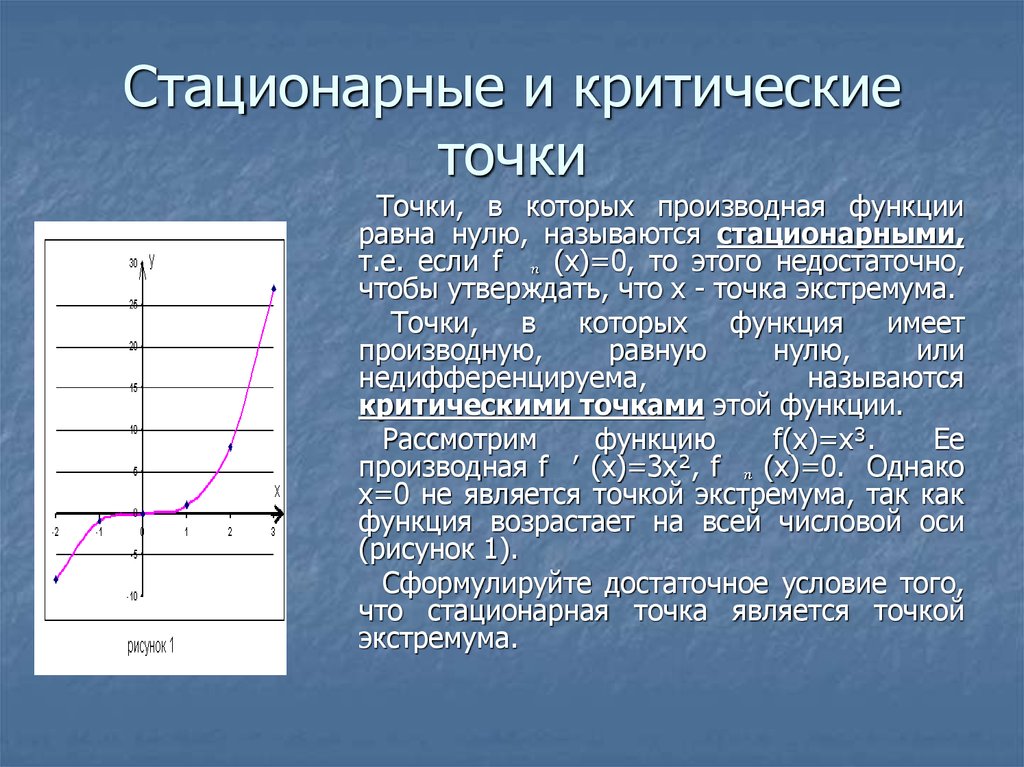
Что такое критические точки?
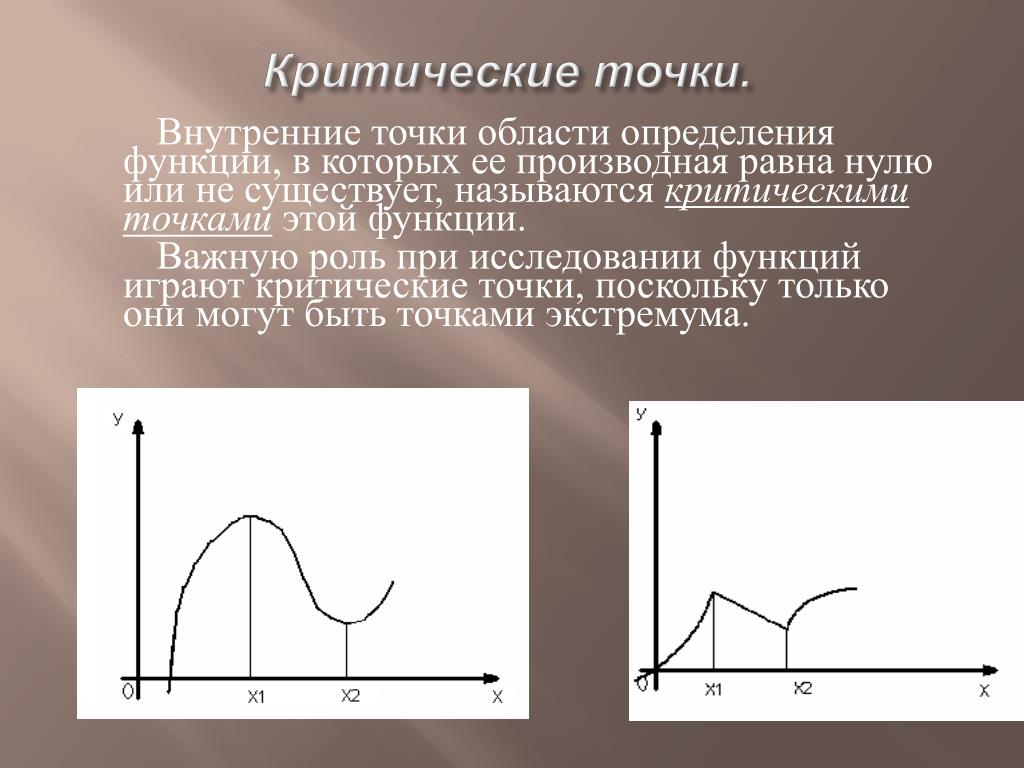
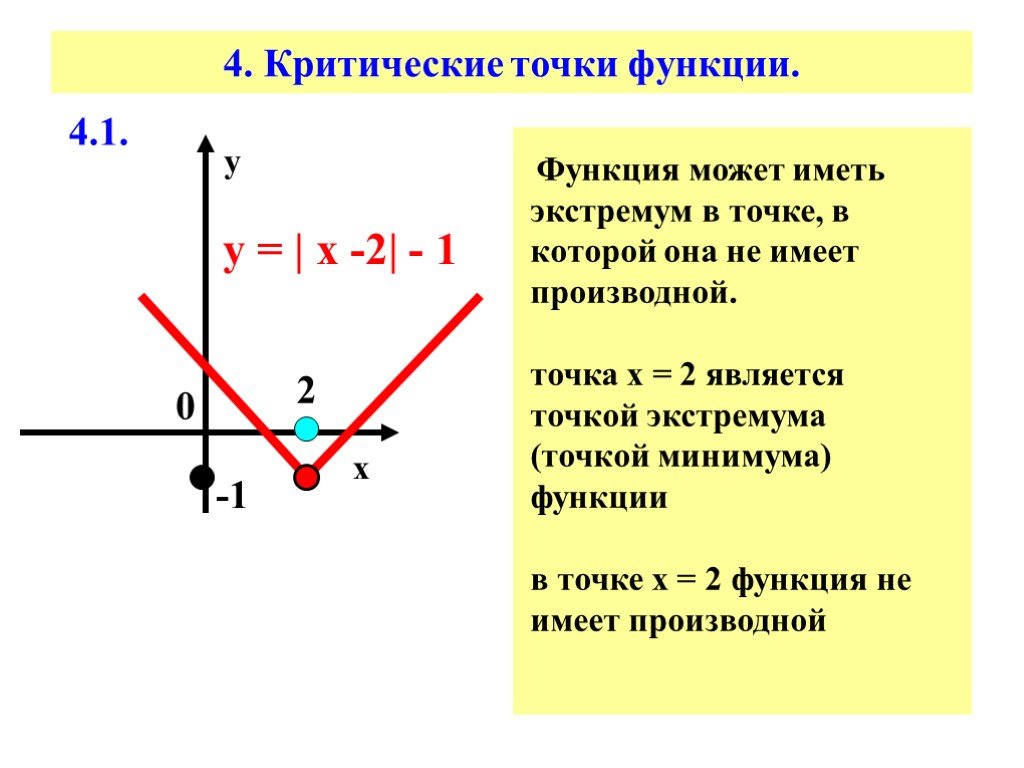
Критическая точка — это точка в заданной области определения функции, где производная функции либо равна нулю, либо не определена, и сама функция существует в этой точке.
Почему мы узнаем о критических точках?
Критические точки появляются повсюду в физике и математике, и их можно использовать, чтобы дать нам полезную информацию о том, что происходит в физическом явлении. Возьмем, к примеру, движение снаряда. Допустим, мы подбрасываем мяч в воздух с некоторой скоростью и под некоторым углом над горизонтом. Путь снаряда (мяча) при постоянном/отсутствующем сопротивлении снаряда будет иметь форму параболы.
Мы можем использовать критические точки, чтобы определить, когда наш мяч переходит от восходящего полета к падению на Землю. В свою очередь, мы можем использовать эту информацию для определения максимальной высоты шара.
Если у нас есть разумно приближенное уравнение для вертикального положения мяча по времени, мы можем взять производную от этого уравнения положения, чтобы найти скорость изменения вертикального положения мяча по отношению к изменению во времени. Затем мы можем решить для момента времени, когда производное уравнение (скорость) равно нулю. Это в основном говорит нам , когда мяч перестает двигаться вверх и начинает падать вниз.
Другими словами, это позволит нам узнать, в какой момент времени мяч достиг максимальной высоты. Затем мы можем взять это значение для времени, ввести его в наше уравнение положения, и это скажет нам , какова максимальная высота мяча в данном случае.
Другой способ использования критических точек — это интерпретация набора данных.
Допустим, мы строим небольшую модель ракеты, которая может развернуть парашют и безопасно упасть на землю после достижения максимальной высоты.
С помощью акселерометра мы можем измерить ускорение, которое видит ракета, и использовать эти данные для автоматического раскрытия парашюта после того, как ракета достигнет максимальной высоты. Какое это имеет отношение к критическим точкам?
Итак, когда ракета находится на стартовой площадке перед запуском, акселерометр покажет значение 1 g, или однократное ускорение, вызванное силой тяжести Земли (9,81 м ⁄ с 2 ). При взлете показания акселерометра превышают 1 g при ускорении вверх. Когда ракетный двигатель сгорит, ракета все еще будет двигаться вверх в небо, но начнет замедляться. Когда ракета, наконец, достигнет своей максимальной высоты, акселерометр приблизится к отсчету 0 g, когда она перейдет в режим свободного падения.
Это будет критическая точка данных о местоположении, потому что, когда ракета переходит от движения вверх к падению на Землю, скорость изменяется от положительного значения (при условии, что движение вверх положительное) до отрицательной скорости.
Другими словами, производная кривой положения (скорости) будет равна нулю на максимальной высоте ракеты, сообщая нашей системе, что раскрытие парашюта допустимо.
Как найти критические точки функции?
Критические точки x = c находятся при следующих условиях:
- f ‘(c) равно нулю ИЛИ f ‘(c) не определено
- f(c) существует
Где c — критическая точка, удовлетворяющая обоим условиям, f ‘(c) — производная входной функции f(x) , оцененная при x = c
Этапы поиска критических точек заданной функции ф(х) :
- Возьмите производную от f(x) , чтобы получить f ‘(x)
- Найти x значений, где f ‘(x) = 0 и/или где f ‘(x) не определено
- Подставьте значения, полученные на шаге 2, в f(x) , чтобы проверить, существует ли функция для значений, найденных на шаге 2.
9{2} — 16 = 0 \\ \\ & \hspace{3ex} \Rightarrow \hspace{2ex} \text{После решения для } x \text{ получаем } x =4,-4\\ \\ & \ hspace{3ex} \Rightarrow \hspace{2ex} c =4,-4\\ \\ & \text{4.) Так как наш домен} \hspace{1ex} — \infty < x < \infty \hspace{1ex } \text{(все действительные числа), а наши } c \text{ значения} \\ \\ & \hspace{3ex} \text{являются действительными числами, мы подставим все эти } c \text{ значения в } f(x) \text{ для получения } f(c) \text{.
3}{3}-16(-4) = 42,666666666666664\\ \\ & \hspace{ 3ex} \text{Поскольку } f(x) \text{ существует в } c_{2}, \text{ в } c_{2} есть критическая точка \text{ = } -4\\\end{align} $$ 9{2}} = 0 \\ \\ & \hspace{3ex} \Rightarrow \hspace{2ex} \text{После решения для } x \text{ получаем } x =-1,\frac{1}{2} i\sqrt{3} + \frac{1}{2},- \frac{1}{2}i\sqrt{3} + \frac{1}{2},0\\ \\ & \hspace{ 3ex} \Rightarrow \hspace{2ex} c =-1,\frac{1}{2}i\sqrt{3} + \frac{1}{2},- \frac{1}{2}i\sqrt {3} + \frac{1}{2},0\\ \\ & \text{4.) Так как наш домен} \hspace{1ex} — \infty < x < \infty \hspace{1ex} \text {(все вещественные числа), мы не будем подставлять} \\ \\ & \hspace{3ex} \text{мнимые значения обратно в } f(x) \text{, чтобы найти } f(c) \text{. Вместо этого мы продолжим} \\ \\ & \hspace{3ex} \text{только со значениями } c \text{, которые являются действительными числами.}\\ \\ & \text{5.) Подключаем наши действительные } c \text{ значения в } f(x) \text{ чтобы получить } f(c) \text{, мы получаем:}\\ \\ & \hspace{3ex} f(c_{1}) = \frac{1 }{3(-1)}-\frac{1}{6}(-1)^2 = -0,5\\ \\ & \hspace{3ex} \text{Поскольку } f(x) \text { существует в } c_{1}, \text{ в точке } c_{1} \text{ = } -1\\\\ \\ & \hspace{3ex} f(c_{2}) = \frac{ 1}{3(0)}-\frac{1}{6}(0)^2 = \text{undefined} \\ & \hspace{3ex} \text{При этом значении c критическая точка не существует, поскольку } f (c) \text{ на данный момент не определен.}\\\end{align}$$Калькулятор критических точек был разработан с использованием HTML, CSS и JavaScript. HTML-часть кода создает структуру калькулятора. Эта структура определяет различные важные объекты, такие как само пространство калькулятора, поле для ответов и поле для решения.
CSS затем используется для придания индивидуального стиля калькулятору и элементам ответов, чтобы их было легко читать и использовать по мере необходимости. Все, от стиля кнопки калькулятора, на которую можно нажать, до автоматических полос прокрутки в поле решения, стилизовано с использованием CSS.
Для работы калькулятора используется JavaScript. Это включает в себя нажатия физических кнопок, получение функции ввода пользователя и вывод пользовательских шагов решения, адаптированных к вводу пользователя. Когда все эти компоненты объединяются, мы получаем удобный и удобный калькулятор, отвечающий конкретным потребностям пользователя.
Изучение математики никогда не было проще.
Получите неограниченный доступ к более чем 165 персонализированным урокам и 69интерактивные калькуляторы.
Присоединяйтесь к Voovers+ сегодня
100% без риска. Отменить в любое время.
Калькулятор критической точки— зачем использовать калькулятор критической точки?
Продолжить чтение..
Критическая точка — это термин, широко используемый в математике, и это точка, в которой функция не дифференцируема. У каждой алгебраической функции есть область определения и диапазон, но в критической точке функцию невозможно дифференцировать. А 9Калькулятор критической точки 0029 позволяет легко найти критическую точку любой алгебраической функции. Вы можете понимать термин критическая точка просто как точку, в которой вы не сможете найти градиент.
Это означает, что градиент или уклон в этой точке не определен. Критической точкой многомерной функции является точка, в которой производная равна нулю.
Это означает, что вы не сможете найти производную функции в критической точке. Онлайн-поиск критических точек может вычислить критическую точку одномерной и многомерной функции. Просто используйте Калькулятор критической точки , чтобы найти производную многомерной алгебраической функции в шагах.В следующей статье мы обсудим, как найти критическую точку в шагах:
Критические точки в шагах:Теперь мы решим пример, чтобы объяснить, как мы можем найти критическую точку в шагах . Это объяснило бы методологию того, как найти критическую точку.
Рассмотрим функцию 4×2+ 8xy+ 2y, мы найдем критическую точку многомерной функции 4×2+ 8xy+ 2y. Вы должны признать, что в функции 4×2+ 8xy+ 2y задействованы две функции x и y. Калькулятор критических точек автоматически распознает, является ли функция многофункциональной или функцией с одной переменной. Критические точки необходимы для нахождения области значений алгебраической функции.
Выполняем шаги вычисления производной функции для нахождения критической точки :
Шаг 1:Нам нужно найти производную по «x» и «y» функции 4×2+ 8xy+ 2y. Если вы столкнулись с трудностями при вычислении, просто воспользуйтесь онлайн-калькулятором критических чисел.
Производная по «x»
Теперь производная по «x» равна:
F(x)=4×2+ 8xy+ 2y
Теперь применим степенные правила, и x переходит в «1»
/x = 8x+ 8(1) y+0
/x = 8x+8y+0
/x = 8x+8y
Вычислить производную относительно «x» с помощью калькулятора критических чисел 4×2+ 8xy+ 2y .
Производная по «y»
Теперь производная по «y» равна:
F(y)=4×2+ 8xy+ 2y
Теперь применим степенные правила, и y переходит в «1»
/y = 0+ 8x(1)+ 2(1)
/y = 8x(1)+ 2(1)
/y = 8x+ 2
Калькулятор критической точки можно использовать для нахождения производной по отношению на «у».
Шаг 2:Для нахождения критической точки нам нужно ввести значения производной f'(x,y) = от 0 до нуля.
Сейчас:
/x =0
8x+8y=0————(1)
/y =0
8x+ 2=0——- —-(2)
Для нахождения критического значения мы сравниваем производную по «х» и «у» с нулем.
Шаг 3:
Вычислите значения «x» или «y» из одного уравнения и подставьте значения во второе уравнение:
Теперь рассмотрим уравнение:
8x+ 2=0
Тогда
x = -2/8 или x=-1/4
x=-1/4
Вставьте значения x=-1/4 в уравнении (1) найти значение «y»
8x+8y=0————(1)
8(-¼)+8y=0
Тогда
-2+8y=0
y=2/8=1/4
y =1/4
Калькулятор критической точки удобно использовать для пошагового вычисления производной многомерной алгебраической функции.
3}{3}-16(-4) = 42,666666666666664\\ \\ & \hspace{ 3ex} \text{Поскольку } f(x) \text{ существует в } c_{2}, \text{ в } c_{2} есть критическая точка \text{ = } -4\\\end{align} $$ 9{2}} = 0 \\ \\ & \hspace{3ex} \Rightarrow \hspace{2ex} \text{После решения для } x \text{ получаем } x =-1,\frac{1}{2} i\sqrt{3} + \frac{1}{2},- \frac{1}{2}i\sqrt{3} + \frac{1}{2},0\\ \\ & \hspace{ 3ex} \Rightarrow \hspace{2ex} c =-1,\frac{1}{2}i\sqrt{3} + \frac{1}{2},- \frac{1}{2}i\sqrt {3} + \frac{1}{2},0\\ \\ & \text{4.) Так как наш домен} \hspace{1ex} — \infty < x < \infty \hspace{1ex} \text {(все вещественные числа), мы не будем подставлять} \\ \\ & \hspace{3ex} \text{мнимые значения обратно в } f(x) \text{, чтобы найти } f(c) \text{. Вместо этого мы продолжим} \\ \\ & \hspace{3ex} \text{только со значениями } c \text{, которые являются действительными числами.}\\ \\ & \text{5.) Подключаем наши действительные } c \text{ значения в } f(x) \text{ чтобы получить } f(c) \text{, мы получаем:}\\ \\ & \hspace{3ex} f(c_{1}) = \frac{1 }{3(-1)}-\frac{1}{6}(-1)^2 = -0,5\\ \\ & \hspace{3ex} \text{Поскольку } f(x) \text { существует в } c_{1}, \text{ в точке } c_{1} \text{ = } -1\\\\ \\ & \hspace{3ex} f(c_{2}) = \frac{ 1}{3(0)}-\frac{1}{6}(0)^2 = \text{undefined} \\ & \hspace{3ex} \text{При этом значении c критическая точка не существует, поскольку } f (c) \text{ на данный момент не определен.
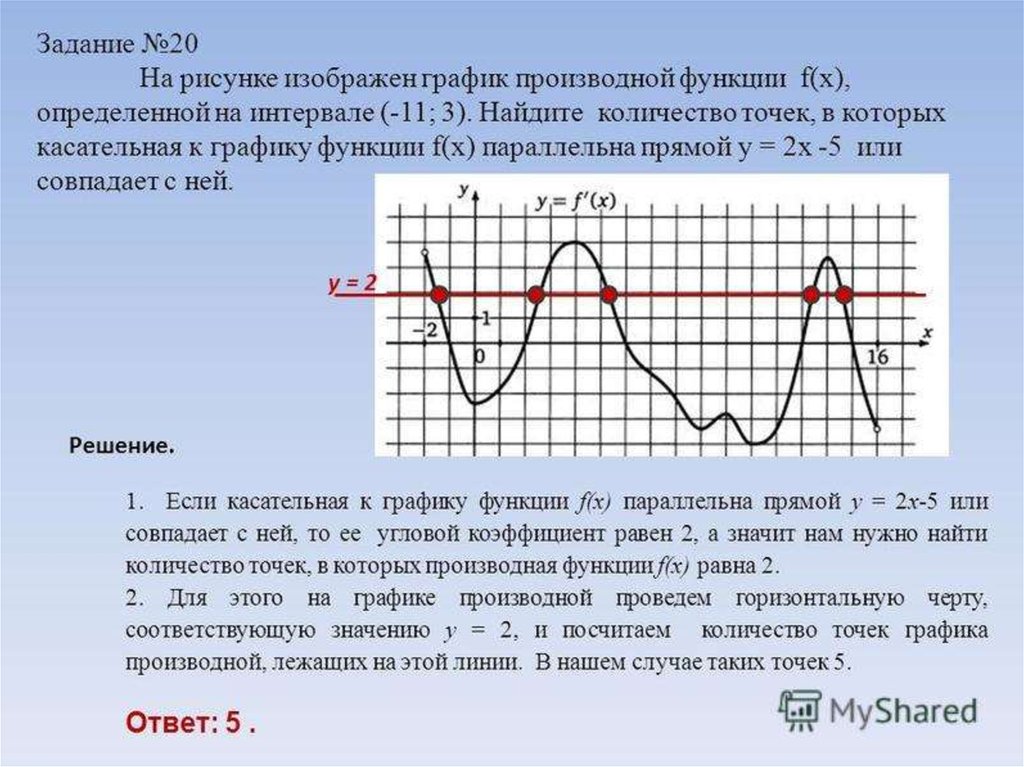
Это означает, что вы не сможете найти производную функции в критической точке. Онлайн-поиск критических точек может вычислить критическую точку одномерной и многомерной функции. Просто используйте Калькулятор критической точки , чтобы найти производную многомерной алгебраической функции в шагах.
