Проектная работа «Математические хитрости при возведение в квадрат двузначных чисел» • Наука и образование ONLINE
Главная Работы на конкурс Предметное образование Физико-математические дисциплины Проектная работа «Математические хитрости при возведение в квадрат двузначных чисел»
Автор: Алякшин Егор Юрьевич
Место работы/учебы (аффилиация): МБОУ «ООШ №4» г. Троицк, Челябинская область, 7 класс
Научный руководитель: Урженко Галина Дмитриевна
Я учусь в 7 классе. По математике у меня оценка «4». Недавно мы проходили тему «Натуральный показатель степени» по этой теме у меня вышло удовлетворительно. Я задумался: Почему? Я знаю все формулы, умею их применять, но за контрольные и самостоятельные работы не получаю оценку выше «4». Наверно, потому, что мне не хватает времени доделать ее до конца. Проанализировав эту ситуацию, я понял, что много времени трачу на вычисления. Тогда я начал искать в интернете ответ на вопрос: Как научиться быстро возводить в степень двузначные числа? И наткнулся на книгу Ингве Фогта «Математические трюки для быстрого счета».
Умение выполнять расчеты необходимо каждому человеку. Без умения считать невозможно, жить в современном мире. Конечно, есть калькулятор, но он не всегда под рукой.
Устный счет – математические вычисления, осуществляемые человеком без помощи дополнительных устройств (компьютер, калькулятор, счёты и т.п.).
Цель: изучить и научиться применять некоторые способы быстрого возведения в степень двузначных чисел, для производства которых, достаточно устного счета или применения ручки и бумаги.
Объект исследования: возведение в степень чисел начинающихся и заканчивающихся на 5; возведение в квадрат числа методом «Обратной пирамиды».
Для достижения данной цели необходимо решить следующие задачи:
- рассмотреть основной прием возведения двузначных чисел в квадрат;
- научиться возведению в степень числа начинающихся и заканчивающихся на 5; возведение в квадрат числа методом «Обратной пирамиды»;
- изучить метод возведения в квадрат трехзначного числа.
Методы исследования: изучение теории по выбранной теме, анализ литературы, практическое применение знаний, умений и навыков.
Актуальность выбранной темы. Мой интерес к теме возник на уроках математики, при изучении темы «Степень с натуральным показателем». При этом я заметил, что не только у меня, но и у моих одноклассников возникали трудности при возведении двузначных чисел в степень. Современная жизнь делает эти задачи актуальными, так как сфера практического применения быстрого счета безгранична. Без умения считать современном обществе просто трудно было бы существовать.
Гипотеза. Научиться быстро считать легко. Все умеют считать, но считать быстро умеют единицы.
Загрузка…
Физико-математические дисциплины
Проект «История Шатурского края в математических задачах»
В жизни каждого человека на Земле есть уголок, который остается дорогим для тебя на всю жизнь, даже, если ты уезжаешь.
Это место, где ты родился, чаще всего и вырос. А зовется оно малой родиной. Малая родина – это не только место, где ты родился, там…
Посмотреть работу
Физико-математические дисциплины
Исследовательский проект «Математические расчёты потребления и экономии воды»
Доступна к просмотру полнотекстовая версия работы
Проблема: неразумное и нерациональное потребление воды человеком несмотря на то, что запасы пресной воды с каждым годом уменьшаются. Актуальность. Вода — не только ценный, но и относительно дорогой ресурс, который нужно беречь. Нерациональное использ…
Посмотреть работу
Физико-математические дисциплины
Исследовательский проект «Фонтан Герона, как вечный двигатель»
Актуальность: Фонтаны улучшают микроклимат в доме, дарят нам радость, ощущение уюта и комфорта.
Движущаяся вода, которая тихонько плещется или брызжет вверх, оказывает успокаивающее воздействие на слух, зрение. Цель работы: Путём систематизации и обо…
Посмотреть работу
Физико-математические дисциплины
Исследовательский проект «Математика в программировании»
Я очень люблю урок математики. А также мое любимое занятие — это компьютерные игры. В этом году я много узнал о программировании и научился сам создавать компьютерные игры. Мое исследование началось с момента серьезного увлечения программированием. Я…
Посмотреть работу
Физико-математические дисциплины
Проект «Исследование теплопроводности различных строительных материалов»
Так как в нашей стране продолжается осваивание различных удалённых краёв, в которых погодные условия очень суровы, поэтому нахождение оптимального материала для утепления зданий довольно актуально.
Гипотеза: утепление дома будет качественным и безопа…
Посмотреть работу
Мероприятие завершено
10 класс И | сайт учителя информатики
Программирование здесь.
Техника безопасности (плакат, тест)
Модуль 1. Информация и информационные процессы
1. Информатика и информация. Информационные процессы (презентация К. Ю. Полякова)
1.1. Информация и информационные процессы.
1.2. Измерение информации (тест)
1.3. Структура информации
1.4. Иерархия. Деревья (слайды 38-47)
Деревья (тест)
Префиксная и постфиксная формы (тест)
1.5. Графы (слайды 48-80, тест)
1.6. Кодирование и декодирование (презентация К. Ю. Полякова)
1.6.1. Язык и алфавит. Кодирование (тест)
1.6.2. Декодирование (тест)
1.6.3. Алфавитное измерение информации (тест)
Контрольная работа модуль 1 (25.09.2018)
Модуль 2.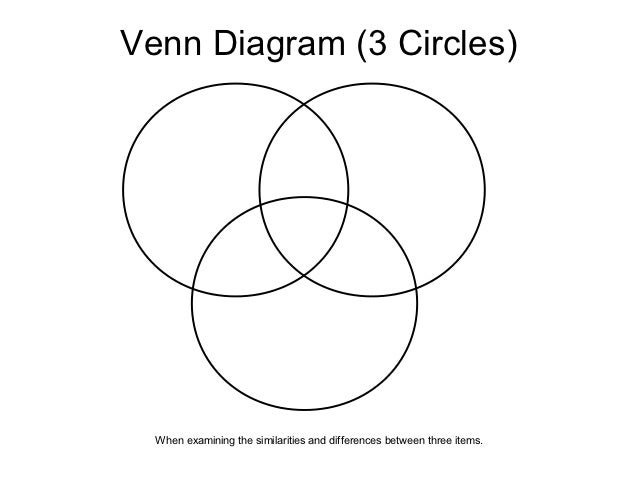
Системы счисления (презентация К. Ю. Полякова)
2.1. Системы счисления (§ 9, слайды 2-11)
2.2. Позиционные системы счисления (§ 10, слайды 12-26, тест)
2.3. Двоичные системы счисления (§ 11, слайды 27-30)
2.4 Восьмеричная система счисления (§ 12, слайды 38-49)
2.5. Шестнадцатеричная система счисления (§ 13, слайды 50-63)
2.6 Двоичная арифметика (слайды 31-34)
Контрольная работа модуль 2 (23.10.2018)
Модуль 3. Кодирование информации (презентация К. Ю. Полякова)
3.1. Кодирование символов (§ 13, слайды 3-9)
3.2. Кодирование графической информации (§ 14, слайды 10-39)
3.3. Кодирование звуковой информации (§ 15, слайды 40-49)
3.4. Хранение в памяти ПК целых чисел (§ 16-17)
3.5. Арифметические и логические (битовые) операции. Маски (§ 28)
3.6. Хранение в памяти вещественных чисел (§ 29)
3.7. Выполнение арифметических операций с нормализованными числами (§ 30)
Подготовка к контрольной работе (на Решу ЕГЭ варианты 1171906, 1777137)
Контрольная работа модуль 3 (17.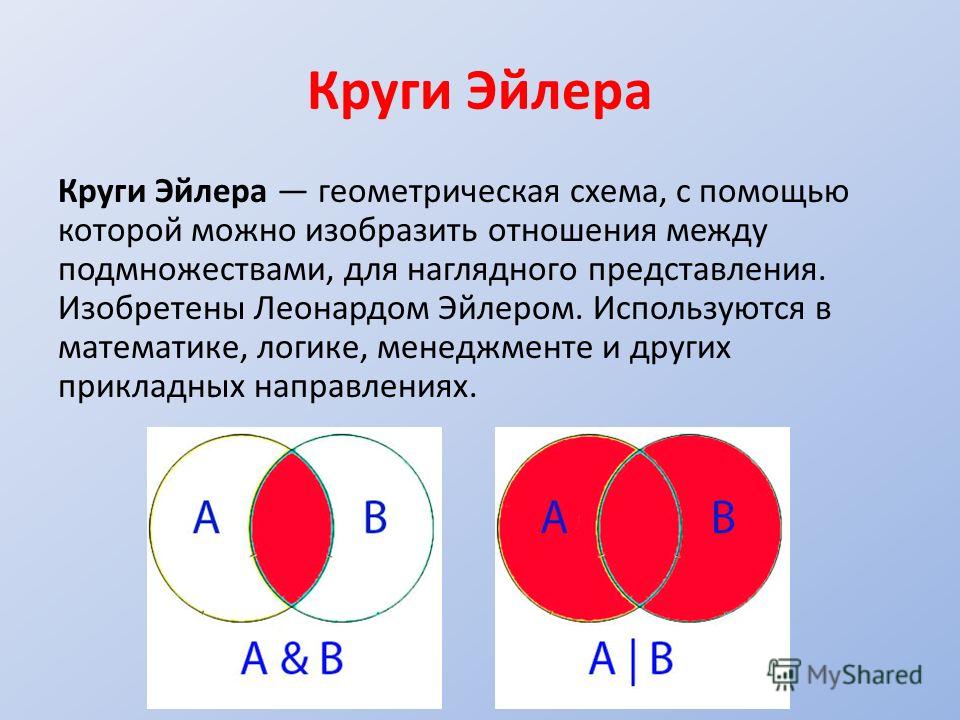
11.2018)
Модуль 4. Логические основы компьютеров (презентация К. Ю. Полякова)
4.1. Основные логические операции (слайды 6-18, 24-25, тест)
Таблицы истинности (тест)
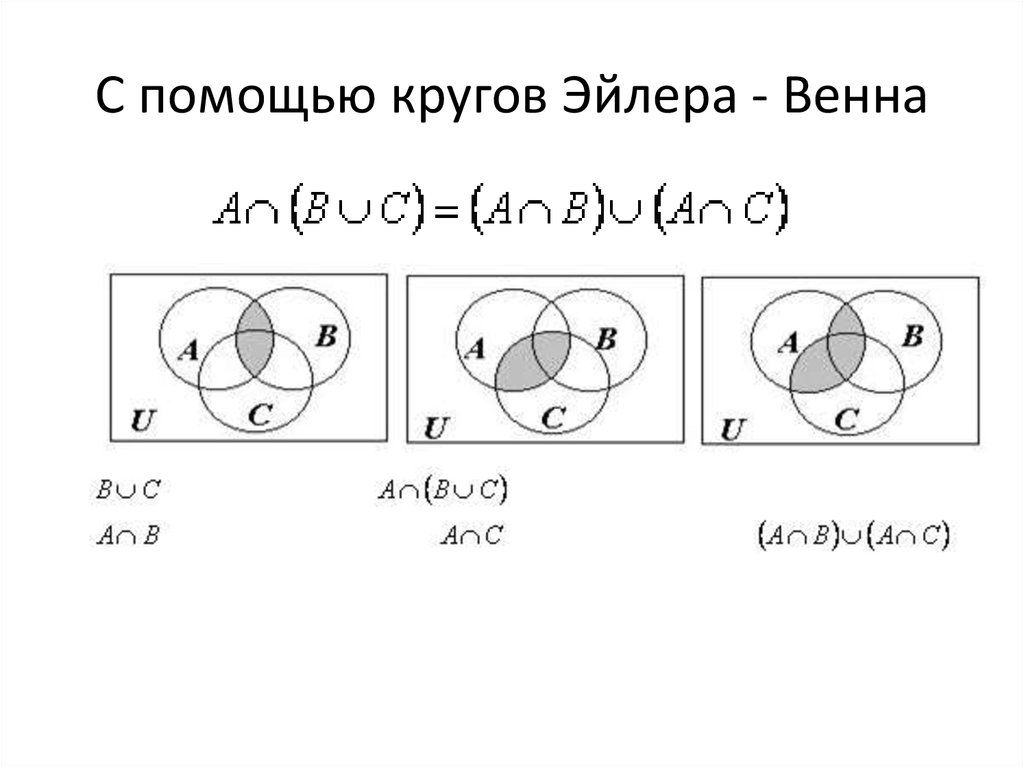
4.2. Круги Эйлера (слайды 27-36)
4.3. Законы алгебры логики (§ 21, презентация, тест)
Все законы в одной таблице
4.4. Логические схемы. Логические элементы компьютера (§ 24)
4.5. Синтез логических выражений (§ 22, презентация)
Контрольная работа модуль 4 (18.12.2018)
Модуль 5 Аппаратное и программное обеспечение компьютеров
Даты докладов и исполнители — здесь
5.1. История вычислительной техники (презентация К.Ю.Полякова)
5.2. Устройство компьютера (презентация К.Ю.Полякова)
5.2.1. Принципы устройства компьютеров
5.2.2. Магистрально-модульная организация компьютера.
5.2.3. Процессор
5.
2.4. Память (видео)
5.2.5. Устройства ввода
5.2.6. Устройства вывода
5.3. Программное обеспечение (презентация К.Ю.Полякова)
5.3.1. Что такое программное обеспечение?
5.3.2. Прикладные программы.
5.3.3. Системное программное обеспечение.
5.3.4. Системы программирования
5.3.5. Инсталляция программ.
5.3.6. Правовая охрана программ и данных.
Тест
Контрольная работа модуль 5 (15.01.2019)
Модуль 6 Алгоритмизация и основы программирования. Условный оператор. Циклы.
6.1. Ветвление (повторение)
6.2. Циклы (повторение) (видео)
Тесты К. Ю. Полякова: тест_1, тест_2
6.3. Строки (см. здесь)
Тест
Задачи на 19.02.2019 здесь
Контрольная работа модуль 6 (12.03.2019)
Модуль 7 Массивы
Тесты К.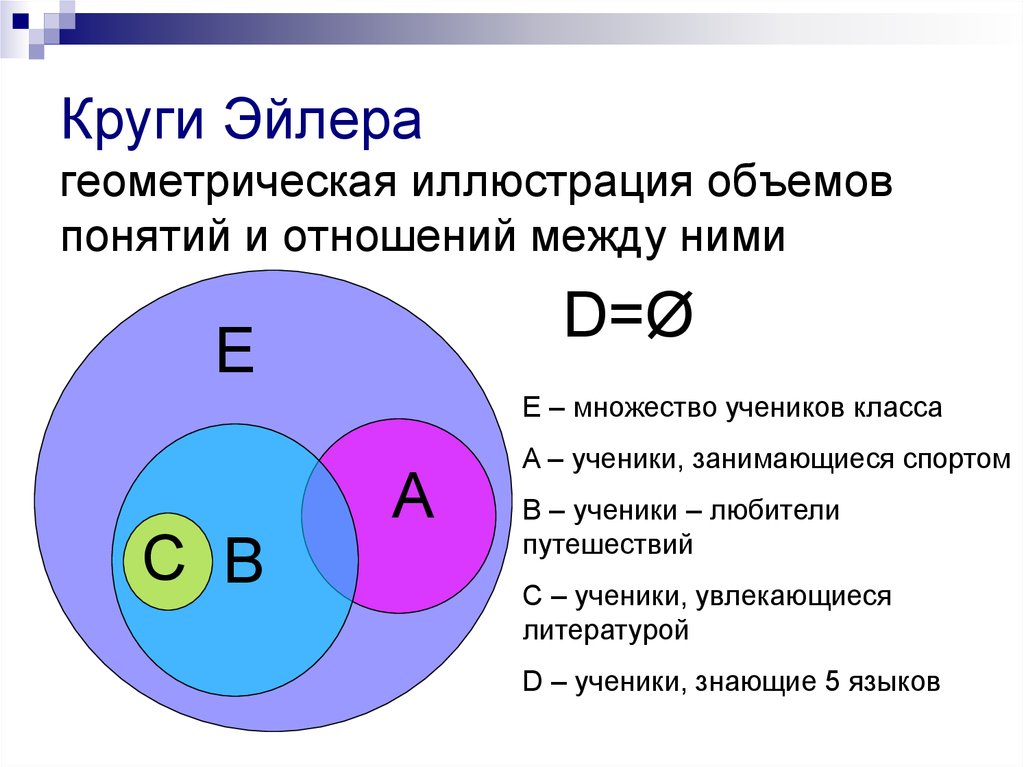
Ю. Полякова: тест_1, тест_2
Тест К. Ю. Полякова — NEW!
Модуль 8 Процедуры и функции
Модуль 9 Рекурсия
Задание в Desmos
Генератор диаграмм Эйлера| Онлайн-инструмент для построения диаграмм Эйлера
Creately уже используют более 8 миллионов человек и тысячи команд.
ВИЗУАЛИЗИРУЙТЕСоздавайте диаграммы Эйлера без усилий
Несколько готовых шаблонов для диаграмм Эйлера и диаграмм Венна для различных сценариев, позволяющих быстро приступить к работе.
Предустановленные цветовые темы и расширенные возможности форматирования текста , чтобы легко выделять и обозначать различные контуры и зоны на диаграммах Эйлера.
Рисование от руки и выделение для рисования сложных диаграмм Эйлера с невыпуклыми контурами.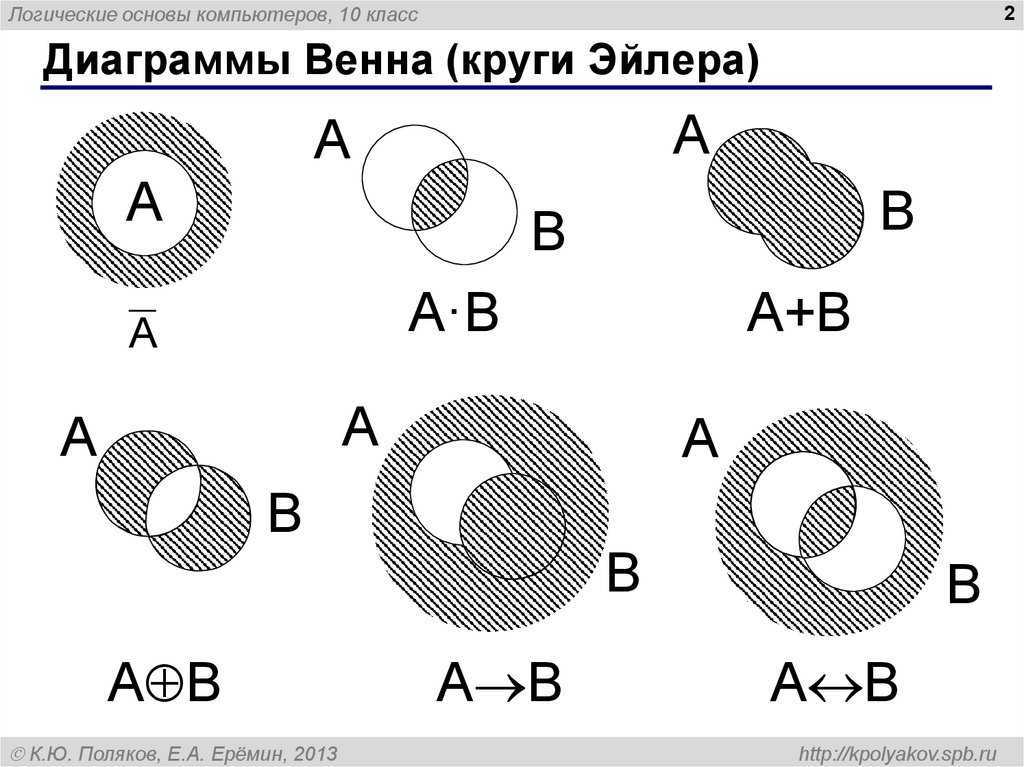
Импортируйте или перетаскивайте изображения , графику и многое другое на холст для создания визуально динамичных диаграмм Эйлера.
Автоматическое рисование с помощью Plus Create . Нарисуйте следующую фигуру и соединитель в правильном положении одним щелчком мыши.
ПОДКЛЮЧАЙТЕ И ОРГАНИЗУЙТЕ
Стройте свои диаграммы
Дополнительные поля данных и пользовательские свойства для отображения подробной информации о том, что содержится в различных зонах диаграммы.
Обширные библиотеки форм для более чем 50 типов диаграмм, графиков и диаграмм для упрощения расширения диаграмм Эйлера дополнительными структурами.
Экспортируйте свои диаграммы в несколько графических форматов , включая PNG, SVG, PDF или JPEGS, для встраивания, печати или совместного использования.
Встроенные инструменты, такие как рамки, режим просмотра и т. д. для удобной организации визуальных элементов на холсте и создания интерактивных презентаций.
СОТРУДНИЧАТЬ
Сотрудничайте с другими в любое время и в любом месте
Курсоры в реальном времени для любого количества участников. Работайте со студентами или коллегами на общем холсте.
Видеоконференцсвязь впилась в платформу, чтобы вы чувствовали себя в одной комнате.
Комментарий с контекстом для обсуждения и последующих действий на одном холсте. Асинхронно!
Автономная синхронизация , чтобы ваша работа всегда синхронизировалась, даже если вы выходите из сети и возвращаетесь.
Что такое диаграмма Эйлера?
Диаграмма Эйлера — это графическое изображение, обычно используемое для иллюстрации отношений между наборами или группами; диаграммы обычно рисуются в виде кругов или овалов, хотя их можно рисовать и в других формах.
Как построить диаграмму Эйлера?
- Включите библиотеку базовых форм Creately или обширную библиотеку шаблонов диаграмм Венна и Эйлера.
- Перетащите круги или любые соответствующие фигуры на холст, чтобы обозначить количество групп, используемых на диаграмме.
- Определите связи между группами и соедините соответствующие фигуры вместе, чтобы визуализировать информацию.
- Продолжайте повторять этот процесс, пока все соответствующие группы не будут отсортированы и связаны соответственно.
- Используйте любую из многочисленных функций дизайна, предлагаемых Creately, для цветового кодирования, выделения и придания вашей диаграмме Эйлера динамичности и презентабельности.
- Завершите работу над диаграммами Эйлера и поделитесь ими с другими в различных графических форматах.
Создайте диаграмму Эйлера
Формула Эйлера и калькулятор тождеств Эйлера
Ниже приведен калькулятор и интерактивный график, который позволяет вам исследовать концепции, лежащие в основе знаменитой и необычной формулы Эйлера:
e iθ = cos( θ ) + i sin( θ )
Когда мы устанавливаем θ = π, мы получаем классический Тождество Эйлера:
e iπ + 1 = 0
Формула Эйлера используется во многих областях науки и техники.
Это очень удобное тождество в математике, так как оно может значительно упростить выполнение многих вычислений, особенно связанных с тригонометрией. Мы видели часть этой концепции в произведениях и частных комплексных чисел ранее. 9п
И формулу, и тождество можно использовать для выполнения вычислений, а также для графических функций. Калькулятор можно использовать для ввода комплексного числа и вычисления различных степеней этого числа, а также для построения графика функции. График можно увеличить или уменьшить, а комплексное число можно изменить, чтобы увидеть, как оно влияет на график.
Формула Эйлера и тождество очень полезны в математике и технике, поскольку они могут значительно упростить выполнение многих вычислений. Попробуйте поиграть с калькулятором и графиком, чтобы увидеть, что вы можете обнаружить!
Формула Эйлера, калькулятор тождества и график
На следующем графике реальная ось (обозначенная «Re») горизонтальна, а воображаемая ось (`j=sqrt(-1)`, обозначенная «Im») вертикальна, как обычно.
У нас есть единичных окружностей , и мы можем изменять угол, образованный отрезком OP.
Точка P представляет комплексное число. Угол θ , разумеется, в радианах.
Чем заняться
- Выберите, будут ли ваши углы выражаться десятичными знаками или числами, кратными π.
- Выберите i или j в качестве символа мнимого числа. (Во многих учебниках используется и для символа мнимого числа, но IntMath, как и многие инженерные тексты, использует j , чтобы попытаться уменьшить путаницу с символом тока в электронике.)
- Вы можете перетащить точку P , чтобы изменить угол θ.
- Когда вы установите θ = π, вы увидите (эквивалент) Тождество Эйлера: e iπ = − 1
Углы: кратные π
Мнимый символ: i j
Формула Эйлера
Прямоугольный и полярный эквиваленты
Для получения дополнительной информации о том, что происходит, и дополнительных пояснений см.
предыдущие страницы,
Комплексные числа и полярная форма комплексного числа
См. также калькулятор полярного преобразования в прямоугольное и прямоугольного в полярное, на котором основано приведенное выше:
Онлайн-калькулятор полярных координат в прямоугольные
Комплексная экспоненциальная форма
В математике комплексная экспоненциальная функция — это функция вида f(z) = ea(z), где z — комплексное число, а a — произвольная комплексная константа. Функция целая, что означает, что она определена и дифференцируема для всех комплексных чисел z. В отличие от вещественно-показательных функций сложные показательные функции не являются взаимно однозначными; то есть два разных комплексных числа могут иметь одинаковый образ под функцией. 9{-би}.
Сложные функции
Комплексная функция — это функция вида f(z) = u(x, y) + iv(x, y), где z = x + iy — комплексная переменная, u и v — вещественнозначные функции две действительные переменные x и y, а i — мнимая единица измерения.
В этой статье будут рассмотрены некоторые свойства сложных функций с упором на формулу Эйлера и тождество Эйлера.
Сложные функции имеют множество приложений в физике и технике, а также в чистой математике. В физике они используются для моделирования волновых явлений, а в технике — для проектирования электрических цепей. В чистой математике они изучаются сами по себе как красивые и интригующие объекты. 9(i*pi) + 1 = 0. Это уравнение важно, потому что оно связывает вместе пять наиболее важных чисел в математике: e, pi, i, 1 и 0.
Дифференциальные уравнения чрезвычайно полезны в математическом моделировании и находят применение в самых разных областях, от физики до экономики. Следовательно, они являются важным инструментом для понимания и прогнозирования изменений.
Если вы хорошо понимаете формулу Эйлера и тождество Эйлера, вы можете относительно легко выполнять широкий спектр вычислений. Это делает формулу бесценным инструментом для математиков, инженеров и других ученых.