круги эйлера примеры задач — 4 рекомендаций на Babyblog.ru
у Милены тут по местным меркам второй класс.
по-нашему — мы бы пошли в первый.
с этого года поменялась программа и усложнились тесты, а нам сдавать тест в мае или июне.
сейчас сижу, смотрю пример теста на офиц сайте (жаль, только один), и глаза на лоб лезут
Математика состоит из двух различных тестов
1) только примеры (сложение, умножение, вычитание, деление). а, еще дроби! примеры есть не самые простые
например, 43+28 = , 86-21 =, 65 +___ = 93
а еще 3/4 от 40 ничего себе пример для семилетки!)
таблицу умножения мы выучили наполовину уже (а Милене только 7 лет) — я думала, мы опережаем, а мы по программе, оказывается)))
2) смешанные задания — напишу основное (всех тем и не переписать)))
— счет денег (когда считаешь фунты и пенсы, предполагается, что умеешь считать более сотни и тп), — это мы освоили
— четные-нечетные числа двухзначные,
— геометрия и фигуры 2д и 3д с вопросами про количество сторон-углов и тп,- почти освоили
— всевозможные единицы измерения (кг, литры, градусы, пинты, ярды и др всякие чисто местные)
— умение определять время (цифровое и аналоговое, писать цифрами, словами, сравнивать, из текстовых задач понимать вопрос), в процессе, половину прорешали
— писать все цифры до ста и записывать примеры СЛОВАМИ
— римские цифры
— логика и всякие последовательности, круги Эйлера (тут по-другому называются) — это то, что мы хорошо умеем
— календарь, дни недели, месяцы, сезоны — ну это как в РФ в первом классе, в процессе
— сравнение чисел до 1000 — это для нас легко, выезжаем на логике)))
— статистика и вероятности (типа определить по количеству «вероятно», «возможно» и тп)
— чтение графиков и решение задач с помощью графиков — такое в первом классе в РФ видела в программе, освоили
— ДРОБИ))) — умение определять, какая дробь по рисунку, сравнение дробей, примеры с дробями, задачи, умение составить дробь из текстовой задачи — это мы уже прорешали, кроме задач
Вообще самая жесть для меня — это то, что в каждом разделе есть задачи текстом, а не только примером, то есть написано же для носителей языка, а Милена догадывается, что спрашивают))))
про тесты по английскому даже писать не буду, я сама ответить не могу, не подумав
Жалко, что Милена расстраивается, когда ошибается.
Математика у нас нормально идет, я стала заниматься с ней каждый день, оплатила ей подписку на сайте местном типа нашего Айкюши, она решает тесты по навыкам, которые на тесте пригодятся прямо по темам.
Кто еще не знает Айкюшу — рекомендую, там программа от 2 лет до 5 класса, постоянно пополняется. Мы там купили подписку на год. Детей очень мотивируют медали и кубки за правильные решения по темам
В общем, я думала, что мы далеко впереди, а мы по программе идем)))
я одного не понимаю, если у них такие нагрузки в школе, почему у них так много бестолочей?))) мне-то казалось, что тут вообще ничего не делают, домашку задают один раз в неделю и она ерундовая совсем. А тесты в итоге сложные
Мне кажется, в РФ мы бы уже в районной олимпиаде участвовали…
Напишите, у кого дети 1-2 класс, как программа, что проходите?
Тест по информатике Отношения между множествами. Отношение «входит в состав» для 6 класса
19.07.2020 Главная › Информатика › 6 класс
Тест по информатике Отношения между множествами.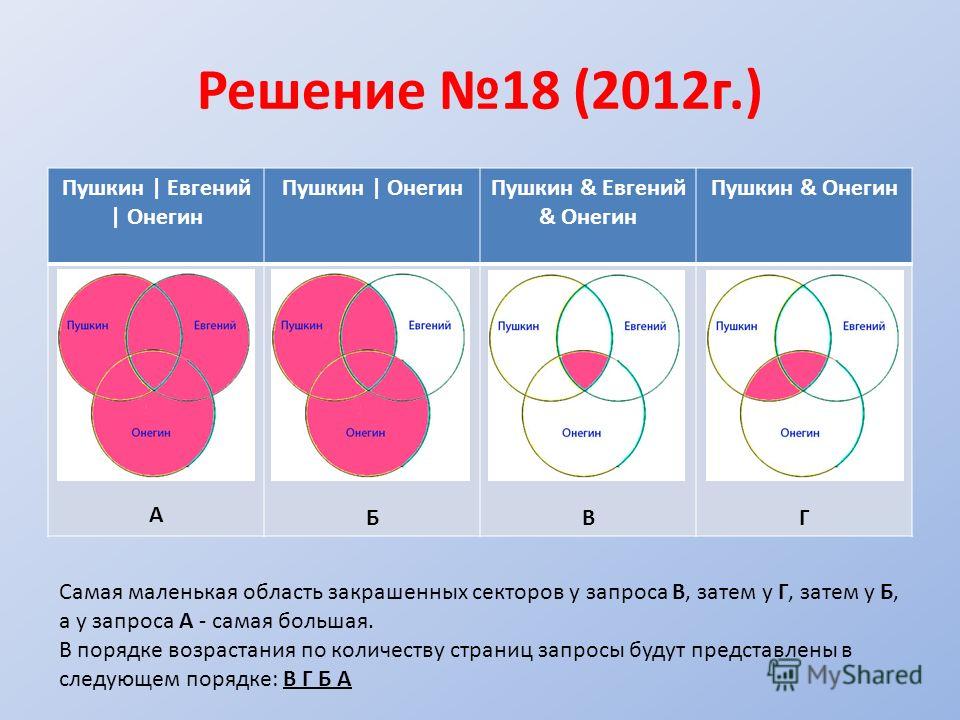
Отношение «входит в состав» для 6 класса с ответами. Тест включает в себя 2 варианта, в каждом варианте 10 заданий с выбором ответа.
1 вариант
1. Какие отношения связывают два множества объектов? Выберите верное утверждение.
1) входит в состав
2) является разновидностью
3) оба утверждения верны
4) все приведённые утверждения не верны
2. Как называется графическое представление отношений множеств элементов?
1) чертёж
2) рисунок
3) круги Эйлера
4) алгоритм
3. Выберите верное утверждение. Если множества А и В «пересекаются», то
1) ровно один элемент принадлежит и множеству А, и множеству В
2) множества А и В имеют общие элементы
3) множества А и В полностью совпадают
4. Пусть множество П — платья, множество К — одежда красного цвета. Выберите «пересечение» множеств П и К.
1) все платья, кроме красного цвета
2) вся одежда красного цвета, кроме платьев
3) красные платья
4) все утверждения не верны
5.
В каком случае множество А является «подмножеством» множества В?
1) каждый элемент множества В является элементом множества А
2) каждый элемент множества А является элементом множества В
3) элементы множеств А и В совпадают
4) все утверждения не верны
6. Пусть множество А — квадраты, а множество В — прямоугольники. Является ли множество А «подмножеством» множества В?
7. В каком случае множество А и множество В «равны»?
1) каждый элемент множества А является элементом множества В
3) если выполняются утверждения и 1, и 2
4) все утверждения не верны
8. Пусть множество А — множество учеников 6а класса (30 человек), а множество В — множество учеников 6г класса (30 человек). Равны ли множества А и В?
1) да
2) нет
9. Что означает отношение: объект А «входит в состав» объекта В?
1) объект В можно разобрать на более мелкие объекты, один из которых — объект А
2) объект А — подмножество множества В
3) оба утверждения верны
4) все утверждения не верны
10.
Пусть объект А — компьютер, а объект В — блок питания. Можно ли сказать, что А «входит в состав» В?
1) да
2) нет
2 вариант
1. Какие объекты связывает отношение «входит в состав»?
1) элемент и множество
2) два множества
4) два элемента из одного множества
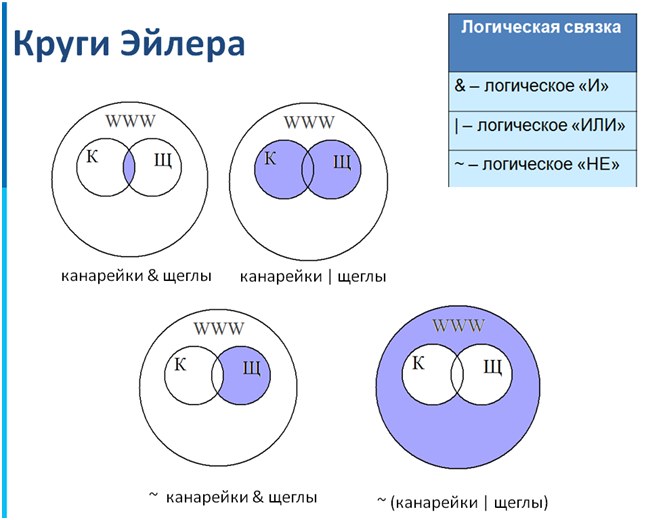
2. Что такое круги Эйлера?
1) чертёж элементов множества
2) схема расположения элементов внутри множества
3) графическое представление отношений множеств
4) алгоритм передвижения элементов множества
3. Выберите верное утверждение. Множества А и В «не пересекаются», если
1) только один элемент принадлежит и множеству А, и множеству В
2) множества А и В имеют общие элементы
3) множества А и В полностью совпадают
4) ни одно утверждение не верно
4. Пусть множество С — сказки, множество П — произведения А.С. Пушкина. Выберите «пересечение» множеств П и С.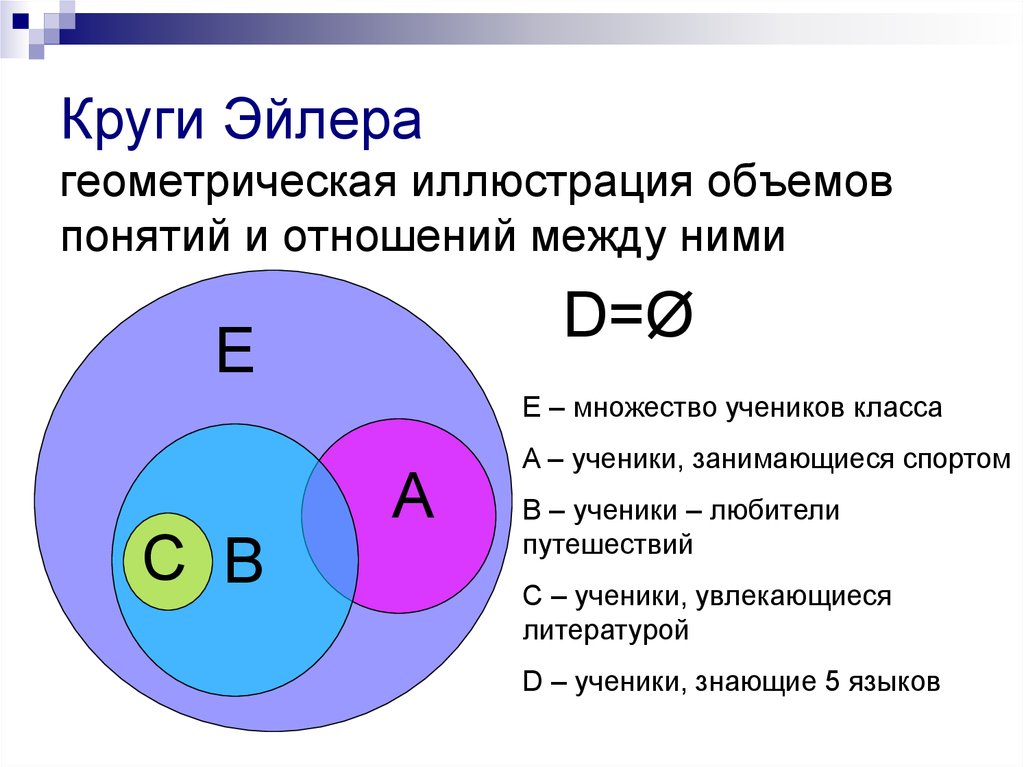
1) все сказки
2) стихи А.С. Пушкина
3) сказки А.С. Пушкина
4) все утверждения не верны
5. В каком случае множество В является «подмножеством» множества А?
1) каждый элемент множества А является элементом множества В
2) каждый элемент множества В является элементом множества А
3) элементы множеств А и В совпадают
4) все утверждения не верны
6. Пусть множество А — автомобили, а множество В — транспорт. Является ли множество А подмножеством множества В?
1) да
2) нет
7. Пусть множество А и множество В «равны». Что является «пересечением» множеств А и В?
1) множество А
2) множество В
3) оба утверждения верны
4) все утверждения не верны
8. Пусть множество А — множество учебников по русскому языку (10 книг), а множество В — множество учебников по математике (10 книг). Равны ли множества А и В?
1) да
2) нет
9. Что означает отношение: объект В «входит в состав» объекта А?
1) объект А можно разобрать на более мелкие объекты, один из которых — объект В
3) оба утверждения верны
4) все утверждения не верны
10.
Пусть объект А — автомобиль, а объект В — двигатель. Верно ли, что В «входит в состав» А?
1) да
2) нет
Ответы на тест по информатике Отношения между множествами. Отношение «входит в состав» для 6 класса
1 вариант
1-3
2-3
3-2
4-3
5-2
6-1
7-3
8-2
9-3
10-2
2 вариант
1-3
2-3
3-4
4-3
5-1
6-1
7-3
8-2
9-1
10-1
PDF-версия
Тест Отношения между множествами. Отношение «входит в состав» для 6 класса
(155 Кб)
Опубликовано: 19.07.2020 Обновлено: 19.07.2020
Мысли об исследованиях – Круг Эйлера
Итак, вы старшеклассник, любите математику, может быть, вы выиграли какие-то олимпиады или посетили математический лагерь. Вы хотите перейти на следующий уровень и провести оригинальное исследование. Это замечательно, и мы благодарим вас за ваш энтузиазм. Но сначала вы должны знать, чего ожидать от математических исследований.
(Осторожно, спойлер: это очень сложно! Даже для профессиональных математиков.)
Во-первых: не выполняйте исследовательский проект по математике, чтобы улучшить свое резюме для колледжа . Это было бы действительно глупо: выдающийся старшеклассник должен рассчитывать потратить около 1000 часов в течение двух лет на исследования, чтобы иметь разумный (но далеко не гарантированный) шанс написать статью, которую можно опубликовать. Даже человек с ограниченным воображением наверняка придумает множество других способов провести 1000 часов, которые гораздо больше помогут при поступлении в колледж. Если это ваша цель, уходите, прежде чем вы сделаете несчастными все вовлеченные стороны.
Вы, возможно, знакомы с «исследованиями» в области биологии в средней школе, когда старшеклассник работает в лаборатории в течение лета, в основном выполняя черную работу, такую как чистка пробирок, и получает в награду статью для публикации или презентации. в конкурсах научной ярмарки.
Существует большое культурное различие между биологией и математикой. В биологии каждый, кто так или иначе участвует в проекте, указан как соавтор, поэтому иногда списки авторов исчисляются сотнями. (См. крайний пример в этой статье.) Но в математике соавторами являются только те люди, которые внесли значительный технический вклад. Не существует математического эквивалента очистки пробирок. (Мы можем стереть свои собственные меловые доски, большое спасибо.) Таким образом, вы просто не можете рассчитывать на то, что поработаете в течение нескольких месяцев летом и вам будет что показать за это. Это просто не работает.
Чтобы заниматься исследованиями в области математики, вы должны быть готовы уделять не менее 10 часов в неделю в течение двух лет. Это должно быть высоким приоритетом. Было бы неплохо запланировать фактические часы, когда вы будете работать над своим исследовательским проектом каждую неделю. По крайней мере, это упражнение даст вам представление о том, действительно ли у вас есть время заниматься математическими исследованиями.
Как правило, изучение математики предполагает замену других видов деятельности, а не добавление к уже существующим.
Время, которое вы отводите на математические исследования, должно быть максимально качественным. Это не время, потраченное на многозадачность или общение, или когда вы, вероятно, устанете. Запланируйте время для исследования перед домашним заданием или другими менее важными делами. Решите, когда и будете ли вы делать домашнюю работу после того, как вы выбрали часы для исследований. Ваша домашняя работа будет расширена, чтобы заполнить все пробелы в вашем расписании, так что у вас не будет времени думать о математике. Но если вы решите делать домашнюю работу, вы можете поместить ее в промежутки между исследованиями, и она все равно будет выполнена. Мы ожидаем, что исследования в области математики станут вашим самым важным видом деятельности, и к ним следует относиться с должным уважением. Невозможно заниматься математическими исследованиями, «когда вы не заняты чем-то другим», потому что вы всегда можете договориться о том, чтобы быть занятым чем-то другим.
«У меня было слишком много домашней работы на этой неделе» никогда не является приемлемым оправданием для того, чтобы не работать над своим исследовательским проектом: если вы выполняете действия профессионального математика, вы теряете право придумывать оправдания на уровне средней школы.
Итак, мы поняли: вы молоды, до сих пор добивались колоссальных успехов в жизни и верите, что можете обмануть систему: работать меньше, но при этом добиваться превосходных результатов. Если это так, вы ошибаетесь. Прежде чем вы начнете серьезно работать над оригинальной проблемой, потребуется много времени, чтобы просто изучить соответствующий фон. Ожидайте потратить несколько месяцев на изучение справочного материала, освоение методов, которые другие использовали для решения связанных проблем. Только тогда вы будете готовы начать думать самостоятельно.
После этого следующая задача — определить подходящую проблему. Проблема, с которой вы начинаете, скорее всего, будет несовершенной: возможно, тривиальной по какой-то глупой причине, возможно, невероятно сложной.
Тем не менее, наверняка будут хорошие проблемы, скрывающиеся очень близко, но найти их сложно, и вы также должны ожидать, что потратите значительное количество времени на их отслеживание.
Никогда нельзя гарантировать успех в исследованиях. Даже если вы очень усердны и все делаете правильно, вы все равно можете не решить проблему или получить бумагу. Большинство исследовательских идей заходят в тупик, и хотя мы поможем вам найти ту, которая имеет больше шансов на успех, чем обычно, мы ничего не обещаем. Неспособность решить проблемы также является ключевой частью исследовательского опыта.
Нет простого способа заниматься математическими исследованиями. Мы не будем рассказывать вам, как решить проблему только потому, что вы уже давно над ней работаете, и нам вас жаль. (Даже если бы мы захотели, мы бы не смогли: мы тоже не знаем, как их решить. Разве не в этом суть?) Из всех возможных областей исследований чистая математика обладает наивысшей затраты на запуск. Очень умные люди думали о математике на протяжении тысячелетий, и заниматься исследованиями — значит доказывать теорему, которую еще никто никогда не доказывал.
Проведение исследований по математике будет самым трудным делом, которое вы когда-либо делали в своей жизни, и, вероятно, самым трудным делом, которое вы когда-либо будете делать.
Конечно, как и во многих других сложных вещах, исследования в области математики имеют большие преимущества. Изучение математики — замечательная вещь, безусловно, самый интересный предмет. Даже не проводя никаких исследований, теоремы и доказательства, которые вы узнаете, разработанные много лет назад другими людьми, достаточны, чтобы вызвать большое счастье у любого, кто захочет приложить усилия, чтобы понять их. И нет большего чувства выполненного долга, чем то, что вы получаете после решения собственной проблемы, особенно когда вы делаете это первым. Даже для признанных математиков такие моменты редки, но они стоят всего отчаяния и чувства неадекватности, которые приходят, когда что-то идет не так, как бывает в большинстве случаев.
Теперь, если вы все еще читаете это и думаете: «А, это хороший способ поступить в колледж», значит, вы пока ничему не научились и вы плохой кандидат для проведения исследований по математике.
Нужно просто уметь читать лучше, чтобы иметь хоть какую-то надежду выучить соответствующий материал. Если это ваша ситуация, уходите и оставьте нас в покое.
Если же у вас есть более благородные цели и вы хотите глубоко изучать математику ради нее самой, ради ее собственной выгоды, то мы будем рады вам помочь. Добро пожаловать в клуб!
Вот так:
Нравится Загрузка…
Диаграммы Венна и Эйлера, ключ к упражнениям
Большинство упражнений в классе должны говорить сами за себя (но, пожалуйста, сообщите, если это не так!). Тот, который, возможно, доставил вам проблемы, следующий:
Упражнение 6: Напишите функцию, которая позволяет генерировать трехстороннюю диаграмму Венна без предварительного вычисления вручную размеров различных групп и перекрытий.
Подсказка: для этого вам, скорее всего, потребуется использовать функции, описанные на странице справки setdiff.
Бонусный балл : Если вы сможете понять, как написать функцию, чтобы вам не приходилось вручную вводить названия категорий при каждом ее запуске, вы получите золотую звезду за день.
threeway.Venn <- function(A,B,C,cat.names = c("A", "B", "C")){
сетка.новая страница()
площадь1 <- длина (А)
площадь2 <- длина (B)
площадь3 <- длина (С)
n12 <- длина (пересечение (A, B))
n23 <- длина (пересечение (B, C))
n13 <- длина (пересечение (A, C))
n123 <- длина (пересечение (пересечение (A, B), пересечение (B, C )))
venn.plot <- draw.triple.venn(
площадь1 = площадь1,
площадь2 = площадь2,
площадь3 = площадь3,
n12 = n12,
n23 = n23,
n13 = n13,
n123 = n123,
категория = cat.names,
кат.поз = с(0,180,0),
fill = c("синий", "красный", "зеленый"),
альфа = 0,3,
лти = "пусто",
секс = 2,
кат.цех = 2,
cat.col = c("синий", "красный", "зеленый")
)
grid.draw (венн. сюжет)
}
Пример графика, сделанного с помощью этой функции
библиотека (ВеннДиаграмма)
## Загрузка требуемого пакета: grid
наборA <- 1:10
установитьB <- 8:13
установитьC <- 8:15
threeway.Venn(setA, setB, setC, cat.names = c("setA", "setB", "setC"))
Упражнение 7:
Проведите, как вам кажется, интересные сравнения. Создавайте диаграммы Венна, чтобы визуализировать совпадения между различными группами. Найдите две группы, у которых есть совпадения, которые, как вы подозреваете, либо больше, либо меньше, чем вы ожидаете случайно.
Приведенный ниже пример взят из набора данных «фильмы». Я смотрел на совпадения фильмов с низким бюджетом и высокими рейтингами.
библиотека (ggplot2) low.budget <- subset(фильмы, бюджет <150000)$title high.budget <- subset(фильмы, бюджет > 2.5e+07)$title длина (малобюджетный) #1064
## [1] 1064
high.rating <- subset(movies, rating > 8)$title low.rating <- подмножество (фильмы, рейтинг < 2) $ title длина (высокий.рейтинг) #4072
## [1] 4072
длина(пересечение(низкий.бюджет, высокий.рейтинг)) #243
## [1] 243
сетка.новая страница()
venn.plot <- draw.pairwise.venn(area1 = 1064, area2 = 4072, cross.area = 243,
scaled = F, category = c("высокий.рейтинг", "низкий.бюджет"), fill = c("синий",
"красный"), альфа = 0,3, lty = "пусто", cex = 2, cat.