Простые и не очень способы того, как вычислить кубический корень :: SYL.ru
Сколько гневных слов произнесено в его адрес? Порой кажется, что кубический корень невероятно сильно отличается от квадратного. На самом деле разница не настолько велика. Особенно, если понять, что они только частные случаи общего корня n-ой степени.
Зато с его извлечением могут возникнуть проблемы. Но чаще всего они связаны с громоздкостью вычислений.
Что нужно знать о корне произвольной степени?
Во-первых, определение этого понятия. Корнем n-ой степени из некоторого «а» называется такое число, которое при возведении в степень n дает исходное «а».
Причем бывают четные и нечетные степени у корней. Если n — четное, то подкоренное выражение может быть только нулем или положительным числом. В противном случае вещественного ответа не будет.
Когда же степень нечетная, то существует решение при любом значении «а». Оно вполне может быть и отрицательным.
Во-вторых, функцию корня всегда можно записать, как степень, показателем которой является дробь. Иногда это бывает очень удобным.
Например, «а» в степени 1/n как раз и будет корнем n-ой степени из «а». В этом случае основание степени всегда больше нуля.
Аналогично «а» в степени n/m будет представлено, как корень m-ой степени из «аn».
В-третьих, для них справедливы все действия со степенями.
- Их можно перемножать. Тогда показатели степеней складываются.
- Корни можно разделить. Степени нужно будет вычесть.
- И возвести в степень. Тогда их следует перемножить. То есть ту степень, которая была, на ту, в которую возводят.
В чем сходства и различия квадратного и кубического корней?
Они похожи, как родные братья, только степень у них разная. И принцип их вычисления одинаков, различие только в том, сколько раз должно число на себя умножиться, чтобы получить подкоренное выражение.
А о существенном отличии было сказано чуть выше.
Но повториться не будет лишним. Квадратный извлекается только из неотрицательного числа. В то время, как вычислить кубический корень из отрицательной величины не составит труда.
Извлечение кубического корня на калькуляторе
Каждый человек хоть раз делал это для квадратного корня. А как быть если степень «3»?
На обычном калькуляторе имеется только кнопочка для квадратного, а кубического — нет. Здесь поможет простой перебор чисел, которые трижды умножаются на себя. Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.
А что в инженерном виде калькулятора в компьютере? Ура, здесь есть кубический корень. Эту кнопочку можно просто нажать, и программа выдаст ответ. Но это не все. Здесь можно вычислить корень не только 2 и 3 степени, но и любой произвольной. Потому что есть кнопка у которой в степени корня стоит «у». То есть после нажатия этой клавиши потребуется ввести еще одно число, которое будет равно степени корня, а уже потом «=».
Извлечение кубического корня вручную
Этот способ потребуется, когда калькулятора под рукой нет или воспользоваться им нельзя.
Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.
Сначала посмотреть, а не получается ли полный куб от какого-нибудь целого значения. Может быть под корнем стоит 2, 3, 5 или 10 в третьей степени?
В противном случае нужно будет считать столбиком. Алгоритм не самый простой. Но если немного попрактиковаться, то действия легко запомнятся. И вычислить кубический корень больше не будет проблемой.
- Мысленно разделить подкоренное выражение на группы по три цифры от десятичной запятой. Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
- Определить число, куб которого меньше целой части подкоренного выражения. Его записать в промежуточный ответ над знаком корня. А под этой группой расположить его куб.
- Выполнить вычитание.
- К остатку приписать первую группу цифр после запятой.
- В черновике записать выражение: а2 * 300 * х + а * 30 * х2 + х3. Здесь «а» — это промежуточный ответ, «х» является числом, которое меньше получившегося остатка с приписанными к нему числами.
- Число «х» нужно записать после запятой промежуточного ответа. А значение всего этого выражения записать под сравниваемым остатком.
- Если точности достаточно, то расчеты прекратить. В противном случае нужно возвращаться к пункту под номером 3.
Наглядный пример вычисления кубического корня
Он нужен потому, что описание может показаться сложным. На рисунке ниже показано, как извлечь кубический корень из 15 с точностью до сотых.
Единственной сложностью, которую имеет этот метод, заключается в том, что с каждым шагом числа увеличиваются многократно и считать в столбик становится все сложнее.
- 15> 23, значит под целой частью записана 8, а над корнем 2.
- После вычитания из 15 восьми получается остаток 7. К нему нужно приписать три нуля.
- а = 2. Поэтому: 22 * 300 * х +2 * 30 * х2 + х3 < 7000, или 1200 х + 60 х2 + х3< 7000.
- Методом подбора получается, что х = 4. 1200 * 4 + 60 * 16 + 64 = 5824.
- Вычитание дает 1176, а над корнем появилось число 4.
- Приписать к остатку три нуля.
- а = 24. Тогда 172800 х + 720 х2 + х3< 1176000.
- х = 6. Вычисление выражения дает результат 1062936. Остаток: 113064, над корнем 6.
- Снова приписать нули.
- а = 246. Неравенство получается таким: 18154800х + 7380х2 + х3< 113064000.
- х = 6. Расчеты дают число: 109194696, Остаток: 3869304. Над корнем 6.
1200 * 4 + 60 * 16 + 64 = 5824.Ответом получается число: 2, 466. Поскольку ответ должен быть дан до сотых, то его нужно округлить: 2,47.
Необычный способ извлечения кубического корня
Его можно использовать тогда, когда ответом является целое число. Тогда кубический корень извлекается разложением подкоренного выражения на нечетные слагаемые. Причем таких слагаемых должно быть минимально возможное число.
К примеру, 8 представляется суммой 3 и 5. А 64 = 13 + 15 + 17 + 19.
Ответом будет число, которое равно количеству слагаемых.
Так корень кубический из 8 будет равен двум, а из 64 — четырем.
Если под корнем стоит 1000, то его разложением на слагаемые будет 91 + 109 + 93 + 107 + 95 + 105 + 97 + 103 + 99 + 101. Всего 10 слагаемых. Это и есть ответ.
Как найти куб корень из числа
Автор Сфера закона На чтение 11 мин Просмотров 3 Опубликовано
Содержание
- Простые и не очень способы того, как вычислить кубический корень
- Что нужно знать о корне произвольной степени?
- В чем сходства и различия квадратного и кубического корней?
- Извлечение кубического корня на калькуляторе
- Извлечение кубического корня вручную
- Наглядный пример вычисления кубического корня
- Кубический корень. Извлечение кубического корня
- Алгоритм извлечения кубического корня
- Кубический корень
- Калькулятор кубического корня
- Алгоритм извлечения кубического корня
- Как находить кубический корень из числа
- Калькулятор кубического корня
- Алгоритм извлечения кубического корня
Простые и не очень способы того, как вычислить кубический корень
Сколько гневных слов произнесено в его адрес? Порой кажется, что кубический корень невероятно сильно отличается от квадратного.
Зато с его извлечением могут возникнуть проблемы. Но чаще всего они связаны с громоздкостью вычислений.
Что нужно знать о корне произвольной степени?
Во-первых, определение этого понятия. Корнем n-ой степени из некоторого «а» называется такое число, которое при возведении в степень n дает исходное «а».
Причем бывают четные и нечетные степени у корней. Если n — четное, то подкоренное выражение может быть только нулем или положительным числом. В противном случае вещественного ответа не будет.
Когда же степень нечетная, то существует решение при любом значении «а». Оно вполне может быть и отрицательным.
Во-вторых, функцию корня всегда можно записать, как степень, показателем которой является дробь. Иногда это бывает очень удобным.
Например, «а» в степени 1/n как раз и будет корнем n-ой степени из «а». В этом случае основание степени всегда больше нуля.
Аналогично «а» в степени n/m будет представлено, как корень m-ой степени из «а n ».
В-третьих, для них справедливы все действия со степенями.
- Их можно перемножать. Тогда показатели степеней складываются.
- Корни можно разделить. Степени нужно будет вычесть.
- И возвести в степень. Тогда их следует перемножить. То есть ту степень, которая была, на ту, в которую возводят.
В чем сходства и различия квадратного и кубического корней?
Они похожи, как родные братья, только степень у них разная. И принцип их вычисления одинаков, различие только в том, сколько раз должно число на себя умножиться, чтобы получить подкоренное выражение.
А о существенном отличии было сказано чуть выше. Но повториться не будет лишним. Квадратный извлекается только из неотрицательного числа. В то время, как вычислить кубический корень из отрицательной величины не составит труда.
Извлечение кубического корня на калькуляторе
Каждый человек хоть раз делал это для квадратного корня.
А как быть если степень «3»?
На обычном калькуляторе имеется только кнопочка для квадратного, а кубического — нет. Здесь поможет простой перебор чисел, которые трижды умножаются на себя. Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.
А что в инженерном виде калькулятора в компьютере? Ура, здесь есть кубический корень. Эту кнопочку можно просто нажать, и программа выдаст ответ. Но это не все. Здесь можно вычислить корень не только 2 и 3 степени, но и любой произвольной. Потому что есть кнопка у которой в степени корня стоит «у». То есть после нажатия этой клавиши потребуется ввести еще одно число, которое будет равно степени корня, а уже потом «=».
Извлечение кубического корня вручную
Этот способ потребуется, когда калькулятора под рукой нет или воспользоваться им нельзя. Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.
Сначала посмотреть, а не получается ли полный куб от какого-нибудь целого значения.
Может быть под корнем стоит 2, 3, 5 или 10 в третьей степени?
В противном случае нужно будет считать столбиком. Алгоритм не самый простой. Но если немного попрактиковаться, то действия легко запомнятся. И вычислить кубический корень больше не будет проблемой.
- Мысленно разделить подкоренное выражение на группы по три цифры от десятичной запятой. Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
- Определить число, куб которого меньше целой части подкоренного выражения. Его записать в промежуточный ответ над знаком корня. А под этой группой расположить его куб.
- Выполнить вычитание.
- К остатку приписать первую группу цифр после запятой.
- В черновике записать выражение: а 2 * 300 * х + а * 30 * х 2 + х 3 . Здесь «а» — это промежуточный ответ, «х» является числом, которое меньше получившегося остатка с приписанными к нему числами.
- Число «х» нужно записать после запятой промежуточного ответа. А значение всего этого выражения записать под сравниваемым остатком.
- Если точности достаточно, то расчеты прекратить. В противном случае нужно возвращаться к пункту под номером 3.
Наглядный пример вычисления кубического корня
Он нужен потому, что описание может показаться сложным. На рисунке ниже показано, как извлечь кубический корень из 15 с точностью до сотых.
Единственной сложностью, которую имеет этот метод, заключается в том, что с каждым шагом числа увеличиваются многократно и считать в столбик становится все сложнее.
- 15> 2 3 , значит под целой частью записана 8, а над корнем 2.
- После вычитания из 15 восьми получается остаток 7. К нему нужно приписать три нуля.
- а = 2. Поэтому: 2 2 * 300 * х +2 * 30 * х 2 + х 3 2 + х 3 2 + х 3 2 + х 3
Источник
Кубический корень. Извлечение кубического корня
Кубический корень из a , обозначающийся как 3 √a или как a 1/3 — решение уравнения x 3 = a (обычно подразумеваются вещественные решения).
Кубический корень — нечётная функция. В отличие от квадратного корня, кубический корень может быть извлечён и из отрицательных чисел.
Онлайн калькулятор для расчета кубического корня для положительных и отрицательных чисел.
Алгоритм извлечения кубического корня
Перед началом необходимо разделить число на тройки (целую часть — справа налево, дробную — слева направо). Когда Вы достигли десятичной запятой, в конце результата необходимо поставить десятичную запятую.
- Найдите число, куб которого меньше первой группы цифр, но при её увеличении на 1 она становиться больше. Выпишите найденное число справа от данного числа. Под ним запишите число 3.
- Запишите куб найденного числа под первой группой цифр и произведите вычитание. Результат после вычитания запишите под вычитаемым. Далее снесите следующую группу цифр.
- Далее найденный промежуточный ответ заменим буквой a. Вычислите по формуле 300× a 2 × x+30× a × x 2 +x 3 такое число x , что его результат меньше нижнего числа, но при увеличении на 1 становится больше. Запишите найденное x справа от ответа. Если достигнута необходимая точность, прекратите вычисления.
- Запишите под нижним числом результат вычисления по формуле 300 × a 2 × x+30 × a × x 2 +x 3 и произведите вычитание. Перейдите к пункту 3.
Запишите найденное x справа от ответа. Если достигнута необходимая точность, прекратите вычисления.Источник
Кубический корень
Кубический корень из a, обозначающийся как или как a 1/3 — решение уравнения x 3 = a (обычно подразумеваются вещественные решения).
Кубический корень — нечётная функция. В отличие от квадратного корня, кубический корень может быть извлечён и из отрицательных чисел.
Калькулятор кубического корня
Онлайн калькулятор для расчета кубического корня для положительных и отрицательных чисел.
Алгоритм извлечения кубического корня
Перед началом необходимо разделить число на тройки (целую часть — справа налево, дробную — слева направо).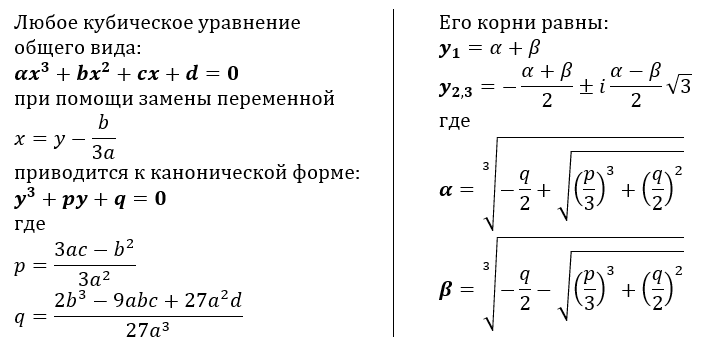
- Найдите число, куб которого меньше первой группы цифр, но при её увеличении на 1 она становиться больше. Выпишите найденное число справа от данного числа. Под ним запишите число 3.
- Запишите куб найденного числа под первой группой цифр и произведите вычитание. Результат после вычитания запишите под вычитаемым. Далее снесите следующую группу цифр.
- Далее найденный промежуточный ответ заменим буквой a. Вычислите по формуле 300× a 2 × x+30× a × x 2 +x 3 такое число x, что его результат меньше нижнего числа, но при увеличении на 1 становится больше. Запишите найденное x справа от ответа. Если достигнута необходимая точность, прекратите вычисления.
- Запишите под нижним числом результат вычисления по формуле 300 × a 2 × x+30 × a × x 2 +x 3 и произведите вычитание. Перейдите к пункту 3.
Источник
Как находить кубический корень из числа
Кубический корень. Как извлечь квадратный корень из большого числа без калькулятора мы уже разобрали. В этой статье рассмотрим как извлечь кубический корень (корень третьей степени). Оговорюсь, что речь идёт о натуральных числах. Как вы думаете, сколько времени нужно, чтобы устно вычислить такие корни как:
Совсем немного, а если потренируетесь два-три раза минут по 20, то любой такой корень вы сможете извлечь за 5 секунд устно.
*Нужно отметить, что речь идёт о таких числах стоящих под корнем, которые являются результатом возведения в куб натуральных чисел от 0 до 100.
Так вот, число а, которое мы будем находить – это натуральное число от 0 до 100. Посмотрите на таблицу кубов этих чисел (результаты возведения в третью степень):
Вы без труда сможете извлечь кубический корень из любого числа в этой таблице. Что нужно знать?
1. Это кубы чисел кратных десяти:
Я бы даже сказал, что это «красивые» числа, запоминаются они легко.
Выучить несложно.
2. Это свойство чисел при произведении.
Его суть заключается в том, что при возведении в третью степень какого-либо определённого числа, результат будет иметь особенность. Какую?
Например, возведём в куб 1, 11, 21, 31, 41 и т.д. Можно посмотреть по таблице.
1 3 = 1, 11 3 = 1331, 21 3 = 9261, 31 3 = 26791, 41 3 = 68921 …
То есть, при возведении в куб числа с единицей на конце в результате у нас всегда получится число с единицей в конце.
При возведении в куб числа с двойкой на конце в результате всегда получится число с восьмёркой в конце.
Покажем соответствие в табличке для всех чисел:
Знания представленных двух моментов вполне достаточно.
Извлечь кубический корень из 21952.
Данное число находится в пределах от 8000 до 27000. Это означает, что результат корня лежит в пределах от 20 до 30. Число 29952 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце.
Таким образом, результат корня равен 28.
Извлечь кубический корень из 54852.
Данное число находится в пределах от 27000 до 64000. Это значит, что результат корня лежит в пределах от 30 до 40. Число 54852 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 38.
Извлечь кубический корень из 571787.
Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 571787 заканчивается на 7. Такой вариант возможен только тогда, когда в куб возводится число с тройкой в конце. Таким образом, результат корня равен 83.
Извлечь кубический корень из 614125.
Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 614125 заканчивается на 5. Такой вариант возможен только тогда, когда в куб возводится число с пятёркой в конце. Таким образом, результат корня равен 85.
Думаю, что вы теперь без труда сможете извлечь кубический корень из числа 681472.
Конечно, чтобы извлекать такие корни устно, нужна небольшая практика. Но восстановив две указанные таблички на бумаге, вы без труда в течение минуты, в любом случае, такой корень извлечь сможете.
После того, как нашли результат обязательно сделайте проверку (возведите его с третью степень). *Умножение столбиком никто не отменял 😉
На самом ЕГЭ задач с такими «страшненькими» корнями нет. Например, в Задаче 27125 требуется извлечь кубический корень из 1728. Думаю, что это теперь для вас не проблема.
Если вы знаете какие-то интересные приёмы вычислений без калькулятора, присылайте, со временем опубликую. На этом всё. Успеха Вам!
Онлайн калькулятор для расчета кубического корня для положительных и отрицательных чисел.
Кубический корень из a, обозначающийся как или как a 1/3 — решение уравнения x 3 = a (обычно подразумеваются вещественные решения).
Кубический корень — нечётная функция. В отличие от квадратного корня, кубический корень может быть извлечён и из отрицательных чисел.
Калькулятор кубического корня
Онлайн калькулятор для расчета кубического корня для положительных и отрицательных чисел.
Алгоритм извлечения кубического корня
Перед началом необходимо разделить число на тройки (целую часть — справа налево, дробную — слева направо). Когда Вы достигли десятичной запятой, в конце результата необходимо поставить десятичную запятую.
- Найдите число, куб которого меньше первой группы цифр, но при её увеличении на 1 она становиться больше. Выпишите найденное число справа от данного числа. Под ним запишите число 3.
- Запишите куб найденного числа под первой группой цифр и произведите вычитание. Результат после вычитания запишите под вычитаемым. Далее снесите следующую группу цифр.
- Далее найденный промежуточный ответ заменим буквой a. Вычислите по формуле 300× a 2 × x+30× a × x 2 +x 3 такое число x, что его результат меньше нижнего числа, но при увеличении на 1 становится больше. Запишите найденное x справа от ответа. Если достигнута необходимая точность, прекратите вычисления.
- Запишите под нижним числом результат вычисления по формуле 300 × a 2 × x+30 × a × x 2 +x 3 и произведите вычитание. Перейдите к пункту 3.
Запишите найденное x справа от ответа. Если достигнута необходимая точность, прекратите вычисления.В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.
Количество источников, использованных в этой статье: 14. Вы найдете их список внизу страницы.
Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.
Если под рукой есть калькулятор, извлечь кубический корень из любого числа не составит никаких проблем. Но если калькулятора нет или вы просто хотите произвести впечатление на окружающих, извлеките кубический корень вручную. Большинству людей описываемый здесь процесс покажется довольно сложным, но с практикой извлекать кубические корни станет намного легче. Перед тем как приступить к чтению данной статьи, вспомните основные математические операции и вычисления с числами в кубе.
Источник
Что такое кубический корень? (Ответы на 7 часто задаваемых вопросов) – JDM Educational
Кубический корень может помочь нам найти длину стороны куба с заданным объемом. Кубический корень также может помочь нам решить кубические уравнения (где есть член x 3 ). Тем не менее, полезно знать, как работают кубические корни.
Итак, что такое кубический корень? Кубический корень C из числа N удовлетворяет уравнению N = C 3 (проще говоря: «N равно C в кубе»). Кубический корень из N — это число C, которое нужно умножить само на себя 3 раза, чтобы получить N. Мы также можем написать C = 9.0003 3 √N для обозначения кубического корня из N.
Конечно, когда мы говорим о кубическом корне из N, мы обычно имеем в виду главный кубический корень из N. Помните, что каждое действительное число (кроме нуля) имеет три кубические корни: один действительный кубический корень и два кубических корня, которые являются комплексными числами с ненулевыми мнимыми частями.
В этой статье мы поговорим о кубических корнях и ответим на некоторые распространенные вопросы о них. Мы также рассмотрим несколько примеров того, как находить кубические корни вручную (на случай, если у вас никогда не будет калькулятора или компьютера).
Начнем.
Что такое кубический корень?
Для числа N кубическим корнем из N является число C, которое удовлетворяет уравнению C = 3 √N [C равно кубическому корню из N]
Вот еще один способ выразить эту идею словами: кубический корень из N — это число C, которое вы умножаете само на себя 3 раза, чтобы получить №
Если нам известен объем куба, мы можем найти длину стороны, взяв кубический корень из объема.Помните, что в дополнение к главному кубическому корню из действительного числа N (действительному) есть еще два кубических корня (оба комплексные).
Например:
- Главный кубический корень из -1 равен -1 (действительное число), поскольку (-1) 3 = -1.
- Еще один кубический корень из -1 равен (1/2) + i(√3/2) (это комплексное число).
- Еще один кубический корень из -1 равен (-1/2) + i(√3/2) (это комплексное число).
Давайте посмотрим на таблицу первых нескольких действительных кубических корней, которые являются целыми числами (целыми числами).
Таблица кубических корней
В таблице ниже показаны целые числа «идеального куба» и их кубические корни.
| N | 3 √n |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 |
| 1 | 1 |
| 1 | 1 | 0087
| 8 | 2 |
| 27 | 3 |
| 64 | 4 |
| 125 | 5 |
| 216 | 6 |
| 343 | 7 |
| 512 | 8 |
| 729 | |
| 1000 | 10 |
.
Это может помочь вам при факторизации суммы или разности кубов.
Вы также можете использовать эту таблицу в качестве руководства при поиске кубических корней вручную (подробнее об этом позже).
Имеет ли кубический корень два ответа?
Кубический корень из действительного числа имеет один действительный ответ, а также два сложных ответа.
Настоящий ответ называется главным кубическим корнем.
Мы можем использовать комплексные числа для записи двух дополнительных кубических корней действительного числа N (помимо главного кубического корня, который является действительным числом).Вы можете найти все комплексные кубические корни действительного числа N, решив уравнение:
Как найти кубический корень вручную
Чтобы найти 3 √N вручную, начните с куба целых чисел (1 3 = 1, 2 3 = 8, 3 3 = 27 и т. д. ). Найдите первое число S такое, что S 3 > N.
Тогда мы знаем, что S – 1 < 3 √N < S.
Возьмите среднее значение S – 1 и S, а затем возведите его в куб.
Если результат больше N, попробуйте меньшее число; в противном случае попробуйте большее число и повторите процесс.
Напомним:
- Во-первых, мы «связали» 3 √N между двумя целыми числами, S – 1 и S. Мы делаем это путем кубирования целых чисел (1 3 = 1, 2 3 = 8). , 3 3 = 27 и т. д.), пока не найдем результат S 3 , больший, чем N. среднее значение конечных точек и кубирование результата. Если мы получаем что-то большее, чем N, мы берем меньшее число. Если мы получаем что-то меньшее, чем N, мы берем большее число.
Это поможет увидеть пример того, как это работает, так что давайте посмотрим на один из них.
Пример: как найти кубический корень из 10 вручную
Наш первый шаг — связать кубический корень из 10 между двумя целыми числами.
Итак, мы перечислим идеальные кубики, пока не найдем один больше n = 10:
- 1 3 = 1
- 2 3 = 8
- 3 3 = 27
Мы останавливаемся на S = 3, так как 3 3 = 27 является первым целым числом в кубе, большим, чем N = 10.
Это означает, что наша граница находится в интервале S – 1 < 3 √N < S, или 2 < 3 √10 < 3.
На шаге 2 мы находим более точное число для √10, повторяя следующий процесс.
Сначала возьмем среднее между конечными точками нашего интервала: (2 + 3) / 2 = 2,5.
Далее куб средней мы нашли: 2,5 3 = 15,625.
Теперь, поскольку результат 15,625 больше 10, нам нужно меньшее число.
Теперь наша граница 2 < 3 √10 < 2,5.
Повторение процесса:
Сначала возьмите среднее значение конечных точек: (2 + 2,5) / 2 = 2,25.
Далее, куб среднего мы нашли: 2,25 3 = 729/65, или 11 & (25/64).
Теперь, поскольку результат 729/64 больше 10, нам нужно меньшее число.
Теперь наша граница 2 < 3 √10 < 2,25.
Повторение процесса:
Сначала возьмем среднее значение конечных точек: (2 + 2,25) / 2 = 2,125.
Затем кубизируйте среднее значение, которое мы нашли: 2,125 3 = 4913/512 или чуть меньше 10.
Теперь, поскольку результат 4913/520 меньше 10, нам нужно большее число.
Теперь наша граница 2,125 < 3 √10 < 2,25.
Повторение процесса:
Сначала возьмем среднее значение конечных точек: (2,125 + 2,25) / 2 = 2,1875.
Далее, куб среднего мы нашли: 2,1875 3 = 42,875/4,096.
Теперь, поскольку результат 42 875/4 096 больше 10, нам нужно меньшее число.
Теперь наша граница 2,125 < 3 √10 < 2,1875.
На данный момент ширина границы составляет всего около 1/16 (0,0625). Если мы сейчас возьмем среднее значение двух конечных точек, мы получим значение, которое находится в пределах 1/32 (0,03125) от 3 √10.
Если нам нужна большая точность, мы можем продолжать повторять описанный выше процесс, чтобы сократить ширину граничного интервала вдвое.
Итак, мы берем (2,125 + 2,1875)/2 = 2 и (5/32) в качестве значения кубического корня из 10. ошибка около 0,025/10 = 0,25%).
Мы видим, что граничный интервал становится меньше с каждым шагом, который мы предпринимаем, чтобы вручную найти кубический корень из 10.
(Вы можете научиться находить квадратные корни вручную здесь).
Можно ли извлечь корень из отрицательного числа? (Может ли кубический корень быть отрицательным?)
Вы можете извлечь кубический корень из отрицательного числа. Результатом будет отрицательное действительное число (для главного кубического корня).
Другими словами, кубический корень может быть отрицательным, но только тогда, когда мы берем кубический корень из отрицательного числа.
Если N — отрицательное действительное число, то его кубический корень равен – 3 √|N|. То есть:
- Возьмите абсолютное значение N, чтобы получить |N|, положительное действительное число.
- Возьмем главный кубический корень из |N| чтобы получить положительное действительное число, 3 √|N|.
- Возьмите отрицательный результат этого положительного кубического корня, чтобы получить отрицательное действительное число, – 3 √|Н|.
Например: чтобы найти кубический корень из -64:
- Возьмите абсолютное значение -64, чтобы получить |-64| = 64.
- Возьмите главный кубический корень из 64, чтобы получить 4.
- Возьмите отрицательный результат этого кубического корня, чтобы получить -4.
Мы легко можем проверить этот ответ:
- (-4) 3
- =(-4)*(-4)*(-4) = 60(-4) ) [произведение двух отрицаний положительно]
- = -64 [произведение отрицательного и положительного отрицательно]
Почему кубический корень из отрицательного числа отрицателен?
Кубический корень любого отрицательного числа должен быть отрицательным из-за четности (четной или нечетной) показателей степени.
Помните, что:
- Отрицательное число, возведенное в четную степень, является положительным.
- Отрицательное число, возведенное в нечетную степень, является отрицательным.
- Положительное число, возведенное в любую степень (четную или нечетную), является положительным.
Итак, кубический корень из отрицательного числа должен быть отрицательным. Положительное число, возведенное в третью степень, никогда не могло дать нам отрицательного результата.
Может ли кубический корень из положительного числа быть отрицательным?
Кубический корень из положительного числа не может быть отрицательным из-за четности показателей (см. выше).
Отрицательное число, возведенное в третью степень (показатель степени 3), должно быть отрицательным, поскольку 3 нечетно. Таким образом, отрицательное число в кубе не может быть положительным, а положительное число не может иметь отрицательный кубический корень.
Можете ли вы извлечь кубический корень из нуля?
Вы можете извлечь кубический корень из нуля. Результат просто нулевой. Есть два способа доказать это.
Во -первых, мы можем легко показать, что 0 3 = 0:
- 0 3
- = 0*0*0
- = 0*0
- 9007 = 00012 9007 = 0*0
- 9007 = 00012 = 0*0
- 9003
Мы также можем показать, что x = 0 является единственным решением кубического уравнения x 3 = 0:
- x 3 = 0
- x*x*x = 0
- x = 0 или x = 0 или x = 0 [x = 0 — тройной действительный корень уравнения]
Является ли кубический корень из X непрерывным?
Функция кубического корня f(x) = 3 √x непрерывна.
Мы можем видеть его график ниже:
Однако обратите внимание, что f(x) = 3 √x не дифференцируема при x = 0, так как мы получаем отрицательный показатель степени, потому что:
- f(x) = 3 √x
- f(x) = x 1/3 [степень 1/3 эквивалентна извлечению кубического корня]
- ‘7 9000 (x) = (1/3)x -2/3 [по степенному правилу для взятия производных]
- f'(x) = 1/(3 3 √(x 2 ))
Мы видим, что x = 0 даст нам нулевой знаменатель в производной.
Заключение
Теперь вы знаете немного больше о кубических корнях, а также ответы на некоторые распространенные вопросы о них. Вы также знаете процедуру нахождения кубических корней вручную, на всякий случай!
Надеюсь, эта статья оказалась вам полезной.
Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.
Не забудьте подписаться на наш канал YouTube и получать обновления о новых математических видео!
Подпишитесь на наш канал на YouTube!
Кубический корень C из числа N удовлетворяет уравнению N = C3 (проще говоря: «N равно C в кубе»). Кубический корень из N — это число C, которое вы умножаете само на себя 3 раза, чтобы получить N. Мы также можем написать C = 3√N, чтобы обозначить кубический корень из N.
Как найти кубический корень? – Метод простой факторизации, метод оценки
Кубический корень любого числа – это другое число, которое при двукратном умножении само на себя дает число, кубический корень которого необходимо определить. Куб корня представлен символом ∛. Кубический корень любого числа также можно представить в виде показателя степени как число в степени ⅓. Кубический корень любого действительного числа, скажем «k», его кубический корень можно записать как ∛k или (k)⅓.
Мы должны понимать, что куб и кубические корни являются обратными математическими операциями. Итак, кубический корень кубического числа — это само число.
Как найти кубический корень?
Кубический корень любого действительного числа получается либо методом простой факторизации, либо методом оценки, когда число, квадратный корень которого нужно найти, является совершенным кубическим числом. Однако в большинстве случаев очень рекомендуется запоминать кубы и кубические корни как минимум первых 25 натуральных чисел. Это поможет учащимся и преподавателям добиться отличных результатов на конкурсных экзаменах. В таблице ниже приведены кубы и кубические корни первых 20 натуральных чисел.
Cubes and Cube Roots of the First 20 Natural Numbers
Number | Cube | Cube Root | Number | Cube | Кубический корень | |||||||
1 | 1 | 1. | 50 9 0 50 9 90 509 0 110509 1331 | 2.224 | ||||||||
2 | 8 | 1.260 | 12 | 1728 | 2.289 | |||||||
3 | 27 | 1,442 | 13 | 2197 | 2,351 | |||||||
4 | ||||||||||||
4 | ||||||||||||
1.587 | 14 | 2744 | 2.410 | |||||||||
5 | 125 | 1.710 | 15 | 3375 | 2,466 | |||||||
6 | 216 | 1,817 | 16 777 | 16 | 16 | 16 777 | 16 7779309309 | .2.520 | ||||
7 | 343 | 1.913 | 17 | 4913 | 2.571 | |||||||
8 | 512 | 2.000 | 18 | 5832 | 2,621 | |||||||
2.080 | 19 | 6859 | 2.668 | |||||||||
10 | 1000 | 2.154 | 20 | 8000 | 2,714 |
000
0509 4096
Как найти кубический корень методом простой факторизации?
В этом методе число, кубический корень которого необходимо найти, полностью разлагается на простые множители.
Одинаковые простые множители сгруппированы таким образом, что три одинаковых множителя образуют одну группу. Для определения кубического корня собирают и перемножают по одному фактору из каждой группы.
Шаг 1:
Данное число полностью разложено на простые множители. Всегда рекомендуется начинать деление с наименьшего возможного простого числа, а затем переходить к большему простому числу, когда частное не полностью делится на выбранное число.
Заданное число, кубический корень которого необходимо определить, равно 74088. Разложение на простые множители можно резюмировать, как показано на рисунке ниже.
(Изображение скоро будет загружено)
Шаг 2:
Запишите число, кубический корень которого нужно определить, как произведение их простых чисел.
Число 74088 можно записать как произведение своих простых чисел:
74088 = 2 x 2 x 2 x 3 x 3 x 3 x 7 x 7 x 7
Шаг 3:
Разделите множители на группы, состоящие из из трех одинаковых факторов.
74088 как произведение его простых чисел переписывается как:
74088 = 2 x 2 x 2 x 3 x 3 x 3 x 7 x 7 x 7
Шаг 4:
Кубический корень числа находится как произведение одного множителя, взятого из каждой группы на шаге 3.
Итак, кубический корень числа 74088 равен 2 x 3 x 7 = 42
Как вычислить Найдите кубический корень методом оценки?
В методе оценки мы разделяем число на группы, а затем оцениваем его кубический корень. Шаги, которые необходимо выполнить при определении кубического корня методом оценки, описаны ниже.
Шаг 1:
Данный номер разбит на группы по 3 цифры, начиная с самой правой цифры номера. Если какое-либо число опущено без образования группы из трех цифр, слева от него добавляются нули, чтобы сделать его группой из 3 цифр. Однако мы должны позаботиться о том, чтобы разрядное значение цифры не изменилось добавлением нулей.
Попробуем найти кубический корень числа 74088.
Итак, чтобы найти кубический корень числа 74088, нужно разбить число на группы по три цифры, начиная с разряда единицы.
074 088
Шаг 2:
Из первой группы, начиная справа, запишите цифру единицы.
Первая самая правая группа на шаге 1 — это 088, а цифра на месте ее единицы — 8.
Шаг 3:
Оцените цифру на месте единицы кубического корня данного числа, используя справочную таблицу, приведенную ниже.
Digit in the Unit’s place of the number | Digit in the Unit’s place of its Cube Root | Digit in the Unit’s place of the number | Digit in the Unit’s place of its Cube Root |
1 | 1 | 6 | 6 |
8 | 2 | 3 | 7 |
7 | 3 | 2 | 8 |
4 | 4 | 9 | 9 |
5 | 5 | 0 | 0 |
Цифра в разряде единиц, полученная на шаге 1, равна «8», и, следовательно, цифра единицы кубического корня числа 74088 также равна «2».
Шаг 4:
Теперь рассмотрим вторую группу справа. Отметьте совершенные кубические числа, между которыми лежит это число. Предположим, что число в этой группе лежит между A3 и B3 и ближе к B3, тогда десятый разряд его кубического корня считается B.
В данном числе 74088 вторая группа из 3 цифр справа — 074.
Это число лежит между двумя совершенными кубическими числами 64 и 125, т. е. 43 и 53. Поскольку 74 ближе к 64, т. е. 43, десятичная цифра кубического корня числа 74088 равна 4.
Кубический корень числа 74088, найденный с помощью оценки Метод равен 42.
Интересные факты
Куб и кубический корень являются обратными операциями, и, следовательно, кубический корень из кубического числа — это само число.
Кубический корень совершенного кубического числа всегда является целым числом.
Методы простой факторизации и оценки можно использовать только для нахождения кубических корней идеальных кубов. Чтобы определить кубические корни несовершенных кубов, можно воспользоваться несколькими приемами.
Кубические корни | Ярлык, чтобы найти кубический корень числа |
You are here: Home / Что такое ведическая математика / Кубические корни в ведической математике
by Rahul Bhangale 6 комментариев
Cube-Roots
Факты:
- Кубики от 1 до 10
Номер | Куб | Куб заканчивается | Таким образом, так как видимые кубы имеют четкие окончания, перекрытия нет. Таким образом, если заданное число является полным кубом, то последняя цифра поможет найти кубический корень. |
1 | 1 | 1 | |
2 | 8 | 8 (дополнительно 2) | |
3 | 27 | 7 (дополнение 3) | |
4 | 64 | 4 | |
5 | 125 | 5 | |
6 | 216 | 6 | |
7 | 343 | 3 (дополнение 7) | |
8 | 512 | 2 (дополнение 8) | |
9 | 729 | 9 | |
10 | 1000 | 0 |
- Кубические корни необходимо сгруппировать в группу по 3 из R -> L. Таким образом, количество сформированных групп будет == Количество цифр в кубическом корне. Например (для идеальных кубов).
- 1728 будут сгруппированы как 1 , 728 . Таким образом, его кубический корень будет из 2 цифр 84604519 и будет сгруппирован как 84 604 519 . Таким образом, его кубический корень будет равен 3 9.1219 цифр.300763 будут сгруппированы как 300 763. Таким образом, его кубический корень будет состоять из 2 цифр.
- Всегда 1-я группа будет определять 1-ю цифру кубического корня. Найдите идеальный куб, который <= 1-й группы, и его кубический корень будет 1-й цифрой кубического корня данного числа.
Таким образом, количество сформированных групп будет == Количество цифр в кубическом корне. Например (для идеальных кубов).Для приведенных выше примеров
| Куб | Совершенный куб <= 1-я группа | Кубический корень из столбец 2 | 1-я цифра кубического корня данного числа. (3-я точка) | Последняя цифра кубического корня данного числа. | Количество цифр в кубическом корне данного числа (2-я точка) | Требуется кубический корень |
| 1 728 | 1 | 1 | 1 | 2 | 2 | 12 |
| 84 604 519 | 64 | 4 | 4 | 9 | 3 | 4 _ 9 |
| 300 763 | 216 | 6 | 6 | 7 | 2 | 67 |
- Как видно из приведенной выше таблицы, когда у нас есть 2 группы, мы можем напрямую записать кубический корень (2 цифры), т. е. вычисление кубического корня из числа, имеющего <= 6 цифр, очень просто и не требует дополнительных шагов. Но если у нас более 2 групп, нам нужно использовать другую логику.
- Трехзначное число (cba) может быть записано как a+10b+100c. Его куб: (A + 10B + 100C) 3 = A 3 + 1000B 3 + 10 000 000C 3 + 30A 2 B + 300A 2 C + 300AB 2 + 30 000. AC 2 + 3 000 000,000BC 2 + 30 000B 2 C + 6000ABC. = 10 000 000C 3 + 1 000 000 x 3BC 2 + 10 000 x (3AC 2 + 3B 2 в) + 1000 х (б 3 +6абв) + 100 х (3а 2 в + 3аб 2 ) + 10 х 3а 2 б + а 3 .
Места
Десять лакхов/
1 миллион
лакхов
Десять тысяч
Тысячи
Сотни
Десятки
Блок
с 3
3bc 2
3ac 2 + 3b 2 c
б 3 +6абв
3а 2 с + 3аб 2
3а 2 б
3
е. вычисление кубического корня из числа, имеющего <= 6 цифр, очень просто и не требует дополнительных шагов. Но если у нас более 2 групп, нам нужно использовать другую логику.Метод аргументации (кубический корень ведической математики для трехзначного числа):
Это метод устранения процесса рассуждения методического.