Квадратное уравнение с 1 корнем: Квадратные уравнения с 1 корнем пример. Квадратные уравнения

Содержание

Полное приведенное квадратное уравнение пример. Решение квадратных уравнений, формула корней, примеры

Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.

С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».

Какие же квадратные уравнения называются полными? Это уравнения вида ах 2 + b x + c = 0 , где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.

D = b 2 – 4ас.

В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.

Если дискриминант отрицательное число (D

Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),

тогда х 1 = (-b — √D)/2a , и х 2 = (-b + √D)/2a .

Например. Решить уравнение х 2 – 4х + 4= 0.

D = 4 2 – 4 · 4 = 0

x = (- (-4))/2 = 2

Ответ: 2.

Решить уравнение 2х 2 + х + 3 = 0.

D = 1 2 – 4 · 2 · 3 = – 23

Ответ: корней нет .

Решить уравнение 2х 2 + 5х – 7 = 0 .

D = 5 2 – 4 · 2 · (–7) = 81

х 1 = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5

х 2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1

Ответ: – 3,5 ; 1 .

Итак представим решение полных квадратных уравнений схемой на рисунке1.

По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида

ах 2 + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х 2 = 0, ошибочно можно решить, что

а = 1, b = 3 и с = 2. Тогда

D = 3 2 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня.

А это неверно. (Смотри решение примера 2 выше).

Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах 2 , затем с меньшим – bx , а затем свободный член с.

При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.

Полное квадратное уравнение называется приведенным, если коэффициент при х 2 равен единице и уравнение примет вид х 2 + px + q = 0 . Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент

а , стоящий при х 2 .

На рисунке 3 приведена схема решения приведенных квадратных
уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.

Пример. Решить уравнение

3х 2 + 6х – 6 = 0.

Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.

D = 6 2 – 4 · 3 · (– 6) = 36 + 72 = 108

√D = √108 = √(36 · 3) = 6√3

х 1 = (-6 — 6√3)/(2 · 3) = (6 (-1- √(3)))/6 = –1 – √3

х 2 = (-6 + 6√3)/(2 · 3) = (6 (-1+ √(3)))/6 = –1 + √3

Ответ: –1 – √3; –1 + √3

Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам, приведенным на схеме рисунка D 1 = 3 2 – 3 · (– 6) = 9 + 18 = 27

√(D 1) = √27 = √(9 · 3) = 3√3

х 1 = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3

х 2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3

Ответ: –1 – √3; –1 + √3 . Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x 2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного
уравнения рисунок 3.

D 2 = 2 2 – 4 · (– 2) = 4 + 8 = 12

√(D 2) = √12 = √(4 · 3) = 2√3

х 1 = (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3

х 2 = (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3

Ответ: –1 – √3; –1 + √3.

Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Рассмотрим задачу. Основание прямоугольника больше высоты на 10 см., а его площадь равна 24 см². Найти высоту прямоугольника. Пусть х сантиметров — высота прямоугольника, тогда его основание равно (х +10) см. Площадь этого прямоугольника равна х (х + 10) см². По условию задачи х (х + 10) = 24. Раскрывая скобки и перенося число 24 с противоположным знаком в левую часть уравнения, получаем: х ² + 10х -24 = 0. При решении этой задачи было получено уравнение, которое называют квадратным.

Квадратным уравнением называется уравнение вида

ax ²+bx +c= 0

где a, b, c — заданные числа, причем а ≠ 0, а х — неизвестное.

Коэффициенты a, b, c квадратного уравнения обычно называют так:

a — первым или старшим коэффициентом, b — вторым коэффициентом, c — свободным членом. Например в нашей задаче старший коэффициент равен 1, второй коэффициент 10, свободный член -24. Решение многих задач математики и физики сводится к решению квадратных уравнений.

Решение квадратных уравнений

Полные квадратные уравнения. Первым делом надо заданное уравнение привести к стандартному виду ax ²+ bx + c = 0. Вернемся к нашей задаче, в которой уравнение может быть записано как х (х + 10) = 24 приведем его к стандартному виду, раскроем скобки х ² + 10х — 24 = 0, решим это уравнение с помощью формулы корней квадратного уравнения общего вида.

Выражение под знаком корня в этой формуле называется дискриминант D = b ² — 4ac

Если D>0, то квадратное уравнение имеет два различных корня, которые можно найти по формуле корней квадратного уравнения.

Если D=0, то квадратное уравнение имеет один корень.

Если D

Подставим значения в нашу формулу а = 1, b = 10, c = -24.

получаем D>0, следовательно у нас получится два корня.

Рассмотрим пример где D=0, при этом условии должен получится один корень.

25x ² — 30x + 9 = 0

Рассмотрим пример где D

2x ² + 3x + 4 = 0

Число, стоящее под знаком корня (дискриминант) отрицательное, ответ запишем так: уравнение не имеет действительных корней.

Решение неполных квадратных уравнений

Квадратное уравнение ax ² + bx + c = 0 называют неполным, если хотя бы один из коэффициентов b или c равен нулю. Неполное квадратное уравнение, есть уравнение одного из следующих видов:

ax ² = 0,

ax ² + c = 0, c ≠ 0,

ax ² + bx = 0, b ≠ 0.

Рассмотрим несколько примеров, решим уравнение

Разделив обе части уравнения на 5, получим уравнение х ² = 0, в ответе будет один корень х = 0.

Рассмотрим уравнение вида

3х ² — 27 = 0

Разделив обе части на 3, получим уравнение х ² — 9 = 0, или его можно записать х ² = 9, в ответе будет два корня х = 3 и х = -3.

Рассмотрим уравнение вида

2х ² + 7 = 0

Разделив обе части на 2, получим уравнение х ² = -7/2. Это уравнение действительных корней не имеет, так как х ² ≥ 0 для любого действительного числа х .

Рассмотрим уравнение вида

3х ² + 5х = 0

Разложив левую часть уравнения на множители, получим х (3х + 5) = 0, в ответе будет два корня х = 0, х =-5/3.

Самое главное при решении квадратных уравнений, привести квадратное уравнение к стандартному виду, выучить наизусть формулу корней квадратного уравнения общего вида и не запутаться в знаках.

2 + j * w + k равный 0, где «i» и «j» — первый и второй коэффициент соответственно, «k» — константа, которую иногда именуют «свободным членом», а «w» — переменная. Его корнями окажутся все значения переменной, при которых оно превращается в тождество. Такое равенство допустимо переписать, как произведение i, (w — w1) и (w — w2) равное 0. В этом случае очевидно, что если коэффициент «i» не обращается в ноль, то функция в левой части станет нулевой только в случае, если x принимает значение w1 или w2. Эти значения являются результатом приравнивания многочлена к нулю.

Для нахождения значения переменной, при котором квадратный многочлен обращается в ноль, используется вспомогательная конструкция, построенная на его коэффициентах и названная дискриминантом. Эта конструкция рассчитывается согласно формуле D равняется j * j — 4 * i * k. Зачем она используется?

Она говорит, имеются ли действительные результаты.
Она помогает их высчитать.

Как это значение показывает наличие вещественных корней:

Если оно положительное, то можно найти два корня в области действительных чисел. (1/2).
Нахождение результата в соответствии с формулой (-j +/- d) / (2 * i).
Подстановка полученного результата в исходное равенство для проверки.

Некоторые частные случаи

В зависимости от коэффициентов решение может несколько упрощаться. Очевидно, что если коэффициент перед переменной во второй степени равен нулю, то получается линейное равенство. Когда коэффициент перед переменной в первой степени нулевой, то возможны два варианта:

многочлен раскладывается в разность квадратов при отрицательном свободном члене;

при положительной константе действительных решений найти нельзя.

Если свободный член нулевой, то корни будут {0; -j}

Но есть и другие частные случаи, упрощающие нахождение решения.

Приведенное уравнение второй степени

Приведенным именуют такой квадратный трёхчлен, где коэффициент перед старшим членом — единица. Для данной ситуации применима теорема Виета, гласящая, что сумма корней равняется коэффициенту при переменной в первой степени, помноженному на -1, а произведение соответствует константе «k». 2 + 18 * i * j * k * m.

Допустим, дискриминант превосходит ноль . Это значит, что имеется три корня в области действительных чисел. При нулевом есть кратные решения. Если D

Видео

Наше видео подробно расскажет о вычислении дискриминанта.

Не получили ответ на свой вопрос? Предложите авторам тему.

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

Не имеют корней;
Имеют ровно один корень;
Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .

Дискриминант

Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

Если D
Если D = 0, есть ровно один корень;
Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:
x 2 − 8x + 12 = 0;
5x 2 + 3x + 7 = 0;
x 2 − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

x 2 − 2x − 3 = 0;
15 − 2x − x 2 = 0;
x 2 + 12x + 36 = 0.

Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

x 2 + 9x = 0;
x 2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:

Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
Если же (−c /a )

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:
x 2 − 7x = 0;
5x 2 + 30 = 0;
4x 2 − 9 = 0.

x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.

5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.

Более простым способом. Для этого вынесите z за скобки. Вы получите : z(аz + b) = 0. Множители можно расписать: z=0 и аz + b = 0, так как оба могут давать в результате ноль. В записи аz + b = 0 перенесем второй вправо с другим знаком. Отсюда получаем z1 = 0 и z2 = -b/а. Это и есть корни исходного .

Если же имеется неполное уравнение вида аz² + с = 0, в данном случае находятся простым переносом свободного члена в правую часть уравнения. Также поменяйте при этом его знак. Получится запись аz² = -с. 2 — 4*a*c. Значение D может быть больше, меньше или равно нулю. Если D больше или меньше нуля, то корня будет два, если D=0, то остается всего один корень, более точно можно сказать, что D в этом случае имеет два равнозначных корня. Подставьте известные коэффициенты a, b, c в формулу и вычислите значение.

После того как вы нашли дискриминант, для нахождения х воспользуйтесь формулами: x(1) = (- b+sqrt{D})/2*a; x(2) = (- b-sqrt{D})/2*a, где sqrt — это функция, означающая извлечение квадратного корня из данного числа. Посчитав эти выражения, вы найдете два корня вашего уравнения, после чего уравнение считается решенным.

Если D меньше нуля, то он все равно имеет корни. В школе данный раздел практически не изучается. Студенты вузов должны знать о том, что появляется отрицательное число под корнем. От него избавляются выделяя мнимую часть, то есть -1 под корнем всегда равно мнимому элементу «i», который умножается на корень с таким же положительным числом. К примеру, если D=sqrt{-20}, после преобразования получается D=sqrt{20}*i. После этого преобразования, решение уравнения сводится к такому же нахождению корней, как было описано выше.

Теорема Виета заключается в подборе значений x(1) и x(2). Используется два тождественных уравнения: x(1) + x(2)= -b; x(1)*x(2)=с. Причем очень важным моментом является знак перед коэффициентом b, помните, что этот знак противоположен тому, который стоит в уравнении. С первого взгляда кажется, что посчитать x(1) и x(2) очень просто, но при решении вы столкнетесь с тем, что числа придется именно подбирать.

Элементы решения квадратных уравнений

По правилам математики некоторые можно разложить на множители: (a+x(1))*(b-x(2))=0, если вам посредством формул математики удалось преобразовать подобным образом данное квадратное уравнение, то смело записывайте ответ. x(1) и x(2) будут равны рядом стоящим коэффициентам в скобках, но с противоположным знаком.

Также не стоит забывать про неполные квадратные уравнения. У вас может отсутствовать какое-то из слагаемых, если это так, то все его коэффициенты просто равны нулю. 2 или x ничего не стоит, то коэффициенты а и b равны 1.

Квадратные трехчлены и параметры

Вводные замечания и простейшие примеры
Пример 1. При каких значениях a уравнение ax² + 2x + 1 = 0 имеет два различных корня?
Решение.
Данное уравнение является квадратным относительно переменной x при a№ 0 и имеет различные корни, когда его дискриминант
т. е. при a < 1.
Кроме того, при a = 0 получается уравнение 2x + 1 = 0, имеющее один корень.
Таким образом, a О (–Ґ; 0) И (0; 1).
Правило 1. Если коэффициент при x² многочлена второй степени содержит параметр, необходимо разбирать случай, когда он обращается в нуль.
Пример 2. Уравнение ax² + 8x + c = 0 имеет единственный корень, равный 1. Чему равны a и c?
Решение. Начнем решение задачи с особого случая a = 0, уравнение имеет вид 8x + c = 0. Это линейное уравнение имеет решение x₀ = 1 при c = – 8.
При a № 0 квадратное уравнение имеет единственный корень, если
Кроме того, подставив корень x₀ = 1 в уравнение, получим a + 8 + c = 0.
Решая систему двух линейных уравнений, найдем a = c = – 4.
Теорема 1.
Для приведенного квадратного трехчлена y = x² + px + q (при условии p²і 4q)
сумма корней x₁ + x₂ = – p, произведение корней x₁x₂ = q, разность корней равна
а сумма квадратов корней x₁² + x₂² = p² – 2q.
Теорема 2.
Для квадратного трехчлена y = ax² + bx + c с двумя корнями x₁ и x₂ имеет место
разложение ax² + bx + c = a(x – x₁)(x – x₂), для трехчлена с одним корнем x₀ – разложение
ax² + bx + c = a(x – x₀)².
Замечание. Часто про квадратные уравнения с дискриминантом, равным нулю и имеющим, соответственно, один корень, говорят, что оно имеет два совпадающих корня (?). Это связано с разложением многочлена на множители, приведенным в теореме 2. (Правильно говорить и понимать в этом случае нужно «один корень кратности два». – Прим. ред.)
Будем обращать внимание на эту тонкость и выделять случай единственного корня кратности 2.
Пример 3. В уравнении x² + ax + 12 = 0 определить a таким образом, чтобы разность корней уравнения равнялась единице.
Решение. Разность корней
откуда a = ± 7.
Пример 4. При каких a сумма квадратов корней уравнения 2x² + 4x + a = 0 равна 6?
Решение. Запишем уравнение в виде
откуда x₁² + x₂² = 4 – a = 6 и a = – 2.
Пример 5. При всех a решить уравнение ax² – 2x + 4 = 0.
Решение. Если a = 0, то x = 2. Если a № 0, то уравнение становится квадратным. Его дискриминант
равен D = 4 – 16a. Если D < 0, т. е. a > ,
уравнение решений не имеет. Если D = 0, т. е. a = ,
x = 4. Если D > 0, т. е. a < ,
уравнение имеет два корня
Расположение корней квадратного трехчлена
Графиком квадратного уравнения является парабола, а решениями квадратного уравнения – абсциссы точек пересечения этой параболы с осью Ox. Основой решения всех задач этого параграфа является изучение особенностей расположения парабол с заданными свойствами на координатной плоскости.
Пример 6. При каких a корни уравнения x² – 2ax + a² – a – 6 = 0 имеют разные знаки?
Решение (рис. 1).
Квадратное уравнение либо не имеет решений (график – парабола вида D), либо имеет один или два положительных корня (парабола C), либо имеет один иди два отрицательных корня (парабола A), либо имеет корни разных знаков (парабола B).
Легко сообразить, что последний тип парабол, в отличие от прочих, характеризуется тем, что f(0) < 0. Таким образом, f(0) = a² – a – 6 < 0, откуда 0 < a < .
Данное решение допускает обобщение, которое мы сформулируем как следующее правило.
Правило 2. Для того чтобы уравнение ax² + bx + c = 0
имело два разных корня x₁ и x₂ таких, что x₁ < M < x₂, необходимо и достаточно, чтобы a•f(M) < 0.
Пример 7. При каких a уравнение x² – 2ax + a² – a – 6 = 0 имеет два разных корня одного знака?
Решение. Нас интересуют параболы типа A и C (см. рис. 1). Они характеризуются тем, что
откуда a О (– 6; – 2) И (3; + Ґ).
Пример 8. При каких a уравнение x² – 2ax + a² – a – 6 = 0 имеет два разных положительных корня?
Решение. Нас интересуют параболы типа C на рис. 1.
Чтобы уравнение имело корни, потребуем
Так как оба корня уравнения по условию должны быть положительными, то и абсцисса вершины параболы, лежащая между корнями, положительна: x₀ = a > 0.
Ордината вершины f(x₀) < 0 в силу того, что мы потребовали существование корней, поэтому если, кроме того, потребовать выполнение условия f(x₀) > 0, то в силу непрерывности исследуемой функции найдется точка x₁О (0; x₀) такая, что f(x₁) = 0. Очевидно, что это меньший корень уравнения.
Итак, f(0) = a² – a – 6 > 0, и, собирая все условия вместе, получим систему
с решением a О (3; + Ґ).
Пример 9. При каких a уравнение x² – 2ax + a² – a – 6 имеет два разных отрицательных корня?
Решение. Изучив параболы типа A на рис. 1, получим систему
откуда a О (– 6; – 2).
Обобщим решение предыдущих задач в виде следующего правила.
Правило 3. Для того чтобы уравнение ax² + bx + c = 0 имело два разных корня x₁ и x₂, каждый из которых больше (меньше) M, необходимо и достаточно, чтобы
Пример 10. Функция f(x) задается формулой
Найдите все значения параметра a, при которых уравнение f(x) = 0 имеет хотя бы одно решение.
Решение. Все возможные решения данного уравнения получаются как решения квадратного уравнения
x² – (4a + 14)x + 4a² + 33a + 59 = 0
с дополнительным условием, что хотя бы один (очевидно, больший) корень x₂і a.
Естественно, чтобы уравнение имело корни, должно быть = – 5(a + 2) і 0,
откуда a Ј – 2.
Графиком левой части выделенного уравнения является парабола, абсцисса вершины которой равна x₀ = 2a + 7. Решение задачи дают два типа парабол (рис. 2).
A: x₀і a, откуда a і – 7. В этом случае больший корень многочлена x₂і x₀і a.
B: x₀ < a, f(a) Ј 0, откуда .
В этом случае также больший корень многочлена x₂і a.
Окончательно .

Три решения одного неравенства
Пример 11. Найти все значения параметра a, при которых неравенство x² – 2ax + a² + 2a – 3 > 0
выполняется:
1) при всех значениях x;
2) при всех положительных значениях x;
3) при всех значениях x О [– 1; 1].
Решение.
Первый способ.
1) Очевидно данное неравенство выполняется при всех x, когда дискриминант отрицателен, т. е.
= a² – (a² + 2a – 3) = – 2a + 3 < 0,
откуда a >.
2) Чтобы лучше понять то, что требуется в условии задачи, применим простой прием: на координатной плоскости нарисуем какие-нибудь параболы, а потом возьмем и закроем левую относительно оси Oy полуплоскость. Та часть параболы, которая останется видимой, должна быть выше оси Ox.
Условие задачи выполняется в двух случаях (см. рис. 3):
A: график функции y = x² – 2ax + a² + 2a – 3 лежит выше оси Ox, т. е. D < 0, откуда a > ;
B: оба корня (может быть, один, но двукратный) уравнения x² – 2ax + a² + 2a – 3 = 0 находятся левее начала координат. По правилу 3 это условие эквивалентно системе неравенств D і 0, x₀Ј 0 и f(0) і 0.
Однако при решении данной системы первое неравенство можно опустить, так как если даже какое-то значение a не удовлетворяет условию D і 0, то оно автоматически попадает в решение пункта A. Таким образом, решаем систему

откуда a Ј – 3.
Объединяя решения пунктов A и B, получим
ответ:
3) Условие задачи выполняется в трех случаях (см. рис. 4):
A: график функции y = x² – 2ax + a² + 2a – 3 лежит выше оси Ox, т. е. D < 0, откуда a > ;
B: оба корня (может быть, один кратности 2) уравнения x² – 2ax + a² + 2a – 3 = 0 находятся левее – 1. Это условие эквивалентно, как мы знаем из правила 3, системе неравенств D і 0, x₀ < – 1, f(– 1) > 0;
C: оба корня уравнения x² – 2ax + a² + 2a – 3 = 0 находятся правее 1.
Это условие эквивалентно D і 0, x₀ > 1, f(1) > 0.
Однако в пунктах B и C, также как и в решении предыдущей задачи, неравенство, связанное с дискриминантом, можно опустить.
Соответственно получаем две системы неравенств
Рассмотрев все случаи, получим результат: a >
в пункте
в C.
Ответ задачи – объединение этих трех множеств.
Второй способ. Для того чтобы выполнялось условие каждого из трех пунктов задачи, наименьшее значение функции
y = x² – 2ax + a² + 2a – 3 на каждом из соответствующих промежутков должно быть положительно.
1) Вершина параболы y = x² – 2ax + a² + 2a – 3 находится в точке (a; 2a – 3), поэтому наименьшее значение функции на всей числовой прямой равно 2a – 3, и a > .
2) на полуоси xі 0 наименьшее значение функции равно f(0) = a² + 2a – 3, если a < 0, и f(a) = 2a – 3, если a і 0. Разбирая оба случая, получим
3) Наименьшее на отрезке [– 1; 1] значение функции равно
Поскольку наименьшее значение должно быть положительно, получаем системы неравенств
Решение этих трех систем – множество
Третий способ. 1) Вершина параболы y = x² – 2ax + a² + 2a – 3
находится в точке (a; 2a – 3). Нарисуем на координатной плоскости множество, которое образуют вершины всех парабол при различных a (рис. 5).
Это – прямая y = 2x – 3. Напомним, что каждой точке этой прямой соответствует свое значение параметра, и из каждой точки этой прямой «выходит» парабола, соответствующая данному значению параметра. Параболы, целиком находящиеся над осью Ox, характеризуются условием 2a – 3 > 0.
2) Решениями этого пункта являются все решения первого пункта, и, кроме того, параболы, для которых a – отрицательны, и f(0) = a² + 2a – 3 і 0.
3) Из рис. 5 видно, что нас интересуют параболы, для которых либо a отрицательно и f(– 1) = a² + 4a – 2 > 0,
либо a положительно и f(1) = a² – 2 > 0.
Уравнения и неравенства, сводящиеся к квадратным
Пример 12. При каких значениях a уравнение 2x⁴ – 2ax² + a² – 2 = 0 не имеет решений?
Решение. Сделав замену y = x², получим квадратное уравнение f(y) = 2y² – 2ay + a² – 2 = 0.
Полученное уравнение не имеет решения, когда D < 0. Кроме того, первоначальное уравнение не имеет решений, когда корни уравнения f(y) = 0 отрицательны.
Эти условия могут быть записаны в виде совокупности
откуда
Пример 13. При каждом значении параметра a решить уравнение cos x sin 2x = asin 3x.
Решение. Так как 2cos x sin 2x = sin x + sin 3x и sin 3x = 3sin x – 4sin³ x,
то уравнение запишется в виде sin x (sin² x (4a – 2) – (3a – 2)) = 0.
Отсюда получаем решения x = pn, n О Z при любом a. Уравнение
имеет решения
не совпадающие с решениями первого уравнения, только при условии
Последние ограничения эквивалентны
Ответ: x = pn, n О Z при любом a; кроме того,
Пример 14. Найти все значения параметра a, при каждом из которых неравенство
a² + 2a – sin² x – 2acos x > 2 выполняется для любого числа x.
Решение. Преобразуем неравенство к виду cos² x – 2acos x + a² + 2a – 3 > 0
и сделаем замену t = cos x. Важно заметить, что параметр t пробегает значения от – 1 до 1, поэтому задача переформулируется в таком виде: найти все a такие, что
t² – 2at + a² + 2a – 3 > 0
выполняется при всех t О [– 1; 1]. Эту задачу мы уже решили ранее.
Пример 15. Определить, при каких значениях a уравнение log₃ (9^x + 9a³) = x имеет решения, и найти их.
Решение. Преобразуем уравнение к виду 9^x – 3^x + 9a³ = 0
и, сделав замену y = 3^x, получим y² – y + 9a³ = 0.
В случае, когда дискриминант отрицательный, уравнение решений не имеет. Когда дискриминант
D = 1 – 36a³ = 0, уравнение имеет единственный корень ,
и x = – log₃ 2. Наконец, когда дискриминант положительный, т. е. ,
исходное уравнение имеет один корень ,
а если, кроме того, выражение 1 – положительно,
то уравнение имеет еще второй корень .
Итак, окончательно получаем
,
решений нет при остальных a.
Пример 16. Для каждого значения параметра a решить уравнение sin⁴ x + cos⁴ x + sin ²x + a = 0.
Решение. Так как
уравнение перепишем в виде sin² x – 2sin x – 2a – 2 = 0.
Пусть y = sin 2x, тогда y² – 2y – 2a – 2 = 0 (| y | Ј 1).
График функции, стоящей в левой части уравнения, – парабола с вершиной, абсцисса которой y₀ = 1; значение функции в точке y = – 1 равно 1 – 2a; дискриминант уравнения равен 8a + 12. Это означает, что больший корень y₂ уравнения y² – 2y – 2a – 2 = 0, даже если он существует, больше 1, и соответствующее уравнение sin 2x = y₂ решений не имеет.
Случай 1. если дискриминант отрицательный, т. е. a < – ,
уравнение решений не имеет.
Случай 2. Если дискриминант равен
получаем уравнение
Случай 3. Если дискриминант больше 0, т. е.
и, кроме того, f(– 1) > 0, то уравнение y² – 2y – 2a – 2 = 0 имеет корень
лежащий между – 1 и 1. Соответствующее уравнение – имеет решения.
Случай 4. Если f(– 1) = 0, т. е. получаем уравнение
Случай 5. Если дискриминант больше 0, т. е. и, кроме того, f(– 1) < 0, то уравнение y² – 2y – 2a – 2 = 0 имеет корни
а уравнения не имеют решений.
Ответ: если то решений нет;
если
если
если
(Случаи отдельно выделять не следует:

описывает все возможные решения. – Прим. ред.)
Задачи для самостоятельного решения
1. При каких значениях a уравнение ax² – 4x + 5 = 0 не имеет корней?
2. При каких значениях a уравнение x² – 2ax – 1 = 0 имеет два различных корня?
3. При каких значениях a уравнение 2x² + (3a + 1)x + a² + a + 2 = 0 имеет хотя бы один корень?
4. Уравнение ax² + bx + 5 = 0 имеет единственный корень, равный 1. Чему равны a и b?
5. При каких значениях параметра a корни квадратного уравнения 5x² – 7x + a = 0 относятся как 2 к 5?
6. В уравнении ax² + 8x + 3 = 0 определить a таким образом, чтобы разность корней уравнения равнялась единице.
7. При каких a сумма квадратов корней уравнения x² – 2ax + 2(a + 1) = 0 равна 20?
8. При каких b и c уравнение c + bx – 2x² = 0 имеет один положительный и один отрицательный корень?
9. Найти все значения параметра a, при которых один корень уравнения x² – (a + 1)x + 2 = 0 больше a, а другой меньше a.
10. Найти все значения параметра a, при которых уравнение x² + (a + 1)x + 2 = 0 имеет два разных корня одного знака.
11. При каких значениях a все получающиеся корни уравнения (a – 3)x² – 2ax + 6a = 0 положительны?
12. При каких a все получающиеся корни уравнения (1 + a)x² – 3ax + 4a = 0 больше 1?
13. Найти все значения параметра a, для которых оба разных корня уравнения x² + x + a = 0 будут больше, чем a.
14. При каких значениях a оба корня уравнения 4x² – 2x + a = 0 заключены между – 1 и 1?
15. При каких значениях a уравнение x² + 2(a – 1)x + a + 5 = 0 имеет хотя бы один положительный корень?
16. Функция f(x) задается формулой
Найдите все значения параметра a, при которых уравнение f(x) = 0 имеет хотя бы одно решение.
17. При каких a неравенство (a² – 1)x² + 2(a – 1)x + 2 > 0 верно для всех x?
18. При каких значениях параметра a неравенство ax² + 2x > 1 – 3a справедливо для всех положительных x?
19. При каких значениях a уравнение x⁴ + (1 – 2a)x² + a² – 1 = 0 не имеет решений?
20. При каких значениях параметра a уравнение 2x⁴ – 2ax² + a2 – 2 = 0 имеет одно или два решения?
21. При каждом значении a решить уравнение acos x cos 2x = cos 3x.
22. Найти все значения параметра a, при каждом из которых неравенство cos² x + 2asin x – 2a < a² – 4 выполняется для любого числа x.
23. При всех a решить уравнение log₂ (4^x + a) = x.
24. При каждом значении параметра a решить уравнение sin² x + asin² 2x = sin .
Ответы.
1.2: Свойство извлечения квадратного корня, завершение квадрата и квадратичная формула
Последнее обновление
Сохранить как PDF
Идентификатор страницы
38237
Решение квадратных уравнений с помощью свойства квадратного корня 9{ 2 } + b x + c = 0\), где \(a, b\) и \(c\) – действительные числа, а \(a ≠ 0\).
Квадратные уравнения могут иметь два действительных решения, одно действительное решение или не иметь действительного решения — в этом случае будет два комплексных решения.
Рассмотрим несколько определений, относящихся к комплексным числам:
Комплексное число — это число в форме \(a+bi\), где \(a\) и \(b\) — действительные числа. Действительная часть равна \(a\), а мнимая часть равна \(bi\).
Воображаемая единица 9{ 2 } — 9 & = 0 \\ ( 2 x + 3 ) ( 2 x — 3 ) & = 0 \end{aligned}\)
\(\begin{array} { c } { 2 x + 3 = 0 \quad \text { или }\quad 2 x — 3 = 0 } \\ { 2 x = — 3 \quad \quad\:\:\:2 x = 3 } \\ { x = — \frac { 3 } { 2 } \quad\quad\:\:\:\: x = \frac { 3 } { 2 } } \end{array}\)
Набор решений \( \Big\{ ± \dfrac{ 3}{2}\Большой\}\). Здесь мы используем \(±\) для записи двух решений в более компактной форме.
Альтернативный метод, который можно использовать для более простого решения этого уравнения, состоит в том, чтобы сначала выделить \(x^{2}\), а затем извлечь квадратный корень из обеих частей уравнения. Помимо простоты, этот метод позволяет решать уравнения, не учитывающие фактор. Продолжая приведенный выше пример, чтобы проиллюстрировать этот альтернативный подход: 9{ 2 } & = \frac { 8 } { 9 } \\
x & = \pm \sqrt { \frac { 8 } { 9 } } && \text{Квадратный корень с обеих сторон. Помните } \pm \text{ !!!}\\
& = \pm \frac { 2 \sqrt { 2 } } { 3 } && \text{Упрощение. } \quad \textbf{Набор решений: } \Big\{ ± \frac { 2 \sqrt { 2 } } { 3 } \Big\} \end{aligned}\)
Полноту этих двух решений можно проверить .
Проверка \(x = — \frac { 2 \sqrt { 2 } } { 3 }\) Проверка \(x = \frac { 2 \sqrt { 2 } } { 3 }\) 9{ 2 } & = -25 && \text{Изолировать квадрат члена}\\
x & = \pm \sqrt { — 25 } && \text{Квадратный корень с обеих сторон. Помните } \pm \text{ !!!}\\
& = \pm \sqrt {- 1} \cdot \sqrt{25} &&\text{Упрощение. } \\
& = \pm i \cdot 5 \\
& = \pm 5 i &&\textbf{Набор решений: } \{ ± 5i \}\end{aligned}\)
Свойство Square Root также может использоваться в уравнениях, которые имеют выражение в квадрате, а не просто переменную в квадрате. 9{ 2 } & = 9 && \text {Можно использовать свойство Square Root. Член в квадрате уже выделен.}\\
x + 5 & = \pm \sqrt { 9 } && \text{Квадратный корень с обеих сторон. Помните } \pm \text{ !!!}\\
x + 5 & = \pm 3 &&\text{Упрощение. }\\
x & = — 5 \pm 3 \end{aligned}\)
Теперь разделите «плюс-минус» на два уравнения и решите каждое по отдельности.
\(\begin{array} {l} { x = — 5 + 3 \quad\text { or } \quad x = — 5 — 3 } \\ { x = — 2 \quad\quad\quad \quad \quad x = — 8 } \\ 9{ 2 } & = \frac { 5 } { 2 } \\
x — 2 & = \pm \sqrt { \frac { 5 } { 2 } } && \text{Квадратный корень с обеих сторон. Помните } \pm \text{ !!!}\\
x & = 2 \pm \frac { \sqrt { 5 } } { \sqrt { 2 } } \cdot \color{Cerulean}{ \frac { \sqrt { 2 } } { \sqrt { 2 } } } &&\text{Обоснуйте знаменатель.} \\
x & = 2 \pm \frac { \sqrt { 10 } } { 2 } &&\text{Упростите. }\\
x & = \frac { 4 \pm \sqrt { 10 } } { 2 } &&\quad \textbf{Набор решений: } \Bigg\{ \frac { 4 — \sqrt { 10 } } { 2 } , \frac { 4 + \sqrt { 10 } } { 2 }\Bigg\} \end{aligned}\) 92=-\dfrac{4}{5} & \text{Выделение квадрата члена} \\
x=\pm \sqrt{\dfrac{4}{5}} && x=\pm \sqrt{\dfrac{ -4}{5}} & \text{Квадратный корень с обеих сторон. Помните } \pm \text{ !!!}\\
x=\pm \dfrac {\sqrt{4}} {\sqrt{5}} && x=\pm \dfrac {\sqrt{-4}} {\sqrt{5}} & \text{Упрощение. } \\
x=\pm \dfrac {2} {\sqrt{5}} \dfrac{\sqrt{5}}{\sqrt{5}} && x=\pm \dfrac {2i} {\sqrt{ 5}} \dfrac{\sqrt{5}}{\sqrt{5}} & \\
x=\pm \dfrac {2\sqrt{5}}{5} && x=\pm \dfrac {2i\ кврт{5}}{5} и 9{ 2 } + 9 = 0\)
Ответить
а) \( \pm \dfrac { \sqrt { 6 } } { 2 } i \) б) \(x=4±\sqrt{5}\) c) \(\dfrac { 1 }{ 3 } \pm \dfrac { \sqrt{2}}{2} i\)
Завершение квадрата
Не все квадратные уравнения можно разложить на множители или решить в исходной форме, используя свойство квадратного корня. В этих случаях мы можем использовать метод решения квадратное уравнение , известное как , завершающее квадрат . Используя этот метод, мы добавляем или вычитаем члены к обеим сторонам уравнения, пока у нас не получится идеальный квадратный трехчлен с одной стороны от знака равенства. Затем мы применяем свойство квадратного корня. Чтобы завершить квадрат, старший коэффициент \(a\) должен быть равен \(1\). Если это не так, то разделите все уравнение на \(a\), прежде чем начинать полный процесс возведения в квадрат. Затем мы можем использовать следующие процедуры для решения квадратного уравнения путем завершения квадрата. 92\) ) создадут трехчлен, который является идеальным квадратным биномом.
Добавьте квадрат половины коэффициента \(x\) к обеим частям уравнения.
Преобразуйте полученный трехчлен в биномиальный квадрат.
Используйте свойство Square Root, чтобы найти \(x\). Помните знак \(±\) !!
Этот метод можно использовать для решения ЛЮБОГО квадратного уравнения, тогда как факторинг работает только в некоторых случаях. {2} + 3x+4=0\). 9{ 2 } & = \frac { — 7 } { 4 } && \text{Решить, используя свойство квадратного корня } \\
x + \frac { 3 } { 2 } & = \pm \sqrt { \frac { — 1 \cdot 7 } { 4 } } \\
x + \frac { 3 } { 2 } & = \pm \frac { i \sqrt { 7 } } { 2 } \\
x & = — \ frac { 3 } { 2 } \pm \frac { \sqrt { 7 } } { 2 } i &&\quad \textbf{Набор решений: } \Bigg\{ — \frac { 3 } { 2 } \pm \frac { \sqrt { 7 } } { 2 } i \Bigg\}
\end{aligned}\)
До сих пор во всех примерах старший коэффициент был равен \(1\). Если это не так, удалите его. Это можно сделать, разделив обе стороны знака равенства на старший коэффициент перед завершением квадрата. 92 & = \frac { -5 } { 3 } \\
x -2 & = \pm \sqrt { \frac { -5 } { 3 } } && \text{Решите, используя свойство квадратного корня } \\
x & = 2 \pm \frac { i \sqrt { 5 } } { \sqrt{3} } \cdot \frac{\sqrt{3}}{\sqrt{3}}\\
x & = \frac { 6 } { 3 } \pm \frac { i\sqrt { 15 } } { 3 }
&&\quad \textbf{Набор решений: } \Bigg\{ \frac { 6 \pm i\sqrt { 15 } } { 3 } \Bigg\}\\
\end{aligned}\)
Пример \(\PageIndex{12}\):
Решите, заполнив квадрат: \(2 x ^ { 2 } + 5 x — 1 = 0 \). 9{ 2 } & = \frac { 33 } { 16 } \\
x + \frac { 5 } { 4 } & = \pm \sqrt { \frac { 33 } { 16 } } && \text{Решите, используя квадрат корневое свойство } \\
x + \frac { 5 } { 4 } & = \pm \frac { \sqrt { 33 } } { 4 } \\
x & = — \ frac { 5 } { 4 } \pm \ frac { \sqrt { 33 } } { 4 }
&&\quad \textbf{Набор решений: } \Bigg\{ \frac { — 5 \pm \sqrt { 33 } } { 4 } \Bigg\}\\
\ end{aligned}\)
Попробуйте \(\PageIndex{13}\)
Решите, заполнив квадрат. 9{ 2 } — 2 х + 1 = 0\)
Ответить
а) \(x=3±\sqrt{22}\) б) \(x = 1 \pm 3 \sqrt { 2 }\) c) \(x = \frac { 1 } { 3 } \pm \frac { \sqrt { 2 } } { 3 } i\)
Квадратная формула
Четвертый метод решения квадратного уравнения заключается в использовании квадратной формулы 9{2}-4(\color{OliveGreen}{2}\color{black}{)}(\color{OliveGreen}{-15}\color{black}{)}}}{2(\color{OliveGreen} {2}\color{black}{)}} \\ &=\frac{7 \pm \sqrt{49+120}}{4} \\
&=\frac{7 \pm \sqrt{169}} {4} \\
&=\frac{7 \pm 13}{4}
\end{aligned}\)
\( \textbf{Набор решений: } \Big\{ -\dfrac{3}{2 }, 5 \Big\} \text{ потому что } x = \dfrac{7-13}{4}=\dfrac{-6}{4}=-\dfrac{3}{2} \text{ и } x =\dfrac{7+13}{4} = \dfrac{20}{4} =5\)
Пример \(\PageIndex{15}\): 9{2}-4(\color{OliveGreen}{3}\color{black}{)}(\color{OliveGreen}{-2}\color{black}{)}}}{2(\color{OliveGreen} {3}\color{black}{)}} \\ &=\frac{-6 \pm \sqrt{36+24}}{6} \\ &=\frac{-6 \pm \sqrt{60} {6} \\
&= \frac{-6 \pm 2 \sqrt{15}}{6} = \frac{\cancel{2}(-3 \pm \sqrt{15})}{\cancel {6}} = \frac{-3 \pm \sqrt{15}}{3} \\
&\qquad\qquad\qquad \text{ или } =\frac{-6}{6} \pm \frac {2\sqrt{15}}{6} =-1 \pm \frac{\sqrt{15}}{3}
\end{aligned}\)
Набор решений можно записать двумя способами: \( \Big\{ \dfrac{-3 \pm \sqrt{15}}{3} \Big\} \) или \( \Big\{ -1 \pm \dfrac{\sqrt{15}}{3} \ Большой\}\) 9{2}-4 (1)(4)}}{2(1)} \\
&=\frac{-2 \pm \sqrt{-12}}{2} \\
&=\frac{- 2 \pm 2 i \sqrt{3}}{2} \\
&=-1 \pm i \sqrt{3} & \text{Набор решений: } \{2,-1 \pm i \sqrt{3 }\}
\end{aligned} }
\end{array}\)
Используя этот метод, мы смогли получить набор всех трех корней \(\{2,-1 \pm i \sqrt{3 }\}\), одно действительное и два комплексных.
Иногда разложение на множители приводит к квадратичному коэффициенту, который необходимо решить с помощью квадратичной формулы или завершить квадрат. 92-4(3)(15)=-80\) Будет два комплексных решения.

Наверх
Была ли эта статья полезной?
Тип изделия
Раздел или Страница
Показать страницу TOC
да
Теги
На этой странице нет тегов.
Корни квадратных уравнений и их связь со значениями параметров а, b и с, а также кубическое расширение
Корни квадратных уравнений и их связь со значениями параметров а, b и с, а также кубическое расширение
Корни квадратных уравнений, их связь со значениями параметров и кубическое расширение
Автор: Эл Бирнс
В этой статье мы попытаемся изучить некоторые закономерности для корней и то, как эти корни связаны со значениями параметров a, b и c в квадратном уравнении. Затем будут предложены расширения для дальнейших исследований с использованием этих наблюдений.
Для начала рассмотрим уравнение x² + bx + 1 = 0 в плоскости xb. График этого уравнения показан ниже; горизонтальная ось — это ось x, а вертикальная ось — ось b:
Если изобразить различные значения параметра b в виде линий на плоскости xb, то можно получить интересную информацию о количестве действительных корней квадратного уравнения x² + bx + 1 = 0 и информацию о знаках этих корней. Например, если мы выберем b = 2, уравнение будет иметь единственный отрицательный корень:
.
х² + 2х + 1 = 0; какие значения x удовлетворяют этому уравнению?
Если мы разложим это квадратное уравнение, мы получим x² + 2x + 1 = (x + 1)² = 0; поэтому у этого квадратного уравнения есть один корень, значение которого x = -1. Но как этот результат соответствует графику x² + bx + 1 = 0. Что еще более важно, можем ли мы разработать шаблон, который поможет улучшить нашу интуицию о числе и знаках корней квадратного уравнения на основе значений a, б и в.
Давайте просто рассмотрим x² + bx + 1 = 0. Мы определили, что когда b имеет значение 2, существует один отрицательный корень со значением x = -1. На плоскости эти два уравнения, изображенные вместе, выглядят так:
Обратите внимание на точку, в которой прямая b = 2 и график квадратного уравнения x² + bx + 1 = 0 касаются друг друга. Графики двух уравнений котангенсивны в одной точке, что очень интересно, учитывая, что при решении приведенного выше уравнения мы нашли единственный корень. Это значение корня, x = -1, также может быть представлено на плоскости как точка касания между линией b = 2 и уравнением x² + bx + 1 = 0 в виде упорядоченной пары (-1, 2).
Итак, наша интуиция может подсказать, что число действительных корней будет соответствовать тому, сколько раз прямая b = a (где a — действительное число) пересекает кривую x² + bx + 1 = 0. Кроме того, значения Координата x пар порядков, обозначающих точки пересечения этих двух кривых, должна указывать значения корней уравнения x² + bx + 1 = 0. Давайте проверим эту интуицию. Рассмотрим квадратное уравнение x² + bx + 1 = 0 и прямую b = 3.
Итак, теперь мы имеем ситуацию, в которой наша интуиция может подсказать, что квадратное уравнение x² + 3x + 1 = 0 имеет два действительных корня, каждый из которых имеет отрицательное значение. Используя график, давайте сделаем первоначальное предположение о значениях корней: я бы предположил, что x = -2,62 и x = -0,382. Эти предположения были получены с помощью графического калькулятора:
В качестве проверки воспользуемся более традиционным методом получения значения корней квадратного уравнения, более «устойчивым» к простой факторизации, квадратной формулой:
х = (-3+√(5)/2) и (-3-√(5)/2)
Действительно, после вычислений эти значения совпадают с теми значениями, которые мы предсказали для корней! При рассмотрении других значений для линии b = a мы можем продолжить укреплять наши предположения. Рассмотрим прямую b=0 и квадратное уравнение x² + bx + 1 = 0. Основываясь на графике этих двух кривых на плоскости и точках, в которых они совпадают, какие предположения мы могли бы сделать о числе и знаках вещественной корни уравнений?
Я рискну предположить, что квадратное уравнение x² + x + 1 = 0 не имеет действительных корней, в значительной степени потому, что кривые x² + bx + 1 = 0 и b = a; 2 > a > -2 не совпадают в диапазоне 2 > a > -2. На самом деле, как только мы воспользуемся квадратичной формулой, мы увидим, что x² + 1x + 1 = 0 не имеет действительных корней:
х = (-1+√(-3)/2) и (-3 — √(-3)/2). Опять же, наша интуиция была верна!
Давайте проверим еще два значения b, чтобы завершить нашу стратегию наблюдения за значениями и количеством действительных корней квадратных уравнений. Последние два значения b, которые мы нанесем на график, будут линиями b = -2 и b = -3.
Линия b = -2 обозначена красным цветом, а линия b = -3 обозначена синим цветом. Действительно, при сравнении графика и развитой нами интуиции мы видим, что квадратное уравнение x² + -2x + 1 = 0 и уравнение x² + -3x + 1 = 0 имеют один положительный действительный корень и два положительных действительных корня соответственно. Алгебраическое обоснование см. ниже:
х² + -2х + 1 = (х — 1)² = 0; реальный корень: х = 1
Использование квадратичной формулы для получения корней для x² + -3x + 1 = 0:
x = (3+√(5)/2) и (3 — √(5)/2), что указывает на наличие двух положительных действительных корней.
Можно ли распространить эти наблюдения на уравнения высших степеней? Рассмотрим кубическое выражение следующего вида:
В данном исследовании нас будет особенно интересовать случай, когда b = -2.
Используя интуицию, которую мы сформировали в отношении того, что пересечение этих двух кривых может сказать нам о действительных корнях квадратного уравнения, давайте расширим свое мышление до графика кубического выражения, показанного выше x ³ + -2x² + x + 1 = 0. Моя первоначальная догадка заключалась бы в том, что выражение имеет 1 действительный корень со значением x пары порядка, которая описывает точку, в которой линия b = -2 и кривая x ³ + -2x² + x + 1 = 0 совпадают. Используя Graphing Calculator, мы можем определить значение этой точки с относительной точностью:
Таким образом, значение этого корня приблизительно равно -0,465571. Давайте проверим с помощью алгебры:
х ³ + -2x² + x + 1 = 0
х (х² — 2х + 1) = -1
х (х — 1)² = -1
х(х — 1)² — 1 = 0
Пусть х = -0,465571
(-. 465571)((-.465571) — 1)² — 1 = 0
После завершения вычислений мы видим, что с учетом ошибки, вызванной округлением, значение -0,465571 удовлетворяет уравнению и, следовательно, очень близко к значению фактического действительного корня кубического уравнения!

Вернуться к началу
Вернуться на мою студенческую страницу
квадратных уравнений и функций | Алгебра 1
Дополнительные темы
по квадратным уравнениям и функциям
Популярные учебные пособия
по квадратным уравнениям и функциям
Как решить квадратное уравнение с двумя решениями с помощью графика?
Одним из многих способов решения квадратного уравнения является построение его графика и определение его пересечения с осью x. Следуйте инструкциям, поскольку этот учебник покажет вам, как построить график квадратного уравнения, чтобы найти решение. Проверьте это!
Как найти ось симметрии квадратичной функции?
Ось симметрии — это вертикальная линия, проходящая через вершину квадратного уравнения. Есть даже формула, которая поможет найти его! В этом уроке вы увидите, как найти ось симметрии для заданного квадратного уравнения.
Как найти вершину квадратичной функции?
Вершина квадратного уравнения — это точка минимума или максимума уравнения. Знаете ли вы, что можно использовать формулу для оси симметрии, чтобы найти вершину квадратного уравнения? Посмотрите этот урок и узнайте, как это делается!
Как составить таблицу квадратичной функции?
Когда вы пытаетесь построить график квадратного уравнения, очень полезно составить таблицу значений. Чтобы выяснить, какие значения x использовать в таблице, сначала найдите вершину квадратного уравнения. Таким образом, вы можете выбрать значения с любой стороны, чтобы увидеть, что делает график по обе стороны от вершины. Чтобы узнать, как составить таблицу значений для квадратного уравнения, ознакомьтесь с этим руководством!
Как найти нули квадратичной функции на графике?
Нули квадратного уравнения — это точки, в которых график квадратного уравнения пересекает ось x. В этом уроке вы увидите, как использовать график квадратного уравнения, чтобы найти нули уравнения. Взглянем!
Как решить квадратное уравнение с помощью факторинга?
Одним из многих способов решения квадратного уравнения является его разложение на множители. В этом уроке вы увидите, как факторизовать квадратное уравнение, используя метод факторинга «догадка и проверка». Затем используйте свойство нулевого произведения, чтобы найти решение!
Как решить квадратное уравнение, используя квадратную формулу?
Одним из многих способов решения квадратного уравнения является использование квадратной формулы. Квадратичная формула обычно выбирается, когда другие методы не работают или их трудно использовать. В этом уроке вы узнаете, как решить квадратное уравнение с помощью квадратной формулы!
Как решить квадратное уравнение, составив квадрат?
Одним из многих способов решения квадратного уравнения является завершение квадрата. В этом методе вы хотите превратить одну часть уравнения в идеальный квадратный трехчлен. В этом учебном пособии вы пошагово пошагово решаете квадратное уравнение, заполняя квадрат. Проверьте это!
Как построить график квадратичной функции?
Когда вы пытаетесь построить график квадратного уравнения, очень полезно составить таблицу значений. Прежде чем составить таблицу, сначала найдите вершину квадратного уравнения. Таким образом, вы можете выбрать значения с любой стороны, чтобы увидеть, что делает график по обе стороны от вершины. Посмотрите этот урок, чтобы узнать, как построить график квадратного уравнения!
Как найти значения a, b и c квадратичной функции?
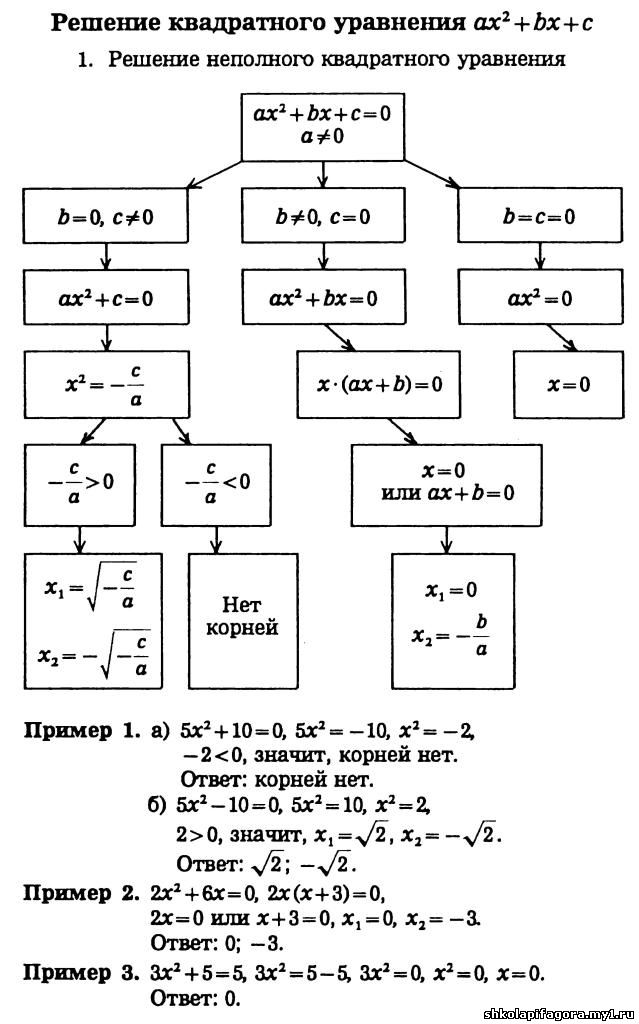Когда вы имеете дело с квадратными уравнениями, очень полезно определить a, b и c. Эти значения используются для нахождения оси симметрии, дискриминанта и даже корней по квадратичной формуле. Несомненно, важно знать, как идентифицировать эти значения в квадратном уравнении. Этот урок покажет вам, как!
Как построить график квадратного уравнения без решения?
Одним из многих способов решения квадратного уравнения является построение его графика и определение его пересечения с осью x. Следуйте инструкциям, поскольку этот учебник покажет вам, как построить график квадратного уравнения, чтобы найти решение. Проверьте это!
Как найти дискриминант квадратного уравнения с двумя решениями?
В квадратном уравнении дискриминант помогает определить количество действительных решений квадратного уравнения. В этом уроке вы узнаете, как найти дискриминант квадратного уравнения и использовать его для определения количества решений!
Как использовать дискриминант для определения количества решений квадратного уравнения?
В квадратном уравнении дискриминант помогает определить, сколько действительных решений имеет квадратное уравнение. В этом уроке вы узнаете, как найти дискриминант квадратного уравнения и использовать его для определения количества решений!
Как найти дискриминант квадратного уравнения с 1 решением?
В квадратном уравнении дискриминант помогает определить количество действительных решений квадратного уравнения. В этом уроке вы узнаете, как найти дискриминант квадратного уравнения и использовать его для определения количества решений!
Как найти дискриминант квадратного уравнения без решений?
В квадратном уравнении дискриминант помогает определить количество действительных решений квадратного уравнения. В этом уроке вы узнаете, как найти дискриминант квадратного уравнения и использовать его для определения количества решений!
Как определить, будет ли вершина квадратичной функции максимумом или минимумом?
Вершина квадратного уравнения является максимумом или минимумом функции. Но как узнать, будет ли это максимум или минимум? Посмотрите этот урок и найдите ответ на этот вопрос!
Как определить, что квадратное уравнение не имеет реальных решений, используя квадратную формулу?
Одним из многих способов решения квадратного уравнения является использование квадратной формулы. Квадратичная формула обычно выбирается, когда другие методы не работают или их трудно использовать. В этом уроке вы узнаете, как решить квадратное уравнение с помощью квадратной формулы!
Как использовать метод квадратного корня для решения квадратного уравнения с двумя решениями?
Одним из многих способов решения квадратного уравнения является использование метода квадратного корня. Следуйте этому руководству и узнайте, как использовать метод квадратного корня для решения квадратного уравнения. Взглянем!
Как определить, представляет ли график линейную, экспоненциальную или квадратичную функцию?
Графики бывают самых разных форм и размеров. В алгебре чаще всего встречаются три основных типа графиков: линейный, квадратичный и экспоненциальный. Ознакомьтесь с этим руководством и узнайте, как определить, представляет ли график линейную, квадратичную или экспоненциальную функцию!
Как построить график родительской квадратичной функции y=x2?
Имеешь дело с графиками квадратных уравнений? Сначала вы должны узнать о графе родительской функции! Все графики квадратных уравнений начинают выглядеть так до их преобразования. Проверьте это!
Как решить текстовую задачу, разложив квадратное уравнение на множители?
Как решить текстовую задачу с помощью квадратичной формулы?
Когда вы отправляете посылку по почте, вам нужна коробка подходящего размера. Но что делать, если у вас нет коробок? Просто сделайте из картона! Следуйте этому руководству, чтобы увидеть, как математика может помочь вам вычислить размеры коробки, созданной из куска картона!
Что такое вершина квадратичной функции?
Каждое квадратное уравнение имеет либо максимум, либо минимум, а вы знали, что эта точка имеет особое имя? В квадратном уравнении эта точка называется вершиной! Взгляните на вершину квадратного уравнения, просмотрев этот урок.
Что такое ось симметрии квадратичной функции?
Вы когда-нибудь замечали, что левая часть графика квадратного уравнения очень похожа на правую часть графика? На самом деле эти стороны просто зеркальные отражения друг друга! Если бы вы разрезали график квадратного уравнения вертикально пополам в вершине, вы бы получили эти симметричные стороны. Та вертикальная линия, которую вы разрезаете, имеет особое имя. Она называется осью симметрии. Чтобы узнать об оси симметрии, посмотрите этот урок!
Что такое парабола?
Если построить график линейной функции, получится линия. Если вы начертите квадратичную функцию, вы получите то, что называется параболой. Парабола имеет тенденцию выглядеть как улыбка или хмурый взгляд, в зависимости от функции. Посмотрите этот урок и узнайте больше о параболах!
Что такое максимум квадратичной функции?
Когда вы имеете дело с квадратичными функциями, очень вероятно, что вы встретите максимум и минимум. В этом уроке рассматривается максимум квадратичной функции. Проверьте это!
Что такое минимум квадратичной функции?
Когда вы имеете дело с квадратичными функциями, очень вероятно, что вы встретите максимум и минимум. В этом уроке рассматривается минимум квадратичной функции. Проверьте это!
Что такое квадратичная функция?
Вы не можете пройти алгебру, не видя квадратичных функций. Графики квадратичных функций представляют собой параболы; они имеют тенденцию выглядеть как улыбка или хмурый взгляд. В этом уроке вы познакомитесь с квадратичными функциями, посмотрите на их графики и увидите несколько примеров квадратичных функций!
Что такое дискриминант?
В квадратном уравнении дискриминант помогает определить количество действительных решений квадратного уравнения. Выражение, используемое для нахождения дискриминанта, — это выражение, стоящее под радикалом в квадратной формуле! В этом уроке вы познакомитесь с дискриминантом квадратного уравнения!
Что такое квадратное уравнение?
Вы не можете пройти алгебру, не видя квадратных уравнений.
No related posts.