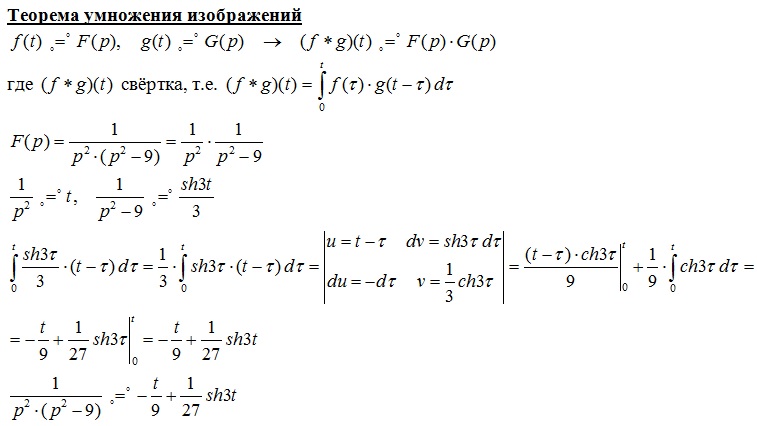04.2. Теорема Чебышева
Закон больших чисел занимал большое место в работах П. Л. Чебышева. Первое доказательство этого закона было дано им в его магистерской диссертации «Опыт элементарного анализа теории вероятностей» (1845 г.). Однако это доказательство касалось частных случаев. Но уже в 1846 г. П. Л. Чебышев нашел более общее элементарное доказательство (на основе рассмотрения экстремальной задачи).
Окончательное разрешение этого вопроса с доказательством закона больших чисел в общем виде было достигнуто П. Л. Чебышевым в 1866 г. в Мемуаре «О средних величинах», где на основе точного установления свойств математических ожиданий П. Л. Чебышев приходит к строгому доказательству закона больших чисел
Теорема Чебышева. Если дисперсии попарно независимых случайНых величин не превосходят данного положительного числа С, тО Вероятность того, что абсолютное отклонение средней арифметической таких величин от средней арифметической их математических ожиданий меньше какого-нибудь данного числа, с возрастанием количества случайных величин становится сколь угодно близкой к единице.
Для доказательства теоремы преобразуем левую часть неравенства Чебышева, приняв , где П — Количество независимых величин X, Y, Z, …, а E — произвольное положительное число. Это позволит заменить условие
Равносильным ему
,
А поэтому неравенство Чебышева примет вид
.
Так как по условию теоремы , то
D(X)+D(Y)+…+D(V) £ NC.
Соответствующая замена правой части усиливает неравенство и дает
.
Этим доказана теорема Чебышева, так как с возрастанием числа N разность становится сколь угодно близкой к единице, т. е. .
Следствие. Полученный в доказанной теореме результат не нарушится, если вместо случайных величин X, Y, …, U, V перейти к случайным величинам
, Имеющим равные математические ожидания а и одинаково ограниченные дисперсии. Такие случайные величины могут, например, выражать независимые результаты по сериям измерений одной и той же величины.
Соответствующая запись
Непосредственно следует из теоремы Чебышева.
Возвращаясь в правой части этого неравенства от C к D(X), будем иметь
.
Пользуясь этим следствием из Теореглы Чебышева, можно доказать теорему Бернулли.
Пусть случайная величина Х представляет число появлений события А в каждом из независимых испытаний, т. е. принимает ЗНачения 1 или 0. Тогда сумма выразится числом Т Появлений события А при П испытаниях, средняя арифметическая такой случайной величины — частостью , ее математическое ожидание — вероятностью Р появления события A в отдельном испытании и дисперсия — произведением
При достаточно большом числе П.
Переходя к пределу при , получаем
Этим доказана как частный случай теоремы Чебышева теорЕМа Бернулли: С вероятностью, сколь угодно близкой к единице, можно утверждать, что при неограниченном возрастании Чисш П неЗАвисимых испытаний частость появления наблюдаемого события как угодно мало отличается от его вероятности в отдельном испытании.
Переход к использованию частичного1) содержания закона больших чисел для решения соответствующих задач требует некоторого предварительного общего разъяснения.
Практика требует, чтобы по интересующим нас событИЯм мы располагали надежными данными о достоверности или невозможности их наступления. Опыт показывает, что при вероятности, близкой к единице, данное событие почти обязательно наступает, а при очень малой вероятности оно практически не имеет места, и всякие расчеты, построенные на возможном его появлении, лишены реального смысла. Но эти соображения не могут найти своего практического приложения, пока они не обоснованы необходимыми цифровыми расчетами. Только тогда высказанный здесь принцип практической уверенности будет полезен в применении к решению практических задач, когда он подкреплен данными надежной оценки. На этом фоне выявляется особая практическая важность закона больших чисел, раскрывающего те условия, при которых вероятность появления события становятся сколь угодно близкой к единице (или к нулю).
Доказанные теоремы и связанные с ними неравенства дают ответы на ряд интересных в этом смысле вопросов: начиная с какого числа испытаний заданная вероятность отклонения будет находиться в требуемых границах; какова граница возможного отклонения при заданных значениях
Эти соображения должны дать учащемуся направление в практически полезном применении предлагаемых здесь примеров и упражнений.
Пример 4. При каком числе независимых испытаний вероятность выполнения неравенства превысит 0.96, если вероятность появления события в отдельном испытании ?
Решение. Условие Р > 0,96 равносильно неравенству
.
Отсюда .
Подстановка значений , и дает
.
Таким образом, требуемое задачей неравенство выполняется при числе независимых испытаний, начиная со 132.
Пример 5. При штамповке пластинок из пластмассы по данным ОТК брак составляет 3%. Найти вероятность того, что при просмотре партии в 1000 пластинок выявится отклонение от установленНОго процента брака меньше чем на 1%.
Решение. Здесь следует определить при , и .
По теореме Бернули искомая вероятность ,
Где .
Таким образом, искомая вероятность Р ³ 0,709.
Пример 6. Партия деталей для оборудования завода распределена по ящикам, имеющим одинаковый вес (нетто). Из каждого ящика на выборку берется по одной детали и определяется ее вес. Известно, что дисперсия по каждому из ящиков не превышает 4. Установить (применяя теорему Чебышева), при каком числе ящиков отклонение среднего выборочного веса дЕТали от общего среднего веса ее менее чем на 0,2 Кг определится вероятностью, ПРевышающей 0,95.
Решение. По условию имеем: , причем здесь С = 4, E = 0,2.
Поэтому число ящиков определится из урАВнЕНия
,
Которое дает 100:N=0,05. Таким образом, П= 2000.
Таким образом, П= 2000.
Упражнения
Применяя теорему Бернулли, решить задачи 1, 2.
1. Вероятность положительного исхода отдельного испытания P=0,8. ОЦЕнить вероятность того, что при 1000 независимых повторных испытаний отклонение частости положительных исходов от вероятности при отдельном испытании по своей абсолютной величине будет меньше 0,05.
Отв.
2. Вероятность наличия зазубрин на металлических брусках, заготовленных для обточки, равна 0,2. Оценить вероятность того, что в партии из 1000 брусков отклонение числа пригодных брусков от 800 не превышает 5%.
Отв.
Применяя Тeopeму Чебышева, решить задачи 3, 4.
3. Для каждой из 1500 независимых случайных величин дисперсия не превышает 3. Оценить вероятность того, что отклонение средней арифметической этих СЛучайных величин от средней арифметической их математических ожиданий не превысит (по своей абсолютной веЛИчине) числа 0,4.
Отв. Р > 0,9875.
4. Известно, что дисперсия каждой из данных независимых случайных величин не превышает 4. Найти то число этих величин, при котором вероятность отклонения их средней арифметической от средней арифметической их математических ожиданий не более чем на 0.25 превысит 0.99.
Отв. N > 6400.
| < Предыдущая | Следующая > |
|---|
9. Закон больших чисел
Следующие утверждения и теоремы составляют содержание группы законов, объединенных общим названием Закон больших чисел.
Лемма 1 (неравенство Маркова)
,
Где М(Х) — математическое ожидание Х.
Следствие 1. Так как события и противоположные, то неравенство Маркова можно записать в виде
.
Пример 9.1. Оценить вероятность того, что в течение ближайшего дня потребность в воде в населенном пункте превысит 150 000 л, если среднесуточная потребность в ней составляет 50 000 л.
Решение. Используя неравенство Маркова в виде , получим .
Ответ: .
Пример 9.2. Среднее число солнечных дней в году для данной местности равно 90. Оценить вероятность того, что в течение года в этой местности будет не более 240 солнечных дней.
Решение. Согласно неравенству , имеем .
Ответ: .
Лемма 2 (неравенство Чебышева).
Для любой случайной величины Х, имеющей конечную дисперсию и любого.
Следствие 2. Для любой случайной величины Х С конечной дисперсией и любого
.
Пример 9.3. Длина изготавливаемых деталей является случайной величиной, среднее значение которой 50 мм. Среднеквадратичное отклонение этой величины равно 0,2 мм. Оценить вероятность того, что отклонение длины изготовленной детали от ее среднего значения по абсолютной величине не превзойдет 0,4 мм.
Решение. Для оценки вероятности используем неравенство Чебышева
,
.
Ответ: .
Пример 9.4. Среднесуточное потребление электроэнергии в населенном пункте равно 20 000 кВт/ч, а среднеквадратичное отклонение — 200 кВт/ч. Какого потребления электроэнергии в этом населенном пункте можно ожидать в ближайшие сутки с вероятностью, не меньшей 0,96?
Решение. Воспользуемся неравенством Чебышева . Подставим в правую часть неравенства вместо величину , сделаем ее большей или равной 0,96:
.
Следовательно, в этом населенном пункте можно ожидать с вероятностью не меньшей 0,96 потребление электроэнергии , т. е. .
Ответ: от 19 000 до 21 000.
Теорема Чебышева. Если последовательность независимых случайных величин с математическими ожиданиями и дисперсиями , ограниченными одной и той же постоянной , то какова бы ни была постоянная
.
При доказательстве предельного равенства используется неравенство
,
Которое вытекает из неравенства Чебышева.
Пример 9.5. За значение некоторой величины принимают среднеарифметическое достаточно большого числа ее измерений. Предполагая, что среднеквадратичное отклонение возможных результатов каждого измерения не превосходит 5 мм, оценить вероятность того, что при 1000 измерений неизвестной величины отклонение принятого значения от истинного по абсолютной величине не превзойдет 0,5 мм.
Предполагая, что среднеквадратичное отклонение возможных результатов каждого измерения не превосходит 5 мм, оценить вероятность того, что при 1000 измерений неизвестной величины отклонение принятого значения от истинного по абсолютной величине не превзойдет 0,5 мм.
Решение. Воспользуемся неравенством
.
По условию , , Итак, искомая вероятность
Ответ:
Частными случаями теоремы Чебышева являются теоремы Бернулли и Пуассона.
Теорема Бернулли. При неограниченном увеличении числа независимых опытов частость появления Некоторого события А сходится по вероятности к его вероятности Р = Р(А):
,
Где — сколь угодно малое положительное число.
При доказательстве теоремы Бернулли получаем такую оценку
, которая применяется на практике.
Теорема Пуассона. Если производится Независимых опытов и вероятность появления события А в -м опыте равна , то при увеличинении Частость события А сходится по вероятности к среднеарифметическому вероятностей :
,
Где — сколь угодно малое положительное число. При доказательстве этой теоремы используется неравенство
При доказательстве этой теоремы используется неравенство
,
Имеющее практическое применение.
Пример 9.6. При контрольной проверке изготавливаемых приборов было установлено, что в среднем 15 шт. из 100 оказывается с теми или иными дефектами. Оценить вероятность того, что доля приборов с дефектами среди 400 изготовленных будет по абсолютной величине отличаться от математического ожидания этой доли не более чем на 0,05.
Решение. Воспользуемся неравенством
.
По условию , . В качестве Р возьмем величину, полученную при проверке для доли брака .
Итак, .
Ответ: .
Пример 9.7. Вероятность того, что изделие является качественным, равна 0,9. Сколько следует проверить изделий, чтобы с вероятностью не меньшей 0,95 можно было утверждать, что абсолютная величина отклонения доли качественных изделий от 0,9 не превысит 0,01?
Решение. Воспользуемся неравенством
.
По условию , , . Подставим в правую часть вышеприведенного неравенства эти значения
.
Ответ: .
| < Предыдущая | Следующая > |
|---|
2.5: Эмпирическое правило и теорема Чебышева
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 559
Цели обучения
- Узнать, что подразумевает значение стандартного отклонения набора данных о том, как данные отклоняются от среднего значения, как описано Эмпирическое правило и Теорема Чебышева .
- Использовать эмпирическое правило и теорему Чебышева, чтобы делать выводы о наборе данных.
Вероятно, вы хорошо понимаете, что среднее значение набора данных говорит об этом наборе данных. В этом разделе мы начинаем изучать, что стандартное отклонение может сказать нам о характере набора данных.
В этом разделе мы начинаем изучать, что стандартное отклонение может сказать нам о характере набора данных.
Мы начинаем с изучения определенного набора данных. В таблице \(\PageIndex{1}\) показан рост в дюймах \(100\) случайно выбранных взрослых мужчин. Гистограмма относительной частоты для данных показана на рисунке \(\PageIndex{1}\). Среднее значение и стандартное отклонение данных округлены до двух знаков после запятой: \(\bar{x}=690,92\) и \(\сигма = 1,70\).
| 68,7 | 72,3 | 71,3 | 72,5 | 70,6 | 68,2 | 70,1 | 68,4 | 68,6 | 70,6 |
| 73,7 | 70,5 | 71,0 | 70,9 | 69,3 | 69,4 | 69,7 | 69,1 | 71,5 | 68,6 |
| 70,9 | 70,0 | 70,4 | 68,9 | 69,4 | 69,4 | 69,2 | 70,7 | 70,5 | 69,9 |
| 69,8 | 69,8 | 68,6 | 69,5 | 71,6 | 66,2 | 72,4 | 70,7 | 67,7 | 69,1 |
| 68,8 | 69,3 | 68,9 | 74,8 | 68,0 | 71,2 | 68,3 | 70,2 | 71,9 | 70,4 |
| 71,9 | 72,2 | 70,0 | 68,7 | 67,9 | 71,1 | 69,0 | 70,8 | 67,3 | 71,8 |
| 70,3 | 68,8 | 67,2 | 73,0 | 70,4 | 67,8 | 70,0 | 69,5 | 70,1 | 72,0 |
| 72,2 | 67,6 | 67,0 | 70,3 | 71,2 | 65,6 | 68. 1 1 | 70,8 | 71,4 | 70,2 |
| 70,1 | 67,5 | 71,3 | 71,5 | 71,0 | 69,1 | 69,5 | 71,1 | 66,8 | 71,8 |
| 69,6 | 72,7 | 72,8 | 69,6 | 65,9 | 68,0 | 69,7 | 68,7 | 69,8 | 69,7 |
Если мы просмотрим данные и подсчитаем количество наблюдений, которые находятся в пределах одного стандартного отклонения от среднего, то есть находятся между \(69,92-1,70=68,22\) и \(69,92+1,70=71,62\). ) дюймов, их всего \(69\). Если мы подсчитаем количество наблюдений, которые находятся в пределах двух стандартных отклонений от среднего значения, то есть находятся между \(690,92-2(1,70)=66,52\) и \(69,92+2(1,70)=73,32\) дюймов, их всего \(95\). Все измерения находятся в пределах трех стандартных отклонений от среднего, то есть между \(69,92-3(1,70)=64,822\) и \(69,92+3(1,70)=75,02\) дюймов. Эти подсчеты не являются совпадениями, но согласуются со следующим результатом, который оказался широко применимым.
Все измерения находятся в пределах трех стандартных отклонений от среднего, то есть между \(69,92-3(1,70)=64,822\) и \(69,92+3(1,70)=75,02\) дюймов. Эти подсчеты не являются совпадениями, но согласуются со следующим результатом, который оказался широко применимым.
Приблизительно \(68\%\) данных лежат в пределах одного стандартного отклонения от среднего, то есть в интервале с конечными точками \(\bar{ x}\pm s\) для выборок и с конечными точками \(\mu \pm \sigma\) для популяций; если набор данных имеет приблизительно колоколообразную гистограмму относительной частоты, то (Рисунок \(\PageIndex{2}\))
- приблизительно \(95\%\) данных лежат в пределах двух стандартных отклонений от среднего, то есть в интервале с конечными точками \(\bar{x}\pm 2s\) для проб и с конечными точками \( \mu \pm 2\sigma\) для популяций; и
- примерно \(99,7\%\) данных лежит в пределах трех стандартных отклонений от среднего, то есть в интервале с конечными точками \(\bar{x}\pm 3s\) для выборок и с конечными точками \(\mu \pm 3\sigma\) для популяций.

Два ключевых момента в отношении эмпирического правила заключаются в том, что распределение данных должно быть примерно колоколообразным, и что проценты верны только приблизительно. Эмпирическое правило не применяется к наборам данных с сильно асимметричным распределением, и фактический процент наблюдений в любом из интервалов, указанных в правиле, может быть больше или меньше, чем указано в правиле. Мы видим это на примере роста мужчин: эмпирическое правило предполагало 68 наблюдений между 1(68,22) и 1(71,62) дюймами, но мы посчитали 1(69).\).
Пример \(\PageIndex{1}\)
Рост \(18\)-летних мужчин имеет колоколообразное распределение со средним значением \(69,6\) дюймов и стандартным отклонением \(1,4\) дюймов.
- Примерно какая доля всех таких мужчин имеет рост от \(68,2\) до \(71\) дюймов?
- Какой интервал с центром в среднем должен содержать примерно \(95\%\) всех таких мужчин?
Решение :
Эскиз распределения высот приведен на рисунке \(\PageIndex{3}\).
- Поскольку интервал от \(68,2\) до \(71,0\) имеет концы \(\bar{x}-s\) и \(\bar{x}+s\), по эмпирическому правилу относительно \ (68\%\) всех \(18\)-летних мужчин должны иметь рост в этом диапазоне.
По эмпирическому правилу кратчайший такой интервал имеет концы \(\bar{x}-2s\) и \(\bar{x}+2s\). Поскольку \[\bar{x}-2s=69,6-2(1,4)=66,8 \nonnumber\] и \[ \bar{x}+2s=69,6+2(1,4)=72,4 \nonnumber\]
рассматриваемый интервал — это интервал от \(66,8\) дюймов до \(72,4\) дюймов.
Рисунок \(\PageIndex{3}\): Распределение ростаПример \(\PageIndex{2}\)
Результаты тестов IQ имеют колоколообразное распределение со средним \(\mu =100\) и стандартным отклонение \(\сигма=10\). Обсудите, что Эмпирическое правило подразумевает в отношении людей с показателями IQ \(110\), \(120\) и \(130\).
Решение :
Схема распределения коэффициента интеллекта представлена на рисунке \(\PageIndex{3}\). {th}\).
{th}\).
Эмпирическое правило применяется не ко всем наборам данных, а только к тем, которые имеют форму колокола, и даже в этом случае формулируется в терминах приближений. Результат, применимый к любому набору данных, известен как теорема Чебышева.
Теорема Чебышева
Для любого набора числовых данных
- не менее \(3/4\) данных лежат в пределах двух стандартных отклонений от среднего, то есть в интервале с конечными точками \(\bar{x }\pm 2s\) для выборок и с конечными точками \(\mu \pm 2\sigma\) для популяций; 92\) данных лежат в пределах \(k\) стандартных отклонений от среднего, то есть в интервале с конечными точками \(\bar{x}\pm ks\) для выборок и с конечными точками \(\mu \pm k\sigma\) для популяций, где \(k\) — любое положительное целое число, большее \(1\).

Рисунок \(\PageIndex{4}\) дает наглядную иллюстрацию теоремы Чебышева.
Рисунок \(\PageIndex{4}\): Теорема ЧебышеваВажно обратить особое внимание на слова «по крайней мере» в начале каждой из трех частей теоремы Чебышева. Теорема дает минимум доля данных, которая должна лежать в пределах заданного числа стандартных отклонений от среднего значения; истинные пропорции, найденные в указанных областях, могут быть больше, чем гарантирует теорема.
Пример \(\PageIndex{3}\)
Размер выборки \(n=50\) имеет среднее значение \(\bar{x}=28\) и стандартное отклонение \(s=3\). Что можно сказать о количестве наблюдений, лежащих в интервале \((22,34)\), не зная ничего другого о выборке? Что можно сказать о количестве наблюдений, лежащих за пределами этого интервала?
Решение :
Интервал \((22,34)\) формируется путем сложения и вычитания двух стандартных отклонений от среднего. По теореме Чебышева в этот интервал попадает не менее \(3/4\) данных. Поскольку \(3/4\) от \(50\) равно \(37,5\), это означает, что в интервале находится не менее \(37,5\) наблюдений. Но нельзя взять дробное наблюдение, поэтому мы заключаем, что по крайней мере \(38\) наблюдений должно лежать внутри интервала \((22,34)\).
Поскольку \(3/4\) от \(50\) равно \(37,5\), это означает, что в интервале находится не менее \(37,5\) наблюдений. Но нельзя взять дробное наблюдение, поэтому мы заключаем, что по крайней мере \(38\) наблюдений должно лежать внутри интервала \((22,34)\).
Если не менее \(3/4\) наблюдений находятся в интервале, то не более \(1/4\) из них вне его. Поскольку \(1/4\) от \(50\) равно \(12,5\), не более \(12,5\) наблюдений находятся вне интервала. Так как снова часть наблюдения невозможна, \(x\; (22,34)\).
Пример \(\PageIndex{4}\)
Количество транспортных средств, проезжающих через оживленный перекресток между \(8:00\; утра\) и \(10:00\; утра\) и записывались каждое утро буднего дня в прошлом году. Набор данных содержит \(n=251\) чисел. Среднее значение выборки равно \(\bar{x}=725\), а стандартное отклонение выборки равно \(s=25\). Определите, какое из следующих утверждений должно быть верным.
- Приблизительно \(95\%\) утра в будние дни в прошлом году количество транспортных средств, проезжающих через перекресток с \(8:00\; утра\) до \(10:00\; утра\), составляло от \(675\) и \(775\).

- Не менее \(75\%\) утренних будних дней прошлого года количество транспортных средств, проезжающих через перекресток с \(8:00\; утра\) до \(10:00\; утра\), составляло между \ (675\) и \(775\).
- По меньшей мере \(189\) будних дней в прошлом году количество транспортных средств, проезжающих через перекресток с \(8:00\; утра\) до \(10:00\; утра\), составляло \(675\) и \(775\).
- Не более \(25\%\) будних дней утром в прошлом году количество транспортных средств, проезжающих через перекресток с \(8:00\; утра\) до \(10:00\; утра\), было либо меньше чем \(675\) или больше \(775\).
- Максимум \(12,5\%\) утра в будние дни прошлого года количество транспортных средств, проезжающих через перекресток с \(8:00\; утра\) до \(10:00\; утра\), было меньше \(675\).
- Не более \(25\%\) будних дней утром в прошлом году количество транспортных средств, проезжающих через перекресток с \(8:00\; утра\) до \(10:00\; утра\), было меньше \(675\).

Решение :
- Поскольку не указано, что гистограмма относительной частоты данных имеет форму колокола, эмпирическое правило не применяется. Утверждение (1) основано на эмпирическом правиле и поэтому может быть неверным.
- Утверждение (2) является прямым приложением части (1) теоремы Чебышева, поскольку \(\bar{x}-2s\), \(\bar{x}+2s = (675,775)\). Это должно быть правильно.
- Утверждение (3) говорит то же самое, что и утверждение (2), поскольку \(75\%\) от \(251\) равно \(188,25\), поэтому минимальное целое число наблюдений в этом интервале равно \(189\). ). Таким образом, утверждение (3) определенно верно.
- Утверждение (4) говорит то же самое, что и утверждение (2), но другими словами, и поэтому определенно верно.
- Утверждение (4), которое определенно верно, утверждает, что не более \(25\%\) времени через перекресток проезжало либо менее \(675\), либо более \(775\) транспортных средств.
 Утверждение (5) говорит, что половина этого \(25\%\) соответствует дням с небольшим трафиком. Это было бы правильно, если бы известно, что гистограмма относительной частоты данных симметрична. Но это не указано; возможно, все наблюдения вне интервала (\(675,775\)) меньше, чем \(75\). Таким образом, утверждение (5) может быть неверным.
Утверждение (5) говорит, что половина этого \(25\%\) соответствует дням с небольшим трафиком. Это было бы правильно, если бы известно, что гистограмма относительной частоты данных симметрична. Но это не указано; возможно, все наблюдения вне интервала (\(675,775\)) меньше, чем \(75\). Таким образом, утверждение (5) может быть неверным. - Утверждение (4) определенно верно, а утверждение (4) влечет за собой утверждение (6): даже если каждое измерение, лежащее вне интервала (\(675,775\)) меньше, чем \(675\) (что возможно, поскольку симметрия неизвестно), даже в этом случае самое большее \(25\%\) всех наблюдений меньше, чем \(675\). Таким образом, утверждение (6) заведомо должно быть правильным.
- Эмпирическое правило представляет собой аппроксимацию, применимую только к наборам данных с колоколообразной гистограммой относительной частоты. Он оценивает долю измерений, находящихся в пределах одного, двух и трех стандартных отклонений от среднего значения.
- Теорема Чебышева — это факт, применимый ко всем возможным наборам данных.
 Он описывает минимальную долю измерений, которые должны лежать в пределах одного, двух или более стандартных отклонений от среднего значения.
Он описывает минимальную долю измерений, которые должны лежать в пределах одного, двух или более стандартных отклонений от среднего значения.
Эта страница под названием 2.5: Эмпирическое правило и теорема Чебышева распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Аноним
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 3,0
- Программа OER или Publisher
- Издатель, имя которого нельзя называть
- Показать оглавление
- нет
- Теги
- Теорема Чебышева
- Эмпирическое правило
- источник@https://2012books.
 lardbucket.org/books/beginning-statistics
lardbucket.org/books/beginning-statistics
Калькулятор теоремы Чебышева + пошаговое решение
Калькулятор теоремы Чебышева
Введите число стандартных отклонений от среднего значения. Это должно быть положительное число больше единицы.*
Ответ:
55,56%
Для любого распределения не менее 55,56% значений данных будут находиться в пределах 1,5 стандартных отклонений от среднего . То есть от 1,5 стандартных отклонений ниже среднего до 1,5 стандартных отклонений выше среднего. 92 = 2,25 $$
2. Затем разделите 1 на ответ из шага 1 выше: $$ \frac{1}{2,25} = 0,44444444444444 $$
3. Вычтите ответ на шаге 2 выше из числа 1: $$ 1 — 0,4444444444444 $$ $$ = 0,55555555555556$$
4. Умножьте на 100, чтобы получить процент. Здесь мы округляем не более чем до 2 знаков после запятой. $$ = 55,56\% $$
Содержание
Как пользоваться калькулятором теорем Чебышева
Вы можете использовать калькулятор теорем Чебышева для распределения любой формы. Калькулятор показывает наименьший процент значений данных в «k» стандартных отклонениях от среднего. Затем вы получите пошаговое объяснение того, как сделать это самостоятельно. Вам не нужно среднее значение и стандартное отклонение, чтобы использовать этот калькулятор.
Калькулятор показывает наименьший процент значений данных в «k» стандартных отклонениях от среднего. Затем вы получите пошаговое объяснение того, как сделать это самостоятельно. Вам не нужно среднее значение и стандартное отклонение, чтобы использовать этот калькулятор.
Вы можете использовать Калькулятор теорем Чебышева в качестве учебного пособия. Лучший подход — сначала просмотреть пример решения для нескольких разных задач и понять шаги, показанные в решении. Затем попробуйте решить задачу самостоятельно, используя ту же стратегию, а затем проверьте свою работу с помощью калькулятора. Ты получил это!
Объяснение теоремы Чебышева
Так что же такое теорема Чебышева в статистике и для чего она используется? Мы используем теорему Чебышева или правило Чебышева для оценки процента значений в распределении в пределах ряда стандартных отклонений. то есть любой дистрибутив любой любой формы. Это означает, что мы можем использовать правило Чебышева для искаженных правых распределений, искаженных левых распределений, бимодальных распределений и т. д. По этой причине оценка является консервативной. Мы используем слова «по крайней мере» при описании процента значений данных. Вы увидите использование «по крайней мере» в задачах по теореме Чебышева и ответах, приведенных ниже. Вы можете использовать приведенный выше Калькулятор теорем Чебышева, чтобы увидеть решения любой проблемы, которая у вас может возникнуть.
д. По этой причине оценка является консервативной. Мы используем слова «по крайней мере» при описании процента значений данных. Вы увидите использование «по крайней мере» в задачах по теореме Чебышева и ответах, приведенных ниже. Вы можете использовать приведенный выше Калькулятор теорем Чебышева, чтобы увидеть решения любой проблемы, которая у вас может возникнуть.
Если вы знаете, что распределение, с которым вы работаете, представляет собой распределение в форме колокола, и вы хотите найти процент значений данных в пределах 1, 2 или 3 стандартных отклонений, вы можете использовать калькулятор эмпирических правил, калькулятор процента распределения в форме колокола. Учителя и учебники часто обсуждают теорему Чебышева и эмпирическое правило вместе. Важно помнить, что мы используем эмпирическое правило только с колоколообразными распределениями.
- Теорема Чебышева / Правило Чебышева – используется для распределения любой формы 92} $ значений данных будет в пределах k стандартных отклонений от среднего.
 Значение для k должно быть больше 1. Используя правило Чебышева в статистике, мы можем оценить процент значений данных, которые отличаются на 1,5 стандартных отклонения от среднего. Или мы можем оценить процент значений данных, которые отличаются на 2,5 стандартных отклонения от среднего значения. Калькулятор теоремы Чебышева, приведенный выше, позволит вам ввести любое значение k больше 1. Калькулятор Чебышева также покажет вам полное решение с применением формулы теоремы Чебышева.
Значение для k должно быть больше 1. Используя правило Чебышева в статистике, мы можем оценить процент значений данных, которые отличаются на 1,5 стандартных отклонения от среднего. Или мы можем оценить процент значений данных, которые отличаются на 2,5 стандартных отклонения от среднего значения. Калькулятор теоремы Чебышева, приведенный выше, позволит вам ввести любое значение k больше 1. Калькулятор Чебышева также покажет вам полное решение с применением формулы теоремы Чебышева.Теорема Чебышева Примеры задач
Теперь мы покажем, как применять формулу Чебышева на конкретных примерах. Эти практические задачи по теореме Чебышева должны дать вам представление об использовании теоремы Чебышева и о том, как интерпретировать результат.
Пример 1
Распределение результатов тестов учащихся смещено влево. Используя правило Чебышева, оцените процент оценок учащихся в пределах 1,5 стандартных отклонений от среднего значения.
Решение:
Значение k в этой задаче равно 1,5, поэтому подставим 1,5 в формулу Чебышева: 92 = 2,25 $$
Разделите 1 на 2,25
$$ \frac{1}{2,25} = 0,4444 $$
Вычтите 0,4444 из 1
$$ 1 – 0,4444 = 0,5556 $$
Умножьте на 100, чтобы преобразовать ответ в процент
$$ 0,5556 \cdot 100 = 55,56% $$Интерпретация:
По крайней мере, 55,56% результатов тестов в распределении с асимметрией влево находятся в пределах 1,5 стандартных отклонений от среднего. То есть от 1,5 стандартных отклонений ниже до 1,5 стандартных отклонений выше среднего.
То есть от 1,5 стандартных отклонений ниже до 1,5 стандартных отклонений выше среднего.Пример 2
Распределение кредитных баллов учащихся смещено вправо. Используя правило Чебышева, оцените процент кредитных баллов в пределах 2,5 стандартных отклонений от среднего. 92 = 6,25 $$
Разделите 1 на 6,25
$$ \frac{1}{6,25} = 0,16 $$
Вычтите 0,16 из 1
$$ 1 – 0,16 = 0,84 $$
Умножьте на 100, чтобы преобразовать ответ в процент
$$ 0,84 \cdot 100 = 84% $$Интерпретация:
По крайней мере, 84% кредитных баллов в асимметричном правом распределении находятся в пределах 2,5 стандартных отклонений от среднего. То есть от 2,5 стандартных отклонений ниже до 2,5 стандартных отклонений выше среднего.Вы можете ввести 1,5 и 2,5 в Калькулятор теоремы Чебышева выше, чтобы проверить те же результаты, что и здесь.
Теорема Чебышева в Excel
Альтернативой использованию Калькулятора теорем Чебышева является вычисление теоремы Чебышева в Excel.
 Вы можете скачать связанную таблицу здесь.
Вы можете скачать связанную таблицу здесь.Загрузить: Калькулятор теоремы Чебышева Электронная таблица Excel
Электронная таблица, ссылка на которую приведена здесь, содержит формулы, необходимые для применения теоремы Чебышева в Excel. Части электронной таблицы объясняются в трех шагах ниже.
- В ячейку A2 введите количество стандартных отклонений. В качестве примера я использую 1,2 стандартных отклонения. 92)*100 . Используйте ячейку A2 для обозначения числа стандартных отклонений.
- Нажмите Enter, и получите ответ в ячейке B2. Округлите до сотых, и ответ составит 30,56%.
Интерпретация: по крайней мере 30,56% значений данных находятся в пределах 1,2 стандартных отклонения от среднего значения.
Теорема Чебышева Практические задачи с учетом среднего и стандартного отклонения
Нет необходимости знать среднее значение или стандартное отклонение, чтобы использовать правило Чебышева, но если задача предоставляет эти значения, вы можете интерпретировать результат дальше.
 Например, давайте посмотрим на приведенные выше примеры, но на этот раз предположим, что задачи дают среднее значение и стандартное отклонение.
Например, давайте посмотрим на приведенные выше примеры, но на этот раз предположим, что задачи дают среднее значение и стандартное отклонение.Пример 1
Распределение результатов тестов учащихся смещено влево. Используя правило Чебышева, оцените процент оценок учащихся в пределах 1,5 стандартных отклонений от среднего значения. Среднее значение = 70, стандартное отклонение = 10.
Решение:
Используя формулу Чебышева вручную или приведенный выше калькулятор теорем Чебышева, мы нашли решение этой задачи равным 55,56%. Теперь давайте включим данное среднее значение и стандартное отклонение в интерпретацию.
Сначала рассчитайте 1,5 стандартных отклонения.
$$ \text{1,5 стандартных отклонения} = 1,5 \cdot 10$$
$$\text{1,5 стандартных отклонения} = 15 $$
Затем вычтите и прибавьте 1,5 стандартных отклонения от/к среднему, 70.
$ 70 $ – 15 = 55 $
$ 70 + 15 = 85 $ $
Итак, теперь интерпретация задачи выглядит следующим образом: по крайней мере 55,56% результатов теста в распределении с асимметрией влево находятся между 55 и 85.
Пример 2
Распределение кредитных баллов студентов смещено вправо. Используя правило Чебышева, оцените процент кредитных баллов в пределах 2,5 стандартных отклонений от среднего. Среднее значение = 400, стандартное отклонение = 120.
Решение:
Используя формулу Чебышева вручную или приведенный выше калькулятор теорем Чебышева, мы нашли решение этой задачи равным 84%. Теперь давайте включим данное среднее значение и стандартное отклонение в интерпретацию.
Сначала рассчитайте 2,5 стандартных отклонения.
$$ \text{2,5 стандартных отклонения} = 2,5 \cdot 120$$
$$\text{2,5 стандартных отклонения} = 300 $$
Затем вычтите и прибавьте 2,5 стандартных отклонения от/к среднему, 400.
$$ 400 – 300 = 100 $$
$$ 400 + 300 = 700 $$
Итак, теперь интерпретация проблемы выглядит следующим образом: по крайней мере 84% кредитных баллов в распределении с перекосом вправо находятся между 100 и 700.Другие сложные практические задачи, проверенные с помощью калькулятора теоремы Чебышева
Вот несколько сложных практических задач, в которых используется теорема Чебышева.

Пример 1
Распределение результатов тестов 800 учащихся смещено влево. Используя правило Чебышева, каково наименьшее количество баллов в пределах 2 стандартных отклонений от среднего? 92 = 4 $$
Разделите 1 на 4
$$ \frac{1}{4} = 0,25 $$
Вычтите 0,25 из 1
$$ 1 – 0,25 = 0,75 $$
Теперь умножьте на 800, чтобы получить 75% из 800. Это наименьшее число баллов учащихся в пределах 2 стандартных отклонений от среднего.
$$ 0,75 \cdot 800 = 600 $$Интерпретация:
По крайней мере 600 оценок учащихся в распределении с асимметрией влево находятся в пределах 2 стандартных отклонений от среднего. То есть от 2 стандартных отклонений ниже до 2 стандартных отклонений выше среднего. 92 $$
Извлеките квадратный корень из 5,29100529101
$$ \sqrt{5,29100529101} = k $$
$$ k = 2,3 $$Интерпретация: согласно теореме Чебышева не менее 81,1% значений данных в распределении находятся в пределах 2,3 стандартных отклонений от среднего значения.

Вы можете убедиться, что 2.3 является правильным ответом, введя его в Калькулятор теорем Чебышева выше. Вы должны получить ответ около 0,8110.Тест по теореме Чебышева – проверьте свои знания
Тест по теореме Чебышева
Проверьте свои знания теоремы Чебышева с помощью этого онлайн-теста. Вы можете сначала попробовать выполнить работу вручную, затем проверить свою работу с помощью Калькулятора теорем Чебышева.
Общие примечания
Вопросы, связанные с теоремой Чебышева на вводных занятиях по статистике, обычно не слишком сложны. Ключевыми фразами, на которые следует обратить внимание, являются тип распределения. Если вы видите фразу «распределение в форме колокола» или «нормальное распределение», то вам не следует использовать правило Чебышева для оценки процентов в распределении. Поэтому вместо этого используйте эмпирическое правило. В вопросах, требующих использования правила Чебышева, будет указано, что распределение не является колоколообразным, скошено вправо, скошено влево, бимодально, j-образно и т.

- В ячейку A2 введите количество стандартных отклонений. В качестве примера я использую 1,2 стандартных отклонения. 92)*100 . Используйте ячейку A2 для обозначения числа стандартных отклонений.





 Утверждение (5) говорит, что половина этого \(25\%\) соответствует дням с небольшим трафиком. Это было бы правильно, если бы известно, что гистограмма относительной частоты данных симметрична. Но это не указано; возможно, все наблюдения вне интервала (\(675,775\)) меньше, чем \(75\). Таким образом, утверждение (5) может быть неверным.
Утверждение (5) говорит, что половина этого \(25\%\) соответствует дням с небольшим трафиком. Это было бы правильно, если бы известно, что гистограмма относительной частоты данных симметрична. Но это не указано; возможно, все наблюдения вне интервала (\(675,775\)) меньше, чем \(75\). Таким образом, утверждение (5) может быть неверным. Он описывает минимальную долю измерений, которые должны лежать в пределах одного, двух или более стандартных отклонений от среднего значения.
Он описывает минимальную долю измерений, которые должны лежать в пределах одного, двух или более стандартных отклонений от среднего значения. lardbucket.org/books/beginning-statistics
lardbucket.org/books/beginning-statistics Значение для k должно быть больше 1. Используя правило Чебышева в статистике, мы можем оценить процент значений данных, которые отличаются на 1,5 стандартных отклонения от среднего. Или мы можем оценить процент значений данных, которые отличаются на 2,5 стандартных отклонения от среднего значения. Калькулятор теоремы Чебышева, приведенный выше, позволит вам ввести любое значение k больше 1. Калькулятор Чебышева также покажет вам полное решение с применением формулы теоремы Чебышева.
Значение для k должно быть больше 1. Используя правило Чебышева в статистике, мы можем оценить процент значений данных, которые отличаются на 1,5 стандартных отклонения от среднего. Или мы можем оценить процент значений данных, которые отличаются на 2,5 стандартных отклонения от среднего значения. Калькулятор теоремы Чебышева, приведенный выше, позволит вам ввести любое значение k больше 1. Калькулятор Чебышева также покажет вам полное решение с применением формулы теоремы Чебышева. То есть от 1,5 стандартных отклонений ниже до 1,5 стандартных отклонений выше среднего.
То есть от 1,5 стандартных отклонений ниже до 1,5 стандартных отклонений выше среднего.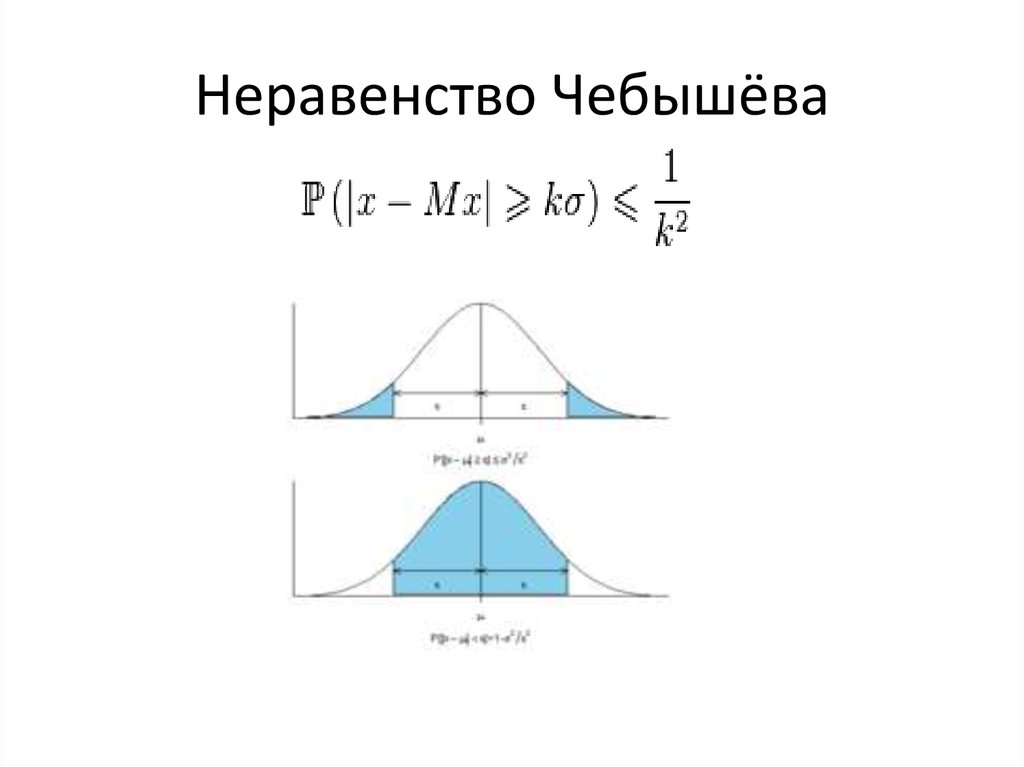 Вы можете скачать связанную таблицу здесь.
Вы можете скачать связанную таблицу здесь. Например, давайте посмотрим на приведенные выше примеры, но на этот раз предположим, что задачи дают среднее значение и стандартное отклонение.
Например, давайте посмотрим на приведенные выше примеры, но на этот раз предположим, что задачи дают среднее значение и стандартное отклонение.