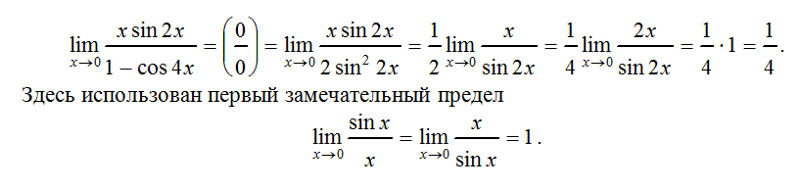2x`. adfree_icon_web_accordion. Ab Padhai karo bina ads ke.cos2x. Natural Language; Math Input. Use Math Input Mode to directly enter textbook math notation. Try it. ×. Have a question about using Wolfram|Alpha?acum 6 zile — Cos2x is one of the double angle trigonometric identities as the angle is a multiple of 2, or, double of x. The cosine of an angle is calculated …Free Pre-Algebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators step-by-step.Cos 2x is also called a Double angle formula as they have 2 or double angles in the trigonometric functions. Practice Cos 2x formula examples and other …Solve your math problems using our free math solver with step-by-step solutions. Our math solver supports basic math, pre-algebra, algebra, trigonometry, …15 feb. 2022 — The cos(2x) graph is a transformation of the cos(x) graph that multiplies any given angle x x by 2. The following table shows the x- and y- …solid on cosx-cos2x. Author: Steve Simon. GeoGebra Applet Press Enter to start activity.
2(x)} …7 mar. 2020 — Bu yazıda cos2x sin2x ifadelerinden bahsedecek yani yarım açı formüllerini vereceğiz. Sin2x = 2.sinx.cosx. Cos2x = cos2x – sin2x…. simplification sin2x +cos2x = 1 Dividing by cos2x cos2xsin2x +1 = cos2x1 … cos (2x) + c2′ sin (2x) – 2 c1 sin (2x) + 2 c2 cos (2x) We will ask that.Si (x) = Cos (2x) Significa que: P = 2*pi / 2 = pi Cada intervalo “pi” en . Multiply and divide the given expression by π π 2 sin 2 π 15, we get.cos2x = cos(x + x) = cosx?cosx – senx?senx. Ou cos2x = cos2 x – sen2 x … Sabendo que sen x = 12/13 e cos x = 5/13, determine o valor de sen 2x e cos 2x.7 apr. 2013 — cos2x + sin2x = 1 1 + tan2x = sec2x cot2x + 1 = csc2x Cofunction …1. sin2x + cos2x = 1 sin x cos x 2. tan x ; cot x ; tanx.cotx = 1 sin2x … + cosx) cos x sin x cos2x = 1 – sin2x = (1 – sinx)(1 + sinx) 1 1 3.Zadanie MATURA 2012: Rozwiąż równanie cos2x + 2 = 3cosx (p. rozszerzony). Teoria potrzebna do zadania: Wykres funkcji y=cos x.2 cos x = 1, sin (2x) = cos x, 2 + cos 2x = 3 cos x,. … Nov 6, 2015 tan2x −cot2x = sin2x cos2x −.
5/2 44 points …The sine of any angle is just it’s y-value on the unit circle. ответ здесь | Решите , 1)sin2x=sin(x-pi/3) 2)cos(x-pi/6)=cos(pi/5) 3)cos2x=sin(pi/3+x) …Integral from 0 to pi 6sin2xdx: integral of 6sin2xdx (-3)cos2x+c. The table shows some more examples of Area = intydx=intsin x dx, between the limits x=0 …4 iul. 2022 — Identities related to sin2x, cos2x, tan2 x, sin3x, cos3x and tan3x. Unit-II: Algebra. 1. Complex Numbers and Quadratic Equations (10 Periods).Click to rate this post!
[Total: 1 Average: 5]
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
пределы — $\lim\limits_{x \to 0}{\frac{\cos x — \cos 2x}{1 — \cos x}}$
спросил
Изменено 6 лет, 1 месяц назад
Просмотрено 1к раз
$\begingroup$
Упражнение:
$$\lim\limits_{x \to 0}{\frac{\cos x — \cos 2x}{1 — \cos x}}$$
Я разместил свое решение ниже, однако, если есть более элегантные подходы, не стесняйтесь включать свои собственные решения.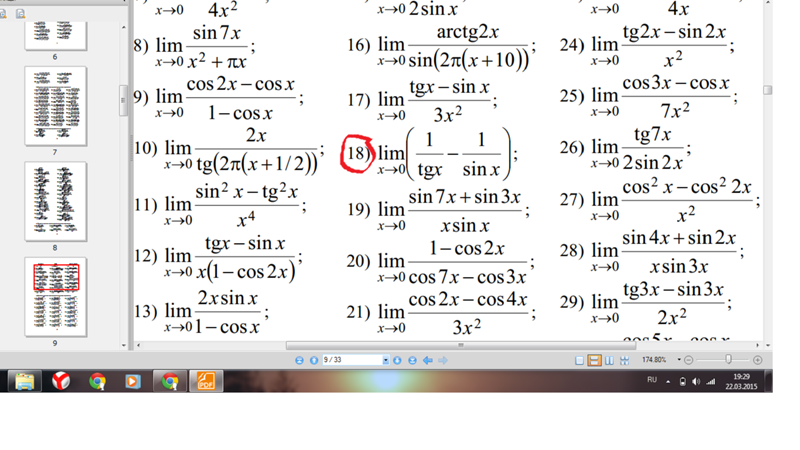
2(x)-1$$ 92(x)=(1-\cos(x))(2\cos(x)+1)$$
Таким образом, находим
$$\frac{\cos(x)-\cos(2x) }{1-\cos(x)}=2\cos(x)+1$$
Таким образом, ограничение равно $3$.
$\endgroup$
3
$\begingroup$
Если дважды применить правило Лопиталя, $$ \lim\limits_{x \to 0}{\frac{\cos x — \cos 2x}{1 — \cos x}}=\lim\limits_{x \to 0}{\frac{-\sin x + 2 \sin 2x}{\sin x}}=\lim\limits_{x \to 0}{\frac{-\cos x +4 \cos 2x}{\cos x}}=\frac{-1+4 }1=3. $$ 92}}$ $= 3$
Ответ:
$$\lim\limits_{x \to 0}{\frac{\cos x — \cos 2x}{1 — \cos x}} = 3$$
$\endgroup$
1
$\begingroup$
Если мы вычислим напрямую, то получим дробь $\frac{0}{0}$. Итак, используя правило Лопиталя: $$ \lim_{x \rightarrow 0} \frac{\cos x — \cos 2x}{1-\cos x} «=» \lim_{x \rightarrow 0} \frac{-\sin x + 2\sin 2x}{\sin x} $$
Теперь, если мы еще раз вычислим напрямую, мы получим дробь $\frac{0}{0}$.