Бесконечные пределы и асимптоты
Помимо конечных пределов, у последовательностей бывают бесконечные (см. раздел Пределы и ограниченность в главе 5). У функций тоже!
12.1Бесконечные пределы в конечных точках
12.1.1Существование предела и ограниченность
Из лекции 5 мы знаем, что сходящаяся последовательность ограничена. Для функций можно сформулировать аналогичное утверждение.
Теорема 1. Пусть функция f(x) имеет предел при x→x0. Тогда она ограничена на некоторой проколотой окрестности точки x0. Иными словами, найдутся такие C и δ∗>0, что для всех x∈˚Uδ∗(x0) выполняется неравенство |f(x)|<C.
Доказательство. По определению предела, для всякого ε>0 найдётся такое δ=δ(ε)>0, что для всех x из проколотой δ-окрестности x0 выполняется неравенство |f(x)−b|<ε.
Положим δ∗:=δ(1) (то есть возьмём ε=1). Тогда для всех
x из проколотой δ∗-окрестности точки x0 выполняется неравенство
|f(x)−b|<1. По неравенству треугольника,
Тогда для всех
x из проколотой δ∗-окрестности точки x0 выполняется неравенство
|f(x)−b|<1. По неравенству треугольника,
|f(x)|≤|f(x)−b|+|b−0|<1+|b|.
Положим C=1+|b|. Тогда ˚Uδ∗(x0) — искомая окрестность точки x0. Теорема доказана.∎
Доказательство очень похоже на доказательство аналогичной теоремы для последовательностей, и даже проще: в случае с последовательностями нужно было отдельно рассматривать начальный отрезок. За это мы платим тем фактом, что утверждение об ограниченности распространяется не на всю область определения функции, а лишь на некоторую проколотую окрестность точки x0.
Пример 1. Рассмотрим функцию f(x)=1/x. Она имеет предел при x→1, однако не является ограниченной на всей области определения.
12.1.2Бесконечные пределы
В том случае, когда функция не является ограниченной ни в какой проколотой
окрестности точки x0, она не может иметь предела в этой точке. Однако,
опять аналогично ситуациям с последовательностями, мы можем определить, что
означает, что функция стремится к бесконечности в точке x0.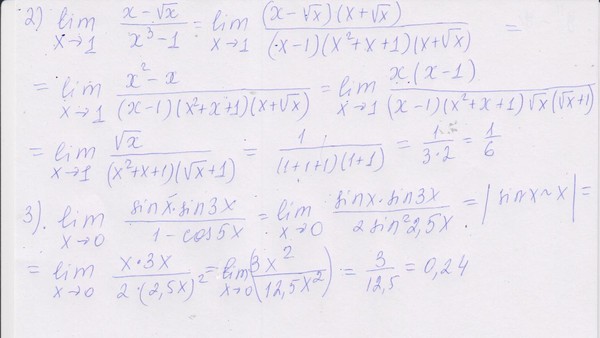
Определение 1. Пусть функция f(x) определена в некоторой проколотой окрестности точки x0. Говорят, что её предел в этой точке равен бесконечности, если для всякого C найдётся такая δ>0, что для всех x из проколотой δ-окрестности точки x0 выполняется неравенство: |f(x)|>C. Формально:
∀C∈R ∃δ>0 ∀x∈R:0<|x−x0|<δ⇒|f(x)|>C.
∀C∈R ∃δ>0 ∀x∈R:0<|x−x0|<δ⇒|f(x)|>C.
Записывают:
limx→x0f(x)=∞.
Пример 2. Функция f(x)=1x стремится к бесконечности при x→0. Дейстительно, возьмём любоое C. Если C≤0, условие |1/x|>C выполнено автоматически. Если C>0, положим δ=1/C. Тогда если |x|<δ, то |1/x|=1/|x|>1/δ=C.
Пример 3. Функция
f(x)={1/x,x∈Q,0,x∉Q,
не является ограниченной ни в какой проколотой окрестности точки x=0
(поскольку сколь угодно близко к нулю существуют рациональные числа), но
при этом не стремится к бесконечности при x→0 (поскольку сколь угодно
близко к нулю существуют иррациональные числа, в которых функция принимает
значение 0).
Опять же, аналогично последовательностям, помимо просто бесконечности, бывает плюс бесконечность и минус бесконечность:
Определение 2. Пусть функция f(x) определена в некоторой проколотой окрестности точки x0. Говорят, что её предел в этой точке равен плюс бесконечности (минус бесконечности), если для всякого C найдётся такая δ>0, что для всех x из проколотой δ-окрестности точки x0 выполняется неравенство: f(x)>C (соответственно, f(x)<C).
Упражнение 1. Запишите эти три определения в кванторах.
Пример 4. Неверно, что 1/x→+∞ при x→0: когда x приближается к нулю слева (то есть становится очень маленьким по модулю, но отрицательным), 1/x становится большим по модулю, но тоже отрицательным. В то же время, 1/(x2)→+∞ при x→0: знаменатель всегда положительный при x≠0, и когда он маленький по модулю, дробь становится очень большой.
Наконец, можно рассматривать односторонние бесконечные пределы.
Упражнение 2. Придумайте определения для утверждений limx→x+0f(x)=+∞,
limx→x+0f(x)=−∞, limx→x−0f(x)=+∞,
limx→x−0f(x)=−∞ самостоятельно, объединяя определение
2 и определения 11 и 12
из лекции 10.
Упражнение 3. Снова рассмотрим функцию f(x)=1/x. Докажите, что
limx→0+1x=+∞
и
limx→0−1x=−∞.
Определение 3. Заметим, что если функция стремится к какой-нибудь из бесконечностей
(неважно, плюс, минус или просто бесконечности) когда x стремится к x0
с какой-нибудь стороны, график y=f(x) приближается к вертикальной прямой
x=x0 когда x приближается к x0 (слева или справа). В этом случае
прямая x=x0 называется
Пример 5. Рассмотрим функцию
f(x)=x−1×2−1.
Знаменатель обнуляется в двух точках: x=1 и x=−1. При приближении к
точке x=−1 знаменатель стремится к нулю, а числитель к −2. Значит, дробь
стремится к бесконечности (без знака, т.к. знаменатель может быть
положительным или отрицательным, в зависимости от того, с какой стороны
приближаемся). У функции есть вертикальная асимптота x=−1. В точке x=1
обнуляется и числитель, и знаменатель. Чтобы найти предел в этой точке,
сократим дробь на (x−1). Получится выражение 1/(x+1). Оно имеет предел,
равный 1/2 при x→1. Значит, вертикальной асимптоты x=1 у функции
нет.
В точке x=1
обнуляется и числитель, и знаменатель. Чтобы найти предел в этой точке,
сократим дробь на (x−1). Получится выражение 1/(x+1). Оно имеет предел,
равный 1/2 при x→1. Значит, вертикальной асимптоты x=1 у функции
нет.
Рис. 12.2: У функции f(x)=x−1×2−1 есть единственная вертикальная асимптота: x=−1.
12.2Пределы на бесконечности
Другой тип пределов функций, связанный с бесконечностями — это предел при x стремящемся к бесконечности.
12.2.1Конечные пределы на бесконечности и горизонтальные асимптоты
Определение 4. Пусть функция f(x) определена для всех достаточно больших по модулю значений x, то есть найдётся такое C∗, что f(x) определена для всех x, для которых |x|>C∗. Говорят, что предел функции f(x) при x стремящемся к бесконечности равен b, если для всякого ε>0 найдётся такое C, что для всех x, если |x|>C, то |f(x)−b|<ε.
Определение 5. Пусть функция f(x) определена для всех достаточно больших значений x, то
есть найдётся такое C∗, что f(x) определена для всех x>C∗. Говорят,
что предел функции f(x) при x стремящемся к плюс бесконечности равен
b, если для всякого ε>0 найдётся такое C, что для всех x>C
верно неравенство |f(x)−b|<ε.
Говорят,
что предел функции f(x) при x стремящемся к плюс бесконечности равен
b, если для всякого ε>0 найдётся такое C, что для всех x>C
верно неравенство |f(x)−b|<ε.
Определение 6. Пусть функция f(x) определена для всех достаточно больших по модулю отрицательных значений x, то есть найдётся такое C∗, что f(x) определена для всех x<C∗. Говорят, что предел функции f(x) при x стремящемся к минус бесконечности равен b, если для всякого ε>0 найдётся такое C, что для всех x<C верно неравенство |f(x)−b|<ε.
Обозначения:
limx→∞f(x)=b,limx→+∞f(x)=b,limx→−∞f(x)=b.
Упражнение 4. Докажите, что если limx→∞f(x)=b, то limx→+∞f(x)=b и limx→−∞f(x)=b. Верно и обратное: если limx→+∞f(x)=b и limx→−∞f(x)=b, то limx→∞f(x)=b. Докажите и это.
Пример 6. Функция f(x)=1/x стремится к нулю при x→∞. (Докажите!)
Пример 7. Функция f(x)=ex стремится к нулю при x→−∞, а предел при x→+∞ не существует.
Определение 7. Если функция стремится к какому-то числу при x→+∞ или x→−∞,
её график приближается к горизонтальной прямой y=b.
Рис. 12.3: Прямая y=0 является горизонтальной асимптотой функции f(x)=(sinx)/x.
Вопрос 1. Сколько вертикальных асимптот может быть у функции?
Сколько угодно, даже бесконечное число.
Верный ответ. Это правда. Например, у тангенса их бесконечно много.
Тоже не больше двух.
Неверный ответ. У функции f(x)=1/(x(x−1)(x+1)) их три!
Сколько угодно, но конечное число.
Неверный ответ. Что насчёт тангенса?
Вопрос 2. Рассмотрим два предела: предел функции limx→+∞sin(πx) и предел последовательности limn→∞sin(πn). Что вы можете про них сказать?
Они оба существуют, но не равны.
Неверный ответ.
Этого не может быть из определения предела по Гейне.
Они оба существуют и равны.
Неверный ответ. Это вряд ли. Функция sinπx может принимать значения 1 или −1 для сколь угодно больших x.
Они оба не существуют.
Неверный ответ. А что вы можете сказать про последовательность {sin(πn)}? Найдите несколько её членов.
Предел функции существует, а предел последовательности нет.
Неверный ответ. Этого не может быть из определения предела по Гейне.
Предел последовательности существует, а предел функции нет.
Верный ответ. И правда! Последовательность на самом деле состоит из нулей и её предел равен нулю. А функция sinπx может принимать значения 1 или −1 для сколь угодно больших x, и значит не имеет предела.
12.2.2Бесконечные пределы на бесконечности
Мы рассмотрели бесконечные пределы в конечных точках и конечные пределы на
бесконечности. Можно скрестить ужа с ежом и получить бесконечные пределы
при x стремящемся к бесконечности.
Можно скрестить ужа с ежом и получить бесконечные пределы
при x стремящемся к бесконечности.
Определение 8. Пусть функция f(x) определена для всех достаточно больших значений x, то есть найдётся такое C∗, что f(x) определена для всех x>C∗. Говорят, что предел функции f(x) при x стремящемся к плюс бесконечности равен плюс бесконечности, если для всякого D найдётся такое C, что для всех x>C верно неравенство f(x)>D. Записывают:
limx→+∞f(x)=+∞.
Упражнение 5. Придумайте определения для остальных комбинаций бесконечностей.
Пример 8. Функция f(x)=x2 стремится к плюс бесконечности при x→∞, а функция f(x)=x3 стремится просто к бесконечности при x→∞.
Пример 9. Рассмотрим функцию
f(x)=11+e−x.
При x→+∞ функция e−x стремится к нулю (она равна 1/ex, и раз ex становится очень-очень большим, e−x становится очень близким к нулю). По арифметике пределов,
limx→+∞11+e−x=11+0=1.
При x→−∞ функция e−x стремится к плюс бесконечности. В этом случае знаменатель дроби также стремится к плюс бесконечности. Поскольку числитель равен 1, значение дроби стремится к нулю (см. утверждение 2 из лекции 7, где шла речь про «арифметику бесконечностей»). Значит
limx→−∞11+e−x=0.
У нашей функции две горизонтальные асимптоты: y=0 и y=1. (И вообще это важная функция — так называемая «сигмоида», встречается в эконометрике и нейросетях.)
Рис. 12.4: У функции f(x)=1/(1+e−x) две горизонтальные асимптоты: y=0 и y=1.
12.2.3Наклонные асимптоты
Пусть limx→∞f(x)=∞. Тогда функция не может иметь горизонтальных асимптот. Однако её график по-прежнему может приближаться к какой-нибудь прямой — только не горизонтальной.
Пример 10. Рассмотрим функцию
f(x)=x+1x.
Её предел при x→∞ равен бесконечности, и когда x стремится к
бесконечности, график функции неограниченно приближается к прямой y=x.
Рис. 12.5: У функции f(x)=x+1x есть наклонная асимптота y=x.
Действительно, давайте возьмём большое значение x=x0 и посчитаем «расстояние по вертикали» между графиком функции и прямой y=x для этого значения x. (Иными словами, мы проведём вертикальную прямую x=x0 и посмотрим на расстояние между точками пересечения этой прямой и графиков y=f(x) и y=x.) Это расстояние вычисляется как |f(x)−x|=|1/x|. Оно стремится к нулю при x→∞.
Определение 9. Прямая y=kx+b называется наклонной асимптотой функции f(x) (или её графика), если хотя бы один из пределов
limx→+∞(f(x)−(kx+b)),
или
limx→−∞(f(x)−(kx+b))
равен нулю.
Как искать наклонные асимптоты? На эту тему есть рецепт.
Утверждение 1. Наклонная асимптота y=kx+b при x→+∞ у функции f(x) существует
тогда и только тогда, когда существуют пределы
limx→+∞f(x)x=k;limx→+∞(f(x)−kx)=b. (12.1)(12.2)
При этом они обязаны равняться указанным значениям (k и b).
(12.1)(12.2)
При этом они обязаны равняться указанным значениям (k и b).
Доказательство. Докажем в одну сторону. Пусть y=kx+b является наклонной асимптотой функции f(x) при x→+∞. Тогда
limx→+∞f(x)x=limx→+∞f(x)−(kx+b)+(kx+b)x==limx→+∞(f(x)−(kx+b)x+k+bx)=k
limx→+∞f(x)x==limx→+∞f(x)−(kx+b)+(kx+b)x==limx→+∞(f(x)−(kx+b)x+k+bx)=k
Предел первого слагаемого равен нулю, поскольку числитель стремится к нулю (по предположению), а знаменатель к бесконечности.
Со вторым пределом ещё проще:
limx→+∞(f(x)−kx)=limx→+∞((f(x)−(kx+b)+b)=b.
limx→+∞(f(x)−kx)==limx→+∞((f(x)−(kx+b)+b)=b.
В обратную сторону. Пусть существует предел (12.2) и он равен b. Тогда
limx→+∞(f(x)−(kx+b))=limx→+∞(f(x)−kx)−b=b−b=0.
limx→+∞(f(x)−(kx+b))==limx→+∞(f(x)−kx)−b=b−b=0.
Утверждение доказано. ∎
∎
Конечно, можно сформулировать и доказать аналогичное утверждение для x→−∞.
Таким образом, чтобы найти наклонные асимптоты, нужно сперва найти предел (12.1). Если он не существует, наклонной асимптоты (для этой бесконечности) точно нет. Если существует, нужно найти предел (12.2). Если этот предел существует, прямая y=kx+b является наклонной асимптотой.
Пример 11. Может так случиться, что предел (12.1) существует, а предел (12.2) нет. Например, это верно для функции f(x)=sinx.
12.3Заключение
Главная цель математического анализа — научиться «заглядывать в бесконечность». В этой лекции мы серьезно продвинулись в этом навыке.
← Предыдущая глава Следующая глава →
0 lim
0 limВы искали 0 lim? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 1 0 lim, не
исключение.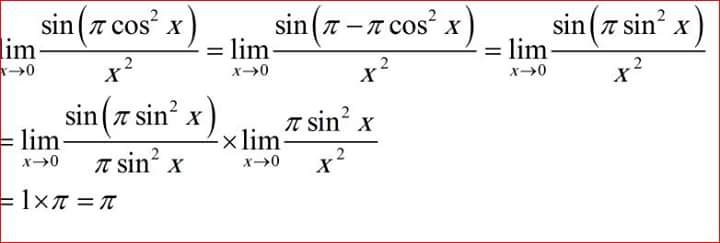 Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «0 lim».
Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «0 lim».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 0 lim,1 0 lim,1 lim,1 x предел,cosx x предел,lim,lim 0,lim 0 1,lim 0 x,lim 0 бесконечность,lim 1,lim 1 0,lim 1 x 1,lim 1 равен,lim a x,lim a x a lim x,lim f x бесконечность,lim n,lim n стремится к бесконечности,lim n стремится к бесконечности n,lim n стремится к бесконечности как решать,lim sin,lim sinx,lim tgx,lim x,lim x 0,lim x 0 1 x 0,lim x 0 x 1 x,lim x 0 x sinx,lim x 1,lim x 2 a 2 x a,lim x a 1 x 1,lim x n 1 x 1,lim x бесконечность,lim x стремится,lim x стремится к,lim x стремится к 0,lim x стремится к 0 sinx x,lim x стремится к 0 x tgx,lim x стремится к 0 как решать,lim x стремится к 1,lim x стремится к бесконечности,lim x стремится к бесконечности x,lim x стремится к бесконечности как решать,lim алгебра,lim в математике,lim в математике что это,lim в математике это,lim как решить,lim математика,lim пределы,lim решение,lim стремится к 0,lim стремится к бесконечности,lim формулы,lim функции,lim что значит,lim что такое,lim что это,lim что это в математике,lim что это в физике,lim это,lim это в математике,lim это что,x lim,x lim 0,алгебра lim,виды пределов,вычисление лимитов,вычисление предела,вычисление предела функции,вычисление пределов,вычисление пределов с подробным решением,вычисление пределов функции,вычисление пределов функций,вычисления пределов,вычислите предел,вычислите предел функции,вычислите пределы,вычислить предел,вычислить предел функции,вычислить предел функции lim,вычислить пределы,вычислить пределы функции,вычислить пределы функций,вычислить функции пределы,если предел равен 0,если предел стремится к бесконечности,как вычислить предел,как вычислить предел функции,как вычислить пределы,как вычислять пределы,как вычислять пределы функции,как искать пределы,как найти предел,как найти предел функции,как найти предел функции примеры решения,как найти пределы,как находить предел,как находить пределы,как находить пределы функций,как понять пределы,как посчитать предел,как решать lim,как решать предел функции,как решать пределы функции,как решить lim,как решить предел,как решить пределы,как считать предел,как считать пределы,как считать пределы функций,лим в математике,лим математика,лим что такое в математике,лимит алгебра,лимит найти,лимит функции,лимиты и пределы,лимиты математика,математика lim,математика лим,математика пределы функций объяснение с нуля,математика решение пределов,найдите предел,найдите предел функции lim,найдите пределы,найти предел,найти предел lim x стремится к бесконечности,найти предел функции,найти пределы,найти пределы как,найти пределы функции,найти пределы функций,найти указанные пределы,нахождение предела,нахождение предела функции,нахождение пределов,нахождение пределов функции,понятие предела,предел,предел 0 1,предел 1,предел 1 0 равен,предел 1 x,предел 1 x 1,предел 1 равен 0,предел x 1 x,предел в алгебре,предел как найти,предел как находить,предел как посчитать,предел как решать,предел как считать,предел посчитать,предел при x стремящемся к 0,предел при х стремящемся к бесконечности,предел равен 0 когда,предел решение,предел стремится к бесконечности,предел стремится к нулю,предел стремящийся к бесконечности,предел функции,предел функции в математике это,предел функции в точке примеры решения,предел функции вычисление предела функции,предел функции как найти,предел функции как решать,предел функции примеры,предел функции решение,предел функции формулы,предел функции это в математике,предел функций,предел х в степени х,предел х при х стремящемся к бесконечности,предел х стремится к 0,предел х стремится к бесконечности,предел х стремится к бесконечности х,предел что такое,предел что это,предел это,предел это что такое,предела,предела значение,предела решение,пределе,пределов функции решение,пределы,пределы lim,пределы и лимиты,пределы как вычислить,пределы как искать,пределы как найти,пределы как понять,пределы при х стремится к бесконечности,пределы решать,пределы решение,пределы решить,пределы стремящиеся к бесконечности,пределы функции,пределы функции как решать,пределы функции примеры,пределы функции решение,пределы функций,пределы функций примеры,пределы что такое,пределы что это,пределы это,пределы это что,придел это,примеры предел функции,примеры пределы функции,расчет пределов,решать пределы,решение lim,решение лимитов,решение предел,решение предел функции,решение предела,решение пределов,решение пределов функции,решение пределов функций,решение пределы,решение функции пределов,решение функций пределов,решения пределов,решения пределы,решить предел,решить пределы,стремится к бесконечности,стремится к нулю предел,формулы lim,функции lim,функции пределы как решать,функции пределы примеры,что такое lim,что такое lim в алгебре,что такое lim в математике,что такое в математике lim,что такое в физике lim,что такое предел. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 0 lim. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 1 lim).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 0 lim. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 1 lim).
Решить задачу 0 lim вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
объяснение, теория, примеры решений. Понятие предела в математике
Определение пределов последовательности и функции, свойства пределов, первый и второй замечательные пределы, примеры.
Постоянное число а называется пределом последовательности {x n }, если для любого сколь угодно малого положительного числа ε > 0 существует номер N, что все значения x n , у которых n>N, удовлетворяют неравенству
Записывают это следующим образом: или x n →
a.
Неравенство (6.1) равносильно двойному неравенству
a — ε x n , начиная с некоторого номера n>N, лежат внутри интервала (a-ε , a+ε), т.е. попадают в какую угодно малую ε-окрестность точки а .
Последовательность, имеющая предел, называется сходящейся , в противном случае — расходящейся .
Понятие предел функции является обобщением понятия предел последовательности, так как предел последовательности можно рассматривать как предел функции x n = f(n) целочисленного аргумента n .
Пусть дана функция f(x) и пусть a — предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a . Точка a может принадлежать множеству D(f), а может и не принадлежать ему.
Определение 1. Постоянное число А называется предел функции f(x) при x→ a, если для всякой последовательности {x n } значений аргумента, стремящейся к а , соответствующие им последовательности {f(x n)} имеют один и тот же предел А.
Это определение называют определением предела функции по Гейне, или “на языке последовательностей ”.
Определение 2 . Постоянное число А называется предел функции f(x) при x→a, если, задав произвольное, как угодно малое положительное число ε, можно найти такое δ
>0 (зависящее от ε), что для всех x , лежащих в ε-окрестности числа а , т.е. для x , удовлетворяющих неравенству
0
Это определение называют определением предел функции по Коши, или “на языке ε — δ «
Определения 1 и 2 равносильны. Если функция f(x) при x → a имеет предел , равный А, это записывается в виде
В том случае, если последовательность {f(x n)} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а , то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:
Переменная величина (т.е. последовательность или функция), предел которой равен нулю, называется бесконечно малой величиной.
Переменная величина, предел которой равен бесконечности, называется бесконечно большой величиной .
Чтобы найти предел на практике пользуются следующими теоремами.
Теорема 1 . Если существует каждый предел
(6.4)
(6.5)
(6.6)
Замечание . Выражения вида 0/0, ∞/∞, ∞-∞ 0*∞ являются неопределенными, например, отношение двух бесконечно малых или бесконечно больших величин, и найти предел такого вида носит название “раскрытие неопределенностей”.
Теорема 2.
т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности,
Теорема 3.
(6.11)
где e » 2.7 — основание натурального логарифма. Формулы (6.10) и (6.11) носят название первый замечательного предело и второй замечательный предел.
Используются на практике и следствия формулы (6.11):
(6.12)
(6.13)
(6.14)
в частности предел,
Eсли x → a и при этом x > a, то пишут x →a + 0. Если, в частности, a = 0, то вместо символа 0+0 пишут +0. Аналогично если x→a и при этом x и называются соответственно предел справа и предел слева функции f(x) в точке а . Чтобы существовал предел функции f(x) при x→
a необходимо и достаточно, чтобы . Функция f(x) называется непрерывной в точке x 0 , если предел
Если, в частности, a = 0, то вместо символа 0+0 пишут +0. Аналогично если x→a и при этом x и называются соответственно предел справа и предел слева функции f(x) в точке а . Чтобы существовал предел функции f(x) при x→
a необходимо и достаточно, чтобы . Функция f(x) называется непрерывной в точке x 0 , если предел
(6.15)
Условие (6.15) можно переписать в виде:
то есть возможен предельный переход под знаком функции, если она непрерывна в данной точке.
Если равенство (6.15) нарушено, то говорят, что при x = x o функция f(x) имеет разрыв. Рассмотрим функцию y = 1/x. Областью определения этой функции является множество R , кроме x = 0. Точка x = 0 является предельной точкой множества D(f), поскольку в любой ее окрестности, т.е. в любом открытом интервале, содержащем точку 0, есть точки из D(f), но она сама не принадлежит этому множеству. Значение f(x o)= f(0) не определено, поэтому в точке x o = 0 функция имеет разрыв.
Функция f(x) называется непрерывной справа в точке x o , если предел
и непрерывной слева в точке x o, если предел
Непрерывность функции в точке x o равносильна ее непрерывности в этой точке одновременно и справа и слева.
Для того, чтобы функция была непрерывна в точке x o , например, справа, необходимо, во-первых, чтобы существовал конечный предел , а во-вторых, чтобы этот предел был равен f(x o). Следовательно, если хотя бы одно из этих двух условий не выполняется, то функция будет иметь разрыв.
1. Если предел существует и не равен f(x o), то говорят, что функция f(x) в точке x o имеет разрыв первого рода, или скачок .
2. Если предел равен +∞ или -∞ или не существует, то говорят, что в точке x o функция имеет разрыв второго рода .
Например, функция y = ctg x при x → +0 имеет предел, равный +∞
, значит, в точке x=0 она имеет разрыв второго рода. Функция y = E(x) (целая часть от x ) в точках с целыми абсциссами имеет разрывы первого рода, или скачки.
Функция y = E(x) (целая часть от x ) в точках с целыми абсциссами имеет разрывы первого рода, или скачки.
Функция, непрерывная в каждой точке промежутка , называется непрерывной в . Непрерывная функция изображается сплошной кривой.
Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины. К таким задачам, например, относятся: рост вклада по закону сложных процентов, рост населения страны, распад радиоактивного вещества, размножение бактерий и т.п.
Рассмотрим пример Я. И. Перельмана , дающий интерпретацию числа e в задаче о сложных процентах. Число e есть предел . В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример. Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 ×1,5 = 150, а еще через полгода — в 150× 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 ×
(1 +1/3) 3 ≈ 237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:
ед. превратятся в 200 ден.ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 ×1,5 = 150, а еще через полгода — в 150× 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 ×
(1 +1/3) 3 ≈ 237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:
100×(1 +1/10) 10 ≈ 259 (ден. ед.),
100×(1+1/100) 100 ≈ 270 (ден. ед.),
100×(1+1/1000) 1000 ≈271 (ден. ед.).
При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что предел
Пример 3. 1 .
Пользуясь определением предела числовой последовательности, доказать, что последовательность x n =(n-1)/n имеет предел, равный 1.
1 .
Пользуясь определением предела числовой последовательности, доказать, что последовательность x n =(n-1)/n имеет предел, равный 1.
Решение. Нам надо доказать, что, какое бы ε > 0 мы ни взяли, для него найдется натуральное число N, такое, что для всех n > N имеет место неравенство |x n -1|
Возьмем любое ε > 0. Так как x n -1 =(n+1)/n — 1= 1/n, то для отыскания N достаточно решить неравенство 1/n1/ε и, следовательно, за N можно принять целую часть от 1/ε N = E(1/ε). Мы тем самым доказали, что предел .
Пример 3.2. Найти предел последовательности, заданной общим членом .
Решение.
Применим теорему предел суммы и найдем предел каждого слагаемого. При n → ∞ числитель и знаменатель каждого слагаемого стремится к бесконечности, и мы не можем непосредственно применить теорему предел частного. Поэтому сначала преобразуем x n , разделив числитель и знаменатель первого слагаемого на n 2 , а второго на n . Затем, применяя теорему предел частного и предел суммы, найдем:
Затем, применяя теорему предел частного и предел суммы, найдем:
Пример 3.3 . . Найти .
Решение.
Здесь мы воспользовались теоремой о пределе степени: предел степени равен степени от предела основания.
Пример 3.4 . Найти ().
Решение. Применять теорему предел разности нельзя, поскольку имеем неопределенность вида ∞-∞. Преобразуем формулу общего члена:
Пример 3.5 . Дана функция f(x)=2 1/x . Доказать, что предел не существует.
Решение. Воспользуемся определением 1 предела функции через последовательность. Возьмем последовательность { x n }, сходящуюся к 0, т.е. Покажем, что величина f(x n)= для разных последовательностей ведет себя по-разному. Пусть x n = 1/n. Очевидно, что , тогда предел Выберем теперь в качестве x n последовательность с общим членом x n = -1/n, также стремящуюся к нулю. Поэтому предел не существует.
Пример 3.6 . Доказать, что предел не существует.
Решение. Пусть x 1 , x 2 ,…, x n ,… — последовательность, для которой
. Как ведет себя последовательность {f(x n)} = {sin x n } при различных x n → ∞
Если x n =
p
n, то sin x n = sin (p
n) = 0 при всех n и предел Если же
x n =2
p
n+
p
/2, то sin x n = sin(2
p
n+
p
/2) = sin
p
/2 = 1 для всех n и следовательно предел . Таким образом, не существует.
Предел функции — число a будет пределом некоторой изменяемой величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a .
Или другими словами, число A является пределом функции y = f (x) в точке x 0 , если для всякой последовательности точек из области определения функции , не равных x 0 , и которая сходится к точке x 0 (lim x n = x0) , последовательность соответствующих значений функции сходится к числу A .
График функции, предел которой при аргументе, который стремится к бесконечности, равен L :
Значение А является пределом (предельным значением) функции f (x) в точке x 0 в случае, если для всякой последовательности точек , которая сходится к x 0 , но которая не содержит x 0 как один из своих элементов (т. е. в проколотой окрестности x 0 ), последовательность значений функции сходится к A .
е. в проколотой окрестности x 0 ), последовательность значений функции сходится к A .
Предел функции по Коши.
Значение A будет являться пределом функции f (x) в точке x 0 в случае, если для всякого вперёд взятого неотрицательного числа ε будет найдено соответствующее ему неотрицательно число δ = δ(ε) такое, что для каждого аргумента x , удовлетворяющего условию 0 , будет выполнено неравенство | f (x) A | .
Будет очень просто, если вы понимаете суть предела и основные правила нахождения его. То, что предел функции f (x) при x стремящемся к a равен A , записывается таким образом:
Причем значение, к которому стремится переменная x , может быть не только числом, но и бесконечностью (∞), иногда +∞ или -∞, либо предела может вообще не быть.
Чтоб понять, как находить пределы функции , лучше всего посмотреть примеры решения.
Необходимо найти пределы функции f (x) = 1/ x при:
x → 2, x → 0, x → ∞.
Найдем решение первого предела. Для этого можно просто подставить вместо x число, к которому оно стремится, т.е. 2, получим:
Найдем второй предел функции . Здесь подставлять в чистом виде 0 вместо x нельзя, т.к. делить на 0 нельзя. Но мы можем брать значения, приближенные к нулю, к примеру, 0,01; 0,001; 0,0001; 0,00001 и так далее, причем значение функции f (x) будет увеличиваться: 100; 1000; 10000; 100000 и так далее. Т.о., можно понять, что при x → 0 значение функции, которая стоит под знаком предела, будет неограниченно возрастать, т.е. стремиться к бесконечности. А значит:
Касаемо третьего предела. Такая же ситуация, как и в прошлом случае, невозможно подставить ∞ в чистом виде. Нужно рассмотреть случай неограниченного возрастания x .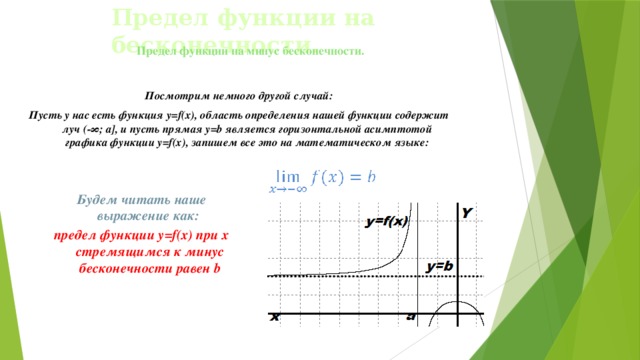 Поочередно подставляем 1000; 10000; 100000 и так далее, имеем, что значение функции f (x) = 1/ x будет убывать: 0,001; 0,0001; 0,00001; и так далее, стремясь к нулю. Поэтому:
Поочередно подставляем 1000; 10000; 100000 и так далее, имеем, что значение функции f (x) = 1/ x будет убывать: 0,001; 0,0001; 0,00001; и так далее, стремясь к нулю. Поэтому:
Необходимо вычислить предел функции
Приступая к решению второго примера, видим неопределенность . Отсюда находим старшую степень числителя и знаменателя — это x 3 , выносим в числителе и знаменателе его за скобки и далее сокращаем на него:
Ответ
Первым шагом в нахождении этого предела , подставим значение 1 вместо x , в результате чего имеем неопределенность . Для её решения разложим числитель на множители , сделаем это методом нахождения корней квадратного уравнения x 2 + 2 x — 3 :
D = 2 2 — 4*1*(-3) = 4 +12 = 16 → √ D = √16 = 4
x 1,2 = (-2 ± 4) / 2 → x 1 = -3; x 2 = 1.
Таким образом, числитель будет таким:
Ответ
Это определение его конкретного значения или определенной области, куда попадает функция, которая ограничена пределом. 2 стремится к нулю.
2 стремится к нулю.
Обычно переменная величина x стремится к конечному пределу a, причем, x постоянно приближается к a, а величина a постоянна. Это записывают следующим образом: limx =a, при этом, n также может стремиться как к нулю, так и к бесконечности. Существуют бесконечные функции, для них предел стремится к бесконечности. В других случаях, когда, например, функцией замедление хода поезда, можно о пределе, стремящемся к нулю.
У пределов имеется ряд свойств. Как правило, любая функция имеет только один предел. Это главное свойство предела. Другие их свойства перечислены ниже:
* Предел суммы равен сумме пределов:
lim(x+y)=lim x+lim y
* Предел произведения равен произведению пределов:
lim(xy)=lim x*lim y
* Предел частного равен частному от пределов:
lim(x/y)=lim x/lim y
* Постоянный множитель выносят за знак предела:
lim(Cx)=C lim x
Если дана функция 1 /x, в которой x →∞, ее предел равен нулю. Если же x→0, предел такой функции равен ∞.
Для тригонометрических функций имеются исключения из этих правил. Так как функция sin x всегда стремится к единице, когда приближается к нулю, для нее справедливо тождество:
Так как функция sin x всегда стремится к единице, когда приближается к нулю, для нее справедливо тождество:
lim sin x/x=1
В ряде задач встречаются функции, при вычислении пределов которых возникает неопределенность — ситуация, при которой предел невозможно вычислить. Единственным выходом из такой ситуации становится применение правила Лопиталя. Существует два вида неопределенностей:
* неопределенность вида 0/0
* неопределенность вида ∞/∞
К примеру, дан предел следующего вида: lim f(x)/l(x), причем, f(x0)=l(x0)=0. В таком случае, возникает неопределенность вида 0/0. Для решения такой задачи обе функции подвергают дифференцированию, после чего находят предел результата. Для неопределенностей вида 0/0 предел равен:
lim f(x)/l(x)=lim f»(x)/l»(x) (при x→0)
Это же правило справедливо и для неопределенностей типа ∞/∞. Но в этом случае справедливо следующее равенство: f(x)=l(x)=∞
С помощью правила Лопиталя можно находить значения любых пределов, в которых фигурируют неопределенности. (n-1)
(n-1)
Пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции, так как именно с ними чаще всего сталкиваются студенты. Но сначала — самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A , к которому стремится функция при х , стремящемся к определенной точке а . Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim — от английского limit — предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача — найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют базовые операции над матрицами , читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х . Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0 . Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением. n, на него и упрощаем
n, на него и упрощаем
Далее оцениваем вклад каждого слагаемого
Слагаемые 3/8 стремятся к нулю при переменной направляюейся к бесконечности, поскольку 3/8<1 (свойство степенно-показательной функции).
Пример 37.Предел последовательности с факториалами раскрывается розписанням факториала к наибольшему общему множителю для числителя и знаменателя.
Далее на него сокращаем и оцениваем лимит по значению показателей номера в числителе и знаменателе.
В нашем примере знаменатель быстрее растет, поэтому предел равен нулю.
Здесь использована следующее
свойство факториала.
Пример 38.Не применяя правила Лопиталя сравниваем максимальные показатели переменной в числителе и знаменателе дроби.
Так как знаменатель содержит старший показатель переменной 4>2 то и растет он быстрее.
Отсюда делаем вывод, что предел функции стремится к нулю.
Пример 39.Раскрываем особенность вида бесконечность разделить на бесконечность методом вынесения x^4 с числителя и знаменателя дроби. 3 и выполним предельный переход
3 и выполним предельный переход
Пример 41.Имеем особенность типа единица в степени бесконечность.
А это значит, что выражение в скобках и сам показатель надо свести под вторую важную границу.
Распишем числитель, чтобы выделить в нем выражение идентичное знаменателе.
Далее переходим к выражению, содержащем единицу плюс слагаемое.
В степени нужно выделить множителем 1/(слагаемое).
Таким образом получим экспоненту в степени предела дробной функции.
Для раскрития особенности использовали второй предел:
Пример 42.Имеем особенность типа единица в степени бесконечность.
Для ее раскрытия следует свести функцию под второй замечатеьный предел.
Как это сделать подробно показано в приведенной далее формуле
Подобных задач Вы можете найти очень много. Их суть в том, чтобы в показателе получить нужный степень, а он равен обратному значению слагаемого в скобках при единицы.
Таким методом получаем экспоненту. Дальнейшее вычисление сводится к вичислению предела степени экспоненты.
Дальнейшее вычисление сводится к вичислению предела степени экспоненты.
Здесь экспоненциальная функция стремится к бесконечности , поскольку значение больше единицы e=2.72>1.
Пример 43 В знаменателе дроби имеем неопределенность типа бесконечность минус бесконечность, фактически равное делению на ноль.
Чтобы избавиться корня домножим на сопряженное выражение, а дальше по формуле разности квадратов перепишем знаменатель.
Получим неопределенность бесконечность разделить на бесконечность, поэтому выносим переменную в наибольшей степени и сокращаем на нее.
Далее оцениваем вклад каждого слагаемого и находим предел функции на бесконечности
Пример 44.Найти повторные границы
Решение: Вычисляем предел функции двух переменных сначала по y, а дальше – x)
a)
б)
Пример 45. Вычислить повторные границы
Решение: Методика вычисления повторных границ не сложна:
сначала находим границу по одной переменной, считая вторую переменную постоянной.
Далее остается функция от одной переменной, а таких пределов мы разобрали очень много.
а)
б)
В этом задании предел по первой переменной равен нулю, поэтому повторные записываем только для формальности.
Предел в данном случае от порядка нахождения не зависит.
Однако, если взглянуть ответ из предыдущего примера то такое утверждение не всегда выполняется.
Ищите эффективные схемы вычисления пределов на страницах сайта, если возникают проблемы с пределами на экзаменах и модулях — обращайтесь за помощью!
Предел «бесконечности» — подход к исчислению
Подход
к
C A L C U L U S
Содержание | Дом
4
Определение «становится бесконечным»
Пределы рациональных функций
Изменение переменной
БЕСКОНЕЧНОСТЬ вместе со своим символом ∞ не является числом и не местом. Когда в исчислении мы говорим, что функция становится «бесконечной», мы просто имеем в виду, что нет предела ее значениям.
Пусть f ( x ), например, будет . Затем, когда значения x становятся все меньше и меньше, значения f ( x ) становятся все больше и больше. Независимо от того, какое большое число мы назовем, можно будет назвать значение x таким образом, что значение f ( x ) будет больше, чем это число, которое мы назвали.
Тогда мы говорим, что значения f ( x ) становятся бесконечными или стремятся к бесконечности. Мы говорим, что как x приближается к 0, предел f ( x ) равен бесконечности.
Теперь предел — это число — граница. Поэтому, когда мы говорим, что предел бесконечен, мы имеем в виду, что нет числа , которое мы можем назвать.
Учащийся должен знать, что слово бесконечный в том виде, в каком оно используется в исчислении и использовалось исторически, не имеет того же значения, что и в теории бесконечных множеств. См. это из Википедии, особенно взгляды Карла Фридриха Гаусса в разделе «Прием аргументации».
ОПРЕДЕЛЕНИЕ 4. становится бесконечным. Мы говорим, что переменная «становится бесконечной» или «стремится к бесконечности», если, начиная с определенного члена в последовательности ее значений, абсолютное значение этого члена и любого последующего термина, который мы называем, больше, чем любое положительное число, которое мы называем , однако большой.
Когда переменная равна x и принимает только положительные значения, тогда x становится положительно бесконечным. Мы пишем
Если x принимает только отрицательные значения, оно становится отрицательно бесконечным, и в этом случае мы пишем
В обоих случаях мы имеем в виду: Независимо от того, какое большое число M мы назовем, мы дойдем до такой точки в последовательности значений x , что их абсолютные значения станут больше, чем M.
Когда переменная является функцией f ( x ), и она становится положительно или отрицательно бесконечной, когда x приближается к значению c , тогда пишем
Хотя мы пишем символ «lim» для обозначения предела, эти алгебраические утверждения означают: Предел f ( x ), когда x приближается к c , не существует. Опять же, предел — это число. (Определение 2.1.)
Опять же, предел — это число. (Определение 2.1.)
Определение 4 — это определение «становится бесконечным»; это не определение предела.
Что касается символа ∞, мы используем его в алгебраических утверждениях, чтобы показать, что определение становится бесконечным выполнено. Этот символ сам по себе не имеет значения.
| В качестве примера, вот график функции | г | = | 1 х | : |
Давайте посмотрим, что происходит со значениями и , когда x приближается к 0 справа:
Как последовательность значений x становятся очень маленькими числами, затем последовательность значений y , обратных величин, становится очень большими числами. Значения y станут и останутся больше, например, чем 10 100000000 . y становится бесконечным.
Пишем:
Если x приближается к 0 слева, то значения становятся большими отрицательными числами. В этом случае мы пишем
Когда функция становится бесконечной по мере того, как x приближается к значению c , тогда функция разрывна при x = c , а прямая линия x = c является вертикальной асимптотой графика. (Тема 18 Precalculus.) График y = , следовательно, разрывен при x = 0, а прямая линия x = c является вертикальной асимптотой.
Далее рассмотрим случай, когда x становится бесконечным, то есть когда его значения становятся большими положительными числами справа от 0.
В этом случае становится очень маленьким числом, а именно 0. Мы пишем
Мы должны читать это как «предел, когда х становится бесконечным», а не как « х приближается к бесконечности», потому что, опять же, бесконечность не является ни числом, ни местом. С другой стороны, мы могли бы читать это как угодно («ограничение в виде x вызывает головокружение»), если любое выражение, которое мы используем, относится к условию Определения 4.
С другой стороны, мы могли бы читать это как угодно («ограничение в виде x вызывает головокружение»), если любое выражение, которое мы используем, относится к условию Определения 4.
См. Первые принципы элементов Евклида, Комментарий к определениям. В частности, обратите внимание, что определение номинальное ; он утверждает только то, как будет использоваться слово или имя; и мы должны согласиться с этим.
Наконец, когда x становится бесконечным отрицательно, то есть когда оно принимает значения крайне слева от 0 (-∞), тогда снова приближается к 0. Мы пишем
Другими словами, всякий раз, когда x становится бесконечным положительно или отрицательно, значения y = приближаются к горизонтальной линии y = 0. Эта линия называется горизонтальной асимптотой графика.
| Задача 1. Оценить |
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
При загар x не существует. (Тема 15 и Тема 18 тригонометрии.)
По мере приближения x слева, тангенс x становится больше, чем любое число, которое мы можем назвать. (Определение 4.)
Пределы рациональных функций
Рациональная функция — это частное полиномов (раздел 6 предварительного исчисления). Он будет иметь такой вид:
| f ( x ) г ( x ) |
, где f и g — многочлены ( g 0).
Помимо постоянного члена, каждый член многочлена будет иметь множитель x n ( n ≥ 1). Поэтому исследуем следующие пределы.
c может быть любой положительной константой. Учащийся должен заполнить каждую правую часть.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала сделай сам!
| 1) | = | 0 | |
| 2а) | = | ∞ | |
| n четный. | |||
| 2б) | = | ∞ | |
| n нечетный. | |||
| 2в) | = | −∞ | |
| № нечетный. | |||
| Сравните y = | 1 х | выше, где n = 1, |
| 3) | = | ∞ | |
| 4) | = | ∞ | |
Пример. Докажите: Докажите: |
Решение . Разделите числитель и знаменатель на наибольшую степень x . В этом случае разделите их на x 2 :
Согласно приведенному выше пункту 1 предел каждого члена, содержащего x , равен 0. Следовательно, по теоремам темы 2 мы имеем требуемый ответ.
В подобных случаях первый шаг: Разделите числитель и знаменатель на степень x , которая стоит в старшем члене любого из них.
| Задача 2. | = | 4 |
Результат следует после деления числителя и знаменателя на x .
| Задача 3. | = |
Другими словами: Когда числитель и знаменатель имеют одинаковую степень,
, тогда предел, когда x становится бесконечным, равен частному старших коэффициентов.
Задача 4.
| = | = | = | 0. |
Далее рациональная функция обратна приведенной выше:
| = | = | ∞ |
Эта задача иллюстрирует:
Когда степень знаменателя больше степени числителя, то есть когда преобладает знаменатель, тогда предел, когда x становится бесконечным, равен 0. Но когда преобладает числитель, — когда степень числителя больше — тогда предел, когда x становится бесконечным, составляет .
Изменение переменной
Учитывайте это ограничение:
Вместо того, чтобы приближать переменную к 0, мы иногда предпочитаем, чтобы она стала бесконечной. В этом случае мы делаем замену переменной. Ставим x = или , это не имеет значения. Ибо x , приближающееся к 0, эквивалентно тому, что z становятся бесконечными. Затем
Ставим x = или , это не имеет значения. Ибо x , приближающееся к 0, эквивалентно тому, что z становятся бесконечными. Затем
При замене x на , мы позволяем z стать бесконечными. Лимит остается 1.
Где это всплывет? В пределе, из которого мы вычисляем число e :
(Урок 15.)
Проблема 5. В приведенном выше пределе измените переменную на n , и пусть он станет бесконечным.
Следующий урок: Производная
Содержание | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
| 1 | Найдите производную — d/dx | натуральное бревно х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найдите производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найдите производную — d/dx | грех(2x) | |
| 23 | Найдите производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) по x | |
| 42 | Найдите производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценить интеграл 9бесконечность | ||
| 45 | Найдите производную — d/dx | х/2 | |
| 46 | Найдите производную — d/dx | -cos(x) | |
| 47 | Найдите производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найдите производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | предел, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найдите производную — d/dx | лог х | |
| 86 | Найдите производную — d/dx | арктан(х) | |
| 87 | Найдите производную — d/dx | бревно натуральное 5х92 |
| 1 | Найдите производную — d/dx | натуральное бревно х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | 92)|||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найдите производную — d/dx | грех(2x) | |
| 23 | Найдите производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) по x | |
| 42 | Найдите производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценить интеграл 9бесконечность | ||
| 45 | Найдите производную — d/dx | х/2 | |
| 46 | Найдите производную — d/dx | -cos(x) | |
| 47 | Найдите производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найдите производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | предел, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найдите производную — d/dx | лог х | |
| 86 | Найдите производную — d/dx | арктан(х) | |
| 87 | Найдите производную — d/dx | бревно натуральное 5х92 |
Исчисление — Пределы
Пределы при стремлении x к бесконечности
Интуитивно мы можем понять, что по мере того, как \(x\) становится все больше и больше,
1\(/x\) становится все меньше и меньше. Предел 1\(/x\) как \(x\)
стремится к бесконечности равно нулю. Мы пишем это как:
Предел 1\(/x\) как \(x\)
стремится к бесконечности равно нулю. Мы пишем это как:
\[\lim_{x\стрелка вправо \infty}\frac{1}{x}=0\]
Обратите внимание, что используется знак равенства, предел равен нулю.
Другой способ записи:
\[\frac{1}{x}\стрелка вправо 0 \text{ as } x\стрелка вправо \infty \]
Вместо этого мы используем стрелки, 1\(/x\) никогда не равно нулю, но стремится к нуль.
Делать , а не смешивать «lim» и стрелки или выражения и знак равенства; выберите одну из форм выше!
В общем случае мы называем предел \(A\) и записываем его как
\[\lim_{x\стрелка вправо \infty}f(x)=A \]
Точного определения предела нет в программе. Неофициально это означает что значение \(f(x)\) можно сделать настолько близким к \(A\), насколько мы хотим, если мы просто выберем \(x\) достаточно большим.
Горизонтальные асимптоты
Если функция \(f(x)\) имеет предел \(A\) при стремлении \(x\)
до бесконечности, то график \(f(x)\) будет все ближе и ближе к
строка \(y=A\). Линия \(y=A\) является горизонтальной асимптотой к \(f(x)\). 92+1} }\)
Линия \(y=A\) является горизонтальной асимптотой к \(f(x)\). 92+1} }\)
Есть ли способ найти горизонтальную асимптоту рациональной функции (что рациональная функция?) без использования электронного устройства? 92+2x-8} \]
Знаменатель равен нулю, когда \(x=2\) и когда \(x=-4\). Функция имеет две вертикальные асимптоты.
Мы можем приблизиться к значению \(x=2\) с двух сторон, либо \(x\lt 2\)
или \(2\lt х\) . Чтобы предел существовал, пределы, которые мы получаем из
два направления должны быть одинаковыми. В этом случае не существует предела, даже бесконечности. Функция
однако имеет вертикальную асимптоту. Иногда мы хотим указать, что выражение имеет разные
пределы в зависимости от того, приближаемся ли мы к пределу слева или справа. Мы используем + (\(x\) больше, чем)
или a — (\(x\) меньше), чтобы различать два случая. 92+2x-8} = -\infty\]
Мы используем + (\(x\) больше, чем)
или a — (\(x\) меньше), чтобы различать два случая. 92+2x-8} = -\infty\]
Трудные пределы
В некоторых случаях вы руководствуетесь здравым смыслом, чтобы найти ограничения:
\[\frac{1}\infty = 0 \hspace{1 см} \frac{1}{0}=\infty \hspace{1 см} 1+\infty=\infty \hspace{1 см} 2\ cdot \infty = \infty\]
(Не пишите так на ↑ экзамене)
В некоторых случаях сложно:
\[\frac{\infty}\infty = ? \hspace{1 см} \frac{0}{0}=? \hspace{1 см} \infty-\infty=? \hspace{1 см} 0\cdot \infty = ?\]
Упражнение 2
Постройте график следующих функций, чтобы найти пределы, если они существуют.
- \( \displaystyle{\lim_{x\стрелка вправо 0}\sin\left(\frac{1}{x}\right)} \)
- \( \displaystyle{\lim_{x\rightarrow 0} x \cdot \sin\left( \frac{1}{x}\right)} \)
- \( \displaystyle{\lim_{x\rightarrow 0} \frac{\sin x}{x} } \)
- \( \displaystyle{\lim_{x\rightarrow 0} \frac{\cos x -1}{x}} \) 9п}\)
Предел sin(x)/x, доказательство
Легко найти предел
\[\lim_{x \rightarrow 0}\frac{\sin x}{x} \]
численно. Если вы хотите доказать, что такое предел, вы должны использовать геометрию.
Если вы хотите доказать, что такое предел, вы должны использовать геометрию.
Чтобы предел стал простым числом, вы должны использовать радианы для измерения углов, это это причина, по которой градусы никогда не используются при вычислениях. Этот предел используется для нахождения производная тригонометрических функций.
Загрузить рабочий лист GeoGebra
Двигай П!Упражнение 4
Используя обозначения в таблице выше:
Найдите площади треугольников \(\Delta OAP\), \(\Delta OAB\) и площадь сектора \(OAP \). Опишите области в терминах \(\alpha \), \(\sin (\alpha)\) и \(\cos (\alpha)\).
Используйте неравенства \(\Delta OAP \lt OAP \lt \Delta OAB \) для нахождения предела
\[\lim_{\alpha \rightarrow 0}\frac{\alpha}{\sin{\alpha}} \]
Переставить неравенства, чтобы найти предел
\[\lim_{\alpha \rightarrow 0}\frac{\sin \alpha }{\alpha} \]
Малин Кристерссон в рамках Creative Commons Attribution-Noncommercial-Share
Alike 2. 5 Швеция Лицензия
5 Швеция Лицензия
www.malinc.se
Исчисление I. Пределы на бесконечности, часть I
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-7: Пределы на бесконечности, часть I
В предыдущем разделе мы видели пределы, которые были бесконечны, и теперь пришло время взглянуть на пределы в бесконечности.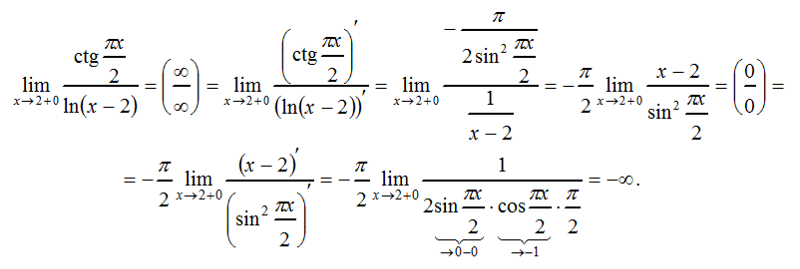 Под пределами на бесконечности мы понимаем один из следующих двух пределов.
Под пределами на бесконечности мы понимаем один из следующих двух пределов.
\[\ mathop {\ lim } \ limit_ {x \ to \ infty} f \ left ( x \ right) \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ mathop {\ lim } \ limit_{x \to — \infty} f\left( x \right)\]
Другими словами, мы собираемся посмотреть, что произойдет с функцией, если мы позволим \(x\) стать очень большим как в положительном, так и в отрицательном смысле. Кроме того, как мы вскоре увидим, эти пределы также могут иметь бесконечное значение.
Во-первых, отметим, что набор фактов из раздела «Бесконечный предел» также сохраняется, если мы заменим \(\mathop {\lim }\limits_{x \to \,c} \) на \(\mathop {\lim }\limits_{x \to \infty} \) или \(\mathop {\lim }\limits_{x \to — \infty} \). Доказательство этого почти идентично доказательству исходного набора фактов с небольшими изменениями, чтобы справиться с изменением предела, и поэтому остается за вами. Нам не понадобятся эти факты в следующих парах разделов, но иногда они потребуются. 9{r}\) определяется для отрицательного \(x\). Это условие здесь, чтобы избежать таких случаев, как \(r = \frac{1}{2}\). Если бы это \(r\) было разрешено, мы бы извлекали квадратный корень из отрицательных чисел, что было бы комплексно, и мы хотим избежать этого на этом уровне.
Нам не понадобятся эти факты в следующих парах разделов, но иногда они потребуются. 9{r}\) определяется для отрицательного \(x\). Это условие здесь, чтобы избежать таких случаев, как \(r = \frac{1}{2}\). Если бы это \(r\) было разрешено, мы бы извлекали квадратный корень из отрицательных чисел, что было бы комплексно, и мы хотим избежать этого на этом уровне.
Обратите внимание, что знак \(c\) не влияет на ответ. Независимо от знака \(c\) у нас все равно будет константа, деленная на очень большое число, что приведет к очень маленькому числу, и чем больше \(x\), тем меньше будет дробь. Знак \(c\) будет влиять на то, в каком направлении дробь приближается к нулю ( т.е. с положительной или отрицательной стороны), но все равно приближается к нулю.
Если подумать, это действительно частный случай последнего факта из фактов в предыдущем разделе. Однако, чтобы увидеть прямое доказательство этого факта, см. раздел «Доказательство различных предельных свойств» в главе «Дополнительно».
Давайте начнем примеры с одного, который приведет нас к хорошей идее, которую мы будем использовать на регулярной основе, относительно пределов на бесконечности для многочленов.
Пример 1 Оцените каждый из следующих пределов. 92} — 8x} \справа)\) Показать решение
Наша первая мысль здесь, вероятно, состоит в том, чтобы просто «подставить» бесконечность в многочлен и «вычислить» каждый член, чтобы определить значение предела. Довольно просто увидеть, что будет делать каждый член в пределе, и поэтому это кажется очевидным шагом, тем более что мы делали это для других пределов в предыдущих разделах.
Итак, давайте посмотрим, что мы получим, если сделаем это. Поскольку \(x\) приближается к бесконечности, то \(x\) в степени может только увеличиваться, а коэффициент при каждом члене (первом и третьем) будет только увеличивать член. Итак, если мы посмотрим, что делает каждый член в пределе, мы получим следующее: 92} — 8x} \справа) = \infty — \infty — \infty \]
Теперь у нас есть небольшая, но легко решаемая проблема. 3}}}} \верно-верно]\]
95}\) в этом случае.
3}}}} \верно-верно]\]
95}\) в этом случае.
Теперь все, что нам нужно сделать, это взять предел двух терминов. В первом случае не забывайте, что поскольку мы выходим в сторону \( — \infty\) и возводим \(t\) в степень 5 th , предел будет отрицательным (отрицательное число возводится в нечетная степень все еще отрицательна). Во втором члене мы снова будем широко использовать приведенный выше факт, чтобы увидеть, что это конечное число.
Следовательно, используя модификацию фактов из предыдущего раздела, значение предела равно 9.п}\]
На самом деле этот факт говорит о том, что когда мы берем предел в бесконечности для многочлена, все, что нам действительно нужно сделать, это посмотреть на член с наибольшей степенью и спросить, что этот член делает в пределе, поскольку многочлен будет иметь такое же поведение.
Вы можете увидеть доказательство в разделе «Доказательство различных предельных свойств» в главе «Дополнительно».
Теперь перейдем к более сложным ограничениям. 4 } + 7}}\]
4 } + 7}}\]
Показать решение
Во-первых, единственная разница между этими двумя состоит в том, что один стремится к положительной бесконечности, а другой — к отрицательной бесконечности. Иногда эта небольшая разница будет влиять на значение лимита, а иногда нет.
Начнем с первого предела, и, как и в нашем первом наборе примеров, может возникнуть соблазн просто «вставить» бесконечность. Поскольку и числитель, и знаменатель являются полиномами, мы можем использовать приведенный выше факт для определения поведения каждого из них. Это дает 94} + 7}} = \frac{\infty }{{ — \infty }}\]
Это еще одна неопределенная форма . В этом случае у нас может возникнуть соблазн сказать, что предел равен бесконечности (из-за бесконечности в числителе), нулю (из-за бесконечности в знаменателе) или -1 (потому что что-то, что делится само на себя, равно единице). Здесь работают три отдельных арифметических «правила», и без работы невозможно узнать, какое «правило» будет правильным, и, что еще хуже, возможно, что ни одно из них не сработает, и мы можем получить совершенно другой ответ, скажем \( — \frac{2}{5}\), чтобы выбрать число совершенно случайно. 94}}}}}\\ & = \frac{{2 + 0 + 0}}{{ — 5 + 0}}\\ & = — \frac{2}{5}\end{align*}\]
94}}}}}\\ & = \frac{{2 + 0 + 0}}{{ — 5 + 0}}\\ & = — \frac{2}{5}\end{align*}\]
В этом случае неопределенная форма не была ни одним из «очевидных» вариантов бесконечности, нуля или -1, поэтому будьте осторожны, делая такого рода предположения с такого рода неопределенными формами.
Аналогично делается второй лимит. Обратите внимание, однако, что нигде в работе над первым пределом мы на самом деле не использовали тот факт, что предел приближался к плюс бесконечности. В этом случае не имеет значения, к какой бесконечности мы идем, мы получим одно и то же значение предела. 92} + 6} }}{{5 — 2x}}\]
Показать решение
Квадратный корень в этой задаче не изменит нашу работу, но немного усложнит ее.
Начнем с первого лимита. В этом случае наибольшая степень \(х\) в знаменателе — это просто \(х\). Итак, нам нужно вынести \(x\) из числителя и знаменателя. Когда мы закончим разложение \(x\), нам понадобится \(x\) как в числителе, так и в знаменателе. 2}}}}}}{{x\left( {\frac{5}{x} — 2} \right)}}\ ]
2}}}}}}{{x\left( {\frac{5}{x} — 2} \right)}}\ ]
Теперь мы не можем просто отменить \(x\). Сначала нам нужно избавиться от полос абсолютного значения. Для этого вспомним определение абсолютной величины.
\[\слева| х \ справа | = \left\{ {\begin{array}{rl}x & {{\mbox{if}}x\ge 0}\\{ — x} & {{\mbox{if}}x <0}\end {массив}} \право.\]
В этом случае мы выходим на плюс бесконечность, поэтому мы можем с уверенностью предположить, что \(x\) будет положительным, и поэтому мы можем просто отбросить столбцы абсолютного значения. Тогда предел 92}}}} }}{{\frac{5}{x} — 2}}\\ & = \frac{{\sqrt 3}}{2}\end{align*}\]
Итак, как мы видели в последних двух примерах, иногда бесконечность в пределе влияет на ответ, а иногда нет. Обратите также внимание, что это не всегда просто меняет знак числа. Иногда он может полностью изменить значение. Мы увидим пример или два из этого в следующем разделе.
Прежде чем перейти к еще паре примеров, давайте еще раз вернемся к идее асимптот, которую мы впервые увидели в предыдущем разделе. Точно так же, как мы можем иметь вертикальные асимптоты, определенные в терминах пределов, мы также можем иметь горизонтальные асимптоты, определенные в терминах пределов.
Определение
Функция \(f(x)\) будет иметь горизонтальную асимптоту в точке \(y=L\), если верно одно из следующих условий.
\[\ mathop {\ lim } \ limit_ {x \ to \ infty} f \ left ( x \ right) = L \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ mathop {\ lim }\limits_{x \to — \infty} f\left( x \right) = L\]
Мы не собираемся здесь много заниматься асимптотами, но это легко привести, и мы можем использовать предыдущий пример, чтобы проиллюстрировать все идеи асимптот, которые мы видели как в этом разделе, так и в предыдущем разделе. Функция в последнем примере будет иметь две горизонтальные асимптоты. Он также будет иметь вертикальную асимптоту. Вот график функции, показывающий это. 94}}}}}{{2 + \frac{3}{t}}}\\ & = \frac{0}{2}\\ & = 0\end{align*}\]
Он также будет иметь вертикальную асимптоту. Вот график функции, показывающий это. 94}}}}}{{2 + \frac{3}{t}}}\\ & = \frac{0}{2}\\ & = 0\end{align*}\]
В этом случае, используя факт 1, мы видим, что числитель равен нулю, и, поскольку знаменатель также не равен нулю, дробь и, следовательно, предел будут равны нулю.
В этом разделе мы сосредоточились на пределах на бесконечности для функций, которые содержат только многочлены и/или рациональные выражения, включающие многочлены. Есть много других типов функций, которые мы могли бы использовать здесь. Это тема следующего раздела.
Чтобы увидеть точное и математическое определение этого типа предела, см. раздел «Определение предела» в конце этой главы.
Интуиционизм в философии математики (Стэнфордская философская энциклопедия)
Люитцен Эгбертус Ян Брауэр родился в Оверши, Нидерланды.
Изучал математику и физику в Амстердамском университете.
где он получил докторскую степень в 1907 году.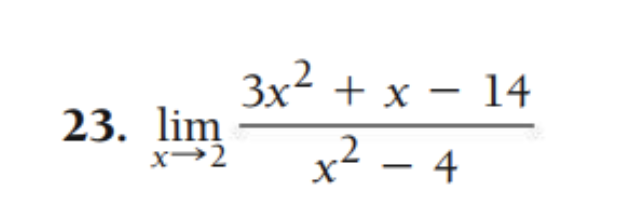 В 1909 году он стал лектором в
того же университета, где он был назначен профессором в 1912, а
должность, которую он занимал до выхода на пенсию в 1951 году. Брауэр был блестящим
математик, проделавший новаторскую работу в топологии и ставший
известен уже в юном возрасте. Всю жизнь он был независимым умом
который преследовал то, во что верил, с пылкой энергией, что принесло
он в конфликте со многими коллегами, в первую очередь с Дэвидом
Гильберт. Были у него и поклонники, и в его доме
хижине» в Бларикуме он приветствовал многих известных математиков
его время. К концу жизни он стал более изолированным, но его
вера в истинность его философии никогда не колебалась. Он умер в машине
несчастный случай в возрасте 85 лет в Бларикуме, через семь лет после смерти
его жена Лиза Брауэр.
В 1909 году он стал лектором в
того же университета, где он был назначен профессором в 1912, а
должность, которую он занимал до выхода на пенсию в 1951 году. Брауэр был блестящим
математик, проделавший новаторскую работу в топологии и ставший
известен уже в юном возрасте. Всю жизнь он был независимым умом
который преследовал то, во что верил, с пылкой энергией, что принесло
он в конфликте со многими коллегами, в первую очередь с Дэвидом
Гильберт. Были у него и поклонники, и в его доме
хижине» в Бларикуме он приветствовал многих известных математиков
его время. К концу жизни он стал более изолированным, но его
вера в истинность его философии никогда не колебалась. Он умер в машине
несчастный случай в возрасте 85 лет в Бларикуме, через семь лет после смерти
его жена Лиза Брауэр.
В возрасте 24 лет Брауэр написал книгу « Жизнь, искусство и жизнь».
Мистицизм (Brouwer 1905), солипсическое содержание которого предвещает
его философия математики. В своей диссертации обоснованы
интуитивизма формулируются впервые, хотя еще не
это имя, а не в их окончательной форме. В первые годы после своего
диссертации, большая часть научной жизни Брауэра была посвящена
топология, область, в которой он до сих пор известен своей теорией
размерность и его теорема о неподвижной точке. Эта работа является частью классического
математика; согласно более поздней точке зрения Брауэра, его фиксированная точка
теорема не верна, хотя аналог, приведенный в терминах
приближения могут быть доказаны в соответствии с его принципами.
В первые годы после своего
диссертации, большая часть научной жизни Брауэра была посвящена
топология, область, в которой он до сих пор известен своей теорией
размерность и его теорема о неподвижной точке. Эта работа является частью классического
математика; согласно более поздней точке зрения Брауэра, его фиксированная точка
теорема не верна, хотя аналог, приведенный в терминах
приближения могут быть доказаны в соответствии с его принципами.
С 1913 года Брауэр все больше посвящал себя
развитие идей, сформулированных в его диссертации, в полную
философия математики. Он не только усовершенствовал философию
интуитивизм, но и переработал математику, особенно теорию
континуум и теория множеств, согласно этим принципам.
К тому времени Брауэр был известным математиком, давшим влиятельные
лекции по интуитивизму в научных Мекках того времени,
Среди них Кембридж, Вена и Геттинген. Его философия была
многими считается неудобным, но рассматривается как серьезная альтернатива
классические рассуждения некоторых из самых известных математиков его
время, даже когда у них было другое мнение по этому вопросу. Курт
Гёдель, который всю жизнь был платоником, был одним из них. Германн
Вейль в какой-то момент написал: «So gebe ich also jetzt meinen eigenen
Versuch Preis und schließe mich Brouwer an» (Weyl 1921,
56). И хотя позже он редко практиковал интуитивистскую математику
при жизни Вейль не переставал восхищаться Брауэром и его интуитивным
философия математики.
Курт
Гёдель, который всю жизнь был платоником, был одним из них. Германн
Вейль в какой-то момент написал: «So gebe ich also jetzt meinen eigenen
Versuch Preis und schließe mich Brouwer an» (Weyl 1921,
56). И хотя позже он редко практиковал интуитивистскую математику
при жизни Вейль не переставал восхищаться Брауэром и его интуитивным
философия математики.
Жизнь Брауэра была полна конфликтов, самый известный из которых был конфликт с Давидом Гильбертом, который в конечном итоге привел к Исключение Брауэра из правления Mathematische Аннален . Этот конфликт был частью Grundlagentreit . потрясшее математическое общество в начале 20-х гг. века и возникшее в результате появления парадоксов и крайне неконструктивные доказательства в математике. Философы и математики были вынуждены признать отсутствие гносеологические и онтологические основы математики. Брауэра интуитивизм — это философия математики, цель которой — предоставить такие фундамент.
2.1 Два акта интуитивизма
Согласно Брауэру, математика — это бесъязыковое творение
разум. Время есть единственное априорное понятие в кантианском смысле. Брауэр
различает два акта интуитивизма :
Время есть единственное априорное понятие в кантианском смысле. Брауэр
различает два акта интуитивизма :
Первый акт интуитивизма:
Полностью отделить математику от математического языка и, следовательно, из явлений языка, описываемых теоретической логикой, признавая, что интуиционистская математика по существу бесъязыковая деятельность разума, берущая свое начало в восприятии хода времени. Это восприятие движения времени может быть описано как распад жизненного момента на две отдельные вещи, одну из которое уступает место другому, но сохраняется памятью. Если двойка рожденное таким образом лишается всех качеств, оно переходит в пустую форму общий субстрат всех двойственностей. И это общее субстрат, эта пустая форма, которая является основной интуицией математика. (Брауэр 1981, 4–5)
Как будет показано в разделе, посвященном математике, первый акт
интуитивизм порождает натуральные числа, но подразумевает строгое
ограничения на допустимые принципы рассуждения, в первую очередь
отказ от принципа исключенного третьего. Благодаря
отказ от этого принципа и исчезновение логической основы
для континуума можно, по словам Брауэра, «страх
что интуитивистская математика обязательно должна быть бедной и анемичной,
и, в частности, не было бы места для анализа» (Брауэр
1952, 142). Второй акт, однако, устанавливает существование
континуум, континуум, обладающий свойствами, не присущими его классическому
аналог. Восстановление континуума основывается на понятии
последовательности выбора, оговоренной во втором акте, т.е. о существовании
бесконечные последовательности, порожденные свободным выбором, которые поэтому не
фиксируется заранее.
Благодаря
отказ от этого принципа и исчезновение логической основы
для континуума можно, по словам Брауэра, «страх
что интуитивистская математика обязательно должна быть бедной и анемичной,
и, в частности, не было бы места для анализа» (Брауэр
1952, 142). Второй акт, однако, устанавливает существование
континуум, континуум, обладающий свойствами, не присущими его классическому
аналог. Восстановление континуума основывается на понятии
последовательности выбора, оговоренной во втором акте, т.е. о существовании
бесконечные последовательности, порожденные свободным выбором, которые поэтому не
фиксируется заранее.
Второй акт интуитивизма:
Допуская два способа создания новых математических объектов: во-первых, в форму более или менее свободно протекающих бесконечных последовательностей ранее приобретенные математические объекты…; во-вторых, в форма математических видов, т. е. свойства, допустимые для ранее приобретенные математические объекты, удовлетворяющие условию что если они верны для определенного математического объекта, они также верны для всех математических объектов, которые были определены как «равно» ему... (Брауэр 1981, 8)
Два акта интуитивизма составляют основу теории Брауэра.
философия; только из этих двух актов Брауэр создает царство
интуиционистской математики, как будет объяснено ниже. Уже из
из этих основных принципов можно сделать вывод, что интуиционизм отличается
от платонизма и формализма, потому что он не предполагает
математическая реальность вне нас, а также не утверждает, что математика
это игра с символами по определенным установленным правилам. В
По мнению Брауэра, язык используется для обмена математическими идеями.
но существование последнего не зависит от первого.
различие между интуиционизмом и другими конструктивными взглядами на
математика, согласно которой математические объекты и аргументы
должно быть вычислимо, заключается в свободе, которую допускает второй акт
при построении бесконечных последовательностей. Действительно, как будет
объясняется ниже, математические следствия второго акта
интуитивизма противоречат классической математике, а потому не
соблюдаются в большинстве конструктивных теорий, поскольку они, как правило, являются частью
классическая математика.
Таким образом, интуитивизм Брауэра стоит особняком от других философий. математики; оно основано на осознании времени и убеждение, что математика есть творение свободного разума, и поэтому не является ни платонизмом, ни формализмом. Это форма конструктивизма, но только в более широком смысле, поскольку многие конструктивисты не принимают всех принципов, в которые верил Брауэр. быть правдой.
2.2 Создающий субъект
Два акта интуитивизма сами по себе не исключают
психологическая интерпретация математики. Хотя только Брауэр
время от времени обращался к этому вопросу, из его сочинений ясно, что
он действительно считал интуитивизм независимым от психологии.
Представление Брауэра о Создание субъекта (Брауэр
1948) как идеализированный разум, в котором математика имеет место уже
абстрагируется от несущественных аспектов человеческого мышления, таких как
ограничения пространства и времени и возможность ошибочных аргументов.
Таким образом, проблема интерсубъективности, требующая объяснения
тот факт, что люди способны общаться, перестает существовать,
поскольку существует только один Создающий Субъект. В литературе также
имя Творческая тема используется для создания темы, но здесь
Используется терминология Брауэра. В (Niekus 2010) утверждается,
что «Создание субъекта» Брауэра не связано с идеализированным
математик. Для феноменологического анализа Создающего Субъекта
как трансцендентальный субъект в смысле Гуссерля см. (ван Аттен
2007).
В литературе также
имя Творческая тема используется для создания темы, но здесь
Используется терминология Брауэра. В (Niekus 2010) утверждается,
что «Создание субъекта» Брауэра не связано с идеализированным
математик. Для феноменологического анализа Создающего Субъекта
как трансцендентальный субъект в смысле Гуссерля см. (ван Аттен
2007).
Брауэр использовал аргументы, связанные с созданием субъекта, для построения контрпримеры к некоторым интуиционистски неприемлемым утверждениям. Там, где слабые контрпримеры, которые будут обсуждаться ниже, показывают только то, что некоторые утверждения в настоящее время не могут быть приняты интуитивно, понятие идеализированного разума доказывает некоторые классические принципы быть ложным. В разделе 5.4 приведен пример формализации понятия Творящего Субъекта. Там же поясняется, что следующий принцип, известный как Схема Крипке , может быть аргументированным с точки зрения Создающего Субъекта:
\[\тег{\({\bf КС}\)}
\существует \альфа(A \leftrightarrow \существует n\, \alpha(n) = 1). \]
\]
В KS , \(A\) распространяется на формулы и \( \alpha\) распространяется на последовательности выбора, которые представляют собой последовательности натуральных чисел, созданные Создающий Субъект, который выбирает свои элементы один за другим. Выбор последовательности и схема Крипке обсуждаются далее в разделе 3.4.
В большинстве философий математики, например в платонизме, математические утверждения не имеют времени. В интуитивизме истина и ложь имеет временной аспект; установленный факт останется таковым, но утверждение, которое становится доказанным в определенный момент времени, не имеет истинностное значение до этой точки. В указанной формализации понятия Создание Субъекта, который был сформулирован не Брауэром, а лишь позднее другими, темпоральный аспект интуитивизма бросается в глаза. подарок.
Важно, поскольку аргументы, использующие понятие «Создание темы», могут
способствовать дальнейшему пониманию интуиционизма как философии
математики, ее роль в развитии области была меньше
влиятельнее, чем два акта интуитивизма, которые непосредственно
привести к математическим истинам Брауэра и тех, кто придет после него
были готовы принять.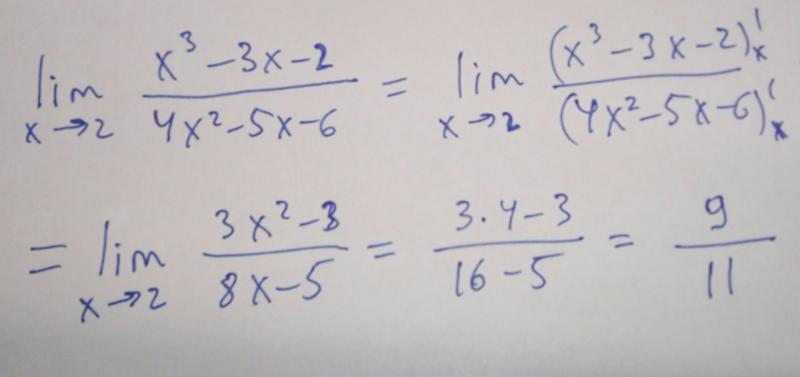
Хотя развитие интуитивизма Брауэром сыграло важную роль в основополагающих дебатах среди математиков на начале 20-го века, далеко идущие последствия его философия математики стала очевидной только после многих лет исследовательская работа. Двумя наиболее характерными чертами интуитивизма являются логические принципы рассуждений, которые он допускает в доказательствах, и полная концепция интуиционистского континуума. Только насколько последнее, интуиционизм становится несравнимым с классическим математика. В этой статье основное внимание уделяется тем принципам интуитивизм, который отличал ее от других математических дисциплин, поэтому другие его конструктивные аспекты будут рассмотрены в меньшей степени. деталь.
3.1 Интерпретация BHK
В интуитивизме знание того, что утверждение A истинно, означает
имея доказательства этого. В 1934 году Аренд Хейтинг, ученица
Брауэр ввел форму того, что позже стало известно как Брауэра-Хейтинга-Колмогорова-интерпретация , которая фиксирует
значение логических символов в интуиционизме и в конструктивизме
в общем тоже. Он неформально определяет, что
интуиционистское доказательство должно заключаться в указании того, как
связки и квантификаторы должны быть интерпретированы.
Он неформально определяет, что
интуиционистское доказательство должно заключаться в указании того, как
связки и квантификаторы должны быть интерпретированы.
- \(\bot\) недоказуема.
- Доказательство \(A\клина B\) состоит из доказательства \(A\) и доказательства из \(В\).
- Доказательство \(A \vee B\) состоит из доказательства \(A\) или доказательства \(В\).
- Доказательством \(A \rightarrow B\) является конструкция, которая преобразует любое доказательство \(A\) в доказательство \(B\).
- Доказательство \(\exists x A(x)\) дается представлением элемента \(d\) области и доказательство \(A(d)\).
- Доказательством \(\forall x A(x)\) является конструкция, которая преобразует каждое доказательство того, что \(d\) принадлежит области, в доказательство \(Объявление)\).
Отрицание \(\neg A\) формулы \(A\) доказано, как только оно было
показано, что не может существовать доказательство \(A\), что означает предоставление
конструкция, которая выводит ложность из любого возможного доказательства \(A\). Таким образом, \(\neg A\) эквивалентно \(A \rightarrow \bot\).
BHK-интерпретация не является формальным определением, поскольку понятие
конструкция не определена и поэтому открыта для различных
интерпретации. Тем не менее, уже на этом неформальном уровне
вынужден отказаться от одного из логических принципов, всегда присутствующих в
классическая логика: принцип исключенного третьего \((A\vee \neg
А)\). Согласно BHK-интерпретации, это утверждение верно
интуитивно, если Создающий Субъект знает доказательство \(A\) или
доказательство того, что \(A\) не может быть доказано. В случае, если ни для \(A\)
ни для его отрицания известно доказательство, утверждение \((A \vee \neg
А)\) не выполняется. Наличие открытых проблем, таких как
Гипотеза Гольдбаха или гипотеза Римана иллюстрирует этот факт.
Но как только найдено доказательство \(А\) или доказательство его отрицания,
ситуация меняется, и для этого конкретного \(A\) принцип \((A
\vee \neg A)\) истинно с этого момента.
Таким образом, \(\neg A\) эквивалентно \(A \rightarrow \bot\).
BHK-интерпретация не является формальным определением, поскольку понятие
конструкция не определена и поэтому открыта для различных
интерпретации. Тем не менее, уже на этом неформальном уровне
вынужден отказаться от одного из логических принципов, всегда присутствующих в
классическая логика: принцип исключенного третьего \((A\vee \neg
А)\). Согласно BHK-интерпретации, это утверждение верно
интуитивно, если Создающий Субъект знает доказательство \(A\) или
доказательство того, что \(A\) не может быть доказано. В случае, если ни для \(A\)
ни для его отрицания известно доказательство, утверждение \((A \vee \neg
А)\) не выполняется. Наличие открытых проблем, таких как
Гипотеза Гольдбаха или гипотеза Римана иллюстрирует этот факт.
Но как только найдено доказательство \(А\) или доказательство его отрицания,
ситуация меняется, и для этого конкретного \(A\) принцип \((A
\vee \neg A)\) истинно с этого момента.
3.2 Интуитивистская логика
Брауэр отверг принцип исключенного третьего на основании
своей философии, но Аренд Хейтинг была первой, кто сформулировал
всеобъемлющая логика принципов, приемлемая для интуиционистской
точка зрения.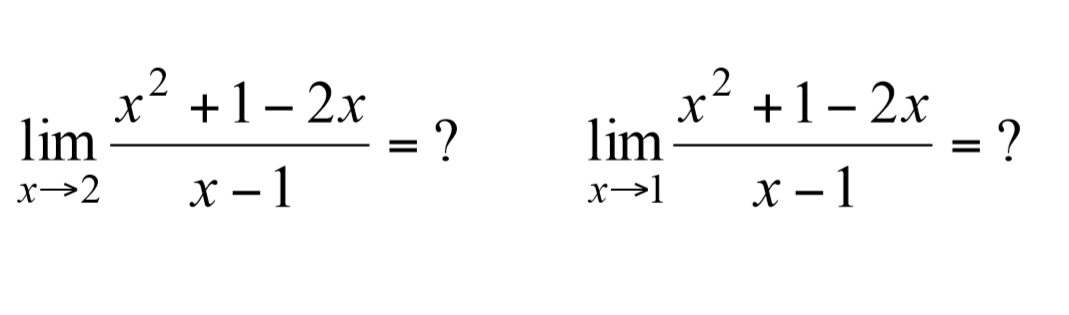 Интуиционистская логика, которая является логикой большинства других
формы конструктивизма, а также часто упоминается как
«классическая логика без принципа исключенного
середина». Обозначается IQC, что означает интуиционистский.
Quantifier Logic, но в литературе встречаются и другие названия. А
возможная аксиоматизация в стиле Гильберта состоит из
принципы
Интуиционистская логика, которая является логикой большинства других
формы конструктивизма, а также часто упоминается как
«классическая логика без принципа исключенного
середина». Обозначается IQC, что означает интуиционистский.
Quantifier Logic, но в литературе встречаются и другие названия. А
возможная аксиоматизация в стиле Гильберта состоит из
принципы
| \(A \клин B \стрелка вправо A\) | \(A \клин B \стрелка вправо B\) | \(А \правая стрелка А \ви Б\) | \(B \rightarrow A \vee B\) |
| \(A \rightarrow (B \rightarrow A)\) | \(\forall x A(x) \rightarrow A(t)\) | \(А(т) \стрелка вправо \существует х А(х)\) | \(\bot \rightarrow A\) |
| \((A \rightarrow (B \rightarrow C)) \rightarrow ((A \rightarrow B) \rightarrow (A \rightarrow C))\) | |||
| \(А \стрелка вправо (В \стрелка вправо А \клин B)\) | |||
| \((A \rightarrow C) \rightarrow ( (B \rightarrow C) \rightarrow (A \vee B \rightarrow C))\) | |||
| \(\forall x (B \rightarrow A(x)) \rightarrow (B \rightarrow \forall x A(x))\) | \(\forall x (A(x) \rightarrow B) \rightarrow (\exists x A(x) \rightarrow B)\) | ||
с обычными дополнительными условиями для последних двух аксиом и правилом Модус Поненс,
\[ \text{из \(A\) и \((A \rightarrow B)\) вывести \(B\)}, \]
как единственное правило вывода. Интуиционистская логика была объектом
исследования с тех пор, как Гейтинг сформулировал его. Уже на
пропозициональном уровне он обладает многими свойствами, которые отличают его от
классическая логика, такая как свойство дизъюнкции:
Интуиционистская логика была объектом
исследования с тех пор, как Гейтинг сформулировал его. Уже на
пропозициональном уровне он обладает многими свойствами, которые отличают его от
классическая логика, такая как свойство дизъюнкции:
\[\тег{\({\bf DP}\)} {\bf IQC} \vdash A \vee B \text{ подразумевает }{\bf IQC} \vdash A \text{ или } {\bf IQC} \vdash B. \]
Этот принцип явно нарушается в классической логике, т.к.
классическая логика доказывает \((A \vee \neg A)\) также для формул, которые
независимо от логики, т. е. для которых оба \(A\) и \(\neg A\) являются
не тавтология. Включение принципа Ex Falso Sequitur
Quodlibet, \((\bot \rightarrow A)\), в интуиционистской логике является
предметом обсуждения для тех, кто изучает замечания Брауэра о
предмет; в van Atten 2008 утверждается, что принцип не
действительны в интуиционизме и что логические принципы действительны согласно
взгляды Брауэра основаны на логике релевантности. Увидеть ван Далена
2004 г. , чтобы узнать больше о Брауэре и Ex Falso Sequitur Quodlibet.
, чтобы узнать больше о Брауэре и Ex Falso Sequitur Quodlibet.
Хотя до сих пор вся логика, используемая в интуиционистских рассуждениях, содержится в IQC , в принципе возможно, что в некоторых момент будет найден принцип, приемлемый с точки зрения интуиционистской точки зрения, которая не охватывается этой логикой. За большинства форм конструктивизма широко распространено мнение, что это никогда не будет иметь место, и поэтому IQC считается логика конструктивизма. Для интуитивизма ситуация менее ясна, потому что нельзя исключить, что в какой-то момент наша интуиционистское понимание может привести нас к новым логическим принципам что мы раньше не понимали.
Одной из причин широкого использования интуиционистской логики является
что он ведет себя хорошо как с точки зрения теории доказательств, так и
с теоретико-модельной точки зрения. Существует великое множество систем доказательств
для него, такие как исчисления Генцена и системы естественного вывода, а также
как различные формы семантики, такие как модели Крипке, модели Бет,
Алгебры Гейтинга, топологическая семантика и категориальные модели. Однако некоторые из этих семантик являются лишь классическими средствами изучения
интуиционистской логики, ибо можно показать, что интуиционистская
доказательства полноты по отношению к ним не может существовать (Крейзель 1962).
Однако было показано, что существуют альтернативные, но мало
менее естественные модели, по отношению к которым имеет место полнота
конструктивно (Вельдман, 1976). Конструктивный характер
интуиционистская логика становится особенно ясной в теории Карри-Ховарда.
изоморфизм, устанавливающий соответствие между дифференцированиями в
логика и термины в просто типизированном \(\lambda\)-исчислении, то есть
между доказательствами и вычислениями. Переписка сохраняется
структуры в том, что сокращение терминов соответствует нормализации
доказательства.
Однако некоторые из этих семантик являются лишь классическими средствами изучения
интуиционистской логики, ибо можно показать, что интуиционистская
доказательства полноты по отношению к ним не может существовать (Крейзель 1962).
Однако было показано, что существуют альтернативные, но мало
менее естественные модели, по отношению к которым имеет место полнота
конструктивно (Вельдман, 1976). Конструктивный характер
интуиционистская логика становится особенно ясной в теории Карри-Ховарда.
изоморфизм, устанавливающий соответствие между дифференцированиями в
логика и термины в просто типизированном \(\lambda\)-исчислении, то есть
между доказательствами и вычислениями. Переписка сохраняется
структуры в том, что сокращение терминов соответствует нормализации
доказательства.
3.3 Натуральные числа
Существование натуральных чисел дается первым актом
интуитивизм, то есть восприятие движения времени и
распад жизненного момента на две отдельные вещи: то, что было,
1, и то, что есть вместе с тем, что было, 2, а оттуда к 3, 4, …
В отличие от классической математики, в интуиционизме вся бесконечность
считается потенциальной бесконечностью. В частности, это случай
для бесконечности натуральных чисел. Поэтому заявления о том, что
к количественной оценке этого набора следует относиться с осторожностью. С другой
стороны, принцип индукции вполне приемлем с
интуитивистская точка зрения.
В частности, это случай
для бесконечности натуральных чисел. Поэтому заявления о том, что
к количественной оценке этого набора следует относиться с осторожностью. С другой
стороны, принцип индукции вполне приемлем с
интуитивистская точка зрения.
Из-за конечности натурального числа в отличие от, для например, действительное число, множество арифметических утверждений конечного то, что верно в классической математике, верно и в интуиционизме. также. Например, в интуитивизме каждое натуральное число имеет простое число. факторизация; существуют вычислимо перечислимые множества, не являющиеся вычислимый; \((A \vee \neg A)\) выполняется для всех свободных кванторов операторы \(А\). Для более сложных утверждений, таких как ван дер Теорема Вардена или теорема Крускала, интуиционистская достоверность не так проста. В самом деле, интуиционистские доказательства оба утверждения сложны и отклоняются от классических доказательств (Коканд 1995, Вельдман 2004).
Таким образом, в контексте натуральных чисел интуиционизм и классический
математика имеет много общего. Только тогда, когда другие бесконечные множества
как действительные числа считаются, что интуиционизм начинает
отличаются более резко от классической математики, и от большинства
и другие формы конструктивизма.
Только тогда, когда другие бесконечные множества
как действительные числа считаются, что интуиционизм начинает
отличаются более резко от классической математики, и от большинства
и другие формы конструктивизма.
3.4 Континуум
В интуиционизме континуум является одновременно расширением и ограничением. своего классического аналога. В полной форме оба понятия несравнимы, поскольку интуиционистские действительные числа обладают свойствами чего нет у классических действительных чисел. Известный пример, чтобы быть обсуждаемой ниже, является теорема о том, что в интуиционизме всякое полное функция на континууме непрерывна. что интуиционистский континуум не удовлетворяет некоторым классическим свойствам, может быть легко видел через слабых контрпримеров . Что он также содержит свойства, которыми классические вещественные числа не обладают, проистекает из существование в интуитивизме последовательностей выбора .
Слабые контрпримеры
слабый контрпример , введенный Брауэром в 1908 г. ,
первые примеры, которые Брауэр использовал, чтобы показать, что переход от
классическая для интуиционистской концепции математики не
без последствий для математических истин, которые могут быть
созданные в соответствии с этими философиями. Они показывают, что определенные
классические утверждения в настоящее время неприемлемы с точки зрения интуиционизма.
точка зрения. В качестве примера рассмотрим последовательность действительных чисел
дается следующим определением: 9{-m} \text{ if } \neg A(m) \wedge m \leq n \wedge \forall k \lt m A(k).
\end{случаи}
\]
,
первые примеры, которые Брауэр использовал, чтобы показать, что переход от
классическая для интуиционистской концепции математики не
без последствий для математических истин, которые могут быть
созданные в соответствии с этими философиями. Они показывают, что определенные
классические утверждения в настоящее время неприемлемы с точки зрения интуиционизма.
точка зрения. В качестве примера рассмотрим последовательность действительных чисел
дается следующим определением: 9{-m} \text{ if } \neg A(m) \wedge m \leq n \wedge \forall k \lt m A(k).
\end{случаи}
\]
Здесь \(A(n)\) — разрешимое свойство, для которого \(\для всех n A(n)\) есть
неизвестно, истинно это или ложно. Разрешимость означает, что в настоящее время для
для любого заданного \(n\) существует (может быть построено) доказательство \(A(n)\)
или из \(\neg A(n)\). На момент написания этой статьи мы могли бы, например,
пусть \(A(n)\) выражает, что \(n\), если оно больше 2, является суммой
три простых числа; \(\forall n A(n)\) затем выражает (исходный)
Гольдбах предположил, что каждое число больше 2 есть сумма
три простых числа. Последовательность \(\langle r_n \rangle\) определяет реальный
число \(r\), для которого утверждение \(r=0\) эквивалентно
утверждение \(\forall n A(n)\). Отсюда следует, что утверждение \((r = 0
\vee r \neq 0)\) не выполняется, и поэтому закон
трихотомия \(\forall x(x \lt y \vee x=y \vee x \gt y)\) неверна на
интуиционистский континуум.
Последовательность \(\langle r_n \rangle\) определяет реальный
число \(r\), для которого утверждение \(r=0\) эквивалентно
утверждение \(\forall n A(n)\). Отсюда следует, что утверждение \((r = 0
\vee r \neq 0)\) не выполняется, и поэтому закон
трихотомия \(\forall x(x \lt y \vee x=y \vee x \gt y)\) неверна на
интуиционистский континуум.
Обратите внимание на тонкую разницу между «\(A\) не
интуиционистски истинен» и «\(А\) интуиционистски
опровержимо»: в первом случае мы знаем, что \(A\) не может иметь
интуиционистское доказательство, второе утверждение выражает, что мы имеем
доказательство ¬ A , т. е. конструкция, которая выводит falsum из
любое возможное доказательство \(A\). Для закона трихотомии мы имеем только что
показано, что это не является интуиционистски верным. Ниже будет показано
что даже вторая более сильная форма говорит о том, что закон опровержим
держится интуитивно. Однако это верно не для всех
утверждения, для которых существуют слабые контрпримеры. Например,
Гипотеза Гольдбаха является слабым контрпримером к принципу
исключенная середина, поскольку \(\forall n A(n)\), как указано выше, в настоящее время
неизвестно, является ли оно истинным или ложным, и поэтому мы не можем утверждать \(\forall n
A(n) \vee \neg \forall n A(n)\) интуитивно, по крайней мере, не при
этот момент. Но опровержение этого утверждения, \(\neg (\forall n
A(n) \vee \neg \forall n A(n))\), неверно в интуиционизме, поскольку
можно показать, что для любого утверждения \(B\) можно вывести противоречие
из предположения, что \(\neg B\) и \(\neg\neg B\) выполняются (и, таким образом,
также из \(B\) и \(\neg B\)). Другими словами, \(\neg\neg (B \vee
\neg B)\) является интуиционистски верным, и поэтому, хотя существуют
слабые контрпримеры к принципу исключенного третьего, его
отрицание ложно в интуиционизме, т. е. интуиционистски
опровержимый.
Но опровержение этого утверждения, \(\neg (\forall n
A(n) \vee \neg \forall n A(n))\), неверно в интуиционизме, поскольку
можно показать, что для любого утверждения \(B\) можно вывести противоречие
из предположения, что \(\neg B\) и \(\neg\neg B\) выполняются (и, таким образом,
также из \(B\) и \(\neg B\)). Другими словами, \(\neg\neg (B \vee
\neg B)\) является интуиционистски верным, и поэтому, хотя существуют
слабые контрпримеры к принципу исключенного третьего, его
отрицание ложно в интуиционизме, т. е. интуиционистски
опровержимый.
Существование действительных чисел \(r\), для которых интуиционист не может решить, положительны они или нет, показывает, что определенные классически тотальные функции перестают быть таковыми в интуиционистской среде, такой как кусочно-постоянная функция
\[ f(r) = \begin{случаи} 0 \text{ если } r \geq 0 \\ 1 \text{ если } г \lt 0. \end{случаи} \]
Существуют слабые контрпримеры ко многим классически верным утверждениям. Построение этих слабых контрпримеров часто следует одному и тому же
шаблон, как в примере выше. Например, аргумент, который показывает
что теорема о промежуточном значении интуиционистски недействительна
работает следующим образом. Пусть \(r\) — действительное число из [−1,1], для которого
\((r\leq 0 \vee 0 \lt r)\) не определено, как в примере
выше. Определим равномерно непрерывную функцию \(f\) на \([0,3]\)
к
Построение этих слабых контрпримеров часто следует одному и тому же
шаблон, как в примере выше. Например, аргумент, который показывает
что теорема о промежуточном значении интуиционистски недействительна
работает следующим образом. Пусть \(r\) — действительное число из [−1,1], для которого
\((r\leq 0 \vee 0 \lt r)\) не определено, как в примере
выше. Определим равномерно непрерывную функцию \(f\) на \([0,3]\)
к
\[ f(x) = \text{min}(x-1,0) + \text{max}(0,x-2) + r. \]
Ясно, что \(f(0) = -1 + r\) и \(f(3) = 1 + r\), откуда \(f\) принимает значение 0 в некоторой точке \(x\) в [0,3]. Если бы такое \(x\) могло быть определяется либо \(1 \leq x\), либо \(x \leq 2\). Поскольку \(f\) равно \(r\) на \([1,2]\), в первом случае \(r \leq 0\) и во втором случай \(0\leq r\), что противоречит неразрешимости утверждения \((r\leq 0 \vee 0 \leq r)\).
Эти примеры, по-видимому, указывают на то, что при переходе от классического к
интуиционистской математике теряется несколько фундаментальных теорем
анализ. Однако это не так, поскольку во многих случаях интуитивизм
восстанавливает такие теоремы в виде аналога, в котором экзистенциальные
утверждения заменяются утверждениями о существовании
приближения с произвольной точностью, как в этом классическом
эквивалентная форма теоремы о промежуточном значении, которая
конструктивно действительный: 9{-н}.
\]
Однако это не так, поскольку во многих случаях интуитивизм
восстанавливает такие теоремы в виде аналога, в котором экзистенциальные
утверждения заменяются утверждениями о существовании
приближения с произвольной точностью, как в этом классическом
эквивалентная форма теоремы о промежуточном значении, которая
конструктивно действительный: 9{-н}.
\]
Слабые контрпримеры — это средство показать, что определенные математические утверждения не верны интуиционистски, но они еще не раскрывают богатство интуиционистского континуума. Только после Введение Брауэром последовательностей выбора сделало интуиционизм приобрел свой особый вкус и стал несравнимым с классическим математика.
Последовательности выбора
Последовательности выбора были введены Брауэром для захвата
интуиция континуума. Поскольку для интуициониста вся бесконечность есть
потенциальные, бесконечные объекты могут быть схвачены только с помощью процесса, который
генерирует их шаг за шагом. Что будет разрешено в качестве законного
Таким образом, конструкция решает, какие бесконечные объекты должны быть
принято. Например, в большинстве других форм конструктивизма только
допускаются вычислимые правила порождения таких объектов, в то время как в
Бесконечности платонизма считаются законченными тотальностями,
существование принимается даже в тех случаях, когда нет порождающих правил.
известен.
Например, в большинстве других форм конструктивизма только
допускаются вычислимые правила порождения таких объектов, в то время как в
Бесконечности платонизма считаются законченными тотальностями,
существование принимается даже в тех случаях, когда нет порождающих правил.
известен.
Второй акт интуитивизма Брауэра приводит к выбору
последовательности, которые наделяют определенные бесконечные множества свойствами,
неприемлемо с классической точки зрения. Последовательность выбора – это
бесконечная последовательность чисел (или конечных объектов), созданная свободным
будут. Последовательность может быть определена законом или алгоритмом, таким как
последовательность, состоящая только из нулей или простых чисел в
порядке возрастания, и в этом случае мы говорим о законоподобии последовательность, или она не может быть подчинена какому-либо закону, и в этом случае она
позвонил беззаконник . Незаконные последовательности могут быть, например,
созданный повторным броском монеты, или попросив Создающего
При условии выбора последовательных номеров последовательности один за другим,
позволяя ему выбрать любое число по своему вкусу. Таким образом, беззаконие
последовательность всегда незакончена, и единственная доступная информация о
это на любом этапе времени является начальным сегментом созданной последовательности
до сих пор. Ясно, что по самой природе беззакония мы никогда не можем
решить, будут ли его значения совпадать с последовательностью, которая
законопослушный. Кроме того, свободная воля способна создавать последовательности, которые начинаются
законопослушным, но для которого в определенный момент закон может быть
снимается, и процесс свободного выбора берет верх над созданием
последующие числа или наоборот.
Таким образом, беззаконие
последовательность всегда незакончена, и единственная доступная информация о
это на любом этапе времени является начальным сегментом созданной последовательности
до сих пор. Ясно, что по самой природе беззакония мы никогда не можем
решить, будут ли его значения совпадать с последовательностью, которая
законопослушный. Кроме того, свободная воля способна создавать последовательности, которые начинаются
законопослушным, но для которого в определенный момент закон может быть
снимается, и процесс свободного выбора берет верх над созданием
последующие числа или наоборот.
Согласно Брауэру, каждое действительное число представлено выбором
последовательность, а последовательности выбора позволили ему уловить
интуиционистский континуум через спорные аксиомы непрерывности.
Брауэр впервые заговорил о последовательностях выбора в своей инаугурационной речи.
(Brouwer 1912), но в то время он еще не относился к ним как к
основная часть его математики. Постепенно их стало больше
важно, и с 1918 года Брауэр начал использовать их таким образом,
объясняется в следующем разделе.
3.5 Аксиомы непрерывности
Принятие концепции последовательности выбора имеет далеко идущие последствия. подразумеваемое. Это оправдывает для интуициониста использование аксиомы непрерывности, из которых можно вывести классически некорректные утверждения. полученный. Самой слабой из этих аксиом является слабая аксиома непрерывности:
\[\tag{\({\bf WC\mbox{-}N}\)} \forall\alpha\существует n A(\alpha,n) \rightarrow \forall\alpha\exists m\exists n \forall\beta\in\alpha(\overline{m})A(\beta,n). \]
Здесь \(n\) и \(m\) варьируются в натуральных числах, \(\alpha\) и
\(\beta\) над последовательностями выбора и \(\beta\in\alpha(\overline{m})\)
означает, что первые \(m\) элементы \(\alpha\) и \(\beta\) равны
равный. Хотя до сих пор никогда не было дано полностью
удовлетворительное обоснование большинства аксиом непрерывности для произвольных
последовательности выбора, даже не у Брауэра, когда они ограничены классом
беззаконные последовательности аргументов, поддерживающих справедливость слабых
Аксиома непрерывности работает следующим образом.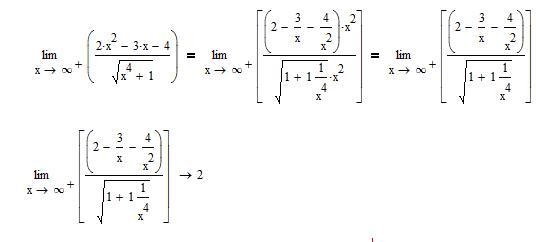 Когда может быть выписка формы
\(\forall\alpha\exists n A(\alpha,n)\) устанавливается
интуитивист? По самой природе понятия незаконной последовательности,
выбор числа \(n\), для которого верно \(A(\alpha,n)\), должен
быть выполнено после того, как известен только конечный начальный сегмент \(\alpha\).
Ибо мы не знаем, как \(\альфа\) будет протекать во времени, и мы
поэтому должны основывать выбор \(n\) на начальном сегменте
\(\alpha\), который известен на тот момент времени, когда мы хотим исправить
\(н\). Отсюда следует, что для любой неупорядоченной последовательности \(\beta\) с
тот же начальный сегмент, что и \(\alpha\), \(A(\beta,n)\) также выполняется.
Когда может быть выписка формы
\(\forall\alpha\exists n A(\alpha,n)\) устанавливается
интуитивист? По самой природе понятия незаконной последовательности,
выбор числа \(n\), для которого верно \(A(\alpha,n)\), должен
быть выполнено после того, как известен только конечный начальный сегмент \(\alpha\).
Ибо мы не знаем, как \(\альфа\) будет протекать во времени, и мы
поэтому должны основывать выбор \(n\) на начальном сегменте
\(\alpha\), который известен на тот момент времени, когда мы хотим исправить
\(н\). Отсюда следует, что для любой неупорядоченной последовательности \(\beta\) с
тот же начальный сегмент, что и \(\alpha\), \(A(\beta,n)\) также выполняется.
Было показано, что аксиома слабой непрерывности непротиворечива.
часто применяется в форме, которая может быть оправдана, а именно в случае в
который предикат \(A\) относится только к значениям \(\alpha\), и
не к свойствам более высокого порядка, которыми он, возможно, обладает.
детали аргумента здесь будут опущены, но он содержит то же самое. ингредиенты как оправдание принципа беззакония
последовательности, и их можно найти в van Atten and van Dalen 2002.
ингредиенты как оправдание принципа беззакония
последовательности, и их можно найти в van Atten and van Dalen 2002.
Слабая непрерывность не исчерпывает интуицию интуиционистов о континууме, ибо с учетом слабой аксиомы непрерывности кажется разумно предположить, что выбор числа \(m\) такого, что \(\forall\beta\in\alpha(\overline{m})A(\beta,n)\), можно сделать явный. Таким образом, \(\forall\alpha\exists n A(\alpha,n)\) подразумевает существование непрерывного функционала \(\Phi\), который для любого \(\alpha\) производит \(m\), который фиксирует длину \(\alpha\) на основание которого \(n\) выбрано. Более формально пусть \(\mathcal{CF}\) — класс непрерывных функционалов \(\Phi\), которые присваивать натуральные числа бесконечным последовательностям, т. е. удовлетворяющим
\[ \forall\альфа\существует m\forall\beta\in\alpha(\overline{m})\Phi(\alpha)=\Phi(\beta). \]
Полная аксиома непрерывности, являющаяся расширением слабого аксиома непрерывности, тогда может быть выражена как:
\[\tag{\({\bf C\mbox{-}N}\)}
\forall\alpha\существует n A(\alpha,n) \rightarrow
\существует \Phi \in \mathcal{CF}\,\forall\alpha A(\alpha,\Phi(\alpha)). \]
\]
С помощью аксиомы непрерывности можно привести некоторые слабые контрпримеры. превратились в подлинные опровержения классически принятых принципы. Например, это означает, что количественная версия принцип исключенного третьего неверен:
\[ \neg\forall\alpha(\forall n\alpha (n)=0 \vee \neg \forall n\alpha (n)=0). \]
Здесь \(\alpha(n)\) обозначает \(n\)-й элемент \(\alpha\). Увидеть что это отрицание имеет место, предположим, рассуждая от противного, что \(\neg\forall\alpha(\forall n\alpha (n)=0 \vee \neg \forall n\alpha (n)=0)\). Это означает, что
\[ \forall\alpha\exists k((\forall n\alpha (n)=0 \wedge k=0) \vee (\neg \forall n\alpha (n)=0 \wedge k=1)). \]
По слабой аксиоме непрерывности для \(\alpha\), состоящего только из нулей
существует число \(m\), фиксирующее выбор \(k\), которое
означает, что для всех \(\beta\in\alpha(\overline{m})\), \(k=0\). Но
существование последовательностей, первые \(m\) элементов которых равны 0, и что
содержат 1 показывают, что этого не может быть.
Этот пример показывает, что принцип исключенного третьего не только не выполняется, а фактически ложно в интуитивизме, приводит к опровержение многих основных свойств континуума. Рассмотрим для пример действительное число \(r_\alpha\), которое является пределом последовательности состоящий из чисел \(r_n\), как указано в разделе о слабом контрпримеры, где \(A(m)\) в определении принимается равным утверждение \(\альфа(м)=0\). Тогда приведенное выше опровержение означает, что \(\neg\forall\alpha(r_\alpha=0 \vee r_\alpha\neq 0)\), и тем самым опровергает закон трихотомии:
\[ \forall x (x \lt y \vee x=y \vee y \lt x). \]
Следующая теорема является еще одним примером того, как аксиома непрерывности опровергает некоторые классические принципы.
Теорема \({\bf (C\mbox{-}N)}\) Каждая полная вещественная функция непрерывна.
Действительно, классический контрпример к этой теореме нигде
непрерывная функция
\[
е (х) =
\begin{случаи}
0 \text{ если \(x\) рациональное число } \\
1 \text{ если \(x\) иррациональное число}
\end{случаи}
\]
не является законной функцией от
интуиционистской точки зрения, поскольку свойство быть рациональным
неразрешимы на действительных числах. Из вышеприведенной теоремы следует, что
континуум неразложим, а в ван Далене 1997 показано, что
это верно даже для множества иррациональных чисел.
Из вышеприведенной теоремы следует, что
континуум неразложим, а в ван Далене 1997 показано, что
это верно даже для множества иррациональных чисел.
Два вышеприведенных примера характерны для того, как аксиомы непрерывности применяются в интуиционистской математике. Они есть единственные аксиомы интуиционизма, противоречащие классическим рассуждениям, и тем самым представляют самые красочные, а также самые противоречивая часть философии Брауэра.
Функции соседства
Существует удобное представление непрерывных функционалов, которое
широко использовался в литературе, но не Брауэром.
сам. Непрерывные функционалы, сопоставляющие числа бесконечным
последовательности могут быть представлены функций окрестности , где
функция окрестности \(f\) есть функция от натуральных чисел
удовлетворяющие следующим двум свойствам (\(\cdot\) обозначает
конкатенация и \(f(\alpha(\overline{n}))\) обозначает значение
\(f\) на коде конечной последовательности
\(\alpha(\overline{n})\)).
\[ \alpha\существует n f(\alpha(\overline{n})) \gt 0 \ \ \ \ \forall n\forall m (f(n) \gt 0 \rightarrow f(n\cdot m) = f(n)). \]
Интуитивно, если \(f\) представляет \(\Phi\), то \(f(\alpha(\overline{n}))=0\) означает, что \(\alpha(\overline{n})\) недостаточно долго для вычисления \(\Phi(\alpha)\) и \(f(\alpha(\overline{n}))=m+1\) означает, что \(\alpha(\overline{n})\) достаточно долго, чтобы вычислить \(\Phi(\alpha)\) и что значение \(\Phi(\alpha)\) равно \(m\). Если \(\mathcal{K}\) обозначает класс функции окрестности, то аксиома непрерывности \({\bf C\mbox{-}N}\) можно перефразировать как \[ \forall \alpha\существует n A(\alpha,n) \rightarrow \существует f \in \mathcal{K}\, \forall m(f(m) \gt 0 \rightarrow \forall \beta \in m A(\beta,f(m-1))), \]
где \(\beta \in m\) означает, что код начального сегмента \(\бета\) это \(м\).
3.6 Теорема о брусе
Брауэр ввел последовательности выбора и аксиомы непрерывности для
охватывают интуиционистский континуум, но только эти принципы
недостаточно, чтобы восстановить ту часть традиционного анализа, которую Брауэр
считается интуиционистски обоснованным, например, теорема о том, что каждый
непрерывная действительная функция на отрезке равномерно непрерывна. По этой причине Брауэр доказал так называемую теорему о стержнях. Это
классически верное утверждение, но доказательство, которое дал Брауэр, многими
вообще не считается доказательством, поскольку использует предположение о
форма доказательства, для которой не предусмотрена строгая аргументация. Это
Причина, по которой теорему о стержнях также называют принципом стержней.
По этой причине Брауэр доказал так называемую теорему о стержнях. Это
классически верное утверждение, но доказательство, которое дал Брауэр, многими
вообще не считается доказательством, поскольку использует предположение о
форма доказательства, для которой не предусмотрена строгая аргументация. Это
Причина, по которой теорему о стержнях также называют принципом стержней.
Наиболее известным следствием теоремы о стержнях является теорема о веерах.
что достаточно для доказательства вышеупомянутой теоремы о равномерном
преемственность, и что будет рассмотрено в первую очередь. И вентилятор, и бар
теоремы позволяют интуиционисту использовать индукцию по некоторым
обоснованные наборы объектов, называемые спредами. Спред — это
интуиционистский аналог множества и отражает идею бесконечности
объекты как всегда растут и никогда не заканчиваются. Спред – это, по сути,
счетно ветвящееся дерево, помеченное натуральными числами или другими конечными
объекты и содержащие только бесконечные пути.
Веер представляет собой конечное разветвление, и принцип веера выражает форму компактности, которая классически эквивалентна Лемма Кенига, классическое доказательство которой неприемлемо с интуиционистской точки зрения. Принцип гласит, что для каждый веер \(T\), в котором каждая ветвь в некоторой точке удовлетворяет свойство \(A\), существует равномерная граница глубины, на которой это свойство выполнено. Такое свойство называется баром для \(Т\).
\[\тег{\({\bf ВЕНТИЛЯТОР}\)} \forall \alpha \in T\существует n A(\alpha(\overline{n})) \rightarrow \существует m \forall \alpha \in T \существует n \leq m A(\alpha(\overline{n})). \]
Здесь \(\alpha \in T\) означает, что \(\alpha\) является ветвью \(T\). принципа FAN достаточно, чтобы доказать упомянутую теорему выше:
Теорема ( FAN ) Каждая непрерывная вещественная функция на отрезке равномерно непрерывна.
Обоснование Брауэром теоремы о веерах — это принцип стержня. для универсального распространения:
\[\тег{\({\bf BI}\)} \начать{выравнивать} & [\forall\alpha\forall n \big( A(\alpha(\overline{n})) \vee \neg A(\alpha(\overline{n})) \big) \клин \forall\alpha\существует n A(\alpha(\overline{n}))\ \клин\\ &\quad \forall\alpha\forall n \big( A(\alpha(\overline{n})) \rightarrow B(\alpha(\overline{n})) \big)\\клин \\ &\quad \forall\alpha\forall n \big( \forall mB(\alpha(\overline{n})\cdot m) \rightarrow B(\alpha(\overline{n})) \big)] \стрелка вправо B(\varepsilon). \end{выравнивание} \]
Здесь \(\varepsilon\) обозначает пустую последовательность, \(\cdot\) —
конкатенация, BI для Bar Induction и
индекс D относится к разрешимости
предикат \(А\). Принцип бара дает интуиционизму
принцип индукции для деревьев; это выражает обоснованность
принцип спредов относительно разрешимых свойств. Расширения
этого принципа, в котором требование разрешимости ослабляется
может быть извлечено из работы Брауэра, но здесь не приводится. Непрерывность и принцип стержня иногда сводятся к одной аксиоме.
называется аксиома непрерывности бара .
Непрерывность и принцип стержня иногда сводятся к одной аксиоме.
называется аксиома непрерывности бара .
Существует тесная связь между принципом бара и функции окрестности, упомянутые в разделе об аксиомах непрерывности. Пусть \(\mathcal{IK}\) — индуктивно определенный класс окрестностей функции, состоящие из всех постоянных ненулевых последовательностей \(\lambda m.n+1\) и такой, что если \(f(0)=0\) и \(\lambda m.f(x\cdot m)\in \mathcal{IK}\) для всех \(x\), затем \(f \in \mathcal{IK}\). утверждение \(\mathcal{K}=\mathcal{IK}\), то есть утверждение, что функции соседства могут быть сгенерированы индуктивно, эквивалентны до БИ Д .
Доказательство Брауэром теоремы о перекладине примечательно тем, что в нем используется
упорядочивающие свойства гипотетического доказательств. Он основан
при условии, что любое доказательство того, что собственность A на
последовательности — это бар, можно разложить на каноническое доказательство это хорошо упорядочено. Хотя это классически верно,
Доказательство этого принципа Брауэром показывает, что причина
принятие его в качестве действительного принципа в интуиционизме отличается
в основном из аргумента, поддерживающего его приемлемость в
классическая математика.
Хотя это классически верно,
Доказательство этого принципа Брауэром показывает, что причина
принятие его в качестве действительного принципа в интуиционизме отличается
в основном из аргумента, поддерживающего его приемлемость в
классическая математика.
3.7 Аксиомы выбора
Аксиома выбора в ее полной форме неприемлема с конструктивной точки зрения, по крайней мере, при наличии некоторых других центральные аксиомы теории множеств, такие как экстенсиональность (Diaconescu 1975). Ибо пусть \(A\) будет утверждением, истинность которого неизвестна или ЛОЖЬ. Тогда принадлежность следующих двух множеств неразрешима.
\[ \начать{выравнивать} X &= \{ x \in \{0,1\} \mid x=0 \vee (x=1 \клин A) \} \\ Y &= \{ y \in \{0,1\} \mid y=1 \vee (y=0 \клин A) \} \end{выравнивание} \]
Наличие функции выбора \(f:\{X,Y\} \rightarrow \{0,1\}\)
выбор элемента из \(X\) и \(Y\) будет означать \((A \vee \neg
А)\). В самом деле, если \(f(X)\neq f(Y)\), то \(X\neq Y\) и, следовательно,
\(\neg A\), тогда как \(f(X)=f(Y)\) подразумевает \(A\).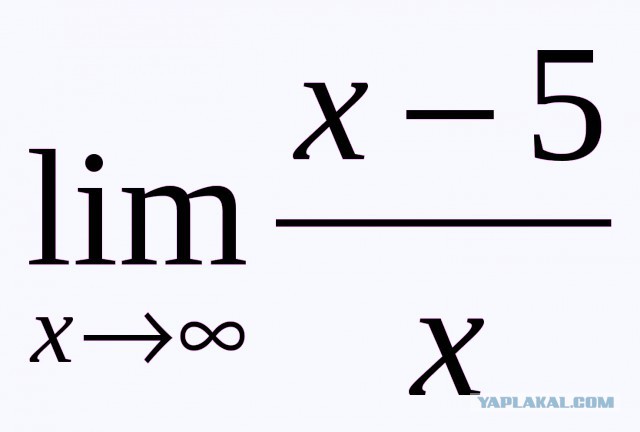 Поэтому выбор
функция для \(\{X,Y\}\) не может существовать.
Поэтому выбор
функция для \(\{X,Y\}\) не может существовать.
Однако существуют определенные ограничения аксиомы, которые приемлемой для интуициониста, например, аксиома исчисляемый выбор , также принятый в качестве легитимного принципа полуинтуиционисты, которые будут обсуждаться ниже: 9\mathbb{N} \для всех m\, mR\alpha(m) \big). \]
Эту схему можно обосновать следующим образом. Доказательство посылки должно предоставить метод, который дает \(m\) число \(n\) такое, что \(мРн\). Таким образом, функция \(\alpha\) натуральных чисел \(\mathbb{N}\) можно построить шаг за шагом: сначала элемент \(m_0\) выбирается так, что \(0Rm_0\), которое будет значением \(\альфа(0)\). Затем выбирается элемент \(m_1\) такой, что \(1Rm_1\), что будет значением \(\alpha(1)\) и так далее. 9\mathbb{N} \big( \альфа(0)=к\ \клин\\ & \forall i\geq 0\, \alpha(i)R\alpha(i+1) \big) \big). \конец{выравнивание}\]
Также в классической математике с осторожностью относятся к аксиомам выбора. и часто прямо упоминается, насколько большой выбор необходим в
доказательство. Поскольку аксиома зависимого выбора согласуется с
важная аксиома классической теории множеств (аксиома детерминированности)
пока полной аксиомы выбора нет, особое внимание уделяется
этой аксиомы и вообще каждый пытается уменьшить количество выбора в
доказательство, если выбор вообще присутствует, к зависимому выбору.
и часто прямо упоминается, насколько большой выбор необходим в
доказательство. Поскольку аксиома зависимого выбора согласуется с
важная аксиома классической теории множеств (аксиома детерминированности)
пока полной аксиомы выбора нет, особое внимание уделяется
этой аксиомы и вообще каждый пытается уменьшить количество выбора в
доказательство, если выбор вообще присутствует, к зависимому выбору.
3.8 Описательная теория множеств, топология и теория топосов
Брауэр был не одинок в своих сомнениях относительно некоторых классических форм.
рассуждений. Это особенно заметно в дескриптивной теории множеств.
которая возникла как реакция на крайне неконструктивные представления
в канторовской теории множеств. Отцы-основатели области,
включая Эмиля Бореля и Анри Лебега как двух главных
фигуры, назывались полуинтуиционистами , а их
конструктивная трактовка континуума привела к определению
Борелевская иерархия. С их точки зрения, такое понятие, как совокупность всех
наборы действительных чисел бессмысленны, и поэтому должны быть заменены
иерархией подмножеств, которые имеют четкое описание.
В Veldman 1999 интуиционистский эквивалент понятия Бореля сформулировано множество и показано, что классически эквивалентные определения борелевских множеств приводят к множеству интуитивно различные классы, ситуация, которая часто возникает в интуитивизм. Для интуиционистского Бореля задается аналог Теорема Бореля об иерархии интуиционистски верна. Доказательство этого факт существенно использует аксиомы непрерывности, обсуждавшиеся выше, и тем самым показывает, как классическая математика может направлять поиск интуиционистские аналоги, которые, однако, должны быть доказаны в совершенно иным путем, иногда используя принципы, неприемлемые с классическая точка зрения.
Другой подход к изучению подмножеств континуума или
топологическое пространство вообще появилось благодаря развитию
формальная или абстрактная топология (Fourman 1982, Martin-Löf 1970,
Самбин 1987). В этой конструктивной топологии роль открытых множеств и
точки перевернуты; в классической топологии открытое множество определяется как
определенное множество точек, в конструктивном случае открытые множества являются
фундаментальное понятие и точки определяются через них. Следовательно
этот подход иногда называют бесточечной топологией.
Следовательно
этот подход иногда называют бесточечной топологией.
Интуиционистский функциональный анализ получил широкое развитие в многие после Брауэра, но поскольку большинство подходов не строго интуитивистское, но и конструктивное в более широком смысле, это исследование здесь больше рассматриваться не будет.
Интуитивизм разделяет основную часть с большинством других форм
конструктивизм. Конструктивизм вообще занимается
конструктивные математические объекты и рассуждения. От конструктивного
доказательств можно, по крайней мере в принципе, извлечь алгоритмы, вычисляющие
элементы и моделировать конструкции, существование которых
установлено в доказательстве. Большинство форм конструктивизма совместимы
с классической математикой, так как они в целом основаны на более строгом
интерпретация кванторов и связок и
конструкции допустимы, а никаких дополнительных предположений не делается.
сделанный. Логика, принятая почти всеми конструктивными сообществами, такова:
то же самое, а именно интуитивистская логика.
Многие экзистенциальные теоремы классической математики имеют конструктивную аналог, в котором экзистенциальное утверждение заменено утверждением о приближениях. Мы видели пример этого, промежуточный теорема о ценности в разделе о слабых контрпримерах выше. Большой части математики могут быть восстановлены конструктивно аналогичным образом. Причина, по которой они не рассматриваются здесь далее, заключается в том, что основное внимание в эта статья посвящена тем аспектам интуитивизма, которые отличают ее от другие конструктивные разделы математики. Для тщательного лечения конструктивизма читатель отсылается к соответствующей статье в эту энциклопедию.
Хотя Брауэр разработал свою математику в точной и
фундаментальным образом, формализация в том смысле, в каком мы ее знаем сегодня, была
только позже другие. Действительно, согласно Брауэру
представление о том, что математика разворачивается внутренне, формализация,
хотя и не является неприемлемым, но ненужным. Другие после него думали
в противном случае, а также формализация интуиционистской математики и
изучение его метаматематических свойств, в частности арифметических
и анализ привлекли многих исследователей. Формализация
интуиционистская логика, на которой базируются все формализации, уже
лечили выше.
Формализация
интуиционистская логика, на которой базируются все формализации, уже
лечили выше.
5.1 Арифметика
Heyting Arithmetic HA в формулировке Аренд Хейтинг является формализацией интуиционистской теории натуральных чисел. (Хейтинг, 1956). Она имеет те же нелогические аксиомы, что и арифметика Пеано. PA , но он основан на интуиционистской логике. Таким образом, это является ограничением классической арифметики и является принятым теории натуральных чисел практически во всех областях конструктивизма. математика. Арифметика Гейтинга обладает многими свойствами, отражающими ее конструктивный характер, например свойство дизъюнкции, которое верно и для интуиционистской логики. Еще одно свойство HA , который PA не разделяет, является числовое свойство существования: (\(\overline{n}\) числовое соответствующее натуральному числу \(n\))
\[\tag{\({\bf НЭП}\)}
{\bf HA} \vdash \exists x A(x) \Rightarrow
\существует n \in {\mathbb N} \, {\bf HA} \vdash A(\overline{n}). \]
\]
То, что это свойство не выполняется в PA , следует из тот факт, что PA доказывает \(\существует x (A(x) \vee \для всех у \нег А(у))\). Рассмотрим, например, случай, когда \(A(x)\) есть формула \(T(e,e,x)\), где \(T\) — разрешимая формула Клини предикат, выражающий, что \(x\) является кодом завершающего вычисление программы с кодом \(e\) на входе \(e\). Если для для каждого \(e\) существовало бы число \(n\) такое, что \({\bf PA}\vdash T(e,e,n) \vee \forall y \neg T(e,e,y)\), то, проверив выполняется ли \(T(e,e,n)\), будет решено, будет ли программа \(e\) завершается на входе \(e\). Это, однако, в общем случае неразрешимо.
Правило Маркова — это принцип, который выполняется как классически, так и интуитивно, но только для HA доказательство этого факт нетривиальный:
\[\тег{\({\bf MR}\)}
{\ bf HA} \ vdash \ forall x (A (x) \ vee \ neg A (x)) \ клин
\neg\neg\exists x A(x) \Rightarrow {\bf HA}
\vdash \существует x A(x). \]
\]
Поскольку HA доказывает закон исключенного третьего для каждого примитивно-рекурсивного предиката следует, что для таких \(A\) вывод \(\neg\neg \exists x A(x)\) в 90_2\)-консервативный над ГА . То есть для примитивно-рекурсивного \(A\): \[ {\bf PA} \vdash \forall x \exists y A(x,y) \Правая стрелка {\bf HA} \vdash \forall x \exists y A(x,y). \] Таким образом, класс доказуемо рекурсивных функций HA совпадает с классом доказуемо рекурсивных функции PA , имущество, которое на основе идеи, лежащие в основе конструктивизма и интуитивизма, могут не прийти сюрприз.
5.2 Анализ
Формализация интуиционистской математики охватывает более
арифметика. Большая часть анализа была аксиоматизирована из
конструктивной точки зрения (Клин 1965, Троэльстра, 1973).
конструктивность этих систем можно установить с помощью функциональных,
теории типов или интерпретаций реализуемости, большинство из которых основано на
или расширения интерпретации диалектики Гёделя
(Гёдель, 1958, Крайзель, 1959), реализуемость Клини (Клин, 1965),
или теории типов (Martin-Löf 1984). В этих интерпретациях
функционалы, лежащие в основе конструктивных утверждений, например, такие как
функция, присваивающая \(y\) каждому \(x\) в \(\forall x\exists y
A(x,y)\), делаются явными различными способами.
В этих интерпретациях
функционалы, лежащие в основе конструктивных утверждений, например, такие как
функция, присваивающая \(y\) каждому \(x\) в \(\forall x\exists y
A(x,y)\), делаются явными различными способами.
В (Скотт, 1968 и 1970) топологическая модель второго порядка
интуиционистская теория анализа представлена там, где реальные
интерпретируются как непрерывные функции из пространства Бэра в
классические реалы. В этой модели схема Крипке, а также
выполняются некоторые аксиомы непрерывности. В (Moschovakis 1973) этот метод
адаптированы для построения модели теорий интуиционистского анализа в
термины последовательностей выбора. Также в этой модели схема Крипке
и выполняются некоторые аксиомы непрерывности. В (Ван Дален 1978) Бет модели
используются для создания модели арифметических последовательностей и последовательностей выбора, которые
удовлетворяют схемам выбора, случаям слабой непрерывности и
Схема Крипке. В этой модели домены в каждом узле являются
натуральные числа, чтобы не приходилось использовать нестандартные модели,
как и в случае с моделями Крипке. Более того, аксиомы CS1–3 создающего субъекта можно
интерпретируется в нем, тем самым показывая, что эта теория непротиворечива.
Более того, аксиомы CS1–3 создающего субъекта можно
интерпретируется в нем, тем самым показывая, что эта теория непротиворечива.
5.3 Беззаконные последовательности
Существуют аксиоматизации беззаконных последовательностей, и все они содержат расширения аксиом непрерывности (Крейзель 1968, Троэльстра 1977). В частности, в форме Аксиомы открытых данных, утверждающей что для \(A(\alpha)\), не содержащего других незаконоподобных параметров кроме \(\альфа\):
\[ A(\alpha) \rightarrow \ существует n \forall \beta \in \alpha (\overline{n}) A(\beta). \]
В (Troelstra 1977) развивается теория незаконных последовательностей (и
оправдано) в контексте интуиционистского анализа. Кроме аксиом
для элементарного анализа он содержит, для беззаконных последовательностей,
усиленные формы аксиом открытых данных, непрерывности,
разрешимость и плотность (плотность говорит о том, что каждая конечная последовательность
начальный сегмент беззаконной последовательности). Что особенно
интересно то, что в этих теориях кванторы над беззаконием
последовательности могут быть исключены, что также можно рассматривать как
предоставление модели законоподобных последовательностей для таких теорий. Другой
классические модели теории беззаконных последовательностей были
построенные в теории категорий в виде моделей пучков (ван дер
Хувен и Мурдейк 1984). В (Moschovakis 1986) теория выбора
вводятся последовательности относительно определенного набора закономерностей,
наряду с классической моделью, в которой получаются беззаконные последовательности
быть именно общими.
Что особенно
интересно то, что в этих теориях кванторы над беззаконием
последовательности могут быть исключены, что также можно рассматривать как
предоставление модели законоподобных последовательностей для таких теорий. Другой
классические модели теории беззаконных последовательностей были
построенные в теории категорий в виде моделей пучков (ван дер
Хувен и Мурдейк 1984). В (Moschovakis 1986) теория выбора
вводятся последовательности относительно определенного набора закономерностей,
наряду с классической моделью, в которой получаются беззаконные последовательности
быть именно общими.
5.4 Формализация создающего субъекта
Создание субъекта, представленное в разделе 2.2, может генерировать выбор. последовательности, которые являются одними из самых важных и сложных математические сущности интуиционизма Брауэра. Несколько философы и математики пытались разработать теорию Создающий Субъект далее математически, а также философски.
В формализации понятия Творящего Субъекта его
временной аспект формализуется с помощью обозначения \(\Box_n A\), т. е.
означает, что Создающий Субъект имеет доказательство А в момент времени n (в каком-то
другие формулировки: переживает истинность \(A\) в момент времени \(n\)).
Георг Крайзель (1967) ввел следующие три аксиомы для
Создание темы, которые вместе обозначаются CS :
е.
означает, что Создающий Субъект имеет доказательство А в момент времени n (в каком-то
другие формулировки: переживает истинность \(A\) в момент времени \(n\)).
Георг Крайзель (1967) ввел следующие три аксиомы для
Создание темы, которые вместе обозначаются CS :
\[\начать{выравнивать} \тег{\({\bf CS1}\)} & \Box_n A \vee \neg \Box_n A \\ & \mbox{(в момент времени \(n\) можно решить, будет ли создан объект создания} \\ & \mbox{ имеет доказательство A)} \\ \тег{\({\bf CS2}\)} & \Box_m A \rightarrow \Box_{m+n}A \\ & \mbox{(Творящий Субъект никогда не забывает, что он доказал)} \\ \тег{\({\bf CS3}\)} & (\exists n \Box_n A \rightarrow A) \wedge (A \rightarrow \neg\neg \exists n \Box_n A)\\ & \mbox{(Тема создания только доказывает, что правда, а что нет} \\ & \mbox{ истинное утверждение невозможно доказать для} \\ & \mbox{ Создание темы)}\\ \конец{выравнивание}\] 9+\)} & \существует n \Box_n A \leftrightarrow A \\ & \mbox{(Тема Создания только доказывает, что правда, а что} \\ & \mbox{ истинно, будет доказано созданием темы в некотором месте} \\ & \mbox{ точка)} \конец{выравнивание}\]
Первая аксиома CS1 бесспорна: в любой момент времени
можно установить, есть ли у Создающего Субъекта доказательство
данное заявление или нет.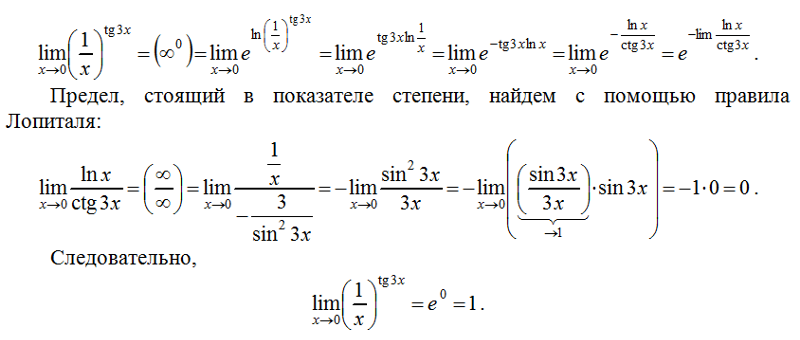 Вторая аксиома CS2 явно использует
тот факт, что Создающий Субъект является идеализацией, поскольку он выражает
что доказательства всегда будут помнить. Последняя аксиома CS3 есть
самая спорная часть формализации Творящего Субъекта,
или лучше, его второй конъюнкт \((A \rightarrow \neg\neg\exists n\Box_n A)\)
есть, которому было присвоено имя Аксиома христианского милосердия Крайзель. Йоран Сундхольм (2014), например, утверждает, что аксиома
Христианская благотворительность неприемлема с конструктивной точки зрения.
А теорема Гёделя о неполноте даже подразумевает, что
принцип ложен, когда \(\Box_n A\) будет интерпретироваться как
доказуема в достаточно сильной системе доказательств, которая, однако,
определенно не та интерпретация, которую имел в виду Брауэр.
Вторая аксиома CS2 явно использует
тот факт, что Создающий Субъект является идеализацией, поскольку он выражает
что доказательства всегда будут помнить. Последняя аксиома CS3 есть
самая спорная часть формализации Творящего Субъекта,
или лучше, его второй конъюнкт \((A \rightarrow \neg\neg\exists n\Box_n A)\)
есть, которому было присвоено имя Аксиома христианского милосердия Крайзель. Йоран Сундхольм (2014), например, утверждает, что аксиома
Христианская благотворительность неприемлема с конструктивной точки зрения.
А теорема Гёделя о неполноте даже подразумевает, что
принцип ложен, когда \(\Box_n A\) будет интерпретироваться как
доказуема в достаточно сильной системе доказательств, которая, однако,
определенно не та интерпретация, которую имел в виду Брауэр.
Учитывая утверждение \(A\), которое не содержит никакой ссылки на время, т. е. нет появления \(\Box_n\), можно определить последовательность выбора по следующему правилу (Brouwer 1953):
\[
\alpha (n) = \left\{ \begin{массив}{ll}
0 & \mbox{ если \(\neg \Box_n A\)} \\
1 & \mbox{, если \(\Box_n A\).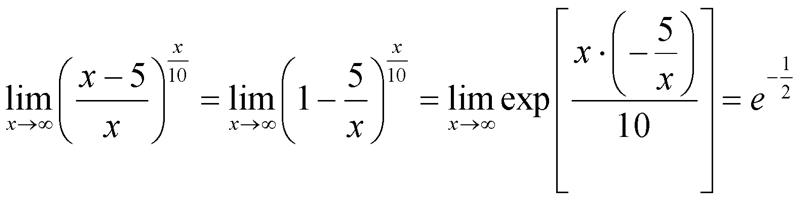 }
\end{массив} \right.
\]
}
\end{массив} \right.
\]
Отсюда следует принцип, известный как схема Крипке. KS , представленный в разделе 2.2, принцип, который в отличие от аксиом теории Создающего Субъекта, не содержит явного ссылка на время: \(\exists \alpha (A \leftrightarrow \exists n \альфа(п) = 1)\).
Используя схему Крипке, аргументы слабого контрпримера могут быть выражено формально без какой-либо ссылки на Создание Субъекта. следующий пример взят из (van Atten 2018). Пусть A будет утверждением для которого в настоящее время \(\neg A \vee \neg\neg A\) не известно. Используя KS , можно получить последовательности выбора \(\alpha_1\) и \(\alpha_2\) такой, что
\[ \neg A \leftrightarrow \exists n \alpha_1(n) = 1 \ \ \ \ \neg\neg A
\leftrightarrow \существует n \alpha_2(n) = 1. \]
9{-m} & \begin{align} &\text{if для некоторых \(m\leq n\), \(\alpha_i(m)=1\) и } \\
& \text{для отсутствия \(k \lt m\), \(\alpha_i(k)=1. \)}
\end{выравнивание}
\end{случаи}
\]
\)}
\end{выравнивание}
\end{случаи}
\]
Тогда для \(r=r_0 + r_1\) оператор \(\neg A \vee \neg\neg A\) следует из \((r\gt 0\vee r\lt 0)\), что показывает, что \((r\gt 0\vee r\lt 0)\) не может быть доказано.
В (van Dalen 1978) построена модель аксиом для Создание Субъекта в контексте последовательностей арифметики и выбора, тем самым доказывая, что они согласуются с интуиционистской арифметикой и определенные разделы анализа. Вышел (ван Дален 1982), Доказано, что CS быть консервативным по арифметике Гейтинга. Математические следствия Схему Крипке можно найти в (van Dalen 1997), где она показано, что KS и аксиомы непрерывности отвергают марковскую принципу, а КС вместе с принципом Маркова подразумевает принцип исключенного третьего.
Крипке показал, что KS подразумевает существование нерекурсивных
функций, результат, опубликованный не им, а Крайзелем (1970).
Ясно, что это подразумевает, что теория CS также подразумевает
существование нерекурсивной функции. Возможный аргумент в пользу CS работает следующим образом. Предположим, что \(X\) является невычислимым, но
вычислимо перечислимое множество и определим функцию \(f\) как
следует:
Возможный аргумент в пользу CS работает следующим образом. Предположим, что \(X\) является невычислимым, но
вычислимо перечислимое множество и определим функцию \(f\) как
следует:
\[ ф (м, п) = \begin{случаи} 0 & \text{ если не \(\Box_m (n \not\in X)\)} \\ 1 & \text{ если \(\Box_m (n \not\in X)\).} \end{случаи} \]
Отсюда следует, что \(n\not\in X\) тогда и только тогда, когда \(f(m,n)=1\) для некоторое натуральное число \(m\), откуда следует, что \(f\) не может быть вычислимый. Ибо если это так, то дополнение \(X\) было бы вычислимо перечислима, что влечет вычислимость \(X\). Так как \(f\) является функции с интуиционистской точки зрения, это устанавливает, что в интуиционизме не все функции вычислимы.
5.5 Фундамент
Формализации, которые должны служить основой для
конструктивная математика является либо теоретико-множественной (Aczel 1978,
Myhill 1975) или теоретико-типовой (Martin-Löf 1984) природы. прежние теории являются адаптацией теории множеств Цермело-Френкеля к
конструктивная установка, тогда как в теории типов конструкции неявные
в конструктивных заявлениях делаются явными в системе. Теория множеств
можно рассматривать как экстенсиональную основу математики, тогда как
теория типов, вообще говоря, интенсиональна.
прежние теории являются адаптацией теории множеств Цермело-Френкеля к
конструктивная установка, тогда как в теории типов конструкции неявные
в конструктивных заявлениях делаются явными в системе. Теория множеств
можно рассматривать как экстенсиональную основу математики, тогда как
теория типов, вообще говоря, интенсиональна.
В последние годы многие модели частей таких основополагающих теорий для появилась интуиционистская математика, некоторые из них упомянутое выше. Особенно в теории топосов (van Oosten 2008) Есть много моделей, которые отражают определенные характеристики интуитивизма. Существуют, например, топосы, в которых все полные действительные функции непрерывный. Функциональные интерпретации, такие как реализуемость, а также интерпретаций в теории типов также можно рассматривать как модели интуиционистская математика и большинство других конструктивных теорий.
5.6 Обратная математика
В обратной математике пытаются установить для математических
теоремы, какие аксиомы нужны для их доказательства.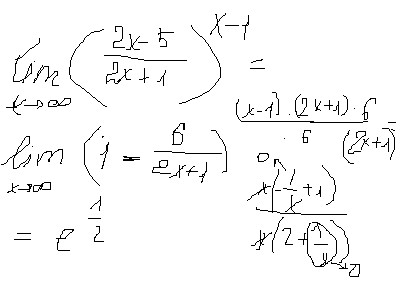 В интуиционистском
обратная математика преследует аналогичную цель, но тогда по отношению к
интуиционистские теоремы: работа над слабой интуиционистской теорией,
аксиомы и теоремы сравниваются друг с другом. Типичные аксиомы
теоремы, с которыми хотелось бы сравнить, — это принцип веера и
принцип стержня, схема Крипке и непрерывность
аксиомы.
В интуиционистском
обратная математика преследует аналогичную цель, но тогда по отношению к
интуиционистские теоремы: работа над слабой интуиционистской теорией,
аксиомы и теоремы сравниваются друг с другом. Типичные аксиомы
теоремы, с которыми хотелось бы сравнить, — это принцип веера и
принцип стержня, схема Крипке и непрерывность
аксиомы.
В (Вельдман 2011) эквиваленты веерного принципа над базовым теории, называемой базовой интуиционистской математикой. это показано, что принцип веера эквивалентен утверждению, что единичный интервал [0,1] обладает свойством Гейне-Бореля, и из этого множества выводятся другие эквиваленты. В (Вельдман 2009) принцип вентилятора показано, что он также эквивалентен приближенной фиксированной точке Брауэра. Теорема. В (Lubarsky et al. 2012) обратная математика применяется к форма схемы Крипке, которая, как показано, эквивалентна некоторые топологические утверждения.
Таких примеров из интуиционистского реверса гораздо больше.
математика. Особенно в более широком поле конструктивного реверса
математике есть много результатов такого рода, которые также
актуально с интуиционистской точки зрения.
Брауэр построил свой интуитивизм с нуля и сделал не комментировать отношения между интуитивизмом и другими существующих философий, но и другие после него. Что-нибудь из этого В этом разделе обсуждаются связи, в частности способ какие интуиционистские принципы могут быть оправданы с точки зрения других философии.
6.1 Феноменология
Связь между интуиционизмом и феноменологией, философией
разработан Эдмундом Гуссерлем, исследовался несколькими авторами,
как при жизни Брауэра, так и десятилетия спустя. Герман Вейль
был одним из первых, кто обсудил связь между
идеи и феноменологический взгляд на математику. Как и Брауэр, Вейл
говорит в своей книге Das Kontinuum (глава 2) о интуитивный континуум , но понятие Вейля основано на
феноменология (сознания) времени. Позже Вейль чувствует, что
Разработка Брауэром реального анализа более верна
представление об интуитивном континууме, чем его собственное (Weyl 1921) и поэтому
становится на сторону Брауэра, по крайней мере, в этом аспекте
(ван Аттен, 2002).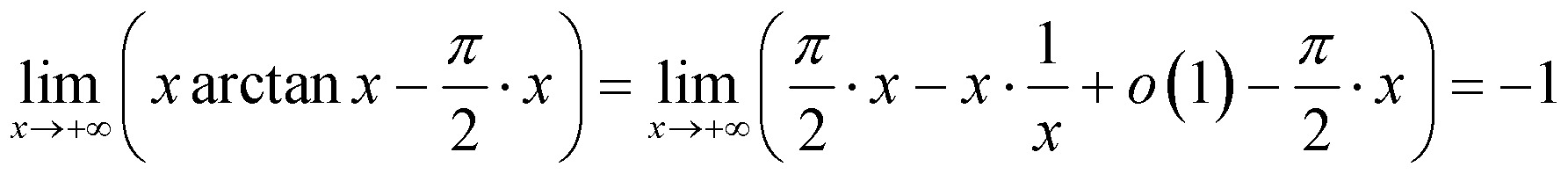
Ван Аттен (2003 en 2007) использует феноменологию для обоснования выбора. последовательности как математические объекты. Автор (2002) критически относится к Брауэровское обоснование последовательностей выбора, которое является мотивом искать философское оправдание в другом месте. Последовательности выбора встречаются в работах Беккера (1927) и Вейля, но они отличаются от Брауэра, и Гуссерль никогда не обсуждали последовательности выбора. публично. Ван Аттен объясняет, как однородность континуум объясняет его неисчерпаемость и неатомарность, два ключевых свойства интуитивного континуума по Брауэру. С использованием тот факт, что эти два существенных свойства присутствуют в определении последовательностей выбора, мы приходим к феноменологическому обоснованию из них.
6.2 Витгенштейн
10 марта 1928 года Брауэр читал в Вене лекцию о своей интуиционистской теории.
основы математики. Людвиг Витгенштейн присутствовал на этой лекции,
убежденный Гербертом Фейглом, который впоследствии писал о часах, которые он
провел с Витгенштейном и другими после лекции: отличный
произошло событие. Внезапно и очень многословно Витгенштейн заговорил
философия – очень долго. Возможно, это был поворот
точка, навсегда с того времени, 1929, когда он переехал в Кембридж
университет, Витгенштейн снова стал философом и начал
огромное влияние .
Внезапно и очень многословно Витгенштейн заговорил
философия – очень долго. Возможно, это был поворот
точка, навсегда с того времени, 1929, когда он переехал в Кембридж
университет, Витгенштейн снова стал философом и начал
огромное влияние .
Другие оспаривают, что лекция Брауэра повлияла на
Мышление Витгенштейна (Hacker 1986, Hintikka 1992, Marion
2003). В какой степени Витгенштейн находился под влиянием
Идеи Брауэра не совсем ясны, но, безусловно, есть
интересные совпадения и разногласия между их взглядами. Марион
(2003) утверждает, что концепция математики Витгенштейна как
описанное в «Трактате», очень близко к описанию Брауэра, и что
Витгенштейн соглашается с отказом от закона исключенного третьего.
(1929 рукопись, стр. 155–156 в Wittgenstein 1994), но не согласен
с аргументами Брауэра против этого. Марион (2003) утверждает, что
Позиция Витгенштейна более радикальна, чем у Брауэра.
что, по мнению первого, недействительность Закона
Исключенное среднее в математике — отличительная черта всех
математические предложения (в отличие от эмпирических предложений) и
не только особенность математики бесконечного, как
для Брауэра.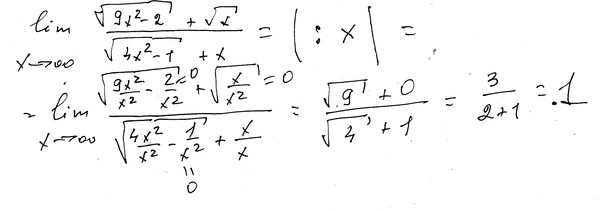
Вельдман (ожидается) обсуждает несколько моментов (не)согласия между Брауэра и Витгенштейна, таких как опасность логики, которая, согласно обоим, может привести к конструкциям без математических содержание. Одно из разногласий, затронутых в статье, касается Витгенштейн считал, что математика — это общее дело. что резко контрастирует с «Созданием субъекта» Брауэра и его считают, что математика — это бесъязыковая деятельность.
6.3 Даммет
Британский философ Майкл Даммет (1975) разработал философская основа интуиционизма, в частности интуиционистского логика. Даммит прямо заявляет, что его теория не является экзегезой Брауэра, а возможная философская теория (в его слов) отказ от классических рассуждений в математике в пользу интуиционистское рассуждение .
Подход Даммета начинается с идеи о том, что выбор одного
логика над другой обязательно должна заключаться в том значении, которое человек придает
логические утверждения. В теории значения, которую использует Даммет, которая
основывается на представлениях Витгенштейна о языке и в
особенно на его идее, что означает использование , значение a
предложение определяется тем, как оно используется. смысл математического утверждения проявляется в использовании
его, и понимание его есть знание
способность использовать заявление. Эта точка зрения поддерживается, кстати, в
которые мы приобретаем математические знания. Когда мы изучаем математический
понятие, мы учимся, как его использовать: как его вычислить, доказать или сделать вывод
от него. И единственный способ установить, что мы поняли
смысл математического утверждения заключается в нашей способности делать
правильное использование высказывания.
смысл математического утверждения проявляется в использовании
его, и понимание его есть знание
способность использовать заявление. Эта точка зрения поддерживается, кстати, в
которые мы приобретаем математические знания. Когда мы изучаем математический
понятие, мы учимся, как его использовать: как его вычислить, доказать или сделать вывод
от него. И единственный способ установить, что мы поняли
смысл математического утверждения заключается в нашей способности делать
правильное использование высказывания.
При таком взгляде на значение центральное понятие в теории значение для математики не есть, как в платонизме, истина, а пруф ; понимание математического утверждения состоит в способности распознать доказательство этого, когда человеку предъявляют один. Это затем, как утверждает Даммет, приводит к принятию интуиционистская логика как логика математических рассуждений.
Интересно, как отмечает сам Даммет (Dummett, 1975), его теория
значение далеко отстоит от представлений Брауэра о математике как
практически безъязыковая деятельность.

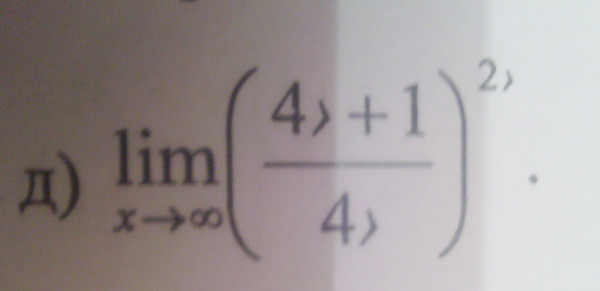
 .. (Брауэр 1981, 8)
.. (Брауэр 1981, 8)