Линейное программирование. Теория
Примеры решенийМетод ГомориГрафический метод Теория игрСимплекс-метод M-задача Теоремы двойственности Одноканальные СМО Задача коммивояжера Транспортная задача
- Классификация экономических моделей
- Линейное программирование
- Микроэкономические модели линейного программирования
- Задача составления кормовой смеси или задача о диете
- Производственная задача
- Задача о раскрое или минимизации отходов (обрезков)
- Задача об использовании мощностей
- Задача о банке
- Модели линейного программирования для решения задач раскроя
- Модель оптимизации рекламной кампании
- Динамические модели линейного программирования
Графический метод решения задач линейного программирования
- Решение систем линейных неравенств графически
- Решение задачи линейного программирования графически
- Графический анализ чувствительности
Симплекс-метод решения задач линейного программирования
- Формулировка основных типов задач ЛП, построение их математических моделей
- Каноническая форма задач линейного программирования
- Симплексный метод решения задач линейного программирования
- Поиск первоначального опорного плана
- Виды записи симплекс-метода
- Двухфазный симплекс-метод
- Матричное описание симплекс-метода
- M-задача
- Симплекс-метод с естественным базисом
- Дробно-линейное программирование
- Построение математической модели для симплекс-задачи
Двойственность в задачах линейного программирования
- Теоремы двойственности.
Двойственность в задачах линейного программирования
- Экономическая интерпретация двойственной задачи и теории двойственности (Анализ решения задачи линейного программирования с помощью теории двойственности)
- Симметричные двойственные задачи
- Несимметричные двойственные задачи
Двойственность в задачах линейного программирования
Целочисленное программирование
- Метод отсечения. Алгоритм Гомори
- Алгоритм Гомори для частично целочисленной задачи линейного программирования
- Целочисленное программирование
- Метод ветвей и границ
Задачи линейного параметрического программирования
Словарь по линейному программированию
Задачу ЛП с двумя переменными можно решить графически, при этом ограничения будут представлять выпуклое множество допустимых решений (в случае его ограниченности – многогранник), а целевая функция F(x) – семейство параллельных прямых. Решение задачи всегда находится в угловой точке, либо в выпуклой линейной комбинации двух угловых точек.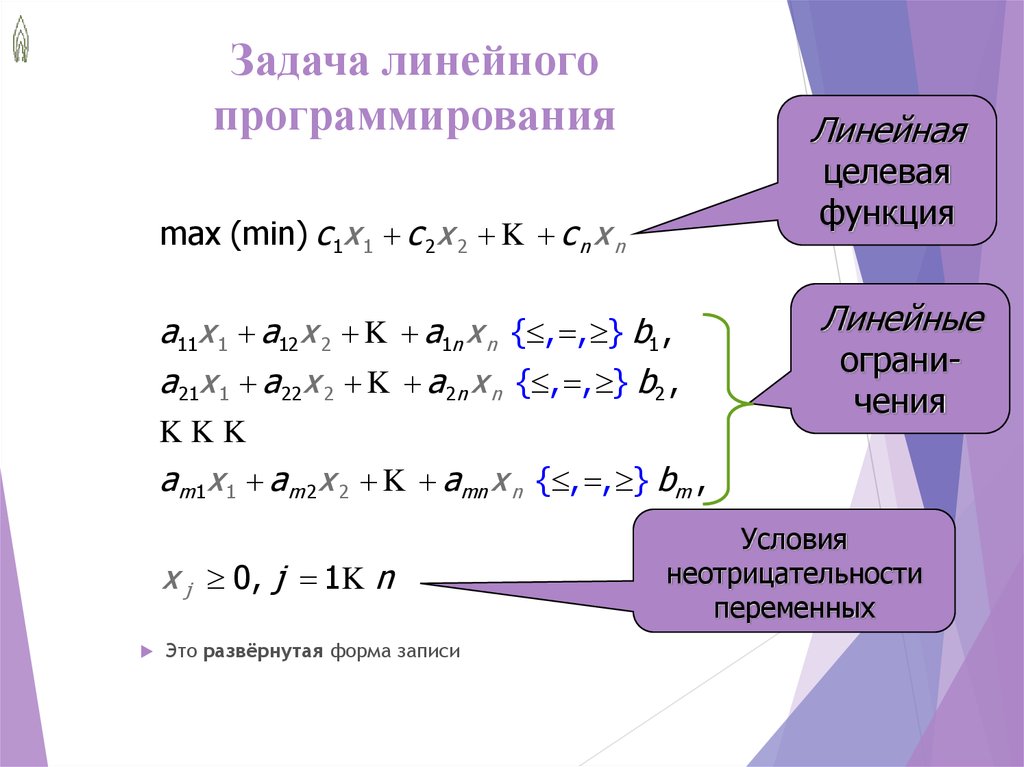
Все алгоритмы решения ЗЛП опираются на каноническую форму задачи. Поэтому число искомых переменных канонической задачи будет больше, чем исходной.
Список рекомендуемой литературы
- Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем. Учебное пособие. – М.,Финансы и статистика, 2005
- Беспалов М.С. Линейное программирование. Владимир: ВлГУ. 1999
- Галкин А.А. Математическая экономика. Владимир: ВлГУ. 2006
- Глухов В.В.Математические методы и модели для менеджмента: учебное пособие. – СПБ;М.;Краснодар:Лань,2005
- Грицюк С.Н.Математические методы и модели в экономике: учебник.- Ростов н/Д:Феникс, 2007
- Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: Учебник. – М.,Изд-во «Дело и сервис», 2004.
- Исследование операций в экономике. Учебное пособие для вузов/Под ред. проф.Н.Ш.Кремера. – М., ЮНИТИ, 2005.
- Кузнецов Б. Т. Математические методы и модели исследования операций: учебное пособие. М.:ЮНИТИ – ДАНА, 2005
- Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. М.: Высшая школа. 1980.
- Кундышева Е.С. Математическое моделирование в экономике: Учебное пособие. – М., Издательско-торговая корпорация «Дашков и Ко», 2004.
- Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании: Учеб.- М.:Дело, 2001
- Орехов А.М. Методы экономических исследований: учебное пособие. – М:ИНФРА – М, 2006
- Орлова А.М. Экономико-математическое моделирование: практическое пособие по решению задач – М.: Вузовский учебник, 2007
- Просветов Г.И.Математические методы в экономике: учебно-методическое пособие. М, Изд-во РДЛ, 2007
- Справочник по математике для экономистов. Под ред. В.И. Ермакова. М.: Высшая школа. 1987.
- Фомин Г.П. Математические методы и модели в коммерческой деятельности: Учебник. — М.: Финансы и статистика, 2005.
- Шевченко В.Н., Золотых Н.Ю. Линейное и целочисленное линейное программирования. — Нижний Новгород: Изд-во Нижегородского государственного университета им. Н.И. Лобачевского, 2004. — 154 с.
- Экономико-математическое моделирование: учебник / ред.И.Н. Дрогобыцкий. М.:Экзамен, 2006
- Экономико-математические методы и модели:учебное пособие / под ред. С.И.Макарова. – М.:КНОРУС, 2007
Т. Математические методы и модели исследования операций: учебное пособие. М.:ЮНИТИ – ДАНА, 2005
— М.: Финансы и статистика, 2005.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Поиск материала «Линейное программирование, учебное пособие, Палий И.А., 2008» для чтения, скачивания и покупки
Ниже показаны результаты поиска поисковой системы Яндекс. В результатах могут быть показаны как эта книга, так и похожие на нее по названию или автору.
Search results:
- Книги по линейному, математическому программированию . ..
Данциг Д. Линейное программирование, его применения и обобщения. Вентцель Е. С. Исследование операций: задачи, принципы, методология. Д. Б. Юдин, Е. Г. Гольштейн Задачи и методы линейного программирования . Грешилов А.А. Прикладные задачи математического программирования. Калихман И. Л., Войтенко М. А. Динамическое программирование в примерах и задачах. Калихман И. Л. Сборник задач по математическому программированию. Карманов В. Г. Математическое программирование.
vk.com
- Скачать Палий И.А. — Линейное программирование
Название: Линейное программирование Автор: Палий И.А. Издательство: Москва Год: 2008 Cтраниц: 256 Формат: pdf Размер: 11 мб Язык: русский.
Рассматриваются следующие темы: построение математических моделей задач линейного программирования, графическое решение задач с двумя переменными, симплекс-метод, теория двойственности, метод потенциалов решения транспортной задачи, паросочетания, потоки в сетях, венгерский алгоритм решения задач о назначениях и транспортной задачи.
litgu.ru
-
Купить эту книгу
- Канцтовары
Канцтовары: бумага, ручки, карандаши, тетради. Ранцы, рюкзаки, сумки. И многое другое.
my-shop.ru
- Линейное программирование | Палий И.А. | download
А. Линейное программирование. Учебное пособие/ И. А. Палий.
Учебное пособие подготовлено в соответствии с требованиями Государственного образовательного стандарта. Рассматриваются следующие темы: построение математи ческих моделей задач линейного программирования. графическое решение задач с двумя переменными, симплекс-метод, теория двойственности, метод потенциалов решения транспортной задачи, паросочетания, потоки в сетях, венгерский алгоритм решения за дач о назначениях и транспортной задачи.
b-ok.
xyz - Палий И.А. Линейное программирование
Учебное пособие подготовлено в соответствии с требованиями Государственного образовательного стандарта. Рассматриваются следующие темы: построение математических моделей задач линейного программирования, графическое решение задач с двумя переменными, симплекс-метод, теория двойственности, метод потенциалов решения транспортной задачи, паросочетания, потоки в сетях, венгерский алгоритм решения задач о назначениях и транспортной задачи.
www.studmed.ru
- Линейное программирование. учебное пособие | Палий…
Учебное пособие подготовлено в соответствии с требованиями Государственного образовательного стандарта. Рассматриваются следующие темы: построение математических моделей задач линейного программирования, графическое решение задач с двумя переменными, симплекс-метод, теория двойственности, метод потенциалов решения транспортной задачи, паросочетания, потоки в сетях, венгерский алгоритм решения задач о назначениях и транспортной задачи.
Изложение теоретического материала сопровождается…libcats.org
- Линейное программирование 2-е изд., испр. и доп. Учебное…
Главная » Ирина Абрамовна Палий » Линейное программирование 2-е изд., испр. и доп.
В результате изучения данного учебного пособия студенты узнают принципы построения математических моделей задач линейного программирования, обоснование симплекс-метода решения задач линейного программирования, основы теории двойственности, основы теории потоков в сетях, обоснование метода потенциалов и венгерского алгоритма решения транспортной задачи, научатся находить решения различных задач линейного…
child-class.ru
- Литература по линейному, математическому программированию…
Палий И. А. Линейное программирование. Учебное пособие / И. А. Палий.
— 256 с ISBN 5-211-03766-9 В учебное пособие включен материал по основным разделам курси «Исследование операций» — линейному программированию, задачам транспортного типа, системам массового обслуживания, системам управления запасами, моделям сетевой оптимизации и т.
diary.ru
- Палий И.А. Линейное программирование
-М.: ЭКСМО, 2008. -257с.Учебное пособие подготовлено в соответствии с требованиями Государственного образовательного стандарта.
Деева Е.М. Методические указания по решению типовых задач по дисциплине Линейная алгебра и линейное программирование (Документ). Кирсанова О.В., Семёнова Г.А. Математическое программирование (типовой расчёт) (Документ). Мощевикин А.П. Презентации лекций «Теория принятия решений» (Документ).
nashaucheba.ru
- Линейное программирование
Учебное пособие. — Воронеж: Изд-во ВГУ, 2001. — 61 с. В учебном пособии излагаются основы линейного программирования: общая постановка задач линейного программирования, формы записи задачи, алгоритм переброса базисных решений системы линейных уравнений, алгоритм симплексного метода, метод искусственного базиса и M-метод решения произвольной задачи линейного программирования, двойственные задачи линейного программирования.
www.studmed.ru
- Учебники, видео, лекции по математическому и линейному…
Линейное программирование: учебники, видео, примеры. В данном разделе мы предлагаем ссылки на лучшие учебные материалы по линейному программированию. Нет времени на изучение? Предлагаем выполнение любых задач линейного программирования на заказ .
Бодров В.И., Лазарева Т.Я., Мартемьянов Ю.Ф., «Математические методы принятия решений» Учебное пособие. Тамбов, 2004. 124 с. Изложены методы линейного и нелинейного программирования, динамическое программирование, игровые методы.
www.MatBuro.ru
- Линейное программирование 2-е изд., испр. и доп. Учебное…
Данное учебное пособие посвящено изучению основ линейного программирования. Изложение теоретического материала сопровождается большим количеством подробно разобранных примеров решения задач, что облегчает усвоение доказательств теорем и принципов работы алгоритмов.
В результате изучения данного учебного пособия студенты узнают принципы построения математических моделей задач линейного программирования, обоснование симплекс-метода решения задач линейного программирования, основы теории…www.litprichal.ru
- Е.Л. Богданова | Примеры задач линейного программирования.
Богданова Е.Л. Оптимизация в проектном менеджменте: линейное программирование: учебное пособие / Е.Л. Богданова, К.А. Соловейчик, К.Г. Аркина.
Пособие имеет учебно-методическое назначение и предназначено для изучения студентами материала раздела линейное программирование дисциплины учебного плана «Проектный менеджмент». В пособии рассмотрены основные методы вычислений раздела исследования операций: линейное программирование на основании примеров в области экономики предприятия.
books.ifmo.ru
- Ирина Абрамовна Палий. Линейное программирование 2-е изд. …
Линейное программирование 2-е изд., испр. и доп. Учебное пособие для академического бакалавриата.
Изложение теоретического материала сопровождается большим количеством подробно разобранных примеров решения задач, что облегчает усвоение доказательств теорем и принципов работы алгоритмов. В результате изучения данного учебного пособия студенты узнают принципы построения математических моделей задач линейного программирования, обоснование симплекс-метода решения задач линейного программирования, основы теории…
referatodrom.ru
- Один из первых вопросов, который возникает у первокурсника, это…
Учебно-методическое пособие содержит теоретические сведения, необходимые для изучения темы «Линейное программирование» учебного курса «Методы оптимизации». Изложение сопровождается примерами решения типовых задач. Приведены задачи для самостоя-тельного решения и 10 вариантов для контрольной работы. Пособие предназначено для студентов, обучающихся по направлению подготовки «Прикладная информатика», а также для преподавателей вузов, инженеров и научных работников.
files.informio.ru
- Microsoft Word — Часть1
Болотникова, О. В. Б79 Линейное программирование: симплекс-метод и двойствен-. ность : учеб. пособие / О. В. Болотникова, Д. В. Тарасов, Р. В. Та-расов. – Пенза : Изд-во ПГУ, 2015. – 84 с. ISBN 978-5-906831-36-1. Работа содержит детальное рассмотрение постановки задач линей-ного программирования, алгоритм симплекс-метода, понятие двой-ственности и задачи целочисленного программирования. Изложение материала сопровождается подробными примерами применения суще-ствующих методов линейного программирования.
dep_vipm.pnzgu.ru
- Ашманов С.А. Линейное программирование
Учебное пособие. — Новосибирск: Изд-во НГУ, 2000 г. — 105 с. В пособии изложен математический аппарат, необходимый для анализа и решения экстремальных задач в конечномерных пространствах. Линейное программирование.
Наглядное пособие / Авторы-составители: Семенкин Е.
С., Семенкина О.Э., Антамошкин А.Н., Терсков В.А., Тынченко В.В. — Красноярск: СФУ, 2007 — 269 слайдов. Содержание: Классификация задач оптимизации. Линейное программирование.www.studmed.ru
- Палий И.А. — Линейное программирование. учебное пособие…
Название: Линейное программирование. учебное пособие. Автор: Палий И.А. Аннотация: Учебное пособие подготовлено в соответствии с требованиями Государственного образовательного стандарта. Рассматриваются следующие темы: построение математических моделей задач линейного программирования, графическое решение задач с двумя переменными, симплекс-метод, теория двойственности, метод потенциалов решения транспортной задачи, паросочетания, потоки в сетях, венгерский алгоритм решения задач о…
lib.mexmat.ru
- «Линейное программирование 2-е изд. , испр. и доп. Учебное…»
В электронной библиотеке ЛитРес можно читать онлайн бесплатно Линейное программирование 2-е изд., испр. и доп. Учебное пособие для академического бакалавриата от Ирины Абрамовны Палий!
Данное учебное пособие посвящено изучению основ линейного программирования. Изложение теоретического материала сопровождается большим количеством подробно разобранных примеров решения задач, что облегчает усвоение доказательств теорем и принципов работы алгоритмов.
www.litres.ru
- ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Учебное пособие составлено в соответствии с требованиями ФГОС подготовки бакалавра по направлению 080500 – Бизнес-информатика с ква-лификацией выпускника «Бакалавр». Пособие содержит теоретическую часть и практические рекомендации по решению типовых задач дисциплины «Линейное программирование», ко-торая входит в цикл общих математических и естественно-научных дисцип-лин и опирается на предшествующие ей дисциплины «Математический ана-лиз» и «Линейная алгебра».
repo.ssau.ru
- Линейное программирование: Руководство к решению задач
Руководство к решению задач Автор: Баскаков С.И. Издательство: М.: Высшая школа Год: 2002 — 2-е изд., дополн. Cтраниц: 214 Формат: pdf Размер: 11 мб Язык: русский Пособие содержит задачи по всем разделам… Параллельное программирование Автор: Качко Е. Г. Название: Параллельное программирование Издательство: Форт Язык: Русский Год: 2011 Формат: pdf, djvu / rar Размер: 14,97 Mb Кол-во страниц: 528 Описание: В учебном пособии изложены методы создания программ с параллельными…
bookskeeper.ru
- Линейное программирование (учебное пособие для студентов)
Учебное пособие для студентов по математике. Линейное программирование. СОДЕРЖАНИЕ. Постановка основной задачи линейного программирования (ОЗЛП) с n переменными. Графический метод решения ОЗЛП с двумя переменными.
www.resolventa.ru
- Васильев Ф.П., Иваницкий А.Ю. Линейное программирование
— 176 с. В книге дается строгое изложение основ теории линейного программирования с использованием минимального аппарата математического анализа и линейной алгебры, без привлечения теории многогранных множеств и теорем отделимости.
Учебное пособие. — Новосибирск: Изд-во НГУ, 2000 г. — 105 с. В пособии изложен математический аппарат, необходимый для анализа и решения экстремальных задач в конечномерных пространствах. Линейное программирование.
www.studmed.ru
- Линейное программирование — Скачать бесплатно
Учебники и пособия для среднего и специального образования. Школьные учебники и пособия, рефераты, шпаргалки. Фантастика.
События книги. Формат: DJVU (1069 Kb). СКАЧАТЬ. Currently 0/5. Рейтинг: 0/5 (Всего голосов: 0). Аннотация.
Линейное программирование.www.rulit.me
- Линейное программирование | Васильев Ф.П., Иваницкий…
Линейное программирование. Васильев Ф.П., Иваницкий А.Ю. Скачать книгу бесплатно (djvu, 1.93 Mb).
libcats.org
- Линейное программирование » Litgu.ru — Литературный гуру
Название: Линейное программирование Автор: Мунасыпов Н.А. Издательство: Оренбург: ООО «Агентство «Пресса» Год: 2015 Страниц: 122 ISBN: 978-5-91854-185-2 Формат: PDF Размер: 10.5 Мб Язык: русский. Учебное пособие содержит основные теоретические положения и алгоритмы решения задач линейного программирования, проиллюстрированные численными примерами.
litgu.ru
- Линейное программирование | Лунгу К.Н. | скачать книгу
Скачать книгу бесплатно (djvu, 1.05 Mb).
Основания геометрии (главы высшей геометрии), ч.
I. Учебное пособие для вузов. Бахвалов С.В., Иваницкая В.П.libcats.org
- Учебное пособие по решению задач
Особое внимание в учебном пособии было уделено вопросам построения математических моделей как основополагающему и наиболее творческому этапу решения задач. В связи с тем, что современное компьютерное программное обеспечение позволяет значительно упростить процесс поиска оптимальных решений, наиболее трудоемкие методы решения задач (симплекс-метод, метод потенциалов, методы оптимизации сетевых моделей) в учебном пособии рассмотрены не были. Часть I. Одноиндексные задачи линейного программирования.
studfile.net
- Линейное программирование. Теория
Список рекомендуемой литературы. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем. Учебное пособие. – М.,Финансы и статистика, 2005. Беспалов М.
С. Линейное программирование.Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: Учебник. – М.,Изд-во «Дело и сервис», 2004. Исследование операций в экономике. Учебное пособие для вузов/Под ред. проф.Н.Ш.Кремера. – м., юнити, 2005.
math.semestr.ru
- Линейное программирование — Скачать бесплатно
Учебное пособие содержит основные теоретические положения и алгоритмы решения задач линейного программирования, проиллюстрированные численными примерами.Пособие предназначено студентам высших учебных заведений, изучающим математическое программирование, исследование операций, методы оптимизации, финансовую математику, экономико-математическое моделирование, и может оказать большую пользу всем, кто интересуется вопросами прикладной математики и приложениями математических методов в…
www.rulit.me
- ЛИНЕЙНОЕ
Пособие «Линейное программирование» разработано в соответствии с программами дисциплин «Математические модели в экономике» и «Моде-лирование в менеджменте» и рассчитано на студентов экономического фа-культета и факультета менеджмента, освоивших курсы линейной алгебры и математического анализа.
Пособие содержит теоретический материал, за-дачи с приведенным решением и достаточное количество задач для органи-зации самостоятельной работы студентов.www.hse.ru
- Линейное и | 1.2. Задача выпуклого программирования
Настоящий учебник является коренной переработкой учебных посо-бий, [10], [11], [7], вышедших в свет более 25 лет назад. Он основан на курсе лекций по дисциплине «Линейное программирование» и, ча-стично, — специальном курсе «Дискретная оптимизация», читаемых для студентов факультета ВМК по специальности «Прикладная математика и информатика». Для понимания основного текста необхожимо выполнить дополняю-щие теоретический материал упражнения, которые вкраплены в основ-ной текст.
www.itlab.unn.ru
- Практическая работа № 1 Графический метод решения задач…
Печатается по решению учебно-методической комиссии экономического отделения Набережночелнинского института (филиала) федерального государственного автономного образовательного учреждения высшего образования «Казанский (Приволжский) федеральный университет», от « 16 » 04 2019 г.
(протокол № 8) Рецензенты: Доктор экономических наук, профессор А.С. Пуряев Доктор экономических наук, профессор А.Н. Макаров Гареева Г.А. Методы линейного программирования: учебно-методическое пособие / Гареева Г.А…kpfu.ru
..
xyz
Изложение теоретического материала сопровождается…
В результате изучения данного учебного пособия студенты узнают принципы построения математических моделей задач линейного программирования, обоснование симплекс-метода решения задач линейного программирования, основы теории…
…
С., Семенкина О.Э., Антамошкин А.Н., Терсков В.А., Тынченко В.В. — Красноярск: СФУ, 2007 — 269 слайдов. Содержание: Классификация задач оптимизации. Линейное программирование.
, испр. и доп. Учебное…»
Линейное программирование.
I. Учебное пособие для вузов. Бахвалов С.В., Иваницкая В.П.
С. Линейное программирование.
Пособие содержит теоретический материал, за-дачи с приведенным решением и достаточное количество задач для органи-зации самостоятельной работы студентов.
(протокол № 8) Рецензенты: Доктор экономических наук, профессор А.С. Пуряев Доктор экономических наук, профессор А.Н. Макаров Гареева Г.А. Методы линейного программирования: учебно-методическое пособие / Гареева Г.А…На данной странице Вы можете найти лучшие результаты поиска для чтения, скачивания и покупки на интернет сайтах материалов, документов, бумажных и электронных книг и файлов похожих на материал «Линейное программирование, учебное пособие, Палий И.А., 2008»
Для формирования результатов поиска документов использован сервис Яндекс.XML.
Нашлось 220 тыс. ответов. Показаны первые 32 результата(ов).
Дата генерации страницы:
Линейное программирование — GeeksforGeeks
Все мы сталкиваемся со многими целевыми ситуациями в повседневной жизни. Вы можете придумать какую-нибудь? Скажем, студент должен выполнить проект за 15 дней, или продавец должен достичь цели по продажам в течение месяца, в то время как другой человек должен купить электронное устройство в пределах бюджета ₹ 500 рупий, пройти через эти ситуации и попытаться выяснить главная цель, которую должен достичь каждый человек в отдельности.
Скажем, какова цель студента в этом случае, да, она хочет получить максимальный балл в этом проекте, можете ли вы сказать мне цель продавца в этом случае? Да, он будет стремиться добиться максимально возможных продаж за месяц. Что, по вашему мнению, будет целью человека, покупающего гаджет, он постарается минимизировать стоимость, насколько это возможно, он покупает гаджет, который попадает в бюджет, мы можем видеть, что каждый из этих случаев выше цели каждого из ситуация заключалась в том, чтобы максимизировать выгоды или минимизировать затраты. Такие типы задач относятся к проблемам оптимизации колледжа.
В математике задача оптимизации может включать поиск максимальной прибыли, минимальных затрат или, возможно, минимального использования ресурсов. В нашей повседневной жизни может быть еще много примеров, которые необходимо решить с помощью методов оптимизации. простой, как указано выше, но может усложниться в зависимости от ситуации, мы уже обсудили цель трех данных ситуаций, теперь мы можем посмотреть на важные факторы, мы выявим ограничивающий фактор в каждом случае.
что это значит? хорошо, в каждом случае есть нехватка некоторых ресурсов, как и в первом случае, срок для завершения проекта ограничен время, отведенное для завершения проекта, ограничено только 15 днями, аналогично во втором случае время в ограничивающем факторе человек должен продать максимально возможный продукт в течение одного месяца что вы можете сказать о третьей ситуации что является ограничивающим фактором в этом случае человек должен купить гаджет в рамках заранее определенного бюджета, то есть сумма, на которую вы тратите свои деньги ограничивающий фактор в данном случае этот ограничивающий фактор, то есть нехватка ресурсов, действует как ограничение в поиске наилучших решений заданных задач. Но как решаются эти задачи оптимизации в математике. Все они представляют собой разные методы решения проблем. Основной метод, который мы обсудим, — это линейное программирование. Как он используется для решения задач оптимизации, мы обсудим выше.
линейное программирование — это метод, который помогает нам найти оптимальное решение для данной проблемы, оптимальное решение — это решение, которое является наилучшим возможным результатом данной конкретной проблемы.
Проще говоря, это метод выяснить, как сделать что-то наилучшим образом при заданных ограниченных ресурсах, необходимых для оптимального использования ресурсов для достижения наилучшего возможного результата в конкретной цели. такие как наименьшая стоимость, наибольшая маржа или наименьшее время использования этих ресурсов, имеют альтернативное использование. Ситуация, требующая поиска наилучших значений переменных с учетом определенных ограничений, поддается корректируемому программному анализу. Эти ситуации не могут быть обработаны обычными инструментами исчисления или маржинального анализа. Метод исчисления может обрабатывать только точно равные ограничения, в то время как это ограничение не существует в случае задач линейного программирования. Задача линейного программирования состоит из двух основных частей:
- Первая часть: Это целевая функция, которая описывает основную цель формации максимизировать какую-то доходность или минимизировать какую-то.
- Вторая часть: Это постоянный набор. Это система равенств или неравенств, которые описывают условия или ограничения ограничения, при которых должна выполняться оптимизация.
Это система равенств или неравенств, которые описывают условия или ограничения ограничения, при которых должна выполняться оптимизация.По сути, существует множество различных задач линейного программирования, но в этой статье мы рассмотрим три основные задачи линейного программирования.
- Производственные проблемы: Производственные проблемы — это проблема, связанная с количеством единиц продукции, которые необходимо произвести или продать, чтобы максимизировать прибыль, когда каждый продукт требует фиксированной рабочей силы, машино-часов и сырья.
- Проблемы с диетой: Используется для расчета количества различных видов компонентов, которые должны быть включены в диету, чтобы добиться минимизации затрат и в зависимости от наличия продуктов питания и их цен.
- Проблемы с транспортировкой: Используется для определения графика транспортировки, чтобы найти самый дешевый способ транспортировки продукта с заводов / фабрик, расположенных в разных местах, на разные рынки.
Для того, чтобы решать задачи линейного программирования, вам необходимо иметь четкое представление об основных терминах, используемых при решении первых задач линейного программирования, которые приведены ниже:
- Переменная решения: Переменные, которые конкурируют друг с другом за совместное использование ограниченных ресурсов, таких как продукты, услуги и т. д. Они взаимосвязаны и имеют линейную зависимость, позволяющую решить, какое оптимальное решение является лучшим, называются переменными решения.
- Целевая функция : Задача должна иметь четкую и четко определенную цель, которую можно сформулировать количественно, например, максимизация прибыли или минимизация затрат и т. д. Все эти примеры подпадают под категорию целевой функции.
- Ограничения: Это ограничения, налагаемые на доступные ресурсы, такие как ограниченное количество машин, рабочих материалов и т. д. исследование называется избыточным ограничением.
- Возможное решение: Это множество всех возможных решений в виде переменных, удовлетворяющих константам.
- Оптимальное решение: Это лучшее решение из всех возможных, которое наилучшим образом поддерживает цель задачи.
д. исследование называется избыточным ограничением.Вопрос 1: Компания производит и продает два вида продукции, и стоимость производства каждой единицы a и b составляет 200 и 150 рупий соответственно, каждая единица IELTS прибыль 20 рупий и каждая единица наибольшей прибыли от вас 15 при продаже компания оценивает месячный спрос от А и В до В при максимальной заготовленной единице во всем производственном бюджете на месяц установлен в 50000 рупий сколько единиц должно быть компания производит, чтобы получить максимальную прибыль от своих ежемесячных продаж от a и b? 9
y = количество единиц типа B
x + 2y ≤ 8
и x, y ≥ 0
Рассмотрим уравнение,
3x + y = 9
x = 3
y = 0
и x + 2y = 8
x = 8
y = 0
Теперь мы можем определить максимальное значение Z, оценив значение Z в четырех точках (вершинах), показанных ниже
Вершины | z = 40x + 50y | |||||
|---|---|---|---|---|---|---|
(0, 0) | (0, 0) | (0, 0) | (0, 0). | |||
(3, 0) | Z = 40 × 3 + 50 × 0 = Rs. 120 | |||||
(0, 4) | Z = 40 × 0 + 50 × 4 = руб. 200 | |||||
(2, 3) | Z = 40 × 2 + 50 × 3 = руб. 230 |
0
Максимальная прибыль, Z = рупий. 230
∴ Количество единиц типа A равно 2, а количество единиц типа B равно 3.
Вопрос 2: максимизация Z = 3x + 4y
С учетом ограничений, x + y ≤ 450 , 2x + y ≤ 600 и x, y ≤ 0.
Решение:
Имеем из данных
Ограничения (1)
X + Y0 =
Полагая x = 0, ⇒ 0 + y = 450 ⇒ y = 450
Полагая y = 0, ⇒ x + 0 = 450 ⇒ x = 450
Из, Ограничения (2)
= 60 +2
Положим x = 0, ⇒ 0 + y = 600 ⇒ y = 600
Положим y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300
Теперь у нас есть координата точки Z = 3x + 4y
Вершины | Z = 3x + 4y |
|---|---|
(0,0 133 )0136 | Z = 3 × 0 + 4 × 0 = 0 |
(300, 0) | Z = 3 × 300+ 4 × 0 = 900 |
(150, 300 ) | z = 3 × 150 + 4 × 300 = 1650 |
(0, 450) | Z = 3 × 0 + 4503998 929292929929299292992929929929929929929929929929929929929929929929929929929929929929929929992992999299929929929929929н. , максимум оптимального решения Z = 1800 при координатах x = 0 и y = 450. График приведен ниже. Руководство по оптимизации смешивания с линейным программированием на Python | by Fouad FarajПрименение к реальной задаче оптимизации цементных смесейИзображение автора Практически в любой отрасли, особенно в сфере природных ресурсов, крайне важно принимать наилучшие возможные решения, чтобы максимизировать ценность каждого проекта за счет оптимизации доходов. генерируется за необходимые потраченные ресурсы. Исследование операций — это дисциплина, в которой реальные проблемы описываются математически и оптимизируются для улучшения процесса принятия решений. Схема ниже иллюстрирует оптимальный проект B на основе максимальной чистой стоимости, достигнутой за выделенные ресурсы, в то время как A и C неоптимальны из-за более плохого дизайна или доступности ресурсов. Хотя на первый взгляд самые дешевые или наиболее ценные проекты кажутся интуитивным выбором, на оптимальный часто влияет множество различных и важных переменных, которые необходимо оптимизировать. При хороших операционных исследованиях многие компании, особенно в отраслях, связанных с природными ресурсами, могут лучше стремиться к оптимальным проектам, которые наиболее вероятны. дать максимальную чистую стоимость. К сожалению, для концептуализации и решения этих проблем оптимизации обычно полагаются на дорогостоящее программное обеспечение или внешних консультантов. В этой статье мы покажем, как просто это сделать в программном обеспечении с открытым исходным кодом, таком как Python. Весь код, используемый в этом примере, хранится на GitHub. Задача оптимизации смешивания цемента В этом учебном пособии основное внимание будет уделено реальной задаче оптимизации смешивания цемента из исследовательской работы по цементу и бетону 1977 года [1]. В этом применении известняк, глина, бокситы и обожженный пирит смешиваются наиболее экономичным способом, сохраняя при этом требуемые физические свойства. Каждое из четырех видов сырья имеет различную стоимость в диапазоне от 6 до 230 долларов США за тонну и состоит из различных пропорций ингредиентов. Основные ингредиенты включают кремнезем (SiO2), глинозем (Al2O3), оксид железа (Fe2O3), оксид кальция (CaO) и триоксид серы (SO3), пропорции каждого из которых должны находиться в определенных диапазонах, чтобы обеспечить соответствие цемента требуемым физическим свойствам. . В таблице ниже приведены все соответствующие значения с использованием реальных данных по цементу из [1] и [2]. Сырье, соответствующее процентное содержание ингредиентов и цены. Реальные данные по цементу из [1] и [2]. Изображение автораПрежде чем приступать к какой-либо оптимизации, нам необходимо понять соответствующую терминологию для математического определения рассматриваемой проблемы. Некоторые ключевые номенклатуры включают в себя:
В нашем примере смешивания целевая функция представляет собой просто сумму цены каждого материала, умноженную на долю этого материала для четырех материалов. Если бы мы запустили оптимизацию исключительно так, как показано выше, мы бы просто получили, что все пропорции материалов равны нулю, что дает нам приятную нулевую стоимость, но мы знаем, что это не реальное решение. Ограничения в конечном итоге определяют оптимизацию, поскольку стоимость смеси должна быть минимизирована при соблюдении требований к физическим свойствам. 9Ограничения 0007 определены в [1] и [2] как функции ингредиентов, поэтому мы введем некоторые переменные (от q1 до q6), аналогичные статье [1], как показано ниже. В этом примере ограничения основаны на указанных диапазонах, под которые должен подпадать каждый ингредиент, нескольких различных модулях и определенных элементах продуктов обжига, которые зависят от пропорций ингредиентов. Для компонента линейного программирования статьи существует 14 ограничений , два из них мы разберем ниже в их адаптации Python. Разбивка первых двух ограничений , показывающая, как каждое уравнение транскрибируется в код Python в формате оптимизации scipy. Изображение автора Теперь нужно просто повторить описанный выше процесс для всех 14 ограничений . Ниже приведены оставшиеся 12 ограничений , показанные в обрезанном фрагменте кода Python на GitHub. Наконец-то мы готовы запустить оптимизацию с нашими ограничениями для определения переменных решения , которые минимизируют целевую функцию . Что касается нашего примера, мы получим пропорции каждого материала, которые дают наиболее экономичную смесь, отвечающую требуемым физическим свойствам. Мы будем использовать Операционные исследования предоставляют мощные инструменты для принятия более обоснованных решений. Несмотря на то, что для запуска линейной программы доступно дорогое программное обеспечение, его также можно легко настроить с помощью программного обеспечения с открытым исходным кодом, как показано на примере оптимизации scipy в Python. Независимое кодирование задачи оптимизации также позволяет вносить изменения, которые могут быть недоступны в коммерческом программном обеспечении, которое абстрагирует многие мелкие детали. Решение этих проблем оптимизации может позволить компаниям принимать лучшие решения или улучшать процедуры сложных операций. В этой статье рассматривалась линейная задача, однако существуют и варианты оптимизации более сложных нелинейных программ. Хотя линейные задачи значительно легче вычислить, они часто содержат допущения, которые приводят к неизбежным субоптимальным решениям. В документе, используемом в этом руководстве, это обсуждается более подробно путем сравнения аппроксимации линейной программы с более точной нелинейной программой [1]. Степень, в которой нелинейная программа улучшит ситуацию, вероятно, будет зависеть от достоверности линейности рассматриваемой проблемы. Иногда полезно сделать шаг назад и увидеть реальное применение всей нашей работы с данными. Цемент является ключевым компонентом бетона, который является наиболее широко используемым материалом в строительстве. |
Переменные решения представляют собой долю каждого материала, например, использование 50% известняка и 20% боксита. Мы можем начать с определения ингредиентов с точки зрения наших переменные решения и настроить целевую функцию до минимизировать , как показано ниже.
Обратите внимание, что в Python с минимизацией scipy они должны быть явно выражены в терминах переменных решения .
Перевод всех ограничений в код может показаться непосильным, но важно просто использовать одно уравнение за раз. Запуск кода по одной строке за раз после введения каждого нового ограничения может быть полезен, чтобы убедиться, что нет очевидной ошибки ввода, которую впоследствии будет сложно отловить.
Результаты, представленные в таблице ниже, показывают, насколько схожи пропорции материала для статьи 1977 года [1] с этим руководством по Python. Небольшие различия, вероятно, связаны с округлением или разными методами оптимизации.
В этом руководстве реальная задача оптимизации смешивания цемента была решена менее чем за 30 строк кода. В то время как решение предназначено для конкретных доступных материалов и ограничений , представленных как часть примера, тот же подход применим и масштабируем к любой похожей задаче смешивания.