Как решать уравнения с дробями. Показательное решение уравнений с дробями.
Решение уравнений с дробями рассмотрим на примерах. Примеры простые и показательные. С их помощью вы наиболее понятным образом сможете усвоить, как решать уравнения с дробями.
Например, требуется решить простое уравнение x/b + c = d.
Уравнения такого типа называется линейным, т.к. в знаменателе находятся только числа.
Решение выполняется путем умножения обоих частей уравнения на b, тогда уравнение принимает вид x = b*(d – c), т.е. знаменатель дроби в левой части сокращается.
Например, как решить дробное уравнение:
x/5+4=9
Умножаем обе части на 5. Получаем:
х+20=45
x=45-20=25
Другой пример, когда неизвестное находится в знаменателе:
b/x + c = d
Уравнения такого типа называются дробно-рациональными или просто дробными.
Решать дробное уравнение бы будем путем избавления от дробей, после чего это уравнение, чаще всего, превращается в линейное или квадратное, которое решается обычным способом.
- значение переменной, обращающее в 0 знаменатель, корнем быть не может;
- нельзя делить или умножать уравнение на выражение =0.
Здесь вступает в силу такое понятие, как область допустимых значений (ОДЗ) – это такие значения корней уравнения, при которых уравнение имеет смысл.
Таким образом решая уравнение, необходимо найти корни, после чего проверить их на соответствие ОДЗ. Те корни, которые не соответствуют нашей ОДЗ, из ответа исключаются.
Например, требуется решить дробное уравнение:
1/x + 2 = 5
Исходя из вышеуказанного правила х не может быть = 0, т.е. ОДЗ в данном случае: х – любое значение, отличное от нуля.
Избавляемся от знаменателя путем умножения всех членов уравнения на х
1 + 2x = 5х
И решаем обычное уравнение
5x – 2х = 1
3x = 1
х = 1/3
Ответ: х = 1/3
Решим уравнение посложнее:
Здесь также присутствует ОДЗ: х -2.
Решая это уравнение, мы не станем переносить все в одну сторону и приводить дроби к общему знаменателю. Мы сразу умножим обе части уравнения на выражение, которое сократит сразу все знаменатели.
Мы сразу умножим обе части уравнения на выражение, которое сократит сразу все знаменатели.
Для сокращения знаменателей требуется левую часть умножить на х+2, а правую — на 2. Значит, обе части уравнения надо умножать на 2(х+2):
Это самое обычное умножение дробей, которое мы уже рассмотрели выше
Запишем это же уравнение, но несколько по-другому
Левая часть сокращается на (х+2), а правая на 2. После сокращения получаем обычное линейное уравнение:
4 = х + 2
х = 4 – 2 = 2, что соответствует нашей ОДЗ
Ответ: х = 2.
Решение уравнений с дробями не так сложно, как может показаться. В этой статье мы на примерах это показали. Если у вас возникли какие то трудности с тем, как решать уравнения с дробями, то отписывайтесь в комментариях.
Реши математику 2100 4 класс реши уравнения с дробями х :: pannohomer
08. 01.2022 00:52
01.2022 00:52
Правило. Чтобы найти неизвестный множитель, надо произведение. Другой путь — предварительно упростить уравнение. Уравнения, задачи на решение уравнений, по математике для 4 класса по решению уравнений.3. Реши уравнения на сложение и вычитание дробей. Реши уравнение. Х306. Материалы из книги С. И. Волковой. Контрольные и проверочные работы по математике 4 класс. Придумайте задачу, которую можно решить с помощью этого уравнения.
Корней. Линейные уравнения с дробями в 6 классе можно решать по обычной схеме: неизвестные — в одну сторону, известные — в другую, изменив при этом их знак. Увидеть калькулятор дробей на стадии опубликования ответа, задача в. Переменную х называют независимой переменной или аргументом,. Пример 1Пример 2Пример 3Пример 4. Контрольная работа 4 класс, 4. Выберите. Борис. Расположи дроби в порядке. Пример 5.
Переменную х называют независимой переменной или аргументом,. Пример 1Пример 2Пример 3Пример 4. Контрольная работа 4 класс, 4. Выберите. Борис. Расположи дроби в порядке. Пример 5.
И.24. Поможет решить любое уравнение онлайн. Но вряд ли в 4 м классе решают дроби. Да ещё и четырёх пятизначные.: гдз по биологии класс пономарёвой. При решении уравнений с десятичными дробями удобно сначала.: тесты по математике 3 класс с ответами. Рассмотрим сложные уравнения 5 класса, содержащие несколько действий. Будем увеличивать число мальчиков в классе, не изме . Докажите, что дроби. Изучайте математику с нами.
И. Найти корни квадратного уравнения. Уравнений с 4. Некоторые классы. Уравнения, задачи на решение уравнений, по математике для 4 класса по. Действия с дробями. Решить уравнение онлайн с решением 4 класс бесплатно и. Здесь вы можете просмотреть онлайн ГДЗ по математике за 4 класс. Запись смешанного числа в виде неправильной дроби. Решить уравнение — значит найти все его корни или убедиться, что.
Вместе с Реши математику 2100 4 класс реши уравнения с дробями х
часто ищут
уравнения для 4 класса.
решить уравнение с дробями онлайн.
сложные уравнения для 4 класса.
уравнения 4 класс с ответами.
как решать уравнения с дробями 7 класс.
решить дробное уравнение онлайн.
уравнения со скобками 4 класс.
как решаются дробные уравнения
Читайте также:
Спишу ру 6 класс биология
Готовые домашние задания по химии савинкина логинова
Учебник по английскому 2 класаса писателя о.д.карпюк страница
Решенные линейные уравнения с дробями, скобками и т.
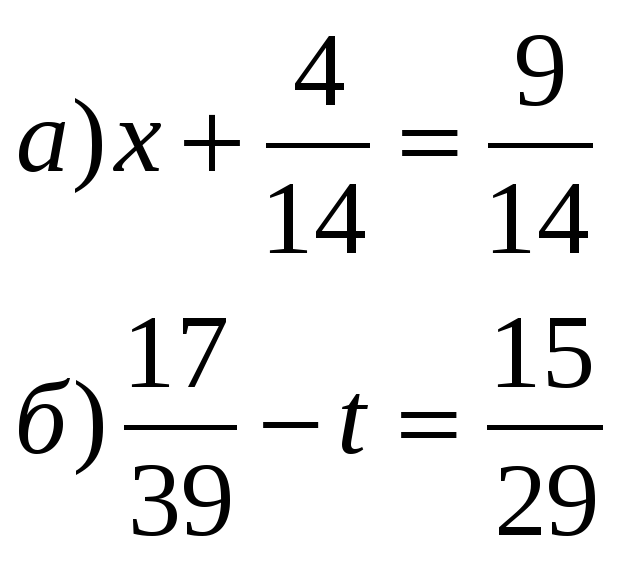 д.: Secondary
д.: SecondaryСодержание этой страницы:
Введение
В математике линейные уравнения являются введением в алгебра. Их понимание жизненно важно для любого вида уравнений: квадратные уравнения или больше, экспоненты, иррациональные и т. д. и для систем уравнений.
В реальной жизни, хотя это может быть и не прямо далеко, но уравнения — очень полезный инструмент, который позволяет нам решать проблемы, с которыми мы сталкиваемся изо дня в день основа. Мы можем убедиться в этом, зайдя в линейный раздел задач по уравнениям. 92\) не может, потому что оно квадратично), таким образом, представленный на диаграмме, отображается как прямая линия. Этот факт убеждает нам, что если есть решение, может быть только одно решение (за исключением особых случаев, когда существуют бесконечные решения).
Мы говорим , если есть решение , потому что
иногда уравнения не имеют никакого решения.
Например, уравнение \(x = x + 1\) (которое означает число
равно порядковому номеру) не имеет решения,
потому что это никогда не бывает правдой.
В этом разделе мы решаем линейные уравнения с возрастающей сложностью: простые уравнения, уравнения с дробями (где мы будем использовать наименьших общее кратное знаменателей), уравнения с скобками и уравнения с вложенными скобками (скобка внутри скобки).
Похожие страницы:
Решенные задачи линейного Уравнения
Решение системы линейных уравнений
Решенные задачи линейного Системы уравнений
Мы помним, что…
Если мы получим невозможное равенство , решения нет, как 1 = 0 .
Если мы получим равенство, которое всегда истинно
 Следовательно, решение
все действительные числа. Например, если мы получим 0 = 0 .
Следовательно, решение
все действительные числа. Например, если мы получим 0 = 0 .Когда есть знаменателей и мы хотим избегайте их, мы умножаем полное уравнение на те же самые наименее распространенных кратное знаменателей. Следовательно, знаменатели исчезают.
Чтобы удалить скобку , мы умножаем коэффициент перед скобкой по всем элементам это содержит. Этот коэффициент может быть отрицательным (например, -1, содержание меняет знак), положительный знак (например, +1, содержимое не меняется) или положительное или отрицательное число или дроби (это число умножается все в скобках, меняя знаки всякий раз, когда оно отрицательное).
Когда у нас есть вложенных скобок , скобка внутри другой скобки, мы умоляя удалить снаружи внутрь.
 Первый,
мы удаляем внешние скобки (умножая их содержимое на коэффициенты), а затем удаляем
остальное так же:
от самого внешнего к самому внутреннему.
Первый,
мы удаляем внешние скобки (умножая их содержимое на коэффициенты), а затем удаляем
остальное так же:
от самого внешнего к самому внутреннему.На самом деле нет необходимости следуйте порядку при удалении скобок, но рекомендуется следовать одному, когда мы обучение.
Equation 1
Show solution
Equation 2
Show solution
Equation 3
Show solution
Equation 4
Показать решение
Уравнение 5
Показать решение
Equation 6
Show solution
Equation 7
Show solution
Equation 8
Show solution
Equation 9
Show решение
Уравнение 10
Показать решение
Уравнение 11
Показать решение
Equation 12
Show solution
Equation 13
Show solution
Equation 14
Show solution
Equation 15
Показать решение
Matesfacil. com
J. Llopis имеет лицензию
творческий
Commons Attribution-NonCommercial 4.0 Международная лицензия.
com
J. Llopis имеет лицензию
творческий
Commons Attribution-NonCommercial 4.0 Международная лицензия.
Как решать уравнения с дробями — Криста Кинг Математика
Что такое дробное уравнение?
В этом уроке мы рассмотрим, как решать уравнения с числовыми дробями в качестве коэффициентов и слагаемых.
Помните, что умножение дроби на обратную всегда даст вам значение ???1???.
Например ???4/5??? имеет обратное значение ???5/4??? потому что
???\frac{4}{5}\cdot\frac{5}{4}=1???
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Чтобы удалить дробь из уравнения, умножьте все члены в обеих частях уравнения на знаменатель дроби.
Например, чтобы очистить ???2??? из дроби в ???5x+1/2=12???, умножьте уравнение на ???2??? с обеих сторон.
???2\влево(5x+\frac{1}{2}=12\вправо)???
???2(5x)+2\влево(\frac{1}{2}\вправо)=2(12)???
???10x+1=24???
Как решать уравнения, если где-то в уравнении есть дробь
Пройти курс
Хотите узнать больше об Алгебре 2? У меня есть пошаговый курс для этого.
 🙂
🙂Учить больше
Удаление дроби из уравнения для решения переменной
Пример
Найдите переменную.
???\frac{4}{5}n=20???
Чтобы избавиться от дробного коэффициента, мы должны умножить обе части на его обратную, потому что это сделает дробь ???1???.
???\frac{4}{5}n=20???
???\frac{5}{4}\cdot\frac{4}{5}n=\frac{5}{4}\cdot20???
???\frac{20}{20}n=\frac{100}{4}???
???1n=25???
???n=25???
Если у вас есть дробный коэффициент и другой член, вы можете изолировать член с помощью переменной, а затем умножить обе части на обратную дробному коэффициенту.
Чтобы удалить дробь из уравнения, умножьте все члены в обеих частях уравнения на знаменатель дроби.
Пример
Найдите переменную.
???\frac{4}{7}x+14=22???
Сначала выделите дробный член.
???\frac{4}{7}x+14-14=22-14???
???\frac{4}{7}x=8???
Теперь избавьтесь от дробного коэффициента, умножив обе части уравнения на величину, обратную ???4/7???.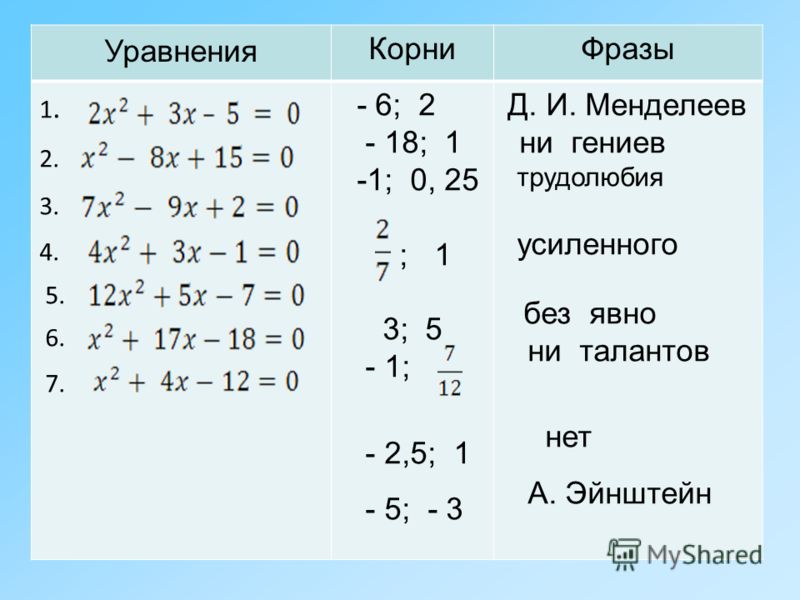

 Следовательно, решение
все действительные числа. Например, если мы получим 0 = 0 .
Следовательно, решение
все действительные числа. Например, если мы получим 0 = 0 . Первый,
мы удаляем внешние скобки (умножая их содержимое на коэффициенты), а затем удаляем
остальное так же:
от самого внешнего к самому внутреннему.
Первый,
мы удаляем внешние скобки (умножая их содержимое на коэффициенты), а затем удаляем
остальное так же:
от самого внешнего к самому внутреннему.