Log a: Формулы и свойства логарифмов — Таловская средняя школа

Содержание

Формулы и свойства логарифмов

Определение

Логарифм числа b по основанию a (log_a b) определяется как показатель степени, в которую надо возвести число a (основание логарифма), чтобы получить число b (Логарифм существует только у положительных чисел).

log_ab = x означает, что a^x = b

Калькулятор логарифмов

log_{-2
График логарифмов
y = log₂ x
Виды логарифмов
log_a b — логарифм числа b по основанию a (a > 0, a ≠ 1, b > 0)
lg b — десятичный логарифм (логарифм по основанию 10, a = 10).
ln b — натуральный логарифм (логарифм по основанию e, a = e).

Формулы и свойства логарифмов

Для любых a > 0, a ≠ 1 и b > 0, x > 0, y > 0 выполняются следующие свойства логарифмов.

a^log_ab = b — основное логарифмическое тождество
log_a 1 = 0 — логарифм единицы
log_a a = 1 — логарифм числа, равного основанию
log_a(x · y) = log_ax + log_ay — логарифм произведения двух положительных чисел
log_a xy = log_ax — log_ay — логарифм частного
log_a 1x = -log_ax
log_a xⁿ = n log_ax — логарифм степени числа
log_aⁿ√x = 1n log_ax — логарифм корня числа
log_aⁿ x = 1n log_a x, при n ≠ 0
log_ax = log_a^c
x^c
log_a x = log_b xlog_b a — формула перехода к новому основанию
log_a x = 1log_x a
(log_a x)′ = 1x ln a — производная логарифма

Скачать Формулы и свойства логарифмов

Логарифмы
Логарифм числа, основное логарифмическое тождество
Формулы и свойства логарифмов
Логарифм произведения. Сумма логарифмов
Логарифм частного. Разность логарифмов
Логарифм степени
Логарифм корня
Логарифмирование
Потенцирование
Десятичный логарифм
Натуральный логарифм
Число е
Логарифмическая функция
Логарифмические уравнения
Логарифмические неравенства

Формулы сокращенного умножения (a ± b)²
Формулы и свойства степеней a
n
Формулы и свойства корней ⁿ√a
Формулы и свойства логарифмов log_a b
Формулы и свойства арифметической прогрессии a_n
Формулы и свойства геометрической прогрессии b_n
Тригонометрические формулы sin x cos x
Обратные тригонометрические формулы arcsin x
Таблица производных ddx
Таблица интегралов ∫x dx
Всі таблиці та формули
Mathway | Популярные задачи
1 Trovare la Derivata — d/dx натуральный логарифм x
2 Вычислим интеграл интеграл натурального логарифма x по x
3 Trovare la Derivata — d/dx e^x
4 Вычислим интеграл интеграл e^(2x) по x
5 Trovare la Derivata — d/dx 1/x
6 Trovare la Derivata — d/dx x^2
7 Trovare la Derivata — d/dx 1/(x^2)
8 Trovare la Derivata — d/dx sin(x)^2
9 Trovare la Derivata — d/dx sec(x)
10 Вычислим интеграл интеграл e^x по x
11 Вычислим интеграл интеграл x^2 по x
12 Вычислим интеграл интеграл квадратного корня из x по x
13 Trovare la Derivata — d/dx cos(x)^2
14 Вычислим интеграл интеграл 1/x по x
15 Вычислим интеграл интеграл sin(x)^2 по x
16 Trovare la Derivata — d/dx x^3
17 Trovare la Derivata — d/dx sec(x)^2
18 Вычислим интеграл интеграл cos(x)^2 по x
19 Вычислим интеграл интеграл sec(x)^2 по x
20 Trovare la Derivata — d/dx e^(x^2)
21 Вычислим интеграл интеграл в пределах от 0 до 1 кубический корень из 1+7x по x
22 Trovare la Derivata — d/dx sin(2x)
23 Trovare la Derivata — d/dx tan(x)^2
24 Вычислим интеграл интеграл 1/(x^2) по x
25 Trovare la Derivata — d/dx 2^x
26 График натуральный логарифм a
27 Trovare la Derivata — d/dx cos(2x)
28 Trovare la Derivata — d/dx xe^x
29 Вычислим интеграл интеграл 2x по x
30 Trovare la Derivata — d/dx ( натуральный логарифм от x)^2
31 Trovare la Derivata — d/dx натуральный логарифм (x)^2
32 Trovare la Derivata — d/dx 3x^2
33 Вычислим интеграл интеграл xe^(2x) по x
34 Trovare la Derivata — d/dx 2e^x
35 Trovare la Derivata — d/dx натуральный логарифм 2x
36 Trovare la Derivata — d/dx -sin(x)
37 Trovare la Derivata — d/dx 4x^2-x+5
38 Trovare la Derivata — d/dx y=16 корень четвертой степени из 4x^4+4
39 Trovare la Derivata — d/dx 2x^2
40 Вычислим интеграл интеграл e^(3x) по x
41 Вычислим интеграл интеграл cos(2x) по x
42 Trovare la Derivata — d/dx 1/( квадратный корень из x)
43 Вычислим интеграл интеграл e^(x^2) по x
44 Вычислить e^infinity
45 Trovare la Derivata — d/dx x/2
46 Trovare la Derivata — d/dx -cos(x)
47 Trovare la Derivata — d/dx sin(3x)
48 Trovare la Derivata — d/dx 1/(x^3)
49 Вычислим интеграл интеграл tan(x)^2 по x
50 Вычислим интеграл интеграл 1 по x
51 Trovare la Derivata — d/dx x^x
52 Trovare la Derivata — d/dx x натуральный логарифм от x
53 Trovare la Derivata — d/dx x^4
54 Оценить предел предел (3x-5)/(x-3), если x стремится к 3
55 Вычислим интеграл интеграл x^2 натуральный логарифм x по x
56 Trovare la Derivata — d/dx f(x) = square root of x
57 Trovare la Derivata — d/dx x^2sin(x)
58 Вычислим интеграл интеграл sin(2x) по x
59 Trovare la Derivata — d/dx 3e^x
60 Вычислим интеграл интеграл xe^x по x
61 Trovare la Derivata — d/dx y=x^2
62 Trovare la Derivata — d/dx квадратный корень из x^2+1
63 Trovare la Derivata — d/dx sin(x^2)
64 Вычислим интеграл интеграл e^(-2x) по x
65 Вычислим интеграл интеграл натурального логарифма квадратного корня из x по x
66 Trovare la Derivata — d/dx e^2
67 Trovare la Derivata — d/dx x^2+1
68 Вычислим интеграл интеграл sin(x) по x
69 Trovare la Derivata — d/dx arcsin(x)
70 Оценить предел предел (sin(x))/x, если x стремится к 0
71 Вычислим интеграл интеграл e^(-x) по x
72 Trovare la Derivata — d/dx x^5
73 Trovare la Derivata — d/dx 2/x
74 Trovare la Derivata — d/dx натуральный логарифм 3x
75 Trovare la Derivata — d/dx x^(1/2)
76 Trovare la Derivata — d/d@VAR f(x) = square root of x
77 Trovare la Derivata — d/dx cos(x^2)
78 Trovare la Derivata — d/dx 1/(x^5)
79 Trovare la Derivata — d/dx кубический корень из x^2
80 Вычислим интеграл интеграл cos(x) по x
81 Вычислим интеграл интеграл e^(-x^2) по x
82 Trovare la Derivata — d/d@VAR f(x)=x^3
83 Вычислим интеграл интеграл 4x^2+7 в пределах от 0 до 10 по x
84 Вычислим интеграл интеграл ( натуральный логарифм x)^2 по x
85 Trovare la Derivata — d/dx логарифм x
86 Trovare la Derivata — d/dx arctan(x)
87 Trovare la Derivata — d/dx натуральный логарифм 5x
88 Trovare la Derivata — d/dx 5e^x
89 Trovare la Derivata — d/dx cos(3x)
90 Вычислим интеграл интеграл x^3 по x
91 Вычислим интеграл интеграл x^2e^x по x
92 Trovare la Derivata — d/dx 16 корень четвертой степени из 4x^4+4
93 Trovare la Derivata — d/dx x/(e^x)
94 Оценить предел предел arctan(e^x), если x стремится к 3
95 Вычислим интеграл интеграл (e^x-e^(-x))/(e^x+e^(-x)) по x
96 Trovare la Derivata — d/dx 3^x
97 Вычислим интеграл интеграл xe^(x^2) по x
98 Trovare la Derivata — d/dx 2sin(x)
99 Вычислить sec(0)^2
100 Trovare la Derivata — d/dx натуральный логарифм x^2
Правила логарифмирования | ChiliMath
В этом уроке вы познакомитесь с общими правилами логарифмирования, также известными как «логарифмические правила». Эти семь (7) логарифмических правил полезны при расширении логарифмов, сокращении логарифмов и решении логарифмических уравнений. Кроме того, поскольку обратная функция логарифма является экспоненциальной функцией, я бы также рекомендовал вам пройтись и освоить правила экспоненты. Поверьте, они всегда идут рука об руку.
Если вас когда-нибудь интересовало, почему правила логарифмирования работают, посмотрите мой урок о доказательствах или обоснованиях свойств логарифмов.
Но если вы считаете, что хорошо усвоили эту концепцию, вы можете просто проверить свои знания с помощью приведенных ниже практических задач.
Практические задачи по правилам логарифмирования
Описание правил логарифмирования
Правило 1: Правило произведения
Логарифм произведения равен сумме логарифмов.
Правило 2: Правило частного
Логарифм отношения двух величин равен логарифму числителя минус логарифм знаменателя.
Правило 3: Степенное правило
Логарифм экспоненциального числа равен произведению показателя степени на логарифм основания.
Правило 4: Правило нуля
Логарифм 1 по любому основанию всегда равен нулю. Пока b положительно, но b \ne 1.
Правило 5: Правило тождества
Логарифм аргумента (внутри скобок), где аргумент равен основанию, равен 1.
Правило 6: Обратное свойство логарифма
Логарифм экспоненциального числа, основание которого совпадает с основанием логарифма, равен показателю степени.
Правило 7: Обратное свойство экспоненты
Возведение логарифма числа в основание равно числу.
Примеры применения правил журнала
Пример 1: Оцените приведенное ниже выражение, используя правила журнала.
{\log _2}8 + {\log _2}4
Выразите 8 и 4 в виде экспоненциальных чисел с основанием 2. Затем примените правило степени, а затем правило идентификации. После этого вы добавляете полученные значения, чтобы получить окончательный ответ.
Ответ: \color{blue}5.
Пример 2: Оцените приведенное ниже выражение, используя правила журнала.
{\log _3}162 — {\log _3}2
Мы не можем выразить 162 в виде экспоненциального числа с основанием 3. Похоже, мы застряли, так как нет правил, которые можно было бы применить в прямом способ.
Правила логарифмирования можно использовать и в обратном порядке! Обратите внимание, что при использовании обратного правила отношения логарифмическое выражение может быть записано как одно логарифмическое число.
Мы сделали это! Применив правила в обратном порядке, мы создали одно выражение журнала, которое легко решить. Окончательный ответ здесь: \color{blue}4.
Пример 3: Оцените приведенное ниже выражение.
Кажется, одновременно происходит много вещей. Во-первых, посмотрите, сможете ли вы упростить каждое из логарифмических чисел. Если нет, начните думать о некоторых очевидных применимых логарифмических правилах.
Наблюдая, мы видим, что задействовано два основания: 5 и 4. Мы можем начать с объединения терминов, имеющих одно и то же основание. Упростим их по отдельности. 95}} \right)
Произведение множителей заключено в скобки. Примените правило продукта, чтобы выразить их в виде суммы отдельных выражений журнала. Старайтесь по возможности упрощать числовые выражения до точных значений. Используйте правило 5 (правило идентификации) как можно чаще, потому что оно может помочь упростить процесс.
Должен признать, что окончательный ответ выглядит «незаконченным». Но нам не стоит беспокоиться, пока мы знаем, что правильно следовали правилам.
Пример 5 : Разверните логарифмическое выражение.
Подход заключается в том, чтобы сначала применить правило отношения к разности двух выражений журнала, поскольку они имеют дробную форму. Затем используйте правило произведения, чтобы разделить произведение факторов на сумму логарифмических выражений.
Пример 6 : Разверните логарифмическое выражение.
У этого числа в знаменателе радикальное выражение. Помните, что символ квадратного корня — это то же самое, что и 9.{{1 \более 2}}}. Как и в задаче № 5, примените правило отношения к журналам, а затем используйте правило продукта.
Пример 7 : Разверните логарифмическое выражение.
Подобная проблема может заставить вас сомневаться, действительно ли вы пришли к правильному ответу, потому что окончательный ответ все еще может выглядеть «незавершенным». Однако если вы правильно применяете правила ведения журналов на каждом этапе, вам не о чем беспокоиться.
Вы могли заметить, что нам нужно сначала применить правило отношения, потому что выражение имеет дробную форму.
Вы также можете быть заинтересованы в:
Правила правил логарифма с ответами
Конденсирование логарифмов
Расширение логаритов
Logarithm Объединенные
Решающие логарифмические уравнения
подтверждают.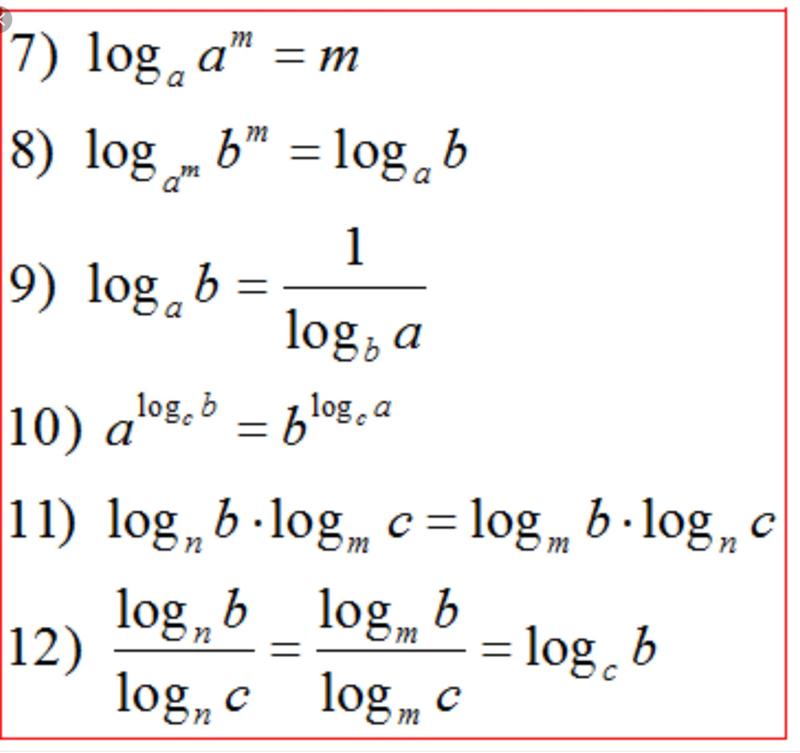
Основная идея и правила для логарифмов
Основная идея
Логарифм противоположен степени. Другими словами, если мы возьмем логарифм числа, мы отменим возведение в степень. 9к=с$$
для любого заданного числа $c$. Другими словами, логарифм дает показатель степени в качестве вывода, если вы даете ему результат возведения в степень в качестве ввода. Чтобы получить все ответы на приведенные выше задачи, нам просто нужно логарифмировать результат возведения в степень $c$, и это даст правильный показатель степени $k$ от $2$. Решением вышеперечисленных проблем являются:
\начать{выравнивать*}
\log_2 8 &= 3\\
\log_2 4 &=2\\
\log_2 16 &= 4\\
\log_2 1 &=0
\конец{выравнивание*}
9к = с
\label{натуральный логб}
\конец{собрать}
для любого числа $c$.
Поскольку использование базы $e$ так естественно для математиков, они иногда просто используют обозначение $\log x$ вместо $\ln x$. Однако другие могут использовать обозначение $\log x$ для логарифма по основанию 10, т.
No related posts.}