Логарифм интерьера: Авторские принты — Логарифм интерьера

LOG компьютерный клуб, Дизайнеры, Наталья Ли

Подберем архитектора или дизайнера для вашего проекта

Подобрать

LOG компьютерный клуб

Стиль необычного интерьера родился под влиянием студии Диснея, выпустившего популярный фильм «Трон: Наследие». Проект называется LOG EVOLUTION, а значит это интерьер из области фантастики.

Наталья Ли

16068

15

Стиль необычного интерьера родился под влиянием студии Диснея, выпустившего популярный фильм «Трон: Наследие». Проект называется LOG EVOLUTION, а значит это интерьер из области фантастики.

Информация

LOG evolution

• Тип файла: Фото
• Помещение : Игровая комната
• Стилистика: Тематические интерьеры

1178

1

0

Информация

LOG evolution

• Тип файла: Фото
• Помещение : Игровая комната
• Стилистика: Тематические интерьеры

1518

0

0

Информация

LOG evolution

• Тип файла: Фото
• Помещение : Игровая комната
• Стилистика: Тематические интерьеры

1736

0

0

Информация

LOG evolution

• Тип файла: Фото
• Помещение : Игровая комната
• Стилистика: Тематические интерьеры

1422

0

0

Информация

LOG evolution

• Тип файла: Фото
• Помещение : Игровая комната
• Стилистика: Тематические интерьеры

1304

0

0

Информация

LOG evolution

• Тип файла: Фото
• Помещение : Игровая комната
• Стилистика: Тематические интерьеры

1596

0

0

Информация

LOG evolution

• Тип файла: Фото
• Помещение : Игровая комната
• Стилистика: Тематические интерьеры

1304

0

0

Информация

LOG evolution

• Тип файла: Фото
• Помещение : Игровая комната
• Стилистика: Тематические интерьеры

988

0

1

Информация

LOG evolution

• Тип файла: Фото
• Помещение : Игровая комната
• Стилистика: Тематические интерьеры

1016

0

0

Информация

LOG evolution

• Тип файла: Фото
• Помещение : Игровая комната
• Стилистика: Тематические интерьеры

1014

0

0

Информация

LOG evolution

• Тип файла: Фото
• Помещение : Санузел
• Стилистика: Тематические интерьеры

947

1

0

Информация

LOG evolution

• Тип файла: Фото
• Помещение : Санузел
• Стилистика: Тематические интерьеры

935

0

0

Информация

LOG evolution

• Тип файла: Фото
• Помещение : Санузел
• Стилистика: Тематические интерьеры

951

0

0

Информация

LOG evolution

• Тип файла: Фото
• Помещение : Игровая комната
• Стилистика: Тематические интерьеры

1385

0

0

Информация

LOG evolution

• Тип файла: Фото
• Помещение : Игровая комната
• Стилистика: Тематические интерьеры

1198

1

0

Понравилась работа? Хотите реализовать нечто подобное?

Заполните форму ниже и автор работы сам свяжется с вами для обсуждения деталей.

Похожие проекты других авторов

Краткое описание заказа:

Ваше имя:

Вы хотите получить ответ:

на телефон:

на почту:

ХV Международный фестиваль архитектуры и дизайна интерьера “Под крышей дома…” — ArchiNews

Учредитель: Департамент градостроительной политики города Москвы

при участии Москомархитектуры

Организаторы: Информационно-аналитический центр  «Дом на Брестской».

Место проведения: Информационно-аналитический центр  «Дом на Брестской»,

г. Москва, 2-я Брестская, д. 6

Конкурс по номинациям:

—  реализованный жилой интерьер;

—  общественный интерьер;

—  декорирование;

—  деталь;

—  реализованный загородный жилой дом;

—  проект-идея загородного дома;

—  коттеджный посёлок;

—  предмет в интерьере

Призы и награды:

— Гран-при за лучший объект;

— первое,  второе и третье места в каждой номинации.

Участнику конкурса необходимо представить

1. заявку;

2. материалы для каталога в электронном виде.

Участнику конкурса предоставляется:

Одно или более конкурсных мест. Одно место соответствует 3 м² площади стены  (высота 2,0 м, ширина 1,4 м) или пола;

Публикация 1 страницы в каталоге фестиваля

Участие в конкурсе БЕСПЛАТНОЕ

Спецпроект: НЕконкурс фестиваля «Интерьер в чужом окне».

Участие в спецпроекте БЕСПЛАТНОЕ

Издается полноцветный каталог фестиваля

Дополнительные услуги:

Широкоформатная печать на принтере и наклейка конкурсных работ

за одно конкурсное место;

Заявки на участие  принимаются  до 20 февраля 2013 г. по адресу:

2-я Брестская ул., д.6, комната 4 или по E-mail: [email protected].

Тел.: (499) 251-26-40, (495) 650-49-97

Сайт: www.dom6.ru

Неконкурс фестиваля

Окно — удивительная вещь. С одной стороны это место для проникновения света, воздуха, звука из одного пространства в другое, средство коммуникации, информации. С другой – барьер, преграда, граница между этими пространствами. Своеобразный КПП (Контрольно-пропускной пункт), со своими правилами, законами, запретами. Прозрачные стекла и плотные шторы, распахнутые ставни и железные решетки. Противоречия и разнообразие. Все это особенности оптики окон: на одно и то же  можно смотреть по-разному. Заглядывать в чужие окна безумно интересно, ведь за ними целый мир. Мир человеческой жизни. Все зависит от видения смотрящего. Настоящему художнику свойственно не только смотреть, но и видеть, а следовательно, и понимать жизнь. На пространство без света сквозь окно смотрел Казимир Малевич. Маяковский, Моор, Соколов-Скаля и другие создатели Окон РОСТА превратили окна в революционные плакаты, увидев за ними светлое будущее. Мир битым стеклом высыпался из картин Магритта. И совсем другой Мир, как на киноэкране скользил по  концептуальным объектам-окнам Ивана Чуйкова.

Интерьер в окне, предметы, вещи, окружение, обстановка, место для жизни, работы, отдыха, одиночества, место первого крика и последнего вздоха.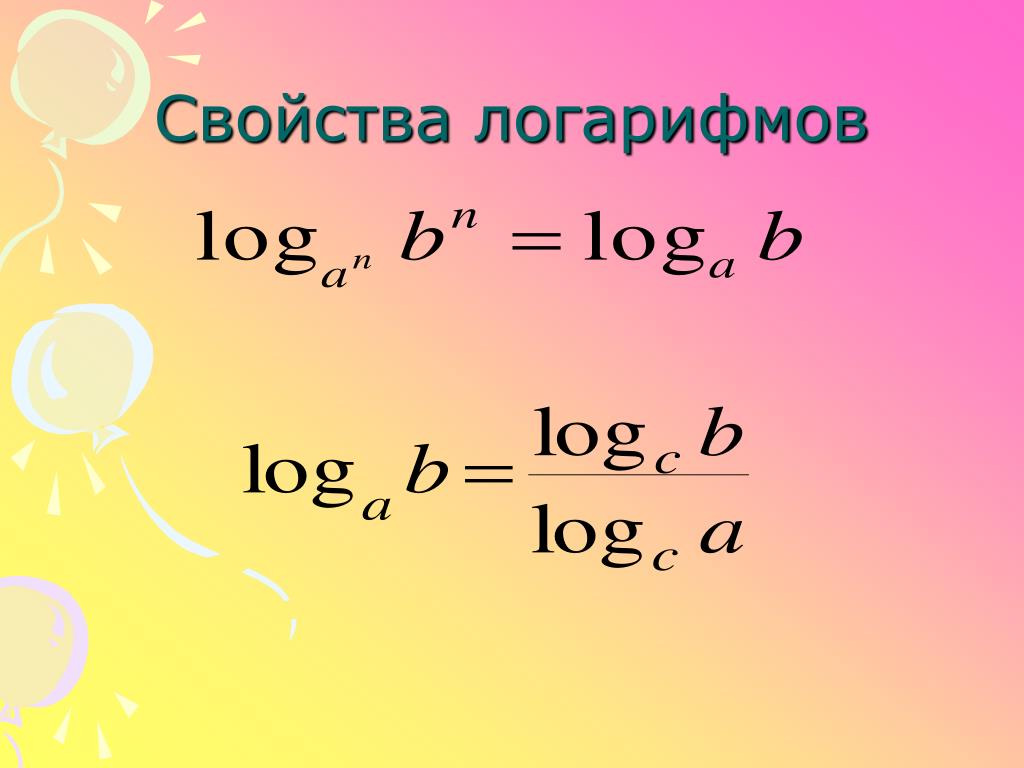 Фрагмент жизни, комната, из которой только что вышли, предел мечтаний, место преступления — набор признаков, указателей, следов, говорящих о жильце интерьера как о Человеке. Все это – поле для деятельности авторов проекта «Интерьер в чужом окне…».

Путешествие от «окна» к «окну», как от остановки к остановке, от стоянки к стоянке это – путешествие в страну людей. Задача участников проекта  — создание картинок, иллюстраций данного путешествия. Авторы должны собрать паззл из предметов, чувств, переживаний, проблем и наполнить его смыслом, как витраж светом. Создать доказательства того, что стоило заглядывать в окно, чтобы это увидеть.

Результат творческих поисков и находок авторов должен быть в конечном итоге выражен в инсталляциях (предметных, фото, видео, текстовых или смешанных), которые на выставке будут помещены в  отдельные замкнутые пространства («комнаты»). Увидеть инсталляции зрители смогут через окна в их стенах.  Площадь таких «комнат» от 1 до 12 квадратных метров. Высота стен 3 метра.

Произведения на стадии эскиза (проекта) проходят предварительный отбор организаторами фестиваля. Эскизы и описания работ представляются в произвольной форме

до 15 февраля 2013 года.

Материалы (эскизы вместе с краткой информацией об авторе) с пометкой «Интерьер в чужом окне…» высылаются на электронный адрес: [email protected] , также могут быть отправлены почтой или принесены лично по адресу: 125047, Москва, 2-я Брестская ул., д.6, комната 4.

Куратор проекта – художник Сергей Яралов (тел.: +7 916 5342615; [email protected] )

Полная информация о проекте размещена на сайте: www.dom6.ru.

Участие в проекте бесплатное.

Выставка будет проходить с 14 по 18 марта.

Москва, Дом на Брестской, ул. 2-я Брестская, д. 6.; Тел.: +7 495 6504997;+7 499 2512640.

Простая английская Википедия, бесплатная энциклопедия

Открытая раковина наутилуса. Его камеры составляют логарифмическую спираль

Логарифмы или бревна являются частью математики. Они связаны с экспоненциальными функциями. Логарифм говорит, какой показатель степени (или степени) необходим для получения определенного числа, поэтому логарифмы являются обратными (противоположными) действиям возведения в степень. Исторически сложилось так, что они были полезны при умножении или делении больших чисел.

Примером логарифма является log2⁡(8)=3 {\displaystyle \log _{2}(8)=3\}. В этом логарифме основание равно 2, аргумент равен 8, а ответ равен 3. В этом случае функция возведения в степень будет: 9{3}=2\times 2\times 2=8\,}

Наиболее распространенными типами логарифмов являются десятичных логарифмов , где основание равно 10, двоичных логарифмов , где основание равно 2, и натуральных логарифмы , где основание e ≈ 2,71828. ^{[1] [2]}

Логарифмы впервые были использованы в Индии во 2 веке до нашей эры. Первым, кто использовал логарифмы в наше время, был немецкий математик Михаэль Штифель (около 1487–1567). {m-n}}. Это основа для понимания логарифмов. Для Stifel m{\displaystyle m} и n{\displaystyle n} должны были быть целыми числами. Джон Напье (1550–1617) не хотел этого ограничения и хотел установить диапазон показателей.

Джон Нейпир работал над логарифмами

Согласно Нейпиру, логарифмы выражают отношения: a{\displaystyle a} имеет такое же отношение к b{\displaystyle b}, как c{\displaystyle c} к d{\displaystyle d}, если разница их логарифмов совпадает. Математически: журнал ⁡ (а) — журнал ⁡ (б) = журнал ⁡ (с) — журнал ⁡ (d) {\ Displaystyle \ журнал (а) — \ журнал (б) = \ журнал (с) — \ журнал (д) )}. Сначала использовалась база e (хотя число еще не было названо). Генри Бриггс предложил использовать 10 в качестве основания для логарифмов, такие логарифмы очень полезны в астрономии.

[2]

Связь с показательными функциями[изменить | change source]

Логарифм говорит, какой показатель степени (или степени) необходим для получения определенного числа, поэтому логарифмы являются обратными (обратными) действиями возведения в степень. {3}=8\}

В этой функции основание равно 2, аргумент равен 3, а ответ равен 8.

У этого экспоненциального уравнения есть обратное ему логарифмическое уравнение:

log2⁡(8)=3 {\displaystyle \log _{2}(8)=3\ }

В этом уравнении основание равно 2, аргумент равен 8, а ответ равен 3.

Сложение имеет одну обратную операцию: вычитание. Кроме того, у умножения есть одна обратная операция: деление. Однако возведение в степень на самом деле имеет два обратные операции: корень и логарифм. Причина, по которой это так, связана с тем фактом, что возведение в степень не является коммутативным.

Следующий пример иллюстрирует это:

• Если x +2=3, то можно использовать вычитание, чтобы узнать, что x =3−2. То же самое, если 2+ x = 3: также получается x = 3−2. Это потому, что x +2 равно 2+ x .
• Если x · 2=3, то можно с помощью деления узнать, что x = 32 {\ textstyle {\ frac {3} {2}}}. Это то же самое, если 2 · x = 3: также получается x = 32{\ textstyle {\ frac {3} {2}}}. Это потому, что x · 2 равно 2 · x .
• Если x ²=3, то можно использовать (квадратный) корень, чтобы узнать, что x = 3{\textstyle {\sqrt {3}}}. Однако, если 2 ^х =3, то один не может использовать корень, чтобы узнать х . Скорее, нужно использовать (двоичный) логарифм, чтобы выяснить, что x = логарифм ₂ (3).
  Это связано с тем, что 2 ^x обычно не совпадает с x ² (например, 2 ⁵ = 32, а 5² = 25).

Логарифмы могут упростить умножение и деление больших чисел, потому что сложение логарифмов — это то же самое, что умножение, а вычитание логарифмов — то же самое, что и деление.

До того, как калькуляторы стали популярными и распространенными, люди использовали таблицы логарифмов в книгах для умножения и деления. ^[2] Та же информация в таблице логарифмов была доступна на логарифмической линейке, инструменте с записанными на нем логарифмами.

Помимо вычислений, логарифм также имеет много других приложений в реальной жизни:

• Логарифмические спирали широко распространены в природе. Примеры включают раковину наутилуса или расположение семян на подсолнухе.
• В химии отрицательное значение логарифма по основанию 10 активности ионов гидроксония (H ₃ O ⁺ , форма H ⁺ принимает в воде) является мерой, известной как рН. Активность ионов гидроксония в нейтральной воде 10 ⁻⁷ моль/л при 25 °C, следовательно, pH равен 7. (Это результат константы равновесия, произведения концентрации ионов гидроксония и гидроксильных ионов в водных растворах, равной 10 ⁻¹⁴ M ² .)
• Шкала Рихтера измеряет интенсивность землетрясений по логарифмической шкале с основанием 10. ^[1]
• В астрономии видимая величина измеряет яркость звезд логарифмически, поскольку глаз также логарифмически реагирует на яркость.
• Музыкальные интервалы измеряются логарифмически как полутона. Интервал между двумя нотами в полутонах равен основанию-2 9.0021 1/12 логарифм отношения частот (или, что то же самое, 12-кратный логарифм по основанию 2). Дробные полутона используются для неравных темпераций. Специально для измерения отклонений от равнотемперированной шкалы интервалы также выражаются в центах (сотых долях равнотемперированного полутона). Интервал между двумя нотами в центах равен логарифму отношения частот по основанию 2 ^1/1200 (или 1200-кратному логарифму по основанию 2). В MIDI ноты пронумерованы по шкале полутонов (логарифмическая абсолютная номинальная высота звука со средней до 60). Для микронастройки на другие системы строя определена логарифмическая шкала, заполняющая диапазоны между полутонами равнотемперированной шкалы совместимым образом. Эта шкала соответствует номерам нот для целых полутонов. (см. микронастройку в MIDI, заархивированном 12 февраля 2008 г. на Wayback Machine ). 9{2}=100\ }

  Логарифмы по основанию e называются натуральными логарифмами. Число e близко к 2,71828, и его также называют константой Эйлера в честь математика Леонарда Эйлера.

  Натуральные логарифмы могут принимать символы loge⁡(x){\displaystyle \log _{e}(x)\,} или ln⁡(x){\displaystyle \ln(x)\,}. ^[3] Некоторые авторы предпочитают использовать натуральные логарифмы в виде log ⁡ (x) {\ displaystyle \ log (x)}, ^[4] , но обычно упоминают об этом на страницах предисловия.

  база	аббревиатура	Комментарии
  2	ld {\ displaystyle \ operatorname {ld}}	Очень распространен в компьютерных науках (двоичный)
  и	ln{\displaystyle \ln} или просто log{\displaystyle \log}	Основанием для этого является постоянная Эйлера e. Это наиболее распространенный логарифм, используемый в чистой математике.
  10	log10{\displaystyle \log _{10}} или log{\displaystyle \log} (иногда также пишется как lg{\displaystyle \lg})	Используется в некоторых науках, таких как химия и биология. {a}) = a} Например, 9{-1}}. Логарифм по основанию b числа a равен логарифму a , деленному на логарифм b . То есть, logb⁡(a)=log⁡(a)log⁡(b){\displaystyle \log _{b}(a)={\frac {\log(a)}{\log(b)}} } Например, пусть a равно 6, а b равно 2. С помощью калькуляторов мы можем показать, что это правда (или, по крайней мере, очень близко): log2⁡(6)=log⁡(6)log⁡(2){\displaystyle \log_{2}(6)={\frac {\log(6)}{\log(2)}} } log2 ⁡ (6) ≈ 2,584962 {\ displaystyle \ log _ {2} (6) \ приблизительно 2,584962} 2,584962≈0,7781510,301029≈2,584970{\displaystyle 2,584962\приблизительно {\frac {0,778151}{0,301029}}\приблизительно 2,584970} Приведенные выше результаты имели небольшую ошибку, но это было связано с округлением чисел. Поскольку представить натуральный логарифм сложно, мы находим, что в терминах десятичного логарифма: пер ⁡ (х) = журнал ⁡ (х) журнал ⁡ (е) ≈ журнал ⁡ (х) 0,434294 {\ displaystyle \ ln (x) = {\ frac {\ log (x)} {\ log (e) )}} \ приблизительно {\ гидроразрыва {\ log (х)} {0,434294}}}, где 0,434294 — приближение логарифма e . Операции с логарифмическими аргументами[change | change source] Логарифмы, которые умножаются внутри своего аргумента, могут быть изменены следующим образом: log⁡(ab)=log⁡(a)+log⁡(b){\displaystyle \log(ab)=\log(a)+\log(b)} Например, log⁡(1000)=log⁡(10⋅10⋅10)=log⁡(10)+log⁡(10)+log⁡(10)=1+1+1=3{\displaystyle \log( 1000)=\log(10\cdot 10\cdot 10)=\log(10)+\log(10)+\log(10)=1+1+1=3} Точно так же логарифм, который делится внутри аргумента, может быть превращен в разность логарифмов (поскольку это обратная операция умножения): log⁡(ab)=log⁡(a)-log⁡(b){\displaystyle \log {\bigg(}{\frac {a}{b}}{\bigg)}=\log(a )-\log(b)} Таблицы логарифмов, логарифмические линейки и исторические приложения[change | изменить источник] До электронных компьютеров ученые ежедневно использовали логарифмы. Логарифмы помогли ученым и инженерам во многих областях, таких как астрономия. До компьютеров таблица логарифмов была важным инструментом. [5] В 1617 году Генри Бриггс напечатал первую таблицу логарифмов. Это было вскоре после основного изобретения Нейпира. Позже люди стали делать таблицы с лучшим охватом и точностью. В этих таблицах перечислены значения log b ( x ) и b x для любого числа x в определенном диапазоне, с определенной точностью, для определенного основания b (обычно б = 10). Например, первая таблица Бриггса содержала десятичные логарифмы всех целых чисел в диапазоне от 1 до 1000 с точностью до 8 цифр. Поскольку функция f ( x ) = b x является обратной функцией log b ( x , она была названа антилогарифмом. [6] Люди использовали эти таблицы для умножения и деления чисел. Например, пользователь искал в таблице логарифм для каждого из двух положительных чисел. Сложение чисел из таблицы даст логарифм произведения. Затем функция антилогарифма таблицы найдет произведение на основе его логарифма. Для ручных вычислений, требующих точности, поиск двух логарифмов, вычисление их суммы или разности и поиск антилогарифма выполняется намного быстрее, чем выполнение умножения более ранними способами. Многие таблицы логарифмов дают логарифмы, отдельно предоставляя характеристику и мантиссу x , то есть целую часть и дробную часть log 10 ( x ). [7] Характеристика 10 · x — это единица плюс характеристика x , и их значения одинаковы. Это расширяет возможности таблиц логарифмов: для таблицы со списком log 10 ( x ) для всех целых чисел x в диапазоне от 1 до 1000 логарифм 3542 аппроксимируется выражением log10⁡(3542)=log10⁡(10⋅354,2)=1+log10⁡(354,2)≈1+log10⁡(354).{\displaystyle \log _{10}(3542)=\log _{ 10}(10\cdot 354,2)=1+\log _{10}(354,2)\приблизительно 1+\log _{10}(354). \,} Другим важным применением была логарифмическая линейка, пара логарифмически разделенных шкал, используемых для вычислений, как показано здесь: Схематическое изображение логарифмической линейки. Начиная с 2 на нижней шкале, добавьте расстояние к 3 на верхней шкале, чтобы получить произведение 6. Логарифмическая линейка работает, потому что она отмечена таким образом, что расстояние от 1 до x пропорционально логарифму x . . Числа отмечаются на скользящих шкалах на расстояниях, пропорциональных разности их логарифмов. Сдвиг верхней шкалы соответствует механическому сложению логарифмов. Например, добавление расстояния от 1 до 2 по нижней шкале к расстоянию от 1 до 3 по верхней шкале дает произведение 6, которое считывается в нижней части. Многие инженеры и ученые использовали логарифмические линейки до 19 века.70-е годы. Ученые могут работать быстрее, используя логарифмическую линейку, чем используя таблицу логарифмов. [8] Постоянная Эйлера–Маскерони Теорема о простых числах ↑ 1.0 1.1 «Полное руководство по логарифму — теория и приложения». Математическое хранилище . 08.05.2016. Проверено 29 августа 2020 г. . ↑ 2.0 2.1 2.2 «логарифм | Правила, примеры и формулы». Британская энциклопедия . Проверено 29 августа 2020 г. . ↑ Вайсштейн, Эрик В. «Натуральный логарифм». mathworld.wolfram.com . Проверено 29 августа 2020 г. . ↑ «Сборник математических символов». Математическое хранилище . 01.03.2020. Проверено 29 августа 2020 г. . ↑ Кэмпбелл-Келли, Мартин (2003), История математических таблиц: от шумеров до электронных таблиц , Оксфордская стипендия онлайн, Oxford University Press, ISBN 978-0-19-850841-0 , раздел 2 ↑ Абрамовиц, Милтон; Стеган, Ирэн А. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт