Логарифмическая регрессия в Excel (шаг за шагом)
Редакция Кодкампа
читать 2 мин
Логарифмическая регрессия — это тип регрессии, используемый для моделирования ситуаций, когда рост или спад сначала быстро ускоряются, а затем со временем замедляются.
Например, следующий график демонстрирует пример логарифмического распада:
Для такого типа ситуации взаимосвязь между переменной-предиктором и переменной-откликом можно хорошо смоделировать с помощью логарифмической регрессии.
Уравнение модели логарифмической регрессии принимает следующий вид:
у = а + b*ln(x)
куда:
- y: переменная ответа
- x: предикторная переменная
- a, b: коэффициенты регрессии, описывающие взаимосвязь между x и

В следующем пошаговом примере показано, как выполнить логарифмическую регрессию в Excel.
Шаг 1: Создайте данныеВо-первых, давайте создадим поддельные данные для двух переменных: x и y :
Шаг 2: возьмите натуральный логарифм переменной-предиктораДалее нам нужно создать новый столбец, представляющий натуральный логарифм переменной-предиктора x :
Шаг 3: Подберите модель логарифмической регрессииДалее мы подгоним модель логарифмической регрессии. Для этого щелкните вкладку « Данные » на верхней ленте, затем щелкните « Анализ данных» в группе « Анализ ».
Если вы не видите Data Analysis в качестве опции, вам нужно сначала загрузить Analysis ToolPak .
В появившемся окне нажмите Регрессия.В появившемся новом окне введите следующую информацию:
Как только вы нажмете OK , отобразятся выходные данные модели логарифмической регрессии:
Общее значение F модели составляет 828,18, а соответствующее значение p чрезвычайно мало (3,70174E-13), что указывает на то, что модель в целом полезна.
Используя коэффициенты из выходной таблицы, мы видим, что подобранное уравнение логарифмической регрессии:
у = 63,0686 – 20,1987 * ln(x)
Мы можем использовать это уравнение для прогнозирования переменной отклика y на основе значения переменной-предиктора x.Например, если x = 12, то мы предсказываем, что y будет 12,87 :
у = 63,0686 – 20,1987 * ln(12) = 12,87
Бонус: не стесняйтесь использовать этот онлайн- калькулятор логарифмической регрессии для автоматического вычисления уравнения логарифмической регрессии для заданного предиктора и переменной отклика.
Дополнительные ресурсыКак выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как выполнить полиномиальную регрессию в Excel
Как выполнить экспоненциальную регрессию в Excel
Антилогарифмический калькулятор | Лучший калькулятор обратного журнала
Что такое логарифм?
Логарифм является обратным значением экспоненты или функции возведения в степень. Допустим, есть 3 числа, обозначенные буквами a, x и n. Тогда отношение, которое они образуют, равно
Допустим, есть 3 числа, обозначенные буквами a, x и n. Тогда отношение, которое они образуют, равно
Если ax = n, где n > 0, a > 0 и a =/ 1
Для лучшего и легкого понимания формула логарифма также записывается как
y = log b x
Введение в Antilog Calculator
Антилогарифмическая функция представляет собой процесс, обратный нахождению логарифма, называемый антилогарифмом. Лог является обратным экспоненте, поэтому антилогарифм также называется возведением в степень.
Калькулятор антилогарифмического вычисления также можно назвать логарифмически-обратным калькулятором. Калькулятор обратного логарифма позволяет пользователю легко вычислить антилогарифм без ручных вычислений.
Вы также можете научиться писать ряды в сигма-калькуляторе онлайн.
Как рассчитать Антилог?
Калькулятор обратного логарифма может мгновенно вычислить антилогарифм, но для ручных вычислений, если «x» является логарифмом заданного числа «n» с заданным основанием «a», тогда n называется антилогарифмом или антилогарифмом «x» к этому base
Итак, если log a n = x, то n = antilog x или x = logb-1 (y) = y. Поскольку log и обратная функция log являются обратными друг другу функциями, это означает, что
Поскольку log и обратная функция log являются обратными друг другу функциями, это означает, что
X = by = blogbx (y) = by и y = logbx = logb(by). Это можно рассчитать с помощью обратного логарифмического калькулятора.
Также узнайте, как рассчитать процент ошибки для решения ошибки в стандартных значениях.
Функция, используемая калькулятором обратного логарифма
Калькулятор обратного логарифма использует обратные логарифмические функции и экспоненциальные функции. Например, логарифм (7) = 0,841 и логарифм (2) = 0,3010, антилогарифмический онлайн-калькулятор рассчитает следующее:
Антилогарифм / инверсия логарифма (3,3010)
Решение: по формуле антилогарифмической или обратной логарифмической
Antilog (3,3010) = 103,3010 = 103 + 0,3010 = 103 x 100,3010 = 1000,2 = 2000
Как узнать Антилог номера?
Найти антилогарифм так же просто, как найти логарифм функции. Даже процесс во многом похож. Чтобы найти антилог числа, прежде всего
- Определите основу вашего нахождения.
 В большинстве случаев обычные числа имеют основание 10.
В большинстве случаев обычные числа имеют основание 10. - Теперь выберите номер, по которому вы хотите найти антилог.
- Увеличить число основания, b x .
- Пересмотрите весь процесс еще раз, чтобы пересмотреть расчеты.
Использование калькулятора антилогарифмов для , чтобы найти антилогарифм числа , всегда полезно, так как вы мгновенно получите быстрые результаты.
Является ли натуральный логарифм (ln) обратным логарифмом?
Натуральный логарифм — это тип логарифма, который поясняет, что натуральный логарифм или ln не является обратным или антилогарифмическим. Как мы знаем, натуральный логарифм — это логарифм с основанием «е», где «е» — экспоненциальная функция.
С другой стороны, антилогарифм или инверсия лога — это полная обратная сторона лога. Обратный журнал находится путем возведения логарифма по основанию «b». Таким образом, мы можем сказать, что натуральный бревно не является антилоганом.
Также попробуйте наш калькулятор факториальных выражений для произведения всех положительных целых чисел, меньших или равных n.
Что такое антилогарифмический калькулятор?
Иногда бывает трудно найти натуральный бревно бесконечности руками. Так зачем же полагаться на обычные методы, когда можно найти антилогарифмический калькулятор онлайн .
Калькулятор обратного логарифма позволяет вычислять обратную логарифмическую функцию. Калькулятор антилогарифмов прост и бесплатен для использования без какой-либо подписки. Вы можете выполнить поиск в Интернете, чтобы найти калькулятор обратного логарифма, или выполнить поиск по запросу Calculatored, чтобы найти этот инструмент.
Calculatored — это онлайн-портал с большим выбором калькуляторов и конвертеров. Вы можете выбрать онлайн-калькулятор антилогарифма для расчета антилогарифма онлайн.
Как пользоваться калькулятором Antilog?
Вычисление обратного логарифма на нашем калькуляторе обратного логарифмического очень легко сделать. Выполните шаги, чтобы вычислить антилогарифм с помощью обратного логарифмического калькулятора.
Выполните шаги, чтобы вычислить антилогарифм с помощью обратного логарифмического калькулятора.
Шаг №1: Введите номер, который вы хотите найти антилог в первом поле
Шаг №2: Введите базу во второе поле
Шаг #3: Нажмите на кнопку «РАССЧИТАТЬ»
Нажав на кнопку, наш научный калькулятор Antilog мгновенно покажет вам результат. Это делает наш онлайн-калькулятор антилогарифма одним из лучших среди других.
Внешние ресурсы:
- Логарифм и антилогарифм.
- Как сделать антилог?
Натуральный логарифм (Ln) Калькулятор
Вычислить натуральный логарифм X по основанию e как log e X :
Ln Калькулятор
Число(X):
Результат:
| Значение y = log e: X9 | 0 |
Что такое натуральный логарифм?
Логарифм (или логарифм) — это математическая операция, обратная возведению в степень. Это означает, что логарифм числа — это степень, в которую нужно возвести основание, чтобы получить это число. Возведение в степень записывается как 𝑥 = b и . Соответствующее логарифмическое обозначение: 𝑦 = log b 𝑥. Если основание равно e, обозначение 𝑥 = e y , а логарифмическое обозначение 𝑦 = log e 𝑥 или 𝑦 = ln 𝑥.
Это означает, что логарифм числа — это степень, в которую нужно возвести основание, чтобы получить это число. Возведение в степень записывается как 𝑥 = b и . Соответствующее логарифмическое обозначение: 𝑦 = log b 𝑥. Если основание равно e, обозначение 𝑥 = e y , а логарифмическое обозначение 𝑦 = log e 𝑥 или 𝑦 = ln 𝑥.
Существует два типа логарифмирования: десятичный логарифм и натуральный логарифм. В обычных обозначениях слово «логарифм» обозначает десятичный логарифм по основанию 10, хотя можно использовать любое основание. Например, log 10 5 записывается просто как log 5. Для любого другого числа всегда указывается основание.
Другой вид логарифма — натуральный логарифм, где по основанию e, то есть число Эйлера. Это иррациональное число и оно равно 2,7182. В этом случае натуральный логарифм обозначается ln или логарифм с основанием e. Например, log e 5 = ln 5. Натуральный логарифм определяет, сколько раз нужно умножить e на себя, чтобы получить 5.
Основное различие между десятичным логарифмом и натуральным логарифмом заключается в основании.
Различия между бревном и натуральным бревном
Разница между log и ln имеет решающее значение для решения математических задач с использованием этих функций. Некоторые из основных различий между этими двумя функциями перечислены ниже.
| журнал | по |
|---|---|
| только log указывает на логарифм с основанием 10, хотя можно использовать и другие основания. Для любого другого основания это указывается явно, но для 10 это может быть опущено. | ln относится к логарифмам с основанием e. |
| Это записывается как 𝑥 = b y в экспоненциальной форме и 𝑦 = log b 𝑥 с использованием логарифмической записи. Если основание равно 10, то 𝑥 = 10 y и 𝑦 = log 10 | Когда основание равно e, обозначение 𝑥 = e y , а логарифмическое обозначение 𝑦 = log e 𝑥 или 𝑦 = ln 𝑥. |
| Логарифмическая функция называется десятичным логарифмом. | ln называется натуральным логарифмом. |
| Логарифмическая функция показывает, сколько раз нужно умножить основание на себя, чтобы получить определенное число, или в какую степень необходимо возвести основание, чтобы получить определенное число. Например, для основания 10 log (100) = 2, что означает, что 10 2 = 100, | Логарифмическая функция показывает, сколько раз нужно умножить «е» на себя, чтобы получить определенное число, или в какую степень нужно возвести «е», чтобы получить определенное число. Например, ln (7.38) ≈ 2 и e 2 = 7,38 |
Формула натурального логарифма
Формула натурального логарифма: 𝑦 = log e 𝑥 = ln 𝑥, что эквивалентно 𝑥 = e y в экспоненциальной форме.
Функция ln и e обратны друг другу. Следовательно, log e (e x ) = ln e y = 𝑥 и e ln (x) = 𝑥
Натуральный логарифм 0 и любого отрицательного числа не определен. Натуральный логарифм 1 равен 0, то есть ln 1 = 0. Натуральный логарифм е равен 1, то есть логарифм e 𝑒 = ln 𝑒 = 1.
Натуральный логарифм 1 равен 0, то есть ln 1 = 0. Натуральный логарифм е равен 1, то есть логарифм e 𝑒 = ln 𝑒 = 1.
Правила естественного журнала
Натуральные журналы подчиняются нескольким правилам, перечисленным ниже.
| правило | пример |
|---|---|
| Правило произведения: $$ ln(x*y) = ln\,x \;+\; лн,у $$ | Например, $$ ln(4*8) = ln\,4 \;+\; ln\,8 = 3,4657 $$ |
| Частное правило: $$ ln({x\over y}) = ln\,x \;-\; лн,у $$ | 9{ln(x)} = x$$|
| Натуральный логарифм отрицательного числа не определен. | |
| Натуральный логарифм 0 не определен. | |
| Натуральный логарифм e равен 1, то есть log e 𝑒 = ln 𝑒 = 1. | |
Области применения
Натуральное бревно и обычное бревно имеют одинаковые области применения. Оба являются очень удобными способами выражения больших чисел.
Ниже приведены некоторые примеры задач, связанных с натуральным логарифмом.
Ответ: В этой задаче ln √𝑒 = ln e 1/2 = (1/2) ln e = 1/2
Ответ: Здесь ln (5x-7) = 3
Когда в круглых скобках ln содержится несколько терминов, полезно явно записать e как основание, а все остальные термины как показатели степени e. При этом мы получаем форму e ln (x) = 𝑥, что помогает в процессе упрощения.
Следовательно, данное уравнение можно записать в виде e пер (5х-7) = е 3 .
Поскольку e ln (x) = 𝑥, указанный выше шаг сводится к 5𝑥 − 7 = e 3 .
Поскольку e является константой, ее степени можно легко найти с помощью калькулятора. Отсюда получаем
5𝑥 − 7 = 20,0855
5𝑥 = 27,0855
𝑥 = 5,4171
Ответ: В ситуациях с экспоненциальным периодом полураспада имеет место .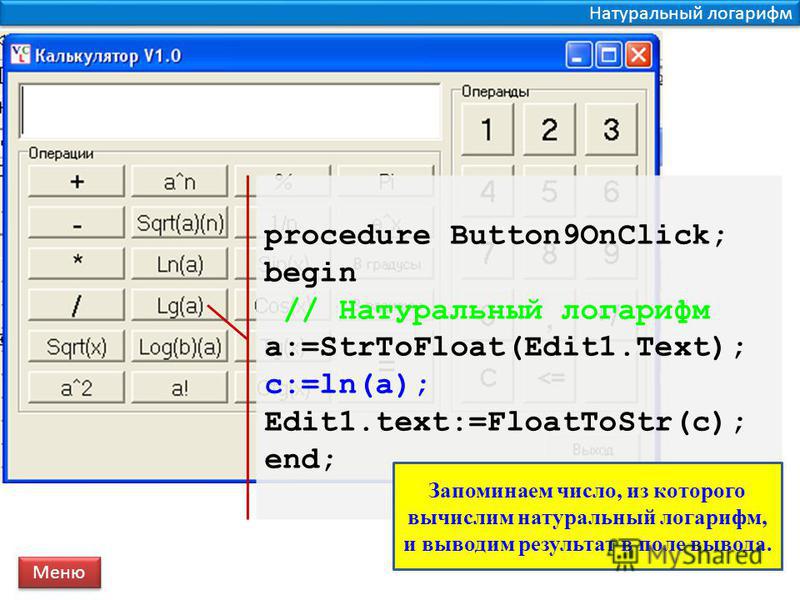


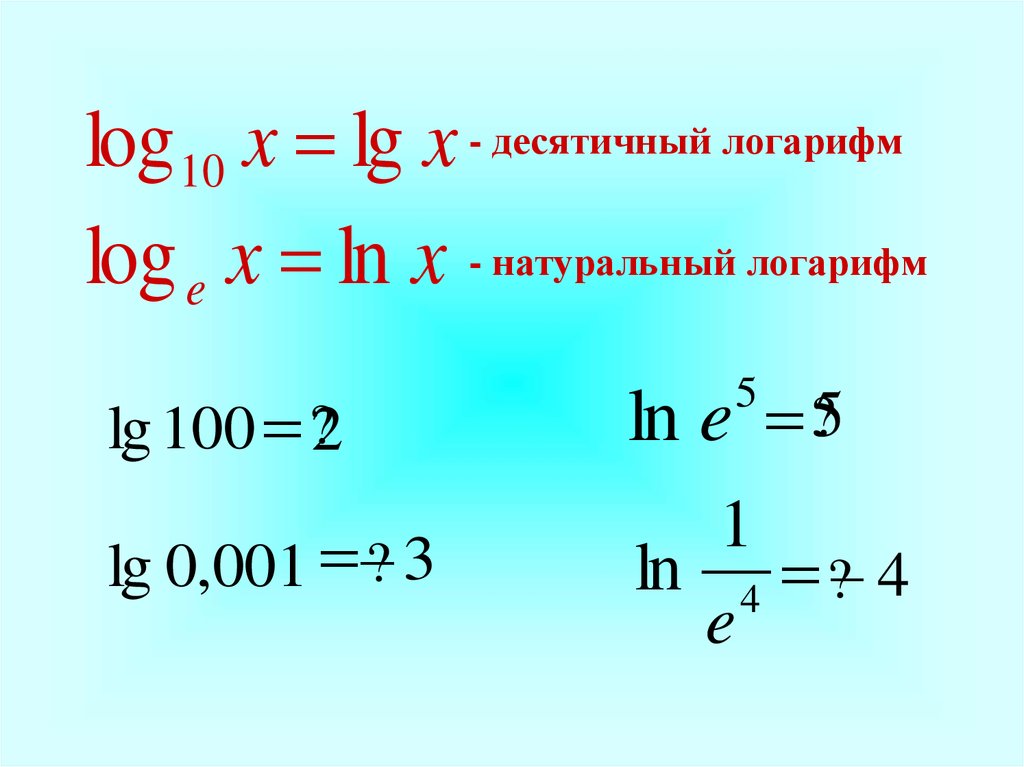 В большинстве случаев обычные числа имеют основание 10.
В большинстве случаев обычные числа имеют основание 10.