Будем говорить, что эти числа представляются единицей с нулями (с последующими нулями, если $n > 0$, и с предшествующими нулями, если $n
Десятичный логарифм числа, представляемого единицей с нулями, равен числу нулей в этом числе, если оно есть единица с последующими нулями, и числу нулей с противоположным знаком, если оно есть единица с предшествующими нулями.
Например:
$lg 0,0001=-4, lg 0,01=-2, lg 1000 = 3, lg 1000000 = 6$.
Десятичный логарифм любого числа, не равного целой степени десяти, является числом дробным (вообще говоря, иррациональным).
Напомним, что всякое число (рациональное или иррациональное) однозначно разлагается на сумму своей целой части и дробней части. При этом целой частью данного числа называется наибольшее целое число, не превосходящее данного; дробная часть любого числа заключена между нулем и единицей:
$3,176 = 3 + 0,176; — 2,143 = — 3 + 0,857 = \overline{3},857$.
Неравенства (3) показывают, что
$- l \leq lg N
т. е. характеристика логарифма $lg N$ равна $-l$.
Итак, характеристика десятичного логарифма положительного числа, меньшего единицы, равна взятому со знаком минус числу нулей в данном числе, предшествующих первой значащей цифре, включая и нуль целых.
Например:
$lg 0,3052 = \overline{1}, \cdots; lg 0,0587 = \overline{2} \cdots; lg 0,0096 = \overline{3}, \cdots$
Мы выяснили, что характеристика десятичного логарифма числа определяется непосредственно по виду самого числа, если оно целое или представлено в виде десятичной дроби. Для определения характеристики, таким образом, не нужны никакие вычисления (и таблицы). Что же касается мантиссы, то она, как правило, берется из таблиц (например, из таблиц Брадиса). При этом следует пользоваться одним замечательным свойством мантиссы: если в логарифмируемом числе перенести запятую на любое количество знаков влево или вправо, то мантисса десятичного логарифма от этого не изменится (изменится только характеристика логарифма).
что такое в математике, вычисление, как правильно решать LG, примеры
Содержание:
- Десятичный логарифм числа – что это такое в математике
- Определение и формулы десятичного логарифма
- График десятичного логарифма
- Как правильно решать задачи на десятичных логарифмах, примеры
- Десятичный логарифм числа – что это такое в математике
- Определение и формулы десятичного логарифма
- График десятичного логарифма
- Как правильно решать задачи на десятичных логарифмах, примеры
Десятичные логарифмы широко применялись в вычислениях до появления компактных калькуляторов.
m\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Логарифм будет иметь смысл только при соблюдении ряда условий:
\(k>0,\;\;k\neq1,\;\;n>0\)
Примечание
Если за основание логарифма взята цифра 10, то такой логарифм называется десятичным. Его принято обозначать знаком lg и не указывать основание, равное 10. Например, правильно записывать lg 20, а не log10 20.
Десятичные логарифмы обладают теми же особенностями, что и любые другие логарифмы при основании больше, чем 1. Например, большему из нескольких положительных чисел будет соответствовать и больший десятичный логарифм. Десятичный логарифм числа, которое больше 0, но меньше 1, будет отрицательным, а больше единицы – положительным.
Десятичные логарифмы обладают рядом характерных признаков:
- Десятичный логарифм положительного целого числа, представленного единицей и следующими за ней нулями, представляет собой целое неотрицательное число, которое будет равно количеству нулей в записи выбранного числа: lg 10=1, lg 10000=4.
- Десятичный логарифм десятичной неотрицательной дроби, записанной как единица с предыдущими нулями, будет равен (-m). В этом случае m – количество нулей, предшествующих единице, в том числе с учетом и нулевой целой части: lg 0,1=-1, lg 0,0001=-4.
- Если умножить число на 10m, то десятичный логарифм увеличится на число m. Это можно записать формулой: lg (a10m) = lg a + lg 10m = lg a + m.
- Если разделить число на 10k, то его десятичный логарифм станет меньше на k.
Определение и формулы десятичного логарифма
Определение
Десятичным логарифмом числа k является решение уравнения: 10n=k
В алгебре свойства десятичных логарифмов описываются целым рядом формул. Их использование позволяет значительно проще решать сложные задачи, снижает вероятность ошибок.
Основными формулами десятичных логарифмов являются:
\(1.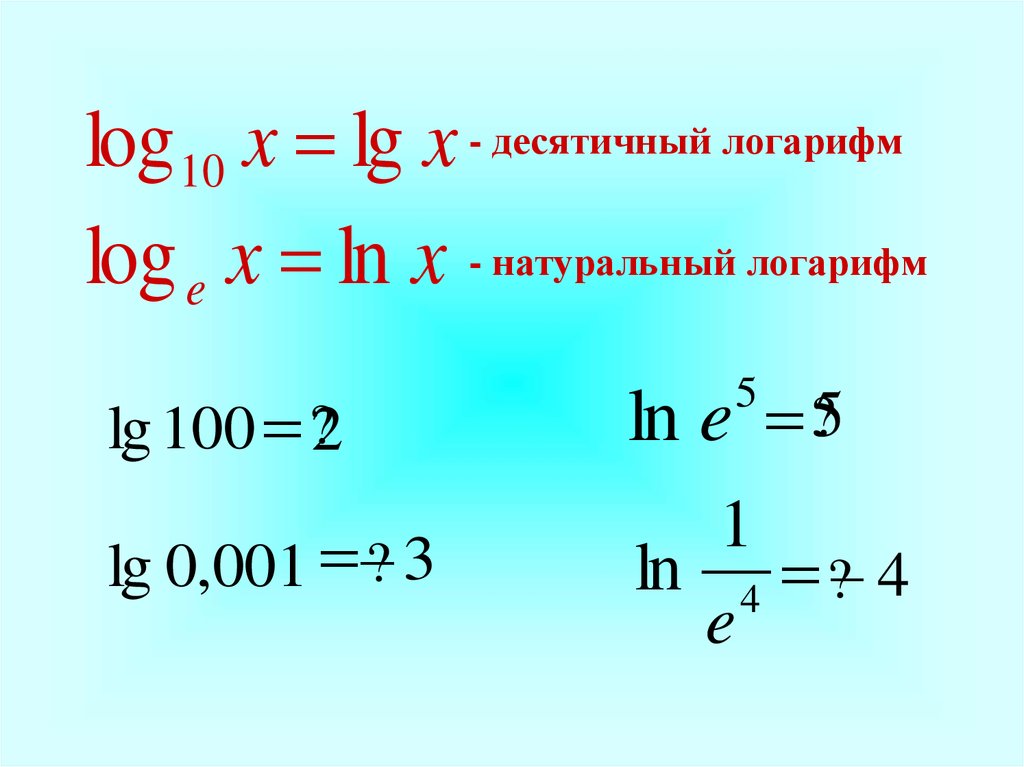
m\right)\;=\;mlg\;(x)\\6.\;lg\;\sqrt[p]x\;=\;\frac{lg\;(x)}p\)
До изобретения калькуляторов вышеописанные формулы использовались очень широко. Например, они позволяют с легкостью выполнить умножение многозначных чисел. Для этого необходимо воспользоваться простым алгоритмом:
- найти по таблице логарифмы заданных чисел;
- в соответствии с третьим свойством сложить их и получить логарифм произведения;
- по полученному логарифму используя таблицу найти и само произведение чисел.
Аналогичным образом можно выполнить и деление многозначных чисел. Только в данном случае логарифмы следует не складывать, а вычитать.
Использование десятичных логарифмов дает возможность даже без калькулятора выполнить извлечение из корня или возведение в степень.
В настоящее время десятичные логарифмы практически полностью вытеснены натуральными. Они сохраняются только в исторически укоренившихся областях математики, например, в построении логарифмической шкалы.
Отрицательные десятичные логарифмы представляют в искусственной форме. В ней они имеют отрицательную характеристику и положительную мантиссу.
Рассмотрим пример:
\(lg\;(0.005)\;=\;\overset-3.69897\\\)
Иначе эту запись можно представить так:
\(lg\;(0.005)\;=\;\overset-3.69897=\;-3\;=\;0.69897=\;-2.30103\\\)
Для перевода десятичного отрицательного логарифма в искусственную форму необходимо увеличить на единицу абсолютную величину характеристики. Над полученным числом поставить знак «минус». Вычесть из девяти все цифры мантиссы кроме последней, не равной нулю.
Ее следует вычесть из десяти. Полученные в ходе вычитания разности записать на тех же местах мантиссы, где находились вычитаемые числа. Нули на конце остаются без изменений.График десятичного логарифма
При рассмотрении логарифмируемого числа в качестве переменной получаем функцию:
\(y\;=\;lg\;(x)\\\)
Она будет определена при всех значениях x больше нуля.
Область значений функции лежит в пределе:
\(E_{(y)}=(-\infty;\;+\infty)\\\)
График десятичного логарифма представляет кривую линию, называемую логарифмикой.
Всюду, где функция определена, она дифференцируема, непрерывна и монотонно возрастает. Ее производную можно задать формулой:
\(\frac d{d_x}=lg\;x\;=\frac{lg\;e}x\\\)
Ось ординат рассматриваемой функции является вертикальной асимптотой, так как
\(\underset{x\rightarrow0+0}{\lim\;lg\;x}=\;-\infty\\\)
Как правильно решать задачи на десятичных логарифмах, примеры
Рассмотрим примеры решения задач с использованием десятичных логарифмов.
Задача 1. Вычислить значение выражения
\(lg\;\left(400\right)\;+\;lg\;\frac1{40}\)
Для решения данного примера воспользуемся формулой суммы:
\(lg\;\left(400\right)\;+\;lg\;\frac1{40}\;=\;lg\;\left(\frac{400\times1}{40}\right)=\;lg\;10\;=\;1\)
Задача 2. Упростите выражение:
\(lg\;\frac18\;-\;3\;lg\;4\)
В данном случае необходимо воспользоваться формулой степени:
\(lg\;\frac18\;-\;3\;lg\;4\;=\;lg\;2^{-3}\;-\;3\;lg\;2^2\;=\;-3lg\;-\;3\times2\;lg\;2\;=\;-9\;lg\;2\)
Задача 3.
3\;=\;3\times2\;lg\frac3{10}\;-\;2\times3\;lg\;3\;=\;6\;lg\;\frac3{10}\;-\;6\;lg\;3\)
Теперь применим свойство частного, откроем скобки и приведем подобные слагаемые:
\(6\;lg\;\frac3{10}\;-\;6\;lg\;3\;=\;6\;(lg\;3\;-\;lg\;10)\;-\;6\;lg3\;=\;6\;lg\;3\;-\;6\;lg\;10\;-\;6\;lg\;3=\;-\;6\;lg\;10=\;-6\times1\;=\;-6\)
Насколько полезной была для вас статья?
Рейтинг: 2.67 (Голосов: 6)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
jpg»> 
Я боялся, что он будет отставать в своих классах. Его учитель математики порекомендовал Алгебратор, который буквально шаг за шагом помог ему решить каждую задачу. Когда мой сын смог вернуться в школу, он стал лучше понимать математику, чем до отъезда. Я бы порекомендовал эту программу всем! 
:
453″ в дробьКалькулятор упрощенного логарифма
- Выражение
- Уравнение
- Неравенство
- Свяжитесь с нами
- Упрощение
- Коэффициент
- Расширение
- GCF 4
- Решить
- График
- Система
- Решить
- График
- Система
- Математический решатель на вашем сайте
- квадратные корни в десятичных дробях
- бесплатный рабочий лист десятичного числа для 5 класса
- бесплатный рабочий лист по упрощению квадратных корней
- прентис холл математика алгебра 1 математика средней школы
- решение сложных уравнений в Excel
- калькулятор экспоненциальной вероятности
- Калькулятор наименьшего общего кратного
- решить любую проблему онлайн
- Два одновременных уравнения Java
- уравнение стандартной формы парабола
- самая сложная математическая задача в мире
- факторные рабочие листы
- тестовых листов с ответами
- формула отношения алгебра
- рабочие листы для умножения и деления целых чисел
- многочлены в кубе множителей
- бесплатных математических таблиц Excel для второго класса
- локальный поиск
- рабочих листов по системам линейных неравенств
- калькулятор упрощения математических выражений
- выражения соотношения алгебры
- рабочие листы закона индексов
- найти калькулятор факторизации lu
- Интерактивные учебники по алгебре для средней школы
- как найти журнал на ti 89
- решение линейных дифференциальных уравнений методом исключения
- Решатель задач построения гиперболы
- умножить разделить целые числа
- как вручную установить программу-калькулятор «ТИ-84»
- предварительная алгебра с пиццами ответы
- самый сложный вопрос по физике
- игры с линейными уравнениями для печати
- разложение биномов в кубе
- преобразовать проценты в целое число
- решение разности частных
- алгебра решатель квадратных уравнений вершина
- смешанное десятичное число 8. 05
- рабочих листов кубических единиц
- финансы+6 класс+деятельность
- лист добавления положительных и отрицательных сторон
- биномиальное разложение на ti-89
- excel «найти процентное изменение
- скачать бесплатно EDEXCEL Бухгалтерский учет на обычном уровне лист с вопросами
- вынесение на множители алгебраических уравнений
- онлайн калькулятор дробей
- решение систем квадратных уравнений с двумя переменными
- Калькулятор логарифмических уравнений
- картинки для графического калькулятора
- рабочих листов на сложение и вычитание целых чисел
- скачать руководство по гидромеханике
- решение задач с рабочим листом дроби
- Рабочие листы дроби 4 класса
- экспоненциальное как рациональное
- преобразование математических сумм в десятичные дроби
- онлайн калькулятор вронскиана
- пошаговый метод преобразования постфикса в преобразование двоичного дерева
- Бесплатные рабочие листы GED
- Кроссворд по современной биологии, глава 17
- ти 89 комплекс Рабочий лист координатной плоскости
- алгебра с рабочими листами
- рабочих листов с переменными
- РЕШЕНИЕ РАДИКАЛОВ
- Калькулятор факторинга квадратичный
- сложение дробей с неизвестным
- «Элементы современной алгебры» задание
- как решить уравнение для параболы и прямой
- значение круговой ионной математики
- треугольников в исходном коде Visual Basic
- программы поля направления фазовая плоскость ti 83
- двухшаговые рабочие листы уравнений бесплатно
- ти 89 однородная ода
- задачи на наивысший общий делитель
- понимание сходных терминов
- математических листов — сложение, вычитание, умножение, деление дробей
- конвертация базовой калькуляторной дроби
- квадратных корней с показателями
- ФОРМУЛА(И) ДЛЯ N-ГО ЧЛЕНА БЕСКОНЕЧНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
- многочлен сложения java
- решатель задач по алгебраическим функциям
- стихотворений с математическими словами
- создание изображений с помощью графического калькулятора
- www.
Наших пользователей:
Эта программа заложила основу для наиболее успешного пошагового решения для обучения алгебре, которое я когда-либо видел или имел удовольствие применять в классе.
Как я упоминал во время нашего предыдущего телефонного разговора, при составлении диаграмм фактических результатов стандартизированного тестирования наших студентов на понимание математики с использованием данных за периоды как до, так и сразу после внедрения вашего программного обеспечения, сравнительная разница действительно очевидна.
Б.Ф., Вермонт
Ваша программа до сих пор была отличной. Я купил это программное обеспечение для моих 13 лет. старая дочь, у которой проблемы с математикой. У нас есть репетитор, который приходит на дом, и благодаря вашему программному обеспечению и ему она получила свою первую пятерку в очень сложном тесте по главе. Как вы, возможно, знаете, иногда, когда вы видите другой подход к проблеме, или иногда просто кто-то другой показывает вам разные способы понимания проблемы, этого достаточно. Ваше программное обеспечение, кажется, дает этот подход к решению проблем таким образом, чтобы его было легко понять. Еще раз спасибо всей семье Терли.
Джейкоб Мэтисон, Флорида
Мой бывший репетитор по алгебре выходил из себя, когда я не мог решить уравнение. В конце концов я устал от нее, поэтому я решил попробовать программное обеспечение. Я так впечатлен этим! Я не могу не подчеркнуть, насколько это здорово!
Моника, Техас
Это программное обеспечение по алгебре дает моей дочери возможность учиться самостоятельно, предлагая факты и полезные советы, прежде чем предлагать ей задачи для решения. Очень хорошо получается. . . Я думаю, что программное обеспечение прекрасно помогает студентам в течение всего года, дополняя любые материалы, которые они получают в обычном классе.
Уильям Маркс, Огайо
Студенты, борющиеся со всевозможными задачами по алгебре, обнаруживают, что наше программное обеспечение спасает им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?
Поисковые фразы, использованные 17 августа 2011 г.
:
05