Таблица значений функции Лапласа | matematicus.ru
Artman Таблицы
Таблица значений функции Муавра Лапласа
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 0,00 | 0,00000 | 0,50 | 0,19146 | 1,00 | 0,34134 | 1,50 | 0,43319 | 2,00 | 0,47725 | 3,00 | 0,49865 |
| 0,01 | 0,00399 | 0,51 | 0,19497 | 1,01 | 0,34375 | 1,51 | 0,43448 | 2,02 | 0,47831 | 3,05 | 0,49886 |
| 0,02 | 0,00798 | 0,52 | 0,19847 | 1,02 | 0,34614 | 1,52 | 0,43574 | 2,04 | 0,47932 | 3,10 | 0,49903 |
| 0,03 | 0,01197 | 0,53 | 0,20194 | 1,03 | 0,34849 | 1,53 | 0,43699 | 2,06 | 0,48030 | 3,15 | 0,49918 |
| 0,04 | 0,01595 | 0,54 | 0,20540 | 1,04 | 0,35083 | 1,54 | 0,43822 | 2,08 | 0,48124 | 3,20 | 0,49931 |
| 0,05 | 0,01994 | 0,55 | 0,20884 | 1,05 | 0,35314 | 1,55 | 0,43943 | 2,10 | 0,48214 | 3,25 | 0,49942 |
| 0,06 | 0,02392 | 0,56 | 0,21226 | 0,35543 | 1,56 | 0,44062 | 2,12 | 0,48300 | 3,30 | 0,49952 | |
| 0,07 | 0,02790 | 0,57 | 0,21566 | 1,07 | 0,35769 | 1,57 | 0,44179 | 2,14 | 0,48382 | 3,35 | 0,49960 |
| 0,08 | 0,03188 | 0,58 | 0,21904 | 1,08 | 0,35993 | 1,58 | 0,44295 | 2,16 | 0,48461 | 3,40 | 0,49966 |
| 0,09 | 0,03586 | 0,59 | 0,22240 | 1,09 | 0,36214 | 1,59 | 0,44408 | 2,18 | 0,48537 | 3,45 | 0,49972 |
| 0,10 | 0,03983 | 0,60 | 0,22575 | 1,10 | 0,36433 | 1,60 | 0,44520 | 2,20 | 0,48610 | 3,50 | 0,49977 |
| 0,11 | 0,04380 | 0,61 | 0,22907 | 0,36650 | 1,61 | 0,44630 | 2,22 | 0,48679 | 3,55 | 0,49981 | |
| 0,12 | 0,04776 | 0,62 | 0,23237 | 1,12 | 0,36864 | 1,62 | 0,44738 | 2,24 | 0,48745 | 3,60 | 0,49984 |
| 0,13 | 0,05172 | 0,63 | 0,23565 | 1,13 | 0,37076 | 1,63 | 0,44845 | 2,26 | 0,48809 | 3,65 | 0,49987 |
| 0,14 | 0,05567 | 0,64 | 0,23891 | 1,14 | 0,37286 | 1,64 | 0,44950 | 2,28 | 0,48870 | 3,70 | 0,49989 |
| 0,15 | 0,05962 | 0,65 | 0,24215 | 1,15 | 0,37493 | 1,65 | 0,45053 | 2,30 | 0,48928 | 3,75 | 0,49991 |
| 0,16 | 0,06356 | 0,66 | 0,24537 | 1,16 | 0,37698 | 1,66 | 0,45154 | 2,32 | 0,48983 | 3,80 | 0,49993 |
| 0,17 | 0,06749 | 0,67 | 0,24857 | 1,17 | 0,37900 | 1,67 | 0,45254 | 2,34 | 0,49036 | 3,85 | 0,49994 |
| 0,18 | 0,07142 | 0,68 | 0,25175 | 1,18 | 0,38100 | 1,68 | 0,45352 | 2,36 | 0,49086 | 3,90 | 0,49995 |
| 0,19 | 0,07535 | 0,69 | 0,25490 | 1,19 | 0,38298 | 1,69 | 0,45449 | 2,38 | 0,49134 | 3,95 | 0,49996 |
| 0,20 | 0,07926 | 0,70 | 0,25804 | 1,20 | 0,38493 | 1,70 | 0,45543 | 2,40 | 0,49180 | 4,00 | 0,49997 |
| 0,21 | 0,08317 | 0,71 | 0,26115 | 1,21 | 0,38686 | 1,71 | 0,45637 | 2,42 | 0,49224 | 4,05 | 0,49997 |
| 0,22 | 0,08706 | 0,72 | 0,26424 | 1,22 | 0,38877 | 1,72 | 0,45728 | 2,44 | 0,49266 | 4,10 | 0,49998 |
| 0,23 | 0,09095 | 0,73 | 0,26730 | 1,23 | 0,39065 | 1,73 | 0,45818 | 2,46 | 0,49305 | 4,15 | 0,49998 |
| 0,24 | 0,09483 | 0,74 | 0,27035 | 1,24 | 0,39251 | 1,74 | 0,45907 | 2,48 | 0,49343 | 4,20 | 0,49999 |
| 0,25 | 0,09871 | 0,75 | 0,27337 | 1,25 | 0,39435 | 1,75 | 0,45994 | 2,50 | 0,49379 | 4,25 | 0,49999 |
| 0,26 | 0,10257 | 0,76 | 0,27637 | 1,26 | 0,39617 | 1,76 | 0,46080 | 2,52 | 0,49413 | 4,30 | 0,49999 |
| 0,27 | 0,10642 | 0,77 | 0,27935 | 1,27 | 0,39796 | 1,77 | 0,46164 | 2,54 | 0,49446 | 4,35 | 0,49999 |
| 0,28 | 0,11026 | 0,78 | 0,28230 | 1,28 | 0,39973 | 1,78 | 0,46246 | 2,56 | 0,49477 | 4,40 | 0,49999 |
| 0,29 | 0,11409 | 0,79 | 0,28524 | 1,29 | 0,40147 | 1,79 | 0,46327 | 2,58 | 0,49506 | 4,45 | 0,50000 |
| 0,30 | 0,11791 | 0,80 | 0,28814 | 1,30 | 0,40320 | 1,80 | 0,46407 | 2,60 | 0,49534 | 4,50 | 0,50000 |
| 0,31 | 0,12172 | 0,81 | 0,29103 | 1,31 | 0,40490 | 1,81 | 0,46485 | 2,62 | 0,49560 | 4,55 | 0,50000 |
| 0,32 | 0,12552 | 0,82 | 0,29389 | 1,32 | 0,40658 | 1,82 | 0,46562 | 2,64 | 0,49585 | 4,60 | 0,50000 |
| 0,33 | 0,12930 | 0,83 | 0,29673 | 1,33 | 0,40824 | 1,83 | 0,46638 | 2,66 | 0,49609 | 4,65 | 0,50000 |
| 0,34 | 0,13307 | 0,84 | 0,29955 | 1,34 | 0,40988 | 1,84 | 0,46712 | 2,68 | 0,49632 | 4,70 | 0,50000 |
| 0,35 | 0,13683 | 0,85 | 0,30234 | 1,35 | 0,41149 | 1,85 | 0,46784 | 2,70 | 0,49653 | 4,75 | 0,50000 |
| 0,36 | 0,14058 | 0,86 | 0,30511 | 1,36 | 0,41309 | 1,86 | 0,46856 | 2,72 | 0,49674 | 4,80 | 0,50000 |
| 0,37 | 0,14431 | 0,87 | 0,30785 | 1,37 | 0,41466 | 1,87 | 0,46926 | 2,74 | 0,49693 | 4,85 | 0,50000 |
| 0,38 | 0,14803 | 0,88 | 0,31057 | 1,38 | 0,41621 | 1,88 | 0,46995 | 2,76 | 0,49711 | 4,90 | 0,50000 |
| 0,39 | 0,15173 | 0,89 | 0,31327 | 1,39 | 0,41774 | 1,89 | 0,47062 | 2,78 | 0,49728 | 4,95 | 0,50000 |
| 0,40 | 0,15542 | 0,90 | 0,31594 | 1,40 | 0,41924 | 1,90 | 0,47128 | 2,80 | 0,49744 | 5,00 | 0,50000 |
| 0,41 | 0,15910 | 0,91 | 0,31859 | 1,41 | 0,42073 | 1,91 | 0,47193 | 2,82 | 0,49760 | ||
| 0,42 | 0,16276 | 0,92 | 0,32121 | 1,42 | 0,42220 | 1,92 | 0,47257 | 2,84 | 0,49774 | ||
| 0,43 | 0,16640 | 0,93 | 0,32381 | 1,43 | 0,42364 | 1,93 | 0,47320 | 2,86 | 0,49788 | ||
| 0,44 | 0,17003 | 0,94 | 0,32639 | 1,44 | 0,42507 | 1,94 | 0,47381 | 2,88 | 0,49801 | ||
| 0,45 | 0,17364 | 0,95 | 0,32894 | 1,45 | 0,42647 | 1,95 | 0,47441 | 2,90 | 0,49813 | ||
| 0,46 | 0,17724 | 0,96 | 0,33147 | 1,46 | 0,42785 | 1,96 | 0,47500 | 2,92 | 0,49825 | ||
| 0,47 | 0,18082 | 0,97 | 0,33398 | 1,47 | 0,42922 | 1,97 | 0,47558 | 2,94 | 0,49836 | ||
| 0,48 | 0,18439 | 0,98 | 0,33646 | 1,48 | 0,43056 | 1,98 | 0,47615 | 2,96 | 0,49846 | ||
| 0,49 | 0,18793 | 0,99 | 0,33891 | 1,49 | 0,43189 | 1,99 | 0,47670 | 2,98 | 0,49856 |
32505
интегральная, локальная, таблицы, примеры задач
Содержание:
- Личность Пьер-Симона Лапласа
- Интегральная теорема Муавра-Лапласа
- Локальная теорема Муавра-Лапласа
- Таблицы
- Примеры решения задач
Содержание
- Личность Пьер-Симона Лапласа
- Интегральная теорема Муавра-Лапласа
- Локальная теорема Муавра-Лапласа
- Таблицы
- Примеры решения задач
Личность Пьер-Симона Лапласа
Пьер-Симон Лаплас известен в качестве ученого из Франции, который изучал и добился высоких результатов в таких научных областях, как математика, механика, физика, астрономия. Популярность исследователю принести труды в области небесной механики, анализ дифференциальных математических соотношений. Лаплас являлся одним из авторов вероятностной теории.
Популярность исследователю принести труды в области небесной механики, анализ дифференциальных математических соотношений. Лаплас являлся одним из авторов вероятностной теории.
Сложно переоценить заслуги ученого в математических и астрономических дисциплинах. Благодаря исследованиям великого научного деятеля, были качественно доработаны практически все направления перечисленных областей. Пьер-Симон Лаплас состоял во Французском Географическом обществе, шести научных академиях и королевских организациях, в числе которых Академия Петербурга (1802 г). Исследователь заслужено был удостоен звания величайшего ученого Франции. С этим перечнем великих научных деятелей можно ознакомиться при посещении Эйфелевой башни в Париже.
Интегральная теорема Муавра-Лапласа
В процессе разбора теоремы для наглядности приведем простой пример. Предположим, что имеется тысяча деталей. Пусть усредненная концентрация бракованных товаров, которыми нельзя пользоваться, составляет 10%. При этом некорректно сделать вывод о наличии 100 единиц брака в рассматриваемой основной партии, так как записанный процент является средним. Возможно, что некачественных деталей всего 101, 98 или другое число. Вычислить, каковы шансы найти в партии ровно 100 изделий с браком, можно с помощью теоремы Муавра-Лапласа в интегральном виде. Данный подход значительно упрощает и сокращает расчеты.
При этом некорректно сделать вывод о наличии 100 единиц брака в рассматриваемой основной партии, так как записанный процент является средним. Возможно, что некачественных деталей всего 101, 98 или другое число. Вычислить, каковы шансы найти в партии ровно 100 изделий с браком, можно с помощью теоремы Муавра-Лапласа в интегральном виде. Данный подход значительно упрощает и сокращает расчеты.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если число опытов равно n, то шансы на успешный результат в интервале от \({K}_{1}\) до \({K}_{2}\) определены таким соотношением: \({{P}_{n}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{{{K}_{2}}-np}{\sqrt{npq}} \right)-F\left( \frac{{{K}_{1}}-np}{\sqrt{npq}} \right)\)
В данном случае функцию F, которая включена в запись выражения, называют функцией Муавра-Лапласа. Ее расчет построен по такому принципу: \(F\left( x \right)=\frac{2}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}{{\int\limits_{0}^{x}{e}}^{-\frac{{{t}^{2}}}{2}}}dt\)
Примечание 1
Заметим, что в процессе вычислений вероятнее всего возникнут сложности с интегрированием. {2}}{2}}\right)\)
{2}}{2}}\right)\)
Таблицы
Таблица значений локальной функции Лапласа:
Таблица значений интегральной функции Лапласа:
Примеры решения задач
Задача 1
Около 5% учащихся вуза ходят в очках. Требуется проанализировать группу из 200 людей, из которых как минимум 10% в очках. Необходимо определить, какова вероятность собрать аудиторию с таким условиями.
Решение
Заметим, что в данном случае целесообразно воспользоваться теоремой Муавра-Лапласа в интегральной форме, то есть:
\({{P}_{n}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{{{K}_{2}}-np}{\sqrt{npq}} \right)-F\left( \frac{{{K}_{1}}-np}{\sqrt{npq}} \right)\)
Здесь также целесообразно воспользоваться следующим соотношением, с которым мы уже успели познакомиться в начале темы:
\(F\left( x \right)=\frac{2}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}{{\int\limits_{0}^{x}{e}}^{-\frac{{{t}^{2}}}{2}}}dt\)
Запишем условия задачи, чтобы было удобно выполнять подстановку числовых значений величин в записанную ранее формулу:
n=200
p=0,05
1-0,05=0,95
Далее определим значение \(\sqrt{npq}\):
\(\sqrt{npq}=\sqrt{200\cdot 0,05\cdot 0,95}=\sqrt{9,5}\approx 3,08\)
Затем вычислим, чему равно np:
\(np=200\cdot 0,05=10\)
Путем подстановки продолжим расчет:
\({{P}_{n}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{200-10}{3,08} \right)-F\left( \frac{20-10}{3,08} \right)= F\left( 61,7 \right)-F\left( 3,25 \right)\)
\(F\left( x \right)=\frac{2}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}{{\int\limits_{0}^{x}{e}}^{-\frac{{{t}^{2}}}{2}}}dt\)
\({{P}_{n}}\left( {{K}_{1}};{{K}_{2}} \right)\approx 0,5-0,49942=0,00058=5,8\cdot {{10}^{-4}}\)
Ответ: \(5,8\cdot {{10}^{-4}}\)
Задача 2
Театральный зал вместимостью в тысячу человек оснащен парой входов, которые доступны без исключения всем зрителям.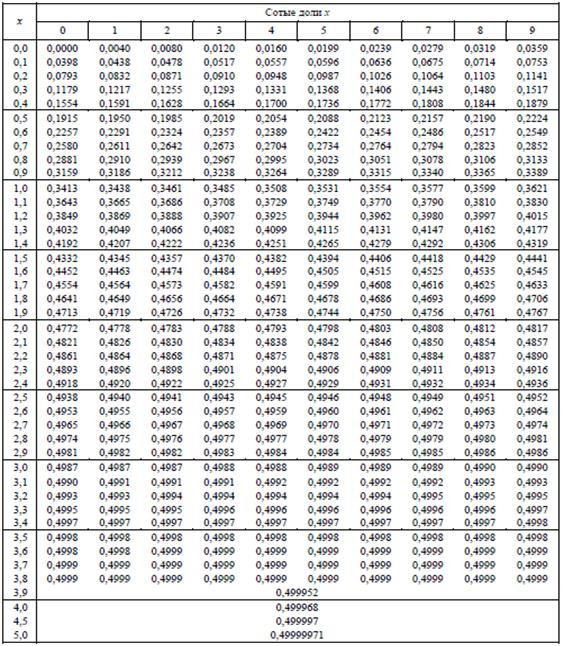 Каждый вход расположен около гардероба. Нужно вычислить количество вешалок в любом из гардеробов, чтобы с вероятностью в 0,99 каждый человек имел возможность оставить верхнюю одежду.
Каждый вход расположен около гардероба. Нужно вычислить количество вешалок в любом из гардеробов, чтобы с вероятностью в 0,99 каждый человек имел возможность оставить верхнюю одежду.
Решение
Запишем данные из условия задачи:
n=1000
\(p=\frac{1}{2}\)
\(q=1-\frac{1}{2}=\frac{1}{2}\)
Воспользуемся рассмотренными ранее формулами и выполним соответствующие вычисления:
\({{P}_{1000}}\left( {{K}_{1}};{{K}_{2}} \right)=0,99\)
Заметим, что при определении интервала значений событий напрашивается следующий вывод:
\({{K}_{1}}=0\)
В таком случае необходимо вычислить, чему соответствует \({K}_{2}\). Обратимся к формулировке теоремы Муавра-Лапласса:
\({{P}_{1000}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{{{K}_{2}}-np}{\sqrt{npq}} \right)-F\left( \frac{{{K}_{1}}-np}{\sqrt{npq}} \right)\)
Отметим, что в данном случае справедливым является следующее равенство:
\(np=1000\cdot \frac{1}{2}=500\)
В результате:
\(\sqrt{npq}=\sqrt{1000\cdot \frac{1}{2}\cdot \frac{1}{2}}=\sqrt{250}=5\sqrt{10}=15,8\)
Путем подстановки численных значений, которые были определены ранее, учитывая, что \({K}_{1}=0\), получим следующее соотношение:
\({{P}_{1000}}\left( {{K}_{1}};{{K}_{2}} \right)\approx F\left( \frac{{{K}_{2}}-500}{15,8} \right)-F\left( \frac{0-500}{15,8} \right)=0,99\)
Рассчитаем значение функции по доказательству:
\(F\left( \frac{-500}{15,8} \right)=-F\left( 31,6 \right)=0,5\)
Таким образом:
\(F\left( \frac{{{K}_{2}}-500}{15,8} \right)+0,5=0,99\)
\(F\left( \frac{{{K}_{2}}-500}{15,8} \right)=+0,49\)
С помощью табличной формы определим близкие к 0,49 значения функции.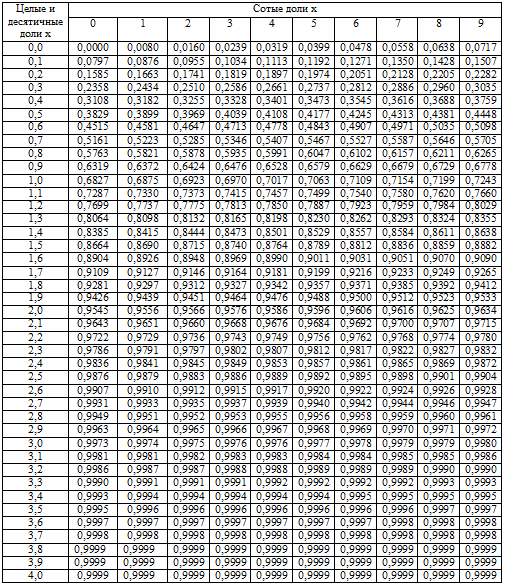 Таковым соответствуют точки 2,32 и 2,34. Выполним вычисления:
Таковым соответствуют точки 2,32 и 2,34. Выполним вычисления:
\(F\left( 2,32 \right)=0,48983\)
\(F\left( 2,34 \right)=0,49036\)
\(\frac{{{K}_{2}}-500}{15,8}=2,33\)
\({{K}_{2}}-500=2,33\cdot 15,8\)
\({{K}_{2}}-500=36,8\)
\({{K}_{2}}\approx 536,8=537\)
Ответ: 537.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Поиск по содержимому
pr.probability — Количественная теорема де Муавра–Лапласа (запрос ссылки)
спросил
Изменено 8 лет, 6 месяцев назад
Просмотрено 2к раз
$\begingroup$
Классическая теорема де Муавра-Лапласа утверждает, что мы можем аппроксимировать нормальное распределение дискретным биномиальным распределением: 92 / (2npq)}.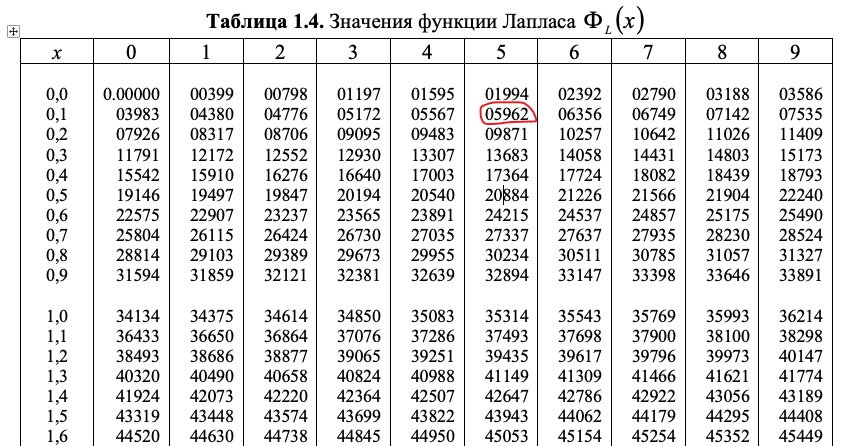 $$
$$
У меня такой вопрос: существуют ли в литературе более точные количественные версии этой теоремы? Есть ли хорошие оценки, как измерить ошибку? К сожалению, я не знаком с предметом, но мне нужен результат такого типа.
Конечно, всегда есть возможность просмотреть существующие доказательства и проверить детали, а также превратить их из «мягких» в «жесткие», но я подозреваю, что это уже должно быть сделано. А может это и не оптимально, может есть хорошие доступные способы.
Может ли кто-нибудь указать мне хорошую ссылку в этом направлении?
- ссылка-запрос
- пр.вероятность
- на.численный-анализ
$\endgroup$
6
$\begingroup$
Во-первых, я думаю, что под «качественным» вы подразумеваете «количественный». Во-вторых, хотя по количественным версиям центральной предельной теоремы имеется огромная литература, канонические результаты можно найти в томе 2 Феллера.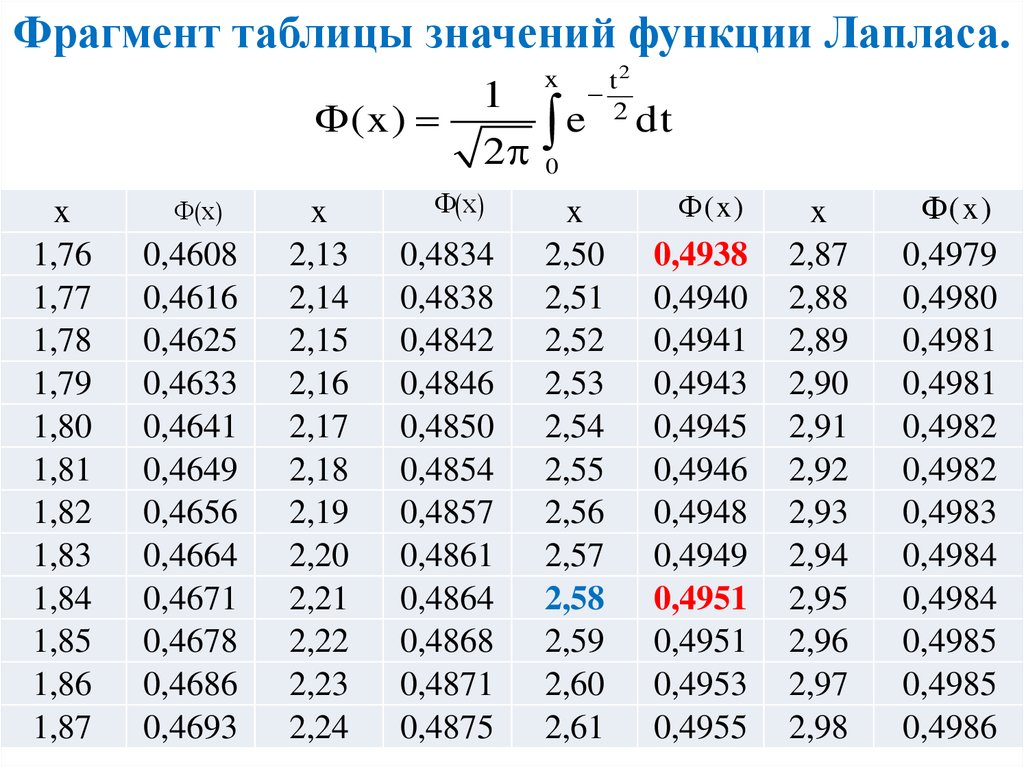 Для центра распределения есть теорема Берри-Эссеена, для хвостов — большие теория отклонений, введение в которую также охвачено Феллером.
Для центра распределения есть теорема Берри-Эссеена, для хвостов — большие теория отклонений, введение в которую также охвачено Феллером.
РЕДАКТИРОВАТЬ Если вас действительно волнует конкретная аппроксимация бинома нормальным (или наоборот ), вы просто говорите о более высоких членах в приближении Стирлинга к факториалу (и, следовательно, к биномиальным коэффициентам). Вы можете прочитать все об этом, например, в Concrete Math Грэма/Кнута/Паташника.
$\endgroup$
4
$\begingroup$
Вас может заинтересовать эта статья (очень точная оценка, очевидно, упущенная из виду большинством людей!)
Дж. Э. Литтлвуд, О вероятности хвоста двучлена дистрибьюция, админ. заявл. Проб. 1 (1969) 43–72.
пересмотрено и исправлено Маккеем
Брендан Д.
Маккей, Об оценке Литтлвуда для бинома Распространение, Достижения в области прикладной теории вероятностей, Vol. 21, № 2 (июнь, 1989), стр. 475-478
$\endgroup$
$\begingroup$
Вам просто нужна локальная предельная теорема для суммы i.i.d. Случайные величины Бернулли. Стандартным справочником (не только по Бернулли с.в.!) являются «Суммы независимых случайных величин» Петрова, в частности глава VII, §3.
$\endgroup$
$\begingroup$
http://www.johndcook.com/normal_ приблизительно_to_binomial.html
$\endgroup$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
теория вероятностей — Нахождение оценки ошибки для теоремы Де Муавра – Лапласа
спросил
Изменено 4 года, 9 месяцев назад
Просмотрено 1к раз
$\begingroup$
Контекст моего вопроса: В одной части моей диссертации я пытаюсь найти верхнюю границу ошибки в нормальном приближении биномиального распределения, следуя стандартному доказательству теоремы Де Муавра–Лапласа с помощью формулы Стирлинга. Для конкретики: пусть $B_n$ имеет биномиальное распределение, а $N$ имеет стандартизированное нормальное распределение. Я хочу найти верхнюю границу для $$\epsilon_n = \sup_{a Я хочу сравнить эту ошибку с самой известной оценкой ошибки теоремы Берри-Эсси для биномиального распределения. Мой вопрос: Знаете ли вы какое-нибудь доказательство в учебнике/статье/статье, где теорема Муавра и Лапласа доказывается с помощью формулы Стирлинга и оценивается полная ошибка? Значение любых встречающихся констант в оценке ошибки также должно быть рассчитано. Можете ли вы указать мне на это доказательство? Обновление: Я повторно задал вопрос в МО, см. https://mathoverflow.net/questions/219253/finding-an-error-estimation-for-the-de-moivre-laplace-theorem-with-stirlings- $\endgroup$ 3 $\begingroup$ Фактически, из статьи Балаша и Тота следует, что
$$
\sup_{a_n\le c $\endgroup$ 5 $\begingroup$ (Примечание:
Я ошибся автором.
Теперь это исправлено.) IIRC,
Книга Успенского «Введение в математическую вероятность».
(опубликовано, возможно, в 1937 г.)
имеет доказательство
Центральная предельная теорема
с явными ограничениями на
срок ошибки. Результат довольно сложный. $\endgroup$ 3 $\begingroup$ Наилучшие двусторонние неравенства для биномиальной функции распределения можно найти в
Теория Вероятность. Appl., 57(3), 539–544. (6 страниц)
Полное доказательство универсальных неравенств для функции распределения биномиального закона
Опубликовано онлайн: 04 сентября 2013 г. Пока я нашел только доказательство, которое показывает, что $\epsilon_n \in O\left(\frac 1{\sqrt n}\right)$. См. это доказательство Мартона Балаша и Балинта Тота (которые также только что рассмотрели $\left|\mathcal P\left(a\le \frac{B_n-np}{\sqrt{np(1-p)}} \le b\ right)-\mathcal P(a \le N \le b)\right|$ без супремума). Другие доказательства вообще не исследуют ошибку (см., например, это доказательство в Википедии).
Пока я нашел только доказательство, которое показывает, что $\epsilon_n \in O\left(\frac 1{\sqrt n}\right)$. См. это доказательство Мартона Балаша и Балинта Тота (которые также только что рассмотрели $\left|\mathcal P\left(a\le \frac{B_n-np}{\sqrt{np(1-p)}} \le b\ right)-\mathcal P(a \le N \le b)\right|$ без супремума). Другие доказательства вообще не исследуют ошибку (см., например, это доказательство в Википедии).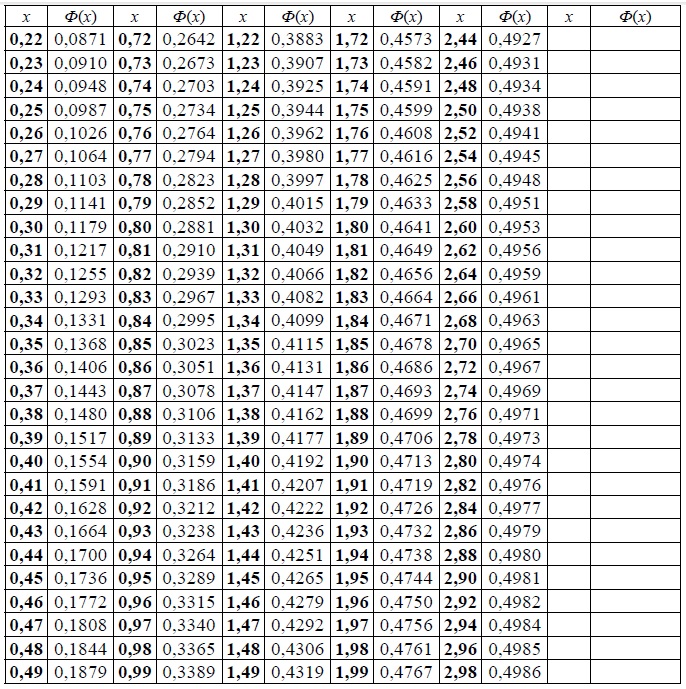

 Маккей, Об оценке Литтлвуда для бинома
Распространение, Достижения в области прикладной теории вероятностей, Vol. 21, № 2 (июнь,
1989), стр. 475-478
Маккей, Об оценке Литтлвуда для бинома
Распространение, Достижения в области прикладной теории вероятностей, Vol. 21, № 2 (июнь,
1989), стр. 475-478