Масштаб. Решение задач — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
ТЕМА
МАСШТАБ
Для изучения темы: «Масштаб» нам
потребуется ответить на ряд вопросов
1. Что такое отношение?
2. Что такое пропорция?
3. Сформулируйте основное свойство пропорции.
4. Где вы уже встречались с «Масштабом»?
5. Сколько сантиметров в одном метре; сколько
сантиметров в одном километре; сколько метров
в одном километре?
Отношение длины отрезка на карте
к длине соответствующего отрезка
на местности называют масштабом
карты.
МАСШТАБ
длина отрезка на карте
длина отрезка на местности
ПРИМЕР
масштаб
В рассмотренном примере масштаб карты
равен 1 : 25 000. Говорят, что карта сделана
в масштабе одна двадцатипятитысячная.
ЗАДАЧА
Длина отрезка на карте 3 см. Найдём длину
соответствующего отрезка на местности, если
масштаб карты 1 : 1 000 000.
Решение:
Обозначим длину отрезка на местности (в сантиметрах)
буквой x и найдём отношение длины отрезка на карте к
длине отрезка на местности: 3 : x, которое и будет равно
масштабу карты.
Значит, 3 : x = 1 : 1 000 000. (получаем пропорцию)
Воспользовавшись основным свойством пропорции находим
x = 3 · 1 000 000 = 3 000 000.
Но 3 000 000 см = 30 000 м = 30 км.
Ответ: длина отрезка на местности 30 км.
Страница 135, № 826
Длина железнодорожной магистрали 3140 км. Какой длины
получится линия, изображающая эту магистраль на карте,
сделанной в масштабе:
а) 1 : 10 000 000,
б) 1 : 2 000 000?
Решение задачи под буквой (а):
Пусть x — длина линии, изображающую эту магистраль на карте.
Переведём 3140 км в см.
3 140 км = 3 140 000 м = 314 000 000 см.
Составим отношение длины линии, изображающую магистраль на карте
к длине этой магистрали на соответствующей местности:
x : 314 000 000.
Прировняем полученное отношение к масштабу:
x : 314 000 000 = 1 : 10 000 000. (получаем пропорцию).
Воспользуемся основным свойством пропорции:
x · 10 000 000 = 314 000 000 · 1.
Решив уравнение получаем x = 31,4 см.
Ответ: длина линии, изображающую железнодорожную магистраль на
карте равна 31,4 см. (задание под буквой (б) решите самостоятельно)!
ДОМАШНЕЕ ЗАДАНИЕ
№ 822
(в № 822 изобразить отрезок в тетради)
№ 824
№ 843
(№ 843 решать по примеру задачи на 5-ом слайде)
№ 844
(выполнять № 844 по примеру № 826)
English Русский Правила
Урок 87. Масштаб | Поурочные планы по математике 6 класс
Цели: ввести понятие масштаба; учить читать масштаб; решать задачи, связанные с понятием масштаба.
Информация для учителя
Задачи, связанные с понятием масштаба, показывают одно из практических применений понятия отношения.
Ход урока
I. Организационный момент
II. Анализ контрольной работы
1. Сообщить результаты контрольной работы.
2. Решить задания, вызвавшие затруднения у учащихся.
III. Устный счет
1. Выразите в километрах:
а) 32 000 000 см; б) 600 000 см; в) 32 000 см; г) 5 000 000 см.
— Что нужно сделать, чтобы выразить данные величины в км? (Так как 1 км = 100 000 см, то нужно разделить на 100 000.)
2. Выразите в метрах:
а) 32 000 000 см; б) 600 000 см; в) 32 000 см; г) 5 000 000 см.
IV. Индивидуальная работа
1 карточка
1. Решить уравнение:
2. На изготовление 14 деталей расходуется 16,8 кг металла. Сколько потребуется металла на изготовление 27 таких деталей?
2 карточка
1. Решить уравнение:
2. Для перевозки угля автомашине грузоподъемностью 6 т надо сделать 10 рейсов.
Сколько придется сделать рейсов автомашине, грузоподъемность которой на 2 т меньше, чтобы перевезти этот груз?
V. Сообщение темы урока
— Сегодня мы познакомимся с масштабом. Именно понятие масштаба показывает нам практическое применение отношений.
VI. Изучение нового материала
1. Подготовительная работа.
— Составьте отношения: а) 1 см к 4000 м; б) 1 см к 120 м; в) 1 см к 10 000 км; г) 1 см к 25 см.
— Что нужно сначала сделать? (Перевести в одинаковые единицы измерения.)
— Давайте все величины запишем в сантиметрах.
Решение:
а) 1 : 400 000; б) 1 : 12 000; в) 1 : 1 000 000 000; г) 1 : 25.
— Мы с вами знаем, что участки земной поверхности, детали машин и многое другое изображают на бумаге в уменьшенном виде.
— Если на карте, плане или чертеже встретите такие отношения, то это масштаб карты, плана или чертежа.
2. Работа над новой темой.
Определение. Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.
Аналогично можно сказать о чертеже или плане.
Масштаб — желз размерный или мерило, мерник, размерник, мера линейная, принятая для чертежа или иной работы. (Из толкового словаря В. И. Даля.)
— Объясните, что обозначают данные масштабы.
Задание: а) проговаривает учитель, дальше учащиеся объясняют по нескольку раз один и тот же масштаб.
Ответ:
а) Если масштаб карты 1 : 400 000, то на этой карте длина каждого отрезка уменьшена в 400 000 раз. На такой карге расстояние, равное 4 км, будет изображаться отрезком в 1 см.
Масштаб карты Говорят, что карта сделана в масштабе одна четырехсоттысячная.
б) Если масштаб карты 1 : 12 000, то на этой карте длина каждого отрезка уменьшена в 12 000 раз. На такой карте расстояние, равное 120 м, будет изображаться отрезком в 1 см.
Масштаб карты Говорят, что карта сделана в масштабе одна двенадцатитысячная.
3. Работа с учебником.
— Самостоятельно разберите задачу 1 на стр. 134.
— Составьте похожую задачу.
Задача. Длина отрезка на карте 15 см. Найдите длину соответствующего отрезка на местности, если масштаб карты 1 : 10 000.
— Что означает масштаб 1 : 10 000?
— Давайте ее решим, оформив краткую запись в виде таблицы.
Решение:
Пусть х (м) — расстояние на местности.
| Расстояние | Масштаб |
На карте На местности |
15 : х = 1 : 10 000
х = 150 000
150 000 см = 1500 = 1,5 км
(Ответ: 1,5 км расстояние на местности.)
VII. Физкультминутка
VIII. Закрепление изученного материала
1. Практическая работа.
№ 820 стр. 134 (под руководством учителя).
— Прочитайте задание. Можем сразу найти расстояние?
— Что нужно знать сначала? (Длину отрезка на карте.
— Как узнать длину отрезка на карте? (Измерить по карте с помощью линейки.)
— Измерьте расстояние на карте. Что означает масштаб 1 : 100 000? (1 см на карте равен 100000 см или 1000 м или 1 км на местности.)
— Запишем решение.
Решение:
Пусть х м — расстояние на местности.
| Расстояние | Масштаб |
На карте На местности |
3 : х = 1 : 100 000
х = 300 000
300 000 см = 3000 м = 3 км
(Ответ: 3 км — расстояние на местности.)
2. Работа над задачей.
№ 821 стр. 134.
— Прочитайте задачу.
— Что известно? Что надо узнать?
— Что означает данный масштаб? (1 см на карте равен 1 000 000 см, или 10 000 м, или 10 км на местности.)
Решение:
Пусть х м — расстояние на местности.
| Расстояние | Масштаб |
На карте На местности |
8,5 : х = 1 : 1 000 000
х = 8,5 · 1 000 000
х = 8 500 000
8 500 000 см = 85 км
(Ответ: 85 км на местности.)
IX. Работа над задачей
№ 835 стр. 136 (один ученик решает на обратной стороне доски, остальные — в тетрадях, самопроверка).
— Прочитайте задачу.
— Составьте краткую запись.
— Решите самостоятельно задачу, составив пропорцию.
Решение:
Пусть х кг — картофеля для 12 порций.
| Количество порций | Масса картофеля |
1 раз 2 раз | 4 п. 12 п. | 0,44 кг х кг |
1,32 кг — картофеля для 12 порций.
(Ответ: 1,32 кг.)
— Кто закончил раньше, помогите товарищу, который с помощью сигнальной карточки зовет вас на помощь.
X. Тест (7 мин)
Вариант I
1. Какая из пропорций верна: а) 2 : 6 = 5 : 15; б) 7 : 8 = 3 : 4; в) 7 : 14 = 8: 15.
2. Неизвестный член пропорции 24 : х = 12 : 4
а) х = 5; б) х = 8; в) х = 11.
3. Неизвестный член пропорции:
а) х = 12; б) х = 8; в) х = 3.
Вариант II
1. Какая из пропорций верна: а) 5 : 7 = 10 : 15; б) 4 : 7 = 8 : 14; в) 4 : 7 = 7 : 15.
2. Неизвестный член пропорции 28 : х = 36 : 9
а) х = 7; б) х = 9; в) х = 6.
3. Неизвестный член пропорции:
а) х = 5; б) х = 9; в) х = 8.
XI. Подведение итогов урока
— Что называют масштабом карты?
— Где в практической деятельности человек пользуется этим понятием?
— Чему равен масштаб чертежа, если на нем детали увеличены в 5 раз? Уменьшены в 50 раз?
Домашнее задание
№ 842, 844, 846 (а) стр.
137. По желанию № 840 стр. 137.
Решение задач, связанных с чертежами геометрических фигур в масштабе: CCSS.Math.Content.7.G.A.1
All Common Core: Math Resources для 7-го класса
7 диагностических тестов 110 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Common Core: Справка по математике для 7-го класса » Геометрия » Решение задач, связанных с чертежами геометрических фигур в масштабе: CCSS.Math.Content.7.G.A.1
Представленный прямоугольник представляет собой масштабированный чертеж прямоугольного двора. Учитывая масштаб, какова фактическая длина двора?
Возможные ответы:
Правильный ответ:
Объяснение:
В этом вопросе нам нужно найти реальный размер длины прямоугольника, поэтому сначала нам нужно вспомнить, какая сторона считается длиной прямоугольника.
В этом примере длина прямоугольника . Мы можем установить пропорцию для определения фактической длины прямоугольника .
Затем мы перемножаем и находим:
Сообщить об ошибке
Представленный прямоугольник представляет собой масштабный чертеж прямоугольного двора. Учитывая масштаб, какова фактическая ширина двора?
Возможные ответы:
Правильный ответ:
Объяснение:
В этом вопросе нам предлагается определить фактический размер ширины прямоугольника, поэтому сначала нам нужно вспомнить, какая сторона считается шириной прямоугольника.
В этом примере ширина прямоугольника равна . Мы можем установить пропорцию для определения фактической длины прямоугольника .
Затем мы умножаем крест и находим:
Сообщить об ошибке
Представленный прямоугольник представляет собой масштабированный чертеж прямоугольного двора.
Учитывая масштаб, какова фактическая ширина двора?
Возможные ответы:
Правильный ответ:
Объяснение:
В этом вопросе нам предлагается определить фактический размер ширины прямоугольника, поэтому сначала нам нужно вспомнить, какая сторона считается шириной прямоугольника.
В этом примере ширина прямоугольника равна . Мы можем установить пропорцию для определения фактической длины прямоугольника .
Затем мы перемножаем и находим:
Сообщить об ошибке
Представленный прямоугольник представляет собой масштабный чертеж прямоугольного двора. Учитывая масштаб, какова фактическая длина двора?
Возможные ответы:
Правильный ответ:
Объяснение:
В этом вопросе нам нужно найти реальный размер длины прямоугольника, поэтому сначала нам нужно вспомнить, какая сторона считается длиной прямоугольника.
В этом примере длина прямоугольника . Мы можем установить пропорцию для определения фактической длины прямоугольника .
Затем мы умножаем крест и находим:
Сообщить об ошибке
Представленный прямоугольник представляет собой масштабированный чертеж прямоугольного двора. Учитывая масштаб, какова фактическая ширина двора?
Возможные ответы:
Правильный ответ:
Объяснение:
В этом вопросе нам предлагается определить фактический размер ширины прямоугольника, поэтому сначала нам нужно вспомнить, какая сторона считается шириной прямоугольника.
В этом примере ширина прямоугольника равна . Мы можем установить пропорцию для определения фактической длины прямоугольника .
Затем мы перемножаем и находим:
Сообщить об ошибке
Представленный прямоугольник представляет собой масштабный чертеж прямоугольного двора.
Учитывая масштаб, какова фактическая длина двора?
Возможные ответы:
Правильный ответ:
Объяснение:
В этом вопросе нам нужно найти реальный размер длины прямоугольника, поэтому сначала нам нужно вспомнить, какая сторона считается длиной прямоугольника.
В этом примере длина прямоугольника . Мы можем установить пропорцию для определения фактической длины прямоугольника .
Затем мы умножаем крест и находим:
Сообщить об ошибке
Представленный прямоугольник представляет собой масштабированный чертеж прямоугольного двора. Учитывая масштаб, какова фактическая ширина двора?
Возможные ответы:
Правильный ответ:
Объяснение:
В этом вопросе нам предлагается определить фактический размер ширины прямоугольника, поэтому сначала нам нужно вспомнить, какая сторона считается шириной прямоугольника.
В этом примере ширина прямоугольника равна . Мы можем установить пропорцию для определения фактической длины прямоугольника .
Затем мы перемножаем и находим:
Сообщить об ошибке
Представленный прямоугольник представляет собой масштабный чертеж прямоугольного двора. Учитывая масштаб, какова фактическая длина двора?
Возможные ответы:
Правильный ответ:
Объяснение:
В этом вопросе нам нужно найти реальный размер длины прямоугольника, поэтому сначала нам нужно вспомнить, какая сторона считается длиной прямоугольника.
В этом примере длина прямоугольника . Мы можем установить пропорцию для определения фактической длины прямоугольника .
Затем мы умножаем крест и находим:
Сообщить об ошибке
Представленный прямоугольник представляет собой масштабированный чертеж прямоугольного двора.
Учитывая масштаб, какова фактическая ширина двора?
Возможные ответы:
Правильный ответ:
Объяснение:
В этом вопросе нам предлагается определить фактический размер ширины прямоугольника, поэтому сначала нам нужно вспомнить, какая сторона считается шириной прямоугольника.
В этом примере ширина прямоугольника равна . Мы можем установить пропорцию для определения фактической длины прямоугольника .
Затем мы перемножаем и находим:
Сообщить об ошибке
Представленный прямоугольник представляет собой масштабный чертеж прямоугольного двора. Учитывая масштаб, какова фактическая длина двора?
Возможные ответы:
Правильный ответ:
Объяснение:
В этом вопросе нам нужно найти реальный размер длины прямоугольника, поэтому сначала нам нужно вспомнить, какая сторона считается длиной прямоугольника.
В этом примере длина прямоугольника . Мы можем установить пропорцию для определения фактической длины прямоугольника .
Затем мы умножаем крест и находим:
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах 110 практических тестов Вопрос дня Карточки Обучение по концепции
Марк Рубин — Шкала решения проблем
Характеристики пункта
Пять пунктов измеряют предпочтение самостоятельного решения проблем (пункты 1, 3, 4, 8 и 9).), а пять измеряют предпочтение взаимозависимого решения проблем (пункты 2, 5, 6, 7, 10). Два пункта были взяты из шкалы Индивидуализм-Коллективизм Триандиса и др. (1986) (пункты 1 и 8), а один был основан на Oyserman, Coon, and Kemmelmeier (2002, стр. 9; пункт 6). Остальные элементы были созданы мной лично.
Подсчет баллов
Исследователи должны поменять местами ответы участников кода либо на независимые вопросы решения проблем, либо на взаимозависимые вопросы решения проблем, а затем вычислить средний балл по всем 10 пунктам. Решение о том, какой набор элементов реверсировать код, зависит от того, хотите ли вы представить независимое решение проблем с высокими оценками и взаимозависимое решение проблем с низкими оценками или наоборот. Например, если вы переоцените ответы на пять взаимозависимых вопросов, то более высокие баллы по шкале будут означать, что у участников более независимый стиль решения проблем.
Надежность и валидность
Rubin et al. (2012) сообщили о доказательствах надежности и достоверности Версии 1 IIPSS. Таким образом, шкала имеет хорошую надежность, однофакторную структуру (собственное значение = 3,96) и хорошую внутреннюю согласованность (αs = 0,77 и 0,80).
Шкала также имеет хорошую конвергентную валидность. Он имеет небольшие и средние корреляции со шкалой реляционно-взаимозависимого самопонимания Кросса и др. (2000) и шкалой экстраверсии Голдберга и др. (2006). Наконец, шкала имеет хорошую прогностическую валидность. Рубин и др. обнаружил, что IIPSS предсказал вероятность того, что участники, по их собственным словам, будут (а) искать в Интернете решение проблемы в университете (т. Е. Самостоятельное решение проблемы) и (б) попросить другого студента помочь им с университетом. проблема (т. е. взаимозависимое решение проблемы). Сантакар и Рубин (2022) недавно представили дополнительные доказательства надежности и достоверности шкалы.
Анализ IIPSS
Существует два подхода к анализу данных IIPSS: (1) рассматривать его как непрерывную переменную в диапазоне от высокой независимости и низкой взаимозависимости, через сочетание обоих типов решения проблем, до низкой независимость и высокая взаимозависимость.
(2) Определите некую точку отсечения, выше и ниже которой вы классифицируете людей как независимых лиц, решающих проблемы, и взаимозависимых лиц, решающих проблемы.
Непрерывный подход является более мощным из двух подходов. Например, вы можете включить IIPSS и производительность на рабочем месте в корреляционный или регрессионный анализ и обнаружить, что чем выше баллы IIPSS отдельных лиц, тем выше их производительность. Если IIPSS закодирован с высокими баллами, указывающими на более независимое решение проблем, то вы можете сделать вывод, что независимые решатели проблем работают лучше, чем взаимозависимые решатели проблем в этой рабочей ситуации. Обратите внимание, что, хотя мы рассматриваем здесь IIPSS как непрерывную переменную, все же имеет смысл говорить о «независимых решателях проблем» и «взаимозависимых решателях проблем» так же, как имеет смысл говорить о «бритых» и «бородатые» лица, хотя между ними нет резкого разрыва (Thouless, 1930).
Категориальный подход менее эффективен, но часто необходим.
Например, если вы рассматриваете независимо-взаимозависимое решение проблем как модераторскую переменную и хотите продемонстрировать, что эффект имеет место для независимых решателей проблем, но не для взаимозависимых решателей проблем, вы можете разделить свою выборку участников исследования на на одно стандартное отклонение выше и ниже среднего значения IIPSS и сравните эффект в каждой из этих двух групп (например, Aiken & West, 199).1). Хотя он популярен, проблема с этим +/- 1 стандартным отклонением заключается в том, что вы теряете большую статистическую мощность, потому что вы исключаете из анализа около 68% ваших участников. Так, например, при выборке из 100 участников этот подход приведет только к 16 участникам в независимой группе решения проблем и 16 участникам во взаимозависимой группе решения проблем. Чтобы свести к минимуму потери выборки, вы можете использовать более свободную точку отсечки. Так, например, вы можете использовать 25-й и 75-й процентили в качестве точек отсечки, чтобы обеспечить большее количество участников в каждой группе (например, n s = 25 вместо 16; Хейс, 2013).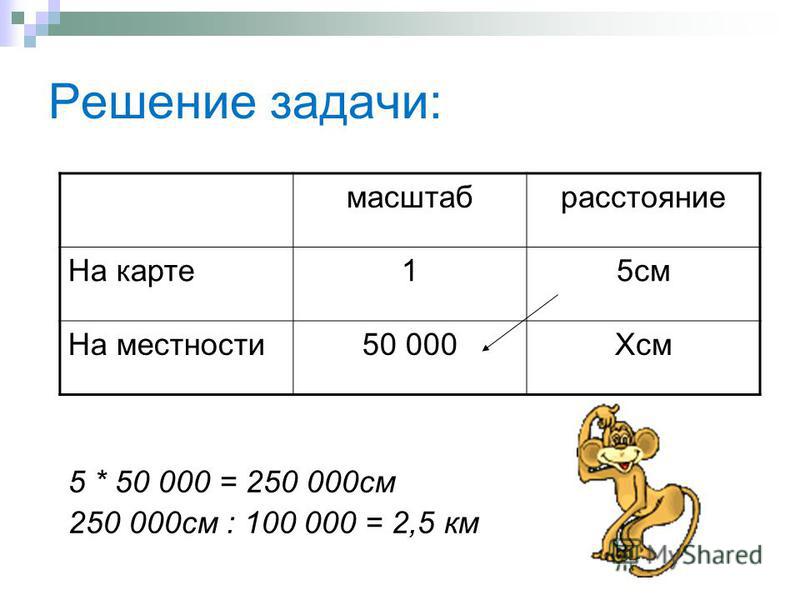
Последние исследования
Виейра (2013) обнаружил, что IIPSS связан с потребностью потребителей прикасаться к предметам перед покупкой.
Seward and Harris (2016) использовали IIPSS в своем расследовании обращения за помощью, связанного с самоубийством.
Akinbobola, Uzonwanne, and Udechukwu (2018) обнаружили, что IIPSS обладает хорошей внутренней надежностью и предсказывает ролевые показатели неакадемического персонала нигерийского университета.
Дорган (2018) не обнаружил существенной разницы в баллах IIPSS между игроками в видеоигры, которые предпочитали играть в однопользовательские, а не многопользовательские игры.
Александр и Беклинг рассмотрели IIPSS в отношении производительности выпускников на рабочем месте.
Эйнсворт и Олдфилд (2019, таблица 3) обнаружили, что среди выборки британских учителей самостоятельное решение проблем имело значительную положительную связь с воспринимаемым конфликтом между убеждениями и практикой преподавания и значительные отрицательные связи с эмоциональным интеллектом, жизненными ориентация и забота о себе.
Санаткар и Рубин (2020) обнаружили, что открытость опыту смягчает связь между IIPSS и невротизмом: самостоятельное решение проблем было связано с высоким уровнем невротизма, но только при низком уровне открытости, возможно, потому, что низкая открытость делает независимым люди, решающие проблемы, чувствуют себя неуверенно в своих способностях решать проблемы.
Разрешения
IIPSS можно использовать бесплатно в исследовательских целях. Разрешение не требуется. Однако масштаб не может быть воспроизведен в коммерческих целях.
Печатная копия
Нажмите здесь , чтобы загрузить печатную копию шкалы для использования в бумажно-карандашных обследованиях.
Ссылка на IIPSS
Первое сообщение о IIPSS было опубликовано в журнальной статье, в которой исследовалась социальная интеграция иммигрантов.
Чтобы обратиться к IIPSS, используйте следующие ссылки:
Rubin, M., Watt, S.E., & Ramelli, M. (2012). Социальная интеграция иммигрантов как функция ориентации на подход-избегание и стиль решения проблем. Международный журнал межкультурных отношений, 36, 498-505. http://dx.doi.org/10.1016/j.ijintrel.2011.12.009 Самозаархивированная версия этой журнальной статьи доступна здесь .
Санаткар, С., и Рубин, М. (2022). Надежность и валидность шкалы независимо-взаимозависимого стиля решения проблем. Международный журнал психологии . http://doi.org/10.1002/ijop.12878
Ссылки
Айкен, Л. С. и Уэст, С. Г. (1991). Множественная регрессия: тестирование и интерпретация взаимодействий. Ньюбери-Парк: Сейдж.
Кросс, С.Э., Бэкон, П.Л., и Моррис, М.Л. (2000). Реляционно-взаимозависимая самоинтерпретация и отношения.