Разработка урока по математике в 10 классе «Метод математической индукции»
Главная / Старшие классы / Алгебра
Скачать
18.35 КБ, 862575.docx Автор: Бугакова Марина Викторовна, 1 Апр 2015
Цель урока — рассмотреть суть метода математической индукции. Научить применять его при доказательстве некоторых утверждений.
Автор: Бугакова Марина Викторовна
Похожие материалы
| Тип | Название материала | Автор | Опубликован |
|---|---|---|---|
| документ | Разработка урока по математике в 10 классе «Метод математической индукции» | Бугакова Марина Викторовна | 1 Апр 2015 |
| документ | Разработка урока по математике в 10 классе «Метод математической индукции» | Бугакова Марина Викторовна | 1 Апр 2015 |
| презентация | Презентация урока физики в 11 классе по теме «Явление электромагнитной индукции . Магнитный поток. Правило Ленца. Закон электромагнитной индукции» Диск | Тишутина Валентина Ивановна | 21 Мар 2015 |
| разное | Методическая разработка урока по математике в 10 классе по теме:»Решение иррациональных неравенств» | Волосожар Марина Ивановна | 1 Апр 2015 |
| разное | Методическая разработка: Метод математической индукции | Гиниятуллин Айрат Минуллович | 16 Фев 2016 |
| презентация | Разработка урока по математике в 9 классе , по теме «Геометрическая прогрессия» | Соколова Елена Сергеевна | 10 Мая 2015 |
| презентация, документ | Научно-исследовательская работа по теме «Метод математической индукции» | Бондаренко Ольга Валентиновна | 4 Апр 2015 |
| документ | Бакланова Анастасия Викторовна | 9 Апр 2015 | |
| документ | Разработка урока по математике в 1 классе «Взаимосвязь компонентов вычитания» | Посредникова Вера Васильевна | 10 Апр 2015 |
| документ | Методическая разработка урока по математике в 1 классе УМК «Школа 2100» по теме «Решение задач изученных видов. Закрепление навыков счета в пределах 10″ | Елена Семеновна Ганичева | 30 Мар 2015 |
| документ | Разработка урока математики в 1 классе по теме: «Вычитание из числа 10. Состав числа 10.» | Ушакова Лариса Викторовна | 30 Мар 2015 |
| разное | Разработка урока по геометрии в 11 классе «Метод координат при решении стереометрических задач» | Уртюкова Мая Андреевна | 23 Сен 2015 |
| разное | Разработка урока по математике в 3 классе «Умножение числа 2» Ход урока. Ход урока. | Кузнецова Марина Егоровна | 15 Дек 2015 |
| разное | метод математической индукции | Барабаш Ирина Викторовна | 11 Апр 2015 |
| разное | Метод математической индукции | Гиниятуллин Айрат Минуллович | 16 Фев 2016 |
| презентация, документ | разработка урока «Формулы приведения» в 10 классе | Цыренова Цыпелма Жадамбаевна | 21 Мар 2015 |
| документ | Разработка урока по литературе в 10 классе «Раскольников и Соня Мармеладова. «Правда» Сони. Анализ эпизода» | Матвеева Елена Юрьевна | 20 Мар 2015 |
| документ | Разработка урока по всемирной истории в 10 классе «Россия в 1917-1939 гг.» | Макарова Елена Геннадьевна | 21 Мар 2015 |
| документ | Разработка урока по всемирной истории в 10 классе «Франция в 1918-1939 гг.» | Макарова Елена Геннадьевна | 21 Мар 2015 |
| документ | Разработка урока в 10 классе по теме: «Перевод целых чисел из одной системы счисления в другую» | Спичкова Наталья Викторовна | 21 Мар 2015 |
| документ | Разработка открытого урока по информатике в 10 классе «Создание видеороликов в программе Киностудия Live» | Иванова Валентина Владимировна | 21 Мар 2015 |
| документ | «Способы словообразования в русском языке» (разработка урока по русскому языку в 10 классе) | Матвеева Мария Ивановна | 9 Апр 2016 |
| разное | Методическая разработка урока по физике в 10 классе по теме «Первый закон термодинамики» | Вилкова Надежда Викторовна | 21 Мар 2015 |
| презентация, документ | Методическая разработка урока по информатике в 10 классе. Подготовка к зачету по разделу «Коммуникационные технологии» — 2014 г. | Носарева Юлия Александровна | 21 Мар 2015 |
| документ | Конспект открытого урока по математике в 1 классе. Тема: «Сложение и вычитание в пределах 10» | Гусельникова Валентина Ильинична | 16 Ноя 2015 |
| План-конспект урока по математике в 10 классе по теме: «Преобразование тригонометрических выражений» | Назарова Маргарита Алексеевна | 1 Апр 2015 | |
| документ | Методическая разработка урока геометрии в 10 классе школы глухих «Решение задачи разными способами». Методическая разработка урока геометрии в 10 классе школы глухих. Первый способ | Богданова Вера Ивановна | 21 Мар 2015 |
| разное | Методическая разработка урока по обществознанию в 10 классе «Единство свободы и ответственности личности» | Котруца Лилия Николаевна | 20 Мар 2015 |
| разное | Разработка урока обществознания в 10 классе по теме «Деятельность — способ существования человека». | Болиевская Оксана Анатольевна | 20 Мар 2015 |
| документ | Разработка урока в 10 классе на тему «Стили речи» по сингапурской методике. | Шамгунова Гулия Сагидулловна | 20 Мар 2015 |
| презентация, документ | Методическая разработка урока в 10 классе по теме «Степенная функция, ее свойства и график» | Иванова Наталья Константиновна | 21 Мар 2015 |
| документ | Разработка урока физики в 10 классе по теме:»Электроемкость. Конденсаторы» | Шуваева Ольга Алексеевна | 21 Мар 2015 |
| документ | Разработка урока физической культуры в 10 классе по теме «Волейбол. Нападающий удар» | Картавцев Андрей Петрович | 21 Мар 2015 |
| разное | Методическая разработка урока по истории в 10 классе на тему: «Суд над князем Александром Невским» | Котруца Лилия Николаевна | 21 Мар 2015 |
| разное | Методическая разработка урока в 10 классе по теме «Площадь криволинейной трапеции» | Заико Илья Валерьевич | 21 Мар 2015 |
| документ | Методическая разработка урока истории в 10 классе по теме «Русско — турецкая война 1877-1878г» | Солтанов Станислав Черменович | 21 Мар 2015 |
| документ | методическая разработка урока в 10 классе по теме «Электризация тел» | Шевякова Наталия Валерьевна | 21 Мар 2015 |
| презентация | Методическая разработка урока «Лауреаты Нобелевской премии по экономике» в 10 классе социально-экономического профиля | Отрокова Ольга Ивановна | 21 Мар 2015 |
| документ | Разработка урока по химии в 10 классе «Каучук» | Донгак-оол Чодураа Кан-ооловна | 20 Мар 2015 |
| документ | Методическая разработка урока геометрии в 10 классе школы глухих по теме «Решение треугольников». Знаю свойства …. | Богданова Вера Ивановна | 21 Мар 2015 |
Занятие 9. Математическая индукция
Известный литературный герой Шерлок Холмс, раскрывая преступления, в качестве метода своей работы использовал дедукцию. Дедуктивные рассуждения – это то, что в математике называют логическими рассуждениями, или переход от общего к частному. И в математической науке дедукция является самым распространенным методом исследования. Правила логических рассуждений были сформулированы два с половиной тысячелетия назад древнегреческим учёным Аристотелем (силлогизмы).
Но есть и еще один способ рассуждений – от частного к общему. Такой метод носит название индукция. Индукция (induction– по-латыни наведение). То есть один или несколько частных случаев «наводят» на общее утверждение, общий вывод делается на основании частных наблюдений. Однако, индуктивный метод имеет весьма существенный недостаток: на основании частных примеров может быть сделан неверный вывод.
Гипотезы, возникающие при частных наблюдениях, не всегда являются правильными. Рассмотрим пример, принадлежащий Эйлеру.
Будем вычислять значение трехчлена n2 +n+41 при некоторых первых значениях n:
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
43 |
47 |
53 |
61 |
71 |
83 |
97 |
113 |
Заметим, что получаемые в результате вычислений числа являются простыми. И непосредственно можно убедиться, что для каждого n от 1 до 39 значение многочлена является простым числом.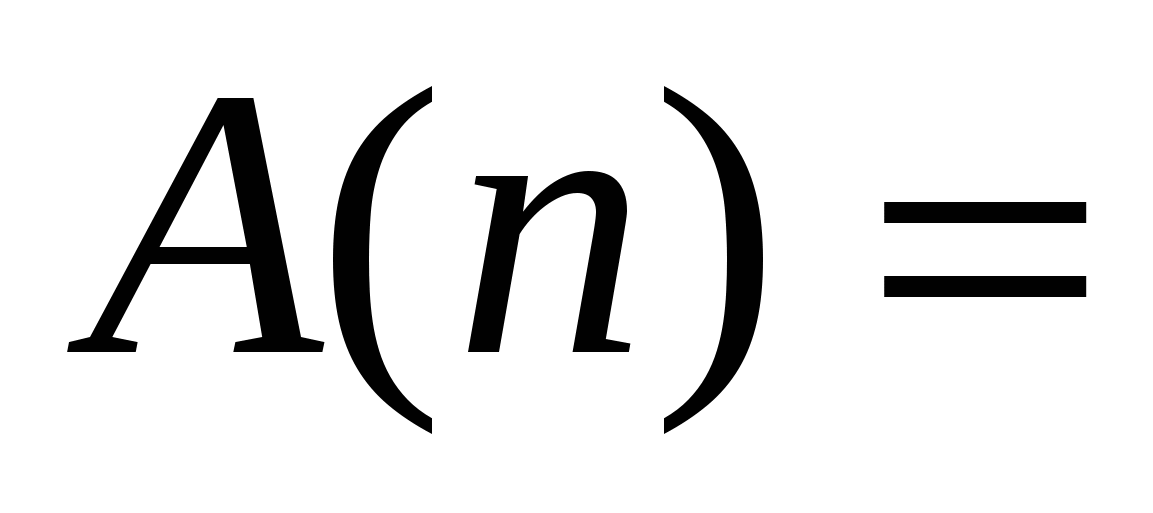
Однако при n=40 получаем число 1681=412, которое не является простым. Таким образом, гипотеза, которая здесь могла возникнуть, то есть гипотеза о том, что при каждом n число n2+n+41 является простым, оказывается неверной.
Таким образом, утверждение может быть справедливым в целом ряде частных случаев и в то же время несправедливым вообще. Поэтому в математике такой метод не используют, но применяют особый метод рассуждений, который называется методом математической индукции (полной индукции, совершенной индукции). Этот метод подразумевает полный перебор всех частных случаев. Однако прямой перебор не всегда возможен (учитывая, что множество чисел, для которых надо проверить то или иное утверждение, бесконечно). Поэтому для доказательства используют следующую схему:
1 шаг. Проверяем истинность утверждения P(п) для п = 1.
2 шаг. Предполагаем, что P(п) истинно для п = к (к — произвольное натуральное число).
3 шаг. Доказываем, что Р(п) истинно, для п = к + 1.
Заменим в левой части равенства первые к слагаемых их суммой из 2-го шага:
В числителе левой части раскроем скобки:
Способом группировки разложим числитель левой части на множители:
Равенство верно.
Задание 2.
(Задача из книги А. Шеня «Математическая индукция», Москва, издательство МЦНМО, 2007)
Игрушка «Ханойские башни» имеет три стержня. На одном находится пирамидка из нескольких колец (уменьшающихся снизу вверх). Эту пирамидку нужно переложить на другой стержень, соблюдая правила игры: нельзя переносить сразу несколько колец и нельзя класть большее кольцо поверх меньшего. Например, пирамидку из двух колец можно переложить так: положить меньшее кольцо на второй стержень, затем большее на третий, а затем меньшее поверх большего. Доказать, что возможно переместить на другой стержень пирамидку из любого числа колец, соблюдая правила игры.
Задание 3.
Задание 4.
Доказать, что для любого натурального n значение выражения 4n +15n-1 кратно 9.
Задание 5.
Доказать, что при любом натуральном n число
делится на 3.
Задание 6.
Доказать, что сумма первых n натуральных нечётных чисел равна квадрату их числа, то есть
Задание 7.
Доказать, что
Задание 8.
Доказать, что сумма квадратов n первых чисел натурального ряда равна
Задание 9.
Доказать, что
Задание 10.
Доказать, что
Задание 11.
Доказать, что
Задание 12.
Доказать, что
Добавить комментарий
Решения NCERT для класса 11 по естественной математике, глава 4
Решения NCERT для класса 11 по естественной математике, глава 4 «Принцип математической индукции» представлены здесь с простыми пошаговыми объяснениями.
Эти решения для Принципа математической индукции чрезвычайно популярны среди учащихся 11 класса, изучающих естественные науки. Все вопросы и ответы из Книги NCERT по математике для 11 класса, глава 4, предоставляются здесь для вас бесплатно. Вам также понравится возможность без рекламы в решениях NCERT от Meritnation. Все решения NCERT для класса 11 по естественной математике подготовлены экспертами и на 100% точны.
Страница № 94:
Вопрос 1:
Докажите следующее, используя принцип математической индукции для всех N ∈ N :
Ответ:
. N ), то есть,
P ( N ): 1 + 3 + 3 2 +… + 3 N –1 =
для N = 1, мы имеем
. P(1): 1 =, что верно.
Пусть P( k ) истинно для некоторого натурального числа k , т. е.
Теперь мы докажем, что P( k + 1) истинно.
Рассмотрим
1 + 3 + 3 2 +… + 3 K –1 + 3 ( K +1) — 1 9003
= (1 + 3 3 (1 + 3 3 (1 + 3 3 (1 + 3 3 (1 + 3 +1) — 1 2 +1) — 1 .
+ 3 2 +… + 3 к –1 ) + 3 к
Таким образом, P ( K + 1) верно, когда P ( K ).
Следовательно, по принципу математической индукции утверждение P( n ) верно для всех натуральных чисел, т. е. n .
Страница № 94:
Вопрос 2:
Докажите следующее, используя принцип математической индукции для всех n ∈ N :
Ответ:
Пусть данный оператор будет P( n ), т. е.
P( n ):
Для n = 1, имеем
P(1): 1 3 = 1 =, что является правдой.
Пусть P( k ) быть истинным для некоторого натурального числа k , т. е.
. теперь докажите, что P(k + 1) верно.
Учитывать
1 3 + 2 3 + 3 3 + … + к 3 + ( к + 1) 3
= (1 3 + 2 3 + 3 3 + ….
+ к 3 ) +
( k + 1) 3
Таким образом, P( k + 1) истинно, если истинно P( k ).
Следовательно, по принцип математической индукции, утверждение P( n ) верно для всех натуральных чисел, т. е. n .
Страница № 94:
Вопрос 3:
Докажите следующее, используя принцип математической индукции для всех n ∈ N :
Ответ:
Пусть данный оператор будет P( n ), т. е.
P( n ):
Для n = 1, имеем
P(1): 1 = что является правдой.
Пусть P( k ) быть истинным для некоторого натурального числа k , т. е.
. теперь докажите, что P( k +1) верно.
Рассмотрим
Таким образом, P( k + 1) истинно, если истинно P( k ).
Следовательно, по
принцип математической индукции, утверждение P( n )
верно для всех натуральных чисел, т.
е. n .
Страница № 94:
Вопрос 4:
Докажите следующее, используя принцип математической индукции для всех n ∈ N : 1.2.3 + 2.3.4 + … + n ( n + 1) ( n + 2) =
Ответ:
Пусть данное утверждение будет P( n ), т.е. + 2.3.4 + … + n ( n + 1) ( n + 2) =
Для n = 1 имеем
P(1): 1.2.3 = 6 =, что является правдой.
Пусть P( k ) истинно для некоторого натурального числа k , т.е.0021 + 1) ( k + 2)
Теперь мы докажем, что P( k + 1) истинно.
Рассмотрим
1.2.3 + 2.3.4 + … + k ( k + 1) ( k + 2) + ( k + 1) ( k + 02) ( k + 02) + 3)
= {1.2.3 + 2.3.4 + … + к ( к + 1) ( к + 2)} + ( к + 1) ( к + 2 ) ( к + 3)
Таким образом, P( k + 1) истинно, если истинно P( k ).
Следовательно, по принципу математической индукции утверждение P( n ) верно для всех натуральных чисел, т. е. n .
Страница № 94:
Вопрос 5:
Докажите следующее, используя принцип математической индукции для всех n ∈ N :
Ответ:
Пусть данный оператор будет P( n ), т. е.
P( n ) :
Для n = 1, имеем
P(1): 1,3 = 3, что является правдой.
Пусть P( k ) быть истинным для некоторого натурального числа k , т. е.
. теперь докажите, что P(k + 1) верно.
Рассмотрим
1,3 + 2,3 2 + 3,3 3 + … + к 3 к + ( к + 1) 3 к +1
= (1,3 + 2,3 2 + 3,3 3 + …+ к. 3 к ) + ( k + 1) 3 k +1
Таким образом, P( k + 1) истинно, если истинно P( k ).
Следовательно, по принцип математической индукции, утверждение P( n ) верно для всех натуральных чисел, т. е. n .
Страница № 94:
Вопрос 6:
Докажите следующее, используя принцип математической индукции для всех n ∈ N :
Ответ:
Пусть данный оператор будет P( n ), т. е.
P( n ):
Для n = 1, имеем
P(1): , что является правдой.
Пусть P( k ) быть истинным для некоторого натурального числа k , т. е.
. теперь докажите, что P(k + 1) верно.
Учитывать
1,2 + 2,3 + 3,4 + … + к .( к + 1) + ( к + 1).( к + 2)
= [1,2 + 2,3 + 3,4 + … + к .( к + 1)] + ( к + 1).( к + 2)
Таким образом, P( k + 1) истинно, если истинно P( k ).
Следовательно, по
принцип математической индукции, утверждение P( n )
верно для всех натуральных чисел, т.
е. n .
Страница № 94:
Вопрос 7:
Докажите следующее, используя принцип математической индукции для всех n ∈ N :
Ответ:
Пусть данный оператор будет P( n ), т. е.
P( n ):
Для n = 1, имеем
, что является правдой.
Пусть P( k ) быть истинным для некоторого натурального числа k , т. е.
. теперь докажите, что P( к + 1) верно.
Рассмотрим
(1,3 + 3,5 + 5,7 + … + (2 к – 1) (2 к + 1) + {2( к + 1) – 1}{2( k + 1) + 1}
Таким образом, P( k + 1) истинно, если истинно P( k ).
Следовательно, по принцип математической индукции, утверждение P( n ) верно для всех натуральных чисел, т. е. n .
Страница № 94:
Вопрос 8:
докажите следующее, используя принцип математической индукции для всех N ∈ N : 1,2 + 2,2 2 + 3,2 2 +… + N .
2 N = ( N .2 N = ( N . – 1) 2 n +1 + 2
Ответ:
Пусть данный оператор будет P( n ), т. е.
P( n ): 1,2 + 2,2 2 + 3,2 2 + … + n .2 n = ( n – 1) 2 n +1 + 2
Для n = 1, имеем
P(1): 1,2 = 2 = (1 – 1) 2 1+1 + 2 = 0 + 2 = 2, что верно.
Пусть P( k ) быть истинным для некоторого положительного целого числа k , т. е.
1,2 + 2,2 2 + 3,2 2 + … + к. 2 к = ( к – 1) 2 к + 1 + 2 … (i)
Мы будем теперь докажите, что P(k + 1) верно.
Рассмотрим
Таким образом, P( k + 1) истинно, если истинно P( k ).
Следовательно, по
принцип математической индукции, утверждение P( n )
верно для всех натуральных чисел, т.
е. n .
Страница № 94:
Вопрос 9:
Докажите следующее, используя принцип математической индукции для всех n ∈ N :
Ответ:
Пусть данный оператор будет P( n ), т. е.
P( n ):
Для n = 1, имеем
P(1): , что является правдой.
Пусть P( k ) быть истинным для некоторого натурального числа k , т. е.
. теперь докажите, что P(k + 1) верно.
Рассмотрим
Таким образом, P( k + 1) истинно, если истинно P( k ).
Следовательно, по принцип математической индукции, утверждение P( n ) верно для всех натуральных чисел, т. е. n .
Страница № 94:
Вопрос 10:
Докажите следующее, используя принцип математической индукции для всех n ∈ N :
Ответ:
Пусть данный оператор будет P( n ), т. е.
P( n ):
Для n = 1, имеем
,
что является правдой.
Пусть P( k ) быть истинным для некоторого натурального числа k , т. е.
. теперь докажите, что P(k + 1) верно.
Рассмотрим
Таким образом, P( k + 1) истинно, если истинно P( k ).
Следовательно, по принцип математической индукции, утверждение P( n ) верно для всех натуральных чисел, т. е. n .
Страница № 94:
Вопрос 11:
Докажите следующее, используя принцип математической индукции для всех n ∈ N :
Ответ:
Пусть данный оператор будет P( n ), т. е.
P( n ):
Для n = 1, имеем
, что является правдой.
Пусть P( k ) быть истинным для некоторого натурального числа k , т. е.
. теперь докажите, что P(k + 1) верно.
Рассмотрим
Таким образом, P( k + 1) истинно, если истинно P( k ).
Следовательно, по принцип математической индукции, утверждение P( n ) верно для всех натуральных чисел, т. е. n .
Страница № 95:
Вопрос 12:
Докажите следующее, используя принцип математической индукции для всех n ∈ N :
Ответ:
Пусть данное утверждение будет P( n ), т. е.
Для n = 1 имеем
, что верно.
Пусть P( k ) истинно для некоторого натурального числа k , т. е.
Теперь мы докажем, что P( k + 1) истинно.
Рассмотрим
Таким образом, P(k + 1) истинно, если P(k ) истинно.
Следовательно, по принципу математической индукции утверждение P( n ) верно для всех натуральных чисел, т. е. п .
Страница № 95:
Вопрос 13:
Докажите следующее, используя принцип математической индукции для всех n ∈ N :
Ответ:
Пусть
данный оператор будет P( n ), т.
е.
For n = 1, имеем
Пусть P( k ) быть истинным для некоторого натурального числа k , т. е.
. теперь докажите, что P( к + 1) верно.
Рассмотрим
Таким образом, P( k + 1) истинно, если истинно P( k ).
Следовательно, по принцип математической индукции, утверждение P( n ) верно для всех натуральных чисел, т. е. n .
Страница № 95:
Вопрос 14:
Докажите следующее, используя принцип математической индукции для всех n ∈ N :
Ответ:
Пусть данный оператор будет P( n ), т. е.
For n = 1, имеем
, что является правдой.
Пусть P( k ) быть истинным для некоторого натурального числа k , т. е.
. теперь докажите, что P(k + 1) верно.
Рассмотрим
Таким образом, P( k + 1) истинно, если истинно P( k ).
Следовательно, по принцип математической индукции, утверждение P( и ) верно для всех натуральных чисел, т. е. n .
Страница № 95:
Вопрос 15:
Докажите следующее, используя принцип математической индукции для всех n ∈ N :
Ответ:
Пусть данный оператор будет P( n ), т. е.
Пусть P( k ) быть истинным для некоторого натурального числа k , т. е.
. теперь докажите, что P( k +1) верно.
Учитывать
Таким образом, P( k + 1) истинно, если истинно P( k ).
Следовательно, по принцип математической индукции, утверждение P( n ) верно для всех натуральных чисел, т. е. n .
Страница № 95:
Вопрос 16:
Докажите следующее, используя принцип математической индукции для всех n ∈ N :
Ответ:
Пусть
данный оператор будет P( n ), т.
е.
Пусть P( k ) быть истинным для некоторого натурального числа k , т. е.
. теперь докажите, что P(k + 1) верно.
Рассмотрим
Таким образом, P( k + 1) истинно, если истинно P( k ).
Следовательно, по принцип математической индукции, утверждение P( n ) верно для всех натуральных чисел, т. е. п .
Страница № 95:
Вопрос 17:
Докажите следующее, используя принцип математической индукции для всех n ∈ N :
Ответ:
Пусть данный оператор будет P( n ), т. е.
For n = 1, имеем
, что является правдой.
Пусть P( k ) быть истинным для некоторого натурального числа k , т. е.
. теперь докажите, что P( к + 1) верно.
Рассмотрим
Таким образом, P( k + 1) истинно, если истинно P( k ).
Следовательно, по принцип математической индукции, утверждение P( n ) верно для всех натуральных чисел, т. е. n .
Страница № 95:
Вопрос 18:
Докажите следующее, используя принцип математической индукции для всех n ∈ N :
Ответ:
Пусть данный оператор будет P( n ), т.е.
Это может быть отметил, что P( n ) верно для n = 1, поскольку .
Пусть P( k ) быть истинным для некоторого натурального числа k , т. е.
. теперь докажите, что P( k + 1) истинно, если истинно P( k ).
Рассмотрим
Следовательно,
Таким образом, P( k + 1) верно, если P( k ) верно.
Следовательно, по принцип математической индукции, утверждение P( n ) верно для всех натуральных чисел, т. е. n .
Страница № 95:
Вопрос 19:
Докажите с помощью принципа математической индукции для всех n ∈ N : n ( n + + 02) ( n + 02) кратно 3.
Ответ:
Пусть данный оператор будет P( n ), т. е.
Р( n ): n ( n + 1) ( n + 5), что кратно 3.
Может быть отметил, что P( n ) верно для n = 1, поскольку 1 (1 + 1) (1 + 5) = 12, что кратно 3.
Пусть P( k ) быть истинным для некоторого положительного целого числа k , т. е.
k ( k + 1) ( k + 5) кратно 3.
∴ k ( к + 1) ( к + 5) = 3 м , где м ∈ N … (1)
Мы теперь докажите, что P( k + 1) истинно, если истинно P( k ).
Рассмотрим
Таким образом, P( k + 1) истинно, если истинно P( k ).
Следовательно, по принцип математической индукции, утверждение P( n ) верно для всех натуральных чисел, т. е. n .
Страница № 95:
Вопрос 20:
докажите следующее, используя принцип математической индукции для всех N ∈ N : 10 2 N — 1 + 1 делится на 11.
Ответ:
данный оператор будет P( n ), т. е.
P( n ): 10 2 п – 1 + 1 шт. делится на 11.
Может быть заметил, что P( n ) верно для n = 1, поскольку P(1) = 10 2.1 – 1 + 1 = 11, которое делится на 11.
Пусть P( k ) быть истинным для некоторого положительного целого числа k , т. е.
10 2 k – 1 + 1 делится на 11.
∴10 2 k – 1 + 1 = 11 м , где м ∈ N … (1)
Мы теперь докажите, что P( k + 1) истинно, если истинно P( k ).
Рассмотрим
Таким образом, P( k + 1) истинно, если истинно P( k ).
Следовательно, по принцип математической индукции, утверждение P( n ) верно для всех натуральных чисел, т. е. n .
Страница № 95:
Вопрос 21:
Докажите следующее, используя принцип математической индукции для всех n ∈ N : x 2 0 y 2 n делится на x + y . Пусть
данный оператор будет P( n ), т. е. P( n ): x 2 n – y 2 n делится на х + у . Может быть
заметил, что P( n ) истинно для n = 1. Это так
потому что x 2 × 1 – г 2 × 1 = х 2 – у 2 = ( х + y ) ( х – y ) делится на ( х + y ). Пусть P( k )
быть истинным для некоторого положительного целого числа k , т.е. x 2 k – г 2 к делится на х + и . ∴ x 2 к – г 2 к = м ( х + y ), где м ∈ N … (1) Мы
теперь докажите, что P( k + 1) истинно, если истинно P( k ). Рассмотрим Таким образом, P( k + 1) истинно, если истинно P( k ). Следовательно, по
принцип математической индукции, утверждение P( n )
верно для всех натуральных чисел, т. е. n . Докажите следующее, используя принцип математической индукции для всех N ∈ N : 3 2 N + 2 — 8 N 
Ответ:
Страница № 95:
Вопрос 22:
Ответ:
Пусть данный оператор будет P( n ), т. е.
P( n ): 3 2 n + 2 – 8 n – 9 делится на 8.
Может быть заметил, что P( n ) верно для n = 1, поскольку 3 2 × 1 + 2 – 8 × 1 – 9 = 64, что делится на 8.
Пусть P( k )
быть истинным для некоторого положительного целого числа k , т.
е.
3 2 к + 2 – 8 k – 9 делится на 8.
∴3 2 k + 2 – 8 к – 9 = 8 м ; где м ∈ N … (1)
Мы теперь докажите, что P( k + 1) истинно, если истинно P( k ).
Рассмотрим
Таким образом, P( k + 1) истинно, если истинно P( k ).
Следовательно, по принцип математической индукции, утверждение P( n ) верно для всех натуральных чисел, т. е. n .
Страница № 95:
Вопрос 23:
Докажите следующее, используя принцип математической индукции для всех N ∈ N : 41 N — 14 N — множества из — 14 N . 27.
Ответ:
Пусть данное высказывание равно P( n ), т. е.
P( n ):41 n – 14 n есть
кратно 27.
Можно заметить, что P( n ) верно для n = 1, поскольку , , кратное 27.
Пусть P( k ) истинно для некоторого положительного целого числа k , т. е.
41 k – 17 из 27
∴41 к – 14 к = 27 м , где m ∈ N … (1)
Теперь мы докажем, что P( k + 1) верно всякий раз, когда P( k ) правда.
Рассмотрим
Таким образом, P(k + 1) истинно, если P(k ) истинно.
Следовательно, по принципу математической индукции оператор P( n ) верно для всех натуральных чисел, т. е. n .
Страница № 95:
Вопрос 24:
Докажите по принципу математической индукции для всех
(2 n +7) < ( n + 3) 2
Ответ:
), т. е.
P( n ): (2 n +7) < ( n + 3) 2
Можно заметить, что P(
1 n) 900 n = 1, так как 2,1 + 7 = 9 < (1 + 3) 2 = 16, что верно.
Пусть P( k ) истинно для некоторого натурального числа k , т.е. теперь докажите, что P( k + 1) истинно, если истинно P( k ).
Рассмотрим
Таким образом, P(k + 1) истинно, если P(k ) истинно.
Следовательно, по принципу математической индукции утверждение P( n ) верно для всех натуральных чисел, т. е. п .
Принцип математической индукции — Infinity Learn
Это концепция, которая помогает доказывать математические результаты и теоремы для всех натуральных чисел. Математическое мышление необходимо, и оно помогает в понимании проблем, с помощью которых мы можем лучше находить решения. Принцип математической индукции — это другой и специфический метод, который используется в задачах алгебры, которые могут быть выражены через n, где n — натуральное число. Принцип математики, связанный с дедуктивным умозаключением. Дедуктивное рассуждение основано на размышлениях и фактах.
То математическое утверждение, которое основано на гипотезе о том, что оно истинно при n = 1, и предполагается, что оно истинно при n = k, затем доказывается при n = k+1.
Давайте разберемся с концепцией принципа математической индукции, теперь мы обсудим его формулировку, ее применение к различным теоремам и формулировкам для натуральных чисел, а также обсудим шаг индукции.
Зарегистрируйтесь и получите бесплатные пробные тесты и учебные материалы
Класс
—Класс 6Класс 7Класс 8Класс 9Класс 10Класс 11Класс 12
Вы ученик Шри Чайтаньи?
НетДа
+91
Проверить OTP-код (обязательно)
Я согласен с условиями и политикой конфиденциальности.
Математическая индукция: По сути, P(n) является знаком принципа математической индукции. Это метод, используемый для доказательства того, что математическое утверждение верно для полностью натуральных чисел n = 1,2,3,……………….n. Для доказательства результата P(n) в этом случае воспользуемся принципом математической индукции, впервые доказанным для n = 1, если P(1) верно, то мы предположили, что P(k) истинно для некоторого натурального числа.
Теперь, используя эту гипотезу, мы докажем, что P(k+1) верно. Если P(k+1) верно. то утверждение будет верным для всех натуральных чисел.
Принцип математической индукции Заявление:- Теперь давайте определим Принцип математической индукции и как его использовать в утверждении в соответствии с шагом.
предположим, что у нас есть данное утверждение P(n), в котором есть натуральное число, такое как
- сначала мы проверяем истинность утверждения для n = 1, если оно истинно для n = 1
- , то мы предположили, что это верно для n = k, где k — некоторое натуральное число,
- , то мы докажем для n = k+1, если оно истинно для P(k+1), следует, что оно верно и для P(k). г.
Тогда P(n) верно для всех натуральных чисел n.
Теперь опишем с помощью диаграммы
Теперь, прежде чем перейти к примеру с принципом математической индукции.
давайте обсудим некоторые важные моменты.
- Первый шаг – констатация факта.
Некоторые математические утверждения верны для n ≥ 5. В этом случае для доказательства результата с использованием принципа математической индукции шаг 1 будет начинаться с n = 5. г. - Шаг 2 является условным свойством. Он не утверждает, что утверждение P(n) верно для n = k. Он говорит, что если утверждение верно для n = k, то оно верно и для n = k+1. Другими словами, мы можем сказать, что мы предполагаем, что P(k) истинно для некоторого натурального числа k, а затем доказываем, что P(k+1) истинно.
Некоторые математические утверждения верны для n ≥ 5. В этом случае для доказательства результата с использованием принципа математической индукции шаг 1 будет начинаться с n = 5.шаг используется для доказательства теоремы или утверждения.
Имеет 3 основных этапа доказательства теоремы
- Базовый шаг: — для этого доказательства для P(n = 1)
- Шаг предположения:- затем предположил, что верно для P(n=k), k — некоторое натуральное число.
- Шаг индукции:- Затем докажите, что для P(k+1)
После решения этих шагов мы можем сказать, что «Принцип математической индукции выполняется» для полностью натурального числа n.
мы поняли применение принципа математической индукции через
Пример:- Докажите, что формула суммы n натуральных чисел, верная для всех натуральных чисел, то есть 1 + 2 + 3 + 4 + + …….+ n = n(n+1) /2 с использованием принципа математической индукции.
Решение: Пусть P(n): 1 + 2 + 3 + 4 + 5 + …. + n = n(n+1)/2
Теперь воспользуемся понятием математической индукции и докажем это с помощью трех шагов индукции.
Базовый шаг: Чтобы доказать истинность P(1).
Для n = 1, LHS = 1
RHS = 1(1+1)/2 = 2/2 = 1
Следовательно, LHS = RHS ⇒ P(1) верно.
Шаг предположения: Предположим, что P(n) истинно для n = k, т. е. P(k) истинно
⇒ 1 + 2 + 3 + 4 + 5 +….+ k = k(k +1)/2 — (1)
Шаг индукции: Теперь мы докажем, что P(k+1) истинно.
Чтобы доказать: 1 + 2 + 3 + 4 + … + (k+1) = (k+1)(k+2)/2
Рассмотрим LHS = 1 + 2 + 3 + 4 + … + (k+1)
= 1 + 2 + 3 + 4 + … k + (k+1)
= (1 + 2 + 3 + 4 + … + k) + k+1
= k(k+1)/2 + k+1 [При использовании ур.
(1)]
= [k(k+1) + 2(k+1)]/2
= (k+1)(k+2)/2 [после взятия общего]
= RHS
Итак, LHS = RHS
⇒ P(n) истинно для n = k+1
Следовательно, по принципу математической индукции P(n) истинно для всех натуральных чисел n.
Важные замечания о принципе математической индукции- В каждом математическом выражении мы предполагается как P(n) для натурального числа n. г.
- Сначала докажем для n = 1, затем предположим, что n = k, а затем докажем для n = k+1.
- Результат «этапа допущения» используется после записи k -го -го терма на следующем шаге (перед (k+1) -го -го терма).
- Если получить правую часть из левой кажется трудным, то упростим левую и правую часть по отдельности и докажем, что они равны.
Математическая индукция на чем основана и к чему относится?
Математическая индукция основана на дедуктивных рассуждениях, и они связаны друг с другом, потому что они связаны, а дедуктивные рассуждения также основаны на логике.