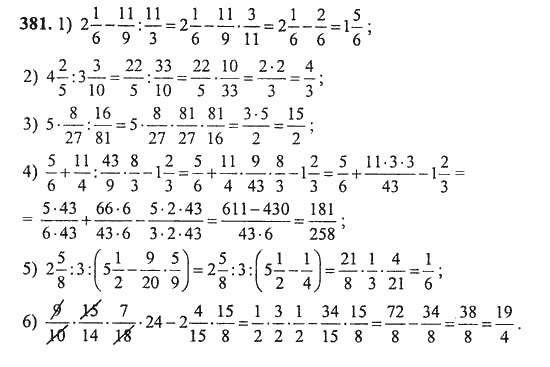Математика 5-6 классы. 23. Равенство дробей. Основное свойство дроби. Сокращение дробей
- Подробности
- Категория: Математика 5-6 классы
Равенство дробей
Для любой дроби можно указать сколько угодно ей равных дробей.
Например, или
Это можно объяснить так: если отрезок разделить пополам, а половину также пополам, то ясно, что половина отрезка равна двум его четвертям, т. е. Также можно показать, что половина равна трем шестым и т. д. (рис. 4.4).
Можно еще сказать, что дроби и определяют одно и то же число; записанное в разных формах. Дроби и так же определяют одно и то же число, записанное в разных формах, и т.
д.
Это свойство называют основным, свойством дроби. С его помощью можно получать дроби, равные данной дроби.
Например,
Равенство (1) можно записать и в обратном порядке:
В таком виде левая часть равенства есть дробь числитель и знаменатель которой имеют общий множитель n.
Если n > 1, то говорят, что можно дробь сократить на n и получить дробь . Говорят еще, что можно разделить числитель и знаменатель на общий множитель n.
Поэтому основное свойство дробей можно сформулировать по-другому:
Если числитель и знаменатель дроби имеют общий множитель, отличный от 1, то дробь можно сократить на этот множитель. При этом получится дробь, равная данной.
Пример. Сократить дроби
Решение.
Если р—натуральное число, то справедливо равенство
Действительно,
Дробь называется несократимой, если ее числитель и знаменатель не имеют общих простых делителей.
Например, дроби несократимые дроби, так как числа 1 и 2, 3 и 4, б и 7, 11 и 8 не имеют общих простых делителей.
Для каждой дроби существует единственная равная ей несократимая дробь.
Например,
Левые части равенств—данные дроби, а правые равные им несократимые дроби.
Чтобы получить несократимую дробь, равную данной дроби, надо сократить данную дробь на наибольший общий делитель ее числителя и знаменателя. Часто наибольший общий делитель числителя и знаменателя указать трудно. В этом случае сокращение дроби выполняют постепенно.
Пример. Сократить дробь
Решение.
Демоверсия ВПР 2023 по математике для 6 класса
Официальная демоверсия проверочной работы по математике для 6 класса.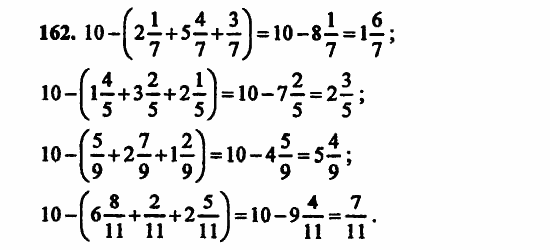
ВПР в 2023 году пройдут с 15 марта по 20 мая. Точные даты устанавливает образовательная организация самостоятельно.
Всего в работе 13 заданий. Время выполнения — 60 минут.
В задании 12 нужно сделать чертёж или рисунок.
В заданиях, после которых есть поле со словами «Решение» и «Ответ», запишите решение и ответ в указанном месте.
Если Вы хотите изменить ответ, зачеркните его и запишите рядом новый.
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором.
При необходимости можно пользоваться черновиком. Записи в черновике проверяться и оцениваться не будут.
→ Демоверсия: vpr_ma-6_demo_2023.pdf
→ Описание работы: vpr_ma-6_opisanie_2023.pdf
Цитата: Система оценивания
Правильное решение каждого из заданий 1–8, 10, 12 оценивается 1 баллом. Задание считается выполненным верно, если ученик дал верный ответ: записал правильное число, правильную величину, изобразил правильный рисунок.
Выполнение каждого из заданий 9, 11, 13 оценивается от 0 до 2 баллов. Максимальный первичный балл – 16.
Рекомендации по переводу первичных баллов в отметки по пятибалльной шкале
«2»: 0–5
«3»: 6–9
«4»: 10–13
«5»: 14–16
Описание ВПР по математике
В заданиях 1–2 проверяется владение понятиями отрицательные числа, обыкновенная дробь.
В задании 3 проверяется умение находить часть числа и число по его части.
В задании 4 проверяется владение понятием десятичная дробь.
Заданием 5
В задании 6 проверяется умение извлекать информацию, представленную в таблицах, на диаграммах.
В задании 7 проверяется умение оперировать понятием модуль числа.
В задании 8 проверяется умение сравнивать обыкновенные дроби, десятичные дроби и смешанные числа.
В задании 9 проверяется умение находить значение арифметического выражения с обыкновенными дробями и смешанными числами.
Задание 10 направлено на проверку умения решать несложные логические задачи, а также на проверку умения находить пересечение, объединение, подмножество в простейших ситуациях.
В задании 11 проверяются умения решать текстовые задачи на проценты, задачи практического содержания.
Задание 12 направлено на проверку умения применять геометрические представления при решении практических задач, а также на проверку навыков геометрических построений.
Задание 13 является заданием повышенного уровня сложности и направлено на проверку логического мышления, умения проводить математические рассуждения.
Успешное выполнение обучающимися заданий 12 и 13 в совокупности с высокими результатами по остальным заданиям говорит о целесообразности построения для них индивидуальных образовательных траекторий в целях развития их математических способностей.
г. Польский | Математические ресурсы
Площадь поверхности: прямоугольники | Цилиндры Объем: Прямоугольники | Цилиндры
3D-объекты: призмы | Пирамиды | Многогранники | Платоновые тела | Грани, вершины и ребра
МАТЕМАТИКА
Математика
Социальные науки
Естествознание
Языкознание
STEM
Альберта Программа обучения
Что ты умеешь делать с математикой слово значит? Используйте этот математический словарь, организованный в алфавитном порядке, чтобы помочь вам понять это.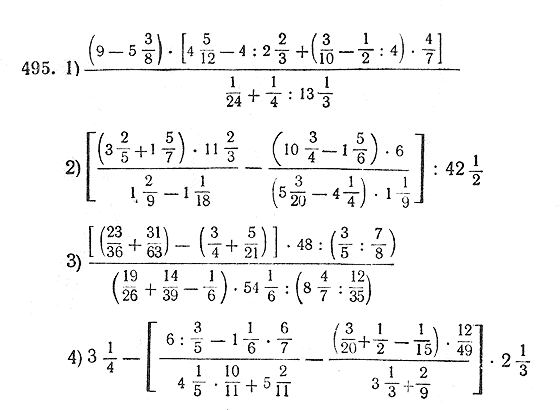
Кризис предотвращен!
Острый угол
для координации
Координатная сетка
до фактора
Дерево факторов до
Отрицательное целое число
Линия номера
к продукту
Правильная фракция
по стандартной форме
Stem и Leaf
до стандартной формы
. к оси Y
Наличие чисел в нашем мире очень важно. Числа постоянно используются в реальных жизненных ситуациях. Многие примеры из реальной жизни могут включать в себя работу с акциями, расчет налогов или подсчет денег, когда вы копите на сноуборд, который вы всегда хотели. В шестом классе мы стремимся научить наших учеников множеству способов использования чисел. Мы работали над стратегиями решения операционных задач на сложение, вычитание, умножение и деление. Студентам предлагается попробовать различные стратегии, которые облегчат им решение их основных фактов.
Понимание чисел
Урок 1 — Изучение больших чисел
Урок 2 — Числа всех нас Операции.0003
Урок 3. Умножение десятичных дробей на целое #
Урок 4. Умножение десятичной дроби <1 на целое #
Урок 5. Деление десятичной дроби на целое #
Урок 7. Деление десятичной дроби <1 на целое #
MathIsFun.com — Десятичные дроби
Дроби и десятичные дроби повсюду в нашей жизни. Вы используете их все время и часто даже не осознаете этого. Кулинария, деньги, спорт, время, игры и медицина — вот лишь несколько примеров использования дробей или десятичных знаков. В рамках этого модуля мы будем работать с этими идеями, чтобы улучшить наши навыки восприятия чисел. Когда вы в последний раз использовали дроби?
MathsIsFun.com [Пояснения, видео и ресурсы для всех понятий]
Пояснения: Дроби | Десятичные числа Дополнительная практика: Дроби | Десятичные дроби
Знакомство с дробями | Дроби больше 1 | Числители и знаменатели | Дроби в числовой строке
Эквивалентные дроби Введение | Визуализация эквивалентных дробей | Сравнение дробей | Упорядочивание дробей
Сравнение дробей с одинаковыми знаменателями | Сравнение дробей с разными знаменателями
Учащиеся будут отвечать на эти вопросы по мере прохождения раздела: [Вопросы о долях и процентах]
Каковы шансы, что Flames выйдут в плей-офф? Насколько вероятно, что «Блю Джейс» обыграют «Янкиз»? Ред Сокс? Если бы учеников в классе спросили, какой у них любимый вид спорта, сколько из них ответили бы на хоккей? Все эти вопросы можно было бы использовать в нашем исследовании статистики и вероятности.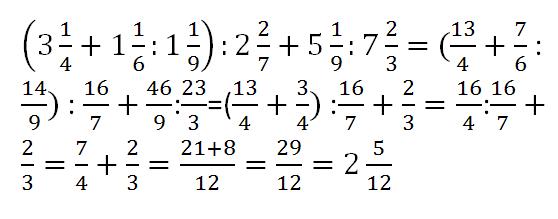
Виртуальные манипуляторы
Линия вероятности
Что такое данные?
Вероятностные игры
Ссылки на статистику и вероятности
Учащиеся будут отвечать на эти вопросы по мере прохождения раздела: [Вопросы по статистике и вероятностям]
Вероятность | Графики | Опросы
Online Room Planner | Введение в геометрию и объяснение | MathsIsFun — Измерение | MathsIsFun — Преобразования
Определения углов | Виртуальные геоборды | Угловые рабочие листы и практика | Интерактивные полигоны
Углы и многоугольники Контрольные вопросы
Урок 1 | Урок 2 | Урок 3 Урок 4 | Урок 6 | Урок 7
Контрольные вопросы по геометрии и измерениям
Урок 1 | Урок 2 | Урок 3 | Урок 4 | Урок 5 | Урок 7 | Урок 8 | Урок 9
Наш мир наполнен большими и маленькими формами, углами, линиями и различными геометрическими формами. Это самая старая математика, самая простая математика: «Какие фигуры подходят друг к другу, чтобы я мог что-то построить?» В этом разделе учащиеся будут изучать мир углов, многоугольников, объема и площади, а также то, как мы можем их измерить.
Наконец, учащиеся изучат 2D- и 3D-формы с их различными характеристиками и узнают, как преобразовывать (перемещать) их по координатным сеткам.
Геометрия | Полигоны | Измерение
Что такое преобразования? | Перевод | Отражение | Вращение | Анимированные трансформации
Математическая площадка: онлайн-трансформации | Практика перевода | Ледяные горки Сальто и повороты | Shapes in Motion
BBC BiteSize Transformations | TranStar: игра-трансформация | Преобразования портала
Измерительные ресурсы
Метрическая система (мм, см, км, м) | Площадь | Периметр | Объем | Масса (Вес) | Часы | Преобразование метрических/имперских единиц
Площадь и периметр геоборда (интерактивный) | Практические листы площади и периметра
Площадь | Периметр | Volume
Нажмите на одну из карточек обзора концепции, чтобы загрузить
Numbers
Place Value | Заказать целые числа | Целые числа | Числовые линии | Оценка целых чисел | Расширенная нотация
Операции
Оценка сумм и разностей целых чисел | Связать сложение и вычитание | Дополнение с перегруппировкой
Свойства дополнения | + & — без перегруппировки | Вычитание с перегруппировкой
Умножение | Одноразрядное деление | Двузначный разряд | Правила делимости | Простые и составные числа
Связать умножение и деление | Прайм-факторизация | Распределительная собственность | Кратные
Дроби
Дроби | Сравните дроби и смешанные числа | Простейшая форма | Сложение и вычитание с разными знаменателями
Сложение и вычитание смешанных чисел | Наименее распространенный кратный | Эквивалентные дроби | Порядок дробей и десятичных знаков
Сложение и вычитание с общими знаменателями | Нахождение части множества | Эквиваленты десятичных и дробных чисел
Наибольший общий делитель
Десятичные числа и проценты
Сравнить денежные суммы | Поместите значение десятичных знаков | Сложение и вычитание десятичных дробей
Умножение десятичных дробей | Проценты | Внесение изменений | Округление десятичных дробей | Поместите десятичную дробь в числовое деление десятичной строки | Эквиваленты десятичных дробей, дробей и процентов
Вероятность
Вероятность как дробь | Комбинации | Определяйте результаты и делайте прогнозы | Найти вероятность | Древовидные диаграммы
Статистика
Медиана | Диапазон | Среднее/среднее | Режим | Гистограммы | Линейные графики | Круговая диаграмма | Двухлинейные графики | Пиктограмма
Сюжеты стеблей и листьев | Гистограммы | Выбор правильного графика
Измерение
Определение времени | Истекшее время | Преобразование единиц времени | Использование календаря | Единицы измерения | Сообщите температуру
Инструменты измерения | Добавление и вычитание измерений | Общепринятые единицы длины | Измерить длину | Периметр
Площадь параллелограмма | Площадь неправильных фигур | Площадь треугольника | Площадь поверхности | Объем
Геометрия
Типы линий | Построение углов | Измерение углов | Классифицировать углы | Классифицировать треугольники | Классифицировать четырехугольники
Твердые фигуры | Похожие фигуры | Линии симметрии | Преобразования | Конгруэнтные фигуры | Ребра, грани, вершины
Объяснение | KhanAcademy: Fraction Intro
Fraction Modeler [Интерактивный]
Explanation
KhanAcademy: Запись смешанных чисел
Explanation
KhanAcademy: Запись неправильных дробей
Explanation | KhanAcademy: Эквивалентные дроби
Объяснение | KhanAcademy: Сравнение Заказ
Объяснение | KhanAcademy: Ratio Intro
KhanAcademy: Ratio Rates Percents
Объяснение | Связанные проценты
KhanAcademy: Значение процента
Дроби 6 класса — основы, задачи и примеры решения
Дроби
Все мы слышали это слово как в области математики, так и в повседневной жизни.
Например, когда мы делим шоколад на две части, это дробь. Когда мы съедаем половину яблока, это дробь. В математике дробь играет очень важную роль, и давайте выясним, как?
Понимание дробей
Дробь состоит из двух частей:
- Числитель : Часть, написанная над горизонтальной чертой, называется числителем.
- Знаменатель : Часть, написанная под горизонтальной чертой спящей линии, называется знаменателем.
Таким образом, число пишется над горизонтальной чертой, а под ней, и тогда такое расположение называется дробью.
Типы фракций
Существует три типа фракций
- Правильная фракция : — Фракция, чье число, меньше, чем денатор.
Пример 2 : 1/4, 5/8, 3/5, 4/7 и т. д.
- Неправильная дробь : Дробь, числитель которой больше или равен знаменателю.
Пример 3 : 5/2, 7/4, 9/7, 13/11, 2/2 и т. д.
- Смешанная дробь : — Сочетание целого числа и дроби вместе называется смешанной дробью .
Пример 4 : Преобразование дроби 17/4 в смешанную дробь.
Пример 5 : Решите приведенный выше пример.
Решение : Чтобы решить это, мы выполним 3 шага
- Умножьте целое число. со знаменателем. (2 х 3 = 6).
- Прибавьте ответ, полученный на шаге 1, к числителю
(6+1=7).
- Поместите результат, полученный на шаге 2, в место числителя, знаменатель останется прежним.
Следовательно, дробь становится 7/3, что является неправильной дробью.
Существует еще одна категория дробей, называемая
Эквивалентные дроби : Те дроби, которые выглядят иначе, но при решении становятся одинаковыми.
- Чтобы найти эквивалентную дробь данной дроби, вы можете умножить числитель и знаменатель данной дроби на одно и то же число.
- Чтобы найти эквивалентную дробь, мы можем разделить и числитель, и знаменатель на одно и то же число.
- Говорят, что дробь находится в простейшей (или наименьшей) форме, если ее числитель и знаменатель не имеют общего делителя, кроме 1, и HCF помогает нам привести дробь к наименьшей форме. . Например, 2/3, 4/3, 5/3 и т. д. — все это дроби.
- совпадает или нет, если да, то дробь с меньшим значением знаменателя будет больше.
- б) Если числитель не один и тот же, попробуйте сделать числитель или знаменатель обеих дробей одинаковыми, а затем выполните предыдущие шаги.
- Обратите внимание, что знаменатели обеих дробей одинаковы.
- Добавьте или вычтите числители, как указано в вопросах.
- Когда знаменатели разные, мы возьмем НОК знаменателей, чтобы сделать знаменатели одинаковыми, и умножим один и тот же множитель на числитель, а затем сложим или вычтем числители, как задано в вопросе.
Дроби, у которых разные знаменатели, называются В отличие от дробей . Например, 2/5, 4/7, ½ и т. д. не похожи на дроби
Сравнение дробей
Сравнение означает определение некоторых характеристик, например, какая из них меньше, а какая больше, когда два или более числа наблюдаются вместе что означает сравнение вместе.
Здесь мы собираемся сравнить две дроби, у которых одинаковые знаменатели, то есть они равны , как и дроби .
Теперь обратите внимание на числитель, та дробь, у которой числитель больше, будет большей дробью.
Пример 7 : Сравните, кто больше 6/7 или 5/7.
Решение : Здесь обе дроби имеют один и тот же знаменатель, и, следовательно, наблюдая за числителями, мы получаем, что 6 больше 5, где 6/7 больше 5/7.
6/7 > 5/7
Когда нам нужно сравнить две дроби, у которых разные знаменатели, то есть они не похожи друг на друга, мы будем сравнивать их следующим образом:
Вычисление операций с дробями
Как известно, сложение, вычитание, умножение и деление являются вычислительными операциями.
Здесь мы изучим только первые две операции вычисления дробей.
Сложение и вычитание дробей
Две дроби с одинаковым знаменателем можно сложить или вычесть, используя два шага:
Пример 8 : Сложите и вычтите 4/5 и 3/5.
Решение : Как мы видим, знаменатели обеих дробей одинаковы, и, следовательно, мы можем складывать и вычитать их, используя числители.
Следовательно, 4/5 + 3/5 = 7/5 и 4/5 – 3/5 = 1/5.
Практические вопросы
Вопрос 1 : Напишите натуральные числа от 102 до 113.